Structural characteristics of a cooperatively rearranging region during the glass transition of a polymer system

Abstract

The correlations between local ordered structures and cooperative motion were investigated by dynamic Monte Carlo (MC) simulation. The fraction of trans-conformation increases with the decrease of temperature, indicating the occurrence of a conformational transition from gauche- to trans-conformations. Due to the relatively high degree of close-packing, the trans-conformations are inclined to form local order. Furthermore, all the segments in the polymer system can be divided into two types: the ordered and the disordered ones. Compared with the ordered segments, the disordered segments have more neighboring vacancy sites, and thus move faster and randomly. Correspondingly, the segments in the local order have fewer neighboring vacancy sites, and exhibit lower mobility, which could only move cooperatively along the parallel direction. Those findings suggest that the cooperatively rearranging regions proposed by Adam and Gibbs contain more local ordered structures.

---

I. Introduction

When amorphous polymeric materials enter the glassy state, their relaxation times will increase dramatically.¹ Amazingly, in despite of the substantial increase of relaxation times, no obvious structural changes were detected by experiments except for the increase of the packing density of chain segments.^2,3 Up to now, though numerous research works have been carried out, the underlying mechanism of glass transition is still a puzzle.

Various theories have been proposed to interpret the mechanism of the glass transition, such as the free volume theory,⁴ the Gibbs–DiMarzio thermodynamic theory,⁵ the Adam–Gibbs theory about cooperative rearrangement,⁶ the energy landscape theory,⁷ the mode-coupling theory,⁸ the coupling theory,⁹ and the liquid fragility,¹⁰ etc. Unfortunately, a comprehensive explanation of the microscopic mechanism of the glass transition is still lacking and thus extreme controversy continues.^11,12

The Adam–Gibbs theory states that the relaxation in a supercooled fluid involves the cooperative motion of molecules, and the structural arrest at glass transition is attributed to the divergence of the size of cooperatively rearranging regions (CRRs).⁶ However, a description of the microscopic details of CRR is not provided by this theory.^13,14 With the rapid development of experimental techniques nowadays, some indirect evidences have been found by using nuclear magnetic resonance^15,16 or fluorescent probe measurements,^17,18 which detect dynamical heterogeneity during glass transition.^15,19 Namely, in different local domains, relaxation occurs with different relaxation times.¹ Since CRR is difficult to be directly observed in experiments, the observation of the dynamical heterogeneity can open up a new way to probe the cooperative motion. Weeks et al. reported that some colloidal particles moved cooperatively and formed large extended clusters the size of which increased as glass transition was approached.¹³ This result received some supports from molecular simulations.^20–22 It was proposed that CCR was composed of the clusters or strings of mobile molecules.²⁰

However, though many outcomes have been achieved, there still exist some unresolved issues, which prevent researchers from obtaining a fully theoretical comprehension of the mechanism of glass transition.^13,14 For instance, the structural characteristics of CRR are still unknown.¹³ As a matter of fact, some structural changes indeed happen during glass transition. For colloidal system, Tanaka et al.^23,24 and Yodh et al.²⁵ detected the formation of some local ordered structures during cooling, and they argued that the development of the local ordered structures may be the origin of the slow dynamics.²³ For polymer system, there is no directly experimental evidence for the formation of the local ordered structures during glass transition. However, it should be noted that Kim et al. detected conformational transition during cooling by Fourier transform infrared spectroscopy,²⁶ which was further demonstrated by molecular simulations.^27–32 The increase of the fraction of trans-conformations may induce the formation of the short-range order in polymers. Binder et al. have observed the formation of clusters with some local orientational orders in polymers based on Monte Carlo (MC) simulation.^33,34 They further suggested that those blocked segments can be released only by means of larger-scale cooperative conformational rearrangements.³³ Nevertheless, no further investigations were carried out to confirm their conjecture. By means of lattice MC simulations, Chen and Ruckenstein systematically investigated the relations between molecular orientation and morphology of copolymer melts confined in cylindrical nanopores, and found that the chain configuration played a key role in the morphology of copolymer melts.^35,36

Previously, we have found that the difference of segmental mobility between the gauche- and trans-conformations is an important reason causing the dynamical heterogeneity. In the present paper, we mainly focus on the relationships between the cooperative motion and the local ordered structures. During cooling, the conformational transition from gauche- to trans-conformations occurs, resulting in the formation of the increasing local orders. Further analysis revealed that the corresponding segments in the small ordered domains are inclined to move along the parallel direction, while the relative large domains are composed of the smaller clusters that move collectively as a single unit.

II. Simulation details

We put 512 model chains, each containing 32 segments, into a 32³ cubic lattice box. In the lattice model, each segment occupies one lattice site. The bonds were oriented either along lattice axes or along diagonals, and then the coordination number of each segment could be as high as 26 (summed over 6 axes, 8 body diagonals, and 12 face diagonals). The occupation density of polymer system was 0.5. Polymer chains could move in the lattice space via a micro-relaxation model,³⁷ which allowed a segment jumping from an occupied site to a neighboring vacancy site, sometimes with partial sliding diffusion along the chain. This micro-relaxation model is similar to the theoretical consideration proposed by de Gennes by combining the jumping and sliding motions together to interpret the changes of T_g in polymer films.^38,39 Thus, we believe that this micro-relaxation model including single segment jumping and sliding motions would provide some resemblances to the molecular motions in real glasses.⁴⁰ In addition, double occupations and bond crossings were forbidden taking into account the volume exclusion of polymer chains. Recently, Hu et al. successfully used the same simulation model to investigate the structural relaxation in ultrathin polymer films.^40,41

The conventional Metropolis sampling algorithm was employed for each step of micro-relaxation with the potential energy penalty

E = cE_c + lE_LJ + ∑f_iE_f (1)

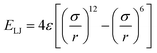where E_c is the potential energy change for non-collinear connection of consecutive bonds along the chain, reflecting the chain flexibility, is the Lennard-Jones potential calculated for non-bonded segments (ε is the characteristic energy well of the potential, σ is the lattice spacing considering the excluded volume, and r is the distance between two segments), E_f represents the frictional barrier for sliding diffusion of segments imposed by other neighboring segments, reflecting the frictional effect of local packing density on mobility of segments, c is the net number of non-collinear connection pairs of bonds along the chain, l is the net number of Lennard-Jones interaction pairs between non-bonded segments within the cut-off distance, and ∑f_i is the sum of neighboring segments around the moving segment along the sliding diffusion path. In the present simulation, 4ε/E_c is fixed at 1, σ is 1 lattice site, the cut-off distance for the Lennard-Jones potential is 3 lattice sites, and kT/E_c (k is the Boltzmann's constant and T the temperature) represents the reduced system temperature (below simplified as T*).

The initially chains were relaxed for 10⁶ MC cycles (each MC cycle was defined as the step when all segments moved once on average) to obtain an equilibrium melt state at T* = 8. Then, the system was cooled gradually from T* = 8 to T* = 0.05 at a cooling rate of 0.01 unit of T* per 100 MC cycles.

III. Results and discussion

In the previous paper, we proposed a parameter, the probability of segment movement (PSM), to directly measure the segmental mobility.³² PSM was defined as the probability of movement of each segment either by jumping into its neighboring empty sites or partial sliding diffusion in one MC cyclewhere n is the number of neighboring vacancy sites around the corresponding segments, ΔE_ij is the energy change of the system caused by a movement of a segment from site i to site j. We could use the mean value of PSM (〈PSM〉) to measure the mobility of the whole polymer system, as depicted in Fig. 1. The value of 〈PSM〉 decreases initially with the decrease of temperature, and then levels off at low temperatures, indicating that the chain segments enter the completely frozen state. The current findings were in line with some experimental results. The single-molecule fluorescence microscopy can be used to detect the motion of single molecules, and thus reflect the segmental mobility in their neighboring domains.⁴² By using the single-molecule fluorescence microscopy, Wöll's group found that the temperature dependence of fraction of mobile molecules in polystyrene films exhibited similar trends with that of PSM.⁴²

Fig. 1 The mean probability of segment movement and the fraction of trans-conformation of the polymer system during cooling.

Some experiments and simulations revealed that the conformational transition from gauche- to trans-conformations occurred during glass transition.^26–32 Similarly, we also observe the conformational changes during cooling in the current simulation. Herein, the two successive bonds that were collinear were treated as a trans-conformation, while the bonds that were nonlinear were considered as a gauche-conformation (a gauche- or trans-conformation is composed of two successive bonds). In the lattice box, one site has 26 neighbors. Thus, for conformations, if the spatial location of the first bond (containing two neighboring sites) is fixed, there are 25 different orientations for the next bond. Among those conformations, only one case belongs to trans-conformation, while the rests gauche ones. By counting the number of the trans-conformations and dividing it by the total number of the trans- and gauche-conformations, the temperature dependence of the fraction of the trans-conformation can be obtained, as also shown in Fig. 1. The fraction of the trans-conformation first increased during cooling, indicating the occurrence of the conformational transition. Below a critical temperature, the trans-conformation fraction became saturated. This critical saturation temperature is almost equal to the critical temperature at which the 〈PSM〉 began to level off, as depicted in Fig. 1. Below the critical temperature, the polymer chains are completely frozen (the value of 〈PSM〉 is close to 0), and thus the conformational transition no longer happens.

The previous simulation revealed that trans-conformations were packed more closely in contrast to the gauche-ones.³² The emergence of local close-packed segments with trans-conformations may cause the formation of local orders. Tanaka et al. have observed the existence of local orders in grassy colloidal system by Brownian dynamic simulation.^23,24 In addition, Koyama et al. also detected the proceeding of local structural orders in amorphous polyethylene with lowering temperature by means of molecular dynamics simulation.⁴³ In order to validate the emergence and evolution of the local order during glass transition, we need to define it in the present simulation. Here, the bonds containing more than five parallel neighbors were considered as the ordered bonds, while those containing less than five parallel neighbors were treated as the disordered bonds. Then, we further define the content of the local order as the fraction of the ordered bonds. The variation of the content of the local order with decreasing temperature was thus tracked, as shown in Fig. 2. During cooling, the content of the local order increases, and then is saturated after the system approaches the completely frozen state. The corresponding critical saturation T* is about 0.2, which is in accordance with the two turning temperatures of the curves in Fig. 1. Namely, when the polymer chains enter the frozen state, both the conformational transition and the development of the local orders stop. Additionally, Fig. 3 visually demonstrates the appearance of the short-range orientational orders in some local domains at several typical temperatures. The trend of the content of the local order during cooling is consistent with the Adam–Gibbs prediction about CCR.⁶ According to the Adam–Gibbs prediction,⁶ the number of segments assembled in CRR increased with the decrease of temperature and diverged on approaching the completely frozen state. Thus, some underlying correlations between the local order and the CRR may exist.

Fig. 2 Variation of content of local order during cooling.

Fig. 3 Snapshots of local orders at several typical temperatures, T* = 0.5, 0.3 and 0.1. The yellow cylinders denote the ordered segments.

In the previous works, the CRR was proposed to be formed by some mobile particles.^13,20,21 However, the reason why the mobile particles move cooperatively is not explained. Since those particles move cooperatively, there should be some structural restrictions on the particle motion. Otherwise, without any structural restrictions, the particles may move randomly rather than cooperatively. Both experiment and simulation results have demonstrated that the particles participating in the cooperative motion prefer to move in parallel direction.^13,20,21 In other words, the movements along other directions would be hindered by some structural restrictions. In order to understand the mechanism of the cooperative motion, the molecular details of structural restrictions must be firstly unveiled.

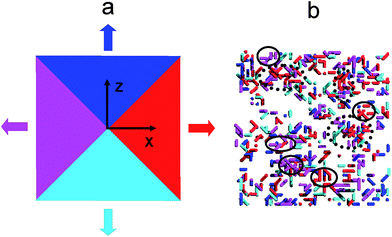
According to the above definition of the local order, the segments in the present simulation can be divided into two types: the ordered and the disordered segments. The former segments were defined as the segments formed by the ordered bonds, while the latter ones were defined as the segments formed by the disordered bonds. Fig. 4(a) shows the mean square displacements (MSDs) of the ordered segments during relaxation at several typical temperatures. During the relaxation process, the ordered segments can move at T* = 0.49 and 0.29, but the values of MSDs decrease with lowering temperature. In addition, the MSD of the ordered segments is lower than that of the disordered ones, as depicted in Fig. 4(b). In order to reveal the relationship between the cooperative motion and the local structures, the movement directions of the ordered segments were probed. As shown in Fig. 5(a), for simplicity, the segmental motions were divided into four parts with different movement directions denoted by different colors. After tracking the motion direction of each ordered segment, we endowed every segment with the corresponding color representing the same direction (motion direction is measured by comparison of the segment coordinates between two different states at 1 and 10 000 MC cycles). From the snapshot in Fig. 5(b), it can be seen that there exist some small local ordered domains, in which nearly all the segments move along the same direction, as circled with black color, implying that the movement of these domains is cooperative. More interestingly, a relatively large ordered domain surrounded with black dots in Fig. 5(b) can be divided into several smaller clusters with different movement directions. Similarly, Glotzer et al. have also observed that a large cluster of mobile particles was composed of several small strings, which moved collectively as a single unit.^21,44

Fig. 4 (a) MSD of local ordered segments during relaxation at several different temperatures (T* = 0.49, 0.29 and 0.09). (b) MSD of local ordered and disordered segments during relaxation at T* = 0.29.

Fig. 5 The cooperative motion of the local orders at T* = 0.29; (a) motion directions were divided into four directions marked by different colors. (b) The snapshot for the local orders with cooperative motion. This snapshot was drawn at 10 000 MC cycles and the segments with same direction were denoted by corresponding colors as used in (a).

To further compare the difference of moving behaviors between the ordered and disordered segments, we count the distribution of movement directions of the local ordered and disordered segments. Firstly, we choose a reference direction (as shown in the inset of Fig. 6(a)), and then calculate the cosine of the angle (cos θ) of the movement direction relative to this reference direction for each segment in the local ordered and disordered domains, respectively. Both of the distributions of the movement angle for the ordered and disordered segments can be obtained, as shown in Fig. 6(a). The probability of high values (bigger than 0.5) of cos θ for the ordered segments is obviously higher than that of the disordered segments, indicating the preference of cooperative motion for the ordered segments. In addition, it can be found that cos θ = 0 (θ = 90°) also shows a relatively high probability. This high probability at θ = 90° is caused by the feature of the lattice model used. As sketched in Fig. 6(b), one lattice site has 26 neighbors, among which 8 neighbors exhibit θ = 90° relative to the reference direction (the red dot arrow in the Fig. 6(b)). Namely, the number of the neighbors with θ = 90° in the lattice model is highest, thus resulting in the high probability.

Fig. 6 (a) The distribution of the angle of the movement direction relative to the reference direction for each segment in the local ordered and the disordered domains, respectively. The definition of movement angle (θ) is illustrated in the inset, in which the dot arrow denotes the reference direction, while the solid arrow represents the movement direction of moving segment. (b) A local lattice domain in the simulation. The red dot arrow denotes the reference direction and the black spheres represent the lattice sites.

The formation of the local ordered structure induces the decrease of neighboring available vacancy volume around the ordered segments. Fig. 7 demonstrates that the mean fraction of vacancy sites in neighboring sites of the ordered segments is apparently lower than that of the disordered ones. Thus, the segmental motion within the local ordered domains is restricted by other neighboring ordered segments. However, the restriction of movement of interior segments within the local ordered domains does not mean that the segments can not move. Actually, those ordered segments can move via the larger-scale cooperative conformational rearrangements. Namely, the external segments have more available neighboring vacancy volumes, and thus they can directly move by jumping or sliding from occupied sites to neighboring vacancy sites. Then, the outside vacancy sites are transferred into the interior of the local ordered domains. Furthermore, the interior segments near the transferred vacancy sites can move subsequently, and the corresponding vacancy sites further diffuse into more inner regions. In this way, the ordered segments can move cooperatively, as sketched in Fig. 8.

Fig. 7 The variations of mean fraction of vacancy sites in the neighboring domains of ordered and disordered segments, respectively, during cooling.

Fig. 8 A sketch of cooperative motion of local ordered segments. The red spheres denote the ordered segments which do not move at our observation time scale, while the purple ones represent the ordered segments participating in the cooperative motion. The white ones denote the vacancy sites, and the yellow ones represent the disordered segments which move randomly. The arrow is used to mark the position exchange between segment and vacancy site.

Since the size of the local ordered structures that prefer to move cooperatively increases during cooling, the relaxation times of the polymer system should be controlled by the cooperative motion of those local orders, as proposed by Tanaka et al.⁴⁵

IV. Conclusions

By means of dynamic Monte Carlo simulation, the micro-structural characteristics of CRR have been explored. With the decrease of temperature, the conformational transition from gauche- to trans-conformation occurs. In some local domains, the segments with trans-conformation are packed more closely, resulting in the formation of local ordered structures. The size of the local orders increases during cooling. In addition, the local orders exhibit obviously lower mobility compared with the disordered segments. Further analysis demonstrates that the segments in the small ordered domains are inclined to move along the parallel direction, while the large domains are composed of several smaller clusters that move collectively as a single unit.

Acknowledgements

The financial supports from the National Basic Research Program of China (973 Program, no. 2012CB821500) and the National Natural Science Foundation of China (no. 21404050 and 21174057) are gratefully acknowledged. The Research Foundation of Jiangsu University (no. 14JDG059) and the Jiangsu Planned Projects for Postdoctoral Research Funds (no. 1402019A) are also appreciated.

Notes and references

1. H. Sillescu, J. Non-Cryst. Solids, 1999, 243, 81.
2. C. A. Angell, Science, 1995, 267, 1924.
3. R. L. Leheny, N. Menon, S. R. Nagel, D. L. Price, K. Suzuya and P. Thiyagarajan, J. Chem. Phys., 1996, 105, 7783.
4. P. J. Flory and T. G. Fox, J. Am. Chem. Soc., 1951, 73, 1904.
5. J. H. Gibbs and E. A. DiMarzio, J. Chem. Phys., 1958, 28, 373.
6. G. Adam and J. H. Gibbs, J. Chem. Phys., 1965, 43, 139.
7. P. G. Debenedetti and F. H. Stillinger, Nature, 2001, 410, 259.
8. W. Götze and L. Sjögren, Transp. Theory Stat. Phys., 1995, 24, 801.
9. K. L. Ngai, R. W. Rendell, A. K. Rajagopal and S. Teitler, Ann. N. Y. Acad. Sci., 1986, 484, 150.
10. C. A. Angell, J. Non-Cryst. Solids, 1985, 1, 73.
11. P. W. Anderson, Science, 1995, 267, 1615.
12. W. B. Hu, Polymer Physics a Molecular Approach, Springer, Vienna, 2013, p. 120.
13. E. R. Weeks, J. C. Crocker, A. C. Levitt, A. Schofield and D. A. Weitz, Science, 2000, 287, 627.
14. M. D. Ediger, Annu. Rev. Phys. Chem., 2000, 51, 99.
15. K. Schmidt-Rohr and H. W. Spiess, Phys. Rev. Lett., 1991, 66, 3020.
16. U. Tracht, M. Wilhelm, A. Heuer, H. Feng, K. Schmidt-Rohr and H. W. Spiess, Phys. Rev. Lett., 1998, 81, 2727.
17. D. Bingemann, R. M. Allen and S. W. Olesen, J. Chem. Phys., 2011, 134, 024513.
18. L. A. Deschenes and D. A. V. Bout, Science, 2001, 292, 255.
19. M. T. Cicerone, F. R. Blackburn and M. D. Ediger, Macromolecules, 1995, 28, 8224.
20. C. Donati, J. F. Douglas, W. Kob, S. J. Plimpton, P. H. Poole and S. C. Glotzer, Phys. Rev. Lett., 1998, 80, 2338.
21. Y. Gebremichael, T. B. Schroder, F. W. Starr and S. C. Glotzer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 051503.
22. F. van Swol and D. N. Petsev, RSC Adv., 2014, 4, 21631.
23. K. Watanabe and H. Tanaka, Phys. Rev. Lett., 2008, 100, 158002.
24. H. Shintani and H. Tanaka, Nat. Phys., 2006, 2, 200.
25. P. Yunker, Z. X. Zhang, K. B. Aptowicz and A. G. Yodh, Phys. Rev. Lett., 2009, 103, 115701.
26. H. S. Shin, Y. M. Jung, T. Y. Oh, T. Chang, S. B. Kim, D. H. Lee and I. Noda, Langmuir, 2002, 18, 5953.
27. X. Yu, R. L. Wu and X. Z. Yang, J. Phys. Chem. B, 2010, 114, 4955.
28. S. Xie, H. Qian and Z. Lu, J. Chem. Phys., 2012, 137, 244903.
29. R. L. Wu, B. Kong and X. Z. Yang, Polymer, 2009, 50, 3396.
30. T. Liang, Y. Yang, D. W. Guo and X. Z. Yang, J. Chem. Phys., 2000, 112, 2016.
31. Z. P. Zhou, W. M. Yang, D. Y. Yan and H. Liu, Macromol. Theory Simul., 2014, 76, 23.
32. Y. J. Nie, X. B. Ye, Z. P. Zhou, W. M. Yang and L. Tao, J. Chem. Phys., 2014, 141, 074901.
33. K. Binder, J. Baschnagel, W. Paul, H. P. Wittmann and M. Wolfgardt, Comput. Mater. Sci., 1995, 4, 309.
34. H. P. Wittmann, K. Kremer and K. Binder, J. Chem. Phys., 1992, 96, 6291.
35. H. Y. Chen and E. Ruckenstein, Polymer, 2010, 51, 968.
36. H. Y. Chen and E. Ruckenstein, Langmuir, 2009, 25, 12315.
37. W. B. Hu and D. Frenkel, Adv. Polym. Sci., 2005, 191, 1.
38. P. G. de Gennes, Eur. Phys. J. E, 2000, 2, 201.
39. P. G. de Gennes, C. R. Acad. Sci., Ser. IV: Phys., Astrophys., 2000, 1, 1179.
40. Q. Y. Tang and W. B. Hu, Phys. Chem. Chem. Phys., 2013, 15, 20679.
41. Q. Y. Tang, W. B. Hu and S. Napolitano, Phys. Rev. Lett., 2014, 112, 148306.
42. B. M. I. Flier, M. C. Baier, J. Huber, K. Müllen, S. Mecking, A. Zumbusch and D. Wöll, J. Am. Chem. Soc., 2012, 134, 480.
43. A. Koyama, T. Yamamoto, K. Fukao and Y. Miyamoto, J. Chem. Phys., 2001, 115, 560.
44. S. C. Glotzer, J. Non-Cryst. Solids, 2000, 274, 342.
45. T. Kawasaki, T. Araki and H. Tanaka, Phys. Rev. Lett., 2007, 99, 215701.

---