Thermal spin transport of a nitroxide radical-based molecule

Abstract

Based on spin-polarized first-principles density functional theory combined with nonequilibrium Green's function method, the thermal spin transport properties of a nitroxide radical-based molecule sandwiched between two Au electrodes are investigated. The results show that opposite spin currents can be induced by applying a temperature difference, rather than bias voltage, between two electrodes. Moreover, a pure spin current and a completely spin-polarized current can be realized by tuning the transverse gate voltage. These results indicate that the nitroxide radical-based molecule is a potential material for spin caloritronic and spintronic applications.

---

1 Introduction

With the aim of miniaturization, molecular electronics has been a very active field of research since its introduction in 1974 by Aviram and Ratner.¹ However, the dissipation of heat energy becomes severe as the electronic devices shrink down to the molecular level, which inevitably leads to high energy consumption and deterioration in the performance and reliability of molecular devices. In this regard, spintronics offers a possibility to reduce the dissipating heat due to the weak spin interactions.^2–4 On the other hand, thermoelectronics opens the door to transform directly the dissipating heat into electric energy.^5–8 Recently, an invigorated research field of spin caloritronics, combining the advantages of both spintronics and thermoelectrics, has drawn considerable interest.^9,10 Especially, the discovery of spin Seebeck effect in 2008 by Uchida et al. advanced dramatically the development of spin caloritronics.¹¹ In this effect, the dissipating heat can be converted into spin voltage, which can be measured via inverse spin Hall effect (ISHE).^12–14 Thus, this indicates that it is possible to apply spin caloritronics in the design of low-power consumption devices.

Much effort has been devoted to find potential nanoscale materials for spin caloritronic applications. Zeng et al. explored thermally induced spin transport in magnetized zigzag graphene nanoribbons and found thermal spin-filtering and magnetoresistance effects.¹⁵ Wu et al. calculated thermal spin-dependent transport through a zigzag silicon carbide nanoribbons heterostructure and found such system can be designed as a highly-efficient multifunctional spin caloritronics device.¹⁶ Su et al. firstly reported a single molecule magnet Mn(dmit)₂ also to be a promising material for spin caloritronic applications.¹⁷ Organic radicals of light elements, with unpaired valence electrons or an open electron shell, have attracted increasing attention in molecular spintronics due to their extremely long spin relaxation times.^18–20 However, the possibility of organic radicals for spin caloritronic applications has never been investigated. It is known that a molecule-containing nitroxides can form stable organic radical species at ambient temperature.²¹ In the present work, using spin-polarized first-principles density functional theory (DFT) combined with nonequilibrium Green's function (NEGF) method, we investigate the thermal spin transport properties of a nitroxide radical-based molecule sandwiched between two Au electrodes. Our results show that the opposite spin currents can be induced by a temperature difference, rather than bias voltage, between the left electrode and the right electrode. Moreover, a pure spin current and a completely spin-polarized current can be realized by tuning the transverse gate voltage.

The remainder of this paper is organized as follows. In Section 2, we briefly describe the simulation model and the computational method. In Section 3, we present the results with associated discussions, and finally a short summary is given in Section 4.

2 Model and method

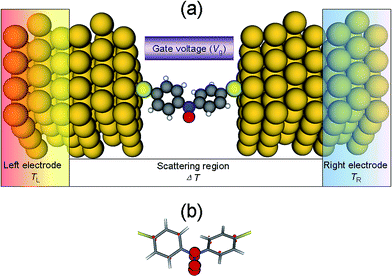
The molecular device is illustrated in Fig. 1(a), the nitroxide radical is connected to the (4 × 4) Au(111) electrodes via phenylthiol groups.²⁰ The sulfur atom is located at the hollow site of each Au surface as this is more energetically favorable than the other absorption sites.²² The initial perpendicular distance between the sulfur atom and the Au surface is set to 1.9 Å, which is a typical Au–S distance²³ and also corresponds to the lowest-energy of our system. As shown in Fig. 1(a), the entire molecular junction can be divided into three regions: the left electrode, the scattering region 2 and the right electrode. Each electrode contains three Au(111) layers, while the scattering region includes the organic radical molecule and seven Au buffer layers to take into account of the molecule–electrode coupling and the electrode screening effect. The transverse gate voltage (V_g) is only applied on the organic radical molecule and has no effect on the Au electrodes. The whole system is relaxed until the force on each atom is less than 0.05 eV Å⁻¹ while the electrode Au atoms are kept fixed.

Fig. 1 (a) The schematic illustration of the thermal spin caloritronic device, in which the nitroxide radical is sandwiched between two Au electrodes via phenylthiol groups. The sulfur atom is located at the hollow site of each Au surface. The thermal spin currents can be induced by applying a temperature difference (ΔT) between the left electrode (T_L) and the right electrode (T_R), i.e., ΔT = T_L − T_R. The gray, blue, red, white, yellow, and golden spheres indicate the carbon, nitrogen, oxygen, hydrogen, sulfur, and gold atoms, respectively. V_g is the transverse gate voltage. (b) The spin density distribution on the central molecule.

The geometric optimization and the sequent thermal spin transport properties are performed within the framework of the Atomistix Toolkit (ATK) package,^24–27 which adopts spin-polarized DFT combined with NEGF method. Norm-conserving Troullier–Martins pseudopotentials²⁸ and a double-ξ plus polarization (DZP) basis set are adopted to describe the core orbitals and the valence electronic orbitals of all the atoms, respectively, except a single-ζ plus polarization (SZP) basis set is adopted for the valence electronic orbitals of Au atoms to achieve a balance between accuracy and computation burden. The exchange–correlation potential is treated at the level of spin-polarized generalized gradient approximation (GGA), with the form of Perdew–Burke–Ernzerhof.²⁹ The Brillouin zone is sampled as a Monkhorst–Pack grid³⁰ using 3 × 3 × 100 k-points and the grid mesh cutoff is set to 200 Ry. The spin-dependent current through the junction is given by the Landauer–Büttiker formula³¹

where e is the electron charge, h is the Planck's constant, f_L(R)(E, T_L(R)) is the Fermi–Dirac distribution function for the left (right) electrode, T_L(R) is the temperature of the left (right) electrode, and T_σ(E) is the spin-resolved transmission function of spin-up (σ = up) and spin-down (σ = dn) electrons and can be defined as

T_σ = Tr[Γ_LG^RΓ_RG^A]_σ, (2)

where G^R(A) is the retarded (advanced) Green's function of the central region and Γ_L(R) is the coupling matrix of the left (right) electrode.

3 Results and discussion

The ground state of optimized free molecule is found to be a doublet-state with an unpaired spin-up electron. However, the presence of an unpaired electron in the free molecule does not necessarily give rise to polarized electron transmission, since charge transfer takes place once the molecule is connected to the electrodes and this maybe extinguish the excess number of spin-up electrons. According to the Mulliken population analysis, the number of excess spin-up electrons of the radical molecule in the junction is still found to be about 0.60e, which is mainly localized on the nitroxide radical group, as demonstrated by the spin density distribution in Fig. 1(b). Then, Fig. 2 plots the corresponding spin-resolved transmission spectrum, where the Fermi level (E_F) has been set as the energy origin. Clearly, the transmission spectrum has an obvious asymmetric feature between spin-up and spin-down electrons, which can be ascribed to the asymmetric alignment between the E_F and spin-polarized frontier molecular orbitals (FMOs). Around the E_F, there are two peaks, at −0.17 eV for spin-up and 0.37 eV for spin-down, which originates from the delocalized highest occupied molecular orbital (HOMO) of spin-up electron and the lowest unoccupied molecular orbital (LUMO) of spin-down electron, respectively, as shown in the insets of Fig. 2. All these characteristics portend a potential way of applying the nitroxide radical-based molecule in the molecular spintronics. Here, we must point out that these two FMOs are calculated from the molecular projected self-consistent Hamiltonian (MPSH), which includes the molecule–electrode interaction.³²

Fig. 2 The spin-resolved transmission spectra. The positions of the HOMO and LUMO for spin-up and spin-down electrons are marked by black square and red circle, respectively. Both the temperatures of T_L and T_R are set as 300 K. The Fermi level (E_F) has been set as the energy origin. The insets show the spatial distribution of HOMO and LUMO orbitals.

Then, we apply different temperatures (T_L and T_R) to the left and right Au electrodes to investigate the thermal spin transport properties of the junction. The thermally induced spin currents versus the temperature difference ΔT (i.e., T_L − T_R) with different T_L (100, 200, and 300 K) and those versus T_L with different ΔT (20, 40, 60 and 80 K) are plotted in Fig. 3(a) and (b), respectively. Interestingly, a distinct spin Seebeck effect can be observed in the junction: the spin-up current (I_up) flows from the left electrode to the right one while the spin-down current (I_dn) flows in the opposite direction. In this process, the dissipating heat is converted into spin voltage. Furthermore, the amplitude of I_up is always larger than that of I_dn at the same ΔT and T_L, and both of them go up almost linearly as ΔT and T_L increase.

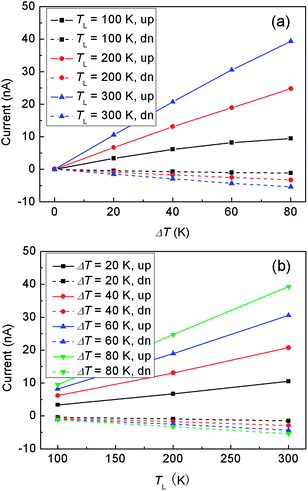Fig. 3 (a) The thermal spin currents versus ΔT with different T_L. (b) The thermal spin currents versus T_L with different ΔT.

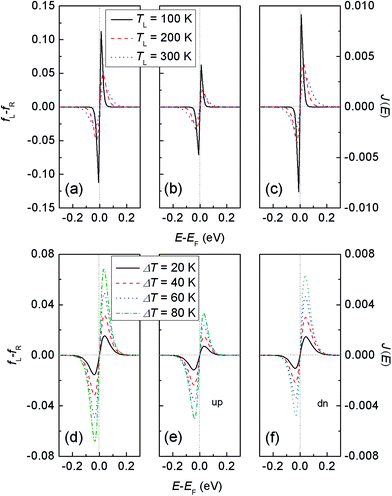
According to the Landauer–Bütiker formula, the thermally induced current is determined not only by the transmission, but also by the difference in the Fermi–Dirac distributions between the left and right electrode, (f_L(E, T_L) − f_R(E, T_R)), which is only dependent on T_L and T_R, i.e., the carrier concentration on the left and right electrode, since the electrodes are the same material. Fig. 4(a) and (d) present the (f_L(E, T_L) − f_R(E, T_R)) with different T_L (ΔT = 40 K) and ΔT (T_L = 300 K), respectively, which shows a typical exponential decaying nature and also a perfect symmetric feature with respect to the E_F. Clearly, f_L − f_R > 0 when the energy is higher than the E_F, so carriers (electrons) with energy greater than the E_F flow from the left electrode to the right one, resulting in a negative current in the opposite direction sine the electron charge e is negative. On the other hand, f_L − f_R < 0 when the energy is lower than the E_F, thus, carriers (holes) with energy smaller than the E_F flow from the left electrode to the right one, leading to a positive current. As shown in Fig. 4(a), although the height of f_L − f_R is decreased, it has a wider spread around the E_F with the increase of T_L if ΔT keeps constant. This means that the transmission with energy far from the E_F can also contribute to the current as T_L increases. On the contrary, as shown in Fig. 4(d), the distribution of f_L − f_R is nearly unchanged, although its height is increased with the increase of ΔT if T_L is fixed, indicating the current is only determined by the transmission close to the E_F.

Fig. 4 (a) The difference in the Fermi–Dirac distributions between the left and right electrode (f_L(E, T_L) − f_R(E, T_R)) for different T_L. (b) The spin-up current spectra for different T_L. (c) The spin-down current spectra for different T_L. In (a)–(c), the ΔT is fixed at 40 K. (d)–(f) Similar to (a)–(c), respectively, except for different ΔT with a fixed T_L = 300 K.

Moreover, it is evident that the positive and negative currents will cancel out each other if the transmission spectrum is symmetric around the E_F. In other words, an asymmetric distribution of the transmission spectrum around the E_F is required to generate the thermally induced current. To further elucidate this point, the current spectra, J_σ(E) = T_σ(E)[f_L(E, T_L) − f_R(E, T_R)], as a function of energy, are shown in Fig. 4(b) and (e) (Fig. 4(c) and (f)) for spin-up electrons (spin-down electrons). Clearly, all these J_σ(E) are asymmetric with respect to the E_F due to the asymmetry of corresponding T_σ(E). To be specific, for spin-up electrons (Fig. 4(b) and (e)), the cover area of J_up(E) below the E_F is larger than that above the E_F at a given T_L and ΔT, resulting in a positive net spin-up current. On the contrary, for spin-down electrons (Fig. 4(c) and (f)), the cover area of J_dn(E) above the E_F is larger than that below the E_F at a certain T_L and ΔT, giving rise to a negative net spin-down current. With the increase of T_L (ΔT) in Fig. 4(b) and (c) (Fig. 4(e) and (f)), the asymmetry of J_σ(E) around the E_F is enhanced. As a result, both the spin-up and spin-down currents increase almost linearly in Fig. 3. Moreover, the cover area of J_dn(E) is obvious smaller than that of J_up(E) due to the spin-down transmission peak T_dn(E) is farther than the spin-up transmission peak T_up(E) from the E_F (Fig. 2). As a result, the amplitude of I_dn is always smaller than that of I_up at the same T_L and ΔT.

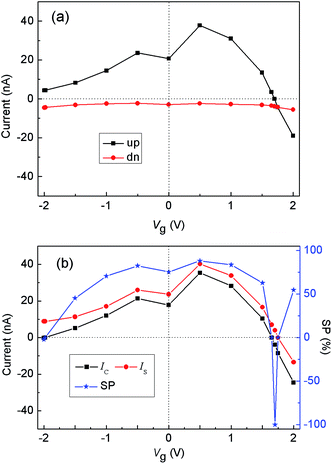
We have shown above that spin Seebeck effect can be obtained in the junction. Next, we prove that it is possible to create a pure spin current I_s (the difference between the spin-up and spin-down currents, i.e., I_s = I_up − I_dn) for vanishingly charge current I_c (the sum of the spin-up and spin-down currents, i.e., I_c = I_up + I_dn), and a completely spin-polarized current by tuning the transverse gate voltage V_g. The former has important applications in ISHE,^13,14 while the later can be used to design a perfect spin-filter. Fig. 4(a) plots the I_up and I_dn as a function of V_g for a fixed T_L (300 K) and ΔT (40 K). At negative V_g, the amplitude of I_up increases firstly, and then decreases slowly. At positive V_g, the amplitude of I_up also increases firstly, then drops quickly to zero at V_g = 1.7 V. After that, I_up changes its sign from positive to negative. On the contrary, the amplitude variation of I_dn is very small. In Fig. 5(b), we present the corresponding I_c and I_s as a function of V_g. Clearly, a pure spin current appears at V_g = −1.98 and 1.65 V, respectively, where I_c = 0 and I_s ≠ 0. Moreover, the spin polarization of charge current (SP = [(|I_up| − |I_dn|)/(|I_up| + |I_dn|)] × 100%) versus V_g is also shown in Fig. 5(b). It is evident that the SP reaches −100% at V_g = 1.7 V, where I_up = 0 and I_dn ≠ 0.

Fig. 5 (a) The thermal spin-up and spin-down currents as a function of gate voltage V_g, where the T_L and ΔT are set as 300 and 40 K, respectively. (b) The spin and charge currents, along with the spin polarization (SP) of the charge current versus V_g.

To understand the variations of I_up and I_dn, in Fig. 6, we plot the spin-resolved transmission spectrum under different V_g. As shown in Fig. 6(a), when negative V_g is applied, the T_up(E) takes place left-shift. Thus, the asymmetric distribution of T_up(E) around the E_F is enhanced firstly, and then is weakened within the nonzero region of f_L − f_R (see the curve of T_L = 300 K in Fig. 4(a) or ΔT = 40 K in Fig. 4(d)) when the negative V_g further increases, resulting in the corresponding increase and decrease of the amplitude of I_up. As shown in Fig. 6(b), when postive V_g is applied, the T_up(E) occurs right-shift and moves from below the E_F to above the E_F. In this process, the asymmetric distribution of T_up(E) with respect to the E_F within the nonzero region of f_L − f_R is enhanced firstly, then is weakened, and then is completely eliminated at V_g = 1.7 V (not shown here), and then is enhanced again with the increase of V_g. As a result, the amplitude of I_up increases firstly, then drops quickly to zero at V_g = 1.7 V, and after that, the I_up changes its sign. On the other hand, as shown in Fig. 6(a) and (b), the T_dn(E) always moves to the left, no matter what V_g is applied. However, because the T_dn(E) is far from the E_F, its shift can hardly affect the asymmetric distribution of T_dn(E) around the E_F within the nonzero region of f_L − f_R. Therefore, the variations of I_dn is very smooth.

Fig. 6 The spin-resolved transmission spectra with different V_g.

4 Summary

In summary, by using spin-polarized first-principles density functional theory combined with nonequilibrium Green's function method, we have investigated the thermal spin transport properties of a nitroxide radical-based molecule sandwiched between two Au electrodes. The numerical results show that the spin Seebeck effect with spin-up and spin-down currents flowing in opposite directions can be realized by applying a temperature difference between two electrodes. The reason is ascribed to the asymmetric distribution the spin-resolved transmission spectra with respect to the Fermi level. Moreover, a pure spin current and a completely spin-polarized current can be achieved by tuning the transverse gate voltage. These results might be helpful in the design of organic radical-based spin caloritronic and spintronic devices.

Acknowledgements

This work was jointly supported by the National Natural Science Foundation of China (Grant no. 11104115), the Science Foundation of Middle-aged and Young Scientist of Shandong Province of China (Grant no. BS2013DX036) and the Doctoral Foundation of University of Jinan, China (Grant no. XBS1004).

References

1. A. Aviram and M. A. Ratner, Chem. Phys. Lett., 1974, 29, 277–283.
2. S. A. Wolf, D. D. Awschalom, R. A. Buhrman, J. M. Daughton, S. von Molnár, M. L. Roukes, A. Y. Chtchelkanova and D. M. Treger, Science, 2001, 294, 1488–1495.
3. I. Žutić, J. Fabian and S. Das Sarma, Rev. Mod. Phys., 2004, 76, 323–410.
4. A. Fert, Rev. Mod. Phys., 2008, 80, 1517–1530.
5. T. T. M. Vo, A. J. Williamson, V. Lordi and G. Galli, Nano Lett., 2008, 8, 1111–1114.
6. G. Joshi, H. Lee, Y. Lan, X. Wang, G. Zhu, D. Wang, R. W. Gould, D. C. Cuff, M. Y. Tang, M. S. Dresselhaus, G. Chen and Z. Ren, Nano Lett., 2008, 8, 4670–4674.
7. J. H. Lee, G. A. Galli and J. C. Grossman, Nano Lett., 2008, 8, 3750–3754.
8. J. Tang, H. T. Wang, D. H. Lee, M. Fardy, Z. Huo, T. P. Russell and P. Yang, Nano Lett., 2010, 10, 4279–4283.
9. G. E. W. Bauer, A. H. MacDonald and S. Maekawa, Solid State Commun., 2010, 150, 459–460.
10. G. E. W. Bauer, E. Saitoh and B. J. van Wees, Nat. Mater., 2012, 11, 391–399.
11. K. Uchida, S. Takahashi, K. Harii, J. Ieda, W. Koshibae, K. Ando, S. Maekawa and E. Saitoh, Nature, 2008, 455, 778–781.
12. S. Valenzuela and M. Tinkham, Nature, 2006, 442, 176–179.
13. E. Saitoh, M. Ueda, H. Miyajima and G. Tatara, Appl. Phys. Lett., 2006, 88, 182509.
14. T. Kimura, Y. Otani, T. Sato, S. Takahashi and S. Maekawa, Phys. Rev. Lett., 2007, 98, 156601.
15. M. Zeng, Y. Feng and G. Liang, Nano Lett., 2011, 11, 1369–1373.
16. D. D. Wu, H. H. Fu, L. Gu, Y. Ni, F. X. Zu and K. L. Yao, Phys. Chem. Chem. Phys., 2014, 16, 17493–17498.
17. Z. Su, Y. An, X. Wei and Z. Yang, J. Chem. Phys., 2014, 140, 204707.
18. A. Rajca, Chem. Rev., 1994, 94, 871–893.
19. C. Herrmann, G. C. Solomon and M. A. Ratner, J. Am. Chem. Soc., 2010, 132, 3682–3684.
20. Y. Matsuura, Chem. Phys. Lett., 2015, 619, 23–26.
21. A. Calder, A. R. Forrester, P. G. James and G. R. Luckhurst, J. Am. Chem. Soc., 1969, 91, 3724–3727.
22. M. Tachibana, K. Yoshizawa, A. Ogawa, H. Fujimoto and R. Hoffmann, J. Phys. Chem. B, 2002, 106, 12727–12736.
23. H. Sellers, A. Ulman, Y. Shnidman and J. E. Eilers, J. Am. Chem. Soc., 1993, 115, 9389–9401.
24. J. Taylor, H. Guo and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 121104(R).
25. J. Taylor, H. Guo and J. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 245407(R).
26. M. Brandbyge, J. L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165401.
27. J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779.
28. N. Troullier and J. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
30. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
31. M. Büttiker, Y. Imry, R. Landauer and S. Pinhas, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 6207.
32. K. Stokbro, J. Taylor, M. Brandbyge, J. L. Mozos and P. Ordejón, Comput. Mater. Sci., 2003, 27, 151–160.

---