Two-photon absorption and two-photon circular dichroism of hexahelicene derivatives: a study of the effect of the nature of intramolecular charge transfer†
Abstract
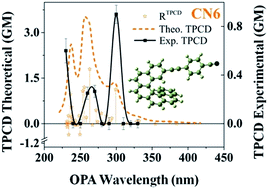
Herein we report on the theoretical–experimental analysis of the one- and two-photon absorption and circular dichroism spectra of two intrinsically chiral aromatic molecules – hexahelicene derivatives – with helical chirality and intramolecular charge transfer (ICT). The primary outcomes of our investigation demonstrate that the TPA cross-section and the amplitude of the TPCD signal of this type of helicenes are strongly affected by the strength of the ICT and the nature of the extension of the electronic delocalization, i.e. beyond (EXO-ICT) or within (ENDO-ICT) the helicene core. These results were corroborated through the comparative theoretical analysis of the corresponding contributions of the magnetic dipole transition moment and the electric quadrupole transition moment to the TPA rotatory strength on a series of five similar helicene derivatives with different molecular electron delocalization disposition. Two-photon absorption (TPA) and two-photon circular dichroism (TPCD) spectra were obtained using the double L-scan technique over a broad spectral range (400–900 nm) using 90 fs pulses at a low repetition rate (2–50 Hz) produced by an amplified femtosecond system. The theoretical simulations were performed using modern analytical response theory within the Time-Dependent Density Functional Theory (TD-DFT) approach using B3LYP and CAM-B3LYP, and the aug-cc-pVDZ and 6-311++G(d,p) basis sets.

 Please wait while we load your content...
Please wait while we load your content...