Polymerization kinetics of a fluorinated monomer under confinement in AAO nanocavities†
Abstract
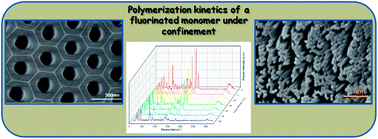
In this work we show for the first time the kinetic study of the radical polymerization of a fluorinated acrylic monomer (MFA) in the confinement of anodic aluminum oxide (AAO) nanocavities. AAO templates with different pore sizes were used as nanoreactors and polymerization kinetics were studied in situ by Raman spectroscopy and in bulk by differential scanning calorimetry (DSC). Afterwards, a mathematical model that describes the effect of nanoconfinement on the polymerization kinetics was derived. Furthermore, similar nanostructures were observed by SEM when in bulk polymerized PFA was infiltrated into the AAO nanocavities. Superhydrophobic surfaces were achieved with the water contact angle of 159°, much higher than its analogous non-nanostructured PFA, 114°. The “lotus effect” was observed in the superhydrophobic surface which has a low sliding angle of 8°.

 Please wait while we load your content...
Please wait while we load your content...