Understanding the binding interaction of imidazole with ZnO nanomaterials and clusters

Abstract

The potential applications of different nanostructured materials in biomedical nanotechnologies and the interaction of nanomaterials with bioactive molecules are of current interest. A bioactive fluorophore 1-(3,5-dimethylphenyl)-2-(furan-2-yl)-4,5-diphenyl-1H-imidazole has been synthesized and characterized by ¹H NMR, ¹³C NMR and mass spectral studies. Electronic properties and the binding interactions of the fluorophore with ZnO nanocrystals of different sizes have been studied using absorption, emission, lifetime and cyclic voltammetric analysis. The strong adsorption of the imidazole on the surface of ZnO nanocrystals is likely due to the chemical affinity of azomethine nitrogen atom of the imidazole and this is likely to result in lowering the HOMO and LUMO energy levels. TEM, SEM and EDS confirm the adsorption of imidazole on the surface of ZnO nanocrystals. Theoretical investigation reveals that small Zn_nO_n clusters (n < 9) and their imidazole–ZnO composites are stabilized in 2D ring geometries whereas the larger cluster Zn₁₀O₁₀ and its imidazole–ZnO composite prefer 3D cage structures. 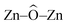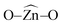The ring to cage crossover of ZnO clusters is studied by analyzing the and bond angles, Zn–O bond length and number of bonds. Binding energy, energy gap, binding site and adsorption strength of imidazole with different ZnO clusters show that Zn²⁺ of ZnO clusters prefer to bind with the azomethine nitrogen atom (N-site) relative to the other binding site (O-site).

---

1. Introduction

The II–VI semiconductor nanocrystals are known for their photostability, high photoluminescence quantum yield, broad absorption spectrum with high molar extinction coefficient and their symmetric, narrow and tunable emission spectrum spanning from the UV to near IR. These properties make them attractive for numerous applications, ranging from light-emitting diodes to bioimaging, biolabeling and sensing with performances that are significantly superior to their organic counterparts.^1,2 Although many smart fluorescent organic dyes have been intensively investigated for sensing a variety of target molecules, following mechanisms such as photoinduced electron transfer (PET) and energy transfer,³ constructing II–VI semiconductor based nanohybrids for recognition and sensing will be an important extension of nanocrystal applications.³ ZnO nanoparticles have unique physical and chemical properties and potential biomedical applications by virtue of their nontoxic nature, low cost, biosafety, biocompatibility and wide usage in daily life such as drug carriers, cosmetics, etc.^4–10 ZnO nanoparticles can kill cancer and activated human T cells, suggesting biotherapeutic functionality of this novel material.¹¹ The photoactive surfaces of the nanoparticles produce reactive oxygen species that can potentially cause oxidative stress which leads to cellular protein, lipid and DNA damage.^12–14

The small size of the ZnO nanoparticles reduces scattering of visible light and provides transparent products which retain UV absorption.¹⁵ There is no evidence that ZnO nanoparticles possess phototoxic risk to humans. There is robust evidence that this substance protects human skin against UV-induced adverse effects, including skin cancer and DNA damage.¹⁵ In medicine, magnetic nanoparticles are used for magnetic cell separation or magnetic resonance imaging (MRI). The development of biocompatible nano sized drug delivery systems for specific targeting of therapeutics is the focus of medical research, especially for the treatment of cancer and diseases of the vascular system.¹⁶ Imidazole nucleus forms the main structure of human organisms, i.e., amino acids, histidine, vitamin B₁₂, DNA component, etc., and also has significant analytical applications utilizing their fluorescence and chemiluminescence properties.¹⁷ The combination of ZnO with biomolecules is particularly intriguing since it opens the door to novel bio- and nanotechnological applications.¹⁸ DFT calculation on ZnO clusters is widely analysed¹⁸ and binding interaction of nano metal oxides with biological molecules viz., adenine, guanine, cytosine, thymine, etc., is of current interest in biomedical nanotechnology.^19–23 Nano ZnO prefers to bind with a ring nitrogen atom (N-site) relative to other binding sites of the DNA bases; adsorption strength of ZnO with the N-site of guanine is much higher than other sites.²⁴ In order to analyse the properties of materials at the nano level a detailed study of nano metal oxide–bioactive molecule interaction is required. Joshi et al.,²⁵ studied the interaction of nanoclusters with tryptophan and the results show that the binding of –COOH group (C-site) with ZnO clusters is energetically more favourable than the other interacting sites such as indole and amine groups in tryptophan.

In continuation of our research interest,²⁶ the present investigation is designed to explore the binding of imidazole derivative on the surface of ZnO nanoparticles with different sizes to tune the recognition properties. The observed enhancement of emission is ascribed to photoelectron (PET) transfer process. For the first time, the binding of bioactive imidazole with ZnO clusters has been analysed in terms of their size, binding energy, geometry, binding site, bond length and HOMO–LUMO energies. The experimental and theoretical results confirm the formation of ≥N–Zn bond in imidazole–ZnO composites. There is an overlap occurring between the d-orbital of zinc and azomethine nitrogen atoms which lead to a greater binding energy for N site.

2. Materials and methods

2.1. Materials and spectral measurements

Furan-2-carbaldehyde, 3,5-dimethylaniline and all other reagents were purchased from Sigma-Aldrich chemicals and used without further purification. The ¹H NMR and proton decoupled ¹³C NMR spectra were recorded at room temperature using a Bruker 400 MHz NMR spectrometer operating at 400 and 100 MHz, respectively. The mass spectra of the samples were obtained using a Thermo Fischer LC-Mass spectrometer in FAB mode. The UV-vis absorption and emission spectra were recorded with a PerkinElmer Lambda 35 spectrophotometer and a PerkinElmer LS55 spectrofluorimeter, respectively. Lifetime measurements were carried out with a nanosecond time correlated single photon counting (TCSPC) spectrometer. The decay was analyzed using DAS6 software. The cyclic voltammetric analysis was performed with a CHI 630A potentiostat-electrochemical analyzer at a scan rate of 100 mV s⁻¹ using 0.1 M tetra(n-butyl)-ammonium hexafluorophosphate as supporting electrolyte with Ag/Ag⁺ (0.01 M AgNO₃) as the reference electrode and Pt electrode as the working electrode under nitrogen atmosphere at room temperature. The energies of the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO)²⁶ were calculated using the following equations, E_HOMO = 4.4 + E_(onset); E_LUMO = E_HOMO − 1239/λ_abs. The powder X-ray diffractogram (XRD) was recorded with a PAN analytical X'Pert PRO diffractometer using Cu K_α rays at 1.5406 Å with a tube current of 30 mA at 40 kV. A JEOL JSM 10LV scanning electron microscope (SEM) equipped with a highly sensitive back scattered detector and low vacuum secondary detector was used to get the SEM image of the sample. The UV-vis diffuse reflectance spectra (DRS) were recorded with a PerkinElmer Lambda 35 spectrophotometer with RSA-PE-20 integrating sphere. The quantum chemical calculations were performed using the Gaussian 03 (ref. 27) package.

2.2. Synthesis of 1-(3,5-dimethylphenyl)-2-(furan-2-yl)-4,5-diphenyl-1H-imidazole

A mixture of furan-2-carbaldehyde (1 mmol), benzil (1 mmol), 3,5-dimethylaniline (1 mmol) and ammonium acetate was stirred at solvent-free condition at 80 °C. The progress of the reaction was monitored by TLC. After completion of the reaction, the mixture was cooled, dissolved in acetone and filtered. The product 1-(3,5-dimethylphenyl)-2-(furan-2-yl)-4,5-diphenyl-1H-imidazole was purified by column chromatography using benzene : ethyl acetate (9 : 1) as the eluent. M.p. 220 °C, anal. calcd for C₂₇H₂₂N₂O: C, 83.05; H, 5.68; N, 7.17; found: C, 83.04; H, 5.66; N, 7.15.¹H NMR (400 MHz, CDCl₃): δ 2.25 (s, 6H), 5.66 (d, J = 3.6 Hz, 1H), 6.26 (q, J = 1.6 Hz, 1H) 6.50 (q, J = 5.2 Hz, 1H), 6.80 (s, 1H), 6.99 (d, J = 3.6 Hz, 2H), 7.10–7.32 (m, 9H), 7.41 (d, J = 1.2 Hz, 1H), 7.44 (d, J = 6.8 Hz, 2H), 7.51 (d, J = 6.8 Hz, 3H). ¹³C NMR (100 MHz, CDCl₃): δ 21.15, 107.64, 109.21, 111.01, 112.08, 125.52, 126.18, 126.51, 126.68, 127.50, 127.88, 128.04, 128.09, 128.20, 128.31, 128.58, 130.21, 130.70, 130.75, 130.81, 130.99, 134.20, 138.44, 138.96, 139.00, 142.35, 142.74. MS: m/z 390 [M⁺].

2.3. Synthesis nanocrystalline ZnO by sol–gel method

To 2.5 mL of 0.2 M zinc acetate solution, aqueous ammonia (1 : 1) was added drop wise to reach a pH of 7/7.2 under continuous stirring and the stirring was continued for another 30 min. The formed glassy like white gel was allowed to age overnight. It was filtered, washed with water and ethanol, dried at 100 °C for 12 h and calcinated at 500 °C for 2 h (heating rate 10 °C min⁻¹) to pale grey solid.

2.4. Synthesis of imidazole–ZnO composite

About 1 mmol of imidazole in dimethyl sulphoxide (1 mL) was added to 1 mmol of ZnO nanoparticles suspended in dimethyl sulphoxide (1 mL) under constant stirring for 3 h. The solid was filtered, washed with dimethyl sulphoxide and dried at 110 °C.

3. Results and discussion

3.1. Characterization of nano ZnO

Fig. 1 displays the X-ray diffraction pattern (XRD) of pristine nano ZnO samples obtained by sol–gel method. The diffraction pattern matches with the JCPDS pattern of zincite (89-7102). The crystal structure of pristine ZnO is primitive hexagonal with crystal constants a and b as 3.249 Å and c as 5.025 Å, respectively. The average crystallite sizes (L) of the sol–gel synthesized ZnO have been deduced as 36 and 19 nm. They have been obtained from the full width at half maximum (FWHM, β) of the most intense peak using the Scherrer equation, L = 0.9λ/β cos θ, where λ is the wavelength of the X-rays used and θ is the diffraction angle. The specific surface areas (S) of the nanocrystals have been obtained using the relationship, S = 6/ρL, where L is the average particle size and ρ is the material density. The results are in accordance with the crystal sizes and the calculated surface area are 28.8 and 56.7 m² g⁻¹.

Fig. 1 X-ray diffraction patterns (XRD) of pristine ZnO (36 nm) (a); ZnO (19 nm) (b); SEM images of pristine ZnO (36 nm) (c) and ZnO (19 nm) (d).

The SEM images of the ZnO samples are displayed in Fig. 1. The particles are flower like; use of PVP as templating agent provides finite morphology. The TEM images (Fig. 2) confirm the nanoparticulate nature of the synthesized samples and the observed crystallite sizes are in general agreement with those obtained by XRD. The TEM image at high resolution is displayed as inset in Fig. 2 which shows lattice fringes of the nanocrystals. The observed d-spacing corresponds to the 100-plane of hexagonal ZnO. A typical EDX spectrum of pristine ZnO is shown in Fig. 2. The absence of signals other than zinc and oxygen confirms the purity of the synthesized samples. The diffused reflectance spectra of the samples are displayed in Fig. 3. The reflectance is presented in terms of the Kubelka–Munk (KM) function. The DRS show the band gaps as 3.18 and 3.20 eV. The observed band gaps are in agreement with the mean crystallite sizes of the synthesized ZnO nanoparticles. The increase in the average crystallite size from 19 to 36 nm has resulted in the decrease of band gap energy from 3.20 to 3.18 eV.

Fig. 2 TEM images of pristine ZnO (36 nm) (a); ZnO (19 nm) (b) and EDX spectrum of pristine ZnO (36 nm) (c).

Fig. 3 Diffused reflectance spectra of pristine ZnO (36 nm) and ZnO (19 nm).

3.2. Electronic spectral analysis

The absorption spectra of the imidazole in the presence of 19 nm or 36 nm-ZnO nanocrystals dispersed at different loading and also in their absence are displayed in Fig. 4. The enhanced absorption is due to the adsorption of the imidazole on ZnO nanocrystals which leads to the formation of the imidazole–ZnO nano composites. The emission spectra of imidazole in the presence of ZnO nanoparticles dispersed at different loading and also in their absence are displayed in Fig. 4. The nanoparticles enhance the emission of imidazole remarkably and the emission in red shifted. This is because of the effective transfer of electron from the excited state of the imidazole to the conduction band of (CB) of the semiconductor nanoparticles. Fluorescence enhancement arises due to the formation of imidazole–ZnO composite. The binding constants (K) of the imidazole with 36 nm- and 19 nm-ZnO have been obtained as 8.8 × 10⁵ and 7.86 × 10⁷ M⁻¹, respectively. Such a large binding constants indicates that imidazole is strongly associated to the surface of nanocrystals by electrostatic interactions. These values show that the binding is stronger with the smaller nanoparticles than with the larger one. This is because of the surface area; the surface area of the former is smaller than that of the latter. The greater interaction of smaller nanocrystals with imidazole is not only due to the large surface area of the smaller nanocrystals but also because of larger surface curvature of the smaller nanocrystals. The larger surface curvature reduces the steric hindrance between the surface binding molecules and provides a large number of unsaturated dangling bonds on the nanocrystal surface and enhances the binding interaction.

Fig. 4 Absorption (a) and emission (b) spectra of imidazole in presence and absence of different sized ZnO nanoparticles.

3.3. Mechanism of enhancement

Several mechanisms for the enhancement are possible; free energy transfer (FRET) from imidazole to nanocrystals and electron transfer from excited imidazole to the CB of nanosemiconductors. On the basis of Forster's energy transfer (FRET) formalism, there are three requirements for FRET to occur from imidazole to nanocrystals, i.e. efficient overlap between emission and absorption spectra of imidazole and nanocrystals, center-to-center distance of imidazole and nanocrystals and coupling between imidazole and nanocrystals transition dipole moments. Therefore the energy transfer efficiency is related not only to the distance between the acceptor ZnO and donor imidazole (r₀) but also to the critical energy transfer distance (R₀). The critical energy transfer distance (R₀), R₀⁶ = 8.8 × 10⁻²⁵K²N⁻⁴φJ, where, K² is the spatial orientation factor of the dipole, N is the refractive index of the medium, φ is the fluorescence quantum yield of the donor and J is the overlap integral of the fluorescence emission spectrum of the donor and the absorption spectrum of the acceptor. According to the equation J = ∫F(λ)ε(λ)λ⁴dλ/F(λ)dλ, where, F(λ) is the fluorescence intensity of the donor and ε(λ) is molar absorptivity of the acceptor, we could calculate the J (1.32 × 10⁻¹¹ (36 nm) and 1.04 × 10⁻¹¹ cm³ LM⁻¹ (19 nm)). Under these experimental conditions, the calculated values of R₀ and r₀ are 9.8 × 10⁻¹⁰ (36 nm) and 1.87 × 10⁻⁹ m (19 nm) and 1.08 (36 nm) and 2.05 nm (19 nm), respectively. The value of K² (= 2/3) and N (0.955) used are from the literature²⁸ and the φ value is from the present study. The obtained donor–acceptor distance (r₀) is consistent with the covalent attachment of imidazole with ZnO nanoparticles. Obviously, the calculated value of R₀ is in the range of maximal critical distance. The energy transfer efficiency (E) was calculated using the formula E = mR₀⁶/(mR₀⁶ + r₀⁶) where, R₀ is the critical distance when the transfer efficiency is 50% and m is the average number of acceptor molecules interacting with one imidazole. A value of m lower than 10 was estimated on the basis of imidazole to nanocrystal concentration ratio, leading to an energy transfer efficiency lower than 0.03 for both the imidazole-composites. This means that the energy transfer from imidazole to nanocrystal is negligible. Therefore, the observed enhancing likely originated from an electron transfer process only. All these results put forward that the optoelectronic behavior of imidazole will be enhanced in the presence of ZnO nanoparticles which implies its potential application in the field of nano-drug carriers.

3.4. Energetics

On the basis of the relative positions of imidazole and ZnO energy levels,²⁹ the interfacial electron injection would be thermodynamically allowed from the excited singlet of the imidazole to the CB of pristine ZnO. Fig. 5 represents the HOMO and LUMO energy levels of an isolated imidazole molecule along with the CB and valence band (VB) edges of ZnO nanoparticles. On illumination at excitation wavelength both the imidazole and nanosemiconductor are excited. Duel emission is expected due to LUMO → HOMO and CB → VB electron transfer. Also possible is electron jump from the excited imidazole to the nanocrystal; the electron in the LUMO of the excited imidazole is of higher energy compared to that in the CB of ZnO nanocrystals. This should lead to quenching of fluorescence in imidazole. However, contrary to the expectations, enhancement of fluorescence is observed in presence of ZnO nanocrystal. This may be because of lowering of the HOMO and LUMO energy levels due to adsorption on ZnO nanoparticles. The polar ZnO surface enhances the delocalization of the π electrons and lowers the HOMO and LUMO energy levels due to adsorption.³⁰ The chemical affinity between the azomethine nitrogen atom of the imidazole and zinc ion on the surface of the metal oxide causes the enhancement. The excited state energy of the imidazole is larger than the CB energy levels of nanosemiconductors.³¹ This makes possible the electron transfer from the excited state of imidazole to the nanoparticle.

Fig. 5 A schematic enhancement mechanism.

To gain more insight into the mechanism of the generation of light from the fluorophore–ZnO composites, the photoexcitation processes have been shown in the Fig. 5. The two types of transition i.e., n–π* and π–π* exists in fluorophore.³¹ Due to the lower availability of the non-bonding electron, the π–π* transition is more prominent, which will give rise to the blue emission around 397 nm. Now, as for as the ZnO nanocrystals, some O²⁻ ions can escape from the host lattice, leading to the formation of oxygen vacancies. This oxygen vacancy centre can trap an electron, leading to defect states formation.³¹ There are three energy levels viz., VB, defect states and CB. ZnO nanocrystals first create positive holes in the VB and negative electrons in the CB after photoexcitation. The hole in the VB can be trapped at the oxygen vacancy sites. Then, this surface trapped hole tunnels back into the particle to recombine with an electron to form the defect states at the surface of the particle. Then recombination of this centre with an electron in the CB gives rise to emission.³¹ Upon photoexcitation of the composites, the π–π* transition of fluorophore gives blue light and the transition between the electron in the CB and hole trapped in the defect states give rise to emission at longer wavelength. The emission intensity of fluorophore bound to ZnO is far larger than that of the isolated molecule. With the fluorophore adsorbed on ZnO the semiconductor is also excited on irradiation. The recombination of the electron in the oxygen vacancies with the hole in the VB results in emission at 416 nm. In addition, emission from the LUMO of the fluorophore adsorbed on ZnO to the CB of ZnO at 416 nm is possible. Due to the additional path opened up for emission the emission intensity is increased. This sensing system was identified to operate under the photoinduced electron transfer (PET) mechanism in which imidazole is the electron donor. We showed that imidazole bound with ZnO nanocrystals through electrostatic interactions resulted in an efficient enhancement.

3.5. Free-energy change (ΔG_et) for electron transfer process

The thermodynamic feasibility of excited state electron transfer reaction has been confirmed by the calculation of free energy change by employing the well known Rehm–Weller expression,³² ΔG_et = E_(ox)^1/2 − E_(red)^1/2 − E_s + C, where, E_(ox)^1/2 is the oxidation potential of imidazole, E_(red)^1/2 is the reduction potential of ZnO nanoparticles, i.e., the CB potential of nanoparticle, E_s is the excited state energy of imidazole and C is the coulombic term. Since the imidazole is neutral and the solvent used is polar in nature, the coulombic term in the above expression can be neglected.³³ The calculated negative value of ΔG_et (−2.09 eV) indicates the thermodynamic feasibility of the electron transfer process³⁴ which further illustrates the strong affinity of imidazole towards ZnO nanocrystal surface.

3.6. Fluorescence lifetime studies

Time-resolved fluorescence experiments using time correlated single photon counting (TCSPC) technique were carried out to analyze the electron transfer process from excited imidazole to nanocrystals. The experimental decay curves were fitted to a biexponentials, f(t) = α₁ exp(−t/τ₁) + α₂ exp(−t/τ₂), where α₁ and τ₁ are respectively, the pre-exponential factor and lifetime of the various excited states involved. Fig. 6 displays the bi exponential decay of imidazole revealing that imidazole is in two excited states – one is likely to be the configuration in which the furfuryl ring is perpendicular with the imidazole ring [excited state I] and the other is the one in which the same is coplanar with the imidazole ring [excited state II]. The X-ray crystal structure³⁵ and theoretical calculation²⁷ show the perpendicular configuration as the most stable one and hence the observed longer lifetime is attributed to the same. The observed biexponential decay indicates that the imidazole–ZnO composite formation is possible with both the conformation of imidazole. The perpendicular conformation of imidazole binds with the nanoparticles is predominant than the other one with the planar conformation. The fluorescence decay curves of all nanoparticles with imidazole were recorded in ethanol. Laser excitation was set at 260 nm and the fluorescence signal was measured at emission wavelength of individual compound. The radiative (k_r) and non-radiative (k_nr) decay of the excited state have been obtained using the quantum yield (Φ) and lifetime (τ). The formula employed to calculate the k_r and k_nr are; k_r = Φ/τ; k_nr = (1/τ) − (Φ/τ); τ = (k_r + k_nr)⁻¹. The lifetime, radiative and non-radiative constants and energy transfer rate constants (k_et) are presented in Table 1. Evaluation of the radiative and non-radiative rates shows that the radiative emission is predominant over the non-radiative emission. ZnO nanocrystals bound to imidazole modifies the fluorescence lifetime. The decay times of imidazole–ZnO composites are distinctly shorter than the imidazole. This is again in line with the occurrence of electron transfer from imidazole to the nanocrystals. The observed lifetimes of both the composites do not differ significantly indicating the same type of bonding in the composites. The substantial shortening of fluorescence lifetime upon conjugation of imidazole with ZnO nanoparticles indicates conclusively that efficient electron transfer from donor imidazole to acceptor ZnO. The rate constants for the electron transfer (k_et) can be calculated by using the equation, k_et = 1/τ_ads − 1/τ and the calculated value of k_et is listed in Table 1. The rate constant for electron transfer is larger for smaller nanoparticles than the larger ones.

Fig. 6 Life time spectra of imidazole along with imidazole–ZnO composites.

Table 1 Bi exponential fitting parameter for fluorescence decay of imidazole and imidazole–ZnO composites

Compound	10^2a1	10^9τ1 (ns)	10^3a2	10^8τ2 (ns)	τavg (ns)	kr 10^−8 S^−1	knr 10^−8 S^−1	ket 10^−8 S^−1
a ZnO – 36 nm.b ZnO – 19 nm.
Imidazole	3.73	2.23	3.70	1.45	3.34	1.68	1.31	—
Imidazole–ZnO composite^a	4.07	2.04	1.47	1.27	2.42	2.48	1.65	1.1
Imidazole–ZnO composite^b	3.32	2.12	0.91	9.84	2.32	2.67	1.64	1.3

---

3.7. Electrochemical measurements

Cyclic voltammetric studies were carried out to probe the efficient binding of ZnO nanoparticles with imidazole. Fig. 7 shows the cyclic voltammogram (CV) of imidazole, imidazole–ZnO (19 nm) and imidazole–ZnO (36 nm) composites. Both the composites show a shift in peak potentials along with decrease in peak current.³⁶ It is evident that the two different sized ZnO nanoparticles have efficient binding with imidazole which supports the electronic spectral results.

Fig. 7 Cyclic voltammogram of imidazole along with imidazole–ZnO composites.

3.8. SEM, EDX and FT-IR spectra of imidazole–ZnO composites

Fig. 8 presents the SEM of imidazole–ZnO composites. The SEM images show that adsorption of imidazole significantly modifies the morphology of the ZnO nanocrystal. EDX spectrum of imidazole–ZnO composites confirms the adsorption of imidazole on ZnO nanocrystalline surface (Fig. 8). The FT-IR spectra of pristine ZnO, imidazole and imidazole–ZnO composites are displayed in Fig. 9. In the case of bare ZnO sample, Zn–O stretching vibration is observed at 447 cm⁻¹. For imidazole–ZnO composites, C=C and C–O–C stretching vibrations are observed around 1509 and 1335 cm⁻¹ in addition to the Zn–O stretching mode at 462 cm⁻¹. The frequency observed around 1600 cm⁻¹ by imidazole and imidazole–ZnO composites corresponds to C=N function. The absorption around 3050 cm⁻¹ is due to [double bond splayed left]C–H of imidazole and imidazole–ZnO composites. The peak at ∼966 cm⁻¹ is likely due to the phenyl C–H stretching.

Fig. 8 (a) SEM image and (b) EDX spectrum of imidazole–ZnO composite.

Fig. 9 FT-IR spectra of bare imidazole, bare pristine ZnO and imidazole–ZnO composites.

3.9. Evidence for linkage

Although there are three basic sites in the imidazole, the azomethine nitrogen is involved in the binding process with ZnO nanoparticles. This is because of the high electron density at the azomethine nitrogen. Hence it is of interest to study the behaviour of nitrogen in acid environment. In order to prove the higher electron density at azomethine nitrogen, we have performed DFT calculation to get the molecular electrostatic potential (MEP) for imidazole, bare ZnO and imidazole–ZnO composites. The MEP map (Fig. 10) shows that nitrogen atoms represent the most negative potential region (dark red). The predominance of green region in the MEP surface corresponds to a potential halfway between the two extremes red and dark blue colour.

Fig. 10 Molecular electrostatic potential (MEP) diagram of bare Zn_nO_n clusters and their imidazole–Zn_nO_n composites.

3.10. Electronic properties of ZnO clusters and imidazole–ZnO composites

In order to get a better insight on the nature of binding of the imidazole with the ZnO surface, DFT calculations have been made with Zn_nO_n (n = 1–9) clusters of different geometries. ZnO, Zn₂O₂, Zn₃O₃, Zn₄O₄ (R), Zn₄O₄ (W), Zn₅O₅, Zn₆O₆ (R), Zn₆O₆ (C), Zn₇O₇ (R), Zn₈O₈ (R) and Zn₉O₉ (R), are the clusters used for the calculation. The optimized geometries of imidazole, bare Zn_nO_n (n = 1–4) clusters and their corresponding imidazole–ZnO composites are shown in Fig. 11 and the optimization parameters, energy gap (E_g) and binding energies (E_b) are given in Table 2. The binding energy (E_b) of ZnO clusters have been calculated by using the equation, E_b = (nE_Zn + nE_O − E_ZnO)/n, where n is the number of ZnO molecules in the cluster. In the optimised bare ZnO clusters, the Zn–O bond length varies from 1.86 to 1.99 Å. The Zn–O bond is mainly ionic with charge transfer from zinc atom to oxygen atom. The energy gap of the ZnO clusters were calculated from the total densities of states (DOS) which is shown in Fig. 12 and the E_g of ZnO, Zn₂O₂, Zn₃O₃, Zn₄O₄ (R) and Zn₄O₄ (W) are 2.68, 2.29, 3.72, 3.88, and 2.24 eV, respectively. As shown in Table 2, the calculated E_b of ZnO, Zn₂O₂, Zn₃O₃, Zn₄O₄ (R) and Zn₄O₄ (W) are 5.89, 6.10, 7.32, 7.72 and 7.20 eV, respectively. The E_b of Zn₄O₄ (R) is larger than those of Zn₂O₂, Zn₃O₃ and Zn₄O₄ (W) clusters and hence Zn₄O₄ (R) is a more stable one. The binding interactions between imidazole with the ZnO clusters have been analysed by binding energy, E_b = E_composite − (E_ZnO + E_imidazole), where E_composite is the total energy of imidazole adsorbed on the ZnO, E_ZnO and E_imidazole are the energies of the ZnO clusters and imidazole, respectively. The E_b of Zn₄O₄ (R) is larger than those of ZnO, Zn₂O₂, Zn₃O₃ and Zn₄O₄ (W) clusters and hence Zn₄O₄ (R) is a more stable one. The energy gap of the ZnO clusters were calculated from the total densities of states (DOS) and the E_g of Zn₂O₂, Zn₃O₃, Zn₄O₄ (R) and Zn₄O₄ (W) are 2.29, 3.72, 3.88, and 2.24 eV, respectively. As shown in Table 2, the calculated E_b of Zn₂O₂, Zn₃O₃, Zn₄O₄ (R) and Zn₄O₄ (W) is 6.10, 7.32, 7.72 and 7.20 eV, respectively. From the optimized parameters and binding energies it is confirmed that the zinc atom of ZnO clusters prefer to bind through the azomethine nitrogen atom of imidazole (N site). There is an overlap occurring between the d-orbital of zinc and azomethine nitrogen atoms which lead to a greater binding energy for N site.³⁵ The calculated binding energy (E_b) is of the order: imidazole–Zn₄O₄ (R) (7.75 eV) > imidazole–Zn₃O₃ (7.34 eV) > imidazole–Zn₄O₄ (W) (7.21 eV) > imidazole–Zn₂O₂ (6.12 eV) > imidazole–ZnO (6.41 eV). This order is further supported by Zn–N bond distance. The Zn–N bond distance of imidazole–Zn₄O₄ (R) composite is shorter (2.01 Å) than those of imidazole–Zn₃O₃ (2.03 Å), imidazole–Zn₄O₄ (W) (2.05 Å), imidazole–Zn₂O₂ (2.08 Å) and imidazole–ZnO (2.07 Å). The preferred imidazole–Zn₄O₄ (R) composite is most favored as compared to other imidazole–ZnO composites. The binding energy of imidazole–Zn₄O₄ (R) is larger than that of imidazole–Zn₄O₄ (W) and the bond distance of the former is shorter than that of the latter. The covalent forces play a key role in deciding the strength of the interaction.³⁷

Fig. 11 Optimized structures of (a) Zn_nO_n clusters (n = 1–4) and (b) imidazole–Zn_nO_n composites (n = 1–4).

Table 2 E_HOMO, E_LUMO, energy gap (E_g), distance Zn–N (Å), binding energies (E_b), optimised energies (E) and dipole moments of imidazole–ZnO composite along with ZnO clusters

Compound	EHOMO	ELUMO	Eg/Eb (eV)	Eb (eV)		Zn–N	E (eV)	D
				N-site	O-site
ZnO	−6.23	−3.55	2.68/5.89					1.26
Zn2O2	−6.0	−3.69	2.29/6.10	—	—	—	—	0.00
Zn3O3	−6.83	−3.11	3.72/7.12	—	—	—	—	0.01
Zn4O4 (R)	−6.84	−2.85	2.98/7.70	—	—	—	—	0.65
Zn4O4 (W)	−6.12	−3.86	2.24/7.19	—	—	—	—	3.21
Imidazole	−5.13	−0.82	4.31	—	—	—	6.50	4.99
Imidazole–ZnO	−3.45	−2.33	1.12	6.41	2.31	2.07	22.4	11.42
Imidazole–Zn2O2	−3.83	−2.54	1.29	6.12	2.42	2.08	28.6	13.97
Imidazole–Zn3O3	−3.32	−2.59	0.73	7.34	3.56	2.03	30.08	16.91
Imidazole–Zn4O4 (R)	−3.29	−2.68	0.61	7.75	3.89	2.01	15.57	12.63
Imidazole–Zn4O4 (W)	−3.58	−2.59	0.99	7.21	2.82	2.05	42.10	4.85

---

Fig. 12 Density of state-plots for imidazole and imidazole–Zn_nO_n composites (n = 1–4).

In the optimized bare ZnO clusters, the Zn–O bond length varies from 1.86 Å to 1.99 Å. Due to the adsorption of imidazole on bare ZnO, the surface structure of the ZnO is slightly distorted. Thus the surface Zn–O bond lengths in the imidazole adsorbed ZnO clusters are expanded by a smaller amount (2.01 Å, 2.08 Å). The Zn–O bonds are mainly ionic in nature and charge transfer occurs from zinc to more electronegative oxygen atoms. This charge transfer occurs in greater amounts in the surface region. To have an understanding of the extent of fractional charge transfer from imidazole to ZnO clusters, we have shown the Mulliken charge of the atoms of imidazole–ZnO composites in Table S1.† The values of the charge transfer give us some understanding of the character of the imidazole–ZnO interactions and also the nature of imidazole adsorption on the ZnO clusters. From the Mulliken charge analysis it is clear that there are relatively large changes in the fractional charge of the atoms which bind to the ZnO nanomaterials and also the atoms adjacent to them. For ZnO clusters the oxygen atom exhibits negative charges, which are donor atoms. Zinc atom exhibits a positive charge, which is an acceptor atom for ZnO clusters. All hydrogen atoms have positive charges. The zinc atom exhibits a more positive charge and the azomethine nitrogen atom exhibits a more negative charge, these two atoms favor the weak interaction of Zn–N bond in imidazole–ZnO clusters. The detailed calculated values of the binding energies for imidazole with different possible attacking sites to the ZnO are summarized in Table 2. The binding energy values suggest that the most preferred attacking site for imidazole to the ZnO surface is azomethine nitrogen atom (N site). The equilibrium Zn–N bond length confirms the interaction regime for covalent forces. Energy gaps of imidazole–ZnO, imidazole–Zn₂O₂, imidazole–Zn₃O₃, imidazole–Zn₄O₄ (R) and imidazole–Zn₄O₄ (W) composites are 1.12, 1.29, 0.73, 0.61 and 0.99 eV, respectively. This shows that binding of imidazole on ZnO clusters induces some changes in the electronic properties and the E_g values are decreased when compared with both bare imidazole and ZnO clusters. The order of changes occurring in the E_g values are, imidazole–Zn₂O₂ (1.29 eV) > imidazole–ZnO (1.12 eV) > imidazole–Zn₄O₄ (W) (0.99 eV) > imidazole–Zn₃O₃ (0.73 eV) > imidazole–Zn₄O₄ (R) (0.61 eV). In addition, more efficient binding has been achieved in the Zn₄O₄ (R). The achieved reduction is 72% [imidazole–ZnO], 70% [imidazole–Zn₂O₂], 83% [imidazole–Zn₃O₃], 86% [imidazole–Zn₄O₄ (R)] and 77% [imidazole–Zn₄O₄ (W)]. The HOMO–LUMO analysis explains the charge transfer taking place within the imidazole–ZnO composites. Fig. 13 shows the HOMO–LUMO electron distribution plots for imidazole–Zn₂O₂, imidazole–Zn₃O₃, imidazole–Zn₄O₄ (R) and imidazole–Zn₄O₄ (W) clusters. Usually the clusters with larger HOMO–LUMO gaps are more stable and chemically inert.³⁸ The above observation shows that the charge transfer occurs in the imidazole–Zn₄O₄ (R) composite are faster than the same in other composites. Similar type of calculations have been made for large sized Zn_nO_n clusters and imidazole–ZnO composites. In the two isomers of Zn₆O₆, the energy of Zn₆O₆ (R) is lower than that of Zn₆O₆ (C) by 26.92 kcal mol⁻¹. In Zn₆O₆ (R), the 12 atoms are stacked to a slightly distorted hexagonal prism where the Zn–O bond lengths on the bottom surfaces are larger than 1.9 Å, and the distances between the adjacent layers are larger than 2.0 Å. It is well-known that the ZnO crystal lattice preferably adopts a hexagonal packed structure so the hexagonal prism should be the most favorable structure and the Zn–O bond length lie between 1.89–2.09 Å.³⁹ The calculation results show that the ring structures of Zn_nO_n where n = 5–10 are the most stable geometries.⁴⁰ The optimised structures, HOMO–LUMO plots, MEP diagram and DOS are given in Fig. S1 and S2.† We have shown the Mulliken charges of the atoms of imidazole–Zn_nO_n composites (n = 5–9) in Table S2.† The zinc atom exhibits a more positive charge and the azomethine nitrogen atom exhibits a more negative charge, these two atoms favor the weak interaction of Zn–N bond in imidazole–ZnO clusters. All these results show that for both bare Zn_nO_n and imidazole–Zn_nO_n composites, the ring structure is more stable for n = 1–9 but when n = 10, the energy decrease and the bond angles of and also reach an extreme and so the ring structures no longer exist. Furthermore, the calculation shows that the Zn₉O₉ cluster less prefers the 2D ring geometry whereas the larger cluster with n = 10 is stabilized in 3D structure; ring to cage structural cross over takes place between Zn₉O₉ and Zn₁₀O₁₀ clusters. The Zn₉O₉ cluster is structurally distorted from planner geometry (D_9h symmetry) to zig-zag ring (C1 symmetry). Hence, the Zn₉O₉ clusters is the onset of 2D to 3D structural cross over in ZnO clusters and the structural zig-zag distortion of Zn₉O₉ is attributed to the behavior of bond angle. Because of the ionic Zn–O bonding, the valence electronic shell is mainly localized on oxygen nuclei while the zinc nuclei act as the localized positive charge centers and the presence of two lone pairs of electrons in the valence shell of oxygen prevents the linear configuration of Zn–O–Zn chains. In the perfect planar Zn₉O₉ structure, is expected to be 135° but the obtained zig-zag structural distortion reduces the to about 124°. For larger cluster (n = 10) zig-zag structural distortion with angle of 124° was obtained. For smaller clusters (n = 1–9), the ring structures with smaller bond lengths and stronger single bond energies were obtained when compared with the cage structures because in 3D structures the atoms are more coordinated, containing more number of bonds and hence the valence electrons are divided into more bonds and gets weaker. In the smaller clusters, the number of bonds are less and the individual bond energy determines the stability. Increasing the cluster size enhances the coordination number and at some point (n = 10) a ring to cage structural transition occurs. The first 3D cluster Zn₁₀O₁₀ favors an intermediate configuration between the ring and cage structures which is composed of two Zn₅O₅ ring structures. The energy gap of ring clusters are larger than 2 eV while the cage clusters exhibit lower energy gap (<2.0 eV) which shows that the energy gap is mainly sensitive to the cluster geometry and not to the cluster size.

Fig. 13 HOMO–LUMO contour maps for imidazole and imidazole–Zn_nO_n composites (n = 1–4).

4. Conclusion

Fluorescent enhancement has been explained and binding constant has been calculated based on photoelectron transfer mechanism and the negative ΔG_et value reveals that the electron transfer process is thermodynamically favourable. SEM with EDX, TEM and electronic spectral analyses show the adsorption of imidazole on the ZnO surface. We have theoretically investigated the interaction of imidazole with different sized Zn_nO_n (n = 1–10) clusters. The order of the binding energies of imidazole–Zn_nO_n clusters are of the order imidazole–Zn₄O₄ (R) > imidazole–Zn₃O₃ > imidazole–Zn₄O₄ (W) > imidazole–Zn₂O₂, indicating imidazole–Zn₄O₄ (R) composite as the most stable one. The bond distances are of the reverse order. The interaction between the imidazole and ZnO clusters is dominated by the hybridization between d-orbitals of zinc and nitrogen atoms and this determines the strength of interaction imidazole with ZnO. Adsorption of the imidazole on the ZnO clusters modifies the electronic properties of the ZnO clusters and the HOMO–LUMO analysis confirms the occurrence of charge transfer. Mulliken charge distribution shows that zinc atom exhibits more positive charge and the azomethine nitrogen atom exhibits a more negative charge. These two atoms form the weak interaction of Zn–N bond (N-site) in imidazole–ZnO composite. The calculation reveals that reduction in the energy gap for imidazole–ZnO composite when compared to bare ZnO and imidazole and Zn₉O₉ cluster less prefers the 2D ring geometry whereas the larger cluster with n = 10 is stabilized in 3D structure; ring to cage structural cross over takes place between Zn₉O₉ and Zn₁₀O₁₀ clusters.

Acknowledgements

One of the authors Prof. J. Jayabharathi is thankful to DST (no. SR/S1/IC73/2010), DRDO (NRB-213/MAT/10-11) and CSIR (no. 3732/NS-EMRII) for providing funds to this research study.

References

1. (a) L. Vayssieres, K. Keis, A. Hagfeldt and S. E. Lindquist, Chem. Mater., 2001, 13, 4395; (b) J. A. Rodriguez, T. Jirsak, J. Dvorak, S. Sambasivan and D. Fischer, J. Phys. Chem. B, 2000, 104, 319.
2. (a) M. Bruchez Jr, M. Moronne, P. Gin, S. Weiss and A. P. Alivisatos, Science, 1998, 281, 2013; (b) I. L. Medintz, H. T. Uyeda, E. R. Goldman and H. Mattoussi, Nat. Mater., 2005, 4, 435; (c) A. R. Clapp, I. L. Medintz, J. M. Mauro, B. R. Fisher, M. G. Bawendi and H. Mattoussi, J. Am. Chem. Soc., 2004, 126, 301; (d) B. P. Aryal and D. E. Benson, J. Am. Chem. Soc., 2006, 128, 15986.
3. P. D. Beer and P. A. Gale, Angew. Chem., Int. Ed., 2001, 40, 486.
4. A. Nel, T. Xia, L. Mädler and N. Li, Science, 2006, 311, 622.
5. S. Rakshit and S. Vasudevan, J. Phys. Chem. C, 2008, 112, 4531.
6. D. S. Bohle and C. J. Spina, J. Am. Chem. Soc., 2007, 129, 12380.
7. H. M. Xiong, Y. Xu, Q. G. Ren and Y. Y. Xia, J. Am. Chem. Soc., 2008, 130, 7522.
8. H. Wang, D. Wingett and M. H. Engelhard, J. Mater. Sci.: Mater. Med., 2009, 20, 11.
9. S. Dhobale, T. Thite and S. L. Laware, J. Appl. Phys., 2008, 104, 094907.
10. C. Hanley, J. Layne and A. Punnoose, Nanotechnology, 2008, 19, 295103.
11. K. M. Reddy, K. Feris, J. Bell, D. G. Wingett, C. Hanley and A. Punnoose, Appl. Phys. Lett., 2007, 90, 213902.
12. A. S. Barnard, Nat. Nanotechnol., 2010, 5, 271.
13. J. Musarrat, Q. Saquib, A. Azam and S. A. H. Naqvi, Int. J. Nanopart., 2009, 2, 402.
14. T. Thomas, K. Thomas, N. Sadrieh, N. Savage, P. Adair and R. Bronaugh, Toxicol. Sci., 2006, 91, 14.
15. K. Schilling, B. Bradford, D. Castelli, E. Dufour, J. F. Nash, W. Pape, S. Schulte, I. Tooley, J. Bosch and F. Schellauf, Photochem. Photobiol. Sci., 2010, 9, 495.
16. (a) R. Jurgons, C. Seliger, A. Hilpert, L. Trahms, S. Odenbach and C. Alexiou, J. Phys.: Condens. Matter, 2006, 18, S2893; (b) A. E. Dunn, D. J. Dunn, M. Lim, C. Boyer and N. T. K. Thanh, Nanoscience, 2013, 2, 225; (c) Z. Yuanbi, Q. Zumin and H. Jiaying, Chin. J. Chem. Eng., 2008, 16, 451; (d) M. Shao, L. Yan, H. Pan, I. Ivanov and B. Hu, Adv. Mater., 2011, 23, 2216; (e) Y. Xie, M. Gong, T. A. Shastry, J. Lohrman, M. C. Hersam and S. Ren, Adv. Mater., 2013, 25, 3433; (f) H. B. Radousky and H. Liang, Nanotechnology, 2012, 23, 502001.
17. A. Mallick, S. C. Bera, S. Maiti and N. Chattopadhyay, Biophys. Chem., 2004, 112, 9.
18. (a) V. Shewale, P. Joshi, S. Mukhopadhyay, M. Deshpande, R. Pandey, S. Hussain and S. P. Karna, J. Phys. Chem. C, 2011, 115, 10426; (b) G. Li, J. Li, C. Zhang, Y. Hu, X. Li, J. Chu, W. Huang and D. Wu, J. Phys. Chem. C, 2009, 113, 21338; (c) K. Kotsis and V. Staemmler, Phys. Chem. Chem. Phys., 2006, 8, 1490; (d) J. M. Matxain, J. E. Fowler and J. M. Ugalde, Phys. Rev. A, 2000, 62, 053201; (e) R. Steudel, Y. Steudel and M. W. Wong, Chem.–Eur. J., 2008, 14, 919; (f) N. Rossler, K. Kotsis and V. Staemmler, Phys. Chem. Chem. Phys., 2006, 8, 697; (g) M. Zhao, Y. Xia, Z. Tanb, X. Liu and L. Mei, Phys. Lett. A, 2007, 372, 39; (h) C. Wang, S. Xu, L. Ye, W. Lei and Y. Cui, J. Mol. Model., 2011, 17, 1075; (i) F. D. Angelis and L. Armelao, Phys. Chem. Chem. Phys., 2011, 13, 467; (j) X. Cheng, F. Li and Y. Zhao, J. Mol. Struct.: THEOCHEM, 2009, 894, 121; (k) A. Choudhury, S. Neeraj, S. Natarajan and C. N. R. Rao, Dalton Trans., 2002, 1535.
19. A. K. Jissy and A. Datta, J. Phys. Chem. Lett., 2014, 5, 154.
20. T. Wang, Y. Hu, L. Zhang, L. Jiang, Z. Chen and N. Y. He, Nano Biomed. Eng., 2010, 2, 31.
21. S. H. Chen, Y. X. Ji, Q. Lian, Y. L. Wen, H. B. Shen and N. Q. Jia, Nano Biomed. Eng., 2010, 2, 15.
22. S. L. Bechara, A. Judson and K. C. Popat, Biomaterials, 2010, 31, 3492.
23. Y. Q. Li, Z. Y. Li, X. P. Zhou and P. Yang, Nano Biomed. Eng., 2010, 2, 24.
24. V. Shewale, P. Joshi, S. Mukhopadhyay, M. Deshpande, R. Pandey, S. Hussain and S. P. Karna, J. Phys. Chem. C, 2011, 115, 10426.
25. P. Joshi, V. Shewale, R. Pandey, V. Shanker, S. Hussain and S. P. Karna, Phys. Chem. Chem. Phys., 2011, 13, 476.
26. (a) C. Karunakaran, J. Jayabharathi and K. Jayamoorthy, Spectrochim. Acta, Part A, 2013, 114, 303; (b) C. Karunakaran, J. Jayabharathi and K. Jayamoorthy, Spectrochim. Acta, Part A, 2013, 112, 417; (c) C. Karunakaran, J. Jayabharathi, R. Sathishkumar and K. Jayamoorthy, Spectrochim. Acta, Part A, 2013, 110, 151; (d) C. Karunakaran, J. Jayabharathi, M. Venkatesh Perumal, V. Thanikachalam and P. K. Thakur, J. Phys. Org. Chem., 2013, 26, 386; (e) C. Karunakaran, J. Jayabharathi and K. Jayamoorthy, Sens. Actuators, B, 2013, 182, 514; (f) C. Karunakaran, J. Jayabharathi, R. Sathishkumar and K. Jayamoorthy, J. Lumin., 2013, 138, 235; (g) C. Karunakaran, J. Jayabharathi, K. Jayamoorthy and P. Vinayagamoorthy, J. Mol. Liq., 2013, 177, 295; (h) C. Karunakaran, J. Jayabharathi, K. Jayamoorthy and P. Vinayagamoorthy, J. Photochem. Photobiol., A, 2012, 247, 16; (i) C. Karunakaran, J. Jayabharathi, K. Jayamoorthy and K. Brindha Devi, Sens. Actuators, B, 2012, 168, 263; (j) C. Karunakaran, J. Jayabharathi, K. Jayamoorthy and K. Brindha Devi, J. Fluoresc., 2012, 22, 1047; (k) C. Karunakaran, J. Jayabharathi, K. Jayamoorthy and K. Brindha Devi, Spectrochim. Acta, Part A, 2012, 89, 187; (l) R. R. Gange, C. A. Koval and G. C. Lisensky, Inorg. Chem., 1980, 19, 2854.
27. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery Jr, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, and J. A. Pople, Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford CT, 2004.
28. L. Cyril, J. K. Earl and W. M. Sperry, Biochemists' Handbook, E. & F. N. Spon, London, 1961, p. 84.
29. J. Hou, L. Huo and C. He, Macromolecules, 2006, 39, 594.
30. (a) H. M. Cheng and W. F. Hsich, Nanotechnology, 2010, 21, 485202; (b) B. Lin, Z. Fu and Y. Jia, Appl. Phys. Lett., 2001, 79, 943.
31. (a) A. Paul, P. K. Mandal and A. Samanta, J. Phys. Chem. B, 2005, 109, 9148; (b) H. M. Cheng and W. F. Hsich, Nanotechnology, 2010, 21, 485202; (c) A. Kar, S. Kundu and A. Patra, J. Phys. Chem. C, 2011, 115, 118.
32. G. J. Kavarnos and N. J. Turro, Chem. Rev., 1986, 86, 401.
33. P. Ramamurthy, S. Parret, F. M. Savary and J. P. Fouassier, J. Photochem. Photobiol., A, 1994, 83, 205.
34. K. Kikuchi, T. Niwa, Y. Takahashi, H. Ikeda and T. Miyashi, J. Phys. Chem., 1993, 97, 5070.
35. J. Jayabharathi, V. Thanikachalam, M. Venkatesh Perumal and N. Srinivasan, J. Fluoresc., 2012, 22, 409.
36. (a) X. Wang, R. Zhang, C. Wu, Y. Dai, M. Song, S. Gutmann, F. Gao, G. Lv, J. Li, X. Li, Z. Guan, D. Fu and B. Chen, J. Biomed. Mater. Res., Part A, 2007, 80, 852; (b) S. Saha and P. Sarkar, Phys. Chem. Chem. Phys., 2014, 16, 15355.
37. (a) C. Arunagiri, A. Subashini, M. Saranya and P. T. Muthiah, Indian J. Pure Appl. Phys., 2013, 3, 78; (b) A. V. Kachynski, A. N. Kuzmin, M. Nyk, I. Roy and P. N. Prasad, J. Phys. Chem. C, 2008, 112, 10721.
38. B. Wang, S. Nagase, J. Zhao and G. H. Wang, J. Phys. Chem. C, 2007, 111, 4956.
39. C. Li, W. Guo, Y. Kong and H. Gao, Appl. Phys. Lett., 2007, 90, 223102.
40. A. Jain, V. Kumar and Y. Kawazoe, Comput. Mater. Sci., 2006, 36, 258.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra15957h

---