Ridges and valleys on charged 1T-MoS₂ sheets guiding the packing of organic cations

Abstract

Using a novel powder X-ray pattern refinement technique, DFT calculations and TEM, we reveal for the first time the three-dimensional structure of hybrid (R₄N)_xMoS₂ layered compounds. Both the precise coordinates of Mo and S atoms in the inorganic layer and the preferred positions of the organic cations relative to them are reported. The distorted geometry of the MoS₂ sheet is found to be the driving force behind the arrangement of cations within the organic layers. The refined atomic coordinates, confirmed by periodic DFT modeling, show octahedral Mo atoms arranged in zigzag chains and the S atoms following the Mo ones, forming “ridges” and “valleys” on the sheet surface. The size of alkylammonium cations is compatible with these valleys, leading to a strong preferred arrangement: the cations exclusively occupy the space between the ridges. This result allows predicting the layer structure and ultimately the composition of the hybrid compound depending on the cation structure. The reported features of the MoS₂ surface are important for understanding of MoS₂-based sensors and hybrid flexible conductors, both relying on charged sheets of MoS₂.

---

1. Introduction

Molybdenum disulfide is an important graphene analog demonstrating semiconducting properties both in bulk¹ and as single layers.²

A single layer of molybdenum disulfide consists of fused MoS₆ polyhedra forming a flat, three atom thick S–Mo–S sandwich.³ Like graphene, these 2D sheets, both monolayerly thin^2,4 or assembled in few-layer particles,^5,6 are considered particularly important components for future nanoelectronic devices,^2,4,6 sensors,^7,8 and electrocatalysts.⁹ Chemical modification of 2D materials like graphene or molybdenum disulfide due to their non-covalent interactions with donor or acceptor molecules is a promising route to fine-tuning their properties for different applications.^6,7,10–12

The unique feature of the MoS₂ layers is the susceptibility of their atomic structure and properties to negative charge transferred onto layers. This charge induces atomic rearrangements^13–17 and changes behavior of the resulting material from semiconducting to metallic.^17–19 The process is usually referred as “2H to 1T phase transition”, but the actual rearrangement may involve at least three separate transitions between structurally distinct phases.²⁰ Several MoS₂ forms were also directly observed in metal-doped MoS₂ under the beam of electronic microscope.²¹ The fully lithiated MoS₂ displays a octahedral modification with Mo atoms organized in ‘diamond’ formation,¹⁵ while Na_xMoS₂ exhibits 2H, 1T and several 1T-based modulated phases depending on the value of x.²²

Still, the detailed structural studies in the literature are limited to purely inorganic systems. As for MoS₂–organic intercalation compounds, the form of MoS₂ and the arrangement of the cations relative to the inorganic layers remain unknown and their elucidation is the main goal of this manuscript.

Hybrid MoS₂-based heterostructures where organic cationic species^16,23–26 (B⁺) are sandwiched between negatively charged sulfide layers are prepared by using the negatively charged MoS₂ sheets as building blocks in self-assembly process (eqn (1)). The resulting particles are 2–10 layers thick.^24,25

The hybrid (B⁺)_x(MoS₂)^x− compounds with alkylammonium cations easily form flexible conductive films.^23,24 As intermediates, they find use in preparation of various mesoporous MoS₂-based materials.^27,28

Studies of similar substances by XRD, EXAFS,^14,16 PDF,¹⁵ TEM,^17,29 electron diffraction^18,29 together with quantum-chemical calculations^30,20 revealed that rearrangements of S–Mo–S network induced by the charge transfer lead to formation of molybdenum zigzag chains and probably change the MoS₆ polyhedra from trigonal prisms (neutral layers) to octahedra (negatively charged layers). However, to the best of our knowledge, structures of hybrid MoS₂–organic layered compounds have been neither resolved at the atomic level by any method nor successfully modeled using quantum-chemical approaches.

The obvious method for determination of the 3D structure of a substance is X-ray diffraction. Unfortunately, the MoS₂-based hybrid compounds do not form single crystals, and their powder XRD patterns contain very few sharp peaks required for typical Rietveld refinement. The usually reported and easily measurable 00l reflections provide only the periodicity in the direction normal to the sulfide sheets and reveal neither the actual positions of the guest molecules between MoS₂ layers nor the exact MoS₂ layer structure. However, the modern developments in the X-ray diffraction theory allow going beyond sharp peaks in the analysis of the powder patterns. The aim of the current study was to extract novel structural information from the full powder patterns of hybrid MoS₂ materials.

The tetramethyl- and tetraethylammonium layered salts (Me₄N)_0.25MoS₂ and (Et₄N)_0.15MoS₂, further referred to as TM and TE respectively, were chosen for detailed study due to their reproducible composition and symmetric guest moiety.

2. Results and discussion

2.1. Structural studies

The diffraction patterns of TM and TE are visually similar, consisting of strong symmetric 00l lines and broad reflections of different origin (Fig. 1). The strong 00l lines indicate that the studied compounds are indeed three-dimensional, and not monolayerly thin.³¹ Besides the reflections in 2θ > 30 region, both patterns contain a weak peak at ≈15.5° 2θ, which does not change position despite the difference in interlayer (00l) distance (11.1733(2) Å in TE and 11.0620(3) Å in TM). This peak, along with other non-00l peaks in the patterns, was indexed in pg plane group with a = 5.6991(12) and b = 3.2001(10) Å (see ESI for details†). These values, corresponding approximately to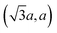 , where a is the unit cell parameter of crystalline¹⁵ 2H-MoS₂, indicate the presence of the 2 × 1 supercell often found³² in charged MoS₂ layers. More notable is the complete absence of the hkl peaks; along with the asymmetric shape of the “plane group” peaks, it indicated that the materials are turbostratically disordered in a manner similar to clays or carbon black.³³ In these structures, layers can move and rotate freely against each other, the hkl peaks disappear, and the hk0 peaks become hk diffraction bands, while the diffraction along the 00l direction still shows normal Bragg reflections.

Fig. 1 The fit of TE (a) and TM (b) powder patterns using the approach outlined in 4.2. Refinement model. Diffraction bands are labeled in red, stars denote the independently refined peaks, and ticks label the 00l and hk0 positions.

There have been reports^34–36 of quantifying the mixtures containing similarly disordered clays using a specially created supercell with scaled reflection intensities to represent the clay phase. In this work, we repurposed this approach for true structure refinement of the (R₄N)_xMoS₂ structure, both of the MoS₂ sheet and of the organic layer, simultaneously including the sharp 00l peaks and wide hk bands in the fit (see 4.2. Refinement model). To our knowledge, the current work is the first application of this model to MS₂ structures or to any system except clays. The main advantage before the more commonly³⁷ used Debye formula modeling is the possibility of direct least squares refinement of the studied structure.

Initially, atomic positions from 2H-MoS₂ were used as starting coordinates for the refinement of the inorganic layer geometry. The models for both TM and TE converged to similar distorted layer structures with zigzag ordering of the Mo atoms, but the unusually close S⋯S distances and unsatisfying fit led to rejection of this model (see ESI for refinement details†).

Thus, we assumed octahedral¹⁴ coordination of Mo atoms (called 1T-MoS₂ in the case of the exotic³⁸ bulk crystalline species). The crystal structure of pure 1T-MoS₂ has never been published, so we started the refinement with sulfur atoms approximately shifted to octahedral positions. It led to a reasonable structural model with a significantly better fit (TE R_wp of 4.339 as compared to 5.762 in the distorted prismatic model).

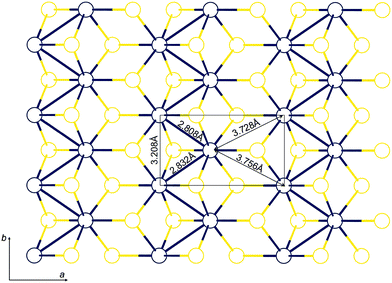
The main features of the resulting structure, distinguishing it from the idealized octahedral one, are zigzag chains of the Mo atoms (Fig. 2) and pronounced displacement of the sulfur atoms (Fig. 3): the S atoms bound to only one Mo chain form ‘ridges’, and sulfur atoms linking two different chains form ‘valleys’ between. These S–S–S valleys are ≈0.5 Å deep, and their effective width matches one of a CH₂ group (see Fig. 3). As an external check, the refined Mo–Mo distances for TM (Table 1) agreed well with the EXAFS data reported in the literature¹⁶ (3.76 Å, 3.15 Å, 2.77 Å). Also this structure is in line with published quantum-chemical calculations³² indicating that the removal of Li from fully-lithiated MoS₂ leads to metastable ZT-MoS₂ with similar arrangement of atoms, since TM is produced via LiMoS₂.

Fig. 2 The MoS₂ layer structure of TE in the distorted octahedral model (final), view in the c direction. Rectangle denotes the refined supercell, Mo–Mo distances are labeled. Et₄N cation is omitted for clarity.

Fig. 3 TM structure, view in the b direction. The spacefill model represents the van der Waals radii of the corresponding elements.

Table 1 The summary of TM and TE final refinements in the distorted octahedral model

	TE	TE calculated^a	TM	DE
a Values provided are averaged over the 3 × 3 × 1 supercell used in the computation.b Calculated as zSridge − zSvalley.
Composition	(Et4N)0.15MoS2	(Et4N)1/6MoS2	(Me4N)0.25MoS2	(Et2NH2)0.16MoS2
a, Å	5.6924(5)	5.6924	5.6925(5)	5.7098(13)
b, Å	3.2083(3)	3.2083	3.2126(3)	3.2187(8)
c, Å	11.168(4)	11.168	11.096(5)	10.017(7)
Rbragg, %	1.380	—	1.714	1.944
Rwp, %	4.507	—	3.542	4.543
Mo–Mo distances, Å	2.808(7)	2.835	2.789(6)	2.852(6)
	2.832(8)	3.220	2.800(6)	2.873(6)
	3.2083(3)	3.753	3.2126(3)	3.2187(8)
	3.737(6)		3.762(4)	3.715(5)
	3.756(6)		3.771(4)	3.731(5)
Mo–Mo–Mo, °	69.35(4)	69.1	70.2(2)	68.42(5)
Mo–S, Å	2.400(5)	2.441	2.400(5)	2.400(5)
Valley depth^b, Å	0.527(5)	0.385	0.561(3)	0.548(5)

---

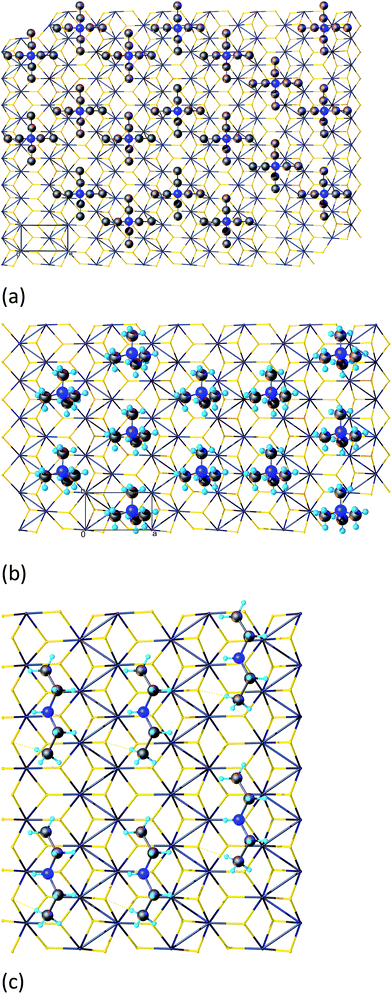
Along with the MoS₂ layer geometry, the refinement revealed the coordinates of the organic moiety within the unit cell: both in TM and TE, organic cations lie in the valleys between the Mo–Mo zigzags. The least squares procedure provided only approximate average occupancies of organic moiety due to correlations with Debye–Waller factor. To obtain precise occupancies and further insight into organic layer structure, we studied possible layer packings by placing maximum number of cations into refined positions on the MoS₂ sheet while avoiding collisions (Fig. 4).

Fig. 4 Example organic layer packing without long-range ordering, generated by expanding experimental unit cells (black rectangle) and randomly removing colliding cations, for TE (a), TM (b) and DE (c). Hydrogen atoms in TE are omitted for clarity.

As we found out, the idealized composition of the organic layers can be estimated by counting the amount of cations fitting in the valleys without violation of the typical intermolecular distances. Optimal C⋯C contact distance between tetraalkylammonium cations is 3.2 Å according to CSD,³⁹ allowing one cation per two unit cells in TM and one per three in TE (Fig. 4). Each unit cell contains two Mo atoms and four S, predicting R₄N/MoS₂ ratio of 0.17 for TE and 0.25 for TM, equal to the experimental composition within the precision of the chemical analysis. The tetraethylammonium cation is large enough to restrict cation placement not only in its “own” valley, but also in the neighboring ones; still, a favorable diagonal arrangement resulting in complete filling of all valleys is possible. It should be noted that above rules define only the local ordering and do not impose any additional long-range periodicity, as can be seen on Fig. 4.

Analysis of TM and TE strongly suggests that the structure of the organic layer is determined by the ridges and valleys on MoS₂ surface and not simply by dense packing of the cations in a given space between “flat” MoS₂ sheets. This hypothesis was checked by preparing the salt of diethylammonium cation and MoS₂ (DE) and analyzing its composition and structure. Indeed, the Et₂NH₂⁺ cation has the same atom count and volume as Me₄N⁺, so we could expect a composition with 0.25 cations per MoS₂ formula unit in the case of dense packing of the organic layer. The diethylammonium cation, however, should occupy the same space as Et₄N⁺ when fitted within a MoS₂ valley, leading to maximum 1/6 cations per MoS₂ if these valleys play the major role. The experimental composition, with 0.16 cations per MoS₂ unit, supports the latter model.

The fit of the DE experimental powder pattern using the same method as TE and TM (see ESI†) also confirms that the linear Et₂NH₂⁺ fragments occupy the space in the valleys of distorted 1T-MoS₂.

2.2. DFT modeling and bonding analysis

In order to verify the refined geometry and quantify the cation–MoS₂ and cation–cation interactions, we aimed to model the hybrid MoS₂ system using ab initio calculations with periodic boundary conditions. The practically feasible computation methods are unsuitable for turbostratically disordered structures, so we constructed an ordered, 3D periodic model to approximate the experimental data using plane wave-based periodic DFT.

Due to the interactions between cations in neighboring valleys, the cation layer packing in TE is the most ordered among the studied compounds. This fact allowed assembling a reasonable periodic approximation of the refined structure using only the [X + 1, Y + 1, Z] operation to fit the cation rows together and ignoring the turbostratic disorder (see ESI† for computational details). This very simplified model still reproduced the experimental Mo layer geometry, including the ridges and valleys, with high precision; the difference in refined and calculated bond lengths was similar to one usually achieved for calculations based on experimental single crystal data (Table 1).

The calculated structure was additionally studied using the R.F.W. Bader's quantum theory of atoms in molecules (QTAIM).⁴⁰ This theory reveals bonding interactions and charge transfer using topological analysis of the total electron density ρ(r). In addition, the energy of weak interactions can be estimated using Esminosa–Molins–Lecomte (EML) correlations initially developed for weak hydrogen bonds^41–43 but further applied to a wide range of interactions,⁴⁴ including those in 2H-MoS₂.⁴⁵

Each cation forms on average 18 S⋯H contacts with the MoS₂ layers, totaling 18.0 kcal mol⁻¹ of interaction energy, and 13 H⋯H contacts with neighboring cations, for 18.2 kcal mol⁻¹ total (Table 2). Thus the interactions within the organic layer are of similar importance for the formation of the structure as the interlayer ones, explaining the stable stoichiometry of MoS₂ hybrid compounds. The organic cations also stabilize the MoS₂ layer by charge transfer (0.17e per cation, measured by integration of ρ(r) over the QTAIM atomic basins). Indeed, excess LiMoS₂ in the reaction mass leads to a two-phase system containing hybrid layered compound and 2H-MoS₂ instead of a single hybrid phase with lowered organic content.

Table 2 Summary of average critical point properties (a.u.) in the 3 × 3 × 1 supercell of hypothetical ordered TE, according to PW-PBE-d modeling

		Count	d, Å	ρ(r)	∇^2ρ(r)	ge(r)	ve(r)	he(r)	EEML, kcal mol^−1
Mo	S	36	2.398	0.096	0.176	0.087	−0.130	−0.043	−40.6
Mo	S	36	2.433	0.090	0.157	0.078	−0.118	−0.039	−36.9
Mo	S	36	2.492	0.082	0.132	0.066	−0.100	−0.033	−31.2
Mo	Mo	18	2.835	0.057	0.087	0.039	−0.056	−0.017	−17.5
H	S	54	3.065	0.007	0.020	0.004	−0.003	0.001	−1.0
H	H	39	2.447	0.008	0.028	0.006	−0.004	0.001	−1.4

---

2.3. Transmission electron microscopy studies

The TE compound, as the most stable one of the studied, was additionally examined using TEM. In agreement with the powder diffraction data, most particles of the material are turbostratically disordered, leading to HRTEM images in the basal projection similar to Fig. 5. This came as a major limitation in our study, meaning that we could analyze only periodic or single-layer fragments in detail, without guarantee that their structure was similar to the bulk of the material: average thickness of the diffracting particles estimated by powder diffraction exceeds 200 nm (20 MoS₂ layers).

Fig. 5 The TEM image of a turbostratically disordered TE particle (basal projection) and its FFT (on the right).

This problem of representativeness of basal projections of these particles became obvious during the examination of the visibly ordered images. The particles fell into two groups: purely hexagonal ones with period of 2.7 Å (see ESI, Fig. S2†) and those with grouping of the spots in twin rows, corresponding to a superperiod of ≈5.75 Å (Fig. 7d). The former can be attributed to 2H-MoS₂ while the latter can only be modeled using the layer structure obtained from XRD data (Fig. 7b and c).

Fig. 6 The TEM image of the side projection of TE and FFT transforms of its fragments with corresponding period values.

Fig. 7 The HRTEM image for a particle with a superperiod (a), its magnified fragment (b) and contrast function simulated from the TE distorted octahedral structural model (c) (modeling parameters: lens defocussing of 63.0 nm, crystal thickness of 28.6 nm); FFT from selected area on “a” (the reflections d₂₀₀ = 0.27 nm and d₁₀₀ = 0.55 nm for TE are labeled).

The powder patterns of TE show no presence of 2H-MoS₂. However, according to previous studies, heating of exfoliated–restacked MoS₂ to 400 K in vacuum leads to 2H-MoS₂ phase,^46,17 and processes of degradation for intercalated MoS₂ particles were observed in the MoS₂—long-chain alkylammonium system under electronic beam.²⁵

The FFT processing of the TEM side projections of the studied particles provides d₀₀₁ distances ranging from 9.16 Å to 11.66 Å (Fig. 6). The mean c-value obtained by refinement of XRD patterns (11.168 Å) lies near the upper end of this range.

The TEM results confirm the presence of hybrid layered compound and of MoS₂ layers showing distorted octahedral structure among the particles of TE. Still, we cannot exclude the possibility that this structure coexists with the prismatic modification similar to 2H-MoS₂, at least in the few-layer samples subjected to electronic irradiation in the microscope. Recently, coexistence of the domains with 1T (octahedral) and 2H (trigonal prismatic) modifications was revealed in TEM studies of MoS₂ layers obtained by removal of Li from LiMoS₂ (ref. 17) or partial lithiation.³²

3. Experimental

3.1. Materials synthesis

Layered compounds of MoS₂ with tetramethyl-, tetraethyl- and diethylammonium cations were obtained according to procedure described elsewhere.⁴⁷ Experimental details of synthese, TEM and powder X-ray diffraction measurements are presented in the ESI.†

3.2. Refinement model

For structure refinement of PXRD patterns of TM, TE and DE we applied the X. Wang implementation^35,36 for TOPAS 4.2 (ref. 48) of the “supercell approach” developed by K. Ufer et al.³⁴ This model relies on the similarity between diffraction from single layers and turbostratically disordered structures. It describes the hk rods and the outline of the corresponding hk0 diffraction bands in the powder pattern by a periodic unit cell of a special form: a “virtual” supercell elongated by a factor N ≥ 10 in the stacking direction, containing one unit cell of the hypothetical ordered structure and N − 1 empty unit cells. After removing the 00l reflections with l ≢ 0 (mod N) and scaling the intensity of the remaining 00l reflections by N, the model provides a simultaneous description of the hk0 bands and 00l peaks.

It is important to state explicitly that shifts and rotations of the layers against each other are not refined and are not even present in the model, assuming a complete absence of positional correlation. The refinement details regarding the line broadening functions, preferred orientation correction and Mo–S restraints can be found in the ESI.†

4. Conclusion

Both the MoS₂ sheet structure and the positions of organic cations in MoS₂–organic hybrid materials were reconstructed from powder X-ray diffraction patterns of these turbostratically disordered compounds. The refinement results were verified by periodic DFT calculations and confirmed by TEM.

The studied compounds demonstrate distorted octahedral (1T) geometry of the MoS₂ sheets, with 2 × 1 orthorhombic supercell as a repeating unit and Mo atoms forming zigzag chains.

The important new feature compared to previously reported structures of similar materials are the displacements of the sulfur atoms: the S atoms above Mo zigzags form ‘ridges’ and between these ridges lie ‘valleys’ 0.5 Å deep. Most notably, the width of the ‘valleys’ is complementary for a CH₂ or a CH₃ group, leading to organic cations packing exclusively in the valleys. This preference is the main cause behind the composition of the studied materials: the amount of cations per MoS₂ unit in the organic layer is determined not by dense packing of the organic cations, but by the amount of the cations fitting in the valley. At the same time, the space above ‘ridges’ is strongly unfavorable for cation placement. This result has strong implications for the surface chemistry of 1T-MoS₂ and materials based on it, such as sensors and flexible conductors. By taking into account the uneven surface of the charged 1T-MoS₂ sheet one can predict both the composition of the surface layer and the preferential placement of molecules in it.

The approach used to obtain and verify the discussed structures can reveal previously inaccessible structural features and thus can be useful for studies of similar inorganic–organic compounds with loosely coupled layers, based on metal dichalcogenides, graphene, BN etc.

Acknowledgements

This work was supported by Russian Foundation for Basic Research (RFBR) grants 12-03-00878 “A”, 14-03-00287 “A” and 13-03-12197 “ofi-m”.

References

1. T. Böker, R. Severin, A. Müller, C. Janowitz, R. Manzke, D. Voß, P. Krüger, A. Mazur and J. Pollmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 235305.
2. K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Phys. Rev. Lett., 2010, 105, 136805.
3. R. G. Dickinson and L. Pauling, J. Am. Chem. Soc., 1923, 45, 1466–1471.
4. D. Lembke and A. Kis, ACS Nano, 2012, 6, 10070–10075.
5. H. S. S. Ramakrishna Matte, A. Gomathi, A. K. Manna, D. J. Late, R. Datta, S. K. Pati and C. N. R. Rao, Angew. Chem., 2010, 122, 4153–4156.
6. M. M. Perera, M.-W. Lin, H.-J. Chuang, B. P. Chamlagain, C. Wang, X. Tan, M. M.-C. Cheng, D. Tománek and Z. Zhou, ACS Nano, 2013, 7, 4449–4458.
7. F. K. Perkins, A. L. Friedman, E. Cobas, P. M. Campbell, G. G. Jernigan and B. T. Jonker, Nano Lett., 2013, 13, 668–673.
8. C. Zhu, Z. Zeng, H. Li, F. Li, C. Fan and H. Zhang, J. Am. Chem. Soc., 2013, 135, 5998–6001.
9. D. Voiry, M. Salehi, R. Silva, T. Fujita, M. Chen, T. Asefa, V. B. Shenoy, G. Eda and M. Chhowalla, Nano Lett., 2013, 13, 6222–6227.
10. Q. Su, S. Pang, V. Alijani, C. Li, X. Feng and K. Müllen, Adv. Mater., 2009, 21, 3191–3195.
11. Y. Li, C.-Y. Xu, P. Hu and L. Zhen, ACS Nano, 2013, 7, 7795–7804.
12. D. Kiriya, M. Tosun, P. Zhao, J. S. Kang and A. Javey, J. Am. Chem. Soc., 2014, 136, 7853–7856.
13. M. A. Py and R. R. Haering, Can. J. Phys., 1983, 61, 76–84.
14. R. A. Gordon, D. Yang, E. D. Crozier, D. T. Jiang and R. F. Frindt, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 125407.
15. V. Petkov, S. J. L. Billinge, P. Larson, S. D. Mahanti, T. Vogt, K. K. Rangan and M. G. Kanatzidis, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 092105.
16. Y. V. Zubavichus, A. S. Golub, N. D. Lenenko, Y. N. Novikov, Y. L. Slovokhotov and M. Danot, J. Mol. Catal. A: Chem., 2000, 158, 231–236.
17. G. Eda, T. Fujita, H. Yamaguchi, D. Voiry, M. Chen and M. Chhowalla, ACS Nano, 2012, 6, 7311–7317.
18. J. Heising and M. G. Kanatzidis, J. Am. Chem. Soc., 1999, 121, 11720–11732.
19. R. Kappera, D. Voiry, S. E. Yalcin, B. Branch, G. Gupta, A. D. Mohite and M. Chhowalla, Nat. Mater., 2014, 13, 1128–1134.
20. M. Kan, J. Y. Wang, X. W. Li, S. H. Zhang, Y. W. Li, Y. Kawazoe, Q. Sun and P. Jena, J. Phys. Chem. C, 2014, 118, 1515–1522.
21. Y.-C. Lin, D. O. Dumcenco, Y.-S. Huang and K. Suenaga, Nat. Nanotechnol., 2014, 9, 391–396.
22. X. Wang, X. Shen, Z. Wang, R. Yu and L. Chen, ACS Nano, 2014, 8, 11394–11400.
23. V. Sánchez, E. Benavente, M. A. Santa Ana and G. González, Chem. Mater., 1999, 11, 2296–2298.
24. H. Tachibana, Y. Yamanaka, H. Sakai, M. Abe and M. Matsumoto, Chem. Mater., 2000, 12, 854–856.
25. N. D. Lenenko, E. N. Semina, V. I. Zaikovskii and A. S. Golub, Mater. Chem. Phys., 2013, 141, 35–41.
26. G. Cetnarowski and G. W. Leach, Langmuir, 2006, 22, 8995–9001.
27. B. A. Vanchura, P. He, V. Antochshuk, M. Jaroniec, A. Ferryman, D. Barbash, J. E. Fulghum and S. D. Huang, J. Am. Chem. Soc., 2002, 124, 12090–12091.
28. L. F. Flores-Ortiz, M. A. Cortés-Jácome, C. Ángeles-Chávez and J. A. Toledo-Antonio, Sol. Energy Mater. Sol. Cells, 2006, 90, 813–824.
29. A. S. Golub, V. I. Zaikovskii, N. D. Lenenko, M. Danot and Y. N. Novikov, Russ. Chem. Bull., 2004, 53, 1914–1923.
30. X. Rocquefelte, F. Boucher, P. Gressier, G. Ouvrard, P. Blaha and K. Schwarz, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 2397–2400.
31. H. S. S. R. Matte, U. Maitra, P. Kumar, B. Govinda Rao, K. Pramoda and C. N. R. Rao, Z. Anorg. Allg. Chem., 2012, 638, 2617–2624.
32. L. Wang, Z. Xu, W. Wang and X. Bai, J. Am. Chem. Soc., 2014, 136, 6693–6697.
33. B. E. Warren, Phys. Rev., 1941, 59, 693–698.
34. K. Ufer, G. Roth, R. Kleeberg, H. Stanjek, R. Dohrmann and J. Bergmann, Z. Für Krist. J. Struct. Phys. Chem. Asp. Cryst. Mater., 2004, 219, 519–527.
35. X. Wang, J. Li, R. D. Hart, A. van Riessen and R. McDonald, J. Appl. Crystallogr., 2011, 44, 902–910.
36. X. Wang, R. D. Hart, J. Li, R. G. McDonald and A. van Riessen, J. Appl. Crystallogr., 2012, 45, 1295–1302.
37. L. Houben, A. N. Enyashin, Y. Feldman, R. Rosentsveig, D. G. Stroppa and M. Bar-Sadan, J. Phys. Chem. C, 2012, 116, 24350–24357.
38. F. Wypych and R. Schöllhorn, J. Chem. Soc., Chem. Commun., 1992, 1386.
39. F. Allen, Acta Crystallogr., Sect. B: Struct. Sci, 2002, 58, 380–388.
40. R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, USA, 1994.
41. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
42. E. Espinosa, C. Lecomte and E. Molins, Chem. Phys. Lett., 1999, 300, 745–748.
43. E. Espinosa and E. Molins, J. Chem. Phys., 2000, 113, 5686.
44. K. A. Lyssenko, Mendeleev Commun., 2012, 22, 1–7.
45. N. G. Naumov, A. A. Korlyukov, D. A. Piryazev, A. V. Virovets and V. E. Fedorov, Russ. Chem. Bull., 2013, 62, 1852–1857.
46. A. S. Goloveshkin, I. S. Bushmarinov, N. D. Lenenko, M. I. Buzin, A. S. Golub and M. Y. Antipin, J. Phys. Chem. C, 2013, 117, 8509–8515.
47. A. S. Golub, Y. V. Zubavichus, Y. L. Slovokhotov, Y. N. Novikov and M. Danot, Solid State Ionics, 2000, 128, 151–160.
48. Bruker, TOPAS 4.2 User Manual, Bruker AXS GmbH, Karlsruhe, Germany, 2009.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental details of syntheses, TEM, powder X-ray diffraction measurements and calculations; CIF files, calculated geometry data, powder datasets. CCDC 1035816–1035818. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4ra15662e

---