Spectroscopic signatures and structural motifs in isolated and hydrated theophylline: a computational study†
Abstract
The spectra and structures of theophylline monomer and dimer and their hydrated complex have been investigated by MP2 and DFT methods. The ground state geometry optimization yields five lowest energy conformers of the Tph1-(H2O)1 complex at the M06-2X/6-311++G(d,p) level of theory for the first time. We investigated the low-lying excited states of bare theophylline by means of coupled cluster singles and approximate doubles (CC2) and TDDFT methods and a satisfactory interpretation of the electronic absorption spectra (Phys. Chem. Chem. Phys., 2012, 14, 10677–10682) is obtained. One striking feature is the coexistence of the blue and red shift of the vertical excitation energy of the optically bright state S1 (1ππ*) of theophylline upon forming a complex with water at C2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C6
O and C6![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O carbonyl sites, respectively. The optimized structure of newly characterized theophylline dimer Form IV is computed for the first time by MP2 and DFT methods. The binding energy of this dimer linked by double N–H⋯O
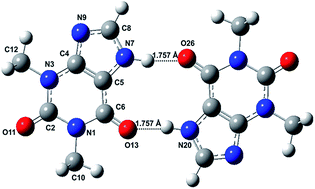
O carbonyl sites, respectively. The optimized structure of newly characterized theophylline dimer Form IV is computed for the first time by MP2 and DFT methods. The binding energy of this dimer linked by double N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds was found to be 88 kJ mol−1 at the MP2/6-311++G(d,p) level of theory. The geometry optimization of dimer Form M has also been performed and it is found that further stability is being conferred to the dimer IV after hydration. Computed IR spectra are found to be in remarkable agreement with the experiment (Cryst. Growth Des. 2010, 10, 3879–3886) and the out of phase (C
C hydrogen bonds was found to be 88 kJ mol−1 at the MP2/6-311++G(d,p) level of theory. The geometry optimization of dimer Form M has also been performed and it is found that further stability is being conferred to the dimer IV after hydration. Computed IR spectra are found to be in remarkable agreement with the experiment (Cryst. Growth Des. 2010, 10, 3879–3886) and the out of phase (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)2 stretching mode shows a tripling of intensity upon dimerisation. The vertical excitation energy of the optically bright state S1 (1ππ*) of the theophylline monomer upon forming dimer IV is shifted towards red as well as blue.
O)2 stretching mode shows a tripling of intensity upon dimerisation. The vertical excitation energy of the optically bright state S1 (1ππ*) of the theophylline monomer upon forming dimer IV is shifted towards red as well as blue.

 Please wait while we load your content...
Please wait while we load your content...