Electric-field-induced structural and electronic changes and decomposition of an energetic complex: a computational study on zinc carbohydrazide perchlorate crystals

Abstract

Periodic first-principle calculations have been performed to study the effects of electric field on the geometric and electronic structures and decomposition mechanism of crystalline zinc carbohydrazide perchlorate (ZnCP). The results show that the influences of external electric field on the crystal and molecular structures are very weak and ZnCP does not undergo a phase transition at an applied field smaller than 7.492 V nm⁻¹. Moreover, the ionic coordination bonds are more susceptible to the electric field mainly because of their weak interatomic interactions as compared to the stronger covalent bonds. In addition, the applied field across the crystal develops instabilities and ZnCP is more sensitive to the field than lead styphnate. At an electric field of 7.492 V nm⁻¹, ZnCP has metallic properties. Interestingly, the electric field redistributes the electron density of the frontier molecular orbitals, but the decomposition mechanism of ZnCP in the presence and absence of the field is similar. Finally, the electric-field-induced decomposition of ZnCP produces many gases and the final decomposed residue is ZnO.

---

1. Introduction

The decomposition reaction of energetic materials can be triggered by various external stimuli, such as impact, friction, heat, static compression, and an electric spark. The influences of temperature and pressure on the structure and properties of explosives have been extensively studied theoretically and experimentally.^1–11 However, except for lead styphnate,¹² theoretical investigations on energetic solids under an external electric field have not been made, although the hazards of energetic materials owing to static charge have been extensively studied experimentally.^13–17 The electrostatic discharge hazard is normally associated with manufacturing and filling operations. And the discharge of static electricity accumulated on a person can supply energy up to 20 mJ, which is possibly bigger than the minimum spark energy required for initiating the energetic materials such as lead styphnate and basic lead azide.¹⁵ Hence, accidents resulting from a static charge can easily occur in the explosive production plant. Moreover, the electric spark sensitivity of various explosives has been the subject of very many articles in the literature.^18–31 The correlations between the spark sensitivity of explosives and their molecular electronic properties have been well established. While the external electric field influences on the structure and properties of energetic materials are still not well understood.

It is known that transition metal carbohydrazide (CHZ) perchlorates, especially the ZnCP, can be widely used as lead-free safe energetic primary explosives. Thereby, the structure, thermal decomposition and sensitivity of ZnCP have been extensively investigated and compared.^32–35 Unfortunately, the geometric and electronic structures and decomposition mechanism under external electric field are often difficult to obtain from experiment for practical reasons. Compared with experiment, simulation can provide more detailed information about variations in crystal and molecular structures, initiation mechanism, and stability of energetic materials under applied electric field. In fact, there are sufficient computational investigations on the structures and properties of materials including single-walled nanotubes,^36–39 diamond nanowires,⁴⁰ graphene nanoribbons,^41–43 graphene-based composites,^44,45 guanine aggregates,⁴⁶ carbon dioxide,⁴⁷ and ultrathin multilayer planar cold cathodes⁴⁸ under external electric field. To the best of our knowledge, there are no such reports on zinc carbohydrazide perchlorate. Thus, in the present work, periodic first-principle calculations have been performed using density functional theory (DFT) to study the effects of electric field on the geometric and electronic structures, decomposition mechanism and stability of crystalline ZnCP.

2. Computational method

The initial structure adopted the experimental crystalline structure³⁴ in which ZnCP contains four [Zn(CHZ)₃](ClO₄)₂ molecules per unit cell in an monoclinic lattice with space group P2₁/n as shown in Fig. 1. The geometry optimization was performed to allow the ionic configuration, cell shape, and volume to change. The total energy of the system was converged less than 1.0 × 10⁻⁵ Ha, the residual force less than 0.002 Ha Å⁻¹, the displacement of atoms less than 0.005 Å. Here we find that the local density approximation (LDA) named PWC⁴⁹ can well reproduce the crystal structure. Therefore, the PWC functional was employed in the present work.

Fig. 1 The experimental unit cell of ZnCP and the orientations of the resultant applied field (green arrow) and its a-, b-, and c-components (yellow arrows) and atomic numbering of the asymmetric unit.

In the geometry relaxation and electronic structure calculation, the effective core potentials, DNP basis set, global orbital cutoff scheme, and DIIS technique were used. The global orbital cutoff was set to 4.4 Å and the SCF tolerance was 1.0 × 10⁻⁶ Ha. Moreover, Brillouin zone sampling was performed by using the Monkhorst–Pack scheme. Our test calculations suggest that the computed structural parameters are not sensitive to the k-point sampling, reasonable accuracy could be obtained by performing each optimization using a (1 × 1 × 1) sampling grid. The band gap and density of states (DOS) of the optimized structures were then determined using the (2 × 2 × 1) k-point sampling grid.

The influence of the external electric field on the structural and electronic properties of crystalline ZnCP was systematically investigated. In the calculation, the electric field is described in terms of the a-, b-, and c-components. Thereby, the static external electric fields are separately applied in the a-, b-, and c-directions. The real strength and orientation of the applied field should be expressed in their resultant vector as displayed in Fig. 1. The magnitudes of the a-, b-, and c-components are equal. And they are 0.001, 0.003, 0.005, 0.007, and 0.009 a.u., that is, 0.514, 1.542, 2.570, 3.598, and 4.626 V nm⁻¹, respectively. As a result, the resultant electric fields applied on the crystal are 0.833, 2.499, 4.160, 5.826, and 7.492 V nm⁻¹, respectively. According to our experience, the influences of external electric field on the structure and property of ZnCP are almost isotropic owing to the similar crystal packing along various directions. Thus, there may not be field direction dependences of the obtained results and conclusions. And only one specific field direction was chosen in the present study. All DFT calculations reported in this work were carried out with the DMol³ code.^50,51

3. Results and discussion

The LDA-PWC functional was selected to fully relax crystalline ZnCP without any constraint in the absence of an electric field. The computed lattice parameters a, b, c, α, β, and γ are 9.750 Å, 8.202 Å, 20.602 Å, 90°, 100.67°, and 90°, respectively. The corresponding experimental values³⁴ are 10.005 Å, 8.428 Å, 21.218 Å, 90°, 100.95°, and 90°, respectively. It is clear that the calculated results are slightly smaller than the measured lattice constants, which is typical for the LDA approximation to DFT. We note that the maximum relative error is only 2.9%. These comparisons confirm that our computational parameters are reasonably satisfactory.

3.1. Crystal structure

To show the effect of external electric field on the crystal structure, Fig. 2 displays the relaxed lattice constants (a, b, c, and β), unit cell volume (V), and density (ρ) of ZnCP at applied electric fields varying from 0 to 7.492 V nm⁻¹. Note that, the lattice parameters of α and γ always equal 90°. As shown in Fig. 2, the length of the three crystallographic axes almost remains constant, indicating that the influence of external electric field on the crystal structure of ZnCP is very weak. However, the lattice parameter of β changes somewhat in the region of low electric fields below 4.160 V nm⁻¹. Above this field, increasing the electric filed makes it varies remarkably. Furthermore, with the increase of electric field, the unit cell volume decreases firstly and then increases. And there is a reverse tendency for the crystalline density. According to ref. 12, the crystal structure variation of ZnCP is much smaller than that of lead styphnate. It implies that ZnCP maybe merely changes its structure and has no phase transition upon the external electric field in range from 0 to 7.492 V nm⁻¹.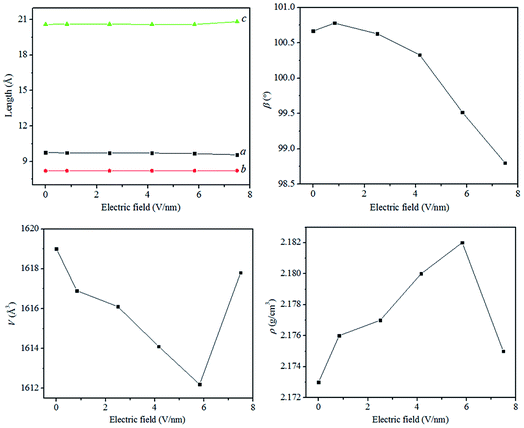

Fig. 2 Calculated lattice constants (a, b, c, and β), unit cell volume (V), and density (ρ) of ZnCP at different resultant electric fields.

3.2. Molecular structure

The electric field causes the changes in not only the unit cell but also the molecular geometry. Some important geometrical parameters including bond lengths and bond angles at various resultant electric fields are presented in Fig. 3 and 4, respectively. From Fig. 3, we can observe the following features. Firstly, the variations of the bond lengths with applied field are quite different. With the electric field increasing from 0 to 7.492 V nm⁻¹, some bonds elongate continuously, others shorten gradually, still others vary arbitrarily. That is, some bonds do not monotonically vary with the increasing electric field, which is similar to lead styphnate. While the bond length variations of ZnCP are much smaller than those of lead styphnate.¹² These observations demonstrate again that crystalline ZnCP may only change its structure and does not undergo a phase transition. Secondly, the changes of the bond lengths in the higher electric field range are much bigger than those at lower electric fields. As is well-known, the electric field force (F) is readily calculated by the following equation:

F = qE

where q is the electric quantity of a point charge, E is the electric field strength. The electric field applied on the crystal is a uniform field and the atomic charge can be considered as a point charge. Thereby, a reasonable explanation may be that the higher the external electric field, the stronger the electric field force is applied on a bond and the easier the bond length changes. Thirdly, the variations of interatomic distances of the covalent bonds are much smaller than those of the ionic coordination bonds of Zn–O and Zn–N. From our earlier reported work,³³ it can be seen that both Zn–O and Zn–N bonds are ionic in nature but have weak covalent character. Also, their atomic charges are moderate, and their bond orders are quite small. Thus, the corresponding interatomic interactions are very weak. Apparently, this is the main reason for which the ionic coordination bonds are more susceptible to the electric field than the covalent bonds. Finally, the maximum changes of the Zn–O, Zn–N, C–O, C–N, N–N, and Cl–O bond lengths are 0.025, 0.037, 0.007, 0.016, 0.004, and 0.019 Å, respectively. And all of them arise at the electric field of 7.492 V nm⁻¹. This results in substantial changes in the electronic structure. Namely, there is a band gap closure in bulk ZnCP at the electric field of 7.492 V nm⁻¹ as presented in the next section.

Fig. 3 Variation of the selected bond lengths with the resultant electric field. Δ_max denotes the maximum variation.

Fig. 4 Variation of the selected bond angles with the resultant electric field. Δ_max denotes the maximum variation.

The selected bond angles that form the three five-membered chelate rings are shown in Fig. 4. Similarly, several features can also be summarized as follows. (i) On the whole, the bond angles change regularly with the increase in electric field. (ii) Most bond angles, especially the O–Zn–N bond angles, have larger variations at higher electric fields. Whereas the maximum change is just 1.4°, suggesting that these chelate rings possess better stability in the presence of the electric field. (iii) The variations of the O1–Zn–N1, O2–Zn–N5, and O3–Zn–N9 bond angles are much bigger than those of the other bond angles.

3.3. Density of states

An analysis of density of states is very helpful to understand the changes in electronic structure caused by external electric field. Fig. 5 presents the calculated total DOS for crystalline ZnCP at different electric fields. Here, we can see that the DOS curve slightly varies at the electric field of 0.833 V nm⁻¹. It reveals that the electronic structure of ZnCP does not have any significant changes. However, in the field range from 2.499 to 7.492 V nm⁻¹, the shape of the DOS curve changes markedly. Moreover, the applied field makes the DOS peaks split and lower, and the electron distribution is more delocalized. More interestingly, the conduction band has a tendency of shifting to the lower energy, consequently leading to a reduction in band gap. When the electric field is increased to 7.492 V nm⁻¹, the case is quite different. In other words, there is a band gap closure between valence and conduction bands in the system. It means that ZnCP has metallic properties at the electric field of 7.492 V nm⁻¹. Such metallization has been also found to occur under heating or hydrostatic compression in other energetic materials.^2–6 The band gap lowering or closing greatly increases the probability of the electronic excitation that may cause the chemical decomposition and the final detonation of explosives.

Fig. 5 Total DOS of ZnCP at various resultant electric fields.

3.4. Band gap and stability

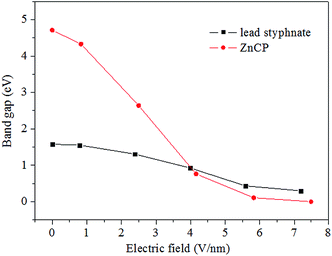
As is well-known, band gap is an important parameter to characterize the electronic structure of solids and retains close connection to some bulk properties. Herein, we discuss the correlation of stabilities (or sensitivity properties) with the band gap. Fig. 6 shows the band gaps of bulk ZnCP and lead styphnate at different resultant electric fields. The results of lead styphnate has been reported previously.¹² Note that, the electric field strength is the component in our previous report, but here the resultant electric field strength is used. Although the a-, b-, and c-components are the same, the resultant fields applied on ZnCP and lead styphnate are not equal, since the magnitudes of their lattice parameter β are different. The resultant electric fields applied on lead styphnate are 0.797, 2.396, 3.990, 5.584, and 7.184 V nm⁻¹, respectively. As depicted in Fig. 6, the band gap of ZnCP sharply decreases with the increment of applied electric field, which differs obviously from lead styphnate. Moreover, at the electric field of 7.492 V nm⁻¹, the band gap of ZnCP disappears, but that of lead styphnate is about 0.3 eV. In conclusion, the band gap reduction of ZnCP is larger than that of lead styphnate. It may be inferred that ZnCP is more sensitive to external electric field. According to the first-principles band gap criterion,⁵² we can conclude that the impact sensitivity for ZnCP becomes more and more sensitive with the external electric field increasing. For energetic materials, the detonation initiation induced by external mechanical stimuli is taken to be an electronic excitation process.^53–56 Thus, a possible explanation may be that the increased impact sensitivity is caused by the increased number of excited states due to optical band gap reduction.

Fig. 6 Band gaps of ZnCP and lead styphnate as a function of electric field.

3.5. Frontier molecular orbitals and decomposition mechanism

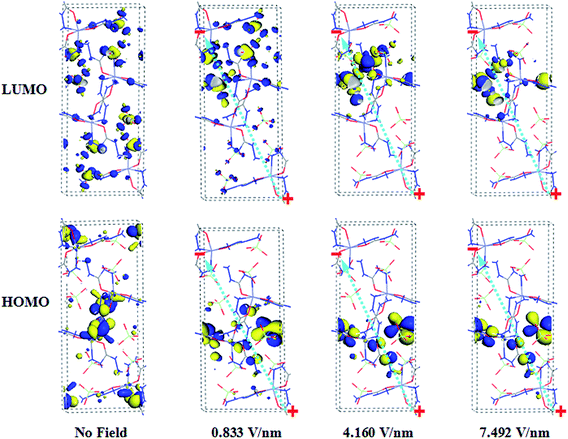
To further investigate the electronic change of ZnCP in the presence of the electric field and its mechanism of electrical decomposition, the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) are analyzed in detail and plotted in Fig. 7. In the absence of the field, the HOMO represents nonbonding orbital occupied by the lone-pair electrons of the carbohydrazide ligands, and the LUMO is donated by the perchlorate ions. As electric field acts on the system, the HOMO and LUMO orbitals still mainly localize on the carbohydrazide ligands and the perchlorate ions, respectively. While the ligands also make a little contribution for the LUMO orbital. And the distribution reduces gradually and slowly with the increasing electric field, which maybe promotes the electrical decomposition of the studied complex.

Fig. 7 Evolution of the distribution of frontier molecular orbitals of ZnCP as a function of the field applied. The positive and negative signs and green arrow denote the anode, cathode and resultant field direction, respectively.

In the presence of the electric field, the double injection of electrons and holes into the ZnCP crystal is from the cathode and anode, respectively. As can be easily seen from Fig. 7, the HOMO orbital approaches the anode and just localizes on the carbohydrazide ligand under the applied field. Hence it is more favorable for the carbohydrazide ligand to combine with holes than for it to combine with electrons. And their combination is represented by

3CN₄OH₆ + 14h⁺ → CO₂ + 5N₂ + H₂O + 2HCN + 14H⁺

where h denotes the hole. And the chemical formula CN₄OH₆ is carbohydrazide ligand. On the contrary, the LUMO orbital is close to the cathode and mostly contributed from the perchlorate ion in the presence of the electric field. Hereby it is more favorable for the perchlorate ion to capture free electrons. And their combination may give rise to the following chemical reaction:

2ClO₄⁻ + 14e⁻ → Cl₂ + 8O²⁻

where e stands for the electron. Subsequently, O²⁻ combines with H⁺ and Zn²⁺, respectively, and generates H₂O and ZnO:

O²⁻ + 2H⁺ → H₂O

O²⁻ + Zn²⁺ → ZnO

As shown in Fig. 7, zinc cation makes no contribution for both HOMO and LUMO orbitals, so that Zn²⁺ does not act as an active center and can not accept holes or electrons at the initial stage of the electrical decomposition. Moreover, Zn²⁺ actually combines with the O²⁻ of perchlorate ion, but not the O²⁻ of carbohydrazide ligand. This is in agreement with the fact that the Zn–O coordination bonds elongate under external electric field.

In the absence of the field, the thermal excitation of electrons from HOMO to LUMO can also result in the aforementioned chemical reactions, since the composition of the frontier molecular orbitals of ZnCP is very similar in the presence and absence of the electric field. Beyond all doubt, the proposed mechanism of electrical decomposition is indirectly supported by the previous experimental observations.^32,34 That is, in the thermal decomposition of ZnCP, the final decomposed residue is ZnO, and the main gas products are CO₂, H₂O, HCN and so on. Unfortunately, the N₂ and Cl₂ cannot be detected by the T-jump/FTIR spectroscopy in the flash pyrolysis of ZnCP. From these discussions, we may infer that the main difference in the process of thermal and electrical decompositions of ZnCP is responsible for the generation of electrons and holes, which is thermal excitation in the thermal case, but field injection in the electrical case.

4. Conclusion

We have performed a detailed theoretical study of electric field effects on the structure, decomposition mechanism and stability of crystalline ZnCP. The obtained results show that the influences of applied field on the crystal and molecular structures are very weak. And the system does not undergo a phase transition as the electric field smaller than 7.492 V nm⁻¹. Moreover, the field effects on the ionic coordination bonds are stronger than those on the covalent bonds, because the interatomic interactions of the coordination bonds are much weaker than those of the others. Furthermore, ZnCP has metallic properties at the field of 7.492 V nm⁻¹ and is more sensitive to external electric field than lead styphnate. As electric field acts on ZnCP crystal, the distribution of frontier molecular orbitals reduces, but their composition varies slightly. Thereby, the mechanism of electrical and thermal decompositions is similar. And the electrical decomposition of ZnCP yields many gases and solid ZnO.

Acknowledgements

This work was supported by the China National “973” project, the Chunhui Program of Ministry of Education of China (Z2014083, Z2014084), the Natural Science Foundation of Chongqing (cstc2011jjA50013), the Scientific and Technological Research Program of Chongqing Municipal Education Commission (KJ131318, KJ1401217), and the Young Talented Researcher Plan of Yangtze Normal University (2014QNRC03).

References

1. K. D. Behler, J. A. Ciezak-Jenkins and R. C. Sausa, High-pressure characterization of nitrogen-rich bis-triaminoguanidinium azotetrazolate (TAGzT) by in situ Raman spectroscopy, J. Phys. Chem. A, 2013, 117, 1737–1743.
2. X. J. Xu, W. H. Zhu and H. M. Xiao, DFT studies on the four polymorphs of crystalline CL-20 and the influences of hydrostatic pressure on ε-CL-20 crystal, J. Phys. Chem. B, 2007, 111, 2090–2097.
3. L. Qiu, W. H. Zhu, J. J. Xiao and H. M. Xiao, Theoretical studies of solid bicyclo-HMX: effects of hydrostatic pressure and temperature, J. Phys. Chem. B, 2008, 112, 3882–3893.
4. Y. Liu, X. D. Gong, L. J. Wang and G. X. Wang, Effect of hydrostatic compression on structure and properties of 2-diazo-4,6-dinitrophenol crystal: density functional theory studies, J. Phys. Chem. C, 2011, 115, 11738–11748.
5. Y. Liu, L. Zhang, G. X. Wang, L. J. Wang and X. D. Gong, First-principle studies on the pressure-induced structural changes in energetic ionic salt 3-azido-1,2,4-triazolium nitrate crystal, J. Phys. Chem. C, 2012, 116, 16144–16153.
6. W. H. Zhu and H. M. Xiao, Ab initio molecular dynamics study of temperature effects on the structure and stability of energetic solid silver azide, J. Phys. Chem. C, 2011, 115, 20782–20787.
7. N. N. Ge, Y. K. Wei, G. F. Ji, X. R. Chen, F. Zhao and D. Q. Wei, Initial decomposition of the condensed-phase β-HMX under shock waves: molecular dynamics simulations, J. Phys. Chem. B, 2012, 116, 13696–13704.
8. M. R. Manaa and L. E. Fried, Nearly equivalent inter- and intramolecular hydrogen bonding in 1,3,5-triamino-2,4,6-trinitrobenzene at high pressure, J. Phys. Chem. C, 2012, 116, 2116–2122.
9. M. Pravica, Y. Liu, J. Robinson, N. Velisavljevic, Z. X. Liu and M. Galley, A high-pressure far- and mid-infrared study of 1,1-diamino-2,2-dinitroethylene, J. Appl. Phys., 2012, 111, 103534.
10. M. Pravica, M. Galley, C. Park, H. Ruiz and J. Wojno, A high pressure, high temperature study of 1,1-diamino-2,2-dinitro ethylene, High Pressure Res., 2011, 31, 80–85.
11. M. R. Manaa and L. E. Fried, The reactivity of energetic materials under high pressure and temperature, Adv. Quantum Chem., 2014, 69, 221–252.
12. Z. Li, H. Huang, T. Zhang, S. Zhang, J. Zhang and L. Yang, First-principles study of electric field effects on the structure, decomposition mechanism, and stability of crystalline lead styphnate, J. Mol. Model., 2014, 20, 2072–2079.
13. M. Auzanneau and M. Roux, Electric spark and ESD sensitivity of reactive solids, Part II: energy transfer mechanism and comprehensive study on E₅₀, Propellants, Explos., Pyrotech., 1995, 20, 96–101.
14. D. Skinner, D. Olson and A. Block-Bolten, Electrostatic discharge ignition of energetic materials, Propellants, Explos., Pyrotech., 1997, 23, 34–42.
15. M. B. Talawar, A. P. Agrawal, M. Anniyappan, D. S. Wani, M. K. Bansode and G. M. Gore, Primary explosives: electrostatic discharge initiation, additive effect and its relation to thermal and explosive characteristics, J. Hazard. Mater., 2006, 137, 1074–1078.
16. D. M. Badgujar, M. B. Talawar, S. N. Asthana and P. P. Mahulikar, Advances in science and technology of modern energetic materials: an overview, J. Hazard. Mater., 2008, 151, 289–305.
17. M. B. Talawar, R. Sivabalan, T. Mukundan, H. Muthurajan, A. K. Sikder, B. R. Gandhe and A. S. Rao, Environmentally compatible next generation green energetic materials (GEMs), J. Hazard. Mater., 2009, 161, 589–607.
18. C. Zhi, X. Cheng and F. Zhao, The Correlation between electric spark sensitivity of polynitroaromatic compounds and their molecular electronic properties, Propellants, Explos., Pyrotech., 2010, 35, 555–560.
19. C. Zhi, X. Cheng and F. Zhao, Relationship between electric spark sensitivity of cyclic nitramines and their molecular electronic properties, Chin. J. Struct. Chem., 2012, 31, 1263–1270.
20. L. Türker, Contemplation on spark sensitivity of certain nitramine type explosives, J. Hazard. Mater., 2009, 169, 454–459.
21. S. Zeman, New aspects of initiation reactivities of energetic materials demonstrated on nitramines, J. Hazard. Mater., 2006, 132, 155–164.
22. S. Zeman, V. Pelikan and J. Majzlik, Electric spark sensitivity of nitramines. Part I. Aspects of molecular structure, Cent. Eur. J. Energ. Mater., 2006, 3, 27–44.
23. V. Zeman, J. Koci and S. Zeman, Electric spark sensitivity of polynitro compounds. Part II. A correlation with detonation velocities of some polynitro arenas, Chin. J. Energ. Mater., 1999, 7, 127–132.
24. V. Zeman, J. Koci and S. Zeman, Electric spark sensitivity of polynitro compounds. Part III. A correlation with detonation velocities of some nitramines, Chin. J. Energ. Mater., 1999, 7, 172–175.
25. S. Zeman and J. Koci, Electric spark sensitivity of polynitro compounds. Part IV. A relation to thermal decomposition parameters, Chin. J. Energ. Mater., 2000, 8, 18–26.
26. J. Koci, V. Zeman and S. Zeman, Electric spark sensitivity of polynitro compounds. Part V. A relationship between electric spark and impact sensitivities of energetic materials, Chin. J. Energ. Mater., 2001, 9, 60–65.
27. M. H. Keshavarz, H. R. Pouretedal and A. Semnani, Reliable prediction of electric spark sensitivity of nitramines: a general correlation with detonation pressure, J. Hazard. Mater., 2009, 167, 461–466.
28. M. H. Keshavarz, Theoretical prediction of electric spark sensitivity of nitroaromatic energetic compounds based on molecular structure, J. Hazard. Mater., 2008, 153, 201–206.
29. M. H. Keshavarz, H. R. Pouretedal and A. Semnani, A simple way to predict electric spark sensitivity of nitramines, Indian J. Eng. Mater. Sci., 2008, 15, 505–509.
30. M. H. Keshavarz, Relationship between the electric spark sensitivity and detonation pressure, Indian J. Eng. Mater. Sci., 2008, 15, 281–286.
31. P. Politzer and J. S. Murray, Detonation performance and sensitivity: a quest for balance, Adv. Quantum Chem., 2014, 69, 1–30.
32. Y. H. Sun, T. L. Zhang, J. G. Zhang, X. J. Qiao and L. Yang, Flash pyrolysis study of zinc carbohydrazide perchlorate using T-jump/FTIR spectroscopy, Combust. Flame, 2006, 145, 643–646.
33. H. Huang, T. Zhang, J. Zhang and L. Wang, Density functional theoretical study of transition metal carbohydrazide perchlorate complexes, Chem. Phys. Lett., 2010, 487, 200–203.
34. S. Qi, Z. Li, T. Zhang, Z. Zhou, L. Yang, J. Zhang, X. Qiao and K. Yu, Crystal structure, thermal analysis and sensitivity property of [Zn(CHZ)₃](ClO₄)₂, Acta Chim. Sin., 2011, 69, 987–992.
35. R. Liu, S. Qi, T. Zhang, Z. Zhou, L. Yang and J. Zhang, Morphological control of zinc tricarbohydrazide perchlorate crystals: theoretical and experimental study, Chin. Sci. Bull., 2013, 58, 1892–1896.
36. L. Wang, Y. Z. Zhang, Y. F. Zhang, X. S. Chen and W. Lu, Electronic structures of S-doped capped C-SWNT from first principles study, Nanoscale Res. Lett., 2010, 5, 1027–1031.
37. M. T. Baei, A. A. Peyghan and M. Moghimi, Electric field effect on (6,0) zigzag single-walled aluminum nitride nanotube, J. Mol. Model., 2012, 18, 4477–4489.
38. M. T. Baei, A. A. Peyghan, M. Moghimi and S. Hashemian, Electric field effect on the zigzag (6,0) single-wall BC2N nanotube for use in nano-electronic circuits, J. Mol. Model., 2013, 19, 97–107.
39. T. H. Cho, W. S. Su, T. C. Leung, W. Ren and C. T. Chan, Electronic and optical properties of single-walled carbon nanotubes under a uniform transverse electric field: a first-principles study, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 235123.
40. J. Zhang, J. X. Cao, X. Chen, J. W. Ding, P. Zhang and W. Ren, Diamond nanowires with nitrogen vacancy under a transverse electric field, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 045417.
41. M. Chattopadhyaya, M. M. Alam and S. Chakrabarti, On the microscopic origin of bending of graphene nanoribbons in the presence of a perpendicular electric field, Phys. Chem. Chem. Phys., 2012, 14, 9439–9443.
42. Y. Ding and Y. Wang, First-principles study of the triwing graphene nanoribbons: junction-dependent electronic structures and electric field modulations, Phys. Chem. Chem. Phys., 2012, 14, 2040–2049.
43. H. Huang, Z. Li, H. J. Kreuzer and W. Wang, Disintegration of graphene nanoribbons in large electrostatic fields, Phys. Chem. Chem. Phys., 2014, 16, 15927–15933.
44. W. Geng, X. Zhao, W. Zan, H. Liu and X. Yao, Effects of the electric field on the properties of ZnO–graphene composites: a density functional theory study, Phys. Chem. Chem. Phys., 2014, 16, 3542–3548.
45. C. Foroutan-Nejad and R. Marek, Potential energy surface and binding energy in the presence of an external electric field: modulation of anion–π interactions for graphene-based receptors, Phys. Chem. Chem. Phys., 2014, 16, 2508–2514.
46. A. K. Jissy and A. Datta, Effect of external electric field on H-bonding and π-stacking interactions in guanine aggregates, ChemPhysChem, 2012, 13, 4163–4172.
47. M. Calvaresi, R. V. Martinez, N. S. Losilla, J. Martinez, R. Garcia and F. Zerbetto, Splitting CO₂ with electric fields: a computational investigation, J. Phys. Chem. Lett., 2010, 1, 3256–3260.
48. R. Z. Wang, H. Yan, B. Wang, X. W. Zhang and X. Y. Hou, Field emission enhancement by the quantum structure in an ultrathin multilayer planar cold cathode, Appl. Phys. Lett., 2008, 92, 142102.
49. J. P. Perdew and Y. Wang, Accurate and simple analytic representation of the electron-gas correlation-energy, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
50. B. Delley, An all-electron numerical-method for solving the local density functional for polyatomic-molecules, J. Chem. Phys., 1990, 92, 508–517.
51. B. Delley, From molecules to solids with the DMol³ approach, J. Chem. Phys., 2000, 113, 7756–7764.
52. W. H. Zhu and H. M. Xiao, First-principles band gap criterion for impact sensitivity of energetic crystals: a review, Struct. Chem., 2010, 21, 657–665.
53. M. M. Kuklja, E. V. Stefanovich and A. B. Kunz, An excitonic mechanism of detonation initiation in explosives, J. Chem. Phys., 2000, 112, 3417–3423.
54. M. M. Kuklja and A. B. Kunz, Compression-induced effect on the electronic structure of cyclotrimethylene trinitramine containing an edge dislocation, J. Appl. Phys., 2000, 87, 2215–2218.
55. T. Luty, P. Ordon and C. J. Eckhardt, A model for mechanochemical transformations: applications to molecular hardness, instabilities, and shock initiation of reaction, J. Chem. Phys., 2002, 117, 1775–1785.
56. W. L. Faust, Explosive molecular ionic crystals, Science, 1989, 245, 37–42.

---