Revealing the properties of the cubic ZrO₂ (111) surface by periodic DFT calculations: reducibility and stabilization through doping with aliovalent Y₂O₃

Abstract

A detailed theoretical study concerning the formation of oxygen vacancies on the clean (111) surface of cubic ZrO₂ and the structural and electronic properties of the (111) surface of yttria-stabilized zirconia (YSZ, 8 mol% Y₂O₃) was carried out using DFT methods in a periodic approach. For the formation of oxygen defects on the clean (111) surface, two different oxygen vacancy positions and two possible spin states for each position were investigated. Large vacancy formation energy, small relaxation and the presence of a highly localized state in the gap characterize the formation of oxygen defects on this surface. Regarding the yttria-stabilized surface, a systematic study of the stability, geometry and electronic structure of seven different configurations for Y atoms and oxygen vacancies on the surface was performed. The doping with Y₂O₃ stabilizes the cubic (111) ZrO₂ surface and is accompanied by large relaxations of the O atoms NN to the vacancies. In addition, Y atoms preferentially occupy positions NNN to the defect. Despite the presence of vacancies in YSZ, no mid-gap states have been observed in any of the studied arrangements. This study allowed identifying an accurate computational protocol and a suitable model of the (111) surface of YSZ, through the characterization of its structural and electronic properties. Both could be used to further elucidate the role of YSZ as electrolyte in SOFC applications, with a view to better clarifying the basic operating principles of low temperature solid oxide fuel cells (LT-SOFCs).

---

I. Introduction

Solid oxide fuel cells (SOFCs) have recently attracted a lot of attention because of their high-energy efficiency, fuel flexibility and low pollutant emissions, which place them as one of the most promising and environmentally friendly in the field of energy conversion devices.¹ Yttria-stabilized zirconia (YSZ) is the most widely used electrolyte for conventional SOFCs operating at high temperature (>800 °C), where YSZ shows high ionic conductivity. However, as a consequence of the drawbacks associated to these operating conditions (such as material degradation, technological complications and high running costs), the current SOFC research is oriented toward the development of novel electrolytes that allow working conditions with lower temperatures (LT-SOFCs). In this regard, composite materials with enhanced conductivity based on a molten salt and an oxide have been recently proposed as promising electrolytes for LT-SOFCs (LT, <600 °C).² Ceria is generally associated with molten carbonates for these composite compounds,^3–5 but the use of YSZ, for instance, could also be envisaged.⁶

A deeper understanding of the structural and electronic properties of these materials constitutes always the first step toward the comprehension of their role as electrolyte in these devices.

Pure zirconia (ZrO₂) exhibits three main crystallographic structures stable at ambient pressure: the monoclinic, tetragonal, and cubic polymorphs. At room temperature, zirconia adopts the monoclinic baddeleyite structure (P2₁/c), stable up to 1480 K where it transforms into the tetragonal polymorph (P4₂/nmc). At around 2650 K, the tetragonal ZrO₂ converts into a cubic fluorite structure (Fm3m).⁷ It has been observed that Zr⁴⁺ ions appear to be too large for an efficiently packed rutile structure and at the same time too small to form the eight-fold coordinated fluorite structure.^8,9 For these reasons, during cooling, the high temperature cubic structure is not stable and distorts first into the lower symmetry tetragonal phases (where Zr cations are still eight-fold coordinated) and finally into the lowest symmetry monoclinic phase (which has seven coordinated Zr cations).

Nonetheless, tetragonal and cubic phases can be stabilized at lower temperatures through doping with aliovalent oxides like yttria (Y₂O₃).⁷ For each pair of aliovalent Y³⁺ ions that substitutes a pair of Zr⁴⁺ cations, one oxygen vacancy must be created to ensure the neutrality of the system.

The first effect of the doping is the partial or complete structural stabilization, depending on the dopant concentration. At room temperature and for low concentrations (2–6 mol% of yttria), the tetragonal structure is stabilized, but this phase separates into monoclinic or cubic-doped structures as a function of temperature and time and is, therefore, called partially stabilized zirconia (PSZ). In the other hand, 8–40 mol% Y₂O₃ is necessary to obtain the fully stabilized cubic structure (YSZ, yttria stabilized zirconia). Over 40 mol%, the system crystallizes as a rhombohedral δ-Zr₃Y₄O₁₂ phase.^9–12

In addition to the structural stabilization, doping of zirconium oxide with yttria has two main consequences: it improves the thermo-mechanical properties and determines the high ionic conductivity because of the presence of oxygen vacancies in the doped material.⁷ The ionic conductivity, together with the number of vacancies, increases with the dopant concentration reaching a maximum at 8 mol% Y₂O₃ and then significantly decreases for higher dopant amount, probably because, at higher Y₂O₃ content, vacancies are trapped in defect complexes.^13,14

The high mechanical strength, the thermal shock resistance, the low thermal conduction and the excellent oxygen ion conduction make YSZ the most common material used as electrolyte in SOFC, oxygen sensors, oxygen pumps and other electrochemical devices, mainly working at temperature higher than 600 °C.^12,15–18

The mechanism of stabilization in YSZ is not completely understood and it is still subject of debate. Decreasing of the coordination number of Zr atoms from eight to a value close to seven (like in monoclinic zirconia), as a consequence of the presence of the oxygen vacancies, is the prevailing explanation, in accordance with the observation that the covalent nature of the Zr–O bond favours structures with lower coordination numbers.¹⁹ This rationalization indirectly implies that oxygen vacancies are associated to Zr⁴⁺ rather than to the Y³⁺ cations, contrarily to the expected electrostatic attraction between the vacancy and the dopant ions.^12,16,19,20

Unfortunately, experimental studies provide conflicting data that do not give clear indication about the nature of the stabilization mechanism. Indeed some of them indicate that vacancies prefer to bind to the dopant,^21,22 while others refer to a preferential association between the vacancies and Zr cations.^23–27 Theoretical studies^{10,12,16,17,19,20,28,29} on the bulk structure of PSZ or YSZ support the latter case in which Y next-nearest neighbour positions (NNN) to the vacancy are energetically favoured with respect to the nearest neighbour (NN) ones. The configuration of Zr, O, Y and oxygen vacancies is however not decisively characterized and the proposed mechanism of stabilization still needs to be better clarified.

The structural characterization of the surfaces of this oxide is also difficult from an experimental point of view. Despite several experiments^30,31 suggesting the presence of a monolayer rich in yttrium on top of a thicker undoped ZrO₂ layer, there is still uncertainty about the locations of the oxygen vacancies and Y atoms.^9,32

Modelling can help investigating structural and electronic properties of the oxide surfaces, providing information that is difficult to obtain experimentally. Some theoretical studies have been already devoted to the description of the structural properties of YSZ or PSZ surfaces,^{8,9,11,15,33,34} but there is not a systematic investigation of dopant and vacancies distribution. This would however be particularly appealing as the knowledge of the geometrical and electronic properties of YSZ surfaces is crucial for SOFC applications of this material.

For these reasons, with the aim to gain further information on the complex surface chemistry of YSZ, clarifying the structure and the impact of the doping on the electronic and chemical properties of YSZ surfaces, we performed first-principles Density Functional Theory (DFT) calculations on the most stable (111) surface of YSZ.^30,35,36 Moreover, while previous theoretical works on YSZ bulk or surfaces were based on various values of dopant concentrations (from 9 to 14 or even 40 mol% of yttria), we focused on the experimental doping amount (8 mol% Y₂O₃) that ensures the highest conductivity and corresponds to the material used in practical SOFC applications.

In particular, we first explored the formation of isolated oxygen defects on the clean (111) ZrO₂ surface. Indeed, the formation of colour centres in zirconia has been extensively described for monoclinic ZrO₂ bulk^20,37 and surfaces,³⁸ for tetragonal ZrO₂ bulk^10,39 and surfaces,¹¹ for cubic zirconia bulk,^12,16,17 while only little information can be found on cubic surfaces.³⁴

The arrangement of Zr, O, Y and oxygen vacancies on the (111) surface was then studied in detail through a systematic study of the stability, geometry and electronic structure of seven different configurations for Y atoms and oxygen vacancies.

II. Computational details

Calculations have been performed in the framework of DFT and using a linear combination of atomic orbitals (LCAO) approach, by means of the periodic CRYSTAL09 (ref. 40) code.

The global hybrid functional PBE0,^41,42 a parameter-free functional mixing 25% of HF exchange in a PBE scheme, has been selected as the exchange-correlation functional of choice. We have already successfully applied this functional to the description of structural and electronic features of zirconia bulk and surfaces.^35,43

For Zr atoms, the small core ECP (effective core pseudo-potential) of Hay and Wadt^44–46 was used to describe the 28 inner core electrons together with a (5sp,4d) → [3sp,2d]⁴⁷ contraction scheme to describe the (4s²4p⁶5s²4d²) valence electrons. The Durand–Barthelat^48,49 large core ECP to replace the 1s core electrons and a (4sp) → [2sp] contraction scheme⁵⁰ for the outer electrons was instead selected as basis set for O atoms. Finally, for the Y atoms, the Hay and Wadt^44–46 small core ECP and the (4sp,2d) → [2sp,1d] contraction scheme⁵⁰ for the (4s²4p⁶5s²4d¹) valence electrons were used. These basis sets have already been shown to perform closely to larger ones.³⁵

The clean (111) surface of cubic ZrO₂ was cleaved from the optimized bulk ZrO₂ structure with lattice parameters a = 5.100 Å.³⁵ In particular, it was modelled by a (2 × 2) supercell with a total of 72 atoms (Zr₂₄O₄₈). To study the formation of colour centres in this surface, two oxygen atoms were removed from the supercell (Zr₂₄O₄₆), but leaving the associated basis set centred in the atomic position of the defect site. Finally, to model the (111) surface of YSZ, in addition to the two vacancies, four Zr atoms of the supercell were replaced by four Y atoms, leading to Zr₂₀Y₄O₄₆ and corresponding to the experimental 8 mol% Y₂O₃ doping amount.

For all the calculations, the reciprocal space was sampled using a Monkhorst–Pack⁵¹ grid with shrinking factors (6 × 6 × 1), corresponding to 13 points in the irreducible Brillouin zone (IBZ) of the supercell. Extrafine⁵² tolerances were considered for the evaluation of Coulomb and exchange series. Finally, geometry optimization were performed keeping the supercell lattice parameters (a = b = 7.196 Å, γ = 120°) constant, while all the atomic positions were allowed to relax, until the maximum and root-mean square atomic forces and displacements were simultaneously less than 4.5 × 10⁻⁴, 3.0 × 10⁻⁴, 1.8 × 10⁻³ and 1.2 × 10⁻³ au, respectively.⁴⁰

The energy of formation of n vacancies (E_fⁿ) on the cubic (111) surface was computed with respect to molecular (1/2O₂) or atomic (O) oxygen as, respectively:

E_fⁿ(O) = E(surface with n vacancies) + nE(O) − E(surface) (2)

where E(surface with n vacancies) is the energy of the system with n vacancies, either in a singlet or triplet spin state, E(O₂) is the energy for the O₂ molecule in its ground state of triplet, E(O) is the energy for the O atom and E(surface) is the energy for the clean surface. The energy of formation for one vacancy (E_f) was then obtained by simply dividing E_fⁿ for the number of vacancies n.

For the (111) YSZ surface, the energy (E_s−f) due to the substitution of Zr atoms with Y atoms and simultaneously to the formation of oxygen vacancies (with respect to O₂ or O) was computed as:

E_s−f(O) = E(doped surface) + 2nE(Zr) + nE(O) − E(surface) − 2nE(Y) (4)

where n is the number of vacancies, E(doped surface) is the energy of the surface containing n vacancies and 2n Y atoms, E(Zr) and E(Y) are the energies of the Zr and Y atoms, respectively.

III. Surface models

The pure cubic zirconia phase belongs to the space group Fm3m and has an fcc sublattice of zirconium atoms and oxygen atoms in the tetrahedral sites. Therefore, Zr atoms are 8-fold, while O atoms are 4-fold coordinated. YSZ bulk has also a fluorite like structure with an fcc cation sub-lattice of Zr and Y atoms and a simple cubic anion sub-lattice of O atoms and oxygen vacancies.

The (111) surface was taken into account for both systems because previous calculations showed that it remains the most stable even after the introduction of dopant atoms.^9,11,15,36 Moreover, following previous results, only the case of oxygen terminated surfaces was taken into account, because they are more stable than the Zr terminated ones.¹¹

Along the normal to the (111) surface there is a sequence of charged planes: the first plane is constituted by oxygen anions, the second by zirconium cations and the third again by oxygen ions. When cubic ZrO₂ crystals are cut along this direction, surface sites with three-fold coordinated oxygen and seven-fold coordinated Zr atoms are formed. In order to ensure the convergence of structural and electronic properties, the clean (111) surface of cubic ZrO₂ was modelled by a (2 × 2) supercell with a depth of 18 atomic layers (six O–Zr–O trilayers) in the direction perpendicular to the surface, for a total of 72 atoms (Zr₂₄O₄₈, Fig. 1).

Fig. 1 Top (left) and lateral (right) views of the (2 × 2) supercell of the (111) ZrO₂ surface. Oxygen atoms are in red, while zirconium atoms are in light blue. Pink for surface vacancies positions, violet for subsurface vacancies positions. Numbers refer to Zr atoms, letters to oxygen atoms. Zirconium atoms numbered 1, 2, 3, and 4 belong to the outermost Zr plane, while 5, 6, 7, and 8 belong to the plane under the subsurface vacancy.

The formation of oxygen defects on the clean surface was studied removing two oxygen atoms from this supercell (Zr₂₄O₄₆). Bogicevic et al.¹² observed that as a consequence of the repulsion between the vacancies, oxygen defects in zirconia tend to align along the [111] direction as third nearest neighbours for high (15–40 mol%) Y₂O₃ concentrations. They also observed that for more dilute composition the vacancies could space themselves at greater distances. The two vacancies were then placed along the [111] direction in a symmetrical way at the top and bottom of the supercell. This ensures to leave enough space between the two vacancies (∼13 Å) to avoid any spurious interactions between defects. Two possible positions for an oxygen vacancy on the (111) surface were tested. From Fig. 1, it is evident that one corresponds to a three-fold coordinated surface oxygen site (indicated as surface vacancy in the following), while the other corresponds to a four-fold coordinated bulk-like site (indicated as subsurface vacancy in the following).

Finally, to obtain a representative model for YSZ we created, as before, two oxygen vacancies, one at the top and the other at the bottom of the ZrO₂ supercell and, at the same time, we substituted four Zr with four Y atoms (Zr₂₀Y₄O₄₆). This allows mimicking the experimental percentage of 8 mol% Y₂O₃. One pair of Y atoms was positioned at the top and the other at the bottom of the supercell in a symmetrical way, each one in correspondence with one oxygen vacancy.

Two and five different configurations of the two Y³⁺ cations with respect to a surface or subsurface vacancy were taken into account, similarly to the work of Ganduglia-Pirovano et al.,⁵³ who studied the formation of oxygen vacancies and the localization of the excess electrons on different pair of sites on the (111) surface of the cubic fluorite structure of CeO₂.

There are four Zr atoms in the outermost Zr plane, three of them (1, 2, and 4 in Fig. 1) are in nearest-neighbour position (NN) to a surface vacancy, while the fourth one (3 in Fig. 1) is in a next nearest-neighbour (NNN) position with respect to it. For a subsurface vacancy, instead, Zr atoms 1, 2, and 3 of the outermost Zr layer and Zr atom 8 which belong to the plane below this defect are in NN positions, while Zr atom 4 on the plane above and Zr atoms 5, 6, and 7 in the plane below it are in NNN positions. If we consider the bulk truncated surface, NN and NNN Zr atoms are at a distance of respectively 2.22 Å and 4.20 Å away from the vacancy.

Hence for a surface vacancy, the two Y atoms can be introduced both NN to the defect or one can be NN and the other NNN to it, for a total of two possible configurations ((1,2)_NN–NN and (2,3)_NN–NNN). For a subsurface vacancy, the two Y atoms could be placed both NN to the defect, or one in NN and the other in NNN positions or they can be both in NNN sites, for a total of five different configurations ((1,2)_NN–NN), (2,8)_NN–NN), (1,4)_NN–NNN, (4,8)_NNN–NN, and (4,6)_NNN–NNN).

IV. Results and discussion

A. Isolated oxygen vacancy on (111) ZrO₂ surface

As a preliminary step toward the study of YSZ, the stability, the structural and electronic properties of the zirconia (111) surface containing only isolated oxygen vacancies were investigated.

When a neutral oxygen atom is removed, two electrons associated to an oxygen anion are left behind in the lattice and a neutral oxygen vacancy (V_O) is formed, with two possible spin states for the resulting system.

The energy of formation (E_f) of one surface or subsurface oxygen vacancy on the (111) surface was computed and reported in Table 1. E_f was calculated with respect to atomic oxygen (O) or molecular oxygen (O₂). The second species is generally preferred as reference in more recent works, because molecular oxygen is used in some oxidation techniques providing the right reference for the chemical potential and because the degeneracy of the ground state of triplet for the O atom is poorly described in DFT.³⁷

Table 1 Formation energy (E_f, in eV) of one surface or subsurface oxygen vacancy (with respect to 1/2 O₂ or to O) on the cubic ZrO₂ (111) surface, as a function of the spin state considered (T for triplet; S for singlet)

	Vacancy	Spin State	Ef (1/2 O2)	Ef (O)
a See ref. 39. Computed for bulk t-ZrO2.b See ref. 38. Computed for bulk m-ZrO2.c See ref. 37. Computed for bulk m-ZrO2.d See ref. 34. Computed for c(111).
This work	Surface	S	8.4	10.2
		T	8.5	10.3
	Subsurface	S	7.0	8.7
		T	7.3	9.1
Other works
GTO/B3LYP			7.2^a	—
PAW/PBE			5.9^b	8.9^b
PAW/GGA-II			—	8.9^c
PAW/PBE			—	8.8^d

---

The obtained values are in agreement with the ones reported in previous theoretical works, which, however, refer to the bulk structure of the tetragonal and monoclinic zirconia phases or to the cubic (111) surface,³⁴ even if in this latter case the role of different oxygen sites was not taken into account.

The singlet state is always found to be the most stable independently of the type of vacancy: it is more stable than the triplet one by 0.3 eV and 0.1 eV for a 4-fold coordinated subsurface and for the 3-fold coordinated surface vacancy, respectively. Considering the difference in stability, the following discussion is based only on the most stable singlet state.

Subsurface vacancies resulted to be the most stable, with formation energies of 1.4 and 1.5 eV (with respect to O₂ and O, respectively) lower than the corresponding energies for the surface one. Indeed, Syzgantseva et al.³⁸ already reported that even if surfaces are more reducible than bulk, due to the decrease in coordination of surface atoms, the most stable vacancy does not always correspond to those created from under-coordinated oxygen site.

The formation energy of the oxygen vacancy can be considered as a measure of the reducibility of the material. These values show that the reduction behaviour of ZrO₂ surfaces from the point of view of energetics is closer to the one of irreducible oxides like MgO (E_f(O) ∼ 10.6 eV and 9.8 eV for surfaces³⁸) rather than to the one of a reducible oxide such as TiO₂ (E_f(O) ∼ 7 eV for the bulk and 5.5–6 eV for surfaces).³⁸ The irreducible nature of ZrO₂ is thus confirmed.

Optimized geometries for the system with a surface or subsurface vacancy are reported in Fig. 2. Structural rearrangements are generally restricted to atoms in NN positions to the vacancy for both a surface and subsurface defect, in particular to NN oxygen atoms. Again, this is similar to a metal oxide like MgO, where F centres are stable and their formation is accompanied by small relaxation of the O atom NN to the defect, indicating electron trapping in the vacancies.^16,38 The surface vacancy is associated to the largest displacements, which cause the NN O atoms to move toward the vacancy and NN Zr atoms to move radially away from it to a distance of 2.39 Å (the distance of NN Zr atoms from the vacancy for the unrelaxed system is 2.22 Å). Smaller relaxations are observed for the most stable system with subsurface vacancies (see Table 2).

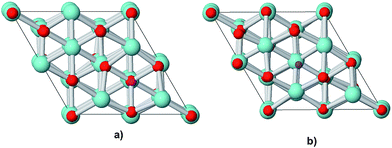Fig. 2 Top view of the supercell for the optimized geometry of the (111) surface with (a) surface or (b) subsurface vacancies.

Table 2 Displacements (in Å, from ideal positions) for the (111) surface with surface or subsurface oxygen vacancies. Atom labels refer to Fig. 1

Vacancy	Label	x	y	z
Surface	Oc(NN)	0.21	0.12	0.00
	Od(NN)	0.00	−0.24	0.00
	Ob(NN)	−0.21	0.12	0.00
	Oe(NNN)	0.00	−0.10	−0.02
	Zr1(NN)	0.03	0.02	−0.05
	Zr2(NN)	0.00	−0.04	−0.05
	Zr3(NNN)	0.00	0.00	0.11
	Zr4(NN)	−0.03	0.02	−0.05
Subsurface	Oe(NN)	−0.09	−0.10	−0.07
	Of(NN)	0.04	−0.13	−0.08
	Oa(NN)	0.09	−0.06	0.02
	Oc(NNN)	0.05	0.07	−0.03
	Zr1(NN)	0.00	−0.09	−0.02
	Zr2(NN)	0.06	0.03	−0.02
	Zr3(NN)	0.07	−0.04	0.04
	Zr4(NNN)	0.00	0.00	−0.08

---

There could be a relationship between relaxation and charge redistribution: the lower stability of the surface vacancies is accompanied by greater relaxation, which is in turn accompanied by a greater redistribution of charge density. Table 3 shows that, on the NN Zr atoms, the atomic charge decreases from +2.17 for the clean surface to +1.97 and +2.01 for a surface and a subsurface vacancy, respectively. Smaller decreases are observed for Zr atoms NNN to the vacancy.

Table 3 Mulliken atomic charges (in e) of selected Zr and O atoms of the clean (111) surface and of system with surface or subsurface vacancies. Atom labels refer to Fig. 1

Label	Clean	Oxygen vacancy
		Surface	Subsurface
Oe	−1.06	−1.06	−1.06
Of	−1.06	−1.06	−1.06
Oa	−1.06	−0.35	−1.06
Oc	−1.12	−1.11	−1.12
Od	−1.12	−1.11	−1.12
Ob	−1.12	−1.11	−0.46
Zr1	2.17	1.97	2.01
Zr2	2.17	1.97	2.01
Zr3	2.17	2.06	2.01
Zr4	2.17	1.97	2.17
Zr8	2.21	2.21	2.04

---

1. Electronic structure of oxygen vacancy. Before discussing the electronic structure of the defective system, we briefly describe the electronic properties of the clean (111) supercell for comparison.

The band structure and the total and atom-projected density of states (DOS) of the cubic (111) surface in Fig. 3 show a wide band between 0 and about −7 eV, which constitutes the top of the valence band (VB) and corresponds to the O-2p states. An appreciable contribution of the Zr-4d states to this band can also be seen from the density of states, indicating the presence of covalent bonding in the solid. The bottom of the conduction band (CB), between 5 and 12 eV, is instead made by the Zr-4d states that are clearly split into two groups, the low energy e_g and the high energy t_2g states, as a consequence of the crystal field associated to the cubic environment (O_h point group symmetry) of the surrounding oxygen ions.

Fig. 3 Band structure (a) and total and atom-projected density of states (b) for the clean (111) ZrO₂ surface.

The computed band gap is 5.48 eV, in line with previous theoretical calculations for ZrO₂ bulk and surfaces^17,35,54,55 and within the range of experimental values, which spread between 4 (EELS⁵⁶) and 6 eV (VUV⁵⁷). This large range of results (2 eV) could be due from one side to an overestimation of the VUV methods⁵⁷ and from the other to the attribution of the low energy part of the EELS states to transitions from the VB to still unassigned localized states in the gap, due to extrinsic defects (defect states or oxygen vacancy) or induced by the disorder in the YSZ solid solution.^57,58

Reduction via surface or subsurface vacancy formation leads to the creation of a defect state in the gap, (see Fig. 4). The two left electrons, which filled the O-sp states, now occupy a newly created vacancy state. Therefore, a new doubly occupied defect energy level appears in the band gap. As we can see from the DOS, it is mostly made by Zr-4d states, so we can imagine that after the removal, these two electrons are moving back from O to Zr, occupying a linear combination of the d orbitals of neighbouring Zr atoms.¹⁷ A small contribution of O-2p states could also be observed in Fig. 4. This defect state is localized in the vacancy region. It resembles a neutral V_O center in alkaline-earth oxides and has the typical structure of an F-center.^16,38,39

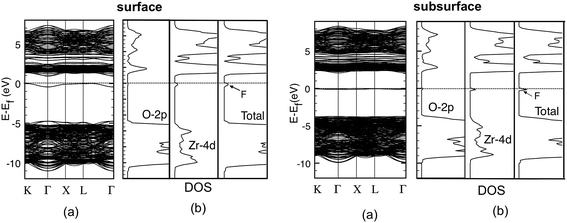Fig. 4 Band structure (a) and total and atom-projected density of states (b) for the system with surface (left) or subsurface (right) oxygen vacancies.

The main difference in the electronic structure of a surface or subsurface vacancy, except for the slightly more flat band structure of the latter system, is in the position of the defect state, which depends on the coordination of the site from which the oxygen atom is removed. For a surface vacancy, the defect level is 4.30 eV above the top of the VB and only 0.92 eV under the bottom of the CB. For the most stable subsurface vacancy, instead, the defect level is 3.58 eV above the top of VB and 2.07 eV under the bottom of the CB (see Table 4). Therefore, the presence of the vacancy state in the gap decreases the effective band gap, which results to be higher in the case of the most stable type of defect, compared to the other surface case.

Table 4 Band gap values (E_g) and positions of the defect level with respect to the valence band (VB) and the conduction band (CB) for surface and subsurface vacancies. All data in eV

Vacancy	Relative to VB	Relative to CB	Eg
Surface	4.30	0.92	5.66
Subsurface	3.58	2.07	5.79

---

Finally, from Fig. 5, it is interesting to note that the defect state is clearly observed both in the DOS of the unrelaxed system, i.e. the structure in which the atoms are in the centro-symmetric fluorite positions, and in that of the relaxed one, i.e. the structure obtained after the geometry optimization.

Fig. 5 Total and atom-projected DOS for the relaxed (plain line) and unrelaxed (dotted line) (111) supercell with a surface (a) or subsurface (b) oxygen vacancy.

B. Y₂O₃-doped (111) surface

When ZrO₂ is doped with Y₂O₃, for each pair of aliovalent Y³⁺ ions that substitutes a pair of Zr⁴⁺ cations, one oxygen vacancy must be created. Hence, since Y has one d-electron less than Zr, this corresponds removing one oxygen atom together with two electrons (O²⁻). For this reason, the corresponding vacancy should be a doubly positively charged vacancy (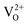) also called F²⁺ centre.

In Table 5, the energy due to the creation of the oxygen vacancies and to the simultaneous substitution of Zr with Y atoms (E_s−f) was reported for all the considered configurations of the four Y³⁺ cations with respect to a surface or subsurface vacancy (Fig. 6). According to eqn (3) and (4), the negative sign of the computed E_s−f values indicate that the doping with Y₂O₃ stabilizes the surface.

Table 5 Energy of substitution and of the formation of oxygen vacancies (with respect to 1/2O₂, E_f(1/2O₂), or with respect to O, E_f(O)) for different configurations of two Y dopant atoms with respect to a surface or subsurface oxygen vacancy on the cubic ZrO₂ (111) surface. All data in eV

Vacancy	Configuration	Ef (1/2O2)	Ef (O)
Surface	(1,2)NN–NN	−28.52	−24.98
	(2,3)NN–NNN	−31.14	−27.59
subsurface	(1,2)NN–NN	−29.43	−25.89
	(2,8)NN–NN	−29.98	−26.43
	(1,4)NN–NNN	−31.08	−27.53
	(4,8)NNN–NN	−30.94	−27.40
	(4,6)NNN–NNN	−32.05	−28.50

---

Fig. 6 Top (left) and top half lateral view (right) of optimized structure of the (2 × 2) supercell for the seven configurations taken into account for Zr₂₀Y₄O₄₆. Oxygen atoms are in red, zirconium atoms in light blue, and yttrium atoms in green. Pink for surface vacancies positions, violet for subsurface vacancies positions.

In particular the preferred configuration for the surface vacancy is (2,3)_NN–NNN. Indeed, for this kind of vacancy there is only one possible NNN position for the Y ions in the outermost zirconium plane and the (2,3)_NN–NNN configuration results to be the most stabilized one.

For a subsurface vacancy, we found the following stabilization order: (1,2)_NN–NN < (2,8)_NN–NN < (4,8)_NNN–NN < (1,4)_NN–NNN < (4,6)_NNN–NNN. Again, the preferred configuration is when the Y³⁺ ions are both NNN to the vacancy and, thus, the vacancy is likely to be bound to Zr⁴⁺ ions rather than to the dopant. Moreover, the most stable subsurface configuration ((4,6)_NNN–NNN), with two Y in NNN position, is 0.91 eV more stable than the most stable surface one.

In summary, subsurface vacancies are favoured and Y³⁺ ions occupy preferentially positions NNN to the defect, in agreement with experimental observations^23–27 and with previous YSZ bulk calculations.^12,17

The observed stability order can be rationalized considering two different aspects related to the doping of zirconia with aliovalent Y₂O₃. On one hand, relative to the host lattice ions Zr⁴⁺ and O²⁻, the dopant ion Y³⁺ and the vacancy can be seen as point defect charge −1 and +2, respectively, so that electrostatic interactions should be predominant. Coulomb considerations thus suggest that Y would most likely be NN to the vacancy. On the other hand, it was observed that the covalent nature of Zr–O bonds favours structure with lower Zr coordination, explaining in this way the higher stability at room temperature of the monoclinic ZrO₂ phase (where Zr atoms are 7-fold coordinated) over the tetragonal and cubic zirconia phases (where Zr atoms are 8-fold coordinated). Thus, if in presence of the vacancies, Zr atoms prefer to be NN to the defects while the Y ions prefer NNN positions, in YSZ there will be a reduction of the average zirconium coordination from 8 to a value closer to 7, similar to the value of monoclinic zirconia. This lowering of the Zr coordination is then at the base of the mechanism of stabilization of cubic zirconia through Y₂O₃-doping. Moreover, in a very simple view, Y³⁺ has a larger radius than Zr⁴⁺ and could thus prefer the eight-fold coordination, whereas the smaller Zr⁴⁺ can better accommodate the contraction of the lattice in the neighbourhood of the vacancy that accompanies its formation. We can then conclude that the stabilization and the preference for defect sites in YSZ is a consequence of a delicate compromise between size effects and electrostatic interactions.

Larger relaxations (between 0.3 and 1 Å) of the oxygen atoms NN to the vacancy with respect to the ones observed for the formation of oxygen vacancies on the pure (111) surface are observed. After the NN O atoms, the Zr atoms NN to the vacancies have the greatest displacements, while the Y atoms are associated to the smallest relaxations. Consequently, Zr atoms NN to the vacancy move away from it, while NN O atoms move toward the defect determining compression regions in the lattice near the defects. Generally, less stable configurations relax more. For Y³⁺ ions that are NN to defect sites, the average Y–O bond length is about 2.0 Å, while for dopant ions NNN to the vacancy it is of about 2.3 Å, very close to the value of the Y–O bond in Y₂O₃.⁵⁹ Considering that Y³⁺ ions are larger than Zr⁴⁺ ions, this confirms that Y³⁺ in NN position are compressed.

1. Electronic structure of Y₂O₃-doped (111) surface. The band gap values for the different configurations are reported in Table 6. These data can be compared with the band gap value obtained for the clean ZrO₂ (111) supercell (5.48 eV) and range between 5.49 and 5.80 eV. Even if the highest value is obtained for the most stable system, no simple correlation between the band gap and the stability or the position of the dopant atoms appear.

Table 6 Computed band gaps (E_g, in eV) for the different configurations of Y atoms with respect to a surface or subsurface vacancy on the (111) surface of YSZ

Vacancy	Configuration	Eg
Surface	(1,2)NN–NN	5.71
	(2,3)NN–NNN	5.65
Subsurface	(1,2)NN–NN	5.49
	(2,8)NN–NN	5.67
	(1,4)NN–NNN	5.61
	(4,8)NNN–NN	5.74
	(4,6)NNN–NNN	5.80

---

Band structure and total and atom-projected DOS of the different configurations (Fig. 7) are alike and show similar properties to the ones of the pure system: the VB is constituted by O-2p states, while the bottom of the CB is associated mainly to Zr-4d. However, there are two main differences. The first one is that Y-4d states also contribute to the bottom of the CB, but they lie at higher energies with respect to the corresponding Zr states. Moreover, it can be observed that when the Y atoms are in NNN position with respect to the vacancy, these Y-4d states are at even higher energies. This means that a stronger interaction with the vacancy determines a higher stabilization of Y-4d orbitals. The second difference is that the e_g − t_2g splitting of the Zr-4d states is present, especially in the least stable configuration (1,2)_NN–NN, but a broadening can be observed as a consequence of the doping and the disorder that the doping creates in the structure.

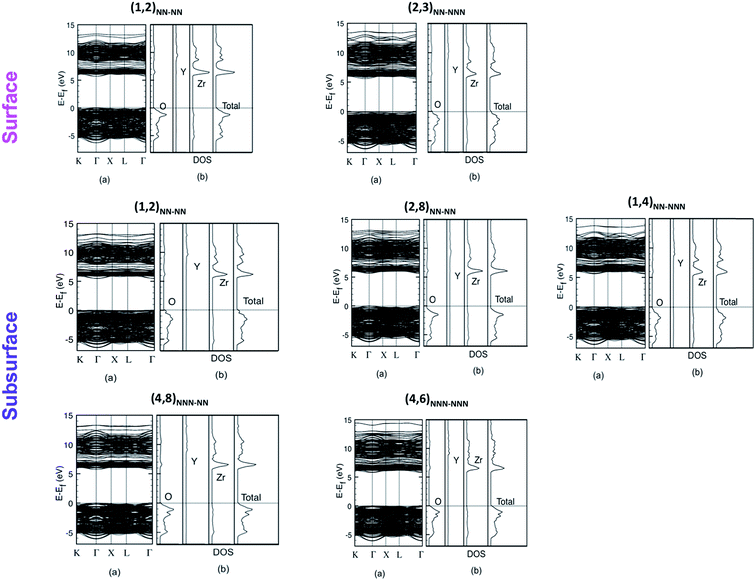Fig. 7 Band structure (a), total and atom-projected DOS (b) of the different configurations of the YSZ (111) surface.

Although an isolated peak, corresponding to an empty colour center () is present in the gap of the unrelaxed YSZ structure for each configuration, no such empty electronic state is observed in the gap of any optimized configuration (see for example the DOS for the unrelaxed and relaxed (4,6)_NNN–NNN configuration in Fig. 8). This result can be explained considering the perturbation in the periodic electrostatic Madelung potential due to the presence of , which increases the potential on the NN sites lowering the energy of the d states of the ions in that position with respect to the energy of the d states of cations far from the defect. This is why a mid-gap empty state is observed in the band structure and DOS of the unrelaxed system. The large relaxations of oxygen atoms NN to the vacancies generate a Madelung field that prevents the formation of the empty electronic state in the gap, compensating the perturbation of the potential in the neighbourhood of the vacancy and thus pushing the d states back in the CB (Fig. 9).^16,37 The deviation from the ideal cubic symmetry is then crucial for the understanding of the electronic properties of YSZ.

Fig. 8 Total and atom-projected DOS for the relaxed (plain line) and unrelaxed (dotted line) (4,6)_NNN–NNN configuration of YSZ.

Fig. 9 Electrostatic potential plots for the (4,6)_NNN–NNN configuration, before (a) and after (b) the relaxation of the system. Yellow for positive and light blue for negative values. Isosurface values of 0.005 au.

V. Conclusions

In this work, the formation of oxygen defects on the (111) surface of cubic zirconia as well as the stabilization of this surface through doping with the aliovalent Y₂O₃ oxide were investigated in detail by periodic DFT calculations. Two possible vacancy positions and two possible spin states for each position were taken into account to study the isolated oxygen vacancies on the clean (111) surface, as well as seven different configurations of Y atoms and oxygen vacancies for the Y₂O₃-doped (111) surface.

Concerning neutral oxygen vacancy (V_O) formed after the removal of O atoms from the clean surface, formation energies ranging between 8 and 10 eV were obtained. These values are close to the ones of irreducible oxide like MgO. The type of site from which the O atom is removed seems also to play an important role, as subsurface vacancies are found to be ∼1.4–1.5 eV more stable than surface ones. Small relaxation accompanies the formation of V_O, suggesting that the two electrons left behind by the removed oxygen atoms are trapped in the vacancy vicinity. Indeed, surface vacancies, which are less stable and relax more in comparison to subsurface one, are also associated to a greater redistribution of charge density. As a consequence of the electrons occupying the vacancy state, a doubly occupied defect energy level appears in the band gap of ZrO₂. These results evidence the different intrinsic conduction properties of zirconia, an ionic conductor, with respect to other oxides, that can be used in composites electrolytes for LT-SOFC applications, as CeO₂. This irreducible nature is important since CeO₂ can suffer, in SOFC operating conditions, of partial reduction of Ce⁴⁺ ions into Ce³⁺ cations, becoming a mixed electron/ion conductor. Naturally, these differences should be taken into account when comparing the properties and performances of different composite in order to elucidate the conduction properties of different composite materials.

As regards the doping with yttria, the computed values for the energy due to the creation of the oxygen vacancies () and simultaneously to the substitution of Zr with Y atoms (E_s−f) confirm, as expected, that doping of the (111) zirconia surface with Y₂O₃ is accompanied by the stabilization of the system. Subsurface vacancies are favoured also in this case and Y ions occupy preferentially the positions NNN to the defect. Indeed, of all the tested configurations, the (4,6)_NNN–NNN, with a subsurface vacancy and two Y atoms both in NNN position to the defect, is found to be by far the most stable. Consequently, Zr⁴⁺ ions should prefer to be NN to the vacancies, with the consequent reduction of their coordination number, which supports the idea that the stabilization mechanism is related to the lowering of the coordination of Zr atoms. Moreover, upon vacancy formation, the lattice contraction is easier when the NN ions are Zr⁴⁺ cations rather then the larger Y³⁺ cations, which instead prefer higher coordination numbers. Large relaxations are observed for all the studied configurations. They are associated to the O atoms NN to the vacancies, which move toward the vacancy, thus determining the contraction of the lattice in the defect region. This deviation from the ideal cubic geometry is fundamental to explain the electronic properties of the system and can be rationalized by electrostatic potential arguments.

In conclusion, this systematic investigation of the dopant and vacancies arrangement on the (111) surface allowed us to clarify the effect of the doping on the structural properties of the YSZ (111) surface, to elucidate the proposed mechanism of stabilization, and to explain the electronic features of YSZ where oxygen vacancies, that determine the ionic conductivity of the material, are present but mid-gap states are not observed. Finally, this work allowed to find a model of the YSZ (111) surface (i.e. the most stable arrangement with Y atoms and oxygen in (4,6)_NNN–NNN configuration) that is reliable (it is derived from a detailed comparison of the structural and electronic features of different configurations) and that has the advantage of reproducing the experimental 8 mol% Y₂O₃ amount. This model could be used in future studies, for example to simulate the oxide-carbonate interface of composite electrolytes, in order to further elucidate the basic operating principles of LT-SOFCs.

References

1. R. M. Ormerod, Chem. Soc. Rev., 2003, 32, 17–28.
2. X. Wang, Y. Ma and B. Zhu, Int. J. Hydrogen Energy, 2012, 37, 19417–19425.
3. X. Wang, Y. Ma, S. Li, A.-H. Kashyout, B. Zhu and M. Muhammed, J. Power Sources, 2011, 196, 2754–2758.
4. M. Benamira, A. Ringuedé, L. Hildebrandt, C. Lagergren, R.-N. Vannier and M. Cassir, Int. J. Hydrogen Energy, 2012, 37, 19371–19379.
5. M. Benamira, A. Ringuedé, V. Albin, R.-N. Vannier, L. Hildebrandt, C. Lagergren and M. Cassir, J. Power Sources, 2011, 196, 5546–5554.
6. A. S. V. Ferreira, T. Saradha, F. L. Figueiredo and F. M. B. Marques, Int. J. Energy Res., 2011, 35, 1090–1099.
7. N. Clausen, M. Ruhle and A. H. Heuer, in Advances in Ceramics, The American Ceramic Society, Columbous, OH, 1984, vol. 12.
8. X. Xia, R. J. Oldman and C. R. A. Catlow, J. Mater. Chem., 2011, 21, 14549–14558.
9. X. Xia, R. Oldman and R. Catlow, Chem. Mater., 2009, 21, 3576–3585.
10. A. Eichler, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 174103–174108.
11. A. Eichler and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 045402–045408.
12. A. Bogicevic, C. Wolverton, G. Crosbie and E. Stechel, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 014106–014114.
13. R. Devanathan, W. Weber, S. Singhal and J. Gale, Solid State Ionics, 2006, 177, 1251–1258.
14. R. Krishnamurthy, Y.-G. Yoon, D. J. Srolovitz and R. Car, J. Am. Ceram. Soc., 2005, 87, 1821–1830.
15. G. Ballabio, M. Bernasconi, F. Pietrucci and S. Serra, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 075417–75426.
16. G. Stapper, M. Bernasconi, N. Nicoloso and M. Parrinello, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 797–810.
17. B. Králik, E. Chang and S. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 7027–7036.
18. A. D. Mayernick, M. Batzill, A. C. T. van Duin and M. J. Janik, Surf. Sci., 2010, 604, 1438–1444.
19. V. Stefanovich, A. L. Shluger and C. R. Catlow, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 11560–11571.
20. S. Fabris, A. T. Paxton and M. W. Finnis, Acta Mater., 2002, 50, 5171–5178.
21. W. L. Roth, R. Wong, A. I. Goldman, E. Canova, Y. H. Kao and B. Dunn, Solid State Ionics, 1986, 18 & 19, 1115–1119.
22. D. Steele and B. E. F. Fender, J. Phys. Chem. Solids, 1974, 7, 1–11.
23. C. R. A. Catlow, A. V. Chadwick, G. N. Greaves and L. M. Moroney, J. Am. Ceram. Soc., 1986, 69, 272–277.
24. B. W. Veal, A. G. McKale, A. P. Paulikas, S. J. Rothman and L. J. Nowicki, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 150, 234–240.
25. P. Li, I. Chen and J. E. Penner-Hahn, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 10082–10089.
26. P. Li, I. Chen and J. E. Penner-Hahn, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 10074–10081.
27. P. Li, I. Chen and J. E. Penner-Hahn, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 10063–10073.
28. L. Jin, Q. Yu, A. Rauf and C. Zhou, Solid State Sci., 2012, 14, 106–110.
29. G. P. Cousland, R. A. Mole, M. M. Elcombe, X. Y. Cui, A. E. Smith, C. M. Stampfl and A. P. J. Stampfl, J. Phys. Chem. Solids, 2014, 75, 351–357.
30. C. Morterra, G. Cerrato and L. Ferrato, Mater. Chem. Phys., 1994, 37, 243–251.
31. M. De Ridder, R. G. Van Welzenis, H. H. Brongersma and U. Kreissig, Solid State Ionics, 2003, 158, 67–77.
32. A. Bernasik, K. Kowalski and A. Sadowski, J. Phys. Chem. Solids, 2002, 63, 233–239.
33. X. Xia, R. J. Oldman and C. R. A. Catlow, J. Mater. Chem., 2012, 22, 8594–8612.
34. M. Shishkin and T. Ziegler, J. Phys. Chem. C, 2008, 112, 19662–19669.
35. C. Ricca, A. Ringuedé, M. Cassir, C. Adamo and F. Labat, J. Comput. Chem., 2015, 36, 9–21.
36. A. Christensen and E. Carter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 8050–8064.
37. A. Foster, V. Sulimov, F. Lopez Gejo, a. Shluger and R. Nieminen, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 224108.
38. O. A. Syzgantseva, M. Calatayud and C. Minot, J. Phys. Chem. C, 2012, 116, 6636–6644.
39. C. Gionco, M. C. Paganini, E. Giamello, R. Burgess, C. Di Valentin and G. Pacchioni, Chem. Mater., 2013, 25, 2243–2253.
40. R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco and M. Llunell, CRYSTAL09 User's Manual, University of Torino, Torino, 2009.
41. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
42. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
43. Y. L. Yang, X. L. Fan, C. Liu and R. X. Ran, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 434, 7–13.
44. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
45. W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298.
46. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283.
47. T. Bredow and M. Lerch, Zeitschrift für Anorg. und Allg. Chemie, 2004, 630, 2262–2266.
48. J. C. Barthelat, P. Durand and A. Serafini, Mol. Phys., 1977, 33, 159.
49. J. C. Barthelat and P. Durand, Gazz. Chim. Ital., 1978, 108, 225–236.
50. Basis set available at the following web site, http://www.crystal.unito.it/basis-sets.php.
51. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
52. The default grid in CRYSTAL09 has 55 radial points and a maxiumum 434 angular points, while the extrafine integration scheme corresponds to 75 radial points and 975 angular points. See ref. 40.
53. M. Ganduglia-Pirovano, J. Da Silva and J. Sauer, Phys. Rev. Lett., 2009, 102, 026101–026104.
54. F. Gallino, C. Di Valentin and G. Pacchioni, Phys. Chem. Chem. Phys., 2011, 13, 17667–17675.
55. T. Bredow, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 144102–144111.
56. D. McComb, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 7094–7102.
57. R. French, S. Glass, F. Ohuchi, Y. Xu and W. Ching, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 5133–5142.
58. L. Dash, N. Vast, P. Baranek, M.-C. Cheynet and L. Reining, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 245116–245117.
59. N. Thromat, C. Noguerra, M. Gautier, F. Jollet and J. P. Duraud, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 7904–79011.

---