Proposed correlation of glass formation ability with critical dosage for the amorphous alloys formed by ion beam mixing†
M. H. Yang,
J. H. Li* and
B. X. Liu
Key Laboratory of Advanced Materials (MOE), School of Materials Science and Engineering, Tsinghua University, Beijing 100084, China. E-mail: lijiahao@mail.tsinghua.edu.cn
First published on 29th January 2015
Abstract
A negative correlation of glass formation ability with the critical dosage, i.e. minimum ion-dosage, is first proposed for the amorphous alloys formed by ion beam mixing (IBM), i.e. the lower the critical ion-dosage (Dc) the better the glass formation ability (GFA), suggesting that Dc could serve as an indicator to the GFA of these alloys. The correlation is not only supported by the results of experiments such as IBM and liquid melt quenching (LMQ), but is also proven to be relevant by thermodynamic calculations. The proposal helps to bridge the gap of experimental data between different producing methods, e.g. making it possible to apply the IBM results to designing alloy compositions when producing metallic glasses by LMQ. The limitations and prospects are also presented in the discussion.
Due to their excellent mechanical, chemical and physical properties, amorphous alloys, i.e. metallic glasses, have been attracting great attention as a prominent class of functional and structure materials.1,2 To date, a great number of binary, ternary and even multicomponent amorphous alloys have been obtained through a variety of powerful producing techniques, such as liquid melt quenching (LMQ), ion beam mixing (IBM), and mechanical alloying (MA).3,4 In order to facilitate the production of amorphous alloys, one of the basic issues is to search for an appropriate method or parameter to indicate the glass-formation ability (GFA) that describes the easiness or difficulty of metallic glass formation. In principle, GFA not only depends on the applied producing techniques, but is also governed by the intrinsic characteristics of the system. In practice, the GFA is evaluated usually by the maximum size (Dmax) of the obtainable metallic glasses, or the minimum cooling speed (Rc) to produce metallic glasses by LMQ, e.g. copper model casting.5 The smaller Rc or the larger Dmax is, the better GFA of the alloy should be. However, there is still lack of a proper parameter to describe the GFA of those amorphous alloys formed by IBM. The present work attempts to solve this problem by correlating the GFA of those amorphous alloys with the dosage of IBM.
Ion beam mixing is a process of far-from equilibrium and is commonly divided into three steps, i.e. the atomic collision cascade, relaxation and delayed period. Generally, the first and second steps are of importance in determining the structural characteristics of the alloy phases, however, the last step has no considerable effect on the structure of alloys. In the first step, when an ion, with the energy higher than a critical value, impacts on the surface and penetrates into the multilayered films, an atomic collision cascade will be triggered, i.e. the impinging ion knocks out an atom from its own site and the knocked-out atom, if its energy is still high enough, will result in secondary collision, third collision, and so on and so forth. The atoms are excited into such violent motion by the impinging ions and knocked-out atoms that not only the crystalline lattices are destroyed but also the interface of multilayered film are smeared out, thus obtaining a highly disordered atomic mixture. Apparently, the uniform mixing is induced by dynamic collision process together with the associated irradiation enhanced diffusion. In the relaxation step, the highly energetic mixture should somehow relax towards equilibrium. However, whether or not the mixture can reach an equilibrium state depends on the kinetics conditions available in IBM.6 An alternatively way of examining the process of ion irradiation is to consider the energy deposition in the surface of the target material and a concept of thermal spike was introduced. As radiation defects created in materials by highly energetic ions are cylindrical, a time-dependent thermal transient process is expressed in cylindrical geometry:
 | (1) |
 | (2) |
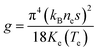 . Here, kB is the Boltzmann's constant, ne is the electron density and s is the speed of sound in the metal.
. Here, kB is the Boltzmann's constant, ne is the electron density and s is the speed of sound in the metal.
From the numerical analysis of the coupled equations, the lattice temperature T(r,t) at each time t and radius r can be calculated. The maximum temperature Tmax(r) reached by the lattice at a radius r from the ion path is dependent on the electronic stopping Se. The temperature of electronic system increases during a time equivalent to the energy deposition time ∼10−15 s. Then the lattice temperature increases mainly because of the electron–phonon interaction. The maximum lattice temperature ∼104 K is reached when both systems are in equilibrium at a mean time equal to Ce(Te)/g(Te), which is of the order of 10−12 s. Above a certain Se threshold, this lattice temperature may exceed the melting temperature Tm of the lattice within a cylinder of radius rm, i.e. latent track, of the order of a few nm. After that time both temperatures decrease and are governed by the thermal conductivity. The molten phase is quenched with an effective cooling rate of the order of 1015 K s−1. Such a high cooling speed makes the kinetic condition for alloy phase formation to be extremely restricted, thus allowing only peculiar phases, i.e. amorphous or simple structured crystalline alloys, to be formed. Considering ion beam induced interface amorphization to take place, when the substrate temperature is decreased lower than some critical value Tr, which is a function of implant conditions, the sign of the growth rate Vr = −dh/dD (where h is the a-layer thickness, and D is the delivered dose) changes. This transition from the crystallization to amorphization regime can also be caused by increasing the accelerating voltage, the beam flux F, and also dependent on irradiation conditions, such as ion species and energy, dopant type and concentration, and a/c interface orientation with respect to the crystallographic axes.7
Based on the above explanation, it can be seen that the key factor in formation of amorphous alloys is to destroy the structure of the crystalline lattices by ion beam. The more stable, or the more difficult to destroy the crystalline lattice, the more difficult the amorphous alloys to be formed. Therefore, to obtain the amorphous alloys, more ion-dosage is required to destroy the crystalline lattice. The corresponding alloy could therefore be considered as a poor glass-former, i.e. the GFA of this alloy is also poor. It suggests that, under the same circumstance such as accelerating voltage and the beam flux, more ion-dosage is needed to produce this amorphous alloy by IBM. Naturally, if the GFA of an alloy is good, then the small ion-dosage is needed to produce this amorphous alloy. For either good or poor glass-former, it is reasonable that there is a critical ion-dosage Dc, i.e. the minimum ion-dosage, less which no uniform amorphous alloys could be obtained. However, the critical ion-dosage Dc for a good glass-former is lower than that for a poor glass-former to produce amorphous alloys. It suggests that there exists a negative correlation between the critical ion-dosage Dc and the GFA of amorphous alloys formed by IBM, i.e. the lower the critical ion-dosage Dc, the better the GFA of an alloy. To verify the relevance of this negative correlation, the IBM experiments were carried out on the Ni–Mo–(Ti,Zr) multilayered films.
In present study, the overall compositions of the Ni–Mo–(Ti,Zr) multilayered films were designed to be Ni40Mo20(Ti1−xZrx)40, x = 0, 0.25, 0.50, 0.75 and 1. The thickness of a multilayered film is designed as about 40 nm to match the irradiating ion range.8 The desired multilayered films were prepared by depositing alternatively pure Ni (99.99%), Mo (99.99%), Ti (99.99%) and Zr (99.99%) at a rate of 0.5 Å s−1 onto newly cleaved NaCl single crystal substrates in an e-gun evaporation system with a vacuum level of 10−6 Pa. The prepared multilayered films were then irradiated by 180 keV xenon ions in an implanter with a vacuum level better than 5 × 10−4 Pa and the irradiation doses were in a range from 1 × 1015 to 7 × 1015 Xe+ per cm2. During the irradiation, the sample holder was cooled by liquid nitrogen (77 K) and the ion beam current density was confined to be about 2 μA cm−2 to avoid an overheating effect. The real compositions of the as-deposited multilayered films were all determined by X-ray fluorescence (XRF). The real compositions are (1) Ni41Mo21Ti38, (2) Ni41Mo18Ti31Zr10, (3) Ni39Mo20Ti21Zr20, (4) Ni40Mo22Ti10Zr28, and (5) Ni40Mo22Zr38, while the designed compositions are (1) Ni40Mo20Ti40, (2) Ni40Mo20Ti30Zr10, (3) Ni40Mo20Ti20Zr20, (4) Ni40Mo20Ti10Zr30, and (5) Ni40Mo20Zr40. It was found that there were few differences between the real compositions and the designed compositions, indicating the accuracy of the film composition controlling. For structural characterization, the Ni–Mo-(Ti,Zr) films at deposition state and upon irradiation were examined by bright field image and selected area diffraction (SAD) of transmission electron microscopy (JEM 200 CX). High-resolution transmission electron microscopy (HRTEM) was also used for analyzing the bright field image of samples. The results of IBM experiment were summarized in Table 1.
| γ* | Ni40Mo20Ti40 | Ni40Mo20Ti30Zr10 | Ni40Mo20Ti20Zr20 | Ni40Mo20Ti10Zr30 | Ni40Mo20Zr40 |
|---|---|---|---|---|---|
| 2.04 | 2.97 | 3.08 | 3.06 | 2.69 | |
| a A, amorphous phases; B, Mo-based bcc solid solutions. | |||||
| 1 × 1015 | A + B | A + B | A + B | A + B | A + B |
| 3 × 1015 | A + B | A | A | A | A + B |
| 5 × 1015 | A + B | A | A | A | A |
| 7 × 1015 | A | A | A | A | A |
The IBM experiment shows that amorphous alloys could be formed in the Ni40Mo20(Ti1−xZrx)40 multilayered films upon irradiation to appropriate dosages. At lower ion-dosage, the mixtures of amorphous and crystalline phases were formed, while the uniform amorphous alloys were obtained with increasing the dosage of ion beam mixing to higher values. Fig. 1(a) shows the bright field image of the Ni40Mo20Ti10Zr30 multilayered films upon irradiation of 1 × 1015 Xe+ per cm2. The corresponding SAD pattern was shown in Fig. 1(b), in which both the diffused halos of amorphous phases and the diffraction rings of crystalline phase could be distinguished. Upon irradiation to the dose of 3 × 1015 Xe+ per cm2, the Ni40Mo20Ti10Zr30 multilayered films turned into an uniform amorphous phase. It can be seen from Fig. 1(c) that the bright field image exhibits a gray matrix of a typical amorphous configuration, which is confirmed by diffused halos, instead of diffraction rings, in the corresponding SAD pattern in Fig. 1(d). One notes that the similar results were also obtained in Ni40Mo20Ti20Zr20 and Ni40Mo20Ti30Zr10 quaternary multilayered films. Besides, Table 1 also shows that the minimum ion-dosages, i.e. critical ion-dosages Dc, to form uniform amorphous phases in the Ni40Mo20(Ti1−xZrx)40 multilayered films are different. For example, to form an uniform Ni40Mo20Ti40 amorphous alloy by IBM in the present study, the ion-dosages should not be less than 7 × 1015 Xe+ per cm2, otherwise only a mixture of amorphous and crystalline phases were obtained, i.e. the corresponding critical ion-dosage Dc = 7 × 1015 Xe+ per cm2. Similarly, the Dc of Ni40Mo20Ti10Zr30, Ni40Mo20Ti20Zr20 and Ni40Mo20Ti30Zr10 are 3 × 1015 Xe+ per cm2, while the Dc of Ni40Mo20Zr40 is 5 × 1015 Xe+ per cm2. According to the above proposal that there is a negative correlation between the Dc and the GFA of alloys, the GFAs of the former three alloys are better than the latter two and the GFA of Ni40Mo20Zr40 is again better than Ni40Mo20Ti40 alloy.
From a theoretical viewpoint, the GFA of an alloy not only depends on the applied producing techniques, but also is governed by the intrinsic characteristics of the system, and therefore the GFA could be estimated from some intrinsic properties of the alloy. In the past, by considering the underlying insights of glass-formation, a dozen of criteria or parameters have been developed to compute the GFA of a variety of alloys. Among them, the most famous one is the reduced glass transition temperature Trg = Tg/Tm proposed by Turnbull, where Tg and Tm stand for the glass transition temperature and the melting point, respectively.9 Later on, Lu et al. confirmed that Trg computed by Tl/Tg shows a better correlation with GFA than that given by Tg/Tm for multicomponent alloy systems, where Tl is liquidus temperature.10 Typically, the Trg value of the known metallic glasses varies between 0.4 and 0.7.11 Based on the considerations of super-cooled liquid stability against crystallization, Inoue et al. proposed another parameter, i.e. the super-cooled liquid region ΔTxg, to indicate the GFA of an alloy.12 It should be noted that this criterion considers only the thermal stability of the glass that has been formed and does not actually consider the ease with which the liquid forms the glass.13 By combining the Trg and ΔTxg to one, Lu and Liu also developed a new parameter γ = Tx/(Tg + Tl) to predict the GFA of metallic glasses.5 With the synthesis of a very large number of BMGs, a number of new parameters, for example, α = Tx/Tl,14 β = Tx/Tg + Tg/Tl,14 δ = Tx/(Tl − Tg),15 and γm = (2Tx − Tg)/Tl (ref. 16) were proposed. Majority of these new parameters were derived using the characteristic temperatures such as Tg, Tx and Tl and their different combinations. Alternatively, by considering the competition of amorphous against crystalline phases and basing thermodynamic analysis, a simple parameter γ* ∝ ΔHamor/(ΔHcryt − ΔHamor) was proposed by Xia et al. to indicate the GFA of metallic glasses.17,18 Here ΔHamor and ΔHcryt stand for the formation enthalpies of the amorphous and competing crystalline phases, respectively. Unlike those parameters derived from characteristic temperatures, the parameter γ* can be obtained by simple thermodynamic calculation, e.g. using Miedema model, avoiding the complicated and time-consuming experimental tests and measurements.19 Besides, the parameter γ* is found to be widely accepted among the research community of metallic glasses.20 For instance, great deals of LMQ experiments have shown a strong correlation of the parameter γ* to the largest sizes of obtained glasses, suggesting that parameter γ* could reasonably reflect the GFA of an alloy.21 Since the critical ion-dosage Dc is proposed to correlate with the GFA of amorphous alloys, a correlation should also exist between the parameter γ* and the critical ion-dosage. In order to prove the assumption, the values of parameter γ* were computed for the Ni40Mo20 (Ti1−xZrx)40 alloys and the calculated results are given in Table 1. Concerning the details of parameter γ* and corresponding thermodynamic calculation, the readers are referred to the ref. 22 and 23 and the appendix below.
Thermodynamic calculation indeed reveals a negative correlation between the parameter γ* and the critical ion-dosage Dc. For example, Table 1 shows that the calculated γ* of Ni40Mo20Ti30Zr10, Ni40Mo20Ti20Zr20 and Ni40Mo20Ti10Zr30 alloys are apparently larger than that of the Ni40Mo20Ti40 and Ni40Mo20Zr40 alloys. Not coincidentally, the critical ion-dosages Dc of the former three are 3 × 1015 Xe+ per cm2, and pronouncedly lower than that of the latter two. Besides, since the γ* values of Ni40Mo20Ti30Zr10, Ni40Mo20Ti20Zr20 and Ni40Mo20Ti10Zr30 alloys are so closed to each other, all around 3, the present study does not distinguish the difference of their critical ion-dosages. The calculated γ* values of Ni40Mo20Ti10Zr30, Ni40Mo20Zr40 and Ni40Mo20Ti40 alloys are 3.06, 2.69 and 2.04, respectively, i.e. smaller and smaller, showing that their GFAs become poorer and poorer. This conclusion is also confirmed by the corresponding critical ion-dosages, i.e. 3 × 1015, 5 × 1015, 7 × 1015 Xe+ per cm2, respectively. This correlation between the γ* and Dc proves that the critical ion-dosage Dc is capable to sever as an indicator of the GFA of alloy, e.g. the lower the critical ion-dosage, the better the GFA of an alloy, the larger the parameter γ* is and vice versa.
In order to further testify the relevance of the obtained conclusion, some IBM experimental data are collected and shown in Fig. 2,24–30 in which the calculated γ* values are also given. One can vividly see from this figure that there exists a negative correlation between the γ* and Dc. With the incensement in critical ion-dosages, the γ* values become smaller and smaller, both showing the corresponding GFA become poorer and poorer. The correlation between the GFA and critical ion-dosage is not only supported by the present IBM experiments and thermodynamic calculation, but also is proven to be relevant by the results of other LMQ. It has been reported that when irradiated to a dose of 5 × 1015 Xe+ per cm2, unique Cu65Zr35 amorphous alloy was obtained by IBM and its composition could be made into bulk metallic glass rods with 2 mm in diameter.31 To take another example, the γ* value and Dc for Ni63Nb28Zr9 and Ni79Nb12Zr9 alloy are 3.72, 0.6 × 1015 Xe+ per cm2 and 2.93, 3 × 1015 Xe+ per cm2, while the critical diameter Dmax of Ni63Nb28Zr9 and Ni79Nb12Zr9 amorphous alloy are about 3 and 1 mm, respectively.32 Compared to the Ni79Nb12Zr9 alloy, the Ni63Nb28Zr9 alloy has a lower Dc, a higher γ* and a larger Dmax, indicating that the alloy with lower Dc is easier to destroy the structure of the crystalline lattices upon IBM, obtaining a larger Dmax. More importantly, this suggest that the present proposed correlation bridge the gap between IBM and LMQ experimental results, e.g. making it possible to apply the Dc to designing the alloy composition in producing metallic glasses by LMQ.
 | ||
| Fig. 2 The correlation between the parameter γ* value and critical ion-dosage Dc of amorphous alloys formed by IBM (a) upon 180 keV, (b) upon 200 keV. | ||
From the above discussion, it can be concluded that there is a negative correlation of GFA with the critical dosage for the amorphous alloys formed by IBM, i.e. the lower the critical ion-dosage Dc the better the GFA, suggesting that Dc could serves as an indicator to GFA of these alloys. Nevertheless, one should be aware that this correlation just holds qualitatively and approximately. In fact, extensive experimental results have shown that due to the extremely restricted kinetic condition, IBM should be executed under an appropriate condition, e.g. the samples should be retained at a relatively low temperature, the ion beam current density should be relatively low to avoid an overheating effect, etc.6,7 Considering the practical experimental procedures, there are some discrepancies to the proposed method. These discrepancies are thought to be based on the following three aspects: (1) the IBM experiments should be carried out under the same circumstance, such as accelerating voltage, ion beam current density and ion irradiation at relatively low temperature, (2) difficulty of precisely determining the minimum ion-doses to keep the melt amorphous without precipitation of any crystals during solidification, (3) limitation of the number of experimental results compared to the entire compositions of the systems. The first and second aspect would not affect the application of the proposed method, as the irradiation dose could be precisely controlled by adjusting the ion current under the same experimental circumstance, thus enabling researchers to trace the details of the amorphous phase formation. For the third aspect, it indicates that not all the compositions have been studied due to the scientific and application interests.
Conclusions
In summary, the critical ion-dosage, Dc, could be considered as an indicator to the glass formation ability (GFA) of the alloy formed by ion beam mixing (IBM). The correlation of the critical dosage Dc with the GFA, i.e. the lower the Dc, the better the GFA, is not only supported by the results of experiments such as IBM and liquid melt quenching (LMQ), but also proven to be relevant by thermodynamic calculations. The proposal correlation helps to bridge the gap of experimental data between different producing methods, e.g. making it possible to apply the IBM results to designing the alloy composition in producing metallic glasses by LMQ.Acknowledgements
The authors are grateful for the financial support from the National Natural Science Foundation of China (51131003), the Ministry of Science and Technology of China (973 Program 2011CB606301, 2012CB825700), and the Administration of Tsinghua University.References
- A. Inoue, Acta Mater., 2000, 48, 279–306 CrossRef CAS.
- Z. P. Lu, H. Bei and C. T. Liu, Intermetallics, 2007, 15, 618–624 CrossRef CAS PubMed.
- A. Inoue, T. Zhang and T. Masumoto, Mater. Trans. JIM, 1989, 30, 965–972 CrossRef CAS.
- H. W. Kui, A. L. Greer and D. Turnbull, Appl. Phys. Lett., 1984, 45, 615–616 CrossRef CAS PubMed.
- Z. P. Lu and C. T. Liu, Acta Mater., 2002, 50, 3501–3512 CrossRef CAS.
- B. X. Liu, W. S. Lai and Q. Zhang, Mater. Sci. Eng., R, 2000, 29, 1–48 CrossRef.
- I. P. Jain and G. Agarwal, Surf. Sci. Rep., 2011, 66, 77–172 CrossRef CAS PubMed.
- J. F. Ziegler, J. P. Biersack and U. Littmark, The Stopping and Range of Ions in Solids, Pergamon Press, New York, 1985, ch. 2, pp. 79–82 Search PubMed.
- D. Turnbull, Contemp. Phys., 1969, 10, 473–483 CrossRef CAS.
- Z. P. Lu, H. Tan, Y. Li and S. C. Ng, Scr. Mater., 2000, 42, 667–673 CrossRef CAS.
- Z. Y. Suo, K. Q. Qiu, Q. F. Li, J. H. You, Y. L. Ren and Z. Q. Hu, Mater. Sci. Eng., A, 2010, 528, 429–433 CrossRef PubMed.
- A. Inoue, T. Zhang and T. Masumoto, Mater. Trans. JIM, 1990, 31, 177–183 CrossRef CAS.
- M. C. Weinberg, J. Non-Cryst. Solids, 1994, 167, 81–84 CrossRef CAS.
- K. Mondal and B. S. Murty, J. Non-Cryst. Solids, 2005, 351, 1366–1371 CrossRef CAS PubMed.
- Q. Chen, J. Shen, D. Zhang, H. Fan, J. Sun and D. G. Mccartney, Mater. Sci. Eng., A, 2006, 433, 155–160 CrossRef PubMed.
- X. H. Du, J. C. Huang, C. T. Liu and Z. P. Lu, J. Appl. Phys., 2007, 101, 086108 CrossRef PubMed.
- L. Xia, S. S. Fang, Q. Wang, Y. D. Dong and C. T. Liu, Appl. Phys. Lett., 2006, 88, 171905 CrossRef PubMed.
- L. Xia, W. H. Li, S. S. Fang, B. C. Wei and Y. D. Dong, J. Appl. Phys., 2006, 99, 026103 CrossRef PubMed.
- F. R. De Boer, R. Boom and W. C. Mattens, Cohesion in Metals: Transition Metal Alloys, North-Holland, Amsterdam, 1989, ch. 2, pp. 79–82 Search PubMed.
- X. Ji, Y. Pan and F. Ni, Mater. Des., 2009, 30, 842–845 CrossRef CAS PubMed.
- A. H. Cai, X. Xiong, Y. Liu, W. K. An, G. J. Zhou, Y. Luo, T. L. Li and X. S. Li, J. Non-Cryst. Solids, 2013, 376, 68–75 CrossRef CAS PubMed.
- T. L. Wang, J. H. Li and B. X. Liu, Phys. Chem. Chem. Phys., 2009, 11, 2371–2373 RSC.
- N. Li, J. H. Li and B. X. Liu, RSC Adv., 2014, 4, 20616–20619 RSC.
- Y. Li, S. H. Liang, N. Li, J. H. Li and B. X. Liu, Mater. Chem. Phys., 2013, 141, 960–966 CrossRef CAS PubMed.
- M. H. Yang, N. Li, J. H. Li and B. X. Liu, J. Alloys Compd., 2014, 606, 7–10 CrossRef CAS PubMed.
- N. Li, J. H. Li, Y. Y. Wang and B. X. Liu, Intermetallics, 2014, 44, 73–76 CrossRef CAS PubMed.
- N. Li, J. H. Li, J. B. Liu and B. X. Liu, Appl. Surf. Sci., 2014, 290, 495–498 CrossRef CAS PubMed.
- Y. Li, T. L. Wang, N. Ding, J. B. Liu and B. X. Liu, Sci. China: Technol. Sci., 2012, 55, 1–6 Search PubMed.
- W. C. Wang, H. F. Yan, F. Zeng and B. X. Liu, Scr. Mater., 2007, 57, 583–586 CrossRef CAS PubMed.
- T. L. Wang, W. C. Wang, J. H. Li and B. X. Liu, J. Alloys Compd., 2010, 493, 154–157 CrossRef CAS PubMed.
- T. L. Wang, W. T. Huang, W. C. Wang and B. X. Liu, Mater. Lett., 2010, 64, 96–98 CrossRef CAS PubMed.
- F. S. Santos, C. S. Kiminami, C. Bolfarini, M. F. de Oliveira and W. J. Botta, J. Alloys Compd., 2010, 495, 313–315 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra15180a |
| This journal is © The Royal Society of Chemistry 2015 |

