An X-ray absorption spectroscopy investigation of the coordination environment of electrogenerated Ni(II)-pseudohalide complexes arising from the anodic polarization of Ni electrodes in DMSO solutions of NCO⁻, NCS⁻ and NCSe⁻ ions

Abstract

X-ray absorption near edge spectroscopy (XANES) and extended X-ray absorption fine structure (EXAFS) were used to provide direct information in solution on the coordination state of electrogenerated products from anodically polarized nickel electrodes in pseudohalide-ion-containing dimethyl sulfoxide (DMSO) solvent (i.e. NCX⁻, X = O, S, Se) in the presence of a supporting electrolyte of tetrabutylammonium perchlorate (TBAP). Electrogenerated solutions and model solutions representative of the chemical speciation in electrolyzed systems (prepared by mixing Ni(II) and pseudohalide ion solutions in DMSO), were also examined. In general for Ni(II) interacting with NCS⁻ and NCSe⁻, the complex ion generated appears to be 6-coordinate [Ni(NCX)(DMSO)₅]⁺, while EXAFS/XANES data of the Ni/cyanate system suggest an average coordination number of 5, which in reality is due to the electrogenerated solution containing a mixture of 4 coordinate (tetrahedral) [Ni(NCO)₄]²⁻ and octahedral [Ni(DMSO)₆]²⁺ species. These observations of the octahedral geometry for the Ni(II)/thiocyanate and Ni(II)/selenocyanate systems and 5-coordinate geometry in the Ni(II)/cyanate systems (being electrogenerated products of anodic polarisation of Ni in the DMSO-supported pseudohalide ion electrolytes) agree with the differences in colour observed between samples. EXAFS/XANES measurements combined with IR spectroelectrochemical analyses of solutions provide a versatile way of analyzing these electrochemical systems without the need for isolating compounds from the electrolyte.

---

Introduction

Electrochemical studies of nickel in non-aqueous solvents are important for understanding its behaviour in applications such as battery and supercapacitor technology and as a catalyst for organic molecule synthesis.^1,2 Non-aqueous solvents are widely used in electrodeposition of metals where it is desirable to avoid the evolution of hydrogen.^2,3 However the dissolution behaviour of nickel metal electrodes in these solvents, particularly in the presence of co-ordinating ionic species, has received relatively little attention.⁴ Characterization of the nickel complexes formed in these environments is problematic, since the ions cannot be isolated from solution and their co-ordination environment is highly dependent on the concentrations of Ni and the complexing ligands. The solvent itself may also co-ordinate to Ni. Infrared spectroscopy can yield information about the species co-ordinating to Ni, but not their geometry or number. The colour of the solution may give insight into the likely co-ordination geometry due to ligand field splitting effects, but provides no direct chemical information into the co-ordinating species. NMR spectroscopy can give more qualitative information into co-ordination numbers, but the technique requires relatively high concentrations, and in the case of Ni the NMR peaks are broadened due to paramagnetism of the Ni²⁺ ion.⁵ X-ray absorption spectroscopy can provide information on the average Ni valence, co-ordination geometry, and number of co-ordinating species of ions in solution,^6–11 including electrochemically generated unstable solution species.¹²

The particular system under study here is complexes of Ni with pseudohalide ions (NCO⁻, NCS⁻, NCSe⁻) in dimethylsulfoxide (DMSO) and dimethylformamide (DMF) – solvents commonly used in the chemical and fibre industries.^13,14 In a previous study, Ni was anodically dissolved in DMSO and DMF in the presence of pseudohalide ions with tetrabutylammonium perchlorate (TBAP) as a supporting electrolyte, in an IR spectroelectrochemical cell.¹⁵ This enables direct correlations to be made between the electrochemical response and the chemical species observed.^16–27 The pseudohalide ions are easily identified from the ν(CN) stretching mode, which occurs in a region of the IR spectrum that is relatively unpopulated by other vibrational frequencies. Model solutions consisting of different Ni:pseudohalide ion ratios were synthesised and their IR spectra compared to those from the spectroelectrochemical study in an attempt to identify the complexes formed. Cyanate (NCO⁻) containing solutions were blue in colour, thought to be due to the formation of [Ni(NCO)₄]²⁻. In solutions containing NCS⁻ or NCSe⁻ ions, it was proposed that a [Ni(pseudohalide)_x(solvent)_6−x]^(2−x)+ complex was produced. However, neither the geometries nor the degree of substitution x could be conclusively determined for either compound from the IR spectra.

XAS was used to study both the electrogenerated and model solutions of Ni in DMSO in the presence of NCO⁻, NCS⁻, and NCSe⁻, to ascertain the actual co-ordination environment of these complexes. The results, combined with earlier IR spectroscopy and electrochemistry work, provide a clearer picture on the nature of the complexes and how they are formed. This has implications on how Ni might be used as an electrode in non-aqueous applications where pseudohalide ions may be present.

Experimental section

Solvents: Anhydrous DMSO (99.9%) was used as the solvent for all experiments. The pseudohalide salts used in experiments, i.e. potassium cyanate (KOCN, >96%), potassium thiocyanate (KSCN, >99%), and potassium selenocyanate (KSeCN, >97%) as well as other incidental chemicals that were needed in electrochemical, XAS work and in model solution preparations, i.e. nickel oxide (NiO, >99%), tetrabutylammonium perchlorate (>98%) were all supplied by Aldrich Chemical Co, Ltd. and used as received. The nickel nitrate (Ni(NO₃)₂·6H₂O, >99%) contained waters of crystallization which were partially removed by drying in an oven at 50 °C for 2–3 hours. This led to the originally blue salt turning a green colour after heating. Not all water was removed as confirmed by IR spectroscopic analysis. This was not believed to significantly affect the results.

Electrogenerated solutions for XAS analysis were produced using a thin layer electrochemical cell as described previously¹⁵ containing a nickel working electrode, Pt secondary electrode and AgCl/Ag reference electrode. In general, the electrolyte solutions prepared for electrochemical experiments had a pseudohalide salt concentration of 0.05 mol L⁻¹ in DMSO with 0.1 mol L⁻¹ TBAP as a supporting electrolyte.

Model solutions were prepared by mixing partially dehydrated (heated in an oven at 50 °C for 2–3 hours) Ni(NO₃)₂·6H₂O and potassium pseudohalide salts with NCX⁻ : Ni²⁺ mole ratios of 2 : 1 in DMSO. These solutions had Ni²⁺ concentrations of 0.025 mol L⁻¹.

Liquid samples and standards were loaded into a custom made cell which was constructed by affixing Kapton™ tape to both sides of a Perspex holder which had a circular cavity of 1 cm diameter by 2 mm thickness. Liquid was injected into this Kapton™-sealed cavity (∼2.5 mL) via syringe. The liquid-filled cell was then flash frozen in liquid nitrogen and measured in a closed-cycle He cryostat (T < 10 K) at the XAS beamline at the Australian Synchrotron (Melbourne, Australia). Samples were frozen to avoid the formation of bubbles due to ionization of the solution by the X-ray beam. Freeze quenching has also been used in past studies to prolong the lifetime of electrochemically generated unstable species.¹² To verify that freezing did not alter the co-ordination environment of the complexes, the IR spectra of frozen samples were recorded and showed no difference compared to liquid samples. The nominal beam size at the sample was 2 × 0.5 mm (horizontal × vertical height). Frozen samples were measured in fluorescence mode using a Canberra 100-element Ge detector. Data were collected at the Ni K-edge (8333 eV) up to k = 12 Å⁻¹. The photon energy was controlled using a Si(111) double-crystal monochromator operating at the peak of the rocking curve (“fully tuned”), higher harmonics were rejected using X-ray mirrors. Solid standards (NiO) were measured in transmission mode by thoroughly mixing powders in cellulose powder. Liquid standard solutions were prepared as nominally 0.05 mol L⁻¹ solutions of the dried nickel nitrate in distilled water and in neat DMSO solvent.

The following samples were measured:

Sample 1: NiO, powder standard

Sample 2: Ni(NO₃)₂ dissolved in water, liquid standard

Sample 3: Ni(NO₃)₂ dissolved in DMSO solvent, liquid standard

Sample 4: KOCN + Ni(NO₃)₂ 2 : 1 in DMSO model solution

Sample 5: KSCN + Ni(NO₃)₂ 2 : 1 in DMSO model solution

Sample 6: KSeCN + Ni(NO₃)₂ 2 : 1 in DMSO model solution

Sample 7: Ni/KOCN solution generated by anodic polarization of a Ni electrode at +800 mV (AgCl/Ag) in DMSO producing a blue solution. N.B. +800 mV (AgCl/Ag) is where the Ni(II)/cyanate complex ion produced by anodic polarization of the Ni electrode occurs at maximum intensity (when detected via IR spectroelectochemistry).¹⁵ The concentration of the Ni(II) complex ions being analysed in the electrogenerated solutions was expected to be lower than those in the model solutions (i.e. <0.05 mol L⁻¹).

Data were processed using either beamline software (Average 2.0) or software developed in-house to remove diffraction peaks (arising from frozen solvent crystals). These software packages allow scans from entire detector elements (or parts of scans, in the case of the in-house software) to be removed. The data from remaining elements were dead-time corrected and averaged. The EXAFS data were processed and analyzed using Athena and Artemis²⁸ with FEFF6.²⁹ The background subtraction and normalization procedures were carried out using standard routines with default parameters determined by the Athena software. The data were fitted in R-space with k¹, k², and k³ weightings simultaneously. The Fourier transformed data were not phase shift corrected.

Results

XANES

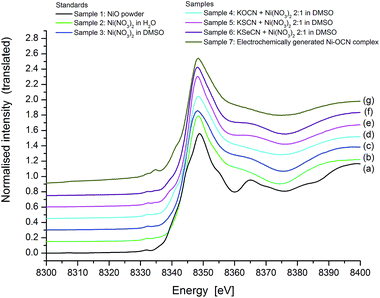
The XANES part of the spectrum can be used for 'fingerprinting' the valence state of the Ni complex ions being probed (from the position of the absorption edge, E₀), and their co-ordination environment (from the intensity and position of peak features near the edge).

Fig. 1 shows the XANES spectra for all standards and samples collected. Ni(II) ions tend to adopt octahedral or tetrahedral geometries,⁵ although square planar, 5-co-ordinate trigonal bipyramid and square pyramid geometries have also been observed. In many transition metals the XANES spectra for these different coordination geometries are reasonably distinct, but for Ni the differences can be subtle.^30–32 According to the literature, the following conclusions can be drawn: a weak pre-edge peak feature at ∼8333 eV corresponds to a 1s–3d electronic transition, which is forbidden in true centrosymmetric molecules.³⁰ Thus it is more prominent in tetrahedrally co-ordinated Ni than octahedrally co-ordinated Ni. However, distortion of octahedral Ni(II) complexes will also result in this pre-edge peak feature being observed. Square planar and square pyramidal Ni often show a prominent feature or peak on the edge at ∼8338 eV corresponding to the 1s–4p_z transition.³⁰ For Ni(II) in solution, the first minimum above the edge is lower in energy for 6 co-ordinate Ni (8375 eV) than 4 co-ordinate Ni (8380 eV).³⁰ Other features present in XANES spectra, including the intensity of the “white line” (first maximum) and position of subsequent maxima, depend on the ligand species attached and cannot be used as a general fingerprint of co-ordination geometry. Similarly the average slope of the edge depends on the ligand hardness.³⁰ The position of the edge can also shift by up to 2 eV as a result of ligands conjugated through O or N, to S.³⁰

Fig. 1 XANES data collected for standards: (a) NiO powder, (b) Ni(NO₃)₂ in H₂O, (c) Ni(NO₃)₂ in DMSO, (d) to (f) represent samples of model solutions with pseudohalide ion to nickel ratios of 2 : 1, hence (d) is Ni/NCO⁻ (Sample 4), (e) is Ni/NCS⁻ (Sample 5), (f) is Ni/NCSe⁻ (Sample 6) and (g) represents the sample of electrochemically generated Ni complex ions with NCO⁻ from the thin layer electrochemical cell (Sample 7).

From an examination of the XANES spectra from the present study in Fig. 1, the following was noted. There is a small peak at 8332 eV in all of the spectra shown in Fig. 1, which corresponds to the 1s–3d electronic transition. All of the Ni samples and standards in solution have similar shapes, i.e., the white line at 8348 eV, a shoulder at 8365 eV, a minimum at 8374–8376 eV, and subsequent oscillations. The two liquid standards (Ni(II) in H₂O and Ni(II) in DMSO; Fig. 1(b) and (c)) are expected to adopt symmetric octahedral geometries^5,33 and display similar spectra to octahedral Ni(II) ions in solution.³⁴ The samples containing coordinated NCX⁻ ligands (X = O, S, Se) show a shoulder below the edge at 8340 eV which is not present in the two liquid standards. This indicates a degree of asymmetry, possibly arising from having two different species of co-ordinating ligands (NCX⁻ and DMSO solvent molecules). For both the model and electrochemically generated samples with coordinated NCO⁻ (Fig. 1(d) and (g)), the intensity of this feature is noticeably higher than the samples with NCS⁻ and NCSe⁻. This is most likely a 1s–4p_z transition as observed in the XANES of species possessing square planar and square-pyramidal geometries, and, by implication, in distorted octahedral geometries also.^30–32 This may indicate that the Ni(II) complex with NCO⁻ has a different co-ordination geometry, or adopts a mixture of different co-ordination geometries.

The shoulder above the edge at 8365 eV is significantly lower in intensity for the two samples with coordinated NCO⁻ ligands compared to the other samples and solution standards.

The peak at 8335 eV for the electrochemically generated Ni/NCO⁻ sample (Fig. 1(g)) is due to a monochromator ‘glitch’. The reason it is only seen in this sample is due to the lower concentration of Ni in the electrochemically generated solution (relative to model solutions), which results in a lower overall absolute intensity.

In conclusion it appears that the Ni complexes with NCS⁻ and NCSe⁻ in the model solutions are mostly octahedral in geometry, with varying degrees of distortion depending on the ligand, arising from the mixture of co-ordination species (NCX⁻ and DMSO). However the Ni complexes with NCO⁻ appear to have a different geometry, or possibly a mixture of geometries. The XANES spectra of the Ni/cyanate system produced by anodic dissolution of Ni in 0.05 mol L⁻¹ KOCN to the 2 : 1 KOCN : Ni(II) model solution (Fig. 1(g) and (d), respectively) are similar, indicating that the model solutions are accurate representations of the co-ordination environment existing in the electrochemically generated solutions, as also proven by IR spectroscopy.¹⁵ For this reason, and because the Ni(II) complex ion species can be prepared in higher concentrations than what would be produced in the electrochemical experiments, the bulk of the study presented here concentrates on the model solutions.

EXAFS

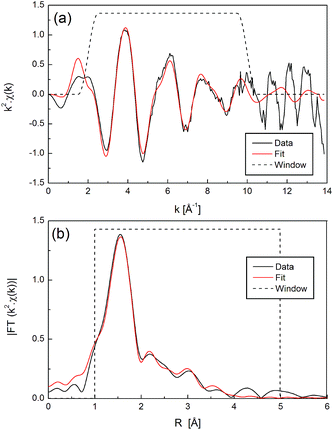
The EXAFS region of the XAS spectra was analyzed to gain more information about the average coordination environment around the Ni(II) centres under study.

The NiO powder standard was fitted simultaneously for k¹, k² and k³ weightings in R-space, using a FEFF model based on the NiO crystal structure to a radial distance of R = 6 Å. All single- and multiple-scattering paths were used to fit the data to R = 5 Å. The data and fit for k² weighting is shown in Fig. 2, and for all k-weightings in Fig. S1.† The parameters used are given in Table S1.† In the EXAFS equation, the co-ordination number, N, and the amplitude parameter, S₀², are combined as a product. For NiO, N is known to be 6. The value of S₀² obtained from the fit is 0.78 ± 0.07, which is within the usual expected range of 0.7–1.1.³⁵ When fitting the samples, the unknown co-ordination number can be obtained if one assumes that S₀² has this same value.

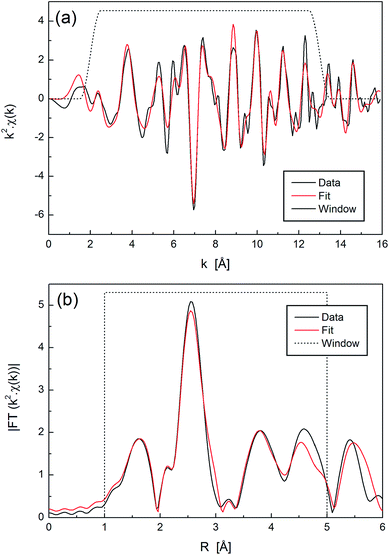Fig. 2 EXAFS data and fit for NiO powder standard (‘Sample 1’) in (a) k-space and (b) R-space, with k² weighting.

The same analysis method (constructing a model based on a known crystal structure) cannot be applied to complex ions in solution due to the lack of long-range order. Instead, a collection of single-scattering paths was used to fit the data, with constraints imposed on various parameters as appropriate.

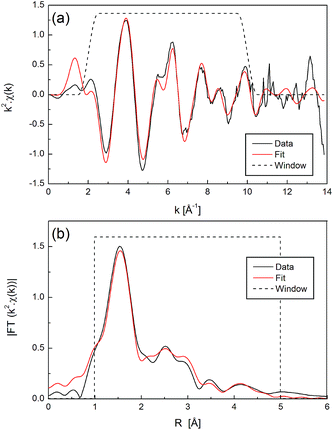
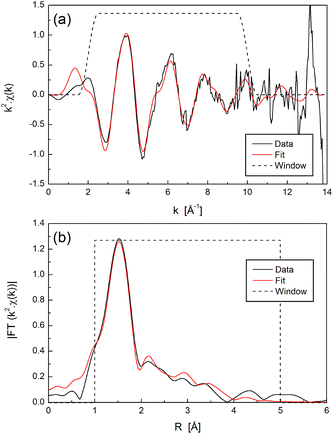
First we consider the two Ni(NO₃)₂ standards dissolved in H₂O and DMSO, shown in Fig. 3 and 4 respectively. A prominent peak in both spectra is observed at R ≈ 1.5 Å, corresponding to the first nearest neighbour shell. For Ni²⁺ in H₂O, a model was constructed using only oxygen atoms, since hydrogen is not usually observed in EXAFS. Two paths representing the first and second solvation shells were estimated to be located at 2.0 and 4.0 Å. Seven parameters were used: amplitude (amp), σ² (Debye–Waller Factor) and Δr (to account for the difference in the shell radius between the model and actual data) for each path, and ΔE₀ (same for both paths). A full list of parameter values is given in Table S2.† The data and fit for k² weighting are shown in Fig. 3, and for all k-weightings in Fig. S2.†

Fig. 3 EXAFS data and fit for Ni²⁺ in H₂O standard (Ni(NO₃)₂ dissolved in water, ‘Sample 2’) in (a) k-space and (b) R-space, with k² weighting.

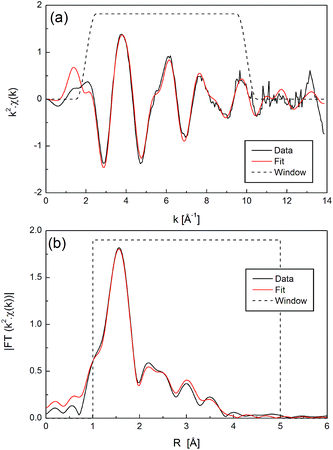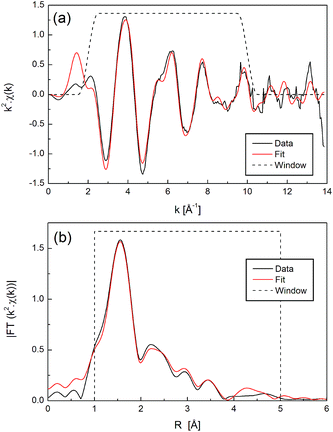
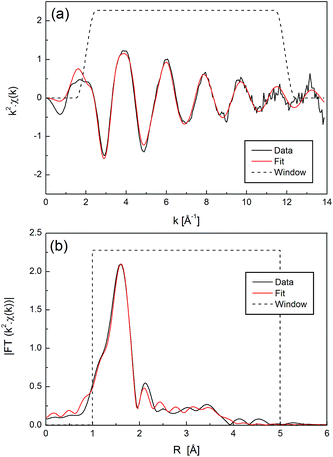
Fig. 4 EXAFS data and fit for Ni²⁺ in DMSO standard (Ni(NO₃)₂ dissolved in DMSO solvent, ‘Sample 3’) in (a) k-space and (b) R-space, with k² weighting.

For Ni²⁺ in DMSO, it is assumed that the oxygen atom, with its lone electron pairs, is closest to the Ni²⁺ ion. A collection of single-scattering paths to represent the oxygen, sulphur, and two carbon atoms of DMSO at appropriate path distances based on the molecular geometry was used. This gave a good fit to the data and used 9 parameters, which are given in Table S3.† The data and fit for k² weighting are shown in Fig. 4, and for all k-weightings in Fig. S3.†

When comparing the product N × S₀² for the three standards and dividing by the value of S₀² obtained from the NiO fit of 0.78 ± 0.07, it is possible to obtain values for the co-ordination number of Ni²⁺ in the two liquid standards (Table 1). These are the same as each other within uncertainty. The average co-ordination numbers may be 5 or 6 within uncertainty, but are most likely to be 6. According to literature,^5,33 the predominant species in such solutions are likely to be [Ni(H₂O)₆]²⁺ and Ni(DMSO)₆²⁺. This is consistent with the XANES spectra of Ni²⁺ in H₂O and in DMSO which are very similar to one another, and to literature data for octahedrally co-ordinated Ni²⁺ ions.³⁴

Table 1 Extraction of co-ordination numbers for standards. The co-ordination number is calculated assuming that the global value of S₀² of 0.78 ± 0.07, as obtained from the NiO standard, applies to all samples

Sample	N in model	Fitted value of S0^2	N × S0^2	Calculated coordination number, N
NiO	6	0.78 ± 0.07	4.68 ± 0.42	6.00 ± 0.60
Ni(NO3)2 in H2O	1	4.00 ± 0.15	4.00 ± 0.15	5.13 ± 0.65
Ni(NO3)2 in DMSO	1	4.16 ± 0.20	4.16 ± 0.20	5.33 ± 0.74

---

We now consider the nickel DMSO-pseudohalide complexes, which are expected (based on assumptions of octahedral coordination geometry as suggested by XANES) to have the average stoichiometry [Ni(NCX)_n(DMSO)_m]^(2−x)+ (X = O, S, or Se), most likely with n = 1 and m = 5, resulting in a 6-co-ordinate, possibly distorted, octahedral geometry.

The first question that arises when proposing a model structure for this complex is: which terminus of the pseudohalide ion complexes to Ni²⁺? We begin by considering the case of a Ni(II) complex containing NCSe⁻ as the coordinated pseudohalide ion. Selenium has the highest atomic number of the species studied and will therefore lead to different spectral responses at different k-weightings compared to lower atomic number species such as C, N, and O (specifically, at higher k-weightings Ni–Se components will show an increase in intensity relative to Ni–C, Ni–N and Ni–O components).

A model was constructed from a collection of single-scattering paths as follows. The DMSO molecule was included with paths based on the Ni²⁺ in DMSO standard. The number of parameters for the DMSO molecule was reduced by fixing the amplitude ratios of the four paths, and using a single amplitude scale factor, and common σ² parameter. The NCX⁻ (X = O, S, or Se) molecule was modelled in two different ways. In the first, three separate paths were included corresponding to N, C, and either O, S, or Se at appropriate distances from the central Ni atom. These paths shared a common σ² parameter, and each had separate independent parameters for ‘amp’ and Δr. This resulted in a total number of parameters of 13. For consideration of the case involving Ni(II) coordinated to NCSe⁻, models were constructed for both Ni–NCSe and Ni–SeCN. The Ni–NCSe model gave a much more stable fit than Ni–SeCN, indicating that the pseudohalide ion is complexed to the Ni(II) central atom via the nitrogen atom – an observation that is consistent with IR data reported by previous workers.^36–38 Therefore in considering Ni(II) complexes coordinated to the other pseudohalide ions, similar models were also constructed for Ni–NCS and Ni–NCO. (However, note that due to the similarity in atomic number between N and O, it is impossible to distinguish between Ni–NCO and Ni–OCN by EXAFS alone.) A list of the fitted values for the parameters for each sample is given in Table S4,† and the data and fits are shown in Fig. S4–S7.†

Although the first method gave reasonable fits and values for the amplitude parameters, the shell radii for some of the atoms – particularly Ni–N and Ni–C in the Ni-NCX ligand – resulted in unphysical bond lengths for N–C (<1.0 Å) in the NCX⁻ molecule. For collinear paths, multiple scattering can often be significant. Since all ions in the NCX⁻ series are linear, a second model was constructed that included multiple scattering paths for NCX⁻. Once again, single-scattering paths were used for DMSO. This resulted in more realistic values for N–C bond lengths within the NCX⁻ molecules. Note that the Ni–X (X = O, S, Se) distances are indicative only as these are close to the limit of the fitting range used. Once again both Ni–NCX and Ni–XCN models were considered, and for X = Se and S the Ni–XCN model failed (these results are not shown). The fitted values of the parameters are given in Table 2, and the data and fits are shown for k²-weighting in Fig. 5–9 and all k-weightings in Fig. S8–S11.†

Table 2 Parameters used in EXAFS fits with a multiple-scattering model for NCX⁻ and a single-scattering model for DMSO

Parameter	X = O	X = S	X = Se	Echem X = O
a Set to 3 × σ^2 (NCX^− single scattering).b For the DMSO paths, amp(O) = scale × 4.14, amp(C) = scale × 4.61.c X = S only.
#Parameters	12	14	13	12
Independent points	20.0	20.0	20.0	20.0
k-range	2.0–10.0	2.0–10.0	2.0–10.0	2.0–10.0
R-range	1.0–5.0	1.0–5.0	1.0–5.0	1.0–5.0
k-weights used	1, 2, 3	1, 2, 3	1, 2, 3	1, 2, 3
Reduced χ^2	106	484	301	32.5
ΔE^0 (all paths)	−4.1 ± 1.0	−5.7 ± 2.5	−4.8 ± 1.4	−6.4 ± 1.3
σ^2 (DMSO paths)	0.005 ± 0.004	0.005 ± 0.007	0.003 ± 0.003	0.004 ± 0.005
σ^2 (NCX^− single scattering paths)	0.002 ± 0.004	0.002 ± 0.005	0.001 ± 0.005	0.001 ± 0.003
σ^2 (NCX^− multiple scattering paths)	0.005 ± 0.011^a	0.007 ± 0.015^a	0.018 ± 0.010	0.004 ± 0.008^a
Scale (DMSO)^b	0.71 ± 0.13	0.94 ± 0.45	0.70 ± 0.19	0.62 ± 0.09
amp_O (DMSO)^c		3.34 ± 0.87
amp_S (DMSO)^c		2.87 ± 1.36
amp (NCX^−)	0.52 ± 0.49	0.64 ± 1.10	1.34 ± 1.10	0.59 ± 0.32
r_O (DMSO)	2.06 ± 0.01	2.06 ± 0.03	2.08 ± 0.026	2.04 ± 0.01
r_S (DMSO)	3.19 ± 0.03	3.14 ± 0.02	3.14 ± 0.04	3.15 ± 0.03
r_C1 (DMSO)	3.87 ± 0.09	3.94 ± 0.09	3.98 ± 0.063	3.95 ± 0.07
r_C2 (DMSO)	4.18 ± 0.05	4.13 ± 0.09	4.16 ± 0.063	4.05 ± 0.10
r_N (NCX^−)	1.99 ± 0.15	1.97 ± 0.19	2.01 ± 0.05	1.98 ± 0.06
r_C (NCX^−)	3.10 ± 0.09	3.00 ± 0.26	3.34 ± 0.14	3.09 ± 0.14
r_X (NCX^−)	4.14 ± 0.07	4.84 ± 0.06	5.11 ± 0.08	4.31 ± 0.06

---

Fig. 5 EXAFS data and fit for 2 : 1 KOCN + Ni²⁺ in DMSO model solution (‘Sample 4’) in (a) k-space and (b) R-space, with k² weighting. Single-scattering paths were used for DMSO, and multiple-scattering paths for NCO⁻.

Fig. 6 EXAFS data and fit for 2 : 1 KSCN + Ni²⁺ in DMSO model solution (‘Sample 5’) in (a) k-space and (b) R-space, with k² weighting. Single-scattering paths were used for DMSO, and multiple-scattering paths for NCS⁻.

Fig. 7 EXAFS data and fit for 2 : 1 KSeCN + Ni²⁺ in DMSO model solution (‘Sample 6’) in (a) k-space and (b) R-space, with k² weighting. Single-scattering paths were used for DMSO, and multiple-scattering paths for NCSe⁻.

Fig. 8 EXAFS data and fit for electrochemically generated Ni²⁺ : NCO⁻ complex ions in DMSO solution (‘Sample 7’) in (a) k-space and (b) R-space, with k² weighting. Single-scattering paths were used for DMSO, and multiple-scattering paths for NCO⁻.

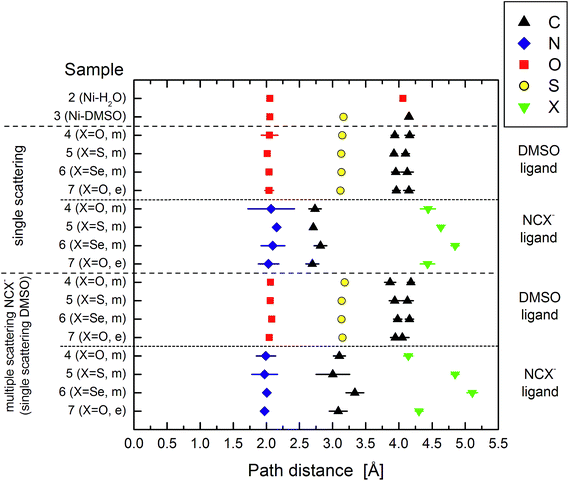
Fig. 9 shows the path distances graphically for the two approaches used (i.e. single scattering only for all and multiple scattering (NCX⁻) and single scattering (DMSO)). Given that the NCX⁻ ligand is linear, the bond distances can be directly read off the graph. For all of the fits that were performed using a single-scattering model (as labelled in Fig. 9) for NCX⁻, the N–C bond is less than 1 Å, which is unreasonable, even though the reduced χ² is lower for these fits. The N–C bond acquires values >1 Å when multiple scattering paths are included. This demonstrates the necessity of including multiple scattering paths for the linear NCX⁻ ligand. As mentioned above, the Ni–X (X = O, S, Se) distances are indicative only as these are close to the upper limit of the fitting range used. However these show consistent trends with size, as expected, and the model and electrochemically generated Ni–NCO data yield quite consistent distances for the furthest Ni–O shell of this ligand.

Fig. 9 Graphical representation of path distances obtained from EXAFS fitting. Sample ID numbers have been described in the experimental section. ‘m’ = 2 : 1 NCX⁻ : Ni²⁺ model solutions, ‘e’ = electrochemically generated solution.

The overall co-ordination environment can be ascertained by considering the various amp (S₀²) parameters. If we assume that the co-ordination numbers of the Ni²⁺ in H₂O and Ni²⁺ in DMSO liquid standards are both 6, then we can obtain the co-ordination numbers for both types of ligands in the [Ni(NCX)_x(DMSO)_6−x]^(2−x)+ complex ions, i.e. N(DMSO) and N(NCX⁻). These values are given in Table 3.

Table 3 Extraction of co-ordination numbers for samples from fits with single scattering paths for DMSO and multiple scattering paths for NCX⁻

Sample	N(DMSO)	N(NCX^−)	Total N
a Based on Ni–O path from DMSO only, since the uncertainties on amplitude for the Ni–S and Ni–C paths were large (∼50%).
4 (Model Ni–NCO)	4.3 ± 0.4	0.8 ± 0.4	5.0 ± 0.8
5 (Model Ni–NCS)^a	4.8 ± 1.5	0.9 ± 0.8	5.7 ± 2.3
6 (Model Ni–NCSe)	4.2 ± 0.5	1.9 ± 0.8	6.1 ± 1.3
7 (Echem Ni–NCO)	3.7 ± 0.3	0.9 ± 0.2	4.6 ± 0.5

---

The average co-ordination numbers obtained from the model including multiple-scattering NCX⁻ paths showed 6-co-ordinate Ni for NCSe⁻ and NCS⁻, and 5-co-ordinate Ni for NCO⁻.

Discussion

The XAS results complement earlier IR studies on the nickel pseudohalide-DMSO complexes by providing quantitative measures of the average co-ordination numbers of each species and an understanding of the co-ordination geometry. These measurements were performed on complex ions in solution at relatively low concentrations. Both IR and XAS experiments indicate that the complex ion species formed in the presence of SCN⁻ and SeCN⁻ are [Ni(NCS)(DMSO)₅]⁺ and [Ni(NCSe)(DMSO)₅]⁺ respectively, whilst in the case of the cyanate, both the model and electrochemically generated solutions are blue in colour due to the presence of some [Ni(NCO)₄]²⁻ ions as reported in other literature.^39,40 The mode of bonding to the pseudohalide ion in all cases is via the nitrogen atom^36,37,41 the IR spectra show a change in the C–N stretch frequency but no change in the C–X (X = O, S, Se) frequency for the co-ordinated ligand compared to the free ligand; and fitting the EXAFS data with a Ni–X–C–N model failed for X = S, Se. Due to the linear geometry of the pseudohalide molecules, it was important to include collinear multiple scattering paths in the EXAFS fits. Both the XAS and IR spectra show that the model Ni–OCN solution is representative of the electrochemically generated Ni–OCN complex in DMSO.

It is important to note that the XAS analyses reported describe an average snapshot of all Ni species in the sample being studied. Hence the interpretation about specific complex ion species and the co-ordination environment around the Ni²⁺ ion must take this into account.

For instance in the case of the model solutions involving Ni²⁺/SCN⁻ or Ni²⁺/SeCN⁻, the “coordination numbers” extracted for the Ni/pseudohalide species detected are 4.8 (∼5) DMSO molecules and 0.9 (∼1) NCS⁻ ion bonded to one Ni²⁺ ion and 4.2 (∼4) DMSO molecules and 1.9 (∼2) NCSe⁻ ions bonded to one Ni²⁺ ion. Overall these results confirm that the bonding in these Ni²⁺ complexes for these particular pseudohalide ligands are octahedral as suggested in the previous work.¹⁵ The difference in the relative coordination numbers of Ni²⁺ and NCS⁻/NCSe⁻ in the multiple scattering entries for the table are not regarded as being statistically significant in light of the large errors in N. It is believed that because of the relative concentrations used in making the model solutions and what is also actually used in the IR spectroelectrochemical experiments that the stoichiometry of the Ni-thiocyanate and selenocyanate complex ions that have been detected are mono or dipseudohalide complexes with the remainder of the attached ligands being coordinated solvent molecules (DMSO). Pilarczyk et al.³³ indicated in studies investigating the dissolution of Ni(SCN)₂ in DMSO that the charge-neutral dithiocyanate complex of Ni(II) forms but that this complex cannot be detected or distinguished when observing UV/Vis spectra. Pilarcyzk et al. stated through conductivity measurements that the monothiocyanate complex ion of Ni(II) must also exist in such solutions. The EXAFS/XANES technique will only see an average of the (frozen) solution environment and this may also have some influence on the N numbers determined for DMSO and NCX⁻. The previous paper¹⁵ published on this system suggested that on the basis of model solution IR data that a mono-pseudohalide complex was more likely to form, i.e. [Ni(DMSO)₅(NCX)]⁺ (X = S, Se). The alternative species (to this terminally bonded complex) that could be considered to exist in solution is a bridging complex such as (DMSO)₄Ni(NCS)₂Ni(DMSO)₄. According to Nelson et al.⁴² the ν(CN) stretches of bridged metal thiocyanate complexes (i.e. M–NCS–M) occur over a wider range of values and tend toward higher numbers than are observed in terminal M–NCS complexes. The possibility of a bridged complex was considered in EXAFS calculations but cursory processing of data in the present study using this bridging M–NCS–M model did not yield any changes in the overall results obtained from when the original models (assuming terminal bonding) were used, and also resulted in too many free parameters to yield a statistically meaningful result. Hence for both the Ni-thiocyanate and Ni-selenocyanate systems, it is believed that the stoichiometry of the system is at least a monopseudohalide Ni(II) ion, though it is plausible that dipseudohalide ion substitutions may also be possible (though no change to IR frequencies of coordinated thiocyanate or selenocyanate reflect this in the model solution IR data) with the remainder being coordinated solvent molecules. This was made most obvious at least in the thiocyanate system case from the colour of solutions where the Ni(II) thiocyanate complex ion present in model solutions produced a greeny colour while colours of the tetrahedral tetrathiocyanatonickelate(II) species or salts are blue^40,43 as is the case for solids containing the dithiocyanatonickelate(II) complex.⁴⁴

In the case of the Ni/cyanate systems, the EXAFS/XANES data have given a distinctly different result for overall coordination numbers to Ni of ligands. In general (see Table 3)), an average coordination of 5 is observed for Ni. Although 5-coordinate Ni(II) complexes are possible,⁴⁵ what is believed to be the situation here is that the EXAFS/XANES measurement depicts an average environment in which tetrahedral Ni(II) cyanate complexes (i.e. [Ni(NCO)₄]²⁻, responsible for the blue colour in these solutions,¹⁵ are mixed with other Ni(II) species which have an octahedral environment, e.g. [Ni(DMSO)₆]²⁺.³³ Hence there is a mixture of 4 and 6 coordinate species present in both the electrochemically generated solution and the model solution so that the EXAFS/XANES method effectively is sensing on average a “5-coordinate species” based on the calculated N numbers. This also accounts for the different features observed for Ni–NCO XANES compared to the other, octahedrally co-ordinated, Ni–NCS and Ni–NCSe samples and standards. It is strongly believed that the “6 coordinate” species is [Ni(DMSO)₆]²⁺ because the N values for DMSO in the “average” 5 coordinate complex are weighted toward the DMSO ligand.

Conclusion

XANES and EXAFS were used to directly probe the coordination state of electrogenerated Ni(II) pseudohalide complex ions from anodic polarisation of Ni electrodes in polar aprotic solvents containing pseudohalide ions, NCO⁻, NCS⁻ and NCSe⁻. In addition, model solutions of NCO⁻, NCS⁻ and NCSe⁻ were measured due to their being proven to be realistic models of the cell solutions after anodic dissolution of Ni in earlier reported work.

Comparison of the XANES spectra collected for the model solution and electrogenerated system samples from this study with 6-, 5-, and 4-co-ordinated Ni shows that the sample spectra appear to match the octahedral geometry best of all of these, although some distortion is likely due to the presence of a Ni pre-edge peak (attributed in the literature to 1s–4p_z transition) at 8340 eV. The average co-ordination environment around Ni in the presence of NCO⁻ is different to that of NCS⁻ and NCSe⁻ (which both appear to be octahedral with some distortion) and may be a mixture of complexes having different geometries.

In the EXAFS studies, two structural models were used to fit the data and hence gain information on the coordinative environment around Ni(II) in the model and electrogenerated solutions: one using single scattering paths for both DMSO and NCX⁻ ligands, and one using single scattering paths for DMSO and including both single and multiple scattering paths for NCX⁻. Reasonable bond distances were only obtained using the model which included multiple scattering for NCX⁻.

Models were constructed using both Ni–X–C–N and Ni–N–C–X for X = Se, S, and O. For X = Se and S, fits to models where Ni was complexed by N were far more stable than those where Ni was complexed by Se or S, where several parameters tended towards unphysical values. That the ligand binds to the Ni centre through the nitrogen atom was in agreement with the wider inorganic chemical literature in this area. For X = O, either Ni–O–C–N or Ni–N–C–O gave acceptable fits. This is not surprising given the similarity in atomic number between N and O; however it is believed that in common with the NCS⁻ and NCSe⁻ based systems, and earlier IR studies of the Ni/NCO⁻ system, that the mode of bonding of NCO⁻ to Ni(II) is Ni–NCO.

The average co-ordination numbers obtained from the model including multiple-scattering NCX⁻ paths showed 6-co-ordinate Ni for NCSe⁻ and NCS⁻, and 5-co-ordinate Ni for NCO⁻. In terms of the realistic situation existing in solution, this difference is a result of XAS being a number averaging technique. In the Ni/cyanate system, the result of “5-coordinate Ni” has likely resulted from there being a mixture of coordination geometries in solution, for instance [Ni(DMSO)₆]²⁺ and [Ni(NCO)₄]²⁻. In contrast, the results for the Ni/thiocyanate and Ni/selenocyanate systems indicate a monoisothiocyanatonickelate(II) or monoisoselenocyantonicklate(II) species which has an octahedral geometry. This is consistent with the differences observed in the XANES spectra, and with the different colours observed with the solutions themselves.

Acknowledgements

Portions of this research were undertaken on the X-ray Absorption Spectroscopy (XAS) Beamline at the Australian Synchrotron, Victoria, Australia. We thank the New Zealand Synchrotron Group for travel funding to use this facility. Emeritus Professor Brian Nicholson of Waikato University is also acknowledged for valuable advice received throughout this study.

References

1. T. C. Girija and M. V. Sangaranarayanan, J. Power Sources, 2006, 156, 705–711.
2. D. Aurbach and I. Weissman, in Nonaqueous Electrochemistry, ed. D. Aurbach, Marcel Dekker, New York, 1999, pp. 1–52.
3. W. Simka, D. Puszczyk and G. Nawrat, Electrochim. Acta, 2009, 54, 5307–5319.
4. A. M. Vecchio-Sadus, J. Appl. Electrochem., 1993, 23, 401–416.
5. F. A. Cotton and G. Wilkinson, Advanced Inorganic Chemistry: A Comprehensive Text, 4th, completely rev. from the original literature edn, Wiley, New York, 1980.
6. J. M. Charnock, D. Collison, C. D. Garner, E. J. L. McInnes and J. F. W. Mosselmans, J. Phys. IV, 1997, 7, C2–C657 -C652-658.
7. Y. Inada and S. Funahashi, Anal. Sci., 1997, 13, 373–377.
8. Y. Inada, H. Hayashi, K. Sugimoto and S. Funahashi, J. Phys. Chem. A, 1999, 103, 1401–1406.
9. J. Krakowiak, D. Lundberg and I. Persson, Inorg. Chem., 2012, 51, 9598–9609.
10. F. F. Xia, D. Zeng, H. B. Yi and C. Fang, J. Phys. Chem. A, 2013, 117, 8468–8476.
11. J. Yeo, M. H. Cheah, M. I. Bondin and S. P. Best, Aust. J. Chem., 2012, 65, 241–253.
12. S. P. Best, S. J. Borg and K. A. Vincent, in Spectroelectrochemistry, ed. W. Kaim and A. Klein, Royal Society of Chemistry, Cambridge, GBR, 2008, pp. 1–30.
13. F. Bellucci, C. A. Farina and G. Faita, Electrochim. Acta, 1981, 26, 731–733.
14. L. Ercolano, T. Monetta and F. Bellucci, Corros. Sci., 1993, 35, 161–167.
15. L. K. H. K. Alwis, M. R. Mucalo and B. Ingham, J. Electrochem. Soc., 2013, 160, H803–H812.
16. K. Ashley, Talanta, 1991, 38, 1209–1218.
17. K. Ashley and S. Pons, Chem. Rev., 1988, 88, 673–695.
18. G. A. Bowmaker, J.-M. Leger, A. Le Rille, C. A. Melendres and A. Tadjeddine, J. Chem. Soc., Faraday Trans., 1998, 94(9), 1309.
19. B. Bozzini, M. Kazemian Abyaneh, B. Busson, G. P. de Gaudenzi, L. Gregoratti, C. Humbert, M. Amati, C. Mele and A. Tadjeddine, J. Power Sources, 2013, 231, 6–17.
20. K. Brandt, E. Vogler, M. Parthenopoulos and K. Wandelt, J. Electroanal. Chem., 2004, 570, 47–53.
21. M. A. El-Attar, N. Xu, D. Awasabisah, D. R. Powell and G. B. Richter-Addo, Polyhedron, 2012, 40, 105.
22. C. Korzeniewski, in Handbook of Vibrational Spectroscopy, ed. J. M. Chalmers and P. R. Griffiths, John Wiley, New York, 2002, p. 2700.
23. C. A. Melendres, G. A. Bowmaker, K. A. B. Lee and B. Beden, J. Electroanal. Chem., 1998, 449, 215–218.
24. M. J. Smieja, M. D. Sampson, K. A. Grice, E. A. Benson, J. D. Froehlich and C. P. Kubiak, Inorg. Chem., 2013, 52, 2484.
25. R. M. Souto, F. Ricci, L. Spyrkowicz, J. L. Rodriguez and E. Pastor, J. Phys. Chem. C, 2011, 115, 3671.
26. N. Xu, J. Lilly, D. R. Powell and G. B. Richter-Addo, Organometallics, 2012, 31, 827.
27. Y. Y. Yang, J. Ren, H.-X. Zhang, Z.-Y. Zhou, S.-G. Sun and W.-B. Cai, Langmuir, 2013, 29, 1709.
28. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537.
29. M. Newville, J. Synchrotron Radiat., 2001, 8, 322.
30. G. J. Colpas, M. J. Maroney, C. Bagyinka, M. Kumar, W. S. Willis, S. L. Suib, N. Baidya and P. K. Mascharak, Inorg. Chem., 1991, 30, 920.
31. M. G. Kim and J. Cho, J. Mater. Chem., 2008, 18, 5880.
32. E. Montargès-Pelletier, V. Chardot, G. Echevarria, L. J. Michot, A. Bauer and J. L. Morel, Phytochemicals, 2008, 69, 1695.
33. M. Pilarczyk, W. Grzybkowski and L. Klinszporn, J. Chem. Soc., Faraday Trans. 1, 1989, 85, 3395–3402.
34. T. J. Strathmann and S. C. B. Myneni, Geochim. Cosmochim. Acta, 2004, 68, 3441.
35. S. D. Kelly, S. R. Bare, N. Greenlay, G. Azevedo, M. Balasubramanian, D. Barton, S. Chattopadhyay, S. Fakra, B. Johannessen, M. Newville, J. Pena, G. S. Pokrovski, O. Proux, K. Priolkar, B. Ravel and S. M. Webb, J. Phys.: Conf. Ser., 2009, 109, 012032.
36. K. Nakamoto, Infrared and Raman Spectra of Inorganic and Coordination Compounds, 5th edn, John Wiley & Sons, Inc., New York, 1997.
37. A. H. Norbury, in Advances in Inorganic Chemistry and Radiochemistry, ed. H. J. Emeleus and A. G. Sharpe, Academic Press, Inc (London) Ltd., New York, 1975, vol. 17, pp. 231–386.
38. M. Pilarczyk, W. Grzybkowski and L. Klinszporn, Bull. Pol. Acad. Sci., Chem., 1987, 35, 559–567.
39. J. P. Fackler Jr, G. E. Dolbear and D. Coucouvanis, J. Inorg. Nucl. Chem., 1964, 26, 2035–2037.
40. D. Forster and D. M. L. Goodgame, J. Inorg. Nucl. Chem., 1964, 26, 2035.
41. M. Pilarczyk, W. Grzybkowski and L. Klinszporn, Bull. Pol. Acad. Sci., Chem., 1987, 35, 559–567.
42. S. M. Nelson and T. M. Shepherd, J. Inorg. Nucl. Chem., 1965, 27, 2123–2125.
43. D. Forster and D. M. L. Goodgame, J. Chem. Soc., 1965, 262–267.
44. A. W. Downs, B. A. Gotz and A. E. McCarthy, Inorg. Nucl. Chem. Lett., 1974, 11, 365–366.
45. M. D. Santana, A. A. Lozano, G. Garcia, G. Lopez and J. Perez, Dalton Trans., 2005, 104–109.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra14940h

---