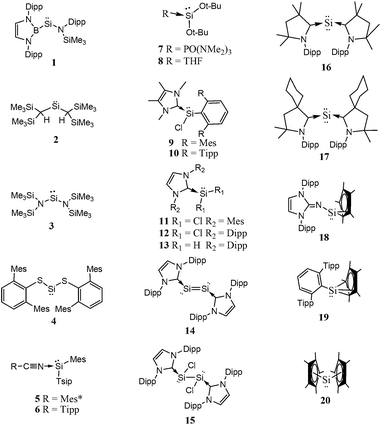
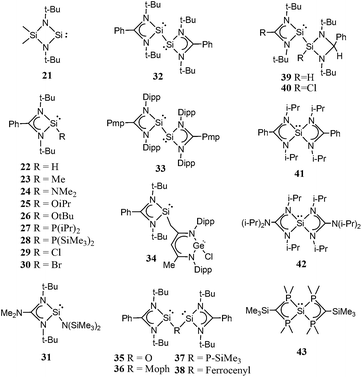
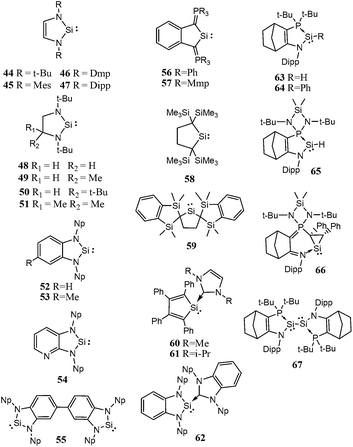
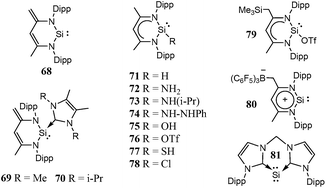
Open Access Article
Open Access ArticleCan low-valent silicon compounds be better transition metal ligands than phosphines and NHCs?†
Zsolt
Benedek
and
Tibor
Szilvási
*
Department of Inorganic and Analytical Chemistry, Budapest University of Technology and Economics, Szent Gellért tér 4, 1111 Budapest, Hungary. E-mail: szilvasitibor@ch.bme.hu
First published on 10th December 2014
Abstract
We investigated the potential application of experimentally characterized low-valent silicon compounds as transition metal ligands by computing the most important ligand properties, σ-donor and π-acceptor ability, ligand-to-metal charge transfer, and steric parameters and compared them to the generally used carbene and phosphine ligands. We found that several recently synthesized donor-stabilized low-valent silicon compounds can compete or even exceed the favorable features of commonly used carbene and phosphine ligands regarding all investigated ligand properties. We derive the general principles behind the enhanced features and conclude how even better low-valent silicon ligands can be designed with a slight modification of known compounds. Using our results as a database, one can choose an appropriate silicon-based ligand for transition metal catalysis.
Introduction
Transition metal catalysts are being used in almost every field of chemistry, and applications in industry are on the increase, even at the production level.1 To gain new, enhanced catalytic properties one of the best options would be to modify the ligation of the transition metal centre.2Traditionally, phosphine ligands were used, later, the successful application of carbenes, especially N-heterocyclic carbenes (NHC), broadened the list of potential transition metal ligands.3–7 This raises the question whether other low-valent group 14 compounds,8 especially silylenes, can be used for the same purpose.
Silylenes were used as transition metal catalyst ligands for the first time in 2001 by Fürstner,9 though the first transition metal silylene complex had been synthesized in 1977,10 and even this late recognition was not followed by other examples until the recent studies of Driess and Hartwig.11–15 In the last two years, some examples were reported in which low-valent silicon compounds served as catalyst ligands in C–H borylation of arenes,11 in hydrosilylation of ketones,12 or in cycloaddition reactons,13 but the low number of such attempts is quite surprising taken into account that the number of isolated low-valent silicon compounds is increasing year by year.16
Though, several study theoretical work have been reported on metal–silylene complexes to date,17,18 detailed comparative study between different ligand systems, such as analog carbenes, silylenes, and germylenes, is very scarce; only Boehme and Frenking19 published from this point of view in 1998. They analysed the electronic structure of analogue imidazole-2-ylidene carbene, silylene, and germylene and concluded that the carbene analogue is stronger σ-donor than the silylene analogue but they did not discuss other catalytic aspects. In the last fifteen years, however, several novel low-valent silicon compounds became available, including acyclic, four-, five- and six-membered ring structures, and even silicon(0) compounds20 (1–81, Schemes 1–5)21–73 which could have very distinctive features applying them as ligands to transition metals in catalytic processes. Especially, because most of them have no carbene analogue in the literature and calculations suggest that some analogous carbene structures are not even stable on the potential energy surface.74,75 Therefore, the previously suggested comparison for σ-donor strength of carbenes and silylenes is not viable to suggest ligands with enhanced features.19
 | ||
| Scheme 5 Definition of functional groups present in silicon compounds on Schemes 1–4. | ||
Thus, we investigated many known low-valent silicon compounds to completely explore their potential utilization in transition metal catalysis. We considered four important features that influence the reaction rate: σ-donor and π-acceptor ability, ligand-to-metal charge transfer (LMCT) and steric factors. To gain full insight, we intended to make comparison between low-valent silicon compounds and regularly applied transition metal ligands such as phosphines and carbenes in order to examine whether low-valent silicon compounds can serve as better alternatives of conventional ligands in practice. Therefore, we analysed 2,6-diisopropyl-phenyl substituted imidazol-2-ylidene (82, Scheme 6) as the most frequently used carbene ligand,6,7 and triphenylphosphine (83) and tricyclohexylphosphine (84) as model compounds3–5 for aryl and alkyl substituted phosphine ligands, respectively, as well. Since the significance of different features depends on the catalytic reaction (on the rate-determining step), we regard our results as a database of potential low-valent silicon-based ligands (see ESI†) from which one can find suitable silicon-based ligand for transition metal catalysed reactions. Based on the large number of data, we derived the main principles that govern the enhanced features of newly synthesized low-valent silicon compounds as ligands to transition metals.
Computational details
Geometry optimizations and NBO charge analyses were carried out at B97-D/6-31G* level, with Def2-TZVP basis on heavier atoms (Fe, Br, Ge, Pd) where relativistic effects are expected to be considerable.76–81 Single point energy calculations on every optimized structure were carried out at B97-D/Def2-TZVP level. B97-D density functional has already been successfully applied to calculate geometries and electronic properties of low-valent silicon compounds.82–87 Stationary points on the potential energy surface (PES) were characterized by harmonic vibrational frequency calculations. Transition states (TS), with one imaginary frequency, were confirmed by intrinsic reaction coordinate (IRC) calculations. Calculations were performed using Gaussian 09 program.88Results and discussion
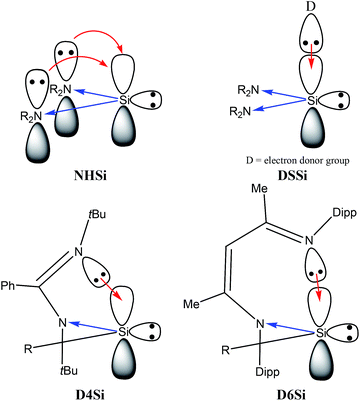
Based on chemical intuition, we constructed five classes of low-valent silicon compounds, which only differ in minor structural parts, similarly to previous classifications;15,16 donor stabilized acyclic low-valent silicon compounds (DASi, 5–15), donor stabilized four membered ring low-valent silicon compounds (D4Si, 22–42), donor stabilized six membered ring low-valent silicon compounds (D6Si, 69–79), N-heterocyclic silylenes (NHSi, 21, 44–55, 68, 80), donor stabilized N-heterocyclic silylenes (DSSi, 60–67, 69, 70). We note that we did not attempt to fit all compounds into classes as many of them show standalone features thus we handled these results separately. However, this partial characterization could help us to make transparency of the results and to easily draw general conclusions on the properties of different silicon ligand systems. Table 1 contains the average, standard deviation (in parenthesis), and the best results of the class with its reference number [in bracket] in case of every ligand class for every investigated properties.| σ-donor strength [kJ mol−1] | π-acceptor ability [−] | LMCT [e] | Buried volume [−] | |
|---|---|---|---|---|
| DASi | 1210 (5%) | 0.12 (54%) | −0.35 (32%) | 0.598 (17%) |
| [1352, 15] | [0.22, 5] | [−0.60, 7] | [0.427, 8] | |
| D4Si | 1165 (4%) | 0.15 (36%) | −0.38 (15%) | 0.469 (24%) |
| [1278, 42] | [0.24, 33] | [−0.49, 42] | [0.357, 30] | |
| D6Si | 1181 (3%) | 0.17 (18%) | −0.39 (11%) | 0.557 (7%) |
| [1222, 73] | [0.24, 71] | [−0.44, 75] | [0.525, 72] | |
| NHSi | 982 (4%) | 0.24 (35%) | −0.24 (19%) | 0.394 (13%) |
| [1023, 51] | [0.42, 80] | [−0.29, 21] | [0.346, 21] | |
| DSSi | 1193 (3%) | 0.10 (59%) | −0.35 (13%) | 0.564 (23%) |
| [1241, 67] | [0.19, 64] | [−0.41, 70] | [0.405, 60] | |
| 82 | 1176 | 0.18 | −0.21 | 0.543 |
| 83 | 1072 | 0.0 | −0.20 | 0.322 |
| 84 | 1031 | 0.0 | −0.26 | 0.374 |
Usual theoretical method of quantifying σ-donor strength, which is important to promote oxidative addition,89,90 is to measure proton affinities or borane stabilization energies.91,92 We performed preliminary calculations on both borane stabilization energies and proton affinities and found the same trends. Therefore, we focus only on proton affinities in the discussion where large proton affinities (PA) characterize strong σ-donating systems. Results of our calculations on PA values are depicted on Fig. 1. Data can be found in table format in the ESI (ESI, Table S1†).
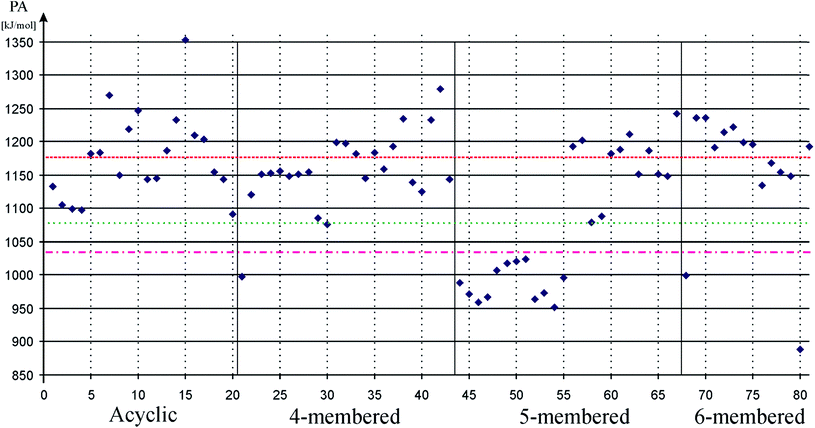 | ||
| Fig. 1 Proton affinity (PA) of low-valent silicon compounds in kJ mol−1 to measure σ-donor strength. Acyclic, 4-membered, 5-membered, and 6-membered signs refer to the ring based grouping of low valent silicon compounds (see Schemes 1–5), which is also indicated by vertical solid lines. Horizontal dashed, dotted-dashed, and dotted lines show proton affinity of carbene (82, 1176 kJ mol−1), phenyl substituted phosphine (83, 1031 kJ mol−1), and cyclohexyl substituted phosphine (84, 1072 kJ mol−1), respectively. Horizontal solid lines and vertical gray dotted lines are presented to guide one's eyes. Note that 5-membered ring silylene, which was previously used as a model compound for low-valent silicon compounds, shows extraordinarily low PA. | ||
Table 1 unambiguously confirms our first observation from Fig. 1: the average PA of NHSi, which are mostly five-membered cyclic molecules, is outstandingly low, which is consistent with the early results of Boehme and Frenking.8 However, other classes show strikingly different character. The average of DASi, D4Si, D6Si, and DSSi classes (1210, 1165, 1181, 1193 kJ mol−1, respectively) are much higher than that of NHSi (982 kJ mol−1). They easily outperform model phosphine ligands (1031 and 1072 kJ mol−1), and are in the same range as NHC (1176 kJ mol−1); the calculated average of three classes (DASi. D6Si, and DSSi) even exceeds it. This deviation among classes can be analysed best on NHSi and DSSi on an unbiased way because most of the compounds in these two groups differ only in a donor structure coordinated to the vacant orbital of the silicon centre (Scheme 7).
PA, and thus σ-donor strength, is mostly determined by the electron density on the low-valent silicon centre, thus, by electron donating or withdrawing effects of neighbour functional groups and by the presence or absence of additional stabilizing electron donors to the vacant orbital. Donor-free NHSis with two electronegative nitrogen atoms next to the silicon are not favourable for strong σ-donor ligands because adjacent nitrogen atoms with high electronegativity strongly withdraw electron density in the σ-system and push electron density weakly in the π-system. However, because of the weak π-donation, additional electron donating group can coordinate to the silicon atom (Scheme 7) which significantly increases the electron density on the silicon centre and enhances the reactivity of the lone pair, that is, the σ-donor ability. As a concrete example: the PA of 68 (NHSi) is only 999 kJ mol−1 but the PA of the NHC stabilized analogue 69 (DSSi) is 1235 kJ mol−1 – much larger than that of NHC–, indicating that NHC stabilized NHSi can be stronger σ-donor than simple NHC alone.
To gain deeper insight we compared and analysed groups D4Si and D6Si in detail because they differ only in the length of the backbone. In groups D4Si and D6Si, the silicon centre has three bonds which can be interpreted as a silylene with an additional N-donation to the ‘empty’ p-orbital (Scheme 7) that increases the electron density on the silicon (compared to NHSi), thus, the σ-donating ability of the molecule itself, similarly to DSSi, (the average of D4Si and D6Si is 1165 and 1181 kJ mol−1, respectively). In D4Si, however, the short backbone hinders the efficient orbital interaction of the lone pair of the donating N atom and the vacant orbital of the silicon centre. The N–Si–N bond angle is 67.9° in 22 the parent compound of D4Si, in contrast to D6Si where the overlapping of the orbitals is ideal (the N–Si–N bond angle is 88.2° in 71 the parent compound of D6Si). These results are also supported by PA data as well. The PA of 22, parent molecule of D4Si, is 1120 kJ mol−1 while the PA of 71, parent molecule of D6Si, is 1190 kJ mol−1, 70 kJ mol−1 higher than that of 22.
Interestingly, double donation to the vacant orbital of the silicon centre is also known in D4Si (41–43). The very large PA of 41 and 42 (1233 kJ mol−1 and 1278 kJ mol−1, respectively) suggest that double donation pushes the limit of σ-donating ability much higher than NHC (1176 kJ mol−1). Double donating compounds are not known in the case of D6Si, however, based on these results; they should have even stronger σ-donating ability.
Donation to the empty orbital in D4Si and D6Si provide extra thermodynamic stability of the silylene (compared to NHSi), which makes it possible to substitute one adjacent nitrogen easily as the large number of synthesized analogues suggest. Therefore, varying the substituents may result in molecules with different σ-donating ability.
Substitution of hydrogen by chlorine, a more electronegative atom, reduces σ-donating ability in line with the suggested picture in Scheme 7. The PA of 29 (1085 kJ mol−1) is decreased by 35 kJ mol−1 compared to 22, whereas the PA of 78 (1154 kJ mol−1) is also reduced by 35 kJ mol−1 compared to 71. Interestingly, the difference between the PA of 29 and 78 is 69 kJ mol−1 which is – considering rounding errors – the same as the difference between the PA of 22 and 71 (70 kJ mol−1) suggesting that the analysed backbone length and substitution effects show additive features. With strong electron donor groups such as ferrocene (38), in which bonding the low-valent silicon atoms to negatively charged cyclopentadienyl rings provide anomalously high electron density on the Si centre, the σ-donating ability can be easily boost up in consistent with the recent results of Driess;11,13 the PA of 38 is 1235 kJ mol−1 which is even much larger value than that of NHC (1176 kJ mol−1). Unfortunately, the six-membered ring analogue of 38 is still missing, however, because of the revealed additive features, it could have very strong σ-donating ability; it is an interesting synthetic target compound.
We used P–H rotational barrier method (see details in the ESI†) for quantifying π-acceptor properties that was introduced for carbene ligands93 and in the same time we show its efficiency for silylenes.94 Calculated relative rotational barriers are depicted in Fig. 2. Data can be found in table form in the ESI (Table S2†).
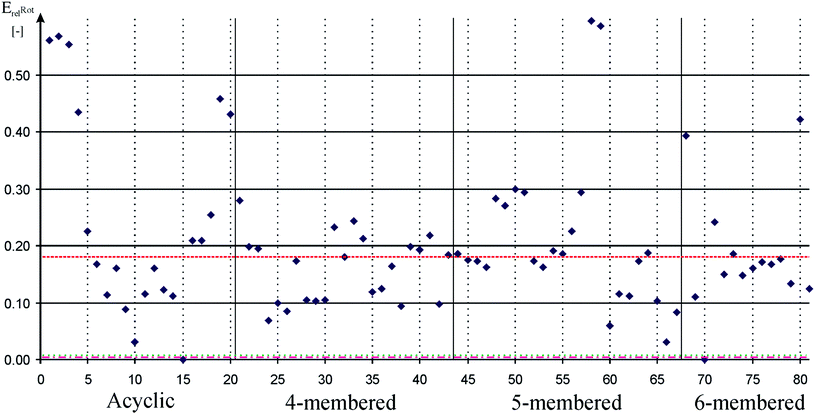 | ||
Fig. 2 Relative rotational barrier of P–H bond around Si–P bond in low-valent silicon compounds compared to SiH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) PH to measure π-acceptor ability. Acyclic, 4-membered, 5-membered, and 6-membered signs refer to the ring based grouping of low valent silicon compounds (see Schemes 1–5) which is also indicated by vertical solid lines. Horizontal dashed, dotted-dashed, and dotted lines indicate the relative rotational barrier in phosphinidene adduct of carbene (82, 0.18), phenyl substituted phosphine (83, ∼0.00), and cyclohexyl substituted phosphine (84, ∼0.00), respectively. Horizontal solid lines and vertical gray dotted lines are presented to guide one's eyes. Note that there are several low-valent silicon compounds with very large rotational barrier. PH to measure π-acceptor ability. Acyclic, 4-membered, 5-membered, and 6-membered signs refer to the ring based grouping of low valent silicon compounds (see Schemes 1–5) which is also indicated by vertical solid lines. Horizontal dashed, dotted-dashed, and dotted lines indicate the relative rotational barrier in phosphinidene adduct of carbene (82, 0.18), phenyl substituted phosphine (83, ∼0.00), and cyclohexyl substituted phosphine (84, ∼0.00), respectively. Horizontal solid lines and vertical gray dotted lines are presented to guide one's eyes. Note that there are several low-valent silicon compounds with very large rotational barrier. | ||
Taking into account that ability of σ-donation derives from large electron density around the silicon, it can be concluded that strong σ-donor molecules are in general weak π-acceptors and vice versa.15 Trends of average proton affinity and relative rotation barrier values shown in Table 1 seem to meet this intuitive expectation. NHSi has the largest average π-acceptor ability (0.24), as there is no direct electron donor group on the ‘vacant’ orbital, only the adjacent N atoms forms weak conjugation in the π-system. The trend is obviously shown by 80 (NHSi) which has the largest P–H rotational barrier among NHSi (0.42) and by far the smallest PA (888 kJ mol−1). Both extreme results can be explained by the positive charge in the π-system. Donor-stabilized analogue group of NHSi, DSSi, has the smallest average π-acceptor ability (0.10) much smaller than that of NHSi which is a direct consequence newly formed dative bond of the silicon centre. The average π-acceptor ability of DASi is very close to the value of DSSi (0.12), and D4Si and D6Si are also in the same range (0.15 and 0.17, respectively) especially considering the relatively large standard deviation (∼20–60%), – note that standard deviation of σ-donor ability is only 3–5% and the larger values mentioned above also stem from the large rounding error (rounding of 0.15 ± 0.01 gives 13% deviation). Nevertheless, the general trends are still clear within groups, similarly to σ-donor trend but with opposite sign: e.g. the parent compound of D4Si, 22, which lacks any donation of the H atom to the ‘vacant’ orbital of the silicon centre, has one of the largest values in the group (0.20) while electron donor modification, such as NMe2, 24, immediately drops the π-acceptor ability (0.09).
In spite of the aforementioned results, we cannot conclude that low-valent silicon compounds have generally weak π-acceptor ability because several successful syntheses, especially acyclic compounds, which cannot be classified into groups, modify the overall picture. Remarkable π-acceptor ability is expected in the absence of significant electron donation to the ‘vacant’ orbital of the silicon centre, for example, in the case of R–Si–R′ acyclic structure (1, 2, 3, 4, 19, 20; relative barriers: 0.56, 0.57, 0.55, 0.43, 0.46 and 0.43, respectively). The synthesis of these compounds requires large steric bulk groups, kinetically compensating the electron deficient reactive silicon centre, which is also important in reductive elimination step.89,90
Ligand-to-metal charge transfer (LMCT) can be used to gauge the ability of a ligand to encourage oxidative addition,88,89 although in the case of low-valent silicon compounds it measures the recently discussed two electronic properties – σ-donor and π-acceptor strength – simultaneously, because both interactions are strongly present in low-valent silicon – transition metal complexes and influence the overall charge of the transition metal centre. To investigate this property, we chose to study palladium low-valent silicon complexes by computing the NBO charge of the Pd centre because several important catalytic reactions, e.g. Suzuki-reaction, involving Pd as transition metal centre, are well-known with phosphine and carbene ligands as well.95–98
The calculated charge on palladium in palladium low-valent silicon complexes are depicted on Fig. 3. Data can be found in table form in the ESI (Table S3†). Note that in certain cases, geometry optimization of palladium complexes resulted in additional phenyl coordination (10, 15, 17, 56) or chelation (36, 38, 63), which hindered us to compare their results with other complexes. We list these results on Fig. 3 and in Table S3† for the sake of completeness, however, we excluded them from further considerations and they are not included in the results showed in Table 1.
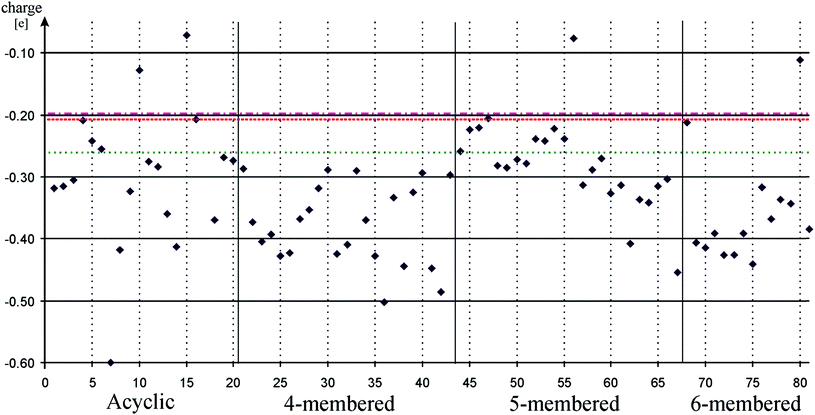 | ||
| Fig. 3 Pd charge in palladium low-valent silicon complexes to measure ligand-to-metal charge transfer. Acyclic, 4-membered, 5-membered, and 6-membered signs refer to the ring based grouping of low valent silicon compounds (see Schemes 1–5) which is also indicated by vertical solid lines. Horizontal dashed, dotted-dashed, and dotted lines indicate the Pd charge in palladium carbene (82, −0.20), palladium phenyl substituted phosphine (83, −0.21), and palladium cyclohexyl substituted phosphine (84, −0.26) complexes, respectively. Horizontal solid lines and vertical gray dotted lines are presented to guide one's eyes. Note that almost all low-valent silicon compounds push more electron density to the metal centre than phosphines or NHC. | ||
Fig. 3 unambiguously shows that most low-valent silicon complexes transfer more charge to the Pd centre than NHC or phosphines. This may suggest that LMCT is mainly associated with σ-donor ability, not π-acceptor ability, however, even NHSi, which has the lowest σ-donor ability and strongest π-acceptor ability among all classes, produces larger LMCT results (average: −0.24) than NHC (−0.20). Also, NHC as a very strong σ-donor (PA: 1176 kJ mol−1), has lower LMCT value (−0.20) than phosphines (−0.21 and −0.26, respectively) (PA: 1031 and 1072 kJ mol−1, respectively). Therefore, we concluded that electronegativity is the main governing principle in LMCT results. It can explain why the less electronegative silicon show uniformly better LMCT results than NHC and phosphines that withdraw their lone pair from Pd centre because of their higher electronegativity. This assumption also explains the anomalously low result of NHC compared to phosphines, in spite of its strong σ-donor ability, owing to the somewhat higher electronegativity of carbon compared to phosphorus.
The same trends can be observed in LMCT results as in case of σ-donor ability, which also enhances the previous findings that LMCT is related to σ-donor ability and is important to oxidative addition step. The NHSi group has the lowest average (−0.24), which is associated with the low σ-donor ability compared to other classes, while donor-stabilized compounds (DASi, D4Si, D6Si, DSSi), with larger σ-donor ability, show enhanced LMCT values (−0.35, −0.38, −0.39, −0.35, respectively).
Interestingly, the averages show similar consistency to PAs in case of σ-donor ability. Even standard deviations (∼10%) show relatively small variability (note that rounding error −0.35 ± 0.01 gives 7% deviation), just like in case of σ-donor ability, except for DASi (32%) which group is structurally more versatile than the others and has an overall higher LMCT value of −0.60 (7). Within classes, the electron donor/withdrawing groups have similar effects to that in case of σ-donor ability. Following the previous examples discussed at σ-donor ability, the LMCT value of parent compound of D4Si, 22, which has no electron withdrawing group, is −0.37, above average of the group, while chlorine modification, 29, reduce the LMCT value to −0.32. Similar observation is possible in the case of D6Si, where LMCT value of 71 is −0.39 which drops to −0.34 with chlorine substitution (78). Double donation to the ‘vacant’ orbital of silicon centre in 41 and 42 boost LMCT toward the Pd atom resulting in the highest LMCT values in D4Si, −0.45 and −0.49, respectively.
Since bulky ligands can hinder oxidative addition and can also promote reductive elimination, steric properties of the ligands has significant influence on the reaction rate.89,90 In order to be able to select the suitable silicon-based ligand for a particular homogenous catalytic reaction, this effect also has to be quantified. Buried volume based methods have a tradition to be used for the quantification of steric properties.99 We implemented standard buried volume method based on previous works100–102 and calculated the coverage of the Pd atom on the optimized geometry of palladium complexes of 1–81, and compared them to that in similar complexes of 82–84. Results of these computations are depicted on Fig. 4. Data can be found in table form in the ESI (Table S4†).
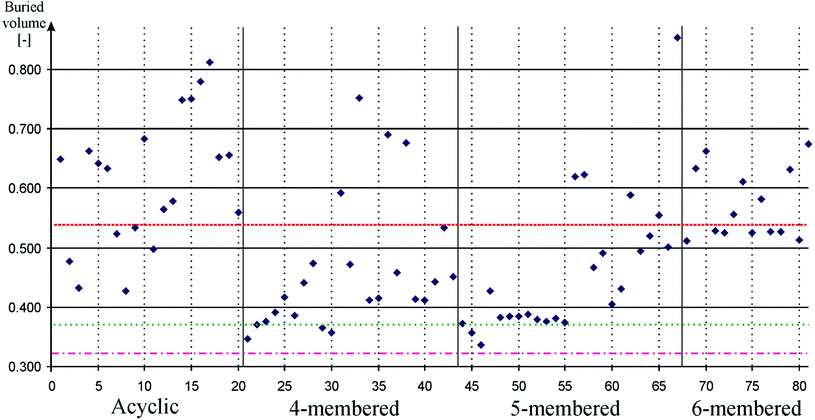 | ||
| Fig. 4 Buried volume of the Pd atom in palladium low-valent silicon complexes to measure steric properties. Acyclic, 4-membered, 5-membered, and 6-membered signs refer to the ring based grouping of low valent silicon compounds (see Schemes 1–5) which is also indicated by vertical solid lines. Horizontal dashed, dotted-dashed, and dotted lines indicate the buried volume on the Pd atom in palladium carbene (82, 0.543), palladium phenyl substituted phosphine (83, 0.322), and palladium cyclohexyl substituted phosphine (84, 0.374) complexes, respectively. Horizontal solid lines and vertical gray dotted lines are presented to guide one's eyes. Note that low-valent silicon compounds indicate versatile steric properties. | ||
Fig. 4 show that low-valent silicon compounds provide versatile opportunities in respect of bulky ligand design. Most four- and five-membered ring low-valent silicon compounds indicate buried volume values well below NHC (0.543) while acyclic and six-membered ring compounds show similar or higher values than that of NHC, though, in all cases there are outliers from this generalized picture which provide evidence that all type of compounds can be effectively modified to increase or decrease bulkiness according to steric demands. Note that the buried volume results of model phosphines compounds 83 and 84 (0.322 and 0.374, respectively) present extremely low values; generally used ligands with complex bulky ligands may produce higher buried volume.
Table 1 confirms all these general points; the average buried volume of NHSi and D4Si show values (0.394 and 0.469, respectively) below the result of NHC (0.543) while D6Si and DSSi indicate average results (0.557 and 0.564, respectively) very close to that of NHC and DASi has larger average (0.598) than that of NHC. Relatively large standard deviations (10–25%) suggest that there are compounds with different bulkiness in every class; therefore, one may choose appropriate ligand system for oxidative addition or reductive elimination considering steric properties and σ-donor or π-acceptor ability at the same time.
To promote oxidative addition, D4Si, D6Si, and DASi indicated excellent results as σ-donors (vide supra). These classes, however, show very distinct steric features. Since oxidative addition is favourable with small buried volume, D4Si seems to be plausible choice (average: 0.469). Moreover, the best buried volume result of the class (30, 0.357) even competes with the extremely low result of model phosphines compounds (0.322 and 0.374). D6Si show very consistent buried volume results (0.557 group average with only 7% standard deviation) because all compounds contain bulky diisopropylphenyl groups. Reduction of the bulky groups, however, may result in an even better transition metal ligand than D4Si compounds because D6Si indicate stronger σ-donor strength than analogue D4Si compounds. Moreover, even DASi can provide alternatives for oxidative addition in spite of its very large average buried volume (0.600), because of the large deviations in the class; buried volume of 8 is only 0.427, smaller than that of the D4Si average.
To promote reductive elimination, NHSi and acyclic structures (1, 2, 3, 4, 19, and 20) are found to be good choice as good π-acceptors (vide supra). Acyclic structures generally show high buried volume values (0.5–0.7), similar or larger than that of NHC (0.543), therefore, they are favourable for promoting reductive elimination as it requires large bulky groups. On the other hand, NHSi shows the smallest average buried volume (0.394) because of their relatively small bulky ligands such as tert-butyl, which may not ideal for reductive elimination, however, some outliers with large bulky groups such as 68 (0.529) with diisopropylphenyl ligand may be more suitable for this purpose.
Conclusions
We investigated the steric and electronic properties of synthetically available low-valent silicon compounds to elucidate their potential application as ligands to transition metals and compared their performance with generally applied carbene and phosphines ligands. We found that several low-valent silicon compounds can compete or even outperform classic carbene and phosphines in all important properties (σ-donor and π-acceptor strength, ligand-to-metal charge transfer, steric properties). We also derived the general principles behind the enhanced features.Due to their advantageous combination of steric and electronic properties, strong σ-donors with small buried volume to promote oxidative addition step or strong π-acceptor ability with large buried volume to enhance reductive elimination, we recommend in general performing transition metal catalysed reactions using low-valent silicon compounds as ligands. Based on the database we created (see ESI†) one can find suitable silicon-based ligand for homogenous catalytic process.
Acknowledgements
We are grateful for generous support of The New Széchenyi Plan TAMOP-4.2.2/B-10/1-2010-0009, the German Chemical Society, the Hungarian Academy of Engineering, the ETDB committee of BUTE, and the Gedeon Richter Plc. We thank the useful comments of Prof. Tamás Veszprémi and the technical help of Dr András Olasz in buried volume calculations. We thank the help of Dr Julianna Oláh to improve the language of our manuscript.Notes and references
- Transition Metals for Organic Syntheses, ed. M. Beller and C. Bolm, Wiley, 2004 Search PubMed.
- Applications of Transition Metal Catalysis in Drug Discovery and Development, ed. M. L. Crawley and B. M.Trost, Wiley, 2012 Search PubMed.
- Ligand electronic effects in homogeneous catalysis using transition metal complexes of phosphine ligands, ed. M. L. Clarke and J. J. R. Frew, RSC Publishing, 2009 Search PubMed.
- Phosphorus(III) ligands in homogeneous catalysis: Design and synthesis, ed. P. C. J. Kamer and P. W. N. M. van Leeuwen, Wiley, 2012 Search PubMed.
- Homogeneous Catalysis with Metal Phosphine Complexes, ed. L. M. Pignolet, Springer, 2013 Search PubMed.
- N-Heterocyclic Carbenes in Transition Metal Catalysis, ed. F. Glorius, Springer, 2007 Search PubMed.
- N-Heterocyclic Carbenes in Transition Metal Catalysis and Organocatalysis, ed. C. S. J. Cazin, Springer, 2011 Search PubMed.
- M. Asay, C. Jones and M. Driess, Chem. Rev., 2011, 111, 354–396 CrossRef CAS PubMed.
- A. Fürstner, H. Krause and C. W. Lehmann, Chem. Commun., 2001, 2372–2373 RSC.
- G. Schmid and E. Welz, Angew. Chem., Int. Ed., 1977, 16, 785–786 CrossRef.
- A. Brück, D. Gallego, W. Wang, E. Irrane, M. Driess and J. F. Hartwig, Angew. Chem., Int. Ed., 2012, 51, 11478–11482 CrossRef PubMed.
- B. Blom, S. Enthaler, S. Inoue, E. Irran and M. Driess, J. Am. Chem. Soc., 2013, 135, 6703–6713 CrossRef CAS PubMed.
- W. Wang, S. Inoue, S. Enthaler and M. Driess, Angew. Chem., Int. Ed., 2012, 51, 6167–6171 CrossRef CAS PubMed.
- M. Stoelzel, C. Präsang, B. Blom and M. Driess, Aust. J. Chem., 2013, 66, 1163–1170 CAS.
- B. Blom, D. Gallego and M. Driess, Inorg. Chem. Front., 2014, 1, 134–148 RSC.
- B. Blom, M. Stoelzel and M. Driess, Chem.–Eur. J., 2013, 19, 40–62 CrossRef CAS PubMed.
- D. G. Musaev, K. Morokuma and N. Koga, J. Chem. Phys., 1993, 99, 7859 CrossRef CAS PubMed.
- P. G. Hayes, C. Beddie, M. B. Hall, R. Waterman and T. D. Tilley, J. Am. Chem. Soc., 2006, 128, 428–429 CrossRef CAS PubMed.
- C. Boehme and G. Frenking, Organometallics, 1998, 17, 5801–5809 CrossRef CAS.
- Some of the low-valent silicon compounds were isolated only in complex form, however, as it did not influence our goal namely to explore the potential effect of low-valent silicon compounds as transition metal ligand, we treated them as other compounds and investigated their free form.
- P. Jutzi, D. Kanne and C. Krüger, Angew. Chem., Int. Ed., 1986, 25, 164 CrossRef.
- C. Zybill and G. Müller, Angew. Chem., Int. Ed., 1987, 26, 669–670 CrossRef.
- H. H. Karsch, U. Keller, S. Gamper and G. Müller, Angew. Chem., Int. Ed., 1990, 29, 295–296 CrossRef.
- M. Veith, E. Werle, R. Lisowsky, R. Köppe and H. Schnöckel, Chem. Ber., 1992, 125, 1375–1377 CrossRef CAS.
- M. Denk, R. Lennon, R. Hayashi, R. West, A. V. Belyakov, H. P. Verne, A. Haaland, M. Wagner and N. Metzler, J. Am. Chem. Soc., 1994, 116, 2691–2692 CrossRef CAS.
- B. Gehrhus, M. F. Lappert, J. Heinicke, R. Boese and D. Bläser, J. Chem. Soc., Chem. Commun., 1995, 1931–1932 RSC.
- R. West and M. Denk, Pure Appl. Chem., 1996, 68, 785–788 CrossRef CAS.
- J. Heinicke, A. Oprea, M. K. Kindermann, T. Kárpáti, L. Nyulászi and T. Veszprémi, Chem.–Eur. J., 1998, 4, 541–545 CrossRef CAS.
- M. W. Boesveld, B. Gehrhus, P. B. Hitchcock, M. F. Lappert and P. v. R. Schleyer, Chem. Commun., 1999, 755–756 RSC.
- M. Kira, S. Ishida, T. Iwamoto and C. Kabuto, J. Am. Chem. Soc., 1999, 121, 9722–9723 CrossRef CAS.
- G.-H. Lee, R. West and T. Müller, J. Am. Chem. Soc., 2003, 125, 8114–8115 CrossRef CAS PubMed.
- N. Takeda, T. Kajiwara, H. Suzuki, R. Okazaki and N. Tokitoh, Chem.–Eur. J., 2003, 9, 3530–3543 CrossRef CAS PubMed.
- B. Gehrhus, P. B. Hitchcock and M. F. Lappert, Z. Anorg. Allg. Chem., 2005, 631, 1383–1386 CrossRef CAS.
- M. Driess, S. Yao, M. Brym, C. van Wüllen and D. Lentz, J. Am. Chem. Soc., 2006, 128, 9628–9629 CrossRef CAS PubMed.
- M. Driess, S. Yao, M. Brym and C. van Wüllen, Angew. Chem., Int. Ed., 2006, 45, 6730–6733 CrossRef CAS PubMed.
- C.-W. So, H. W. Roesky, J. Magull and R. B. Oswald, Angew. Chem., Int. Ed., 2006, 45, 3948–3950 CrossRef CAS PubMed.
- C.-W. So, H. W. Roesky, P. M. Gurubasavaraj, R. B. Oswald, M. T. Gamer, P. G. Jones and S. Blaurock, J. Am. Chem. Soc., 2007, 129, 12049–12054 CrossRef CAS PubMed.
- Y. Wang, Y. Xie, P. Wei, R. B. King, H. F. Schaefer III, P. von, R. Schleyer and G. H. Robinson, Science, 2008, 321, 1069–1071 CrossRef CAS PubMed.
- Y. Mizuhata, T. Sasamori and N. Tokitoh, Chem. Rev., 2009, 109, 3479–3511 CrossRef CAS PubMed.
- A. Meltzer, C. Präsang and M. Driess, J. Am. Chem. Soc., 2009, 131, 7232–7233 CrossRef CAS PubMed.
- Y. Xiong, S. Yao and M. Driess, J. Am. Chem. Soc., 2009, 131, 7562–7563 CrossRef CAS PubMed.
- D. Gau, T. Kato, N. Saffon-Merceron, F. P. Cossío and A. Baceiredo, J. Am. Chem. Soc., 2009, 131, 8762–8763 CrossRef CAS PubMed.
- P. Jutzi, K. Leszczynska, B. Neumann, W. W. Schoeller and H.-G. Stammler, Angew. Chem., Int. Ed., 2009, 48, 2596–2599 CrossRef CAS PubMed.
- R. S. Ghadwal, H. W. Roesky, S. Merkel, J. Henn and D. Stalke, Angew. Chem., Int. Ed., 2009, 48, 5683–5686 CrossRef CAS PubMed.
- S. S. Sen, A. Jana, H. W. Roesky and C. Shulzke, Angew. Chem., Int. Ed., 2009, 48, 8536–8538 CrossRef CAS PubMed.
- A. C. Tomasik, A. Mitra and R. West, Organometallics, 2009, 28, 378–381 CrossRef CAS.
- H. Cui, Y. Shao, X. Li, L. Kong and C. Cui, Organometallics, 2009, 28, 5191–5195 CrossRef CAS.
- P. Zark, A. Schäfer, A. Mitra, D. Haase, W. Saak, R. West and T. Müller, J. Organomet. Chem., 2010, 695, 398–408 CrossRef CAS PubMed.
- H.-X. Yeong, K.-C. Lau, H.-W. Xi, K. H. Lim and C.-W. So, Inorg. Chem., 2010, 49, 371–373 CrossRef CAS PubMed.
- A. C. Filippou, O. Chernov, B. Blom, K. W. Stumpf and G. Schnakenburg, Chem.–Eur. J., 2010, 16, 2866–2872 CrossRef CAS PubMed.
- S.-H. Zhang, H.-X. Yeong, H.-W. Xi, K. H. Lim and C.-W. So, Chem.–Eur. J., 2010, 16, 10250–10254 CrossRef CAS PubMed.
- A. Meltzer, S. Inoue, C. Präsang and M. Driess, J. Am. Chem. Soc., 2010, 132, 3038–3046 CrossRef CAS PubMed.
- W. Wang, S. Inoue, S. Yao and M. Driess, J. Am. Chem. Soc., 2010, 132, 15890–15892 CrossRef CAS PubMed.
- Y. Gao, J. Zhang, H. Hu and C. Cui, Organometallics, 2010, 29, 3063–3065 CrossRef CAS.
- A.-C. Jungton, A. Meltzer, C. Präsang, T. Braun, M. Driess and A. Pennera, Dalton Trans., 2010, 39, 5436–5438 RSC.
- Y. Xiong, S. Yao and M. Driess, Chem.–Asian J., 2010, 5, 322–327 CrossRef CAS PubMed.
- C. Jones, S. J. Bonyhady, N. Holzmann, G. Frenking and A. Stasch, Inorg. Chem., 2011, 50, 12315–12325 CrossRef CAS PubMed.
- S. P. Sarish, S. S. Sen, H. W. Roesky, I. Objartel and D. Stalke, Chem. Commun., 2011, 47, 7206–7208 RSC.
- D. Gau, R. Rodriguez, T. Kato, N. Saffon-Merceron, A. de Cózar, F. P. Cossío and A. Baceiredo, Angew. Chem., Int. Ed., 2011, 50, 1092–1096 CrossRef CAS PubMed.
- M. Asay, S. Inoue and M. Driess, Angew. Chem., Int. Ed., 2011, 50, 9589–9592 CrossRef CAS PubMed.
- R. Rodriguez, D. Gau, Y. Contie, T. Kato, N. Saffon-Merceron and A. Baceiredo, Angew. Chem., Int. Ed., 2011, 50, 11492–11495 CrossRef CAS PubMed.
- S. Inoue, W. Wang, C. Präsang, M. Asay, E. Irran and M. Driess, J. Am. Chem. Soc., 2011, 133, 2868–2871 CrossRef CAS PubMed.
- M. Stoezel, C. Präsang, S. Inoue, S. Enthaler and M. Driess, Angew. Chem., Int. Ed., 2012, 51, 399–403 CrossRef PubMed.
- S. Inoue and K. Leszczynska, Angew. Chem., Int. Ed., 2012, 51, 8589–8593 CrossRef CAS PubMed.
- S. M. I. Al-Rafia, A. C. Malcolm, R. McDonald, M. J. Ferguson and E. Rivard, Chem. Commun., 2012, 48, 1308–1310 RSC.
- A. V. Protchenko, K. H. Birjkumar, D. Dange, A. D. Schwarz, D. Vidovic, C. Jones, N. Kaltsoyannis, P. Mountford and S. Aldridge, J. Am. Chem. Soc., 2012, 134, 6500–6503 CrossRef CAS PubMed.
- B. D. Rekken, T. M. Brown, J. C. Fettinger, H. M. Tuononen and P. P. Power, J. Am. Chem. Soc., 2012, 134, 6504–6507 CrossRef CAS PubMed.
- T. Abe, R. Tanaka, S. Ishida, M. Kira and T. Iwamoto, J. Am. Chem. Soc., 2012, 134, 20029–20032 CrossRef CAS PubMed.
- Y. Xiong, S. Yao, S. Inoue, J. D. Epping and M. Driess, Angew. Chem., Int. Ed., 2013, 52, 7147–7150 CrossRef CAS PubMed.
- K. C. Mondel, H. W. Roesky, M. C. Schwarzer, G. Frenking, B. Niepötter, H. Wolf, R. Herbst-Irmer and D. Stalke, Angew. Chem., Int. Ed., 2013, 52, 2963–2967 CrossRef PubMed.
- B. Blom, S. Enthaler, S. Inoue, E. Irran and M. Driess, J. Am. Chem. Soc., 2013, 135, 6703–6713 CrossRef CAS PubMed.
- N. C. Breit, T. Szilvási, T. Suzuki, D. Gallego and S. Inoue, J. Am. Chem. Soc., 2013, 135, 17958–17968 CrossRef CAS PubMed.
- E. Rivard, Dalton Trans., 2014, 43, 8577–8586 RSC.
- K. Nyíri and T. Veszprémi, Organometallics, 2009, 28, 5909–5914 CrossRef.
- K. Nyíri, T. Szilvási and T. Veszprémi, Dalton Trans., 2010, 39, 9347–9352 RSC.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS PubMed.
- O. Vahtras, J. Almlöf and M. W. Feyereisen, Chem. Phys. Lett., 1993, 213, 514–518 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1997, 107, 8554–8560 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS PubMed.
- T. Szilvási and T. Veszprémi, Organometallics, 2012, 31, 3207–3212 CrossRef.
- T. Szilvási and T. Veszprémi, Organometallics, 2013, 32, 4733–4740 CrossRef.
- Z. Benedek, T. Szilvási and T. Veszprémi, Dalton Trans., 2014, 43, 1184–1190 RSC.
- K. Hansen, T. Szilvási, B. Blom, E. Irran and M. Driess, Chem.–Eur. J., 2014, 20, 1947–1956 CrossRef CAS PubMed.
- N. C. Breit, T. Szilvási and S. Inoue, Chem.–Eur. J., 2014, 20, 9312–9318 CrossRef CAS PubMed.
- S. U. Ahmad, T. Szilvási and S. Inoue, Chem. Commun., 2014, 50, 12619–12622 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- Applied Homogeneous Catalysis with Organometallic Compounds, ed. B. Cornils and W. A. Herrmann, Wiley, 1996 Search PubMed.
- in Homogeneous catalysis: Understanding the Art, ed. P. W. N. M. van Leeuwen, Kluwer Academic Publishers, 2003 Search PubMed.
- N. Fey, A. C. Tsipis, S. E. Harris, J. N. Harvey, G. Orpen and R. A. Mansson, Chem.–Eur. J., 2006, 12, 291–302 CrossRef CAS PubMed.
- J. Jover, N. Fey, J. N. Harvey, G. C. Lloyd-Jones, A. G. Orpen, G. J. J. Owen-Smith, P. Murray, D. R. J. Hose, R. Osborne and M. Purdie, Organometallics, 2010, 29, 6245–6258 CrossRef CAS.
- O. Back, M. Henry-Ellinger, C. D. Martin, D. Martin and G. Bertrand, Angew. Chem., Int. Ed., 2013, 52, 2939–2943 CrossRef CAS PubMed.
- K. Hansen, T. Szilvási, B. Blom, S. Inoue, J. Epping and M. Driess, J. Am. Chem. Soc., 2013, 135, 11795–11798 CrossRef CAS PubMed.
- N. Miyaura and A. Suzuki, Chem. Rev., 1995, 95, 2457–2483 CrossRef CAS.
- G. Altenhoff, R. Goddard, C. W. Lehmann and F. Glorius, Angew. Chem., Int. Ed., 2003, 42, 3690–3693 CrossRef CAS PubMed.
- M. G. Organ, S. Calimsiz, M. Sayah, K. H. Hoi and A. J. Lough, Angew. Chem., Int. Ed., 2009, 48, 2383–2387 CrossRef CAS PubMed.
- T. Szilvási and T. Veszprémi, ACS Catal., 2013, 3, 1984–1991 CrossRef.
- A. C. Hillier, W. J. Sommer, B. S. Yong, J. L. Petersen, L. Cavallo and S. P. Nolan, Organometallics, 2003, 22, 4322–4326 CrossRef CAS.
- I. A. Guzei and M. Wendt, Dalton Trans., 2006, 3991–3999 RSC.
- A. Poater, B. Cosenza, A. Correa, S. Giudice, F. Ragone, V. Scarano and L. Cavallo, Eur. J. Inorg. Chem., 2009, 1759–1766 CrossRef CAS.
- H. Clavier and S. P. Nolan, Chem. Commun., 2010, 46, 841–861 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Details on P–H rotational method, all calculated energies, in Hartree and in kJ mol−1, and geometries are available. See DOI: 10.1039/c4ra14417a |
| This journal is © The Royal Society of Chemistry 2015 |