DOI:
10.1039/C4RA14367A
(Paper)
RSC Adv., 2015,
5, 11297-11308
Size dependence of the equation of state for Ne nanoclusters from an effective two-body potential via molecular dynamics simulations
Received
12th November 2014
, Accepted 7th January 2015
First published on 9th January 2015
Abstract
In this paper we have extended the equation of state (EoS) in terms of particle size for Ne nanoclusters using an effective two-body Hartree–Fock dispersion (HFD)-like potential by molecular dynamics simulations. To take quantum and many-body forces into account, a new simple and accurate empirical expression is used with the HFD-like potential without requiring an expensive three-body calculation. Some features of the EoS criteria, such as the temperature and size dependences of the coefficients, the isothermal bulk modulus and its pressure derivative at the zero-pressure limit, and the isobaric thermal expansion for Ne nanoclusters have been also investigated. The results indicate that the bulk modulus and isobaric expansion coefficient increase as the cluster size decreases.
Introduction
Investigations of clusters and nanoparticles are pursued with several motivations ranging from optimization of the conductivity, magnetic properties, and electronic properties of a material to tailoring substances for use in chemical reactions or for catalysis.1,2
Based on prior studies,3,4 it is clear that quantum effects cannot be ignored for solid neon and that the neglect of these effects will lead to discrepancies when experimental data and classical results are compared. It is also well known that three-body interactions can make a small but significant contribution to properties of solids.5 To obtain quantitative agreement with experiments, pair potentials must be used in conjunction with three-body interactions.6–9
There are many contributions to three-body interactions, but evidences5 indicate that the triple–dipole term of Axilrod and Teller (AT)10 is a fairly good approximation. Nonetheless, the need for three-body calculations, in addition to pair calculations, represents a considerable computational impediment. Solca et al.4 determined melting curve of neon from nonequilibrium MD simulations using ab initio pair-potentials and inclusion of three-body effects at constant pressure. Pahl et al.8 also calculated accurate the melting temperatures for neon and argon using ab initio potentials and inclusion of the AT three-body expression by studying finite clusters and extrapolating the results to infinitely large systems. Schwerdtfeger and Hermann9 performed quantum ab initio calculations for neon triplet and subsequently adjusted the resulting data to an extended triple–dipole AT potential. They concluded that the more complete treatment of three-body force and the four-body force should be considered.
Much work has still to be done for constructing accurate two- and three-body interaction potentials for the rare gases. Solid-state calculations is of great use in the determination of the accuracy of such potentials, which can be further used in cluster simulations.11 The simple Lennard-Jones (LJ) potential one may not get the expected fcc structure for the rare gas solids at medium to large cluster size,12,13 so that the LJ model may become a rather poor approximation for rare-gas clusters when we are interested in structural trends towards the bulk limit.11 Density functional theory (DFT) is currently not capable of accurately describing van der Waals-type clusters (of course, the recent ab initio coupled-cluster calculations give very reasonable results).14 The relativistic ab initio electronic structure calculations including electron correlation are also possible only for the smallest clusters. The most accurate computational quantum methods available are required for describing weak interactions between rare-gas atoms, either in the cluster or in the solid, which currently is a formidable task. Therefore, the use of two-body potentials appears as an important attempt towards the improvement of structure calculations of rare-gas clusters and the solid state.11
We have determined the EoS of neon nanoclusters using a two-body Hartree–Fock dispersion (HFD)-like potential by MD simulation. To take quantum and many-body forces into account, a new simple and accurate empirical expression is used with the HFD-like potential without requiring an expensive three-body calculation. Some features of the EoS criteria, such as the temperature and size dependences of the coefficients, the isothermal bulk modulus and its pressure derivative at the zero-pressure limit, and the isobaric thermal expansion for neon nanoclusters have been investigated.
Intermolecular potentials
Systems of spherical molecules, such as the rare gases, have been intensively and successfully studied over a broad range of temperatures and densities using pair interactions of HFD-like model.15–18 Therefore, the reduced HFD-like potential has been used as a classical two-body potential for neon which has been obtained via the inversion of reduced viscosity collision integrals at zero pressure:17| |
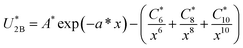 | (1) |
where x = r/σ and U*2B = U2B/ε. The values of the parameters of the HFD-like potential for neon are given in Table 1.
Table 1 The HFD-like parameters of neon used in this work
| Parameter |
Value |
| ε/k (K) |
42.25 |
| σ (Å) |
2.759 |
| A* |
2.0342 × 104 |
| a* |
10.3929 |
| C*6 |
1.2839 |
| C*8 |
7.8407 |
| C*10 |
−8.2396 |
Hauschild and Prausnitz19 proposed a many-body correction term in conjunction with the two-body Kihara potential which was a field term proportional to the 9/10 power of the overall density (ρ0.9) as well as to the attractive-energy contribution from the two-body potential (U2B-Att):
| |
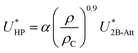 | (2) |
where
α is an adjustable parameter and
ρC is the density at the vapor–liquid critical point.
Abbaspour et al.20–22 have proposed the modified Hauschild and Prausnitz three-body potential in which temperature and density dependence of the coefficient α determined for different pure and mixture fluid systems. This three-body potential was proportional to the attractive-energy contribution from the two-body potential, but it has been demonstrated that the accurate properties of the solids may be well described using the effective two-body potential (with a specially adjusted short-range correcting term) instead of the only three-body exchange interaction. Therefore, we have introduced the following correction term, in conjunction with the classical two-body HFD-like potential, which is a field term proportional to the both repulsive and attractive energy contribution from the two-body potential:
where
β is an adjustable parameter which is dependent on the temperature at constant pressure (according to the work of Hauschild and Prausnitz
19).
We have determined the adjustable parameter β by comparison between prediction of internal energy of solid neon at different temperatures (which corresponds to different densities at constant atmospheric pressure) and experimental data and presented in Fig. 1. Therefore, the β values, which correspond to the difference between the two-body results and the experimental data, not only account for the triple–dipole interaction but also for other effects (such as the quantum effects) which make the calculated values from the pair interaction potential closer to experimental data. According to Fig. 1, the β values are greater at higher densities (and lower temperatures) which correspond to the greater three-body and quantum effects.
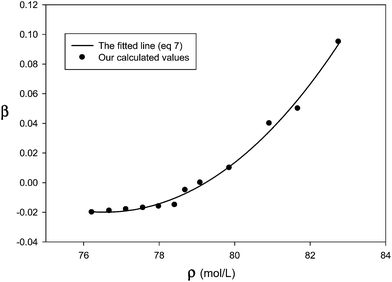 |
| | Fig. 1 Our calculated β values at different densities at atmospheric pressure and the fitted line for the solid neon (the different densities correspond to temperatures from 2–19 K). | |
On the basis of the effective interactions of an extended Lennard-Jones (12, 6, 3) type, Parsafar et al.23 showed that for a wide variety of fluids and solids, the average configurational energy per particle can be given by:
| |
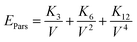 | (4) |
where the temperature dependent parameters
Ki depend on the chemical species as well as the physical state of the system.
Eqn (4) may be rearranged to:
| |
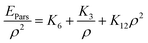 | (5) |
where
ρ = 1/
V is the molar density. Therefore, according to
eqn (5), the total interaction potential (two-body plus many-body interaction potentials) can be presented by:
| |
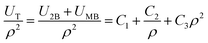 | (6) |
where the
C1,
C2, and
C3 are constants. The
U2B is the two-body potential given by
eqn (1) and
UMB is the many-body potential. In order to verify the validity of the assumption of
eqn (6), the density dependence of the total configurational energy has been studied at different densities at constant atmospheric pressure. For this purpose, the mean value of the quantity
ET/
ρ2 has been calculated for the solid neon, based on the MD results, and its behavior has been compared with the
eqn (6) in
Fig. 2. Solid lines are fitted curves based on the relation given in
eqn (6). The parameters of the fitted curves (
C1,
C2, and
C3) and the
R2 values of the least-squares method used for the regression are given in
Table 2. In general, the
R2 values show good correlation between the simulations results and the predicted relation for the configurational energy. This verifies the applicability of the many-body expression of
eqn (6) for the solid system.
 |
| | Fig. 2 Density dependence of the total configurational energy of the solid system at atmospheric pressure. | |
Table 2 The parameters of the fit to the total configuration energy equation (eqn (6))
| C1 (kJ L2 mol−3) |
C2 (kJ L mol−2) |
C3 (kJ L4 mol−5) |
R2 |
| −11.9660 |
562.9577 |
0.0007 |
0.9952 |
We can derive the density dependence of β by replacing the UMB in eqn (6) by the eqn (3) as:
| |
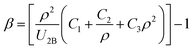 | (7) |
where
Fig. 1 shows the fitted equation (
eqn (7)) to the
β values. Therefore, the total (two-body plus many-body) or the effective interaction potential for the solid systems is as:
| | |
UT = U2B + UMB = U2B(1 + β)
| (8) |
The significance of this equation is that it allows us to use the two-body potentials to predict accurately the properties of solids without incurring the computational cost of the three-body or quantum calculations. In the other words, the new many-body potential not only accounts for the triple–dipole interaction but also for other effects such as the quantum effects and three-body repulsion or many-body terms. This is mainly due to the adjustable parameter, β and its parameters C1, C2, and C3 which is obtained by comparison with the experimental data.
In order to investigate the effect of the many-body potential to the total potential (eqn (8)), we have presented the two-body and total potentials of solid neon at both low and high densities (corresponding to the high and low temperatures, respectively) in Fig. 3. It is shown that the effect of adding UMB to U2B, in order to obtain the effective interaction, is to raise the minimum of U2B and displace it a little to the right. In the other words, the net effect of the UMB is to decrease the effective energy depth (which makes the potential more repulsive) and to increase slightly the mean diameter (which makes the potential profile a bit steeper). It is also shown that these effects are greater in higher densities (and lower temperatures) where the many-body interactions and quantum effects dominate.
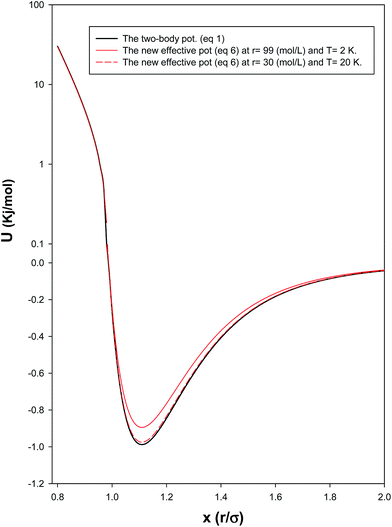 |
| | Fig. 3 Comparison between the two-body and the total potentials at low and high densities for the solid system. | |
Simulation details
We have performed MD simulations for Ne nanoclusters interacting via the new effective potential (eqn (8)). Although the extrapolating the new model of bulk solid to the small nanoclusters, where the contribution of surface atoms is important, leads to some deviations (because the many body contributions differ from bulk to surface atoms), but, as we have discussed in the next section, the model can be applied with reasonable accuracy for bigger nanoclusters. We have also used ideal gas for applying pressure in the Ne nanoclusters.24 The MD simulations have been carried out in a NVT ensemble with periodic boundary conditions (PBC), for the system including the neon nanocluster consisting of 13, 55, 147, 309, 561, 923, and 1415 atoms (corresponding to the magic numbers8,25) and an ideal gas using DL_POLY 4.03.26 Fig. 4 shows the different neon nanocluster used in this work and a Ne nanocluster with 309 atoms immersed in an ideal gas pressure bath with 5 atm pressure at 2 K. (In these simulations, the pressure medium consists of particles that do not interact with each other, but do interact with the Ne atoms in the crystal via a soft-sphere potential of the form 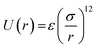 where r denotes the distance between two particles, σ the interaction range, and ε the interaction strength. We may use argon (or any other ideal gas) as the pressure medium in these simulations.24) Recently, Akbarzadeh et al.24 used the similar procedure to obtain the EoS for Ni nanoclusters.
where r denotes the distance between two particles, σ the interaction range, and ε the interaction strength. We may use argon (or any other ideal gas) as the pressure medium in these simulations.24) Recently, Akbarzadeh et al.24 used the similar procedure to obtain the EoS for Ni nanoclusters.
 |
| | Fig. 4 (A) The structures of different neon nanoclusters used in this work. (B) Snapshot of Ne nanocluster (blue) with 309 atoms immersed in an ideal gas (yellow) pressure bath with 5 atm pressure at 2 K. | |
The temperature were controlled by a Nose–Hoover thermostat.27,28 In order to have an isotropic constant pressure on the cluster, the number of gas particles and the gas volume should be much larger than those of the cluster. The equations of motion were integrated using the Verlet–Leapfrog algorithm29 with a time step of 0.001 ps. The system was equilibrated for 1 ns, the averages were computed over the following 2 ns. The cutoff length is chosen to be 10 Å in the simulations. The volume of the clusters were obtained using a volume definition based on a Wigner–Seitz primitive cell.24,30 Additional simulations of bulk neon have been performed with 2048 atoms in a cubic box and the PBC have been applied.
Results and discussion
In order to test our new effective potential, we have compared the simulated internal energies of bulk neon at different temperatures using the two-body (eqn (1)) and the new model (eqn (8)) and the experiment6 in Fig. 5. It is also shown that the new (many-body and quantum) corrected term has significant effect and decreases the classical two-body energy results to get better agreement with the experiment. Although our new model reproduces the energy results in good agreement with the experiment, but the capability of the new potential should be examined for other properties (such as the equation of state).
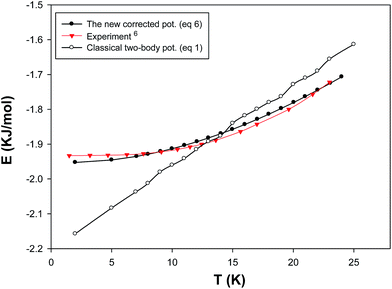 |
| | Fig. 5 Internal energies of solid neon using the two-body and total (two-body plus three-body) potentials. | |
The equations of state (EoS) of solids play an important role in condensed matter physics and geophysics. They provide much information about the nonlinear compression of materials at high pressures, and have been widely applied in engineering and other branches of science.24 The room temperature and high pressure equation of state of solid neon have been experimentally studied using diamond-anvil cell techniques by Finger et al.31 up to 14.4 GPa and by Hemley et al.32 up to 110 GPa. Dewaele et al.33 also investigated crystal structure and the equation of state of neon up to 208 GPa using X-ray diffraction techniques. Hama34 also studied the stability and metallization of solid neon on the basis of muffin-tin augmented-plane-wave (APW) calculation up to pressure of 158 TPa. Although the phase behavior of solid bulk neon has been the subject of many experimental and theoretical investigations, but there is no much known about the neon nanoclusters. Pahl et al.8 calculated the melting temperatures of neon nanoclusters using ab initio potentials including quantum effects. Schwerdtfeger et al.11 investigated the growth patterns of rare-gas clusters. They also calculated the dissociation energies per atom for the cluster structures using an extended LJ potential. They concluded that the per-atom dissociation energies of all the optimized rare gas clusters follow similar qualitative behavior towards the bulk fcc cohesive energy.
In this work, the NVT-MD simulations have been used to calculate the densities of neon nanoclusters using new corrected potential for the temperatures from 2 to 12 K and pressures from 0.1 to 1 GPa. We have then fitted the simulated results to the EoS of Parsafar et al.23 and developed its parameters as functions of temperature and particles size. This EoS gives a good description for all types of fluid, including nonpolar, polar, hydrogen-bonded, and metallic, for temperatures ranging from the triple point to the highest temperature for which experimental data are reported. For solids, the EoS is very accurate for all types considered, including covalent, molecular, metallic, and ionic systems.23
Before further discussions about the EoS of the neon nanoclusters, it is worthwhile to discuss about the stability of the neon nanoclusters especially up to high pressures (1 GPa) used in this work. The neon clusters (with N < 1000) are most stable as complete Mackay icosahedra.8 The number of atoms in the first six shells of the cluster corresponds to the “magic numbers”: 13, 55, 147, 309, 561, and 923.25 These “magic numbers” have been provided by mass spectra in free-jet expansions of rare-gas clusters.35,36 The unusual stability of these clusters is explained by the structure in which one to six completed shells of atoms surround a central atom.25 It is also reported that the clusters of rare gas atoms not bound structurally within a host phase in the earth would be thermodynamically stable in the solid phase at high pressures (above 25 GPa).37 Also, Cheng et al.,38 Molteni et al.,39 and Calvo and Doye40 discussed the influence of pressure on the structure of clusters and even the melting transition.
In order to investigate the stability of the neon nanoclusters especially at high pressures, we have presented the radial distribution functions and snapshots of the Ne13, Ne55, and Ne923 nanoclusters at lowest (P = 1 bar) and highest (P = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bar) pressures at T = 2 K in Fig. 6. According to the snapshots, there is not any significant deformation in the neon nanoclusters with the only exception of Ne13 in which some deformations can be distinguished. It is also shown that the radial distribution functions of the Ne55, and Ne923 nanoclusters at lowest and highest pressures are coincident which is due to the stability of the nanoclusters at high pressures. But the radial distribution function of Ne13 nanocluster shows some small oscillations between the two peaks which is due to its small deformation at high pressures.
000 bar) pressures at T = 2 K in Fig. 6. According to the snapshots, there is not any significant deformation in the neon nanoclusters with the only exception of Ne13 in which some deformations can be distinguished. It is also shown that the radial distribution functions of the Ne55, and Ne923 nanoclusters at lowest and highest pressures are coincident which is due to the stability of the nanoclusters at high pressures. But the radial distribution function of Ne13 nanocluster shows some small oscillations between the two peaks which is due to its small deformation at high pressures.
 |
| | Fig. 6 The radial distribution functions and snapshots of the nanoclusters at lowest (left side) and highest (right side) pressures at T = 2 K. | |
We have also presented the energies (per atom) for neon nanoclusters at low and high pressures in Fig. 7. According to this figure, there is a rapidly increasing stabilization range for the smallest cluster sizes followed by a very slow but monotonous trend towards the experimental energy of bulk neon (fcc solid). In the other words, at least the bigger nanoclusters have similar energies with the bulk solid. Therefore, the new potential can be applied with reasonable accuracy, at least, for bigger nanoclusters. It is also shown that the simulated energies for nanoclusters at high pressure give a much faster convergence towards the solid state as surface effects are smaller than that of the low pressure. In the other words, at higher pressure, the neon nano-clusters have closer energy values to the bulk fcc solid. Therefore, the nanoclusters are more stable at higher pressures than lower pressures.
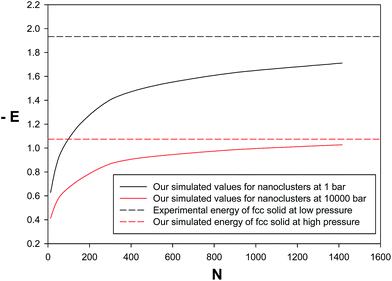 |
| | Fig. 7 Comparison between the energy values of the nanoclusters and bulk solid at lowest (1 bar) and highest pressures (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bar). 000 bar). | |
According to our extended EoS of Parsafar et al.,23 (Z − 1)/ρ2 in terms of ρ may be given as:
| |
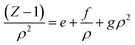 | (9) |
where
Z =
P/
ρRT and
e,
f, and
g are temperature dependent parameters as:
| |
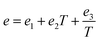 | (10) |
| |
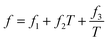 | (11) |
| |
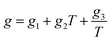 | (12) |
and
ei,
fi, and
gi are size dependent parameters as:
| |
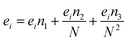 | (13) |
| |
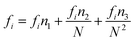 | (14) |
| |
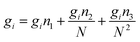 | (15) |
where the values of the parameters
eini,
fini, and
gini are given in
Table 3.
Table 3 The parameters of the new extended EoS (eqn (13)–(15))
| Parameter |
Value |
| e1n1 |
869.93 |
| e1n2 |
−81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 587.27 587.27 |
| e1n3 |
−135![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 034.17 034.17 |
| e2n1 |
−21.85 |
| e2n2 |
1682.59 |
| e2n3 |
−50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990.67 990.67 |
| e3n1 |
−177![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 262.52 262.52 |
| e3n2 |
−10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 612 612![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192.44 192.44 |
| e3n3 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 912 912![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 357.68 357.68 |
| f1n1 |
−104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 739.37 739.37 |
| f1n2 |
−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 267 267![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 784.31 784.31 |
| f1n3 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 034 034![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 994.37 994.37 |
| f2n1 |
4017.32 |
| f2n2 |
140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 055.77 055.77 |
| f2n3 |
−673![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 979.10 979.10 |
| f3n1 |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 549 549![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 324.37 324.37 |
| f3n2 |
56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 415 415![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 139.51 139.51 |
| f3n3 |
−282![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 721 721![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 065.83 065.83 |
| g1n1 |
0.39 |
| g1n2 |
85.47 |
| g1n3 |
727.67 |
| g2n1 |
−0.002 |
| g2n2 |
1.61 |
| g2n3 |
75.82 |
| g3n1 |
27.23 |
| g3n2 |
3208.83 |
| g3n3 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 673.82 673.82 |
The temperature dependences of the parameters of the extended EoS (e, f, and g) have been presented in Fig. 8. Although these parameters are linear versus 1/T for the largest nanocluster, the deviations from linearity become significant for the smaller nanoclusters. Also, the slopes in these figures are the largest (in magnitude) for the smallest nanocluster, which means that the parameters of the effective pair potential are the biggest for this nanocluster.
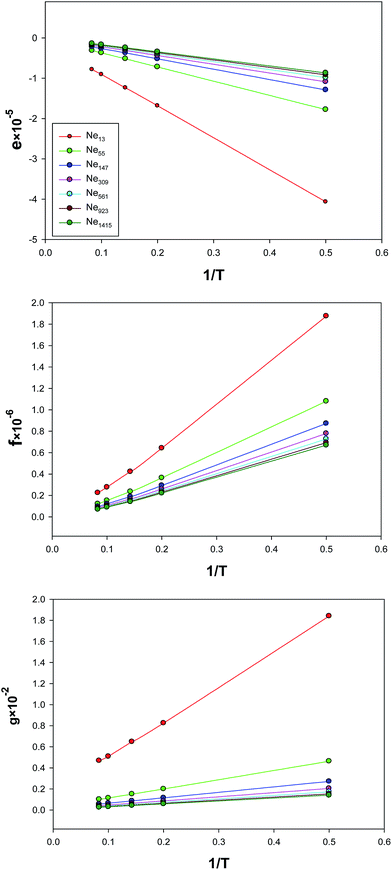 |
| | Fig. 8 Temperature dependence of the parameters, e, f, and g for the different sizes of Ne nanoclusters which are obtained from fitting to the simulation results. | |
The size dependences of the parameters of the extended EoS have been shown in Fig. 9, at five different temperatures. As may be expected, their absolute values become smaller for bigger nanoclusters, due to the smaller fraction of atoms on the surface.
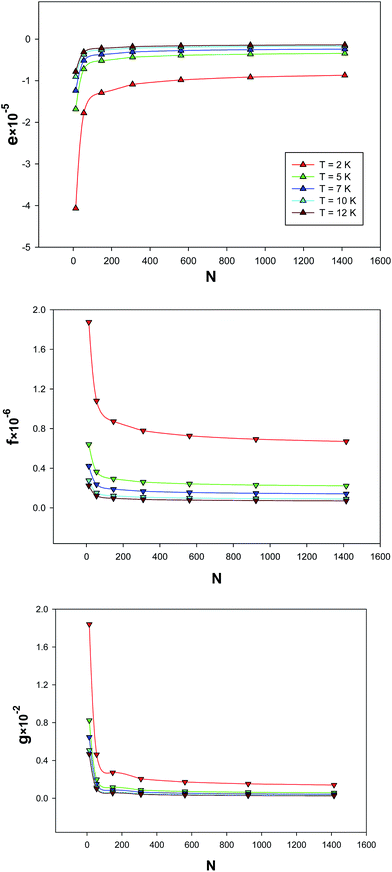 |
| | Fig. 9 Size dependence of the parameters, e, f, and g for the different temperatures which are obtained from fitting to the simulation results. | |
We have presented the graphs of (Z − 1)/ρ2 versus ρ with seven different sizes of nanoclusters at five different temperatures in Fig. 10. These graphs are almost linear for the largest nanocluster but the deviations from linearity become significant for the smaller nanoclusters. It is shown that the agreement between the simulated results and the new EoS are better for smaller nanoclusters. We have also compared our calculated values from the new extended EoS with the experimental data of Anderson et al.41 obtained from high-pressure piston-displacement measurements at T = 4.2 K in Fig. 11. It is shown that our calculated values from the new EoS are in good agreement with the experiment at the bulk limit (N → ∞). The good agreement between our predicted and experimental values indicates the importance of our new effective and isotropic potential. In the other words, the empirical corrected expression (eqn (8)) not only accounts for the quantum effects but also for other effects such as the three-body interactions. This is mainly due to the adjustable parameter β, which is obtained by comparison with the experimental data.
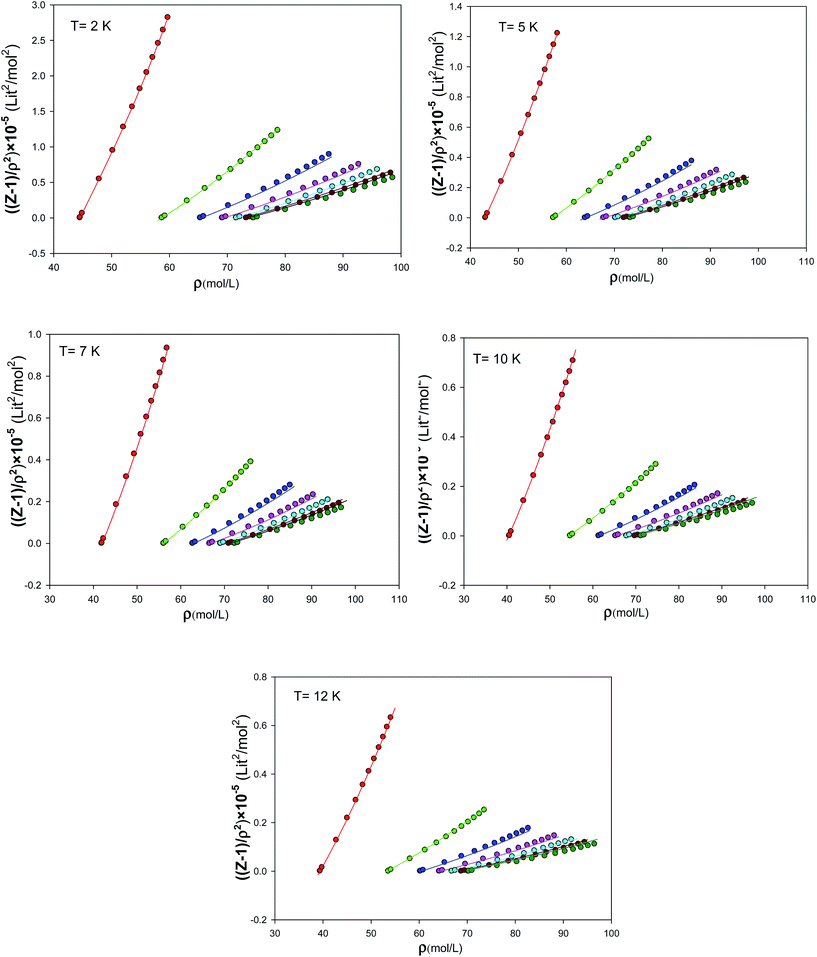 |
| | Fig. 10 The graphs of (Z − 1)/ρ2 versus density for the different sizes of nanoclusters at different temperatures which are obtained from fitting to the simulation results. | |
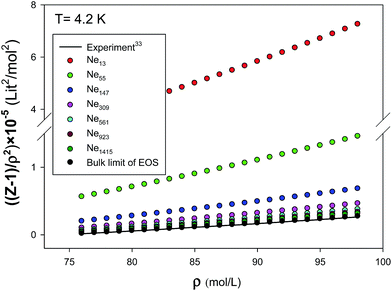 |
| | Fig. 11 Comparison between our new EoS and the experiment for the different sizes of nanoclusters at 4.2 K. | |
We have also presented the bulk modulus, B.M, calculated using the new EoS for different nanoclusters at five different temperatures in Fig. 12. According to these figures, an increase in bulk modulus with decreasing the number of particles can be observed. This effect is called the reverse Hall–Petch effect, which is related to the softening of materials for very small cluster size.42,43 Such behavior is expected, because of the fact that, as the cluster size reduces, proportionally more atoms are on the surface of the cluster. Since surface atoms have less binding energy, compared to the bulk atoms, with a decrease in number of particles, the compressibility is expected to decrease.30 We have also compared the pressure derivative of bulk modulus at zero-pressure limit (B0) from the new extended EoS with the experimental data of Batchelder et al.44 obtained from X-ray measurements of solid neon at T = 4.2 K in Fig. 13. It is shown that our calculated values from the new EoS are in good agreement with the experiment at the bulk limit which corresponds to the importance of the new corrected potential.
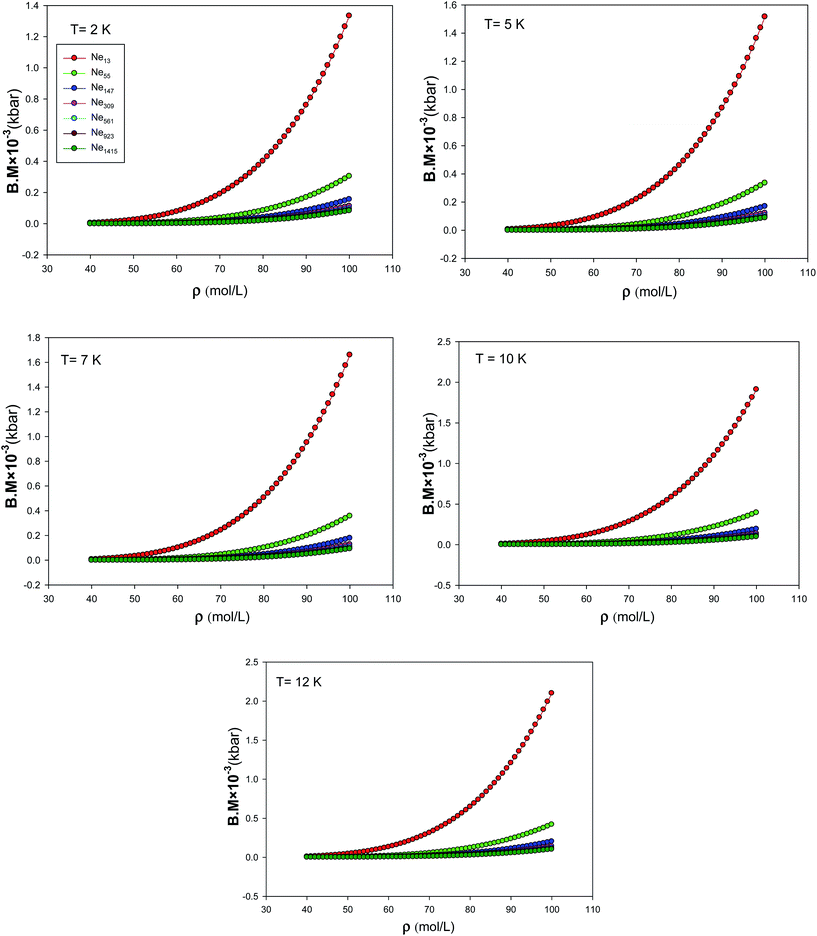 |
| | Fig. 12 The bulk modulus, B.M, calculated using the new EoS for the different nanoclusters at five different temperatures. | |
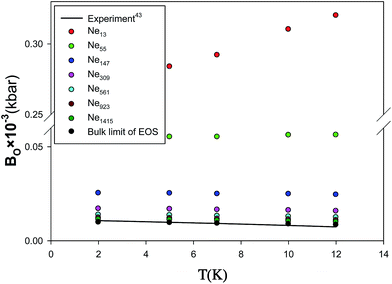 |
| | Fig. 13 Comparison between the pressure derivative of bulk modulus at zero-pressure limit, B0, from the new extended EoS and the experimental data for the different sizes of nanoclusters at 4.2 K. | |
We have also calculated the isobaric expansion coefficient for different cluster sizes at different temperatures and pressures via the extended EoS and these are presented in Fig. 14. According to these figures, an increase on isobaric expansion coefficient with decrease in number of particles can be observed. Since a smaller nanocluster has less binding energy per atom, on average, we may expect that it can be expanded more easily than a bigger cluster with temperature; hence, it has a larger value of the isothermal expansion coefficient. In the other hand, since the isothermal expansion coefficient is related to the lattice anharmonicity, we may conclude that it decreases with the cluster size. Because a smaller cluster has a larger fraction of surface atoms, which experience more asymmetric interactions, compared to the atoms in the bulk.24
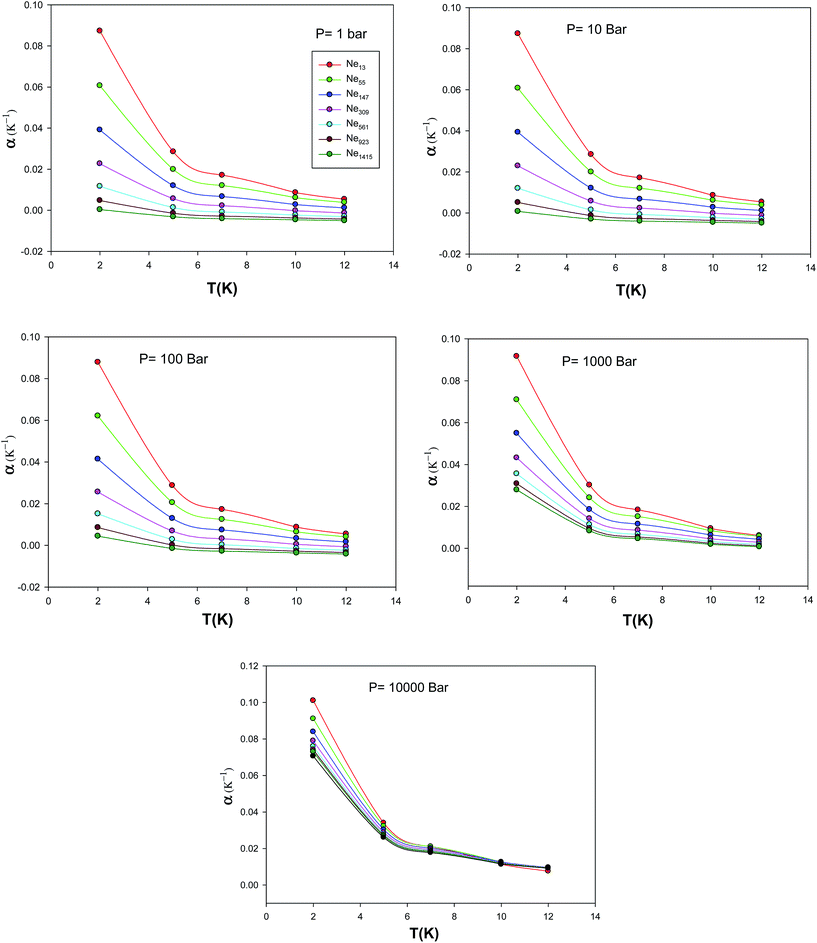 |
| | Fig. 14 The isobaric expansion coefficient, α, calculated using the new EoS for the different nanoclusters at five different pressures. | |
Conclusion
We have extended the EoS of Parsafar et al.23 in terms of density, temperature, and particles size for neon nanoclusters using the effective HFD-like potential from a new simple and accurate empirical expression by the MD simulations. We have also attempted to relate this empirical expression to the known simple quantum and three-body equations. Some features of the EoS criteria, such as the temperature and size dependences of the coefficients, the isothermal bulk modulus and its pressure derivative at the zero-pressure limit, and isobaric thermal expansion for Ne nanoclusters have been investigated. An increase in the bulk modulus with decrease in number of particles of the cluster has been observed. As the cluster size decreases, proportionally more atoms are on the cluster surface. Surface atoms have less binding energy, compared to the bulk atoms; therefore, when the number of particles decreases, the compressibility is expected to decrease. An increase in isobaric expansion coefficient with decrease in number of particles has been observed, which may mean that the anharmonicity increases when the cluster size reduces. Also, a decrease in isobaric expansivity with increase in temperature has been found.
We have also found good agreement between our calculated values of the (Z − 1)/ρ2 and B0 from the new extended EoS at the bulk limit (N → ∞) with the experimental data at T = 4.2 K which indicates the importance of our new effective and isotropic potential. In the other words, the empirical corrected expression (eqn (13)) not only accounts for the quantum effects but also for other effects such as the three-body interactions. This is mainly due to the adjustable parameter β, which is obtained by comparison with the experimental data. It should be also noted although the empirical potential works well for the thermodynamic properties (such as EoS) but it does not seem that the new many-body potential performs well for the transport properties against more realistic approaches.
References
- H. Haberland, Clusters of Atoms and Molecules, Springer, Berlin, 1995 Search PubMed.
- R. L. Johnston, Atomic and Molecular Clusters, Taylor & Francis, London, 2002 Search PubMed.
- A. C. Holt, W. G. Hoover, S. G. Gray and D. R. Shortie, Physica, 1970, 49, 61 CrossRef CAS.
- J. Solca, A. J. Dyson, G. Steinebrunner, B. Kirchner and H. Hubera, J. Chem. Phys., 1998, 108, 4107 CrossRef CAS PubMed.
- J. Barker, M. L. Klein and J. A. Venables, in Rare Gas Solids, Academic Press, New York, 1976 Search PubMed.
- D. Acocella, G. K. Horton and E. R. Cowley, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 8753 CrossRef CAS.
- Y. A. Freiman and S. M. Tretyak, Low Temp. Phys., 2007, 33, 545 CrossRef CAS PubMed.
- E. Pahl, F. Calvo, L. Koci and P. Schwerdtfeger, Angew. Chem., Int. Ed., 2008, 47, 8207 CrossRef CAS PubMed.
- P. Schwerdtfeger and A. Hermann, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 064106 CrossRef.
- B. M. Axilrod and E. Teller, J. Chem. Phys., 1943, 11, 299 CrossRef CAS PubMed.
- P. Schwerdtfeger, N. Gaston, R. P. Krawczyk, R. Tonner and G. E. Moyano, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 064112 CrossRef.
- B. Hartke, Angew. Chem., Int. Ed., 2002, 41, 1468 CrossRef CAS.
- B. W. van de Waal, G. Torchet and M. F. de Feraudy, Chem. Phys. Lett., 2000, 331, 57 CrossRef CAS.
- W. Kohn, Y. Meir and D. E. Makarov, Phys. Rev. Lett., 1998, 80, 4153 CrossRef CAS.
- E. K. Goharshadi and M. Abbaspour, J. Chem. Theory Comput., 2006, 2, 920 CrossRef CAS.
- E. K. Goharshadi, M. Abbaspour, H. Kashani and M. Baherololoom, Theor. Chem. Acc., 2008, 119, 355 CrossRef CAS PubMed.
- M. Abbaspour and E. K. Goharshadi, Theor. Chem. Acc., 2010, 127, 573 CrossRef CAS.
- M. Abbaspour and A. Keyvanloo, J. Mol. Liq., 2013, 177, 1 CrossRef CAS PubMed.
- T. Hauschild and J. M. Prausnitz, Mol. Simul., 1993, 11, 177 CrossRef CAS.
- M. Abbaspour and S. Shakehnia, J. Mol. Liq., 2011, 170, 51 CrossRef PubMed.
- M. Abbaspour and S. N. Borj, Fluid Phase Equilib., 2012, 333, 1 CrossRef CAS PubMed.
- M. Abbaspour and E. Nameni, J. Supercrit. Fluids, 2013, 74, 61 CrossRef CAS PubMed.
- G. A. Parsafar, H. V. Spohr and G. N. Patey, J. Phys. Chem. B, 2009, 113, 11977 CrossRef CAS PubMed.
- H. Akbarzadeh, H. Abroshan, F. Taherkhani and G. A. Parsafar, Solid State Commun., 2011, 151, 965 CrossRef CAS PubMed.
- K. Russel and T. P. Martin, Phys. Rep., 1996, 273, 199 CrossRef.
- I. T. Todorov, W. Smith, K. Trachenko and M. T. Dove, J. Mater. Chem., 2006, 16, 1611 RSC.
- S. Nose, J. Phys.: Condens. Matter, 1990, 2, 115 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef.
- S. J. Zhao, K. Albe and H. Hahn, Scr. Mater., 2006, 55, 473 CrossRef CAS PubMed.
- D. Y. Sun and X. G. Gong, J. Phys.: Condens. Matter, 2002, 14, 487 CrossRef.
- L. W. Finger, R. M. Hazen, G. Zou, H. K. Mao and P. M. Bell, Appl. Phys. Lett., 1981, 39, 892 CrossRef CAS PubMed.
- R. J. Hemley, C. S. Zha, A. P. Jephcoat, H. K. Mao, L. W. Finger and D. E. Cox, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 11820 CrossRef CAS.
- A. Dewaele, F. Datchi, P. Loubeyre and M. Mezouar, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 094106 CrossRef.
- J. Hama, Phys. Lett. A, 1984, 105, 303 CrossRef.
- O. Echt, K. Sattler and E. Recknagel, Phys. Rev. Lett., 1981, 47, 1121 CrossRef CAS.
- I. A. Harris, R. S. Kidwell and J. A. Northby, Phys. Rev. Lett., 1984, 53, 2390 CrossRef CAS.
- A. P. Jephcoat, Nature, 1998, 393, 355 CrossRef CAS PubMed.
- H. Cheng, X. Li, R. L. Whetten and R. S. Berry, Phys. Rev. A, 1992, 46, 791 CrossRef CAS.
- C. Molteni, R. Martonak and M. Parrinello, J. Chem. Phys., 2001, 114, 5358 CrossRef CAS PubMed.
- F. Calvo and J. P. K. Doye, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 125414 CrossRef.
- M. S. Anderson, R. Q. Fugate and C. A. Swenson, J. Low Temp. Phys., 1973, 10, 345 CrossRef CAS.
- R. W. Seigel, G. E. Fougere, G. C. Hadjipanayis and R. W. Seigel, Nanophase Materials, Kluwer, Dordrecht, 1994 Search PubMed.
- A. H. Chokshi, A. Rosen, J. Karach and H. Gletter, Scr. Metall., 1989, 23, 1679 CrossRef CAS.
- D. N. Batchelder, D. L. Losee and R. O. Simmons, Phys. Rev., 1967, 162, 767 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here. 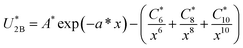
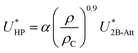

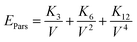
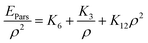
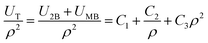

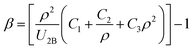

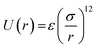 where r denotes the distance between two particles, σ the interaction range, and ε the interaction strength. We may use argon (or any other ideal gas) as the pressure medium in these simulations.24) Recently, Akbarzadeh et al.24 used the similar procedure to obtain the EoS for Ni nanoclusters.
where r denotes the distance between two particles, σ the interaction range, and ε the interaction strength. We may use argon (or any other ideal gas) as the pressure medium in these simulations.24) Recently, Akbarzadeh et al.24 used the similar procedure to obtain the EoS for Ni nanoclusters.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bar) pressures at T = 2 K in Fig. 6. According to the snapshots, there is not any significant deformation in the neon nanoclusters with the only exception of Ne13 in which some deformations can be distinguished. It is also shown that the radial distribution functions of the Ne55, and Ne923 nanoclusters at lowest and highest pressures are coincident which is due to the stability of the nanoclusters at high pressures. But the radial distribution function of Ne13 nanocluster shows some small oscillations between the two peaks which is due to its small deformation at high pressures.
000 bar) pressures at T = 2 K in Fig. 6. According to the snapshots, there is not any significant deformation in the neon nanoclusters with the only exception of Ne13 in which some deformations can be distinguished. It is also shown that the radial distribution functions of the Ne55, and Ne923 nanoclusters at lowest and highest pressures are coincident which is due to the stability of the nanoclusters at high pressures. But the radial distribution function of Ne13 nanocluster shows some small oscillations between the two peaks which is due to its small deformation at high pressures.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 bar).
000 bar).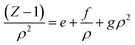
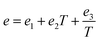
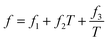
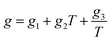
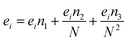
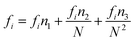
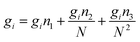
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 587.27
587.27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 034.17
034.17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990.67
990.67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 262.52
262.52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 612
612![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192.44
192.44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 912
912![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 357.68
357.68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 739.37
739.37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 267
267![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 784.31
784.31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 034
034![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 994.37
994.37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 055.77
055.77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 979.10
979.10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 549
549![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 324.37
324.37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 415
415![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 139.51
139.51![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 721
721![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 065.83
065.83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 673.82
673.82







