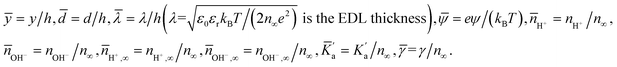Electrostatics of soft charged interfaces with pH-dependent charge density: effect of consideration of appropriate hydrogen ion concentration distribution†
Guang Chen and
Siddhartha Das*
Department of Mechanical Engineering, University of Maryland, College Park, Maryland 20742, USA. E-mail: sidd@umd.edu
First published on 5th December 2014
Abstract
A soft charged interface, represented by a nanoscopically thick charged polyelectrolyte layer (PEL) sandwiched between a rigid solid and an electrolyte solution, forms the central element in the theoretical description of electrodynamics of soft charged biological moieties (e.g., cells, bacteria and viruses), electrohydrodynamics in soft nanochannels, and analysis of properties of non-biological gels and films. In this paper we provide a free energy based theoretical model to quantify the electrostatics of such a soft charged interface with pH-dependent charge density. Our theory considers for the first time the explicit variation of the hydrogen ion concentration inside and outside the PEL and establishes that there cannot be a uniform (within the PEL) distribution of chargeable sites within the PEL. Such uniformity causes unphysical hydrogen ion concentration jump across the PEL–electrolyte interface. In fact we demonstrate that this distribution of chargeable sites on a given polymer must obey at least a cubic variation with distance (within the PEL) in order to address this hydrogen ion concentration jump and at the same time ensure zero hydrogen ion flux at the PEL–rigid-solid interface. We anticipate that these new results will serve as a major stepping-stone towards appropriate modeling of electrodynamics and electrohydrodynamics of soft charged reactive interfaces that are paramount in the description of various micro/nanoscale biological and non-biological problems.
Introduction
A soft charged interface model and the related electrostatics and electrokinetics have often been used to model a number of biological and non-biological phenomena.1–7 Some well-known examples include quantifying electrophoretic properties of cells, bacteria and viruses,8–16 studying bacterial adhesion to surfaces,17–19 interpreting agglutination and shape transition of red blood cells,20,21 specifying properties of non-biological soft charged gels and films,22–25 enhancing electrochemomechanical energy conversion efficiency in polymer-grafted nanochannels,26 designing soft-charged-interface-based double layer capacitors,27 and many more.A soft charged interface is typically described by certain structural and chemical specifications. Firstly, the interface is assumed to be constituted by a layer of charged polyelectrolyte sandwiched between a rigid wall and an electrolyte solution.1–7 This polyelectrolyte layer (or PEL) harbors a particular kind of ion, known as the PEL ions, which remain excluded from the regions outside the PEL; however the electrolyte ions can remain both inside and outside the PEL. For this reason there develops a Donnan potential deep within the PEL, with the PEL–electrolyte interface acting as a semi-permeable membrane.4,28 The second important issue concerns the mechanism of charging of the PEL (or the generation of the PEL ions). Typically this charging occurs due to an acid or a base like reaction, where the chargeable sites on a polyelectrolyte (henceforth denoted as the Polyelectrolyte Chargeable Sites or PCS) dissociates to produce the PEL ions. Of course this dissociation reaction depends on the local value of the hydrogen ion concentration, and therefore the charge density of the PEL (or equivalently the number density of PEL ions) becomes a function of the pH. All the existing studies considering such pH-dependence of the PEL charge density has invariably described the hydrogen ion concentration within the PEL (which in turn dictates the charge density of the PEL) by the Boltzmann distribution.3,17,22–25,29–32 This is inappropriate, since the hydrogen ion concentration distribution within the PEL gets additionally dictated by the chemical reaction that produces the PEL ions. In this paper, we provide a free energy based model that indeed describes the variation of hydrogen ion concentration (within the PEL) taking into consideration the hydrogen-ion-concentration-dependent chemical reaction that produces the PEL ions. In fact, to the best of our knowledge, the present paper is the first study that describes the electrostatics of a charged soft interface, represented as a grafted PEL with a pH-dependent charge density, by explicitly accounting for the hydrogen ion concentration. Of course, there have been several studies on soft matter systems, other than such PEL-grafted systems, that have employed analysis based on the explicit consideration of the pH and pKa of the system.33–36
The central result of our analysis is that there cannot be a uniform distribution of PCS across the depth of the PEL. In case we consider that such a chargeable site is equivalent to a monomer in a polyelectrolyte molecule, this indicates to a non-uniform distribution (across the depth of the PEL) of monomers within the PEL. We show that such non-uniformity is necessary to ensure continuities in the value and in the gradient of the hydrogen ion concentration at the PEL–electrolyte interface. Of course, this extremely important issue has hitherto remained completely unidentified stemming from the sheer disregard of the explicit hydrogen ion concentration distribution in the modeling of electrostatics of soft charged interfaces with pH-dependent charge density. The second important issue on which our study sheds light is the nature of this non-uniformity in the PCS distribution. We establish that this PCS distribution must obey at least a cubic profile, arising from the fact that four different conditions must be satisfied by the PCS distribution. These conditions are the continuities in the value and in the gradient of hydrogen ion concentration distribution at the PEL–electrolyte interface, zero net flux of hydrogen ion concentration at the PEL–rigid-solid interface and constancy in the total number of PCS. We further identify that a profile other than this cubic one, which may satisfy these four conditions, may also represent a viable PCS distribution. For uncharged polymer brushes, where the equilibrium configuration is dictated by the balance of the elastic and volume exclusion effects, the monomer distribution has been identified as a unique quadratic function.37–40 On the contrary, as we demonstrate here, for polyelectrolytes (which of course will also be in form of brushes), where we only consider pH-dependent electrostatic effects (and disregard elastic and volume exclusion effects) this PCS distribution (or equivalently the monomer distribution) is a non-unique function that must at least be cubic. Therefore this paper also provides possibly the first study in quantifying the equilibrium shape of the polyelectrolyte brushes constituting charged PEL – we also discuss certain experimental examples of pH-dependent shape changes of polyelectrolyte brushes,41,42 where our proposed theory can provide useful insights and interpretations.
Results
Electrostatic potential and hydrogen ion concentration profiles for uniform distribution of polyelectrolyte chargeable sites (PCS) within the PEL
We consider a soft charged interface that constitutes the bottom plate of a nanochannel (see Fig. 1). The soft charged interface is represented by a layer of charged polyelectrolyte sandwiched between an electrolyte solution and a rigid surface. Thickness of this PEL is d, whereas the height of the nanochannel is 2h. Here we consider a uniform distribution of the PCS within the PEL. Under these circumstances, we are interested to obtain the equilibrium electrostatic potential and hydrogen ion concentration profiles. The free energy functional dictating the problem is.| F = ∫f[ψ,n±,nH+,nOH−]d3r, | (1) |
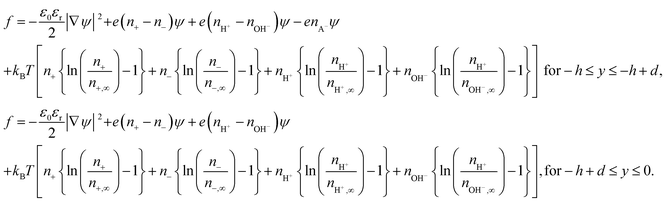 | (2) |
 | ||
| Fig. 1 Schematic of a soft charged nanochannel, with soft charged plates. The PEL ions are shown in green. | ||
In eqn (2), ε0 is the permittivity of free space, εr is the relative permittivity of the medium (assumed identical for the media both inside and outside the PEL4), e is the electronic charge, kBT is the thermal energy, ψ is the electrostatic potential, ni and ni,∞ are the number density and the bulk number density of ion i (i = ±, H+, OH−) and nA− is the number density of the PEL ions. Please note that both the PEL ions and the electrolyte ions (with number densities n±) are assumed to be monovalent.
The PEL ions are assumed to be formed by the dissociation of an acid HA (producing A− ions, which are the PEL ions), and therefore following Das,27 we get
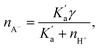 | (3) |
The equilibrium conditions can be obtained by minimizing F with respect to ψ, n±, nH+ and nOH− (see the ESI† for the detailed procedure), resulting in the following two sets of equations in dimensionless variables:
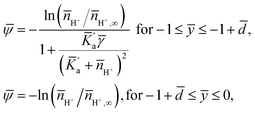 | (4) |
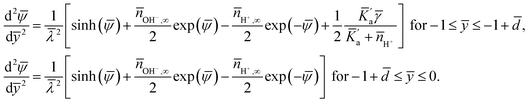 | (5) |
Therefore there are 6 dimensionless parameters dictating the problem: ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+,∞,
H+,∞, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) OH−,∞,
OH−,∞, ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) ,
, ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ,
, ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) ′a,
′a, ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) . Eqn (4) and (5) represent the coupled set of equations that are solved in presence of the following boundary conditions:
. Eqn (4) and (5) represent the coupled set of equations that are solved in presence of the following boundary conditions:
 | (6) |
In order to solve this coupled equation, we first eliminate ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) and obtain the governing equation and the boundary conditions entirely in terms of
and obtain the governing equation and the boundary conditions entirely in terms of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ (see the ESI†), which is then solved numerically to first obtain the hydrogen ion concentration profiles and then the electrostatic potential profiles.
H+ (see the ESI†), which is then solved numerically to first obtain the hydrogen ion concentration profiles and then the electrostatic potential profiles.
Fig. 2(a–e) show the variation of the dimensionless hydrogen ion number density (![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+) and the dimensionless electrostatic potential (
H+) and the dimensionless electrostatic potential (![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) ) profiles for different ranges of the governing parameters. The most important result, evident in all the plots, is the distinct discontinuity in the
) profiles for different ranges of the governing parameters. The most important result, evident in all the plots, is the distinct discontinuity in the ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ profile at the location ȳ = −1 +
H+ profile at the location ȳ = −1 + ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) (i.e., at the PEL–electrolyte interface). Identification of this discontinuity is the most significant discovery of this study. Till date there have been many studies that have considered a pH-dependent charge density of a soft charged interface;3,17,22–25,29–32 however in none of the studies this discontinuity has been identified, since none of the studies cared to consider the explicit hydrogen ion concentration distribution. In other words, these studies simply consider a Boltzmann distribution for the hydrogen ion concentration [i.e., the form expressed in the 2nd part of eqn (4)] both inside and outside the PEL. However, as we demonstrate through an appropriate free energy picture, the dependence of the PEL reaction on the hydrogen ion concentration ensures that the hydrogen ion concentration no longer obeys a Boltzmann distribution inside the PEL. Therefore, we encounter two different
(i.e., at the PEL–electrolyte interface). Identification of this discontinuity is the most significant discovery of this study. Till date there have been many studies that have considered a pH-dependent charge density of a soft charged interface;3,17,22–25,29–32 however in none of the studies this discontinuity has been identified, since none of the studies cared to consider the explicit hydrogen ion concentration distribution. In other words, these studies simply consider a Boltzmann distribution for the hydrogen ion concentration [i.e., the form expressed in the 2nd part of eqn (4)] both inside and outside the PEL. However, as we demonstrate through an appropriate free energy picture, the dependence of the PEL reaction on the hydrogen ion concentration ensures that the hydrogen ion concentration no longer obeys a Boltzmann distribution inside the PEL. Therefore, we encounter two different ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ −
H+ − ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) relationships – one inside the PEL and one outside the PEL [see eqn (4)]. It is precisely for this reason that we encounter two different
relationships – one inside the PEL and one outside the PEL [see eqn (4)]. It is precisely for this reason that we encounter two different ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ −
H+ − ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) relationships at the PEL–electrolyte interface (located at ȳ = −1 +
relationships at the PEL–electrolyte interface (located at ȳ = −1 + ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ), depending on whether we approach the interface from the PEL side or the electrolyte side. Such difference ensures that if there are continuities (at ȳ = −1 +
), depending on whether we approach the interface from the PEL side or the electrolyte side. Such difference ensures that if there are continuities (at ȳ = −1 + ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ) in the value and in the gradient of
) in the value and in the gradient of ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) , there cannot be continuities (at ȳ = −1 +
, there cannot be continuities (at ȳ = −1 + ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ) in the value and in the gradient of
) in the value and in the gradient of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+.
H+.
Here we discuss the effect of individual parameters in dictating the profiles of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ and
H+ and ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) , as well as the discontinuity in the
, as well as the discontinuity in the ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ profile. Fig. 2(a) shows the effect of variation of the dimensionless bulk hydrogen ion concentration
H+ profile. Fig. 2(a) shows the effect of variation of the dimensionless bulk hydrogen ion concentration ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+,∞. Insets of Fig. 2(a) clearly reveal that the extent of discontinuity in
H+,∞. Insets of Fig. 2(a) clearly reveal that the extent of discontinuity in ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ values across the two sides of ȳ = −1 +
H+ values across the two sides of ȳ = −1 + ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) increases with a decrease in the value of
increases with a decrease in the value of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+,∞. Such a behavior can be attributed to the corresponding variation of
H+,∞. Such a behavior can be attributed to the corresponding variation of ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) . Lowering of
. Lowering of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+,∞ will enhance the reaction (HA ↔ H+ + A−) that produces the polyelectrolyte ions A−, thereby augmenting the number density of the A− ions. This happens since lowering of hydrogen ion concentration signals a depletion of the hydrogen ions from the system, thereby favoring the forward reaction that produces H+ ions (of course, along with A− ions). Enhanced number density of A− ensures an enhanced magnitude of
H+,∞ will enhance the reaction (HA ↔ H+ + A−) that produces the polyelectrolyte ions A−, thereby augmenting the number density of the A− ions. This happens since lowering of hydrogen ion concentration signals a depletion of the hydrogen ions from the system, thereby favoring the forward reaction that produces H+ ions (of course, along with A− ions). Enhanced number density of A− ensures an enhanced magnitude of ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) for smaller values of
for smaller values of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+,∞, which in turn enhances the consequence of the disparity in the
H+,∞, which in turn enhances the consequence of the disparity in the ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ −
H+ − ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) relationship [see eqn (4)] leading to a more enhanced discontinuity in the
relationship [see eqn (4)] leading to a more enhanced discontinuity in the ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ profile. Fig. 2(b) demonstrates the effect of variation of the parameter
H+ profile. Fig. 2(b) demonstrates the effect of variation of the parameter ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) . Enhanced
. Enhanced ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) implies enhanced value of the PCS (that dissociate to produce the polyelectrolyte ions A−), thereby enhancing the number density of A− ions. This in turn augments the magnitude of
implies enhanced value of the PCS (that dissociate to produce the polyelectrolyte ions A−), thereby enhancing the number density of A− ions. This in turn augments the magnitude of ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) and the extent of discontinuity in the value of
and the extent of discontinuity in the value of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ (for reasons discussed above) at ȳ = −1 +
H+ (for reasons discussed above) at ȳ = −1 + ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) . Fig. 2(c) represents the effect of variation of the parameter
. Fig. 2(c) represents the effect of variation of the parameter ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) . Enhanced
. Enhanced ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) signifies larger extent of the EDL overlap in the nanochannel, leading to a much weaker gradient in the value of
signifies larger extent of the EDL overlap in the nanochannel, leading to a much weaker gradient in the value of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ and
H+ and ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) values – as a consequence it is the gradient of
values – as a consequence it is the gradient of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ that shows a large discontinuity for weaker
H+ that shows a large discontinuity for weaker ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) at ȳ = −1 +
at ȳ = −1 + ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) . However, since there is relatively less deviation in the value of
. However, since there is relatively less deviation in the value of ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) for different
for different ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) at ȳ = −1 +
at ȳ = −1 + ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) , the discontinuity in the value of
, the discontinuity in the value of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ (at ȳ = −1 +
H+ (at ȳ = −1 + ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ) is similar for different
) is similar for different ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) values. Fig. 2(d) reveals the effect of variation of the parameter
values. Fig. 2(d) reveals the effect of variation of the parameter ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) . Enhanced
. Enhanced ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) increases the magnitude of
increases the magnitude of ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) (ref. 26) (since there is greater total number of A− ions), which in turn increases the extent of jump in
(ref. 26) (since there is greater total number of A− ions), which in turn increases the extent of jump in ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ the profile at ȳ = −1 +
H+ the profile at ȳ = −1 + ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) . Variation of
. Variation of ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) ′a [the corresponding effect on
′a [the corresponding effect on ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ and
H+ and ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) profiles is shown in Fig. 2(e)] produces the most non-trivial and non-monotonic variation of the
profiles is shown in Fig. 2(e)] produces the most non-trivial and non-monotonic variation of the ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ profile. Increase in
H+ profile. Increase in ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) ′a obviously enhances the reaction that produces A− ions, thereby leading to an enhanced magnitude of
′a obviously enhances the reaction that produces A− ions, thereby leading to an enhanced magnitude of ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) and a greater extent of discontinuity in the
and a greater extent of discontinuity in the ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ profile (for reasons discussed above). This description remains perfectly valid for the increase of
H+ profile (for reasons discussed above). This description remains perfectly valid for the increase of ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) ′a from 0.1 to 1. However, when
′a from 0.1 to 1. However, when ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) ′a becomes very large (=10), it effectively indicates a nearly complete dissociation of the chargeable groups (that produce the polyelectrolyte ions A−). Hence for such a case the number density of the PEL ions become effectively pH independent, thereby favoring the fact that
′a becomes very large (=10), it effectively indicates a nearly complete dissociation of the chargeable groups (that produce the polyelectrolyte ions A−). Hence for such a case the number density of the PEL ions become effectively pH independent, thereby favoring the fact that ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ profile will now be dictated by Boltzmann distribution both inside and outside the PEL. Accordingly, there is much weaker discontinuity in the
H+ profile will now be dictated by Boltzmann distribution both inside and outside the PEL. Accordingly, there is much weaker discontinuity in the ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ profile for
H+ profile for ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) ′a = 10, although the magnitude of
′a = 10, although the magnitude of ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) keeps on increasing.
keeps on increasing.
Electrostatic potential and hydrogen ion concentration profiles for non-uniform distribution of polyelectrolyte chargeable sites (PCS) within the PEL: appropriate choice of the distribution of chargeable sites
We have identified that the appropriate consideration of hydrogen ion concentration distribution forbids simultaneous continuities in the gradient and in the value of both the electrostatic potential and the hydrogen ion concentration at the PEL–electrolyte interface. We have further identified that such discontinuities result from the contribution of the electrostatic effect of the PEL ions; this effect introduces a situation where the relationship between![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) and
and ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ are different at the PEL–electrolyte interface [see eqn (4)], depending on whether the interface is approached from the PEL side or from the electrolyte side. This can be addressed only if it is ensured that the electrostatic contribution of the PEL ions is such that there are simultaneous continuities in the values and in the gradient of
H+ are different at the PEL–electrolyte interface [see eqn (4)], depending on whether the interface is approached from the PEL side or from the electrolyte side. This can be addressed only if it is ensured that the electrostatic contribution of the PEL ions is such that there are simultaneous continuities in the values and in the gradient of ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) and
and ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ at the PEL–electrolyte interface. Additionally, the net flux of the hydrogen ions must be zero at the PEL–rigid-wall interface. Given the fact that at that interface
H+ at the PEL–electrolyte interface. Additionally, the net flux of the hydrogen ions must be zero at the PEL–rigid-wall interface. Given the fact that at that interface 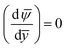 , we must have zero diffusive flux for the hydrogen ions at that interface [i.e.,
, we must have zero diffusive flux for the hydrogen ions at that interface [i.e., 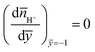 ]. In a framework that does account for all the necessary contributions to the free energy [see eqn (1) and (2)], these issues can only be addressed, by considering a dimensionless concentration (or volume fraction) distribution φ(y) of the chargeable sites. This is exactly analogous to consideration of monomer distribution for uncharged polymer brushes.33–36 Also, φ(y) must satisfy the constraint:
]. In a framework that does account for all the necessary contributions to the free energy [see eqn (1) and (2)], these issues can only be addressed, by considering a dimensionless concentration (or volume fraction) distribution φ(y) of the chargeable sites. This is exactly analogous to consideration of monomer distribution for uncharged polymer brushes.33–36 Also, φ(y) must satisfy the constraint:
 | (7) |
 ].
].
Therefore the revised free energy density f will be expressed as:
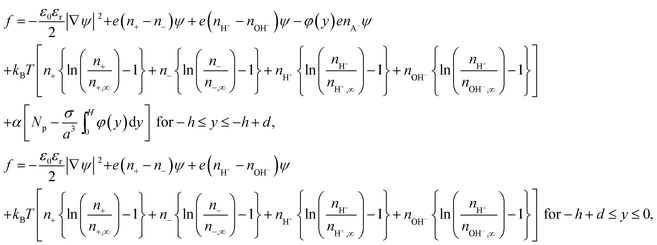 | (8) |
Here the minimization is carried out in terms ψ, n±, nH+, nOH− and φ(y). The resulting equations (in dimensionless form) are (see the ESI† for detailed derivation):
 | (9) |
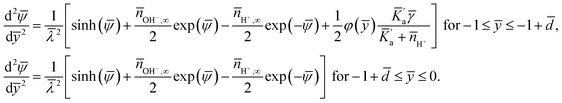 | (10) |
Here too we first eliminate ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) and write all the governing equation and the boundary conditions [see eqn (6)] entirely in terms of
and write all the governing equation and the boundary conditions [see eqn (6)] entirely in terms of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ (see the ESI†). Of course these equations and the boundary conditions will depend on the profile φ. Below we discuss the procedure to obtain φ, which will then allow the solution of the hydrogen ion and the electrostatic potential profiles by employing numerical simulations.
H+ (see the ESI†). Of course these equations and the boundary conditions will depend on the profile φ. Below we discuss the procedure to obtain φ, which will then allow the solution of the hydrogen ion and the electrostatic potential profiles by employing numerical simulations.
The first thing that should be noted about the quantification of the profile φ is that the minimization of F with respect to φ yields only a value for the Lagrange parameter α (see the ESI†), and no information on the functional form of φ. This happens since none of the free energy terms (except for the electrostatic contribution of the PEL ions) depend on φ [see eqn (8)] and this electrostatic contribution of the PEL ions depends only linearly on φ. Therefore, φ can be any function that satisfies all of the three following conditions, along with eqn (7) (see the ESI† for more details)
 | (11) |
The simplest possible choice of φ that satisfies all the above conditions is a cubic equation, expressed as (see the ESI†):
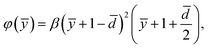 | (12) |
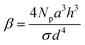 is another dimensionless parameter quantifying the grafting density of the polyelectrolytes. Therefore, now the problem is dictated by seven parameters
is another dimensionless parameter quantifying the grafting density of the polyelectrolytes. Therefore, now the problem is dictated by seven parameters ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+,∞,
H+,∞, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) OH−,∞,
OH−,∞, ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) ,
, ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ,
, ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) ′a,
′a, ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) , β.
, β.
Fig. 3(a–f) show the variation of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ and
H+ and ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) profiles for these parameter values. The most important observation that should be made from these figures is that for all the parameter values, there is no longer any discontinuity in the
profiles for these parameter values. The most important observation that should be made from these figures is that for all the parameter values, there is no longer any discontinuity in the ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ profile. Therefore, using the prescribed remedy of considering a non-uniform distribution of the PCS within the PEL, we do ensure removal of the utterly non-physical result of discontinuous hydrogen ion profiles. Fig. 3(a) demonstrates the effect of considering different values of β. Enhanced β implies enhanced grafting density of the polyelectrolytes in the PEL. This signifies larger number density of the polyelectrolyte ions and hence larger magnitude of
H+ profile. Therefore, using the prescribed remedy of considering a non-uniform distribution of the PCS within the PEL, we do ensure removal of the utterly non-physical result of discontinuous hydrogen ion profiles. Fig. 3(a) demonstrates the effect of considering different values of β. Enhanced β implies enhanced grafting density of the polyelectrolytes in the PEL. This signifies larger number density of the polyelectrolyte ions and hence larger magnitude of ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) . There are two crucial issues associated with Fig. 3(a). Firstly, we find that β = 150 represent a value that reproduces the
. There are two crucial issues associated with Fig. 3(a). Firstly, we find that β = 150 represent a value that reproduces the ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) profile very similar to that of Fig. 2(a). Therefore, for the subsequent plots [Fig. 3(b–f)], we shall work with this value of β. More importantly, consideration of non-uniform distribution of chargeable sites in order to remove the non-physical behavior of the
profile very similar to that of Fig. 2(a). Therefore, for the subsequent plots [Fig. 3(b–f)], we shall work with this value of β. More importantly, consideration of non-uniform distribution of chargeable sites in order to remove the non-physical behavior of the ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ profiles (see Fig. 2) leads to a much steeper
H+ profiles (see Fig. 2) leads to a much steeper ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ profile within the PEL. This behavior is true for the
H+ profile within the PEL. This behavior is true for the ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ profiles for all other plots as well [see Fig. 3(b–f)]. This steepness can be attributed to the fact that
H+ profiles for all other plots as well [see Fig. 3(b–f)]. This steepness can be attributed to the fact that ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ now spans larger ranges of values over a given distance (which is the PEL thickness) in order to remove the corresponding discontinuities (see Fig. 2); hence larger the extent of discontinuity in Fig. 2, steeper will be the corresponding
H+ now spans larger ranges of values over a given distance (which is the PEL thickness) in order to remove the corresponding discontinuities (see Fig. 2); hence larger the extent of discontinuity in Fig. 2, steeper will be the corresponding ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ profile within the PEL. Fig. 3(b) provides the effect of the variation of the parameter
H+ profile within the PEL. Fig. 3(b) provides the effect of the variation of the parameter ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+,∞. Qualitatively the variation is very similar to that depicted in Fig. 2(b), except for the fact that there is no discontinuity in
H+,∞. Qualitatively the variation is very similar to that depicted in Fig. 2(b), except for the fact that there is no discontinuity in ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ profile here. Fig. 3(c) represents the effect of the variation of
H+ profile here. Fig. 3(c) represents the effect of the variation of ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) . For large
. For large ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) (=10), the discontinuity in
(=10), the discontinuity in ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ profile is very large [see Fig. 2(b)]; therefore the
H+ profile is very large [see Fig. 2(b)]; therefore the ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ profile is extremely steep within the PEL. More importantly, we can actually find that
H+ profile is extremely steep within the PEL. More importantly, we can actually find that ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ value at the PEL–rigid-solid interface (i.e., at ȳ = −1) is slightly higher as compared to that in Fig. 2(b). This can be attributed to the corresponding cubic distribution of the PCS constituting the PEL – this cubic distribution ensures greater fraction of PCS at ȳ = −1, which in turn causes greater
H+ value at the PEL–rigid-solid interface (i.e., at ȳ = −1) is slightly higher as compared to that in Fig. 2(b). This can be attributed to the corresponding cubic distribution of the PCS constituting the PEL – this cubic distribution ensures greater fraction of PCS at ȳ = −1, which in turn causes greater ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ concentration at ȳ = −1. Effect of this cubic profile in causing a more augmented value of
H+ concentration at ȳ = −1. Effect of this cubic profile in causing a more augmented value of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ at the PEL–rigid-solid interface is also reflected in Fig. 3(d) that demonstrates the effect of the parameter
H+ at the PEL–rigid-solid interface is also reflected in Fig. 3(d) that demonstrates the effect of the parameter ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) . From eqn (12) we get [φ(ȳ)/β]ȳ=−1 =
. From eqn (12) we get [φ(ȳ)/β]ȳ=−1 = ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) 3/2 – hence this enhancement of
3/2 – hence this enhancement of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ at the PEL–rigid-solid interface is most significant for larger values of
H+ at the PEL–rigid-solid interface is most significant for larger values of ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) (=0.5) [see Fig. 3(e), which illustrates the effect of variation of parameter
(=0.5) [see Fig. 3(e), which illustrates the effect of variation of parameter ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ]. Finally, the non-monotonic behavior of the discontinuity for varying
]. Finally, the non-monotonic behavior of the discontinuity for varying ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) ′a [see Fig. 2(e)], leads to a non-monotonic steepness variation of
′a [see Fig. 2(e)], leads to a non-monotonic steepness variation of ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+ (within the PEL) for the present case where a non-uniform distribution of chargeable sites within the PEL is considered [see Fig. 3(f) that demonstrates the effect of variation of the parameter
H+ (within the PEL) for the present case where a non-uniform distribution of chargeable sites within the PEL is considered [see Fig. 3(f) that demonstrates the effect of variation of the parameter ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) ′a].
′a].
 | ||
Fig. 3 Variation of the dimensionless hydrogen ion number density (top panel) and the dimensionless electrostatic potential profile (bottom panel) for the case where the chargeable sites in a polymer constituting the PEL obey a cubic distribution expressed in eqn (12). For all the figures we maintain the four parameters (i.e., ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+,∞, H+,∞, ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) , , ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) ′a, ′a,![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) ) as equal to unity, ) as equal to unity, ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) = 0.3 and β = 150 except for (a) β = 100, 150, 400, (b) = 0.3 and β = 150 except for (a) β = 100, 150, 400, (b) ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+,∞ = 0.1, 1, 10, (c) H+,∞ = 0.1, 1, 10, (c) ![[small gamma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0c4.gif) = 0.1, 1, 10, (d) = 0.1, 1, 10, (d) ![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) = 0.2, 1, 10 and (e) = 0.2, 1, 10 and (e) ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) =0.1, 0.3, 0.5, (f) =0.1, 0.3, 0.5, (f) ![[K with combining macron]](https://www.rsc.org/images/entities/i_char_004b_0304.gif) ′a = 0.1, 1, 10. In all the figures, the value of the parameter (which is being varied) is indicated at a given plot. It can be clearly seen that there is no more discontinuity in the hydrogen ion concentration at the PEL–electrolyte interface (this interface is located at ȳ = −1 + ′a = 0.1, 1, 10. In all the figures, the value of the parameter (which is being varied) is indicated at a given plot. It can be clearly seen that there is no more discontinuity in the hydrogen ion concentration at the PEL–electrolyte interface (this interface is located at ȳ = −1 + ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) ). Also for all the plots, we use ). Also for all the plots, we use ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) H+,∞ = H+,∞ = ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) OH−,∞. OH−,∞. | ||
Discussions
Here we shall first like to discuss the elements in which the present model compares to the classical equilibrium description of the polymer brushes.37–40 First and foremost, as has been already identified, the present model disregards the contribution of the elastic and the volume exclusion effects, which are paramount in the description of the polymer brushes. The second issue, correlated with the above issue, is that for the present case we can use a fixed value of the thickness of the PEL d. This is an important difference with respect to the case of polymer brushes, where one needs to obtain an equilibrium value of the brush height d.36 We can make such a simplification in the present case since the free energy functional does not depend explicitly on brush height, except for φ [see eqn (8)]. Thirdly, as has already been mentioned in this paper, for the case of polymer brushes, the monomer distribution obeys a quadratic profile37–40 – the monomer concentration is higher at near-wall locations and decays at locations way from the wall. For the present case of the polyelectrolyte brushes, the PCS (which can be considered equivalent to monomers) will obey a non-unique and non-uniform distribution; however, just like the case of polymer brushes, this concentration of the chargeable sites will also decay away from the wall.Here we also attempt to highlight the relevance of the present study in qualitatively interpreting different experimental results on pH-responsive polyelectrolyte brushes. Yameen et al.41 demonstrated that poly (4-vinyl pyridine) brushes undergo a pH-dependent reaction leading a reversible switching between the swollen charged hydrophilic state (at low pH; here the polymer is pyridine) and collapsed, neutral hydrophobic state (at high pH; here the polymer is pyridinium). Here the charging occurs via a base-like reaction, when pyridinium, at a small pH, accepts a proton to form pyridine – this ensures that the charging of the PEL is pH-dependent. Since this charging occurs at a small pH, the pH-dependent PEL charge density will be typically witnessed at this small pH. Hence at such a pH, by the proposed analysis of this study, there needs to be a given non-uniform distribution of the PCS or monomers with the PCS concentration decaying away from the wall, and this ensures this swollen hydrophilic state. On the contrary, at large pH (pH > pKa) when the pyridine loses proton to become uncharged pyridinium. Therefore, at such pH the PEL is uncharged, and therefore there is no constraint on the distribution of the monomers, enforcing them to remain in collapsed, neutral hydrophobic state.
Hou et al.42 employed the pH-dependent shape modulation of poly acrylic acid (PAA) to develop a pH-gating ionic transport in a conical nanochannel. PAA contains a carboxylic acid group, which is assumed to form an intramolecular hydrogen bonding at low pH, whereas at high pH ionizes to form COO− and in the process is assumed to form hydrogen bonding with the surrounding water molecules. Hou et al.42 hypothesized that such a transition from intramolecular to intermolecular hydrogen bonding enforced a structural transition of the PAA molecules, enforcing the conical nanochannel to allow water imbibition at the configuration where there is intermolecular hydrogen bonding (i.e., at larger pH). We can provide an alternate explanation, based on our proposed theory. At large pH, where the PAA molecules have ionized to form COO− (i.e., the PEL has pH-dependent charge density), the PCS (or monomers) will demonstrate a non-uniform distribution, with the PCS concentration decaying away from the wall. Therefore, the drag is also much larger near the wall; since the flow velocity (which is a surface tension driven imbibition) is much weaker closer to the channel walls, this PEL configuration (with greater PCS or monomer concentration at near-wall locations) ensures much weaker overall drag and hence a more enhanced flow rate. On the contrary, for smaller pH, the PEL is uncharged, and hence the PCS or monomers can remain uniformly distributed, thereby inducing a much larger drag force and a weaker flow rate.
Above two examples show that our theory can help to interpret the effects associated with the pH-response-dependent shape changes of polyelectrolyte brushes, and the associated variations in the transport characteristics. Please note that in the above two examples, we only provided qualitative interpretations of the existing experiments based on our new theoretical understanding. Similar such examples, where our theory can provide useful qualitative insights, include the host of experimental studies on transport in soft (polyelectrolyte-grafted) nanochannels/nanopores that are responsive to pH or concentration of a specific ion (Wen et al.43 reviewed several such nanochannels/nanopores). Of course, a more rigorous quantitative comparison will be possible when we actually obtain the unique distribution of the PCS or monomers by considering the elastic and volume exclusion effects in addition to the electrostatic effects. This will be studied in a future publication.
Conclusions
In this paper we provide a rigorous free energy based approach to pinpoint a gross existing error in the modeling of electrostatics of soft charged interfaces, represented as a grafted-PEL system with pH-dependent charge density: we show that for such soft charged interfaces, it is impossible to have a uniform PCS (or monomer) distribution within the PEL. We arrive at this very important conclusion on the basis of the fact that we consider for the first time explicit number density distribution of the hydrogen ions inside and outside the PEL. We argue that the monomer distribution is non-uniform and non-unique; it must at least be a cubic distribution, which is very insightful given the fact that the monomer distribution of the polymer brushes (resulting from the balance of the elastic and volume exclusion effects) should be uniquely quadratic. We also demonstrate that our theory can provide qualitative interpretation of a number of experiments involving pH-response-dependent shape transition in polyelectrolyte brushes.References
- H. Ohshima, Electrophoresis of soft particles, Adv. Colloid Interface Sci., 1995, 62, 189–235 CrossRef CAS
.
- H. Ohshima, Electrical phenomena in a suspension of soft particles, Soft Matter, 2012, 8, 3511–3524 RSC
.
- A. C. Barbati and B. J. Kirby, Soft diffuse interfaces in electrokinetics – theory and experiment for transport in charged diffuse layers, Soft Matter, 2012, 8, 10598–10613 RSC
.
- H. Ohshima, Theory of electrostatics and electrokinetics of soft particles, Sci. Technol. Adv. Mater., 2009, 10, 063001 CrossRef
.
- J. F. L. Duval and F. Gaboriaud, Progress in electrohydrodynamics of soft microbial particle interphases, Curr. Opin. Colloid Interface Sci., 2010, 15, 184–195 CrossRef CAS PubMed
.
- J. F. L. Duval, J. Merlin and P. Anantha, Electrostatic interactions between diffuse soft multi-layered (bio)particles: beyond Debye–Hückel approximation and Deryagin formulation, Phys. Chem. Chem. Phys., 2011, 13, 1037–1053 RSC
.
- K. Makino and H. Ohshima, Soft particle analysis of electrokinetics of biological cells and their model systems, Sci. Technol. Adv. Mater., 2011, 12, 023001 CrossRef
.
- H. Ohshima and T. Kondo, Electrophoretic mobility of a “soft particle” with a nonuniformly charged surface layer as a model for cells, Biophys. Chem., 1993, 46, 145–152 CrossRef CAS
.
- T. Mazda, K. Makino and H. Ohshima, Electrophoretic mobility of red blood cells treated with standardized protease enzymes for use in blood group serology, Colloids Surf., B, 1995, 5, 75–80 CrossRef CAS
.
- R. Bos, H. C. van der Mei and H. J. Busscher, ‘Soft-particle’ analysis of the electrophoretic mobility of a fibrillated and non-fibrillated oral streptococcal strain: Streptococcus salivarius, Biophys. Chem., 1998, 74, 251–255 CrossRef CAS
.
- R. Sonohara, N. Muramatsu, H. Ohshima and T. Kondo, Difference in surface properties between Escherichia coli and Staphylococcus aureus as revealed by electrophoretic mobility measurements, Biophys. Chem., 1995, 55, 273–277 CrossRef CAS
.
- P. J. M. Kiers, R. Bos, H. C. van der Mei and H. J. Busscher, The electrophoretic softness of the surface of Staphylococcus epidermidis cells grown in a liquid medium and on a solid agar, Microbiology, 2001, 147, 757–762 CAS
.
- S. Tsuneda, J. Jung, H. Hayashi, H. Aikawa, A. Hirata and H. Sasaki, Influence of extracellular polymers on electrokinetic properties of heterotrophic bacterial cells examined by soft particle electrophoresis theory, Colloids Surf., B, 2003, 29, 181–188 CrossRef CAS
.
- M. N. Chandraprabha, J. M. Modak and K. A. Natarajan, Soft-particle model analysis of effect of LPS on electrophoretic softness of Acidithiobacillus ferrooxidans grown in presence of different metal ions, Colloids Surf., B, 2009, 69, 1–7 CrossRef CAS PubMed
.
- T. H. Nguyen, N. Easter, L. Gutierrez, L. Huyett, E. Defnet, S. E. Mylon, J. K. Ferri and N. A. Viet, The RNA core weakly influences the interactions of the bacteriophage MS2 at key environmental interfaces, Soft Matter, 2011, 7, 10449–10456 RSC
.
- A. D. Phan, D. A. Tracy, T. L. H. Nguyen, N. A. Viet and T.-L. Phan, Electric potential profile of a spherical soft particle with a charged core, J. Chem. Phys., 2013, 139, 244908 CrossRef PubMed
.
- A. T. Poortinga, R. Bos, W. Norde and H. J. Busscher, Electrical double layer interactions in bacterial adhesion to surfaces, Surf. Sci. Rep., 2002, 47, 1–32 CrossRef CAS
.
- A. J. de Kerchove and M. Elimelech, Relevance of electrokinetic theory for “soft” particles to bacterial cells: Implications for bacterial adhesion, Langmuir, 2005, 21, 6462–6472 CrossRef CAS PubMed
.
- S. Tsuneda, H. Aikawa, H. Hayashi and A. Hirata, Significance of cell electrokinetic properties determined by soft-particle analysis in bacterial adhesion onto a solid surface, J. Colloid Interface Sci., 2004, 279, 410–417 CrossRef CAS PubMed
.
- A. Hyono, T. Mazda, H. Okazaki, K. Tadokoro and H. Ohshima, Analysis
of enzyme-treated red blood cell surface and haemagglutination using a theory of soft particle electrophoresis, Vox Sang., 2008, 95, 131–136 CrossRef CAS PubMed
.
- K. D. Tachev, K. D. Danov and P. A. Kralchevsky, On the mechanism of stomatocyte–echinocyte transformations of red blood cells: experiment and theoretical model, Colloids Surf., B, 2004, 34, 123–140 CrossRef CAS PubMed
.
- S. S. Dukhin, R. Zimmermann and C. Werner, Electrokinetic phenomena at grafted polyelectrolyte layers, J. Colloid Interface Sci., 2005, 286, 761–773 CrossRef CAS PubMed
.
- S. S. Dukhin, R. Zimmermann and C. Werner, Charge density distribution at interfaces between polyelectrolyte layers and aqueous solutions – experimental access and limitations of traditional electrokinetics, J. Colloid Interface Sci., 2008, 328, 217–226 CrossRef CAS PubMed
.
- J. F. L. Duval, D. Kütter, M. Nitschke, C. Werner and R. Zimmermann, Interrelations between charging, structure and electrokinetics of nanometric polyelectrolyte films, J. Colloid Interface Sci., 2011, 362, 439–449 CrossRef CAS PubMed
.
- R. Zimmermann, S. S. Dukhin, C. Werner and J. F. L. Duval, On the use of electrokinetics for unraveling charging and structure of soft planar polymer films, Curr. Opin. Colloid Interface Sci., 2013, 18, 83–92 CrossRef CAS PubMed
.
- S. Chanda, S. Sinha and S. Das, Streaming potential and electroviscous effects in soft nanochannels: towards designing more efficient nanofluidic electrochemomechanical energy converters, Soft Matter, 2014, 10, 7558–7568 RSC
.
- S. Das, Explicit interrelationship between Donnan and surface potentials and explicit quantification of capacitance of charged soft interfaces with pH-dependent charge density, Colloids Surf., A, 2014, 462, 69–74 CrossRef CAS PubMed
.
- S. Chanda and S. Das, Effect of finite ion sizes in an electrostatic potential distribution for a charged soft surface in contact with an electrolyte solution, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 012307 CrossRef
.
- L. P. Yezek, Bulk conductivity of soft surface layers:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Experimental measurement and electrokinetic implications, Langmuir, 2005, 21, 10054–10060 CrossRef CAS PubMed
Experimental measurement and electrokinetic implications, Langmuir, 2005, 21, 10054–10060 CrossRef CAS PubMed .
- S. S. Dukhin, R. Zimmermann and C. Werner, Intrinsic charge and Donnan potentials of grafted polyelectrolyte layers determined by surface conductivity data, J. Colloid Interface Sci., 2004, 274, 309–318 CrossRef CAS PubMed
.
- L. P. Yezek, J. F. L. Duval and H. P. van Leeu, Electrokinetics of diffuse soft interfaces. III. Interpretation of data on the Polyacrylamide/water interface, Langmuir, 2005, 21, 6220–6227 CrossRef CAS PubMed
.
- S. Xue, L.-H. Yeh, Y. Ma and S. Qian, Tunable streaming current in a pH-regulated nanochannel by a field effect transistor, J. Phys. Chem. C, 2014, 118, 6090–6099 CAS
.
- J. R. Kanicky and D. O. Shah, Effect of degree, type, and position of unsaturation on the pKa of long-chain fatty acids, J. Colloid Interface Sci., 2002, 256, 201–207 CrossRef CAS
.
- M. Tollinger, K. A. Crowhurst, L. E. Kay and J. D. Forman-Kay, Site-specific contributions to the pH dependence of protein stability, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 4545–4550 CrossRef CAS PubMed
.
- S. Salenting, L. Sagalowicz and O. Glatter, Self-assembled structures and pKa value of oleic acid in systems of biological relevance, Langmuir, 2010, 26, 11670–11679 CrossRef PubMed
.
- J. V. M. Weaver, R. T. Williams, B. J. L. Royles, P. H. Findlay, A. I. Cooper and S. P. Rannard, pH-Responsive branched polymer nanoparticles, Soft Matter, 2008, 4, 985–992 RSC
.
- Y. B. Zhulina, V. A. Pryamitsyn and O. V. Borisov, Structure and conformational transitions in grafted polymer chain layers. A new theory, Polym. Sci. U.S.S.R., 1989, 31, 205–216 CrossRef
.
- S. T. Milner, Polymer brushes, Science, 1991, 251, 905–914 CrossRef CAS PubMed
.
- S. T. Milner, T. A. Witten and M. E. Cates, A parabolic density profile for grafted polymers, Europhys. Lett., 1988, 5, 413–418 CrossRef CAS
.
- S. P. Adiga and D. W. Brenner, Stimuli-responsive polymer brushes for flow control through nanopores, J. Funct. Biomater., 2012, 3, 239–256 CrossRef CAS PubMed
.
- B. Yameen, M. Ali, R. Neumann, W. Ensinger, W. Knoll and O. Azzaroni, Synthetic proton-gated ion channels via single solid-state nanochannels modified with responsive polymer brushes, Nano Lett., 2009, 9, 2788–2793 CrossRef CAS PubMed
.
- X. Hou, Y. J. Liu, H. Dong, F. Yang, L. Li and L. Jiang, A pH-gating ionic transport nanodevice: asymmetric chemical modification of single nanochannels, Adv. Mater., 2010, 22, 2440–2443 CrossRef CAS PubMed
.
- L. Wen, Y. Tian, J. Ma, J. Zhai and L. Jiang, Construction of biomimetic smart nanochannels with polymer membranes and applications in energy conversion systems, Phys. Chem. Chem. Phys., 2012, 14, 4027–4042 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra13946a |
| This journal is © The Royal Society of Chemistry 2015 |