Interaction of carbon, nitrogen and oxygen with vacancies and solutes in tungsten
Yu-Wei Youa,
Xiang-Shan Konga,
Xue-Bang Wu*a,
C. S. Liu*a,
Q. F. Fanga,
J. L. Chenb and
G.-N. Luob
aKey Laboratory of Materials Physics, Institute of Solid State Physics, Chinese Academy of Sciences, P. O. Box 1129, Hefei 230031, P. R. China. E-mail: xbwu@issp.ac.cn; csliu@issp.ac.cn
bInstitute of Plasma Physics, Chinese Academy of Sciences, Hefei 230031, P. R. China
First published on 18th February 2015
Abstract
Investigating the behaviors of impurities such as carbon, nitrogen and oxygen within tungsten is crucial to understanding the formation of compounds which can substantially influence the physical and chemical properties of tungsten. Using density functional theory method, we have investigated the geometry and energetics of small VacXn, SolXn and SolVacXn (Vac = vacancy, Sol = solute, and X = C, N or O) clusters to probe the aggregation of X in tungsten. We find that vacancy and solute–vacancies show great attraction to X atoms and multiple X atoms can be embedded in the defects. Four C atoms segregate in a vacancy forming a square where the C–C bond forms with the bond length of 1.58 Å, however, it is hard to form N–N (or O–O) bonds in a vacancy although up to six N (or O) atoms can be trapped in a vacancy. The solutes titanium, tantalum, rhenium and osmium present relatively weak attraction to X atoms, and the binding energies of the solute with X rely on the bond length of Sol-X. Moreover, the concentration evolution of VacCn (SolCn) is determined through the law of mass action, and the results show that the concentrations of VacCn (SolCn) depend strongly on temperature, and the initial concentrations of vacancy (Sol) and C. The binding energy of SolVacXn correlates linearly with the volume difference of the system containing a SolVacXn and that with no defects. The aggregation of X atoms in the microstructure of tungsten, forming high X concentration zones, may facilitate the formation of compounds.
1 Introduction
Tungsten (W) possesses many excellent properties such as a high melting point and high resistance to sputtering and chemical erosion, and therefore is used in the Tokamak and, in the near future, the International Thermonuclear Experimental Reactor (ITER).1,2 The mixing of W and C will take place at the strike points of the divertor plates in ITER where W is exposed to high heat and C impurity fluxes, leading to the formation of high C concentrations in the near surface region.3,4 The deposition of C in W will result in the formation of tungsten carbides, such as WC and W2C.5,6 X-ray diffraction measurements showed that C coalesces at the local structure in W and hexagonal tungsten carbide WC forms when the concentrations of C reach 0.1 wt% and 0.8 wt%.7 The formation of carbide often influences the physical and chemical properties of W, for example the formation of a WC layer could prevent the implanted hydrogen isotopes from escaping from W, leading to the increase of hydrogen retention and the formation of blisters in W.3,8–10 The chemical interactions of C-based material with hydrogen isotopes often result in enhanced erosion, especially at elevated surface temperatures (600–800 K).11 The eroded C atoms migrate to other places and re-deposit on the W surface to form thin carbon films. Tungsten carbide is not easily corroded in acidic solutions.12 O is present in the mixed surface layers of W in ITER, and N is often seeded into the edge plasma for radiative cooling.13 The two light elements can also interact with W to form compounds and alter the chemical and physical properties of W. Additionally, C, N and O can be used to stabilize β-phase of W.14Some solute carbides are often introduced to improve the properties of W. Typical examples are the addition of TiC to improve the mechanical properties and reduce microstructure changes and radiation hardening of W by neutron irradiation,15 and the addition of TaC to improve the thermo-mechanical properties of W.16 Moreover, solute Ta is added to reduce deuterium retention in W, and Re is added to improve the creep strength and recrystallization temperature.17,18 Ta, Re, and Os are the primary transmutation solutes in W implanted by high-energy neutrons. For instance, W will be changed to W-11Re-3Os (wt%) alloy after 50 dpa neutron irradiation.19 Theoretical calculations suggest that the concentrations of Re, Os and Ta transmuted from W reach as high as 3.8 at%, 1.4 at% and 0.81 at%, respectively, after five years under fusion power-plant conditions.20 Tanno et al. have found that the presence of Re and Os can suppress void and dislocation loop formations in W under neutron irradiation.21 Besides, both Re and Os precipitate in W after 1.54 dpa irradiation, although Re and Os are far below the solubility limit,22 and the formation of Re and Os precipitates can lead to the hardening and embrittlement of W.21,23
In addition to transmutation solutes, a large number of lattice defects such as vacancies and self-interstitial atoms are produced in W exposed to high temperature and high-energy neutrons in a fusion environment. These lattice defects and solutes interact strongly with light elements,24 slowing down the motion and thus changing the distribution characteristics of the atom in W. The bindings of C atoms with defects and solutes promote the accumulation of atoms to form tungsten (and solute) carbides.7,25 This results in the chemical and physical property modification of W. However, experiments are less clear regarding the interaction strength of C atoms with defects, alloys and transmutation solutes because it is extremely difficult to measure the binding energies of C atoms with defects, alloys and transmutation solutes due to their small sizes. In the present paper, we perform first-principles density functional theory (DFT) calculations on the geometry and energetics of the small clusters VacCn, SolCn and SolVacCn (Vac = vacancy and Sol = solutes including Ti, Ta, Re and Os) in bcc W. Our focus is on the initial stage of tungsten (solute) carbide compounds. To supplement more technical values and gain understanding of the species dependence of tungsten (solute) compounds, we carry out similar modeling calculations on N and O. We find that the attraction of C is weaker than N and O to all the defects considered: vacancy, solute and solute–vacancy, and the attraction of the solute–vacancy is the strongest for C, N and O in most cases. It is possible for multiple C, N and O to bind with a vacancy, solute and solute–vacancy in W.
2 Computational details
The first-principles DFT calculations have been performed using VASP code and ultrasoft pseudopotentials.26,27 The generalized gradient approximation (GGA) of Perdew and Wang function is employed,28,29 and the wave functions expanded in plane–wave basis set with an energy cutoff of 500 eV are used. The calculations have been performed in a 128-atom supercell, using a 3 × 3 × 3 k-point mesh for integration over the Brillouin zone. The atom position and the volume of the supercell are fully optimized, and the structural optimization is truncated when the forces converge to less than 0.01 eV Å−1. The defect formation energy is calculated by:| Ef(X) = E(W + X) − E(W) − E(X), | (1) |
| Ctet–oct | Ntet–oct | Otet–oct | |
|---|---|---|---|
| Present work | 1.47 | 0.72 | −0.27 |
| Ref. 30. | 1.24 | 0.72 | −0.35 |
3 Results and discussion
3.1 Interaction of C, N and O with vacancies
In defect-free W, we have shown that C and N atoms prefer the oct site while O atom favors the tet site in the previous section. The presence of a vacancy can change the site preference of C, N and O, and the vacancy can serve as an attraction center for the dissolved C, N and O atoms. In order to find the equilibrium configuration of C, N and O in a vacancy all the possible oct and tet sites close to a vacancy are calculated. At a vacancy, a single C, N or O atom will spontaneously occupy the first nearest neighbor (1NN) oct site, relaxing towards the vacancy. More precisely, C, N and O atoms are displaced from the oct site to the vacancy by 0.28 Å, 0.23 Å and 0.30 Å, respectively. Similar results have been found for C and N in Fe.31 The binding energy of the X atom to vacancy is calculated with the expression:| Eb(VacXn) = nEint(X) + E(Vac) − E(Vac + nX) − nE(W), | (2) |
3.2 Equilibrium concentration evolution of VacXn
Before considering the equilibrium concentration evolution of VacXn, a phonon spectrum is used to assess the stability of C at the vacancy. As shown in Fig. 3, there is no imaginary frequency in the phonon spectrum of C at the vacancy. This indicates that the configuration of VacC with the C atom positioned at 1NN oct site is stable. In order to avoid too much computation cost, the phonon spectrum of the other VacXn is not calculated. The equilibrium concentration evolution of VacXn can be evaluated through mass action analysis. The mass action framework predicts the equilibrium behavior of the defect towards which the system tries to evolve.33 The concentration development of the VacXn cluster is determined through the law of mass action:
 | (3) |
 | ||
| Fig. 3 The calculated phonon spectrum of the system with a VacC, where the C atom is positioned at 1NN oct site in the vacancy. | ||
 | ||
| Fig. 4 The relative concentrations of VacCn complexes in the temperature range of 400–1600 K. The initial C concentration is assumed to be 1019 cm−3, and vacancy concentration is set to be 1018 cm−3. | ||
3.3 Interaction of isolated C, N or O atom with the solutes
It has been proved that vacancy can act as trapping center for impurities in this and previous work.35 Solute added to W to improve its properties or transmuted from W due to neutron irradiation can also act as potential attraction center for C, N and O. Unfortunately, there is fairly little quantitative or even qualitative experimental and theoretical data regarding the binding energies of C, N and O with the usual substitutional solutes. In order to gain a better understanding of the interactions of C, N, or O with alloying solute, we calculate the binding energy of one isolated interstitial C, N or O atom to the solutes Ti, Ta, Os, and Re using the following equation:| Eb(Sol + nX) = nEint(X) + E(Sol) − E(Sol + nX) − nE(W), | (4) |
 | ||
| Fig. 5 The configurations of 1NN (O1), 2NN (O2, O′2), 3NN (O3, O′3) oct sites, and 1NN (T1), 2NN (T2, T′2), 3NN (T3, T′3) tet sites in the vicinity of a substitutional solutes Ti, Ta, Re and Os. | ||
The binding energies of substitutional solutes Ti, Ta, Re and Os with isolated C, N and O atoms in the 1NN, 2NN and 3NN shells are calculated and presented in Fig. 6(a)–(d). According to the present calculations, the volume of the supercell containing a substitutional Ta atom is 1.84 Å3 larger, and the volumes of the supercells with a Ti, Re and Os atom are 0.64 Å3, 1.01 Å3 and 0.98 Å3, respectively, smaller than the pure W system. Therefore, the substitutional alloying solutes can be divided into two groups, i.e., one group including Ta with a relatively larger atom size and the other group containing Ti, Re and Os with a smaller atom size. From Fig. 6(a), one can see that the solute Ti can bind tightly with the 1NN and 2NN interstitial C and N atoms, and the 1NN (O1 in Fig. 5) binding energy is larger than that of 2NN (O2, O′2). The locations of the 1NN, 2NN and 3NN (O3, O′3) C or N close to Ti are slightly changed, and the bond lengths of Ti–C and Ti–N are 1.93 Å and 1.90 Å, respectively. The bond lengths of Ti–C and Ti–N in W are relatively smaller than in TiC and TiN compounds,37 respectively. The bond length of Ti–N is relatively smaller than Ti–C by 0.03 Å in W, which is very close to the bond length difference of 0.04 Å in compounds.37 However, the 1NN and 2NN tet O atoms move spontaneously to the closest oct site of Ti, where the bond length of Ti–O is 1.88 Å. This is the reason why the binding energies for the 1NN and 2NN are almost the same. The largest binding energies of the 1NN C, 1NN O and 1NN N to Ti reach up to 0.48 eV, 0.80 eV and 0.83 eV, respectively. While the 3NN binding energies for C, N and O are relatively small, suggesting that the influence range of substitutional Ti on C, N and O is confined to the 1NN and 2NN. The investigations for the bindings of Ti with C, N and O are interesting because TiC and TiN are typical compounds known for their high melting point and hardness, thus they are widely used as hard coatings and strengthening phases to improve the mechanical properties of many materials.37 For example, W alloyed with 0.2 wt% TiC exhibits a much lower ductile-to-brittle transition temperature and higher strength than pure W.38
 | ||
| Fig. 6 The binding energies of C and N in the 1-3NN oct sites, O in the 1-3NN tet sites close to (a) Ti, (b) Ta, (c) Re, (d) Os. | ||
In contrast, the 2NN oct site near the large atom Ta is the lowest-energy configuration for C and N, with binding energies of 0.3 eV and 0.4 eV, respectively. The binding energies for O in the 1NN and 2NN shells to Ta are comparable to 0.25 eV because the O atom located at the 2NN tet site near Ta diffuses with no barrier to the 1NN tet site. The 1NN oct site in the vicinity of Ta is unstable for C, exhibiting a repulsive interaction. Solutes Re and Os present a similar attraction role on C and N, where the equilibrium configuration for C or N is the 1NN oct site close to the solutes. The configuration of C or N located at the 2NN oct sites are energetically unstable with a binding energy of ∼−0.2 eV. There are rather weak attractive interactions of the solute Re with N and O atoms. Besides, it is most stable for O to occupy the 2NN tet site to Os. In summary, Ti, Ta, Re and Os can show attraction to C, N and O. The positions of C, N and O in the 1NN, 2NN and 3NN shells of the solutes Re and Os are almost not changed, which differs from Ti and Ta. The trapping role of Ti on isolated C, N and O atoms is the strongest followed by Ta, Re and Os.
The charge density on the (100) plane containing the substitutional solute Ta as well as C and N atoms located at the 1NN and 2NN oct sites are plotted in Fig. 7. Only the 1NN tet site is considered for O because the 2NN tet O can diffuse to the 1NN tet site with no energy barrier. From Fig. 7, one can see that C and N atoms located at 1NN and 2NN oct sites, and O atom at 1NN tet sites can bond tightly with solute Ta and the closest W atoms. Besides, C and N at 1NN oct site can also promote the bonding of W with W atoms (see Fig. 7(a) and (c)). The bonding is exothermic, stabilizing the system and thus resulting the tight binding of the solute with C, N and O atoms. However, the too close distance between the solute and the X atoms results in a coulomb repulsive interaction, which raises the total energy of the system. This may result in the repulsive and nearly no interactions of Ta with the 1NN oct C and N, respectively. The interactions of Ti, Re and Os with N and O may also be analyzed by a similar method.
3.4 Aggregation of C, N or O atoms to the solutes
In this part, we investigate the attraction effect of substitutional solutes on multiple C, N or O atoms in W. In the previous section, we have found that both C and N atoms prefer to occupy the 1NN oct site close to Ti, Re and Os, the 2NN oct site nearby Ta, while O is most energetically favorable to take the 1NN tet site and the 1NN oct site in the vicinity of respectively Ta and Ti, and the 2NN tet site near Os and Re. Based on the results, multiple C, N and O atoms are brought to the possible sites neighboring the substitutional solutes. It is possible to generate a large number of various SolXn cluster geometries with multiple X atoms, even if C and N atoms are restricted to the 1NN and 2NN oct sites, and O is confined to 1NN and 2NN tet sites close to the substitutional solutes. C, N and O atoms are brought one by one to the sites close to the substitutional site, forming a SolXn complex and the possible geometric configurations are examined. By comparing the total energy of the system containing a SolXn complex, the equilibrium states are found for the second and third C, N or O atoms. The binding energies for three C, N and O atoms at ground state with the substitutional solutes Ti, Ta, Re and Os are plotted in Fig. 8. It is noticeable that the reduction in the binding energy of SolXn+1 complex compared with that of SolXn indicates that no more than n X atoms can be bound to the substitutional solute. From the results plotted in Fig. 8, one can see that the smaller solute Ti is capable of catching only one C atom, while Ti has the ability to tightly trap at least three N or O atoms. The binding energies referring to Ti with three N and O atoms reach up to 2.0 eV and 3.8 eV, respectively. The solutes Re and Os present a similar capture effect on C, N and O atoms. It is extremely difficult for the smaller solutes Re and Os to capture more than one C and N atom, however, the two solutes are capable of attracting at least three O atoms. The binding energies of Re and Os with three O atoms reach up to 2.4 eV and 2.7 eV, respectively. In contrast, the larger solute Ta exhibits a strong trapping role on C, N and O atoms, and one Ta could trap no less than three C, N and O atoms. The hybrid configurations using oct and tet sites are also considered. We notice that the 2NN and 3NN oct sites are unstable for C and N atoms due to the presence of solute. Take solute Os as an example. C and N atoms put at 1NN tet migrates to the 1NN oct, while O atom is stable at 1NN oct. Thus the hybrid configurations using oct and tet sites are considered for O atoms. As the first O atom is positioned at the most-stable 2NN tet site, and the second O atom is put at 1NN oct site. The binding energy of the OsC2 in the configuration is 1.05 eV, where the configuration is less stable compared with the most-stable configuration found above. | ||
| Fig. 8 The binding energies for three C, N and O atoms to cluster around solutes Ti (a), Ta (b), Re (c), and Os (d). | ||
The binding strength of the solutes on X atoms can be generally divided into two parts, i.e., the bindings of solute–X and X–X in W. According to the results in the last section and our previous work,39 the interactions of solute–X and X–X in W depend on the separated distance of X from solute and X. Take the interplay of Re with X for example, the interactions of Re with C and N are attractive in the 1NN and 3NN shells, but repulsive in the 2NN shell. While Re is attractive with the 1NN, 2NN and 3NN O atoms. The two C atoms at equilibrium configuration are positioned at the 1NN oct sites, with the distance between the two C atoms of 2.35 Å. However, the interactions of the two C atoms in W at the distance present a strong repulsive effect (see ref. 39). Therefore it is energetically unfavorable for two C atoms to bind with Re. In the similar way, the binding of Ti, Ta, Os and Re with X atoms may be analyzed. The calculated binding energy of solute with X indicates that it is energetically for Ta to attract multiple C, Ti and Ta to capture no less than three N, and Ti, Ta, Os, and for Re to bind at least three O atoms. So it is only energetically favorable for multiple O atoms to bind tightly to all the four solutes. The strong bindings of X atoms to solutes suggest the formation of localized high concentration X atom zones surrounding the solutes. The formation of local high concentration C, N or O atoms around the solutes provides the chance for the formation of solute–C, solute–N and solute–O compounds, or tungsten carbide, nitride or oxide in W. The interaction of C, N and O with vacancies and solutes in W is very local and the amount of C, N and O is low in this work. The increasing amount of C, N and O may lead to the formation of different phases in tungsten, however, the studies of the phases in tungsten require further analysis from the global thermodynamic point of view.
The concentration development of stable SolXn cluster is determined through the law of mass action:
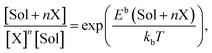 | (5) |
 | ||
| Fig. 9 The relative concentrations of TaCn complexes, unbound vacancies and C atoms in W within the temperature interval of 300–1600 K. | ||
3.5 Aggregation of C, N and O atoms to solute–vacancy complex
Solute–vacancy binding energy is a key quantity controlling the formation of alloying solutes in W. It is possible that C, N or O diffuses through the lattice encountering a solute–vacancy complex and forming a SolVacCn, SolVacNn or SolVacOn complex, influencing the distribution of C, N and O in W. C, N and O may otherwise have a significant effect on the binding of solute–vacancy. So we turn to investigate the binding of C, N and O to the solute–vacancy complex in W in this part. The basic binding energies of Ti, Ta, Re and Os with vacancies in the 1NN and 2NN shells are calculated and compared with the available data by Becquart et al. as summarized in Table 2.From Table 2, one can see that the binding energies obtained here for solute–vacancy in the 1NN and 2NN shells agree well with the reference values, and the maximum difference value is within 0.05 eV for Ti–vacancy in the 2NN shell. The slight difference may originate from the fact that the constant system volume is used in the reference work,40 while variable volume is adopted here. Ti and Ta are energetically unfavorable to form stable solute–vacancy complex, however, Re and Os prefer to aggregate around a vacancy forming solute–vacancy complex. We then investigate the bindings of solute–vacancy with the presence of C, N or O. Since the binding energies of solute–vacancy in the 1NN and 2NN shells are comparable for all four solutes, even the binding energy of Re–vacancy in the 2NN shell is larger than that of 1NN shell, then we take both the 1NN and 2NN solute–vacancy bindings into consideration. C, N or O atoms are brought into the vacancy of the solute–vacancy complex one after another. The ground states of C, N or O atom configurations are found by testing all the possible sites in the vacancy. The binding energies of SolVacCn, SolVacNn or SolVacOn are calculated through the multiple individual point defects, i.e., substitutional solute, vacancy, and nC, N or O atoms.
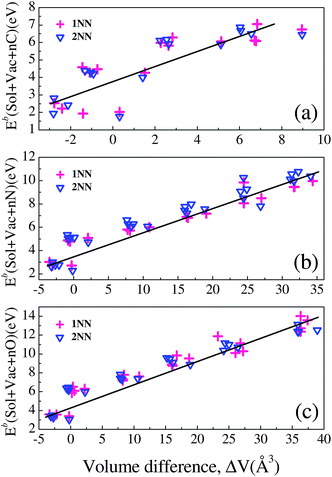
As shown in Fig. 10, one can see that the SolVacCn binding energies fall around the binding energies of VacCn, with most cases that SolVacCn binding energies are larger. This finding is applicable for SolVacNn and SolVacOn complexes in W. In fact, the similar results have been found by Counts et al. for the SolVacH interactions in bcc Fe.41 The incremental binding energies of SolVacXn with the increase of X atom number indicate that the solute–vacancy can attract no less than 4C, N or O atoms. The SolVacXn bindings generally can be divided into the interactions of vacancy with X atoms, vacancy with solute and solute with X atom. From the obtained data in Fig. 10, one can see that the interactions of vacancy with X atoms dominate the bindings of SolVacXn. Meanwhile, the binding energies of SolVacXn correlate tightly with the local stress induced by the presence of the complex in W. The local stress can be expressed by the volume difference of the system having a SolVacXn complex and that containing no defect. The volume difference is defined as: ΔV = V(SolVacXn) − V(Perf), where V(SolVacXn) is the volume of the system containing a SolVacXn complex, and V(Perf) is the volume of the pure system. The correlations of the 1NN and 2NN SolVacXn binding energies with ΔV are calculated and presented in Fig. 11.
Basically, the binding energies of SolVacXn correlate linearly with the volume difference ΔV for C, N and O. The linear relationship is relatively weak for C. From an examination of the microstructure, we find that the main difference between SolVacCn and SolVacNn or SolVacOn is that there is strong covalent bond formation among the C atoms. In general, SolVacXn has larger size and a larger binding energy. The larger size suggests a larger expansion and large stress. The expansion is energetically unfavorable as it is endothermic, thus SolVacXn has a lower binding energy. However, C, N and O prefer to form bonds with W and solute atoms, which can stabilize the system. As the number of C, N or O atoms increase in a vacancy, the volume of the system increases, but there are more covalent bonds formed. The two factors compete and the energy reduced by forming tungsten–X and solute–X bonds may dominate. This results in the stronger binding energy of SolVacXn, although SolVacXn has a relatively larger size.
The diffusion activation energies of Ta, Re and Os in W are found to be 6.23 eV, 6.18 eV and 5.58 eV, respectively, by previous experiments using the radiometric diffusion zone-sectioning method,42 which are much larger than that of a vacancy (1.70 eV). This indicates that a vacancy is more favorable to move to the alloying solutes Re and Os to form a solute–vacancy complex, facilitating the formation of high C, N and O zones. This indicates that the complex can also serve as the aggregation centers for C, N and O. As for Ti and Ta, the bindings of vacancy with the solutes are unfavorable, while the presence of C, N and O promote the binding of the vacancy with the solute. This is interesting because the strong binding of solutes with vacancies benefits the formation of solute precipitates, which can alter the properties of W. Moreover, the aggregation of C, N and O in a solute–vacancy complex can provide an opportunity for the formation of compounds such as carbide, nitride and oxide in W, which can also result in the property change of W.
4 Summary
In summary, we have performed DFT calculations to investigate the geometry and energetics of small VacXn, SolXn and SolVacXn (Vac = vacancy, Sol = Ti, Ta, Re and Os, and X = C, N or O) clusters to elucidate the role of vacancy, solute and solute–vacancy on the aggregation of C, N and O atoms in bcc W. Our results indicate a strong attraction of C, N and O to vacancies, forming locally high C, N and O concentration zones where the binding strength order is approximate to VacOn > VacNn > VacCn. Four C atoms segregate in a vacancy forming a square where the C–C bond forms with a bond length of 1.58 Å, however, it is hard for N (or O) to form covalent bonds in a vacancy although up to six N (or O) atoms can be trapped in a vacancy. The substitutional solutes Ti, Ta, Re and Os present relatively weak attraction to C, N and O. The binding energies of C, N and O with Ti, Ta, Re and Os fall within 0.02–0.83 eV, depending on the bond length of solute–X. Only multiple O atoms can be attracted to all the defects considered. The concentration evolution of VacCn (TaCn) depends strongly on temperature, and the initial concentrations of vacancy (Ta) and C. In most cases, the solute–vacancy complex is the strongest attraction center for C, N and O, and the binding energies of C, N and O with a solute–vacancy complex correlate linearly with the volume difference of the system containing a solute–vacancy –C, –N and –O complexes and that with no defect.Acknowledgements
We acknowledge Dongdong Li for discussing the usage of the law of mass action. This work was supported by the National Magnetic Confinement Fusion Program (Grant no. 2015GB112001), the National Natural Science Foundation of China (nos 11405202, 91126002, and 11375231) and the Strategic Priority Research Program of Chinese Academy of Sciences (Grant no.: XDA03010303), and by the Center for Computation Science, Hefei Institutes of Physical Sciences.References
- R. Neu, V. Bobkov, R. Dux and A. Kallenbach, et al., J. Nucl. Mater., 2007, 363–365, 52–59 CrossRef CAS.
- ITER Physics Basis Editors, et al., Nucl. Fusion, 1999, 39, 2137 CrossRef.
- Y. Ueda, T. Shimada and M. Nishikawa, Nucl. Fusion, 2004, 44, 62 CrossRef CAS.
- R. Kawakami, T. Shimada, Y. Ueda and M. Nishikawa, Jpn J. Appl. Phys., 2003, 42, 7529–7535 CrossRef CAS.
- V. K. Alimov, J. Roth, R. A. Causey, D. A. Komarov, C. Linsmeier, A. Wiltner, F. Kost and S. Lindig, J. Nucl. Mater., 2008, 375, 192–201 CrossRef CAS.
- T. Xiao, A. Hanif, A. P. E. York, J. Sloan and M. L. H. Green, Phys. Chem. Chem. Phys., 2002, 4, 3522–3529 RSC.
- Y. Ueda, M. Fukumoto, I. Sawamura, D. Sakizono, T. Shimada and M. Nishikawa, Fusion Eng. Des., 2006, 81, 233–239 CrossRef CAS.
- T. Shimada, H. Kikuchi, Y. Ueda, A. Sagara and M. Nishikawa, J. Nucl. Mater., 2003, 313–316, 204–208 CrossRef CAS.
- T. Shimada, Y. Ueda and M. Nishikawa, Fusion Eng. Des., 2003, 66–68, 247–251 CrossRef CAS.
- Y. Ueda, T. Funabiki, T. Shimada, K. Fukumoto, H. Kurishita and M. Nishikawa, J. Nucl. Mater., 2005, 337–339, 1010–1014 CrossRef CAS.
- J. Roth, E. Tsitrone, A. Loarte and T. Loarer, et al., J. Nucl. Mater., 2009, 390–391, 1–9 CrossRef CAS.
- K. Essaki, E. J. Rees and G. T. Burstein, Mater. Lett., 2009, 63, 2185–2187 CrossRef CAS.
- K. Schmid, A. Manhard, C. Linsmeier, A. Wiltner, T. Schwarz-Selinger, W. Jacob and S. Mandl, Nucl. Fusion, 2010, 50, 025006 CrossRef.
- M. H. F. Sluiter, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 220102(R) CrossRef.
- H. Kurishita, Y. Amano, S. Kobayashi, K. Nakai, H. Arakawa, Y. Hiraoka, T. Takida, K. Takebe and H. Matsui, J. Nucl. Mater., 2007, 367–370, 1453–1457 CrossRef CAS.
- H. Kurishita and S. Matsuo, et al., Phys. Scr., T, 2014, 159, 014032 CrossRef.
- I. Smid, M. Akiba, G. Vieider and L. Plochl, J. Nucl. Mater., 1998, 258–263, 160–172 CrossRef CAS.
- Y. Zayachuk, M. H. J. Hoen, P. A. Zeijlmans van Emmichoven, D. Terentyev, I. Uytdenhouwen and G. van Oost, Nucl. Fusion, 2013, 53, 013013 CrossRef.
- L. R. Greenwood and F. A. Garner, J. Nucl. Mater., 1994, 212–215, 635–639 CrossRef CAS.
- M. R. Gilbert and J.-C. Sublet, Nucl. Fusion, 2011, 51, 043005 CrossRef.
- T. Tanno, A. Hasegawa, J. C. He, M. Fujiwara, S. Nogami, M. Satou, T. Shishido and K. Abe, Mater. Trans., 2007, 48, 2399–2402 CrossRef CAS.
- T. Tanno, A. Hasegawa, M. Fujiwara, J. C. He, S. Nogami, M. Satou, T. Shishido and K. Abe, Mater. Trans., 2008, 49, 2259–2264 CrossRef CAS.
- Y. Nemoto, A. Hasegawa, M. Satou and K. Abe, J. Nucl. Mater., 2000, 283–287, 1144–1147 CrossRef CAS.
- Y. W. You, D. D. Li, X. S. Kong, X. B. Wu, C. S. Liu, Q. F. Fang, B. C. Pan, J. L. Chen and G. N. Luo, Nucl. Fusion, 2014, 54, 103007 CrossRef.
- M. Rubel, V. Philipps, L. Marot, P. Petersson, A. Pospieszczyk and B. Schweer, J. Nucl. Mater., 2011, 415, S223–S226 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, (R) 558 CrossRef.
- G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 4978 CrossRef CAS.
- D. Nguyen-Manh, Adv. Mater. Res., 2009, 59, 253 CrossRef CAS.
- C. Domain, C. S. Becquart and J. Foct, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 144112 CrossRef.
- Y. L. Liu, H. B. Zhou, Y. Zhang, G. H. Lu and G. N. Luo, Comput. Mater. Sci., 2011, 50, 3213–3217 CrossRef CAS.
- F. A. Kroger and V. J. Vink, in Solid State Physics, ed. F. Seitz and D. Turnbull, Academic, New York, 1956, vol. 3, p. 307 Search PubMed.
- M. Poon, A. A. Haasz and J. W. Davis, J. Nucl. Mater., 2008, 374, 390–402 CrossRef CAS.
- C. S. Becquart and C. Domain, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 255, 23–26 CrossRef CAS.
- X. S. Kong, X. B. Wu, Y. W. You, C. S. Liu, Q. F. Fang, J. L. Chen, G. N. Luo and Z. G. Wang, Acta Mater., 2014, 66, 172–183 CrossRef CAS.
- Y. Yang, C. Yu and J. M. Chen, J. Alloys Compd., 2009, 485, 542–547 CrossRef CAS.
- Y. Kitsunai, H. Kurishita, H. Kayano, Y. Hiraoka, T. Igarashi and T. Takida, J. Nucl. Mater., 1999, 271–272, 423–428 CrossRef.
- X. S. Kong, Y. W. You, C. Song, Q. F. Fang, J. L. Chen, G. N. Luo and C. S. Liu, J. Nucl. Mater., 2012, 430, 270–278 CrossRef CAS.
- C. S. Becquart and C. Domian, Curr. Opin. Solid State Mater. Sci., 2012, 16, 115–125 CrossRef CAS.
- W. A. Counts, C. Wolverton and R. Gibala, Acta Mater., 2010, 58, 4730–4741 CrossRef CAS.
- N. K. Arkhipova, S. M. Klotsman, I. P. Polikarpova, G. N. Tatarinova, A. N. Timofeev and L. M. Veretennikov, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 1788 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2015 |