How do organic gold compounds and organic halogen molecules interact? Comparison with hydrogen bonds

Abstract

An Au⋯X interaction has been predicted in the complexes between the organic gold compound RAu (R = CH₃, C₂H₃, and C₂H) and the organic halogen compound R′X (R′ = CH₃, C₂H, C₂H₃, and CF₃; X = Cl, Br, and I) using quantum chemical calculations. Upon the basis of the anisotropic distribution of molecular electrostatic potentials on the Au and X atoms, two types of structures, represented as GB and XB, respectively, were obtained. In the GB structure, the Au atom acts as a Lewis acid and X is a Lewis base, but reversed roles are found for Au and X in XB. Interestingly, the former structure is far more stable than the latter one. Their difference in stability can be regulated by the substitution and hybridization effects, similarly to those in hydrogen bonds. The partially covalent-interaction nature of GBs was characterized with the large charge transfer and the negative energy density as well as the high interaction energy. GB interaction is dominated by electrostatic and polarization energies, whereas electrostatic and dispersion energies are responsible for the stability of most XB complexes. This is an interesting finding that both patterns of interactions are different in nature even though the two monomers are only different in the spatial orientation for both interactions.

---

1. Introduction

Gold catalysts have been attracting much interest since Haruta et al. reported that gold nanoparticles exhibit unique catalytic activity in CO oxidation at low temperature.¹ Nowadays, gold nanoparticles and its complexes have been widely applied in homogeneous^2–8 and heterogeneous catalyses,^5,9 chemotherapy, protein engineering and gene technology.¹⁰ Intermolecular interactions involving gold atoms probably play important roles in these applications. Gold clusters, as a proton acceptor, are able to form an unconventional hydrogen bond Au⋯H–X (X = N, O, and F).^11–14 On the other hand, due to its remarkably high first electron affinity,¹⁵ gold atom is also able to serve as an electron acceptor in intermolecular interactions, which has been confirmed in complexes of HF⋯AuOH,¹⁶ H₂O⋯AuOH,¹⁷ H₂O⋯AuCH₃,¹⁸ and HCCH⋯AuX (X = OH, F, Cl, Br, CH₃, CCH, CN, and NC).¹⁹ This type of intermolecular interaction was named as Au-bonding by Papadopoulos et al.,¹⁶ which exhibits similar properties with hydrogen bonds, such as synergistic, hybridization, and substitution effects.^17,18

Halogen bond (XB) is one type of highly directional non-covalent interaction between an electron-deficient halogen atom and a Lewis base, represented as R–X⋯B (X is a halogen atom and B is a Lewis base). XBs play important roles in molecular recognition,^20–22 biochemical processes,^23–25 crystal engineering,^26–28 and chemical reactions.^29,30 The capability to form a halogen bond becomes greater for the heavier halogen atom. F atom as a Lewis acid rarely participates in the formation of halogen bond³¹ with the exception that it could form a halogen bond if it is covalently bonded to a strong electron-withdrawing group or the Lewis base in XBs is a sufficiently strong electron donor.³² In most cases, the nature of XB can be illustrated with the concept of σ-hole, a region of positive electrostatic potential on the outer side of the halogen X in a molecule R–X.³¹ This σ-hole determines the direction and strength of XBs. On the other hand, the magnitude of σ-hole depends on the nature of halogen atom, although it can be regulated by the substituent (R) in R–X.³³ For instance, the σ-hole is not found on the Cl atom in CH₃Cl, but the Br and I atoms in CH₃Br and CH₃I have a small σ-hole.³⁴ Experimentally, Legon's group unveiled the differences in geometrical structures between halogen bonds and hydrogen bonds, where the interaction groups of the former are apt to be a collinear configuration while the corresponding part of the latter is not.³⁵ In addition to be a Lewis acid in halogen bonds, halogen atom is also able to act as a Lewis base in hydrogen bonds.³⁶

By analogy with halogen atoms, gold atoms also show dual characters of a Lewis acid and base, thus an interesting point is raised whether there are also two types of interaction modes between gold and halogen atoms? If it is the case, which one is more favorable? In order to address these issues, we performed ab initio calculations for some representative complexes composed of both organic gold compounds (RAu) and organic halogen ones (R′X, X = Cl, Br, and I), where R and R′ are alkyl groups. We focused on the effects of substitution and hybridization on the strengths of interaction modes. It was demonstrated that gold(I)–acetylide complexes exhibit some interesting spectroscopic and photophysical properties,³⁷ thus CF₃X⋯AuCCH complex was studied to compare the effect of hybridization on the interaction mode between organic gold compounds and organic halogen molecules. In order to compare the interactions formed of both gold and halogen atoms, we have analyzed these complexes by means of charge transfer, orbital interactions, electron density difference, topological parameters, and energy decomposition schemes. Finally, we provided some experimental evidences for the existence of such interactions by means of the Cambridge Structural Database (CSD).

2. Computational details

All complexes were optimized using the second-order Møller–Plesset perturbation theory (MP2) with both aug-cc-PVDZ and aug-cc-pVTZ basis sets for all atoms except iodine and gold, for which the aug-cc-pVDZ-PP and aug-cc-pVTZ-PP basis sets were adopted to account for relativistic effects. This method has been used successfully to predict and characterize many complexes involving Au-bonds¹⁹ and halogen bonds.³⁶ All calculations were performed using Gaussian 09 package.³⁸ The frequency calculations were carried out at the same levels to verify that the optimized structures correspond to the local minima on the potential energy surfaces. The interaction energies were calculated by the supermolecular approach including the basis set superposition error (BSSE) correction using the counterpoise method proposed by Boys and Bernardi.³⁹ The interaction energy was also analyzed at the MP2/aug-cc-pVTZ level by the localized molecular orbital energy decomposition analysis (LMOEDA) method⁴⁰ with GAMESS program.⁴¹ It should be mentioned that MP2 overestimates the interaction energies relative to CCSD(T) results and this overestimation can be remedied by using SCS-MP2 or a dispersion-based DFT method.^42,43

Molecular electrostatic potentials (MEPs) on the 0.001 electrons bohr⁻³ contour of the electronic density were calculated with the Wave Function Analysis-Surface Analysis Suite (WFA-SAS) program⁴⁴ at the MP2/aug-cc-pVDZ level. To get a deeper insight into the interaction nature of these complexes in the light of charge transfer and orbital interactions, we performed natural bond orbital (NBO) analyses at the HF/aug-cc-pVTZ(PP) level using NBO 3.1 version⁴⁵ implemented in Gaussian 09. The wavefunctions at the MP2/aug-cc-pVDZ-PP level were used to perform topological analyses for these complexes including both Atoms In Molecules (AIM) and non-covalent interaction (NCI). Electron density, Laplacian, and energy density at bond critical points (BCPs) were analyzed with AIM2000.⁴⁶ NCI maps were plotted with VMD program.⁴⁷

3. Results and discussion

3.1 Two types of interactions

Fig. 1 depicts the MEP maps of C₂H₃Br and C₂H₃Au. It is evident from Fig. 1 that the MEPs on the Br and Au atomic surfaces exhibit a feature of anisotropic distribution: positive MEPs of the Br and Au atoms in the direction opposite to the bonded carbon atom, but negative ones in most other directions, especially along the C–Br and C–Au bonds, respectively. Thus, the Br and Au atoms could serve as both a Lewis acid and a base simultaneously. Furthermore, the positive region of MEPs on the Au atom is larger than that on the Br atom and the negative one on the former is smaller than that on the latter atom (Fig. 1). This indicates that the Au atom is a stronger Lewis acid and the Br atom is a stronger Lewis base. The most positive (V_max) and negative (V_min) MEPs on the halogen and Au atoms in compounds R′X (R′ = CH₃, C₂H₃, C₂H, and CF₃) and RAu (R = CH₃, C₂H₃, and C₂H) are collected in Table 1. It is immediate from Table 1 that for the compounds with the same R′, the value of V_max on the halogen atom increases in the order of Cl < Br < I; and for the ones with the same halogen atom, V_max becomes more positive in the order of R′ = CH₃ < C₂H₃ < C₂H and CH₃ < CF₃, respectively. On the contrary, the value of V_min on the halogen atom becomes more negative in an opposite order. This indicates that the MEPs of the halogen atom depend on its nature and the electron-withdrawing ability of the substituents adjoined with it, that is, the value of V_max on the halogen atom becomes more positive as the halogen is more polarizable and R′ group is more electron-withdrawing. This is consistent with the results of Politzer et al.⁴⁸ Both V_max and V_min on the Au atom are affected by the similar hybridization effect with those on the halogen atom, where the most electron-withdrawing sp-hybridized carbon substituent gives rise to the large V_max. There are some abnormal observations that no positive and negative MEPs are found for the Cl and Au atoms in CH₃Cl and C₂HAu, respectively. We attribute this to the higher electronegativity and lower polarizability of Cl atom (compared with that of Br and I) for the former case, and the stronger electron-withdrawing sp-hybridized C₂H substituent (compared with that of C₂H₃ and CH₃) for the latter.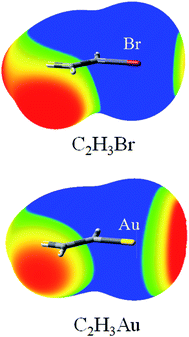

Fig. 1 MEP maps of C₂H₃Br and C₂H₃Au. Blue, less than 0 eV; green, between 0 and 0.05 eV; yellow, between 0.05 and 0.02 eV; red, greater than 0.1 eV.

Table 1 The most positive (V_max, eV) and negative (V_min, eV) MEPs on the halogen and Au atoms calculated at the MP2/aug-cc-pVDZ level

	Vmax	Vmin
CH3Cl	−0.002	−0.027
CH3Br	0.007	−0.025
CH3I	0.022	−0.019
CF3Cl	0.040	0.000
CF3Br	0.047	−0.000
CF3I	0.051	−0.000
C2H3Cl	0.008	−0.023
C2H3Br	0.016	−0.022
C2H3I	0.028	−0.016
C2HCl	0.037	−0.006
C2HBr	0.047	−0.007
C2HI	0.055	−0.004
CH3Au	0.064	−0.015
C2H3Au	0.075	−0.001
C2HAu	0.152	0.048

---

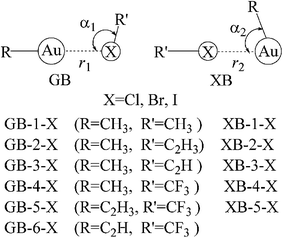
Upon the basis of the anisotropic distribution of MEPs on the Au and X atoms, two types of complex structures between gold and halogen compounds are designed (Fig. 2). Both structures are represented as GB and XB, respectively. In the GB structure, the Au atom acts as the Lewis acid and the X atom is the Lewis base, and the reverse roles are found for the Au and X in the XB structure. Both types of the interactions exist for most complexes with the exception that only GB pattern is obtained for C₂HAu, due to the absence of negative MEPs on the Au atomic surface. Actually, in the optimization of halogen bonded structure of CF₃X⋯AuCCH, it is changed to be the corresponding gold bonded one. Interestingly, XB interaction of CH₃Cl⋯AuCH₃ (XB-1-Cl in Fig. 2), where CH₃Au acts as the Lewis base and CH₃Cl is the Lewis acid, is obtained even the σ-hole is not found on the Cl atom in CH₃Cl. This suggests that there is another type of interaction with the physical picture different from the σ-hole one in the XB structure. Similarly, there is no negative MEPs on the X atom in CF₃X due to the strong electron-withdrawing group CF₃, but GB interaction in CH₃Au⋯XCF₃ (GB-4-X in Fig. 2) is strong enough, indicating that electrostatic interaction is not the only determining factor in the stability of GB structure. We will discuss this in detail in the following section.

Fig. 2 Diagrams of two types of structures.

Table 2 presents the binding distance, the angle along the interaction groups (see the definition in Fig. 2), and the interaction energy in the complexes. The angle R–Au⋯XR′ in the geometries of XBs is smaller than RAu⋯X–R′ in GBs (in context, the angle refers to the bold-font part), and most of the former angle is smaller than 90°, which provides a close contact between X and R groups. In combination with the MEPs of R′X and RAu in Fig. 1, we deduce that the electrostatic attractive interactions exist between the negative MEPs of X in R′X and the positive ones of the R group in RAu. The angle R–Au⋯XR′ in the XB structure becomes larger in the order of Cl < Br < I and CH₃ < C₂H₃ < C₂H, where the influence of the halogen atom is more remarkable than that of the R′ group (Table 1). Both variation trends related with X and R′ groups are consistent with the magnitude of V_min on the X atom of XR′ (Table 1). The most negative MEPs of Cl atom in R′Cl (R′ = CH₃, C₂H₃, and C₂H) indicate that the electrostatic interaction between Cl^δ− of R′Cl and R^δ+ group of RAu is the strongest one, which results in the smallest angle of R–Au⋯ClR′. On the other hand, the angle RAu⋯X–R′ in the geometries of GBs is larger than 90°. In contrast to the electrostatic interaction between X of R′X and R of RAu in XB, instead there is a strong coulomb repulsive interaction between the negative MEPs of X in R′X and the negative ones along the R–Au bond in RAu. As a result, the angle RAu⋯X–R′ in GBs becomes larger in the order of I < Br < Cl, which is in contrast with the variation trend of R–Au⋯XR′.

Table 2 Binding distances (r, Å), angles (α, deg), and interaction energy corrected for BSSE (ΔE, kcal mol⁻¹) in the complexes at the MP2/aug-cc-pVTZ level

	r1	α1	ΔE		r2	α2	ΔE
GB-1-Cl	2.397	101	−17.55	XB-1-Cl	3.467	74	−1.66
GB-1-Br	2.476	98	−19.71	XB-1-Br	3.357	79	−2.32
GB-1-I	2.594	96	−22.69	XB-1-I	3.225	89	−3.59
GB-2-Cl	2.404	101	−15.80	XB-2-Cl	3.456	75	−1.84
GB-2-Br	2.480	98	−18.22	XB-2-Br	3.359	79	−2.51
GB-2-I	2.596	97	−21.52	XB-2-I	3.233	88	−3.77
GB-3-Cl	2.430	104	−11.26	XB-3-Cl	3.373	77	−2.33
GB-3-Br	2.491	102	−14.10	XB-3-Br	3.268	81	−3.24
GB-3-I	2.593	101	−18.21	XB-3-I	3.164	88	−4.97
GB-4-Cl	2.416	103	−11.50	XB-4-Cl	3.355	77	−2.24
GB-4-Br	2.481	100	−14.57	XB-4-Br	3.234	82	−3.20
GB-4-I	2.589	97	−18.51	XB-4-I	3.100	91	−5.15
GB-5-Cl	2.400	103	−12.57	XB-5-Cl	3.377	82	−2.38
GB-5-Br	2.469	100	−15.73	XB-5-Br	3.214	90	−3.35
GB-5-I	2.580	97	−19.71	XB-5-I	3.061	98	−5.38
GB-6-Cl	2.329	104	−21.45
GB-6-Br	2.410	100	−25.25
GB-6-I	2.532	97	−29.93

---

The binding distances in XBs and GBs are longer in the order of I < Br < Cl and Cl < Br < I, respectively. Similarly, the trend of the binding distance in XBs could be demonstrated by the electrostatic interactions between the positive MEPs of X and the negative ones of Au, as well as between the positive MEPs of Au and the negative ones of X in GBs. For instance, the largest positive MEP of I atom in R′I gives rise to the strongest electrostatic interaction between I and Au in XBs, which results in the shortest binding distances in complexes R′I^δ+⋯^δ−AuR compared to other complexes involving Cl and Br atoms. It is obvious from Table 2 that the binding distances in GBs are shorter by ∼1 Å than that in XBs. Such significant difference is correlated with the stronger electrostatic interaction between the positive MEP of Au and the negative one of X in GB than that between the negative MEP of Au and the positive one of X in XB, where the positive MEP of Au is remarkably high (Table 1). Partially, this could also explain the higher interaction energy of GBs than that of XBs. The higher interaction energy suggests that organic gold and halogen compounds prefer to form the GB structures rather the XB ones. With the increase of the halogen atomic number, the interactions of both GBs and XBs become stronger. In the former case, the variation of interaction energy is consistent with the positive MEP on the Au atom and inconsistent with the negative MEP on the halogen atom, while the variation trend for the latter is in agreement with the positive MEP on the halogen atom and not with the negative MEP on the Au atom. This result indicates that the Lewis acid plays a more important role in GB and XB than the Lewis base, similar with that in hydrogen bonds.⁴⁹ The interaction energy of GB in CH₃Au⋯XCH₃ (GB-1-X in Fig. 2) is more negative than that in CH₃Au⋯H₂O complex (−17.20 kcal mol⁻¹),¹⁸ indicating that the heavier halogen atom is a stronger Lewis base than the oxygen atom in GBs. This is different from that in hydrogen bonds, in which the oxygen atom is a stronger Lewis base than the heavier halogen atom.⁵⁰ Generally, the electrostatic interaction is dominant in the formation of strong hydrogen bonds.⁵¹ However, in GB interactions, we predict that there are other types of interaction components besides the electrostatic one, which will be discussed in the Section 3.7.

3.2 Substituent and hybridization effects

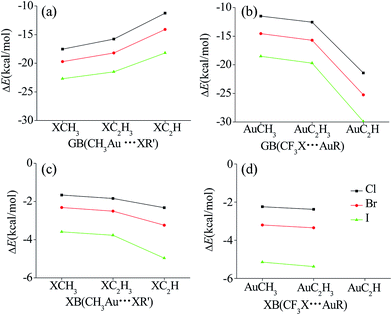
In order to enhance the strength of the XB interaction, we replaced the CH₃ group in CH₃X by CF₃, which is a strong electron-withdrawing group. The XB interaction in CH₃Au⋯XCF₃ (XB-4-X in Fig. 2) becomes stronger than that in CH₃Au⋯XCH₃ (XB-1-X in Fig. 2), characterized with a shorter binding distance and more negative interaction energy for the former structure. The enhancement of XB interaction due to the electron-withdrawing group CF₃ in CF₃X is also related with the nature of X since the increased magnitude of XB interaction energy grows up in the order of X = Cl (−0.58 kcal mol⁻¹) < Br (−0.88 kcal mol⁻¹) < I (−1.56 kcal mol⁻¹). The change of Au⋯X distance in XB is also prominent, shortened by 0.112–0.125 Å in CH₃Au⋯XCF₃. This is due to the large electron-withdrawing ability of CF₃, which significantly increases the positive MEPs of X atom in CF₃X. As a consequence, the electrostatic attractive interaction between X and Au becomes larger, resulting in the short binding distance in CH₃Au⋯XCF₃. By analogy, the decrease of the negative MEPs of X in CF₃X could illustrate the increase of the angle H₃C–Au⋯XCF₃ (XB-4-X in Fig. 2) compared with that in H₃C–Au⋯XCH₃ (XB-1-X). On the contrary, the interaction of GB in GB-4-X is weakened with a longer binding distance and less negative interaction energy. The longer binding distance of GB in CH₃Au⋯XCF₃ is ascribed to the decrease of electrostatic interaction between Au and X, resulting from the decrease of the negative MEPs on X of CF₃X. The decreased magnitude of GB interaction energy is 6.05 kcal mol⁻¹ for CF₃Cl, 5.14 kcal mol⁻¹ for CF₃Br, and 4.18 kcal mol⁻¹ for CF₃I, which is reverse to the increased magnitude of XB interaction energy. Therefore, both types of interactions consisted of the compounds RAu and R′X exhibit different properties. The same substituents of R′X compound lead to a reverse variation trend of the properties for two types of the complexes.

Fig. 3 depicts the effect of spⁿ-C hybridization in R and R′ groups adjoined with atoms Au and X on the interaction energies of GBs and XBs. As the spⁿ-C hybridization in R′X varies from C(sp³) through C(sp²) to C(sp), the interaction energy of GBs becomes less negative in the GB complexes of CH₃Au⋯XR′ (Fig. 3a), while on the contrary, it becomes more negative for the XB complexes of R′X⋯AuCH₃ (Fig. 3c). The R′ group of spⁿ-C hybridization is related with its ability of electron-withdrawing, which is in the order of sp-C > sp²-C > sp³-C. This leads to the V_min value on the halogen atom becoming less negative in the order of CH₃X < C₂H₃X < C₂HX (Table 1). As a consequence, the electrostatic interaction (negative value) between Au and X decreases in the order of CH₃Au^δ+⋯^δ−XCH₃ < CH₃Au^δ+⋯^δ−XC₂H₃ < CH₃Au^δ+⋯^δ−XC₂H. This well demonstrates the variation of the interaction energy with different R′ groups in CH₃Au⋯XR′ (Fig. 3a). In a similar manner, we could explain the trend of interaction energy for the GB complexes in RAu^δ+⋯^δ−XCF₃ (Fig. 3b). On the other hand, the effect of the C hybridization on the strength of XB is also related to the nature of X, and the interaction becomes stronger for the heavier halogen atom. With the same change of the C hybridization in RAu, the interaction energy of GB is more negative in the CF₃X complexes (Fig. 3b), and that of XB is also more negative although its change is very small (Fig. 3d). The former is consistent with the positive MEP on the Au atom in RAu, while the latter is inconsistent with the negative MEP on the Au atom. One can also see that the effect of the C hybridization in RAu on the strength of GB is greater than that in R′X on the XB strength. The hybridization effect in XBs and GBs is similar to that in hydrogen bonds.⁵²

Fig. 3 Dependence of interaction energy of GB and XB on the C hybridization in the complexes (a) (GB-1-X, GB-2-X, GB-3-X), (b) (GB-4-X, GB-5-X, GB-6-X), (c) (XB-1-X, XB-2-X, XB-3-X), and (d) (XB-4-X, XB-5-X).

3.3 AIM and NCI analyses

The existence of GBs and XBs is further characterized with the presence of BCPs between Au and X atoms. Electron density (ρ), Laplacian (∇²ρ), and energy density (H) at the intermolecular BCPs of the complexes are listed in Table 3. It has been confirmed that the type of interactions can be classified in the light of the sign of ∇²ρ and H.⁵³ For the halogen bond with chlorine and bromine as the Lewis acid, both ∇²ρ and H are positive, corresponding to a purely closed–shelled interaction, however, for the halogen bond with iodine as the Lewis acid, ∇²ρ is positive and H is negative, indicating a partially covalent interaction.⁵³ We found that all GB complexes have a positive ∇²ρ and a negative H at the BCPs. Thus, in combination with the high interaction energies as discussed above, GB interactions have the partially covalent nature. GB has a much larger ρ than XB, which is consistent with the strengths of GB and XB interactions. The electron density at the BCPs between Au and X atoms in GBs is out of the range of 0.002–0.04 au suggested for hydrogen bonds.⁵⁴ This confirms the partially covalent nature of GB interactions, which differs from that of hydrogen bonds. Fig. 4 presents the linear relationship between the electron density and the binding distance in the complexes of GBs and XBs. The linear correlation coefficient for this dependence amounts to 0.98–0.99. This shows that the strengths of both GB and XB can be estimated with the electron density at the X⋯Au BCP.

Table 3 Electron density (ρ, au), Laplacian (∇²ρ, au), and energy density (H, au) at the intermolecular bond critical points (BCPs) in the complexes at the MP2/aug-cc-pVDZ level

	ρ	∇^2ρ	H
GB-1-Cl	0.0757	0.2694	−0.0191
GB-1-Br	0.0767	0.2097	−0.0227
GB-1-I	0.0761	0.1311	−0.0266
GB-2-Cl	0.0740	0.2681	−0.0181
GB-2-Br	0.0756	0.2107	−0.0220
GB-2-I	0.0755	0.1338	−0.0261
GB-3-Cl	0.0685	0.2597	−0.0148
GB-3-Br	0.0728	0.2135	−0.0201
GB-3-I	0.0751	0.1398	−0.0257
GB-4-Cl	0.0708	0.2687	−0.0159
GB-4-Br	0.0746	0.2184	−0.0211
GB-4-I	0.0757	0.1413	−0.0262
GB-5-Cl	0.0735	0.2720	−0.0176
GB-5-Br	0.0766	0.2173	−0.0225
GB-5-I	0.0772	0.1373	−0.0274
GB-6-Cl	0.0875	0.3074	−0.0271
GB-6-Br	0.0879	0.2308	−0.0310
GB-6-I	0.0858	0.1339	−0.0343
XB-1-Cl	0.0092	0.0289	0.0009
XB-1-Br	0.0135	0.0384	0.0007
XB-1-I	0.0218	0.0520	−0.0009
XB-2-Cl	0.0094	0.0295	0.0009
XB-2-Br	0.0135	0.0382	0.0007
XB-2-I	0.0215	0.0512	−0.0008
XB-3-Cl	0.0107	0.0343	0.0010
XB-3-Br	0.0155	0.0448	0.0006
XB-3-I	0.0239	0.0560	−0.0014
XB-4-Cl	0.0114	0.0352	0.0010
XB-4-Br	0.0171	0.0467	0.0004
XB-4-I	0.0279	0.0596	−0.0025
XB-5-Cl	0.0109	0.0338	0.0010
XB-5-Br	0.0178	0.0484	0.0003
XB-5-I	0.0301	0.0627	−0.0031

---

Fig. 4 Relationship between the electron density and the binding distance in the complexes of GB (a) and XB (b).

Non-covalent interaction (NCI) analysis is a good supplement to AIM because it can detect some weak interactions, such as van der Waals interactions, and provide the information on repulsive interactions.^55,56 To our knowledge, this technique has not been carried out for Au-bond interaction so far. Thus, we are interested in the new insights that NCI method can provide for the complexes GBs and XBs. NCI involves the reduced density gradient (RDG) and the electron density (ρ). RDG is defined as:

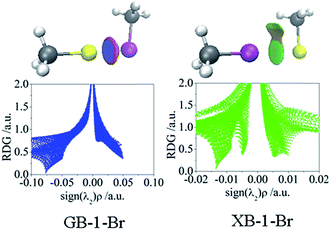
Non-covalent interaction analysis for the Au⋯Br interactions of CH₃Au⋯BrCH₃ (GB-1-Br in Fig. 2) and CH₃Br⋯AuCH₃ (XB-1-Br in Fig. 2) is depicted in Fig. 5, and the analysis for the Au⋯X interactions of all complexes (Fig. 2) is shown in Fig. S1 and S2.† The Au⋯X interactions in all GBs are commonly characterized by a large blue disc surrounded by a red ring of depletion, indicating a strong attractive interaction and a repulsive interaction, respectively. A similar phenomenon has been observed for the Zn–N and Zn–O bonds in Zn^II complexes with 2,2′-bipyridyl.⁵⁷ This repulsive force accounts for the coulomb repulsive interaction between the negative MEPs of Au and the ones along the X–R′ as discussed above.

Fig. 5 Gradient isosurfaces (s = 0.1 au) and plots of the reduced density gradient (RDG) versus the electron density multiplied by the sign of the second Hessian eigenvalue in GB-1-Br and XB-1-Br. Blue, green, orange, and red areas correspond to strong attractive, weak attractive, weak repulsion, and strong repulsion interactions, respectively.

Two low-density, low-gradient spikes are observed for most XB structures except CH₃I⋯AuCH₃ (XB-1-I), C₂H₃I⋯AuCH₃(XB-2-I), C₂HI⋯AuCH₃(XB-3-I), and CF₃I⋯AuCH₃(XB-4-I), corresponding to the halogen bond and the X⋯H interaction between the X atom and the hydrogen atom of R in RAu. The former interaction has a ρ value larger than 0.01 au, indicative of high electrostatic attraction, whereas the latter one shows the characteristics with a high dispersive interaction (ρ < 0.01 au).⁵⁸ Evidently, the weak X⋯H interaction cannot be detected in the AIM maps but could be with the NCI method, and this attractive force results in the small angle R–Au⋯X in XBs (<90°). Four complexes XB-1-I, XB-2-I, XB-3-I, and XB-4-I exhibit a similar feature of NCI with GBs, even the former ones have a lower density.

3.4 NBO analysis

Table 4 presents the second-order perturbation energies (E) in the GBs and XBs. GB is analyzed with two orbital interactions LP_X → BD^*_C–Au and LP_X → LP^*_Au, where LP_X denotes the lone pair orbital of the halogen X, BD^*_C–Au is the C–Au anti-bonding orbital, and LP^*_Au is the lone pair anti-bonding orbital of the gold atom. It is necessary to point out that there are other orbital interactions in GBs. Because they contribute little to the interactions between Au and X, thus we did not discuss them here. XB is also analyzed with two orbital interactions LP_X → LP^*_Au and LP_Au → BD^*_C–X, where LP_Au denotes the lone pair orbital of Au and BD^*_C–X is the C–X anti-bonding orbital. It is obvious from Table 4 that E(LP_X → BD^*_C–Au)_GB is remarkably higher than E(LP_X → LP^*_Au)_GB in most GB complexes except that of C₂H–Au⋯XCF₃ (GB-6-X in Fig. 2), and both terms are important contributions for the strong GB interactions. For the same compound RAu, E(LP_X → LP^*_Au)_GB becomes higher with the increase of X atomic number in R′X, while E(LP_X → BD^*_C–Au)_GB does not have such regular variation, where E(LP_Cl → BD^*_C–Au)_GB is two or three times higher than E(LP_Br → BD^*_C–Au)_GB and E(LP_I → BD^*_C–Au)_GB in most GBs but not in complexes CH₃–Au⋯XC₂H and C₂H–Au⋯XCF₃. The large orbital interaction is consistent with the large interaction energy and the covalent nature of GBs. The orbital interactions in XBs are much weaker than those in GBs, and the LP_Au → BD^*_C–X orbital interaction is predominant in XBs, while the LP_X → LP^*_Au orbital interaction is insignificant in most XBs except that in the complex C₂H₃Au⋯I–CF₃.

Table 4 Second-order perturbation energies (E, kcal mol⁻¹), charge transfer (CT, e), and Wiberg bond index (WBI) in the complexes at the HF/aug-cc-pVDZ level^a

	E1	E2	CT	WBI		E2	E3	CT	WBI
a Note: E1, E2, and E3 are the stabilization energies due to the orbital interactions of LPX → BD^*C–Au, LPX → LP^*Au and LPAu → BD^*C–X, respectively. The charge transfer is the sum of atomic charge on the Lewis acid in the complexes.
GB-1-Cl	129.26	12.89	0.163	0.27	XB-1-Cl	0.14	0.74	−0.003	0.02
GB-1-Br	47.05	15.27	0.206	0.33	XB-1-Br	0.17	1.97	−0.002	0.04
GB-1-I	57.55	21.89	0.263	0.41	XB-1-I	2.28	5.88	−0.003	0.09
GB-2-Cl	122.45	15.55	0.154	0.26	XB-2-Cl	0.08	0.83	−0.002	0.02
GB-2-Br	42.60	27.59	0.196	0.32	XB-2-Br	0.14	2.03	0.000	0.03
GB-2-I	57.44	29.43	0.255	0.41	XB-2-I	0.51	5.68	0.004	0.09
GB-3-Cl	99.18	10.72	0.127	0.22	XB-3-Cl	0.06	1.29	0.002	0.02
GB-3-Br	135.89	16.71	0.170	0.29	XB-3-Br	0.17	3.06	0.008	0.04
GB-3-I	55.36	27.60	0.232	0.38	XB-3-I	0.26	7.39	0.021	0.10
GB-4-Cl	116.44	17.58	0.144	0.24	XB-4-Cl	0.07	1.34	0.003	0.02
GB-4-Br	48.87	26.10	0.187	0.31	XB-4-Br	0.13	3.63	0.012	0.04
GB-4-I	60.59	33.36	0.245	0.40	XB-4-I	2.40	10.72	0.027	0.11
GB-5-Cl	123.46	14.67	0.150	0.25	XB-5-Cl	0.09	1.20	0.002	0.02
GB-5-Br	45.81	32.91	0.195	0.32	XB-5-Br	0.20	3.44	0.008	0.05
GB-5-I	59.55	30.63	0.253	0.41	XB-5-I	7.90	10.19	0.017	0.13
GB-6-Cl	31.41	78.68	0.178	0.32
GB-6-Br	41.02	99.42	0.225	0.39
GB-6-I	48.73	131.41	0.288	0.49

---

The charge transfer and Wiberg bond index (WBI) of the Au⋯X interaction in the complexes are also presented in Table 4. It is interesting to note that the charge transfer in GBs is much greater than that in XBs. The positive charge transfer in GBs confirms the roles of the Lewis acid and base for the Au and X atoms, respectively. The charge transfer in GBs is in the range of 0.127–0.288e, larger than those in hydrogen bonds. In contrast, the charge transfer in XBs is very small, and even it is close to zero in some complexes, indicating that the charge transfer plays a minor role in XBs.

In GBs, WBI varies from 0.22 in CH₃Au⋯ClC₂H (GB-3-Cl in Fig. 2) to 0.49 in C₂HAu⋯ICF₃ (GB-6-I in Fig. 2), where the bond order of Au⋯I interaction in the latter is close to one-half single bond, giving a further evidence for the partially covalent nature of GBs. In XBs, WBI is much smaller than that in GBs, with the largest WBI at the Au⋯I interaction close to 0.1.

3.5 Electron density shift

Fig. 6 and 7 illustrate the electron density difference of the RAu⋯BrR′ complexes in GBs and XBs, respectively, which is generated by the subtraction of the electron density in the complex from the sum of the electron densities of the isolated subsystems, of which the structure is the one in the optimized complex. The electron density shifts in all complexes are shown in Fig. S3 and S4.† For GB complexes, there are three common features: (1) there is a region (blue) of density depletion on the Au atom, (2) a density loss on both sides of the halogen atom which is toward and opposite to the Au atom, respectively; (3) there is an area (red) of density accumulation between the Au and X atoms. These features are different from those observed in hydrogen bonds,⁵⁹ where the Lewis base atom has an increased density and no buildup of electron density is present between the Lewis base atom and the proton.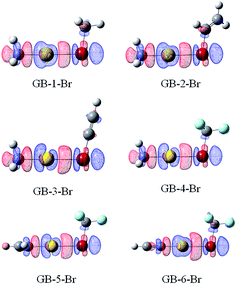

Fig. 6 Electron density shifts of GB–Br (iso = 0.002). Red regions indicate increased electron density, while blue regions represent decreased electron density.

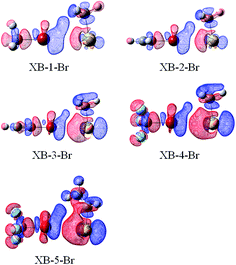Fig. 7 Electron density shifts of XB–Br (iso = 0.0002). Red regions indicate increased electron density, while blue regions represent decreased electron density.

For R′Br in XBs, density depletion is observed on the σ-hole of the halogen atom, which is slightly distorted towards the R group of RAu. This supports the weak steric interactions between the halogen atom and the R group of RAu. It is also found that there is a buildup of the electron density on the X lone pair, mainly at one side of X facing to the R group in RAu. Simultaneously, electron loss occurs on the hydrogen atoms, facing to the X atom, of R in RAu. This indicates that the X⋯R attractive interaction between the X atom of R′X and the R group of RAu in the XB structures is actually the X⋯H interaction. On the other hand, the Au atom has a significant density accumulation on its lone pair in RAu. It is evident that the density shifts in the XB complexes are not prominent than those in the GBs, consistent with the strengths of XBs and GBs.

3.6 Energy decomposition

A decomposition of interaction energy provides a valuable insight in understanding the physical pictures of GBs and XBs. The physical components from GAMESS including electrostatic (ES), exchange (EX), repulsion (REP), polarization (POL), and dispersion (DISP) energies for some representative complexes are presented in Table 5. In GBs, the remarkable overlap of molecular orbitals between both organic compounds results in a large EX and also a much larger REP. The magnitude of POL is close to that of ES, and the former is a little larger than the latter for the strong GBs, indicating that both components make a comparable contribution to the total interaction energy of GB interactions. The large POL suggests that the orbitals undergo a significant change in their shapes, a typical character in the formation of covalent bonds, confirming the partially covalent nature of GBs. In addition, the DISP contribution to GBs is also not negligible.

Table 5 Electrostatic energy (ES), exchange energy (EX), repulsion energy (REP), polarization energy (POL), dispersion energy (DISP), and interaction energy (E_int) in the selected complexes at the MP2/aug-cc-pVTZ level. All are in kcal mol⁻¹

	ES	EX	REP	POL	DISP	Eint
GB-1-Cl	−32.44	−64.52	118.27	−27.14	−11.71	−17.53
GB-1-Br	−35.53	−73.07	133.85	−31.49	−13.08	−19.31
GB-1-I	−36.94	−83.13	151.10	−38.21	−14.84	−22.03
GB-2-Br	−33.22	−70.85	129.87	−30.61	−13.06	−17.87
GB-3-Br	−26.25	−63.59	116.96	−27.91	−12.82	−13.60
GB-4-Br	−28.82	−67.97	125.17	−29.06	−13.73	−14.40
GB-5-Br	−28.08	−66.81	123.15	−30.56	−13.59	−15.89
GB-6-Br	−29.24	−68.96	128.85	−36.94	−18.32	−24.61
XB-1-Cl	−2.19	−8.07	13.39	−0.81	−4.01	−1.69
XB-1-Br	−4.67	−13.98	23.72	−1.71	−5.63	−2.27
XB-1-I	−9.27	−26.19	45.2	−4.97	−8.16	−3.39
XB-2-Br	−4.67	−13.53	23.14	−1.69	−5.69	−2.45
XB-3-Br	−5.81	−14.69	26.04	−2.44	−6.25	−3.16
XB-4-Br	−6.42	−16.28	28.95	−2.99	−6.39	−3.13
XB-5-Br	−6.43	−17.35	30.65	−3.19	−6.99	−3.30

---

Similarly, both EX and REP are relatively the largest in XBs. In contrast to that in GBs, the POL term is the smallest in XBs, even it becomes larger for the stronger XBs. DISP component is comparable with ES in XBs, and the former is larger than the latter in the weak XBs. This indicates that the Au⋯X interactions with moderate or strong strength is dominated by electrostatic and dispersion energies, which is different from conventional halogen bonds with the electrostatic nature.⁴⁸

When the CH₃ group in CH₃Br is replaced by CF₃, ES in GBs is decreased by 18.9%, POL by 7.7%, and EX by 7.0%, while DISP has a small increase in magnitude, thus the substitution effect of CF₃ in the electron donor of GBs is governed mainly by electrostatic interaction. When the same substitution occurs in XBs, POL is increased by 74.8%, ES by 37.5%, EX by 16.4% and DISP by 13.5%, indicating that the substitution effect of CF₃ in the electron acceptor of XB is controlled jointly by polarization and electrostatic interactions. It is obvious from Table 5 that the substituent has a greater effect on the each energy component in XBs than that in GBs.

3.7. CSD search

The Au⋯X (X = Cl, Br, and I) interactions exist in a number of crystal structures, although no roles of Lewis acid and base are identified for both gold and halogen atoms in these crystal structures. It would be very helpful to find supporting structural information from accurately determined molecule structures deposited in the CSD. To obtain experimental evidence for the Au⋯X interactions, we performed a survey of the CSD (version 5.33, updates November 2011).⁶⁰ Only crystal structures with no disorder and errors as well as R-factor less than 0.1 were considered. Based on the van der Waals radii (Au, 1.66 Å; Cl, 1.75 Å; Br, 1.85 Å; I, 1.95 Å)⁶¹ and the covalent radii (Au, 1.24 Å; Cl, 0.99 Å; Br, 1.14 Å; I, 1.33 Å),⁶² the criteria of the intermolecular distances are chosen for Au⋯Cl (2.23–3.41 Å), Au⋯Br (2.38–3.51 Å), and Au⋯I (2.57–3.64 Å). About 142 crystal structures are found and the proportions for Au⋯X (X = Cl, Br, and I) interactions are shown in Fig. 8. Obviously, it is found that the structures with Au⋯Cl interactions are more abundant than those with Au⋯Br and Au⋯I interactions in crystal structures.

Fig. 8 Respective proportions of Au⋯X (X = Cl, Br, I) interactions in the CSD search results and three crystal structures involving Au⋯X (X = Cl, Br, I) interactions. Distances are in the angstroms.

Three selected crystal structures searched from the CSD (codes CAGCOE,⁶³ GUBVAB,⁶⁴ ZOLKUG⁶⁵) are presented in Fig. 8. In the CAGCOE structure, two almost parallel Au⋯Cl contacts with a distance of 3.999 Å are formed between two molecules, in which both Cl atoms are the Lewis base. The second structure selected is GUVBAB that has two Au⋯Br interactions (3.435 Å and 3.443 Å). The Br atom acts as the role of Lewis acid in the Au⋯Br interaction with a shorter distance but the role of Lewis base in the Au⋯Br interaction with a longer distance. In crystal structure of ZOLKUG, the role of I atom in the Au⋯I interaction is similar to that in the stronger Au⋯Br interaction.

4. Conclusion

Complexes between the organic gold compound RAu (R = CH₃, C₂H₃, and C₂H) and the organic halogen compound R′X (R′ = CH₃, C₂H₃, C₂H, and CF₃; X = Cl, Br, and I) have been studied at the MP2/aug-cc-pVTZ(PP) level. The results of this study support the following statements:

(1) There are two types of Au⋯X interactions between RAu and R′X, denoted by GB and XB, due to the dual roles of Lewis acid and base for both Au and X atoms. In GB, the Au in RAu is the Lewis acid and X in R′X is the Lewis base, while the reverse roles are found in XB. The existence and characterization of the GB and XB interactions are also confirmed by the NCI index in combination with the AIM graph.

(2) GBs are more favorable to be formed between the compounds of organic gold and halogen than XBs. GBs exhibit the nature of partially covalent interaction, having the large interaction energy, small binding distance, negative energy density, big charge transfer and orbital interactions. GB becomes stronger with the more polarizable halogen. Even the most negative MEP on the X atomic surface in CF₃X is very small, the binding energy of GB is also high. The Lewis acid plays a greater important role in the GB interactions than the Lewis base.

(3) Substitution and hybridization have similar effects on the strengths of both interactions with that on the hydrogen bonds. The hybridization effect is more prominent for GBs than XBs. The effect of the substitution and hybridization on the strength of XBs is related to the nature of X, where iodine bond is most affected.

(4) GB complexes present a different electron density shift from the hydrogen bonds. A density loss occurs on the Lewis base X atom, and more interestingly, the density accumulation is observed between X and Au atoms. The electrostatic interaction between X and H of R′ group in XB can also be detected with the electron density shift.

(5) Polarization energy has comparable contribution to GBs with electrostatic energy, while XB interaction is dominated by electrostatic and dispersion energies.

(6) CSD search shows the importance of Au⋯X interactions in crystal structures.

It is interesting to note that even the geometrical structures are similar for GB and XB, they exhibit significant differences in their features and especially in nature. This figures out the different roles of the weak intermolecular interaction with the same monomers in different spatial orientation.

Acknowledgements

This work was supported by the Graduate Innovation Foundation of Yantai University (YJSZ201410), the National Natural Science Foundation of China (21403127), the Outstanding Youth Natural Science Foundation of Shandong Province (JQ201006), and the Program for New Century Excellent Talents in University (NCET-2010-0923).

References

1. M. Haruta and M. Date, Appl. Catal., A, 2001, 222, 427–437.
2. A. S. K. Hashmi, Chem. Rev., 2007, 107, 3180–3211.
3. D. J. Gorin, B. D. Sherry and F. D. Toste, Chem. Rev., 2008, 108, 3351–3378.
4. E. Jimenez-Nunez and A. M. Echavarren, Chem. Rev., 2008, 108, 3326–3350.
5. A. Arcadi, Chem. Rev., 2008, 108, 3266–3325.
6. Z. G. Li, C. Brouwer and C. He, Chem. Rev., 2008, 108, 3239–3265.
7. H. Schmidbaur and A. Schier, Organometallics, 2010, 29, 2–23.
8. A. Corma, A. Leyva-Perez and M. J. Sabater, Chem. Rev., 2011, 111, 1657–1717.
9. A. S. K. Hashmi and G. J. Hutchings, Angew. Chem., Int. Ed., 2006, 45, 7896–7936.
10. R. Huschka, A. Barhoumi, Q. Liu, J. A. Roth, L. Ji and N. J. Halas, ACS Nano, 2012, 6, 7681–7691.
11. E. S. Kryachko and F. Remacle, Chem. Phys. Lett., 2005, 404, 142–149.
12. E. S. Kryachko and F. Remacle, Nano Lett., 2005, 5, 735–739.
13. E. S. Kryachko, A. Karpfen and F. Remacle, J. Phys. Chem. A, 2005, 109, 7309–7318.
14. N. Hanne and J. Martin, Angew. Chem., Int. Ed., 2006, 45, 4369–4371.
15. P. Neogrady, V. Kello, M. Urban and A. J. Sadlej, Int. J. Quantum Chem., 1997, 63, 557–565.
16. A. Avramopoulos, M. G. Papadopoulos and A. J. Sadlej, Chem. Phys. Lett., 2003, 370, 765–769.
17. Q. Z. Li, H. Li, R. Li, B. Jing, Z. B. Liu, W. Z. Li, F. Luan, J. B. Cheng, B. A. Gong and J. Z. Sun, J. Phys. Chem. A, 2011, 115, 2853–2858.
18. Q. Z. Li, H. Li, B. Jing, R. Li, Z. B. Liu, W. Z. Li, F. Luan, J. B. Cheng, B. A. Gong and J. Z. Sun, Chem. Phys. Lett., 2010, 498, 259–262.
19. H. Li, Q. Z. Li, R. Li, W. Z. Li and J. B. Cheng, J. Chem. Phys., 2011, 135, 074304.
20. P. Metrangolo, H. Neukirch, T. Pilati and G. Resnati, Acc. Chem. Res., 2005, 38, 386–395.
21. M. G. Chudzinski, C. A. McClary and M. S. Taylor, J. Am. Chem. Soc., 2011, 113, 10559–10567.
22. A. Caballero, F. Zapata, N. G. White, P. J. Costa, V. Félix and P. D. Beer, Angew. Chem., Int. Ed., 2012, 51, 1876–1880.
23. P. Auffinger, F. A. Hays, E. Westhof and P. S. Ho, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 16789–16794.
24. A. R. Voth, F. A. Hays and P. S. Ho, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6188–6193.
25. H. Matter, M. Nazare, S. Gussregen, D. W. Will, H. Schreuder, A. Bauer, M. Urmann, K. Ritter, M. Wagner and V. Wehner, Angew. Chem., Int. Ed., 2009, 48, 2911–2916.
26. P. Metrangolo, F. Meyer, T. Pilati, G. Resnati and G. Terraneo, Angew. Chem., Int. Ed., 2008, 47, 6114–6127.
27. P. Metrangolo, Y. Carcenac, M. Lahtinen, T. Pilati, K. Rissanen, A. Vij and G. Resnati, Science., 2009, 323, 1461–1464.
28. C. B. Aakeröy, N. R. Champness and C. Janiak, CrystEngComm, 2010, 12, 22–43.
29. S. Walter, F. Kniep, E. Herdtweck and S. Huber, Angew. Chem., Int. Ed., 2011, 50, 7187–7197.
30. A. Bruckmann, M. A. Pena and C. Bolm, Synlett, 2008, 6, 900–902.
31. J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296.
32. P. Politzer, J. S. Murray and M. C. Concha, J. Mol. Model., 2007, 13, 643–650.
33. K. E. Riley, J. S. Murray, J. Fanfrlík, J. Řezáč, R. J. Solá, M. C. Concha, F. M. Ramos and P. Politzer, J. Mol. Model., 2011, 17, 3309–3318.
34. P. Politzer, P. Lane, M. C. Concha, Y. Ma and J. S. Murray, J. Mol. Model., 2007, 13, 305–311.
35. A. C. Legon, Angew. Chem., Int. Ed., 1999, 38, 2686–2714.
36. P. P. Zhou, W. Y. Qiu, S. Liu and N. Z. Jin, Phys. Chem. Chem. Phys., 2011, 13, 7408–7418.
37. D. Konkolewicz, S. Gaillard, A. G. West, Y. Y. Cheng, A. Gray-Weale, T. W. Schmidt, S. P. Nolan and S. Perrier, Organometallics, 2011, 30, 1315–1318.
38. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, T. Vreyen Jr, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Octhterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009.
39. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–558.
40. P. F. Su and H. Li, J. Chem. Phys., 2009, 13, 014102.
41. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. J. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363.
42. S. Grimme, J. Antony, T. Schwabe and C. Muck-Lichtenfeld, Org. Biomol. Chem., 2007, 5, 741–758.
43. B. M. Wong, J. Comput. Chem., 2009, 30, 51–56.
44. F. A. Bulat, A. Toro-Labbe, T. Brinck, J. S. Murray and P. Politzer, J. Mol. Model., 2010, 16, 1679–1691.
45. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
46. R. F. W. Bader, AIM2000 Program, v. 2.0, McMaster University, Hamilton, Canada, 2000.
47. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
48. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748–7757.
49. L. Bian, J. Phys. Chem. A, 2003, 107, 11517–11524.
50. E. S. Kryachko and T. Zeegers-Huyskens, J. Phys. Chem. A, 2002, 106, 6832–6838.
51. J. Graton, F. Besseau, A. Brossard, E. Charpentier, A. Deroche and J. Y. Le Questel, J. Phys. Chem. A, 2013, 117, 13184–13193.
52. S. Scheiner, S. J. Grabowski and T. Kar, J. Phys. Chem. A, 2001, 105, 10607–10612.
53. I. Rozas, I. Alkorta and J. Elguero, J. Am. Chem. Soc., 2000, 122, 11154–11161.
54. U. Koch and P. L. A. Popelier, J. Phys. Chem. A, 1995, 99, 9747–9754.
55. E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. T. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
56. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J. P. Piquemal, D. N. Beratan and W. T. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
57. I. Cukrowski, J. H. de Lange and M. Mitoraj, J. Phys. Chem. A, 2014, 118, 623–637.
58. K. E. Riley and P. Hobza, J. Chem. Theory Comput., 2008, 4, 232–242.
59. S. Scheiner and T. Kar, J. Phys. Chem. A, 2002, 106, 1784–1789.
60. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388.
61. A. Bondi, J. Phys. Chem., 1964, 68, 441–451.
62. P. Pyykkö and M. Atsumi, Chem.–Eur. J., 2009, 15, 186–197.
63. U. Siemeling, T. Klemann, C. Bruhn, J. Schulz and P. Štěpnička, Z. Anorg. Allg. Chem., 2011, 637, 1824–1833.
64. P. Chandraskaran, J. T. Mague and M. S. Balakrishna, Dalton Trans., 2009, 5478–5486.
65. Z. Assefa, B. G. McBurnett, R. J. Staples and J. P. Fackler, Inorg. Chem., 1995, 34, 4965–4972.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra13627f

---