Two series of novel 3D potentially porous heterometallic Cu–Ln coordination frameworks assembled by 3,4-pyridinedicarboxylic acid with different topologies and channels: syntheses, structures, luminescence and magnetic properties

Abstract

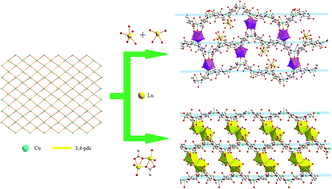
Self-assembly of rare earth salts, Cu(NO₃)₂ and 3,4-pyridinedicarboxylic acid (3,4-pdcH₂) resulted in the formation of two series of 3 d–4f heterometallic coordination polymers: [Ln₂Cu₃(3,4-pdc)₆(H₂O)₁₂]·mH₂O·nCH₃OH (Ln = Eu (1, m = 22, n = 0), Gd (2, m = 22, n = 0) and Tb (3, m = 15.5, n = 5)) and [LnCu(3,4-pdc)₂(OAc)(H₂O)₃]·8H₂O (Ln = Ho (4), Er (5)). Their structures have been determined by single-crystal X-ray diffraction analyses and further characterized by elemental analyses, IR spectra, PXRD and TGA. The structures of isomorphous complexes 1–3 (Form I) are constructed with irregular (4,4)-connected 2D [Cu₃(3,4-pdc)₆(H₂O)₃]_n sheets pillared by Ln(H₂O)₄, showing an intriguing 3D 3⁶·4¹⁸·5³·6 framework with the treatment of the Ln₂Cu₃ unit as an 8-connected node. Complexes 4 and 5 (Form II) are constructed with (4,4)-connected 2D [Cu(3,4-pdc)₂(H₂O)]_n sheets pillared by bimetallic units Ln₂(OAc)₂(H₂O)₄, exhibiting a fascinating 3D architecture with (4,8)-connected fluorite (4¹²·6¹²·8⁴)(4⁶)₂ topology. There exist different 1D channels in the polymers of Form I and Form II, in which solvent molecules are accommodated. Moreover, their luminescence and magnetic properties have been investigated.

---

Introduction

The rational design and construction of novel metal–organic frameworks (MOFs) has attracted great attention; MOFs with flexible or rigid microporous channels have potential applications in selective molecular recognition and separation,¹ physical gas storage,² sensors,³ ion-exchange⁴ and heterogeneous catalysis.⁵ Among these, there are extensive research interests in the assembly of 3d–4f heterometallic coordination polymers not only due to their fascinating topologies and intriguing architectures, but also their potential applications in magnetism, luminescent materials, adsorption and chemical sensing.⁶ The preparation of 3d–4f heterometallic microporous MOF is still a great challenge for the following reasons: (a) competitive reactions between transition and lanthanide metals chelated to the same ligand tends to homometallic complexes rather than heterometallic polymers; (b) the higher coordination numbers and versatile geometries of lanthanide frequently causes structural interpenetration that gives rise to a reduced cavity volume or even a nonporous structure.^5b,7

Although it is not yet possible to prepare fully predictable 3d–4f microporous MOFs, the selective combination of metal centers, bridging ligands and co-ligands is an effective strategy for rational design and creative synthesis of desired frameworks. Thus, in designing extended porous 3d–4f MOFs, judicious selection of the properties of ligands, such as shape, functionality, flexibility, symmetry, length, and substituent group is crucial to the construction of target polymers.⁸ Because multidentate ligands containing N and O atoms have different affinities to transition and lanthanide metal ions, a typical approach to construct 3d–4f MOFs is reacting 3d and 4f metallic ions with a multidentate bridging ligand containing both N- and O-donor atoms. And π-conjugated organic molecules are commonly used as linkers due to their rigidity, which often prevents interpenetration of the network, and the majority of them are based on rigid backbones functionalized with multicarboxylate groups or heterocyclic groups for metal–ligand coordination. Nitrogen-containing heterocyclic carboxylate, such as pyridine-carboxylic and imidazole-carboxylic acid, as multi donor ligands, have been demonstrated to be interesting structural and versatile building blocks for producing coordination polymers, and have also been picked out to synthesize 3d–4f polymers during the past few decades.^6a,c,7,9 3,4-Pyridinedicarboxylic acid (3,4-pdcH₂) is an efficient ligand, which contains a number of N or O coordination sites and rich coordination modes. Polymeric structures of 3,4-pdc complexes with alkaline, transition, and lanthanide metals were reported in which the 3,4-pdc ligand has shown good multi-connecting ability resulting in diversified structures.¹⁰ Whereas, complexes based on 3,4-pdc ligand containing both lanthanide and transition metals are still rare, only a series of Ln–Ag heterometallic coordination polymers constructed from 3,4-pdc ligand have been reported.^10e Herein, we report the syntheses, crystal structures, luminescence and magnetic properties of five heterometallic 3d–4f complexes [Eu₂Cu₃(3,4-pdc)₆(H₂O)₁₂]·22H₂O (1), [Gd₂Cu₃(3,4-pdc)₆(H₂O)₁₂]·22H₂O (2), [Tb₂Cu₃(3,4-pdc)₆ (H₂O)₁₂]·15.5H₂O·5CH₃OH (3), [HoCu(3,4-pdc)₂(OAc)(H₂O)₃]·8H₂O (4) and [ErCu(3,4-pdc)₂(OAc)(H₂O)₃]·8H₂O (5), in which two series of Cu–Ln polymers exhibit different topologies and potentially microporous channels.

Results and discussion

Syntheses

Acting as multi-dentate ligand, 3,4-pdc possesses the capability to bridge metal centers in various coordination modes, and we got potentially porous Cu–Ln 3D framework successfully. The hydrothermal method is a very popular synthetic technique in preparing porous MOFs, while it seemed inapplicable in this 3,4-pdc 3d–4f system. From the entropic point of view, synthesis at a higher temperature could reduce terminal ancillary ligands.⁷ Comparing with 2,n-pdc (n = 3–6), chelating ability of 3,4-pdc is weak, thus the high coordination number of lanthanide with water or other solvent molecules seems inevitable. For synthesizing the potentially porous framework under mild condition, diffusion method was used in the self-assembly process. The synthetic strategy employed for complexes 4 and 5 in Form II was triggered after complexes 1–3 in Form I had been structurally characterized. Seeing that crystalline isomorphous complexes of Ho(III) and Er(III) in Form I could not be obtain by the same diffusion method, which probably due to the difference of lanthanide ions, we wondered whether polymers with different 3D structure could be constructed by adding another auxiliary organic ligand to replace coordinated water molecules which located on Ln(III) ion. Acetate has been used extensively in coordination chemistry and could be introduced easily into the coordination polymers by using lanthanide acetate. In the self-assembly process, acetate combined with Ln(III) ion in starting material successfully remain in the final MOF and take place of some coordinated water molecules of Ln(III) ion, thus we got another series of potentially porous 3d–4f framework in Form II (Ln = Ho(III) or Er(III)). By contract, using lanthanide acetate of Eu, Gd and Tb as reactant, we could not get crystalline product suitable for X-ray analysis. Microcrystalline solid precipitated from solution were examined by PXRD, in which polymer in Form I existed in the mixture. The structural distinctions of Form I and Form II are tentatively attributed to the introduction of acetate and the influence of different Ln cations in the construction of MOFs. Complexes 1–5 are all stable in air at ambient temperature and are almost insoluble in common solvents such as water, alcohol, acetonitrile, chloroform, acetone, and toluene, being consistent with their polymeric nature.

Crystal structures of [Eu₂Cu₃(3,4-pdc)₆(H₂O)₁₂]·22H₂O (1), [Gd₂Cu₃(3,4-pdc)₆(H₂O)₁₂]·22H₂O (2) and [Tb₂Cu₃(3,4-pdc)₆(H₂O)₁₂]·15.5H₂O·5CH₃OH (3). The single-crystal X-ray analyses of complexes 1–3 reveal that they are isomorphous and crystallize in the same monoclinic space group P2₁/n, in which the complicated 3D structures are all built up with basic unit [Ln₂Cu₃(3,4-pdc)₆(H₂O)₁₂]. Thus, we choose complex 1 as a representative example to describe here in detail.

The asymmetric unit of the 3D framework in 1 contains two crystallographically independent europium ions, three copper ions, six 3,4-pdc ligands and twelve coordinated water molecules (Fig. 1). Eu1(III) and Eu2(III) ions are both nine-coordinated with distorted tricapped trigonal prismatic geometry: four carboxylate oxygen atoms from two 3,4-pdc ligands and five oxygen atoms of coordinated water molecules for Eu1; five carboxylate oxygen atoms from three 3,4-pdc ligands and four oxygen atoms of coordinated water molecules for Eu2 (Fig. S1, ESI†). Three crystallographically independent Cu(II) ions exhibit two different coordination geometries (Fig. S2, ESI†). Cu1 and Cu3 atoms are both five-coordinated with tetragonal–pyramidal geometry, in which the equatorial plane is occupied by two N atoms and two O atoms from four different 3,4-pdc ligands, and the axial position is occupied by one water molecule. The Cu2 atom has a slightly distorted octahedron geometry with three oxygen atoms and two nitrogen atoms from four distinct 3,4-pdc ligands and one oxygen atom from coordinated water molecule. The coordination modes of 3,4-pdc in structurally characterized complexes 1–5 are summarized in Chart 1. As can be seen, the nitrogen atom always links copper atom, the 4-carboxyl group prefers connecting to copper atom in a monodentate or bidentate fashion, and the 3-carboxyl group tends to ligate lanthanide metal in a bidentate or monodentate fashion or even be free. Six 3,4-pdc ligands in 1 adopt four different coordination modes, in which three 3,4-pdc ligands adopt mode I, another three 3,4-pdc ligands adopt mode II, III and IV, respectively. Except ligand in Form IV, which link two metal ions, the other 3,4-pdc ligand all affords a three-connecting node linking three metal ions.

Fig. 1 Local coordination environments of Eu(III) and Cu(II) ions in complex 1 (hydrogen atoms are omitted for clarity).

Chart 1 Representations of coordination modes I–IV of 3,4-pdc.

The 3D structure of complex 1 is complicated. Firstly, each Cu(II) ion connects four 3,4-pdc ligands and each 3,4-pdc ligand bridges two Cu(II) ions, forming an extended irregular (4,4)-connected 2D plane, which is composed by asymmetric unit [Cu₃(3,4-pdc)₆(H₂O)₃] (Fig. 2a). Eu(H₂O)₅ (for Eu1) and Eu(H₂O)₄ (for Eu2) spacers lay between the layers, while only Eu(H₂O)₄ acting as pillars to further construct the 3D infinite structure (Fig. 2b). In total, Eu1 ion is linked to four Cu(II) ions (two Cu1, one Cu2 and one Cu3) through 3,4-pdc ligands; Eu2 linked to six Cu(II) ions (one Cu1, two Cu2 and three Cu3); while every Cu(II) ion is linked to four adjacent Cu(II) ions and three (for Cu1), three (for Cu2) or four (for Cu3) Eu(III) ions, in which the different Eu⋯Cu and Cu⋯Cu distances are list in Table 2. Simplifying 3,4-pdc ligands as nodes, the connecting mode of metal ions are shown in Fig. 2c and d.

Fig. 2 (a) 2D network constructed by [Cu₃(3,4-pdc)₆(H₂O)₃] in 1 viewed along the c axis, (b) 3D framework viewed along the a axis, purple polyhedrons represent Eu2 ions which act as pillars, (c) 2D network showing the connecting modes of Cu(II) and Eu1, 3,4-pdc ligands are simplified as nodes, (d) 3D framework showing the connecting modes of Cu(II) and Eu(III) ions, (e) the 8-connected topological structure of 1.

Table 1 Crystal data and structure refinement for complexes 1–5

Complex	1	2	3	4	5
Empirical formula	C42H50Cu3Eu2N6O40	C168H344Cu12Gd8N24O232	C94H180Cu6Tb4N12O113	C64H124Cu4Ho4N8O84	C32H62Cu2Er2N4O42
Mr	1773.42	8433.15	4303.42	3263.59	1636.46
T/K	113(2)	113(2)	113(2)	113(2)	113(2)
λ/Å	0.71073	0.71073	0.71073	0.71073	0.71073
Crystal system	Monoclinic	Monoclinic	Monoclinic	Monoclinic	Monoclinic
Space group	P2(1)/n	P2(1)/n	P2(1)/n	P2(1)/c	P2(1)/c
a/Å	13.945(3)	13.958(3)	13.934(3)	10.792(2)	10.632(2)
b/Å	30.633(6)	30.682(6)	30.722(6)	13.889(3)	13.862(3)
c/Å	20.585(4)	20.529(4)	20.494(4)	19.739(4)	19.498(4)
β/°	98.79(3)	98.82(3)	98.71(3)	100.91(3)	99.98(3)
V/Å^3	8690(3)	8688(3)	8672(3)	2905.1(10)	2830.3(10)
Z	4	1	2	1	2
Dc [g cm^−3]	1.355	1.612	1.648	1.865	1.920
μ/mm^−1	2.222	2.333	2.441	3.525	3.788
F(000)	3508	4236	4332	1620	1624
Crystal size/mm	0.20 × 0.18 × 0.12	0.20 × 0.18 × 0.15	0.20 × 0.18 × 0.16	0.20 × 0.19 × 0.18	0.20 × 0.19 × 0.19
θ range for data	1.62–25.02°	1.33–25.02°	1.62–25.02°	1.92–25.50°	2.94–25.49°
Limiting indices h, k, l	−16 to 16, −36 to 36, −20 to 24	−16 to 16, −36 to 36, −19 to 24	−16 to 16, −36 to 36, −24 to 24	−13 to 13, −15 to 16, −23 to 23	−12 to 12, −11 to 16, −14 to 23
Reflections measured	59 176	65 189	87 730	23 098	10 839
Unique reflections	15 079	15 266	15 307	5383	5239
R(int)	0.0543	0.0489	0.0490	0.0659	0.0323
Max./min. transmission	0.7764 and 0.6649	0.7210 and 0.6526	0.7584 and 0.6411	0.5539 and 0.5110	0.5330 and 0.5179
Parameters	895	1300	1246	392	439
GOF	1.068	1.070	1.032	1.252	1.039
R1, wR2 [I > 2σ(I)]	0.0402/0.1055	0.0528/0.1422	0.0612/0.1630	0.0579/0.1432	0.0344/0.0784
R1, wR2 (all data)	0.0482/0.1096	0.0606/0.1489	0.0670/0.1675	0.0665/0.1457	0.0409/0.0833
Δρ(max./min.)/e Å^−3	1.590/−1.560	1.994/−1.892	2.985/−2.376	1.910/−1.494	1.238/−1.505

---

Table 2 Eu⋯Cu and Cu⋯Cu separation bridged via 3,4-pdc (Å)^a

a Symmetry transformations used to generate equivalent atoms for 1: #1 x − 1, y, z; #2 −x + 3/2, y − 1/2, −z + 1/2; #3 −x + 2, −y, −z + 1; #4 x + 1/2, −y + 1/2, z + 1/2; #5 x − 1/2, −y + 1/2, z + 1/2; #6 −x + 5/2, y − 1/2, −z + 1/2.
For Eu1
Eu(1)⋯Cu(1)	7.670(2)	Eu(1)⋯Cu(1)#1	7.746(2)
Eu(1)⋯Cu(2)	6.747(1)	Eu(1)⋯Cu(3)#2	6.816(1)
For Eu2
Eu(2)⋯Cu(1)#3	6.909(1)	Eu(2)⋯Cu(2)	6.945(2)
Eu(2)⋯Cu(2)#4	6.933(1)	Eu(2)⋯Cu(3)	8.598(1)
Eu(2)⋯Cu(3)#5	7.706(2)	Eu(2)⋯Cu(3)#4	7.706(2)
For Cu⋯Cu
Cu(1)⋯Cu(2)	8.909(2)	Cu(1)⋯Cu(2)#3	8.783(2)
Cu(1)⋯Cu(3)#2	8.863(2)	Cu(1)⋯Cu(2)#6	8.972(2)
Cu(2)⋯Cu(3)	8.873(2)	Cu(2)⋯Cu(3)#6	8.911(2)

---

A better insight into the nature of this intricate framework can be achieved by the application of a topological approach, i.e. reducing multidimensional structures to simple nodes and connection nets. If we select metal ions as nodes, this 3D architecture can be simplified as a 5-nodal (4,6,7,7,8)-connected net with Schläfli symbol of (3⁴·4²)(3⁵·4²·5²·6⁶)(3⁵·4⁵·5⁶·6⁶)(3⁶·4⁶·5⁶·6³)(4¹²·6¹²·8⁴) based on the analysis with TOPOS 4.0 (Fig. S3†),¹¹ which has not been reported as far as we know. If treating the [Eu₃Cu₂] units as individual nodes, this network can be considered as an 8-connected (also see Fig. 2c and d) hex hexagonal primitive topology with a Schläfli symbol of (3⁶·4¹⁸·5³·6) (Fig. 2e), which is also be analysized using TOPOS 4.0. Indeed, the metal–organic frameworks based on nets with coordination numbers ≥8 are rare¹² and very few cases have been found with this topological notation.¹³

Interestingly, the view along the a axis (Fig. 2 and S3, ESI†) shows S-shape channels and smaller hexagonal channels, which are filled with a mass of guest water molecules. As shown in Fig. 3, the dimensions of nanotube which encircle S-shape channel is about 19.5 × 16.9 Å (calculated between opposite metal atoms), showing a 56-member ring (56MR) comprising 2Eu, 6Cu, 32C, 4N and 12O atoms (C, N and O come from eight 3,4-pdc). To the best of our knowledge, 56MR have not been previously reported. In addition, two opposite Eu(H₂O)₅ moieties extend into the void surrounded by 56MR, forming S-shape channel. The PLATON¹⁴ program reveals that the voids in complex 1 occupy 40.9% of the crystal volume (after the removal of the guest water molecules).

Fig. 3 The cross section of the nanotube for 1, which shows 56MRs.

Complexes 2 and 3 posses the similar topology structure and channel with 1, in which the voids occupy 40.9% and 41.6% of the crystal volume, respectively. S-shape channels and smaller hexagonal channels are all filled with a mass of guest water molecules as shown in Fig. S5† for complex 2. The Ln–O distance decreases with increasing lanthanide atomic number (Eu–O 2.415(2)–2.544(2) Å, Gd–O 2.409(2)–2.541(2) Å and Tb–O 2.334(2) −2.527(2) Å), which is interpreted as a result of the lanthanide contraction. As a result, the cell volume of the latter complex is slightly smaller than the former.

Crystal structures of [[HoCu(3,4-pdc)₂(OAc)(H₂O)₃]·8H₂O (4) and [ErCu(3,4-pdc)₂(OAc)(H₂O)₃]·8H₂O (5). The crystal structures of complexes 4 and 5 are isostructural, so 4 is chosen as a representative from two lanthanide compounds. The crystal structure of complex 4, as depicted in Fig. 4, is built up with asymmetric unit [HoCu(3,4-pdc)₂(OAc)(H₂O)₃]·8H₂O, which consists of nine-coordinated Ho(III) unit and five-coordinated Cu(II) unit. The Ho(III) ion is in a distorted tricapped trigonal prismatic coordination environment with a HoO₉ core: four coordinated oxygen atoms derived from two 3,4-pdc ligands, three coordinated oxygen atoms from two acetate ligands and two oxygen atoms of coordinated water molecules. The Cu(II) ion is pentacoordinate in a square pyramidal coordination environment (trigonality factor τ = (α − β)/60 = 0.05, where α = 177.4(2)° and β = 174.4(2)°), in which the equatorial plane was occupied by two N atoms (N1, N2) and two O atoms (O3A, O7B; #A = 1 − x, −1/2 + y, 1/2 − z, #B = −x, −1/2 + y, 1/2 − z) from four different 3,4-pdc ligands, and the axial position was occupied by one oxygen atom (O5) from coordinated water molecule. Due to the Jahn–Teller effect, the axial Cu1–O5 distance (2.301(7) Å) is larger than the other Cu–O distance (1.981(5) and 1.997(5) Å). Both of 3,4-pdc ligands adopt a quadridentate chelating–bridging mode to chelate one Ho(III) ion and link two Cu(II) ions (Mode I in Chart 1). Acetate ligand adopts μ₃-η₂:η₁:η₁ chelating–bridging mode to link two Ho(III) ions, which use two O donor to chelate one Ho(III) ion and also employ its one oxygen atom to link another Ho(III) ion. The Ho⋯Ho distance is 4.117(1) Å; the Ho⋯Cu distances are 7.982(2) and 7.255(2) Å; the Cu⋯Cu distances are 8.958(2) and 8.840(2) Å, respectively.

Fig. 4 Local coordination environments of Ho(III) and Cu(II) ions in complex 4 (hydrogen atoms are omitted for clarity).

Similar to complex 1, Cu(II) ion, which bridged by four 3,4-pdc ligands, could act as 4-connected node, resulting in wavelike (4,4)-connected 2D plane, which is composed by unit [Cu(3,4-pdc)₂(H₂O)] (Fig. 5a). The planes packing along the c axis are further linked by dinuclear Ho(III) units to result in a 3D coordination framework (Fig. 5b). The resulting 3D framework bears two types of rhomboid channels viewed along the a and b axes, which are all filled with lattice water molecules (Fig. S6, ESI†).

Fig. 5 (a) 2D network constructed by [Cu(3,4-pdc)₂(H₂O)] in 4 viewed along the c axis, (b) 3D framework viewed along the b axis, yellow polyhedrons represent Ho(III) ions which act as pillars.

Cross sections (Fig. 6) shows that potentially porous channels along a and b axes are all encircled by 4Ho, 2Cu, 2 acetate and four 3,4-pdc (dimensions of nanotubes are about 16.2 × 9.3 and 11.7 × 8.4 Å, calculated between opposite metal atoms). The difference is that neighbouring Ho(III) and Cu(II) ions are linked through NC₂(COO) spacer of 3,4-pdc around the former channel, while in the latter neighbouring Ho(III) and Cu(II) are linked through C₂(COO)₂ spacer of 3,4-pdc. The void volumes of the channels without the guest molecules, calculated by PLATON, are 34.4% for 4 and 32.8% for 5, respectively.

Fig. 6 Cross sections of the potentially porous channels along the a axis (a) and b axis (b) for 4.

To get further insight into the structure of 4, a topological analysis of this 3D framework was performed. As shown in Fig. 7, one dinuclear Ho(III) unit is surrounded by four 3,4-pdc, two acetate anions and four aqua ligands, which connects eight Cu(II) ions. Therefore, we could defines the bimetallic Ho(III) unit as a eight-connected node. Likewise, although a Cu(II) ion connects eight Ho(III) ions through 3,4-pdc ligands, it actually serves as a four-connected node because two holmium metal atoms bridged by 3,4-pdc constitute a bimetallic core and should be considered as one. As discussed above, the structure of complex 4 is binodal with eight-connected (dinuclear Ho(III) unit) and four-connected (Cu(II) ion) nodes. The framework can be rationalized by considering the shortest circuits starting and ending at dinuclear Ho(III) unit and Cu(II) ion, leading to the formation of a fluorite (4¹²·6¹²·8⁴)(4⁶)₂ topology.

Fig. 7 (a) View showing that the binuclear Ho(III) unit can be simplified to a eight-connected node, (b) schematic representation of the fluorite (4¹²·6¹²·8⁴)(4⁶)₂ topology in 4.

Powder X-ray diffraction and thermal gravimetric analyses

Powder X-ray diffraction (PXRD) analyses were performed on crystalline powders of 1–5. The experimental PXRD patterns are consistent with the corresponding simulated ones from the singlecrystal data, which confirms the phase purity of the products (Fig. S7 and S8, ESI†). For complexes 2–5, simulated PXRD patterns were got from singlecrystal data containing all the crystalline water molecules by the MERCURY software. For complex 1, the scattering from the highly disordered solvent molecules was removed from singlecrystal data, while the simulated PXRD patterns of isomorphous complexes 1–3 are all very similar.

To examine the thermal stability and dehydration properties of these potentially microporous MOFs, thermal gravimetric analysis (TGA) were measured on crystalline samples of 1–5 under nitrogen atmosphere from room temperature to 750 °C (Fig. S9, ESI†). Complexes 1–3 showed similar TGA curves, while 4 and 5 showed similar curves, so complexes 1 and 4 are employed as representatives. The TGA curves indicate that the lattice and coordinated water molecules are removed in a single step in the temperature range 65–180 °C (found, 29.1%; calculated, 29.2%) for polymer 1 and 70–195 °C (found, 23.8%; calculated, 24.4%) for polymer 4, respectively. The weight loss above 305 °C (for 1) and 295 °C (for 4) is sharp, indicating the decomposition of organic ligands. After decomposition of complexes at high temperature, the weight of residue are responded to Eu₂O₃·3CuO for 1 (found 28.3%; calcd 28.1%) and 1/2Ho₂O₃·CuO for 4 (found 33.1%; calcd 32.9%), respectively.

Photoluminescence properties

The ultraviolet and visible spectra of complexes 1–5 show strong absorption signals at 270 nm, which may be attributed to electronic transition of the ligand itself. The photo luminescence properties of solid samples of ligand and complexes were investigated. The free 3,4-pdcH₂ ligand presents a weak fluorescence band with a maximum at 338 nm under excitation at λ = 270 nm, which could be attributed to the π → π* intraligand fluorescence. Complexes 1, 3, 4 and 5 emit moderately intense luminescence bands with a maximum at about 365 nm, upon irradiation with a wavelength of 270 nm (see Fig. S10, ESI†), which originate from intraligand π → π* transition of typically conjugated organic system, but is red-shift to the near visible region. The enhancement of luminescence may be ascribed to a ligand chelating to the lanthanide center, which effectively increases the rigidity of the ligand and reduces the loss of energy by radiationless decay.¹⁵

Complex 1 shows strong emission when excited with 271 nm radiation and the five characteristic emission bands in visible region can be seen from the emitting spectrum of 1. The most intense band at 618 nm is assigned to a ⁵D₀ → ⁷F₂ f–f transition, while the four relatively weak bands at 580, 593, 652 and 699 nm are assigned to ⁵D₀ → ⁷F₀, ⁵D₀ → ⁷F₁, ⁵D₀ → ⁷F₃ and ⁵D₀ → ⁷F₄ transitions, respectively (Fig. 8). The intensity radio of electric dipole ⁵D₀ → ⁷F₂ transition to dipole ⁵D₀ → ⁷F₁ magnetic transition is 4.0, showing that symmetry of coordination environment of Eu(III) ions is low,¹⁶ which is in agreement with the crystal structure analysis that the Eu(III) locates at the asymmetric coordination field. The appearance of the symmetry-forbidden emission ⁵D₀ → ⁷F₀ at 580 nm also indicates that Eu(III) ions in 1 possess the noncentrosymmetric coordination environment. The luminescence spectrum of complex 3 shows the characteristic emission of Tb(III) ion in the visible region with maximum wavelengths of 485, 545, 585 and 621 nm, respectively, which are attributed to ⁵D₄ → ⁷F₆, ⁵D₄ → ⁷F₅, ⁵D₄ → ⁷F₄ and ⁵D₄ → ⁷F₃ transitions of Tb(III) ion, respectively. This luminescent phenomenon was also observed in other reported terbium complexes.^{17 5}D₄ → ⁷F₅ is the most intense transition showing strong green light, which has the largest probability for both electric-dipole and magnetic-dipole induced transitions.

Fig. 8 Solid-state photoluminescence spectra of complexes 1 and 3 at room temperature.

Magnetic properties

Variable-temperature magnetic susceptibility data at the magnetic field of 1000 Oe in the temperature of 1.8–300 K were collected for complexes 1–5.

Fig. 9 shows the temperature dependence of the χ_M and χ_MT curves for complex 1. At 300 K, the χ_MT value of 1 is 3.94 cm³ K mol⁻¹, which is much larger than the calculated value of 1.125 cm³ K mol⁻¹ expected for three independent Cu(II) ion and two independent ground-state Eu(III) ions (J = 0, S = 3, L = 3, ⁷F₀, 0 cm³ K mol⁻¹). The disagreement should be ascribed the presence of thermally populated excited states, as is well-known for Eu(III) complexes (the expected value 1.5 cm³ K mol⁻¹ for one Eu(III) ion calculated by Van Vleck at 293 K).¹⁸ There is a continuous decrease in the values of χ_MT as the temperature is lowered from 300 to 12 K, at which the χ_MT product reaches a minimum value of 1.69 cm³ K mol⁻¹. It should be attributed to the depopulation of the levels with nonzero J values. Upon further lowering the temperature, χ_MT increases dramatically to reach a value of 2.42 cm³ K mol⁻¹ at 1.8 K. The 1/χ_M data above 100 K obey the Curie–Weiss law [χ = C/(T − θ) with C = 5.56 cm³ K mol⁻¹, θ = −114.8 K] (Fig. S11, ESI†). The large negative Weiss constant may reveal the antiferromagnetic couplings within the molecule.

Fig. 9 Temperature dependence of χ_M (○) and χ_MT (▽) for 1, the solid line represents the best fit curve based on the equations indicated in the text.

Obviously, a strictly theoretical treatment of magnetic properties for such a complicated 3D system cannot be carried out. However, to obtain a rough quantitative estimate of the magnetic interaction parameters between paramagnetic species, we assume that the total magnetic susceptibility χ_tot is given by the sum of the isolated Cu(II) and Eu(III) ions. The temperature dependence of the χ_M can be reproduced by eqn (1)–(3), which take into account the seven states ⁷F₀, ⁷F₁, ⁷F₂, ⁷F₃, ⁷F₄, ⁷F₅ and ⁷F₆ generated by the interelectronic repulsion and spin–orbit coupling.¹⁹ N, β, k and g have their usual meaning and λ is the spin–orbit coupling parameter. Then the zJ′ parameter based on the molecular field approximation is introduced (eqn (4)) to roughly simulate the magnetic interactions between the paramagnetic species.^18a,20

where

x = λ/kT (2)

χ_tot = 2χ_Eu + 3χ_Cu (3)

χ_M = χ_tot/[1 − zJ′χ_tot/Ng²β²] (4)

The best fitting for the experimental data gives λ = 226 cm⁻¹, zJ′ = 1.29 cm⁻¹, g_Cu = 2.09. The agreement factor R = ∑(χ_obsd − χ′_cacld)²/∑(χ_obsd)² is 1.06 × 10⁻³. The obtained λ = 226 cm⁻¹ is close to those reported previously,^19a,21 which could be comparable to the value (263 cm⁻¹) deduced from the energy difference between the ground state ⁷F₀ and the lowest-lying split component of ⁷F₁ caused by the crystal field perturbation.

The value of χ_MT of 2 at 300 K is 17.17 cm³ K mol⁻¹, which is slightly higher than the expected value of 16.885 cm³ K mol⁻¹ for two isolated Gd(III) ions in the ⁸F_7/2 ground state with an isotropic g value of 2.00 (C = 7.88 cm³ K mol⁻¹) and three isolated Cu(II) ions (S = 1/2, g = 2.0, C = 0.375 cm³ K mol⁻¹). While the temperature decreases, the χ_MT value remains roughly constant down to 50 K and then it increases and reaches maximum of 17.90 cm³ K mol⁻¹ (Fig. 10). The fitting of experimental data with a Curie–Weiss law leads to C = 17.13 cm³ K mol⁻¹ and θ = 0.20 K (Fig. S12, ESI†). The Gd(III) ion, with an ⁸F_7/2 single-ion (f⁷) ground state, does not possess a first-order orbital moment. So, the contributions of the orbital angular momentum do not need to be taken into consideration. The increase of χ_MT values on cooling and the existence of a positive θ value indicate the presence of weak ferromagnetic interaction between Gd(III) and Cu(II) ions in the complex.²²

Fig. 10 The plots of χ_MT versus T for 2 (■), 3 (●), 4 (▲) and 5 (▼).

At room temperature, the χ_MT product of 3 (Fig. 10) is 25.3 cm³ K mol⁻¹, in good agreement with the expected value of 24.8 cm³ K mol⁻¹ for 3 Cu(II) (C = 0.375 cm³ K mol⁻¹) and 2 Tb(III) (S = 3, L = 3, ⁷F₆, g = 3/2, C = 11.815 cm³ K mol⁻¹). Upon lowering of the temperature, the χ_MT product is roughly constant down to 100 K before exhibiting a slow increase, reaching a maximum of 28.4 cm³ K mol⁻¹ at around 15 K, then decreasing to a minimum value of 27.4 cm³ K mol⁻¹ at 1.8 K. The profile of the χ_MT vs. T curve is strongly suggestive of the occurrence of two competitive phenomena. The decrease of χ_MT on lowering the temperature in the low-temperature region is most probably governed by the depopulation of the Tb Stark levels, while the increase of χ_MT at higher temperature may be attributed to a ferromagnetic interaction between Cu(II) and Tb(III).²³ The plot of 1/χ_M versus T over the whole temperature range obeys the Curie–Weiss law with C = 24.99.23 cm³ K mol⁻¹ and θ = 2.06 K. The C value is comparable with the two Tb(III) and three Cu(II) ions with noninteraction, and the θ value indicates that magnetic interactions between metal ions are very weak. We can not find an accurate fit of the magnetic data for this system.

Although complexes 1–3 are isomorphous, they displays different magnetic behaviors, which mainly arises from the intrinsic natures of different lanthanide ions. Due to the long distance and lack of any important magnetic pathway through pyridine carboxylate ligand, magnetic interactions between adjacent metal ions will be rather weak. The large and different magnetic anisotropy, and complicated Stark energy levels of lanthanide ions from the splitting of individual ^2S+1L_J states, should be responsible for the significant differences of magnetic behaviors in these complexes.

At 300 K, the χ_MT product is 13.38 (for 4) and 11.26 (for 5) cm³ K mol⁻¹ (Fig. 10), respectively, which are all slightly smaller than the expected value for one Cu(II) ion and one Ln(III) ions (Ho: ⁵I₈, g = 5/4, C = 14.06 cm³ K mol⁻¹; Er: ⁴F_15/2, g = 6/5, 11.5 cm³ K mol⁻¹). For 4, as the temperature is lowered, the χ_MT value decreases steadily beyond 50 K, and then decreases in a more abrupt manner, reaching a minimum value of 9.49 cm³ K mol⁻¹ at 1.8 K. For 5, the χ_MT value remains almost unchanged between 300 and 100 K. As temperature further decreases, χ_MT value markedly reduces to 6.21 cm³ K mol⁻¹ at 1.8 K. The magnetic behavior in the whole temperature range for two complexes obey the Curie–Weiss law (for 4: C = 13.43 cm³ K mol⁻¹, θ = −4.57 K; for 5: C = 11.41 cm³ K mol⁻¹, θ = −6.09 K). However, although the χ_MT product decreases and the values of Weiss constant are negative, it is not possible to be sure that this behavior is associated with antiferromagnetic interactions within these complexes due to the presence of strong spin–orbital coupling effects in these Ln(III) ions.

Conclusions

In conclusion, five new potentially microporous 3d–4f MOFs assembled by 3,4-pdc were synthesized, in which introduction of auxiliary acetate ligand and different Ln ions resulted in different topology network. Two series of Cu–Ln polymers were constructed with similar (4,4)-connected 2D Cu sheets and different pillared Ln(III) units, showing hex hexagonal primitive and fluorite topological structures with different channels which are filled by a mass of solvent molecules. Complexes 1 and 3 display strong characteristic emission in the visible region. Magnetic properties of complexes are very different, though the metal magnetic centers are located in the same coordination environment. These results show 3,4-pdc ligands are suitable for constructing of heterometallic frameworks with interesting structures and properties, and these polymers may have potential application in luminescent materials. The 3,4-pdc ligand with various coordination modes combining with other auxiliary ligands can potentially be utilized to constructing novel MOFs with pores and other functionalities, and corresponding work is currently underway in our laboratory.

Experimental

Materials and physical measurements

All of the reagents and solvents employed were commercially available and used directly without further purification. Analyses for C, H and N were carried out on a Perkin-Elmer 240 elemental analyzer. Infrared spectroscopy on KBr pellets was executed on a Bio-Rad FTS 135 spectrometer in the 4000–400 cm⁻¹ regions. The as-synthesized samples were characterized by thermogravimetric analysis (TGA) on a Perkin-Elmer thermogravimetric analyzer Pyris1 TGA up to 1023 K using a heating rate of 10 K min⁻¹ under N₂ atmosphere. The powder X-ray diffraction (PXRD) patterns were measured using a Bruker D8 Advance powder diffractometer at 40 kV, 40 mA for Cu Kα radiation (λ = 1.5418 Å). The spectra of fluorescence were measured by MPF-4 fluorescence spectrophotometer with a xenon arc lamp as the light source. Variable-temperature magnetic susceptibilities were measured on a Quantum Design MPMS-7 SQUID magnetometer using an applied magnetic field of 1000 Oe.

Syntheses of the complexes

The same procedure was employed in the preparation of all heterometallic coordination polymers. In a big test tube, a mixture of Cu(NO₃)₂·3H₂O (0.2 mmol) and 0.2 mmol lanthanide salt (Eu(NO₃)₃·6H₂O, 90 mg for 1; Gd(NO₃)₃·6H₂O, 92 mg for 2; Tb(NO₃)₃·6H₂O, 91 mg for 3; Ho(CH₃COOH)₃·H₂O, 72 mg for 4; Er(CH₃COOH)₃·4H₂O, 83 mg for 5) in 25 mL aqueous solution was layered carefully with water–methanol mixed solvent (15 mL, in 1 : 1 volume ratio) and then layered with a methanol solution (25 mL) of 3,4-pdcH₂ (0.4 mmol) and triethylamine (0.4 mmol). The tube was sealed and left undisturbed at room temperature. Blue block crystals suitable for X-ray analysis were obtained after one week, which were collected by filtration, washed with ethyl ether and dried in air. The yields are ca. 14% (1), 21% (2), 15% (3), 19% (4) and 25% (5) based on lanthanide salt. Elemental analysis (%) calcd for 1 (C₄₂H₈₆Cu₃Eu₂N₆O₅₈): C, 24.05; H, 4.13; N, 4.01; found: C 23.70, H 4.30, N 3.82. Calcd for 2 (C₄₂H₈₆Cu₃Gd₂N₆O₅₈): C 23.93, H 4.11, N 3.99; found: C 23.63, H 4.22, N 3.94. Calcd for 3 (C₄₇H₉₀Cu₃Tb₂N₆O_56.5): C 26.24, H 4.22, N 3.91; found: C 26.65, H 4.27, N 3.95. Calcd for 4 (C₁₆H₃₁CuHoN₂O₂₁): C 23.55, H 3.83, N 3.43; found: C 23.82, H 3.77, N 3.50. Calcd for 5 (C₁₆H₃₁CuErN₂O₂₁): C 23.49, H 3.82, N 3.42; found: C 23.31, H 4.01, N 3.64. IR spectra (KBr, cm⁻¹): complex 1: 3445 (s, br), 1625 (s), 1520 (s), 1449 (m), 1399 (m), 1350 (m), 1270 (m), 1189 (m), 1090 (m), 870 (m), 774 (m), 534 (m); complex 2: 3450 (s, br), 1630 (s), 1520 (s), 1450 (m), 1400 (m), 1352 (m), 1268 (m), 1190 (m), 1090 (m), 875 (m), 775 (m), 530 (m); complex 3: 3445 (s, br), 1630 (s), 1525 (s), 1447 (m), 1398 (m), 1349 (m), 1267 (m), 1188 (m), 1088 (m), 872 (m), 775 (m), 535 (m); complex 4: 3480 (s, br), 1645 (m), 1602 (s), 1510 (s), 1392 (m), 1359 (m), 1281 (m), 1188 (m), 1158 (m), 1110 (m), 1085 (m), 870 (m), 774 (m); complex 5: 3472 (s, br), 1640 (m), 1600 (s), 1510 (s), 1395 (m), 1360 (m), 1280 (m), 1186 (m), 1160 (m), 1112 (m), 1083 (m), 870 (m), 775 (m).

X-ray crystallography

Diffraction data for 1–5 were collected at 113(2) K with a Rigaku Saturn CCD diffractometer equipped with graphite monochromated Mo-K_α radiation by using the ω-scan technique. The data were processed using CrystalClear software²⁴ and corrected for Lorentz and polarization effects. Absorption corrections were applied by using a multiscan program. The structures were solved by direct methods and refined by full-matrix least squares based on F² using the SHELXTL program package.²⁵ Non-hydrogen atoms were subjected to anisotropic refinement. Hydrogen atoms were assigned with common isotropic displacement factors. Hydrogen atoms were included at geometrically calculated positions and refined using a riding model except those bonded to the oxygen atoms in water molecules, which were located on a different Fourier map. In 1, the highly disordered solvent molecules could not be satisfactorily modeled. To resolve these issues, the contribution of the electron density by the remaining water molecule was removed by the SQUEEZE routine in PLATON.¹⁴ Number of solvent water molecules in 1 was obtained by element analysis and TGA. The crystallographic data and refinement parameters of 1–5 are listed in Table 1. Selected bond lengths and angles are listed in Table S1, ESI.†

Acknowledgements

This work was supported by the National Natural Science Foundation of China (no. 21371135), China Postdoctoral Science Foundation (no. 2014M551036) and Natural Science Foundation of Hebei Province under Grant (no. E2013501135).

References

1. (a) P. Cui, Y. G. Ma, H. H. Li, B. Zhao, J. R. Li, P. Cheng, P. B. Balbuena and H. C. Zhou, J. Am. Chem. Soc., 2012, 134, 18892; (b) Q. W. Li, W. Y. Zhang, O. S. Miljanic, C. H. Sue, Y. L. Zhao, L. H. Liu, C. B. Knobler, J. F. Stoddart and O. M. Yaghi, Science, 2009, 325, 855; (c) H. J. Choi and M. P. Suh, J. Am. Chem. Soc., 2004, 126, 15844; (d) L. W. Yan, Z. Wang, M. T. Chen, N. J. Wu, J. B. Lan, X. Gao, J. S. You, H. M. Gau and C. T. Chen, Chem.–Eur. J., 2008, 14, 11601.
2. (a) M. P. Suh, H. J. Park, T. K. Prasad and D. W. Lim, Chem. Rev., 2012, 112, 782; (b) Y. Kubota, M. Takata, T. C. Kobayashi and S. Kitagawa, Coord. Chem. Rev., 2007, 251, 2510.
3. (a) G. Lu and J. T. Hupp, J. Am. Chem. Soc., 2010, 132, 7832; (b) B. L. Chen, L. B. Wang, Y. Q. Xiao, F. R. Fronczek, M. Xue, Y. J. Cui and G. D. Qian, Angew. Chem., Int. Ed., 2009, 48, 500; (c) B. L. Chen, L. B. Wang, F. Zapata, G. D. Qian and E. B. Lobkovsky, J. Am. Chem. Soc., 2008, 130, 6718.
4. (a) J. X. Ma, X. F. Huang, Y. Song, X. Q. Song and W. S. Liu, Inorg. Chem., 2009, 48, 6326; (b) K. S. Min and M. P. Suh, J. Am. Chem. Soc., 2000, 122, 6834.
5. (a) F. Gándara, A. García-Cortés, C. Cascales, B. Gómez-Lor, E. Gutiérrez-Puebla, M. Iglesias, A. Monge and N. Snejko, Inorg. Chem., 2007, 46, 3475; (b) C. D. Wu, A. Hu, L. Zhang and W. B. Lin, J. Am. Chem. Soc., 2005, 127, 8940.
6. (a) Y. J. Cui, Y. F. Yue, G. D. Qian and B. L. Chen, Chem. Rev., 2012, 112, 1126; (b) D. L. Geng, M. M. Shang, D. M. Yang, Y. Zhang, Z. Y. Cheng and J. Lin, J. Mater. Chem., 2012, 22, 23789; (c) B. Zhao, X. Y. Chen, P. Cheng, D. Z. Liao, S. P. Yan and Z. H. Jiang, J. Am. Chem. Soc., 2004, 126, 15394; (d) C. J. Li, Z. J. Lin, M. X. Peng, J. D. Leng, M. M. Yang and M. L. Tong, Chem. Commun., 2008, 6348; (e) X. Feng, Y. Q. Feng, L. Lang, L. Y. Wang, H. L. Song and S. W. Ng, Dalton Trans., 2013, 42, 7741.
7. B. Zhao, P. Cheng, X. Y. Chen, C. Cheng, W. Shi, D. Z. Liao, S. P. Yan and Z. H. Jiang, J. Am. Chem. Soc., 2004, 126, 3012 , and references cited therein.
8. (a) K. Liu, W. Shi and P. Cheng, Coord. Chem. Rev., 2014 DOI:10.1016/j.ccr.2014.10.004; (b) S. Kitagawa, R. Kitaura and S. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334.
9. (a) P. B. Glover, P. R. Ashton, L. J. Childs, A. Rodger, M. Kercher, R. M. Williams, L. Cola and Z. Pikramenou, J. Am. Chem. Soc., 2003, 125, 9918; (b) H. S. Wang, B. Zhao, B. Zhai, W. Shi, P. Cheng, D. Z. Liao and S. P. Yan, Cryst. Growth Des., 2007, 7, 1851.
10. (a) A. M. Plonka, D. Banerjee and J. B. Parise, Cryst. Growth Des., 2012, 12, 2460; (b) X. L. Wang, C. Qin, E. B. Wang, Y. G. Li, C. W. Hu and L. Xu, Chem. Commun., 2004, 378; (c) E. J. Gao, K. H. Wang, M. C. Zhu and L. Liu, Eur. J. Med. Chem., 2010, 45, 2784; (d) M. L. Tong, J. Wang, S. Hu and S. R. Batten, Inorg. Chem. Commun., 2005, 8, 48; (e) C. Qin, X. L. Wang, E. B. Wang and L. Xu, Inorg. Chim. Acta, 2006, 359, 417; (f) Z. B. Han, X. N. Cheng, X. F. Li and X. M. Chen, Z. Anorg. Allg. Chem., 2005, 631, 937; (g) X. J. Gu and D. F. Xue, CrystEngComm, 2007, 9, 471.
11. (a) TOPOS, Version 4.0, http://www.topos.ssu.samara.ru; (b) V. A. Blatov, A. P. Shevchenko and V. N. Serezhkin, Acta Crystallogr., Sect. A: Found. Crystallogr., 1995, 51, 909.
12. O. Delgado Friedrichs, M. O'Keeffe and O. M. Yaghi, Acta Crystallogr., Sect. A: Found. Crystallogr., 2003, 59, 515.
13. P. K. Chen, S. R. Batten, Y. Qi and J. M. Zheng, Cryst. Growth Des., 2008, 9, 2756 , and references cited therein.
14. A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7.
15. (a) Z. Miskolczy, L. Biczók and I. Jablonkai, J. Phys. Chem. A, 2012, 116, 899; (b) T. L. Esplin, M. L. Cable, H. B. Gray and A. Ponce, Inorg. Chem., 2010, 49, 4643; (c) L. N. Jia, L. Hou, L. Wei, X. J. Jing, B. Liu, Y. Y. Wang and Q. Z. Shi, Cryst. Growth Des., 2013, 13, 1570.
16. (a) T. H. Zhou, F. Y. Yi, P. X. Li and J. G. Mao, Inorg. Chem., 2010, 49, 905; (b) C. Z. Xie, B. F. Zhang, X. Q. Wang, B. Yu, R. J. Wang and G. Q. Shen, Z. Anorg. Allg. Chem., 2008, 634, 387.
17. (a) S. F. Tang, J. L. Song, X. L. Li and J. G. Mao, Cryst. Growth Des., 2006, 6, 2322; (b) J. L. Song, C. Lei and J. G. Mao, Inorg. Chem., 2004, 43, 5630; (c) J. L. Song and J. G. Mao, Chem.–Eur. J., 2005, 11, 1417.
18. (a) X. H. Zhou, Y. H. Peng, X. D. Du, C. F. Wang, J. L. Zuo and X. Z. You, Cryst. Growth Des., 2009, 9, 1028; (b) C. J. Chen, N. Wang, Y. Long, J. Y. Gao, W. P. Xie, X. R. Rana and S. T. Yue, CrystEngComm, 2013, 15, 4611.
19. (a) M. Andruh, E. Bakalbassis, O. Kahn, J. C. Trombe and P. Porcher, Inorg. Chem., 1993, 32, 1616; (b) T. Kido, Y. Ikuta, Y. Sunatsuki, Y. Ogawa and N. Matsumoto, Inorg. Chem., 2003, 42, 398.
20. (a) Y. Liao, W. W. Shum and J. S. Miller, J. Am. Chem. Soc., 2002, 124, 9336; (b) Y. Ouyang, W. Zhang, N. Xu, G. F. Xu, D. Z. Liao, K. Yoshimura, S. P. Yan and P. Cheng, Inorg. Chem., 2007, 46, 8454.
21. (a) L. F. Wang, L. C. Kang, W. W. Zhang, F. M. Wang, X. M. Ren and Q. J. Meng, Dalton Trans., 2011, 40, 9490; (b) X. J. Wang, Z. M. Cen, Q. L. Ni, X. F. Jiang, H. C. Lian, L. C. Gui, H. H. Zuo and Z. Y. Wang, Cryst. Growth Des., 2010, 10, 2960.
22. (a) J. Xu, W. P. Sun and M. C. Hong, CrystEngComm, 2011, 13, 3998; (b) N. Xu, W. Shi, D. Z. Liao, S. P. Yan and P. Cheng, Inorg. Chem., 2008, 47, 8748.
23. S. S. Dhers, H. L. C. Feltham, R. Clérac and S. Brooker, Inorg. Chem., 2013, 52, 13685.
24. J. W. Pflugrath, Acta Crystallogr., Sect. D: Biol. Crystallogr., 1999, 55, 1718.
25. G. M. Sheldrick, SHELXL-97, Program for X-ray Crystal Structure Solution, Göttingen University, Germany, 1997.

---

Footnote

† Electronic supplementary information (ESI) available: X-ray structure data in CIF files for 1–5, table of bond lengths and angles, coordination environments of metal ions in 1, topologic network of 1, 3D framework showing 1D channels in 1, 2 and 4, XRD patterns, TGA curves of 1–5, the emission spectra of free 3,4-pdcH₂ ligand and complexes, and other magnetic data. CCDC 1029464 (1), 1029465 (2), 1029467 (3), 1029466 (4) and 1029463 (5). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c4ra13533d

---