Dynamic and static behavior of the E–E′ bonds (E, E′ = S and Se) in cystine and derivatives, elucidated by AIM dual functional analysis

Abstract

Atoms-in-molecules dual functional analysis (AIM-DFA) is applied to the E–E′ bonds (E, E′ = S and Se) in R-cystine (1) and the derivatives of 1, together with MeEE′Me. H_b(r_c) are plotted versus H_b(r_c) − V_b(r_c)/2 at bond critical points (BCPs), where H_b(r_c) − V_b(r_c)/2 = (ħ²/8m)∇²ρ_b(r_c). The plots are analyzed by the polar coordinate (R, θ) representation. Data of perturbed structures around the fully optimized structures are also plotted in this treatment. Perturbed structures are generated using NIV (normal coordinates of internal vibrations). Each plot for an interaction with data of a fully optimized and four perturbed structures gives a curve, which supplies important information. It is expressed by (θ_p, κ_p): θ_p corresponds to the tangent line for the plot measured from the y-direction and κ_p is the curvature. While (R, θ) correspond to the static nature of interactions, (θ_p, κ_p) represent the dynamic nature. The behavior of the E–E′ bonds is well described by (R, θ) and (θ_p, κ_p).

---

Introduction

The E–E′ bonds (E, E′ = S and Se) are of current and continuous interest due to their indispensable role in biological, chemical and physical sciences.^1–7 The S–S bond plays a crucial role in maintaining the three dimensional structures of peptides. On the other hand, the E–E′ bonds show typical behavior in the redox process,⁸ which must be responsible for the highly important biological activities such as detoxification of hydroperoxides in the glutathione peroxidase (GPx) process.^9–21

Scheme 1 summarizes the proposed catalytic mechanism for the antioxidant activity of GPx, which is one of the typical examples of the intervention of E–E′ in biological activities. The mechanism involves the initial oxidation of selenol (R₁-SeH) to produce the corresponding selenenic acid (R₁-SeOH), which reacts with glutathione (GSH) to produce selenenyl sulfide (R₁-SeSG). Then a second molecule of GSH attacks at the sulfur center of R₁-SeSG to regenerate the active form of the enzyme (R₁-SeH) (GPx cycle in Scheme 1). In the overall process, 2 equivalent of GSH is oxidized to the corresponding disulfide (GSSG), while the hydroperoxide is reduced to water.^22,23 When the peroxide concentration is higher than that of the thiol, the selenium center in the selenenic acid (R₁-SeOH) may undergo further oxidation to produce the seleninic acid (R₁-SeO₂H) (another cycle in Scheme 1).

Scheme 1 Proposed catalytic mechanism for the antioxidant activity of GPx.

The behavior of the E–E′ bonds seems well described at first glance, however, it is still of highly importance to clarify the causality in the phenomena of the bonds, with physical necessity. Here, we clarified the dynamic and static behavior of the S–S bond in R-cystine (1), of which structures were determined by the X-ray crystallographic analysis, although the derivatives.²⁴ Similar behavior of the S–Se and Se–Se bonds in the derivatives of 1 (2 and 3, respectively) was also investigated, together with the E–E′ bonds in MeEE′Me (E, E′ = S and Se) (4–6, respectively) (Chart 1). The effect of the hydrogen bonds (HBs) in 1–3 on the dynamic and static nature of the E–E′ bonds must also be of interest.

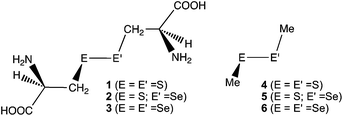Chart 1 Chalcogen–chalcogen bonds in 1–6, examined.

Atoms-in-molecules dual functional analysis (AIM-DFA),^25–28 which we proposed recently, is applied to the E–E′ bonds in 1–6. AIM-DFA is surveyed next, together with the basic concept of the AIM approach introduced by Bader.^29–31

Survey of AIM and AIM dual functional analysis

AIM (atoms-in-molecules method), proposed by Bader,^29–31 enables us to analyze and evaluate the nature of chemical bonds and interactions, together with the classification.^32–36 The bond critical point (BCP; r_c, *) is an important concept in AIM. BCP of (ω, σ) = (3, −1)^29,30 is a point along the bond path at the interatomic surface, where the electron density at BCPs (ρ_b(r_c)) reaches a minimum. Chemical bond or interaction between A and B is denoted by A–B, which corresponds to the bond path between A and B in AIM. A notation A-*-B will be employed for A–B to emphasize the presence of BCP (*) in A–B.

Interactions are classified by signs of ∇²ρ_b(r_c) (Laplacian ρ_b(r_c)) and H_b(r_c) (total electron energy densities). H_b(r_c) are the sum of kinetic energy densities (G_b(r_c)) and potential energy densities (V_b(r_c)) at BCPs, as shown in eqn (1). Eqn (2) represents the relation between ∇²ρ_b(r_c) and H_b(r_c), together with G_b(r_c) and/or V_b(r_c), which is closely related to the Virial theorem.

H_b(r_c) = G_b(r_c) + V_b(r_c) (1)

(ħ²/8m)∇²ρ_b(r_c) = H_b(r_c) − V_b(r_c)/2 (2)

(ħ²/8m)∇²ρ_b(r_c) = G_b(r_c) + V_b(r_c)/2 (2′)

Interactions in the region of ∇²ρ_b(r_c) < 0 are called shared-shell (SS) interactions and they are closed-shell (CS) interactions for ∇²ρ_b(r_c) > 0. H_b(r_c) must be negative when ∇²ρ_b(r_c) < 0, since H_b(r_c) are larger than (ħ²/8m)∇²ρ_b(r_c) by V_b(r_c)/2 with negative V_b(r_c) at all BCPs (eqn (2)). Consequently, ∇²ρ_b(r_c) < 0 and H_b(r_c) < 0 for the SS interactions. The CS interactions are especially called pure CS interactions for H_b(r_c) > 0 and ∇²ρ_b(r_c) > 0, since electrons are destabilized and ρ(r) are depleted at (around) BCPs under the conditions.²⁹ Electrons in the intermediate region between SS and pure CS, which belong to CS, are locally depleted but stabilized at BCPs, since ∇²ρ_b(r_c) > 0 but H_b(r_c) < 0.²⁹ We call the interactions in this region regular CS,^25–27 when it is necessary to distinguish from pure CS. The role of ∇²ρ_b(r_c) in the classification can be replaced by H_b(r_c) − V_b(r_c)/2, since (ħ²/8m)∇²ρ_b(r_c) = H_b(r_c) − V_b(r_c)/2 (eqn (2)).

We proposed AIM-DFA by plotting H_b(r_c) versus H_b(r_c) − V_b(r_c)/2.^26,27 Both axes in the plot are given in energy unit, therefore, distances on the (x, y) [= (H_b(r_c) − V_b(r_c)/2, H_b(r_c))] plane can be expressed in the energy unit, which provides an analytical development. AIM-DFA incorporates the classification of interactions by signs of ∇²ρ_b(r_c) [= (8m/ħ²)(H_b(r_c) − V_b(r_c)/2)] and H_b(r_c). Scheme 2 summarizes the treatment. Interactions of pure CS appear in the first quadrant, those of regular CS in the forth quadrant and data of the SS interactions drop in the third quadrant. No interactions appear in the second one.

R = (x² + y²)^1/2 (3)

θ = 90° − tan⁻¹(y/x) (4)

θ_p = 90° − tan⁻¹(dy/dx) (5)

κ_p = |d²y/dx²|/[1 + (dy/dx)²]^3/2 (6)

k = V_b(r_c)/G_b(r_c) (7)

where (x, y) = (H_b(r_c) − V_b(r_c)/2, H_b(r_c)) and y/x = H_b(r_c)/(H_b(r_c) − V_b(r_c)/2).

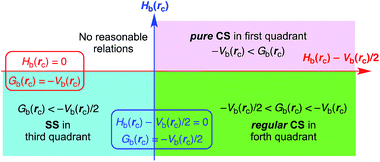Scheme 2 AIM-DFA treatment of interactions: plot of H_b(r_c) versus H_b(r_c) − V_b(r_c)/2 for weak to strong interactions.

In our treatment, data for perturbed structures around fully optimized ones are also employed for the plots, together with the fully optimized structures.^25–28 The method to generate the perturbed structures will be discussed later. The plots of H_b(r_c) versus H_b(r_c) − V_b(r_c)/2 are analyzed employing the polar coordinate (R, θ) representation with the (θ_p, κ_p) parameters.^26–28 The treatment is explained in Fig. 1. R in (R, θ) is defined by eqn (3) and given in the energy unit. R corresponds to the energy for an interaction at BCP. The plots for weak to strong interactions show a spiral stream, as a whole. θ in (R, θ) is defined by eqn (4) and measured from the y-axis. θ controls the spiral stream of the whole plots. Each plot for an interaction shows a specific curve, which provides important information.^26,27,37 The curve is expressed by (θ_p, κ_p). θ_p is defined by eqn (5) and measured from the y-direction, which corresponds to the tangent line of the plot. κ_p is the curvature of the plot (eqn (6)).²⁸ While (R, θ) correspond to the static nature of interactions, (θ_p, κ_p) represent the dynamic nature. Indeed, (θ_p, κ_p) originate mainly from the data of perturbed structures, but they are recognized as the nature at the fully optimized structure. k defined by eqn (7) is also an important and useful parameter in AIM analysis. AIM-DFA will provide an excellent possibility to evaluate, understand and classify weak to strong interactions in a unified form.

Fig. 1 Polar (R, θ) coordinate representation of H_b(r_c) versus H_b(r_c) − V_b(r_c)/2, with the (θ_p, κ_p) parameters.

Methodological details of QC and AIM calculations

Structures of 1–6 were optimized using the Gaussian 09 program package,³⁸ after the conformation research with the Monte-Carlo method³⁹ in the Spartan 02 (ref. 40) for 1–3. At least seven hundred and twenty two conformers were generated for each with the PM3 method.⁴¹ Thirty of most stable conformers by the Monte-Carlo method were re-optimized using the 6-311+G(3d) basis sets⁴² for S and Se and the 6-311++G(d,p) basis sets for O, N, C and H at the M062X level.⁴³ Frequency analysis was performed on three of most stable conformers at the same method for each of 1a–3c, where a represents the most stable conformer with the second and third ones by b and c, respectively. The global minima for 4–6 were determined by usual optimizations with the frequency analysis.

AIM parameters were calculated with the Gaussian 09 program package and analyzed by the AIM2000 program.⁴⁴ Normal coordinates of the internal vibrations (NIV) are employed to generate the perturbed structures necessary to evaluate the dynamic nature of the interactions.²⁸ The k-th perturbed structures in question (S_kw) will be given by the addition of the k-th NIV (N_k) to the coordinates of the standard orientation at the fully optimized structure (S_o) in the matrix representation.²⁸ Eqn (8) explains the treatment. The r(E, E′) values in the perturbed structures were determined as shown by eqn (9) or (9′), where a_o is the Bohr radius (0.52918 Å) with to (E, E′) in the fully optimized structure. Data at w = 0, ±0.05 and ±0.1 were employed for the analysis.^26,27,45 The k-th internal vibration (ν_n) must be located most effectively on E–E′, which corresponding to the selected N_k.

S_kw = S_o + f_kwN_k (8)

r(E, E′) = r_o(E, E′) + wa_o (9)

r = r_o + wa_o (9′)

Results and discussion

Fig. 2 draws the three of most stable conformers for 1–3 (1a–3c). Fig. 2 also shows the stretching modes of 1a–3c, necessary to evaluate the dynamic nature of the E–E′ bonds with NIV. Conformers 1a–3c are stabilized by intramolecular HBs, as shown in Fig. 2. Table 1 collects the optimized E–E′ distances and torsional angles (ϕ(CEE′C)) for 1–6, together with the distances and angles for the intramolecular HBs formed between the different moieties of the E–E′ bonds in 1a–3c.

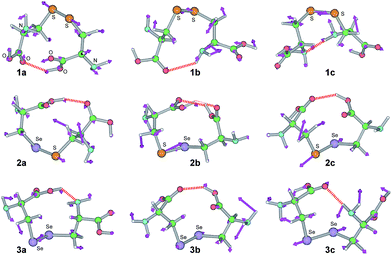Fig. 2 Optimized structures for 1a–3c. Directions of the motions, corresponding to NIV used to generate the perturbed structures, are shown (purple arrows), together with the intramolecular hydrogen bonds (red heavy dotted lines).

Table 1 Optimized E–E′ distances and torsional angles for 1–6, together with the distances and angles for the intramolecular hydrogen bonds in 1a–3c^a

Species^b	ΔErel (kJ mol^−1)	ro(E, E′) (Å)	ϕ(CEE′C) (°)	(A–H⋯B)	ro(A, H) (Å)	ro(B, H) (Å)	∠AHB (°)
a The 6-311+G(3d) basis sets being employed for S and Se with the 6-311++G(d,p) basis sets for O, N, C and H at the DFT level of M062X.b RSH = R-cysteine, for example.
RS-*-SR (1a: C1)	0.0	2.0625	67.7	(O–H⋯O)	0.9780	1.9828	149.8
RS-*-SR (1b: C1)	0.3	2.0471	−82.2	(N–H⋯O)	1.0155	2.4136	134.4
RS-*-SR (1c: C1)	0.7	2.0529	88.5	(N–H⋯N)	1.0210	2.2551	172.3
RS-*-SeR (2a: C1)	0.0	2.1984	−83.9	(O–H⋯O)	0.9850	1.8025	156.4
RS-*-SeR (2b: C1)	15.7	2.1890	84.3	(O–H⋯O)	0.9748	1.8996	142.6
				(O–H⋯O)	0.9743	2.1631	126.4
RS-*-SeR (2c: C1)	17.5	2.2011	94.0	(O–H⋯O)	0.9771	1.8581	142.9
RSe-*-SeR (3a: C1)	0.0	2.3275	88.5	(O–H⋯N)	0.9863	1.8955	137.7
RSe-*-SeR (3b: C1)	1.4	2.3303	93.4	(O–H⋯O)	0.9773	1.8335	145.1
RSe-*-SeR (3c: C1)	3.3	2.3309	90.2	(N–H⋯O)	1.0193	2.0185	167.6
MeS-*-SMe (4: C2)		2.0491	85.0
MeSe-*-SMe (5: C1)		2.1923	85.6
MeSe-*-SeMe (6: C2)		2.3236	86.1

---

Fig. 3 shows contour maps of ρ_b(r_c) drawn on an EE′C plane of 1a–3c. All BCPs expected are clearly detected, containing those on the E–E′, E–C (E′–C) and C–H bonds, together with HBs. AIM-DFA is applied to clarify the static and dynamic behavior of E–E′ in 1–6. Fig. 4 shows the plots of H_b(r_c) versus H_b(r_c) − V_b(r_c)/2 for 1–6. The magnified picture around the data of the fully optimized structures for 2a–2c and 5 is also shown in Fig. 4. AIM parameters corresponding to the static and dynamic behavior of E–E′ are obtained for 1–6, through analysis of the plots in Fig. 4, according to eqn (3)–(6). Table 2 collects the AIM functions and parameters of the static behavior evaluated for 1–6. Table 3 summarizes the AIM parameters of the dynamic behavior evaluated for 1–6.

Fig. 3 Contour maps of ρ_b(r_c) drawn on the E–E′–C planes of 1a–3c, together with BCPs (red solid circles), RCPs (ring critical points: lime green solid squares), and bond paths (solid lines). The counters (ea_o⁻³) are at 2^l (l = ±8, ±7, …, 0) and 0.0047, which corresponds to the molecular surface (heavy line).

Fig. 4 Plots of H_b(r_c) versus H_b(r_c) − V_b(r_c)/2 for 1–6. (a) Whole picture and (b) magnified one around data of fully optimized structures for 2a–2c and 5.

Table 2 Static nature of the E–E′ bonds in 1–6 at full optimized structures^a

Species^b	ρb(rc) (au)	c∇^2ρb(rc)^c (au)	Hb(rc) (au)	R^d (au)	θ^e (°)	k^f
a The 6-311+G(3d) basis sets being employed for S and Se with the 6-311++G(d,p) basis sets for O, N, C and H at the DFT level of M062X.b RSH = R-cysteine, for example.c c∇^2ρb(rc) = Hb(rc) − Vb(rc)/2 where c = ħ^2/8m.d R = [(Hb(rc) − Vb(rc)/2)^2 + Hb(rc)^2]^1/2 (eqn (3)).e θ = 90° − tan^−1[Hb(rc)/(Hb(rc) − Vb(rc)/2)] (eqn (4)).f k = Vb(rc)/Gb(rc) (eqn (7)).
RS-*-SR (1a: C1)	0.1409	−0.0117	−0.0710	0.0719	189.4	−2.495
RS-*-SR (1b: C1)	0.1443	−0.0126	−0.0749	0.0759	189.6	−2.509
RS-*-SR (1c: C1)	0.1432	−0.0124	−0.0737	0.0747	189.6	−2.508
RS-*-SeR (2a: C1)	0.1171	−0.0041	−0.0529	0.0531	184.4	−2.183
RS-*-SeR (2b: C1)	0.1188	−0.0045	−0.0547	0.0548	184.7	−2.195
RS-*-SeR (2c: C1)	0.1166	−0.0040	−0.0525	0.0527	184.4	−2.180
RSe-*-SeR (3a: C1)	0.1020	−0.0042	−0.0431	0.0433	185.6	−2.242
RSe-*-SeR (3b: C1)	0.1021	−0.0046	−0.0432	0.0434	186.0	−2.268
RSe-*-SeR (3c: C1)	0.1023	−0.0046	−0.0435	0.0437	186.1	−2.269
MeS-*-SMe (4: C2)	0.1446	−0.0131	−0.0751	0.0763	189.9	−2.535
MeSe-*-SMe (5: C1)	0.1189	−0.0048	−0.0544	0.0547	185.0	−2.213
MeSe-*-SeMe (6: C2)	0.1036	−0.0050	−0.0445	0.0448	186.4	−2.291

---

Table 3 Dynamic nature of the E–E′ bonds in 1–6 with NIV^a

Species^b	νn^c (cm^−1)	n for νn	kf^d (mdyn Å^−1)	θp^e (°)	κp^f (au^−1)
a The 6-311+G(3d) basis sets being employed for S and Se with the 6-311++G(d,p) basis sets for O, N, C and H at the DFT level of M062X.b RSH = R-cysteine, for example.c Frequency corresponding to the stretching mode of the E-*-E′ bond, where * means the bond critical point in question.d Force constants correspond to νn.e θp = 90° − tan^−1(dy/dx) where (x, y) = (Hb(rc) − Vb(rc)/2, Hb(rc)) (eqn (5)).f kp = |d^2y/dx^2|/[1 + (dy/dx)^2]^3/2 (eqn (6)).
RS-*-SR (1a: C1)	511.3	20	2.060	197.5	0.75
RS-*-SR (1b: C1)	522.5	21	1.118	197.4	0.67
RS-*-SR (1c: C1)	506.8	20	1.947	197.5	0.69
RS-*-SeR (2a: C1)	414.4	18	0.551	188.0	0.34
RS-*-SeR (2b: C1)	423.6	19	1.896	188.4	0.33
RS-*-SeR (2c: C1)	414.7	19	1.440	188.2	0.40
RSe-*-SeR (3a: C1)	301.9	15	1.875	188.9	0.71
RSe-*-SeR (3b: C1)	308.0	16	0.174	189.3	0.77
RSe-*-SeR (3c: C1)	298.7	13	0.938	189.4	0.68
MeS-*-SMe (4: C2)	513.7	6	2.645	197.6	0.66
MeS-*-SeMe (5: C1)	419.7	6	2.072	188.6	0.38
MeSe-*-SeMe (6: C2)	307.7	6	2.730	189.1	0.77

---

The behavior of E–E′ in 1–6 is examined by comparing the (θ, θ_p, R) values with those of the standard ones. The standard values are roughly determined to classify the interactions in question, employing typical weak to strong interactions. Scheme 3 illustrates the standard values for the typical interactions. The results tell us that θ are larger than 180° for SS interactions, which correspond to H_b(r_c) − V_b(r_c)/2 < 0. The θ_p value will play an important role to discuss the characters of CS interactions with θ < 180° (H_b(r_c) − V_b(r_c)/2 > 0). While the character of interactions will be that of CT-TBP (trigonal bipyramidal adducts formed through charge-transfer) such as in Me₂Se(-*-Cl)₂, if θ_p > 180°, it will be that of CT-MC (molecular complexes formed through CT) such as in Me₂S-*-Br₂, when θ_p < 180°, for example. The R values contribute to classify SS, further. Classical chemical bonds of SS are strong for R > 0.15 au but they would be weak when R < 0.15 au.²⁶

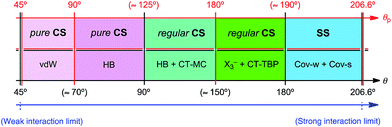Scheme 3 Rough classification of interactions by θ and θ_p.

The (θ/°, θ_p/°, R/au) values for S–S in 1a and 4 are (189.4, 197.5, 0.072) and (189.9, 197.6, 0.076), respectively. While the values for S–Se in 2a and 5 are (184.4, 188.0, 0.053) and (185.0, 188.6, 0.055), respectively, those for Se–Se in 3a and 6 are (185.6, 188.9, 0.043) and (186.4, 189.1, 0.045), respectively. The results show that all E–E′ in 1–6 are classified as the weak covalent bonds, since θ > 180° with R < 0.15 au.²⁶ The nature of E–E′ in 1a–3a is predicted to be very close to that of 4–6, respectively. The strength of E–E′ is reconfirmed in the order of Se–Se ≤ S–Se < S–S. All data of Se–Se, S–Se and S–S in 1–6 appear in the SS region. However, those of Se–Se and S–Se are closer to the regular CS region (θ_p ≈ 189°), relative to the case of S–S (θ_p ≈ 198°). Whereas R for 1a–3a are less than those of 4–6, respectively, the data for 1a–3a seem to appear at the opposite side of the origin in the plots. The discrepancies must be the reflection of the complex contributions from G_b(r_c) and V_b(r_c) to H_b(r_c) and H_b(r_c) − V_b(r_c)/2 in E–E′, according to eqn (1) and (2). It would be difficult to specify the reason for the characteristic behaviour in the plots, based on the data in Tables 2 and 3.

How are the E–E′ bonds affected by the formation of HBs? The formation of intramolecular HBs stabilizes 1–3, relative to the conformers with no such interactions. The A–H⋯B angles are predicted to be around 130–150° for HBs in 1–3, which must be the reflection of the restricted HBs in 1–3. The results may suggest that the intramolecular HBs are formed under somewhat undesirable conditions (see Table 1). The HBs in 1–3 must affect on the stability and the strength of E–E′ in 1–3. The variation of ϕ(CEE′C) in 1–3, relative to the case of 4–6, must be another evidence for the restricted HBs (Table 1). The conformation also affect on the strength of E–E′. In the case of 2, the S–Se bond becomes stronger in the order of 2c ≤ 2a < 2b, although very slightly (see Fig. 4b, Tables 2 and 3). The strength of S–Se seems almost independent of the stability in 2a–c, for example. Namely, such molecules are stabilized through the formation of HBs, but the E–E′ bonds could be sacrificed and somewhat weakened by the distortion.

The nature of the E–E′ bonds in 1–6 is well described with the dynamic nature of (θ_p, κ_p) and the static nature of (R, θ) by applying AIM-DFA.

Conclusion

AIM-DFA is applied to the E–E′ bonds (E, E′ = S and Se) in R-cystine (1) and the derivatives (2 and 3 for the S–Se and Se–Se derivatives, respectively), together with those of MeEE′Me (4–6). The dynamic and static behavior is clarified for E–E′ in 1–6 by the application. The nature of E–E′ in 1–6 is further examined by comparing the (θ, θ_p, R) values with those of the standard ones. The (θ/°, θ_p/°, R/au) values for S–S in 1a and 4 are (189.4, 197.5, 0.072) and (189.9, 197.6, 0.076), respectively. While the values for S–Se in 2a and 5 are (184.4, 188.0, 0.053) and (185.0, 188.6, 0.055), respectively, those for Se–Se in 3a and 6 are (185.6, 188.9, 0.043) and (186.4, 189.1, 0.045), respectively. All E–E′ in 1–6 are classified as the weak covalent bonds. The nature of E–E′ in 1a–3a is very close to that in 4–6, respectively. The strength of the bonds is predicted to be in the order of S–S > S–Se ≥ Se–Se. All data of E–E′ in 1–6 appear in the SS region. However, those of Se–Se and S–Se are closer to the regular CS region (θ_p ≈ 189°), relative to the case of S–S (θ_p ≈ 198°). The A–H⋯B angles in HBs of 1–3 are predicted to be around 130–150°, which must be the reflection of the restricted HBs in 1–3. Indeed, 1–3 are stabilized by the formation of HBs, but the E–E′ bonds could be sacrificed and somewhat weakened by the distortion. The nature of the E–E′ bonds in 1–6 is well described by (θ_p, κ_p) of the dynamic nature and (R, θ) of the static nature obtained through AIM-DFA.

Acknowledgements

This work was partially supported by a Grant-in-Aid for Scientific Research (nos 23350019 and 26410050) from the Ministry of Education, Culture, Sports, Science and Technology, Japan. The support of the Wakayama University Original Research Support Project Grant and the Wakayama University Graduate School Project Research Grant is also acknowledged.

Notes and references

1. (a) Organic Selenium Compounds: Their Chemistry and Biology, ed. D. L. Klayman and W. H. H. Günther, Wiley, New York, 1973; (b) The Chemistry of Organic Selenium and Tellurium Compounds, ed. S. Patai and Z. Rappoport, John-Wiley and Sons, New York, 1986, vol. 1 and 2; (c) Organic Selenium Chemistry, ed. D. Liotta, Wiley-Interscience, New York, 1987; (d) Organoselenium Chemistry, A practical Approach, ed. T. G. Back, Oxford University Press, Oxford, 1999; (e) Organoselenium Chemistry Modern Developments in Organic Synthesis, Topics in Current Chemistry, ed. T. Wirth, Springer, Berlin, Heidelberg, New York, London, Paris, Tokyo, 2000.
2. Chemistry of Hypervalent Compounds, ed. K.-y. Akiba, Wiley-VCH, New York, 1999.
3. (a) W. Nakanishi, Hypervalent Chalcogen Compounds, in Handbook of Chalcogen Chemistry: New Perspectives in Sulfur, Selenium and Tellurium, ed. F. A. Devillanova, Royal Society of Chemistry, Cambridge, 2006, ch. 10.3, pp. 644–668; (b) W. Nakanishi and S. Hayashi, Hypervalent Chalcogen Compounds, in Handbook of Chalcogen Chemistry: New Perspectives in Sulfur, Selenium and Tellurium, ed. F. A. Devillanova and W.-W. du Mont, Royal Society of Chemistry, Cambridge, 2nd edn, 2013, vol. 2, ch. 12.3, pp. 335–372.
4. A. J. Mukherjee, S. S. Zade, H. B. Singh and R. B. Sunoj, Chem. Rev., 2010, 110, 4357.
5. M. Kulcsar, A. Beleaga, C. Silvestru, A. Nicolescu, C. Deleanu, C. Todasca and A. Silvestru, Dalton Trans., 2007, 2187; A. Beleaga, M. Kulcsar, C. Deleanu, A. Nicolescu, C. Silvestru and A. Silvestru, J. Organomet. Chem., 2009, 694, 1308.
6. S. Hayashi and W. Nakanishi, J. Org. Chem., 1999, 64, 6688; W. Nakanishi, S. Hayashi and S. Toyota, J. Org. Chem., 1998, 63, 8790; W. Nakanishi, S. Hayashi and S. Toyota, Chem. Commun., 1996, 371; W. Nakanishi, S. Hayashi and H. Yamaguchi, Chem. Lett., 1996, 947; W. Nakanishi, Chem. Lett., 1993, 2121.
7. W. Nakanishi, S. Hayashi and T. Arai, Chem. Commun., 2002, 2416.
8. W. Nakanishi, S. Hayashi, S. Morinaka, T. Sasamori and N. Tokitoh, New J. Chem., 2008, 32, 1881.
9. (a) W. Brandt and L. A. Wessjohann, ChemBioChem., 2005, 6, 386; (b) S. Gromer, L. A. Wessjohann, J. Eubel and W. Brandt, ChemBioChem., 2006, 7, 1649; (c) L. A. Wessjohann, A. Schneider, M. Abbas and W. Brandt, Biol. Chem., 2007, 388, 997; (d) B. M. Lacey, B. E. Eckenroth, S. Flemer Jr and R. J. Hondal, Biochemistry, 2008, 47, 12810; (e) L. A. Wessjohann and A. Schneider, Chem. Biodiversity, 2008, 5, 375.
10. B. Ren, W. Huang, B. Åkesson and R. Ladenstein, J. Mol. Biol., 1997, 268, 869.
11. W. A. Hendrickson, Science, 1991, 254, 51.
12. A. Ishii, S. Matsubayashi, T. Takahashi and J. Nakayama, J. Org. Chem., 1999, 64, 1084.
13. T. Saiki, K. Goto and R. Okazaki, Angew. Chem., Int. Ed., 1997, 36, 2223; K. Goto, D. Sonoda, K. Shimada, S. Sase and T. Kawashima, Angew. Chem., Int. Ed., 2010, 49, 545.
14. G. Mugesh and H. B. Singh, Chem. Soc. Rev., 2000, 29, 347.
15. K. P. Bhabak and G. Mugesh, Chem.–Asian J., 2009, 4, 974; B. K. Sarma and G. Mugesh, Chem.–Eur. J., 2008, 14, 10603.
16. K. P. Bhabak and G. Mugesh, Chem.–Eur. J., 2009, 15, 9846; K. P. Bhabak and G. Mugesh, Chem.–Eur. J., 2008, 14, 8640; K. P. Bhabak and G. Mugesh, Chem.–Eur. J., 2007, 13, 4594; B. K. Sarma and G. Mugesh, Inorg. Chem., 2006, 45, 5307; P. P. Phadnis and G. Mugesh, Org. Biomol. Chem., 2005, 3, 2476.
17. M. Iwaoka, R. Ooka, T. Nakazato, S. Yoshida and S. Oishi, Chem. Biodiversity, 2008, 5, 359.
18. F. Kumakura, B. Mishra, K. I. Priyadarsini and M. Iwaoka, Eur. J. Org. Chem., 2010, 440.
19. K. Arai, K. Dedachi and M. Iwaoka, Chem.–Eur. J., 2011, 17, 481.
20. S. Yoshida, F. Kumakura, I. Komatsu, K. Arai, Y. Onuma, H. Hojo, B. G. Singh, K. I. Priyadarsini and M. Iwaoka, Angew. Chem., Int. Ed., 2011, 50, 2125 (Angew. Chem., 2011, 123, 2173).
21. D. Manna and G. Mugesh, J. Am. Chem. Soc., 2012, 134, 4269.
22. L. Flohé, E. A. Günzler and H. H. Schock, FEBS Lett., 1973, 32, 132.
23. L. Flohé, Glutathione peroxidase brought into focus, in Free radicals in biology, ed. W. A. Pryor, Academic Press, New York, 1982, vol. 5, pp. 223–253.
24. V. S. Minkov and E. V. Boldyreva, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2009, 65, o245; T. N. Drebushchak, S. V. Bizyaev and E. V. Boldyreva, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2008, 64, o313; V. S. Minkov and E. V. Boldyreva, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2008, 64, o344.
25. W. Nakanishi, S. Hayashi and K. Narahara, J. Phys. Chem. A, 2008, 112, 13593.
26. W. Nakanishi, S. Hayashi and K. Narahara, J. Phys. Chem. A, 2009, 113, 10050.
27. W. Nakanishi and S. Hayashi, Curr. Org. Chem., 2010, 14, 181.
28. W. Nakanishi and S. Hayashi, J. Phys. Chem. A, 2010, 114, 7423.
29. Atoms in Molecules. A Quantum Theory, ed. R. F. W. Bader, Oxford University Press, Oxford, 1990.
30. The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, ed. C. F. Matta and R. J. Boyd, Wily-VCH, Weinheim, Germany, 2007, ch. 1.
31. (a) F. Biegler-König and J. Schönbohm, J. Comput. Chem., 2002, 23, 1489; (b) F. Biegler-König, J. Schönbohm and D. Bayles, J. Comput. Chem., 2001, 22, 545; (c) R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314; (d) R. F. W. Bader, Chem. Rev., 1991, 91, 893; (e) R. F. W. Bader, Acc. Chem. Res., 1985, 18, 9; (f) T. H. Tang, R. F. W. Bader and P. MacDougall, Inorg. Chem., 1985, 24, 2047; (g) R. F. W. Bader, T. S. Slee, D. Cremer and E. Kraka, J. Am. Chem. Soc., 1983, 105, 5061; (h) F. Biegler-König, R. F. W. Bader and T. H. Tang, J. Comput. Chem., 1982, 3, 317.
32. J. M. Molina and J. A. Dobado, Theor. Chem. Acc., 2001, 105, 328.
33. J. A. Dobado, H. Martînez-Garcîa, J. M. Molina and M. R. Sundberg, J. Am. Chem. Soc., 2000, 122, 1144.
34. S. K. Ignatov, N. H. Rees, B. R. Tyrrell, S. R. Dubberley, A. G. Razuvaev, P. Mountford and G. I. Nikonov, Chem.–Eur. J., 2004, 10, 4991.
35. S. K. Tripathi, U. Patel, D. Roy, R. B. Sunoj, H. B. Singh, G. Wolmershäuser and R. J. Butcher, J. Org. Chem., 2005, 70, 9237.
36. R. J. Boyd and S. C. Choi, Chem. Phys. Lett., 1986, 129, 62.
37. See Fig. 2 in W. Nakanishi and S. Hayashi, J. Phys. Chem. A, 2013, 117, 1795.
38. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2009.
39. R. W. B. Ardill, K. J. M. Moriarty and M. Creutz, Comput. Phys. Commun., 1983, 29, 97; M. Creutz, Phys. Rev. Lett., 1983, 50, 1411 , see also P. Bratley, B. L. Fox and L. E. Schrage, A Guide to Simulation, Springer-Verlag, New York, 1987; G. M. Kalos and P. A. Whitlock, Monte Carlo Methods, John Wiley & Sons, New York, 1986; A. R. Leach, Molecular Modelling. Principles and Applications, Addison Wesley Longman, Essex, England, 1996.
40. Spartan ’02 for Windows, Wavefunction, Inc., Irvine, CA, Spartan '02 Windows, Tutorial and User's Guide, Wavefunction, Inc., Irvine, CA, 2001.
41. J. J. P. Stewart, J. Comput. Chem., 1989, 10, 209.
42. In our experience, the 6-311+G(d) basis sets or higher ones are recommended, when usual organic selenium compounds are calculated. For the 6-311+G(3d) basis sets, see: R. C. Binning Jr and L. A. Curtiss, J. Comput. Chem., 1990, 11, 1206; L. A. Curtiss, M. P. McGrath, J.-P. Blaudeau, N. E. Davis, R. C. Binning Jr and L. Radom, J. Chem. Phys., 1995, 103, 6104; M. P. McGrath and L. Radom, J. Chem. Phys., 1991, 94, 511 , for the diffuse functions (+ and ++), see T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. v. R. Schleyer, J. Comput. Chem., 1983, 4, 294 , see for example W. Nakanishi and S. Hayashi, J. Phys. Chem. A, 1999, 103, 6074.
43. Y. Zhao and G. D. Truhlar, Org. Lett., 2006, 8, 5753; E. S. Wheeler and N. K. Houk, J. Chem. Theory Comput., 2010, 6, 395; S. Rayne and K. Forest, J. Mol. Struct.: THEOCHEM, 2010, 948, 102; S. Rayne and K. Forest, Nat. Prec., 2010 DOI:10.1038/npre.2010.4865.1.
44. The AIM2000 program (Version 2.0) is employed to analyze and visualize atoms in molecules: F. Biegler-König, J. Comput. Chem., 2000, 21, 1040 , see also ref. 31b.
45. The bond orders become 1.50 and 0.67 times larger than the initial value if they are calculated at 0.2a_o shorter and longer distances from the initial length, respectively.⁴⁶ The change in the angles could be observed and seems to affect not so much on our discussion to classify various interactions.^28,47.
46. L. Pauling The Nature of the Chemical Bond, Cornell University Press, Ithaca, New York, 3rd edn, 1960, ch. 7, pp. 221–264; L. Pauling, J. Am. Chem. Soc., 1947, 69, 542.
47. See also, W. Nakanishi, S. Hayashi, K. Matsuiwa and M. Kitamoto, Bull. Chem. Soc. Jpn., 2012, 85, 1293.

---

Footnote

† Electronic supplementary information (ESI) available: The fully optimized structures given by Cartesian coordinates for examined molecules and adducts. See DOI: 10.1039/c4ra13276a

---