Computational modelling of the enantioselectivity in the asymmetric 1,4-addition reaction catalyzed by a Rh complex of a S-chiral disulfoxide†
Abstract
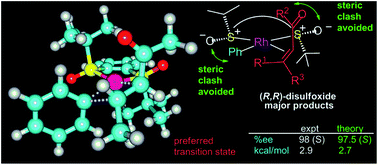
Computational chemistry is a powerful tool for understanding chiral catalysis and aiding future catalyst design. Here we present a DFT (PCM/PBE0/DGDZVP) modelling of the enantioselective step in the 1,4-addition of phenylboronic acid to 5 Michael acceptors catalyzed by Rh ligated with a disulfoxide ligand whose only source of chirality is the sulfur atoms. For all substrates, the predicted absolute configuration was in agreement with the experiment. Using the dispersion-interaction-corrected SMD/M06 method improved the quantitative agreement of predicted and experimental %ee values (within 0.2–0.8 kcal mol−1). The high steric pressure exerted by the bulky tert-butyl groups is the primary determinant of the enantioselectivity.

 Please wait while we load your content...
Please wait while we load your content...