A valley beam splitter of massive Dirac electrons

Abstract

We propose an electrically controllable valley beam splitter of massive Dirac electrons through the valley dependent Goos–Hänchen effect. The device consists of a monolayer graphene grown on a substrate and two ferromagnetic stripes with magnetizations directed along the current direction (the x axis). We found that the transmitted K and K′ valley electron beams exit at different longitudinal positions, and they can be separated spatially. The lateral displacements for the K and K′ valley electron beams, as well as their separations, can be enhanced by the transmission resonances formed between the two ferromagnetic stripes. The spatial separation between the K and K′ valley electron beams can reach values up to several thousands of wavelengths, which indicates that we can collect the two beams at different positions in the experiment. Our results can stimulate further experimental investigation of valley beam splitter in gapped graphene.

---

Introduction

Since the discovery of graphene in 2004,¹ the strictly two-dimensional carbon nano-material has received increasing attention owing to its potential applications in electronic and spintronic devices.^2–9 Charge carriers in graphene behave like relativistic Dirac fermions, described by the Dirac equation, with a dispersion resembling that of an electromagnetic wave.¹⁰ As a result, graphene is also regarded as a promising candidate for optoelectronic applications.^11,12 Currently, a number of optics-like phenomena have been found in graphene, such as the electron lens effect,^13,14 Brewster's angle,¹⁵ and the Goos–Hänchen (GH) effect.¹⁶ The GH effect is an interfacial effect between two media with different refractive indices, which results in a lateral shift of the light beam totally reflected from the dielectric surface. It was predicted by Sir Isaac Newton¹⁷ and realized experimentally by Goos and Hänchen.¹⁸ Until now, a number of studies of the control of electron transport by the GH effect have been undertaken in graphene^{15,16,19–23} such as the giant GH shift in graphene double-barrier structures,¹⁹ the GH effect in a graphene p–n junction,¹⁶ and the valley-dependent GH shift in strained graphene.^15,20

Apart from the spin of an electron, graphene has another degree of freedom: the valley pseudospin, which refers to the two inequivalent Dirac cones at the K and K′ points of the hexagonal Brillouin zone.^24,25 Similar to the electron spin in spintronics, the valley pseudospin in graphene can also be used as a carrier of information, as well as a transmitter of information, and this research area is referred to as valleytronics.^26,27 This opens up new opportunities and directions for the study and development of valley-based electronic devices in graphene. Because the two valleys, K and K′, in clean bulk graphene are related by time-reversal symmetry,²⁸ an important task of graphene valleytronics is to break the time-reversal symmetry and generate uneven distribution of electrons in the valleys. Up to now, several schemes have been proposed to manipulate valley-dependent transport in graphene. Strain effects^{15,20,28–31} can induce pseudomagnetic fields in graphene, and the signs of the effective magnetic fields for the K and K′ valleys are opposite. Other methods, such as the line defects³² and trigonal band warping^33–35 have also attracted detailed studies. Recently, researchers found that a Dirac gap can be induced by growing graphene epitaxially on various substrates,^36,37 such as SiC and BN, and the size of the gap can be from a few to hundreds of meV. This development opens up more possibilities and stimulates more studies in this area.^38–40 In the present study, we propose an electrically controllable valley beam splitter through the valley-dependent Goos–Hänchen effect in a resonant double-barrier structure of gapped graphene.

Device structure

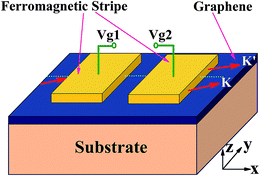
The schematic illustration of the proposed valley beam splitter is shown in Fig. 1. Graphene is epitaxially grown on a substrate, which can induce a Dirac gap in the graphene. Two ferromagnetic stripes with magnetizations along the x-axis are deposited on the graphene to form a double-barrier resonant structure. We need to point out that the two magnetic barriers are also used as top gates for adding two electric potentials, V_g1 and V_g2, to the structure, through which we can control the lateral displacements of the transmitted beams electrically. In this structure, the lateral displacement of an electron beam is valley dependent; thus, there will be a separation between the transmitted beams in the two valleys.

Fig. 1 Schematic illustration of the proposed valley beam splitter. A graphene sheet grown on a substrate is deposited with two ferromagnetic stripes with magnetizations along the x-axis. The two ferromagnetic stripes are also used as the top gates for the two applied electric potentials, i.e. V_g1 and V_g2.

We calculated the Goos–Hänchen lateral shifts along the interface for the electron beams in the two valleys, which are very large compared to the wavelength, and strongly dependent on the parameters of the structure and the electric potentials. We also note that the spatial separation between the K and K′ valley beams can be enhanced by the transmission and reflection resonances formed between the two magnetic barriers. For suitable parameters, the spatial separation between the two valley electron beams can reach values up to several thousands of wavelengths. In our simulation, all of the parameters used are achievable in experiment and some are set according to the experimental values. Therefore, our proposed scheme is very useful for the realization of a practical valley beam splitter and contributes to the development of graphene valleytronics.

Model and calculation

A ferromagnetic stripe can induce an inhomogeneous magnetic field in graphene, which can be well approximated by two magnetic δ functions.^41,42 Thus, we have a constant vector potential in the magnetic barrier region. We assume that the FM stripes are electrically insulated from the graphene layer and that no ferromagnetic proximity effect (spin splitting) is induced in the graphene layer. The motion of the low-energy massive electrons in the presence of a vector potential and an electric potential is described by the Dirac Hamiltonian:
where v_F ≈ 10⁶ ms⁻¹ is the Fermi velocity, are the Pauli matrices for the pseudospin in the sublattice space, is the wave vector, is the vector potential, which in the Landau gauge has the form , τ = ±1 is the valley index, Δ is the mass term induced by the substrate, V is the electric potential, and σ₀ is a unit matrix. Both the vector and the electric potentials are dependent on the x-coordinate to describe the barrier structure. For convenience, we use the two characteristic parameters: the magnetic length l_B = (ħ/eB)^1/2 and the energy E₀ = ħv_F/l_B to express all of the quantities in dimensionless units. In our calculation, we set B = 0.5T; thus, we obtain l_B = 36.8 nm and E₀ = 17.7 meV.

The wave functions in each region for an electron incident from the left into a single magnetic barrier are as follows:

where ψ_L and ψ_R are the wave functions in the left region and the right region, respectively, and ψ_M is the wave function in the magnetic barrier region. The wave vectors are related to E_F and other parameters through and . The electron's wavelength is related to the Fermi energy by . For E_F = 1 (17.7 meV), Δ = 0.5 (8.85 meV) was used in our calculation, and the wavelength was 7.33l_B (269.9 nm). The reflection r_τ and transmission amplitudes t_τ are obtained by matching the wave functions across the boundaries. We obtain the transmission and the reflection amplitudes for the entire double-magnetic barrier structure by combining the scattering matrices using the expression given in pages 125–26 of the ref. 43. Both parallel and antiparallell⁴² (two vector potentials are antisymmetric) magnetization configurations are considered in our study. According to the stationary-phase approximation,⁴⁴ the GH shift for the transmitted beam can be expressed as 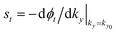where ϕ_t is the phase for the transmission amplitude, defined as ϕ_t = Im(ln(t)) = Im ln(|t|e^iϕ_t).

Results

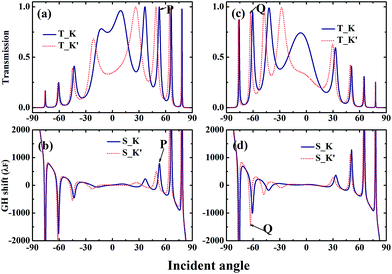
According to the stationary-phase approximation, the GH shift is determined by the derivative of the phase of the transmission amplitude with respect to the transverse wave vector. Thus, it is useful for us to analyze the phases of the transmitted and reflected beams, particularly its dependence on the incident angle (related to the transverse wave vector). In Fig. 2(a), we show the phases of transmission and reflection amplitudes vs. the incident angle for a single magnetic barrier with an electric potential V_g. It is obvious that the phase (blue solid line in Fig. 2(a)) of the transmission amplitude for a single magnetic barrier is independent of the valley index. Thus, the GH displacements of the K and K′ valley electron beams for a single magnetic barrier will be the same, which indicates that the transmitted K and K′ valley electron beams cannot be separated through the GH shift. Both the transmission (blue solid line in Fig. 2(b)) and reflection (red-dotted line in Fig. 2(b)) probabilities are valley independent for a single barrier. It should be noted that the phase of the reflection amplitude (the red-dotted and green-dashed dotted lines in Fig. 2(a)) is dependent on the valley index; thus, we guess that a double-barrier structure with multiple reflections between the barriers may give a valley-dependent transmission phase. For the double-barrier resonant structure, we consider two parallel magnetic barriers and an electric potential barrier (V_g1 = 1, V_g2 = 0). As shown in Fig. 2(c), the transmission amplitude phase is dependent on the valley index in a double-barrier structure, which provides us a method for separating the K and K′ valley electron beams through the GH lateral shift. Moreover, the resonances may play an important role in electron tunneling and the GH shift in the proposed double-barrier structure, which provides us a method to manipulate the transport of electrons.

Fig. 2 (a) The transmission and reflection phases, and (b) transmission and reflection probabilities vs. the incident angle for a single FM barrier for the two valleys. (c) The transmission phase and (d) transmission probability vs. the incident angle for a double-barrier parallel structure for the two valleys. The parameters for the single barrier are E_F = 1, Δ = 0.5, V_g = 1, and L = 1, and the parameters for the double-barrier structure are E_F = 1, Δ = 0.5, V_g1 = 1, V_g2 = 0, L = 1, and W = 2. When the widths of the FM stripes are large, the transmission is small. We therefore consider the width L = 1 and 2 in the results below, and thus reasonable transmission is obtained in the structure.

The angular dependence of the GH shift and transmission probability for our proposed resonant structure vs. the incident angle is presented in Fig. 3. First, it should be noted that the GH shift for both the antiparallel and parallel structures can be up to thousands of Fermi wavelengths, and the spatial separations between the K and K′ valley electrons can be larger than 1000 Fermi wavelengths. For the antiparallel structure (see Fig. 3(a) and (b)), we marked a transmission resonance peak as point P in the figure, and we can see that a large spatial separation occurs at this resonance peak. It is easy to note that the manipulation of transmission resonances provides us a method to control the GH shift. For the parallel structure (see Fig. 3(c) and (d)), similar phenomena are found. For example, the GH shifts of the K and K′ valley electron beams for the Q point in Fig. 3 are larger than 1000 Fermi wavelengths.

Fig. 3 (a) Transmission probability and (b) GH shift vs. the incident angle for the antiparallel structure. (c) Transmission probability and (d) GH shift vs. the incident angle for the parallel structure. The parameters are E_F = 1, Δ = 0.5, V_g1 = 0, V_g2 = 1, L = 1, and W = 15.

In Fig. 4, we show the GH shifts and transmission probabilities of the K and K′ valley electron beams for the antiparallel structure vs. the gate voltages to investigate how the gate voltage can control the GH shift. First, it should be noted that both the transmission and GH shifts of K and K′ valley electron beams are identical when the external gate voltages are zero. Thus, the external gate voltages play an important role in breaking the symmetry of the two valleys. It can be seen from Fig. 4(b) and (d) that the transmission oscillates with the gate voltages, and high transmission probability can be found at resonance peaks. It should also be noted that the GH shifts in Fig. 4(a) and (c) oscillate with the gate voltages with peaks found near the transmission resonance peaks. This indicates that we can electrically manipulate the transport of electron beams through the external gate voltages, which is very useful for the development of graphene-based valleytronic devices. It can be seen from Fig. 4(a) and (c) that the lateral displacements of K and K′ valley electrons can be very large compared to the Fermi wavelength. More importantly, there is a large difference in the displacements of K and K′ valleys, and the two electron beams can be effectively separated.

Fig. 4 GH shifts and transmission probability of K and K′ electron beams for the antiparallel structure plotted as a function of the gate voltage. The parameters for (a) and (b) are E_F = 1, Δ = 0.5, V_g2 = 0, L = 2, W = 15, and θ = π/4, and the parameters for (c) and (d) are E_F = 1, Δ = 0.5, V_g1 = 0, L = 2, W = 13.5, and θ = π/4.

For the parallel structure, we only consider one external gate voltage added to one of the two top gates as the effects of the two top gates are equivalent in the parallel structure. Similarly, we show the GH shifts and transmission of K and K′ valley electron beams in Fig. 5, in which it can be seen that the transmission probability and GH shifts oscillate with the external gate voltage. Similar to the antiparallel structure, we found that large GH shifts occur at the transmission peaks. More interestingly, the GH shifts for the K and K′ valley beams can be negative or positive by changing the external gate voltage, which indicates that we can easily separate the two beams spatially. It can be noted from the results that the spatial separation between the K and K′ valley electron beams can be larger than 4000λ_F, which is quite useful.

Fig. 5 GH shifts and the transmission probability of K and K′ electron beams for the parallel structure plotted as a function of gate voltage. The parameters are E_F = 1, Δ = 0.5, V_g2 = 0, L = 2, W = 13.5, θ = π/4.

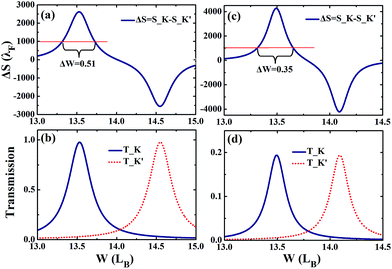
It has been noted in the previous discussion that large GH shift occurs at the transmission peaks; thus, the resonances formed between the two ferromagnetic barriers play a very important role in the transport of electron beams. Therefore, we take a further step to explore how the spatial separation between the two valley electron beams depends on the Fabry–Perot resonances formed between the ferromagnetic stripes (see Fig. 6). We have checked that more Fabry–Perot resonances will be found for the structure with a larger distance between the two barriers. Thus, we now discuss the relationship between the spatial separation of the two transmitted electron beams and the distance between the two magnetic barriers W. We can see that the separation (ΔS) between the K and K′ valleys for both the antiparallel and parallel structures oscillate with W. The oscillating amplitude increases with an increase in W. It should be noted that the peaks in ΔS appear at the resonant peaks of transmission for some values of W, and the spatial separation can be larger than 1000λ_F for the parallel structure. Although the GH shifts appear to depend sensitively on W, it is useful to point out here that the W is expressed in a unit of l_B = 36.8 nm, and a small change of 3 nm (equal to 0.1l_B) in W due to the fabrication error of W does not change the GH shift significantly and affect the usefulness of the proposed structure. In Fig. 7, we show an enlargement of a part of Fig. 6, which shows that a fluctuation of W by ±0.25 (0.17)l_B around W = 13.5l_B in an anti-parallel (parallel) can lower the beam separation but the value is still larger than 1000λ_F. This indicates that even for a dimension fluctuation of ±6.5 nm, the beam separation can still be above 1000λ_F. This shows that the proposed structure can be used as an effective beam splitter.

Fig. 6 (a) The spatial separation and (b) the transmission probability for antiparallel structure plotted as a function of distance between the ferromagnetic stripes. (c) The spatial separation and (d) the transmission probability for the parallel structure. The parameters are E_F = 1, Δ = 0.5, V_g1 = 0, V_g2 = 2, L = 2, and θ = π/4.

Fig. 7 An enlargement of a part of Fig. 6. All the parameters are the same as that of Fig. 6.

Conclusion

In summary, we have proposed an effective valley beam splitter using the GH shift in massive graphene. We investigated theoretically and numerically the valley-dependent GH shifts using the stationary phase approach. It is shown that a valley-unpolarized incident electron beam will be split into two transmitted valley-polarized electron beams, and the transmitted K and K′ electron beams can be detected at different longitudinal positions in the outgoing region. We found that the lateral displacements and transmission probability of K and K′ electron beams can be conveniently modulated by the external gate voltage, incident angle and separation distance between two ferromagnetic stripes. More importantly, the GH shifts for K and K′ electron beams, as well as the spatial separation between them, can be enhanced by the resonances formed between the two ferromagnetic stripes and can be modulated by the gate voltage. As a result, the GH shift can be electrically controlled, which is useful in applications. In our numerical simulation, we found that the spatial separation between K and K′ electron beams can be up to several thousands of Fermi wavelengths, which can be used as an effective beam separator. Our proposed device thus provides us an alternative way to generate pure valley currents and may stimulate further experiments in this direction.

Acknowledgements

This work was supported by the General Research Fund of the Research Grants Council of Hong Kong SAR, China, under Project no. CityU 100311/11, the City University of Hong Kong Strategic Grant (project no. 7004007) and the National Natural Science Foundation of China. (NSFC, Grant no. 11274260).

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666.
2. A. H. C. Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109.
3. N. Tombros, C. Jozsa, M. Popinciuc, H. T. Jonkman and B. J. van Wees, Nature, 2007, 448, 571.
4. C. L. Kane and E. J. Mele, Phys. Rev. Lett., 2005, 95, 226801.
5. R. Zhu and H. Chen, Appl. Phys. Lett., 2009, 95, 122111.
6. Y. Zhang, Y.-W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201.
7. K. S. Novoselov, E. McCann, S. V. Morozov, V. I. Fal'ko, M. I. Kastenel-son, U. Zeitler, D. Jiang, F. Schedin and A. K. Geim, Nat. Phys., 2006, 2, 177.
8. Q. Zhang, K. S. Chan and Z. J. Lin, Appl. Phys. Lett., 2011, 98, 032106.
9. Q. Zhang, Z. J. Lin and K. S. Chan, Appl. Phys. Lett., 2013, 102, 142407.
10. Y. P. Bliokh, V. Freilikher, S. Savel'ev and F. Nori, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 245134.
11. F. Bonaccorso, Z. Sun, T. Hasan and A. C. Ferrari, Nat. Photonics, 2010, 4, 611.
12. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183.
13. V. V. Cheianov, V. Fal'ko and B. L. Altshuler, Science, 2007, 315, 1252.
14. A. G. Moghaddam and M. Zareyan, Phys. Rev. Lett., 2010, 105, 146803.
15. Z. Wu, F. Zhai, F. M. Peeters, H. Q. Xu and K. Chang, Phys. Rev. Lett., 2011, 106, 176802.
16. C. W. J. Beenakker, R. A. Sepkhanov, A. R. Akhmerov and J. Tworzydlo, Phys. Rev. Lett., 2009, 102, 146804.
17. I. Newton, Opticks, Dover Publications, New York, 1952.
18. F. Goos and H. Hänchen, Ann. Phys., 1947, 436, 333.
19. Y. Song, H.-C. Wu and Y. Guo, Appl. Phys. Lett., 2012, 100, 253116.
20. F. Zhai, Y. Ma and K. Chang, New J. Phys., 2011, 13, 083029.
21. X. Chen, J.-W. Tao and Y. Ban, Eur. Phys. J. B, 2011, 79, 203.
22. X. Chen, X. J. Lu, Y. Ban and C.-F. Li, J. Opt., 2013, 15, 033001.
23. M. Sharma and S. Ghosh, J. Phys.: Condens. Matter, 2011, 23, 055501.
24. S. Das Sarma, S. Adam, E. H. Hwang and E. Rossi, Rev. Mod. Phys., 2011, 83, 407.
25. M. O. Goerbig, Rev. Mod. Phys., 2011, 83, 1193.
26. A. Rycerz, J. Tworzydo and C. W. J. Beenakker, Nat. Phys., 2007, 3, 172.
27. D. Xiao, W. Yao and Q. Niu, Phys. Rev. Lett., 2007, 99, 236809.
28. Y. Jiang, T. Low, K. Chang, M. I. Katsnelson and F. Guinea, Phys. Rev. Lett., 2013, 110, 046601.
29. A. Chaves, L. Covaci, K. Y. Rakhimov, G. A. Farias and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 205430.
30. F. Zhai, X. F. Zhao, K. Chang and H. Q. Xu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115442.
31. V. M. Pereira and A. H. Castro Neto, Phys. Rev. Lett., 2009, 103, 046801.
32. D. Gunlycke and C. T. White, Phys. Rev. Lett., 2011, 106, 136806.
33. R. Saito, G. Dresselhaus and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 2981.
34. M. Pereira Jr, F. M. Peeters, R. N. Costa Filho and G. A. Farias, J. Phys.: Condens. Matter, 2009, 21, 045301.
35. J. L. Garcia-Pomar, A. Cortijo and M. Nieto-Vesperinas, Phys. Rev. Lett., 2008, 100, 236801.
36. M. Trushin and J. Schliemann, Phys. Rev. Lett., 2011, 107, 156801.
37. S. Y. Zhou, G.-H. Gweon, A. V. Fedorov, P. N. First, W. A. de Heer, D.-H. Lee, F. Guinea, A. H. Castro Neto and A. Lanzara, Nat. Mater., 2007, 6, 770.
38. X. Zhai and G. Jin, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 235416.
39. D. Moldovan, M. Ramezani Masir, L. Covaci and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 115431.
40. F. Zhai, Nanoscale, 2012, 4, 6527–6531.
41. A. Matulis, F. M. Peeters and P. Vasilopoulos, Phys. Rev. Lett., 1994, 72, 1518.
42. F. Zhai and K. Chang, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 113409.
43. S. Datta, Electronic Transport in Mesoscopic Systems, Cambridge University Press, London, 1995, p. 126.
44. K. Artmann, Ann. Phys., 1948, 437, 87.

---