Estimation of the uncertainty of the measurement results of some trace levels elements in document paper samples using ICP-MS
Abstract
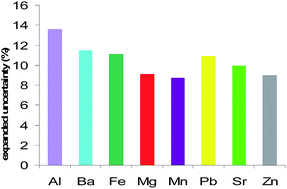
The measurement uncertainty characterizes the dispersion of the quantity values being attributed to the measurand and there are different approaches for uncertainty estimation. This study illustrates the application of the GUM (bottom-up) approach to estimate the measurement results uncertainty for the quantitative determination of Al, Ba, Fe, Mg, Mn, Pb, Sr and Zn from document paper samples using ICP-MS. The measurement uncertainty estimation was done based on identifying, quantifying and combining all the associated sources of uncertainty separately. Certain typical steps were followed: specifying the measurand; identifying the major sources of uncertainty; quantifying the uncertainty components; combining the significant uncertainty components; determining the extended combined standard uncertainty; reviewing the estimates and reporting the measurement uncertainty. For the eight mentioned trace elements the combined standard uncertainties and the expanded uncertainties were determined. The relative measurement uncertainty values lay between 7.7% and 13.6%. In all the five paper samples for each of the eight elements homogenous uncertainty values were obtained. In order to emphasize the uncertainty sources contributions, the percent contribution of the uncertainty components to the combined relative standard uncertainty were graphically represented for the elements determined by ICP-MS in paper samples. The previously validated method proved to be suitable for the intended purpose and when the uncertainty of the measurement results is estimated, it becomes a significant tool for characterizing the elemental composition of the document paper samples. Moreover, the applied approach for the uncertainty estimation enables improving the data quality and decision making.

 Please wait while we load your content...
Please wait while we load your content...