Effect of two-color laser pulse intensity ratio on intense terahertz generation
Abstract
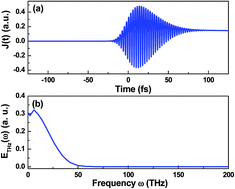
We theoretically demonstrate the effect of the intensity ratio of the two-color laser field on the terahertz generation based on a transient photocurrent model. We show that the terahertz generation depends on the intensity ratio of the two-color laser field at a given total laser intensity, and the optimal intensity ratio for the maximum terahertz generation will decrease with the increase of the total laser intensity. We also show that the final ionization degree can be used to explain the optimal intensity ratio change at different laser intensities. Furthermore, we utilize the increasing rate of electron density and the electron drift velocity to illustrate the physical mechanism of the maximum terahertz radiation generation.

 Please wait while we load your content...
Please wait while we load your content...