DOI:
10.1039/C4RA12530D
(Paper)
RSC Adv., 2015,
5, 9389-9395
Molecular dynamics simulations indicate that DNA bases using graphene nanopores can be identified by their translocation times
Received
16th October 2014
, Accepted 15th December 2014
First published on 15th December 2014
Abstract
The improvement of the resolution of DNA sequencing by nanopore technology is very important for its real-life application. In this paper, we report our work on using molecular dynamics simulation to study the dependence of DNA sequencing on the translocation time of DNA through a graphene nanopore, using the single-strand DNA fragment translocation through graphene nanopores with diameters down to ∼2 nm as examples. We found that A, T, C, and G could be identified by the difference in the translocation time between different types of nucleotides through 2 nm graphene nanopores. In particular, the recognition of the graphene nanopore for different nucleotides can be greatly enhanced in a low electric field. Our study suggests that the recognition of a graphene nanopore by different nucleotides is the key factor for sequencing DNA by translocation time. Our study also indicates that the surface of a graphene nanopore can be modified to increase the recognition of nucleotides and to improve the resolution of DNA sequencing based on the DNA translocation time with a suitable electric field.
1. Introduction
DNA sequencing with nanopores has attracted much attention since DNA translocation through the biological nanopore α-hemolysin was first demonstrated.1 In nanopore sequencing, a negatively charged biological molecule such as DNA2 or RNA3 is electrophoretically driven through a nanopore and its sequence is read off directly by measuring the reduction of the ion current during its translocation through the pore. This provides a promising technology for low-cost and high-throughput DNA sequencing, which is free of fluorescent labeling and enzyme-dependent amplification steps.4,5
It has been reported that DNA sequencing with single-nucleotide resolution could be achieved by a mutant MspA nanopore with phi29 DNA polymerase. This represents great progress in DNA sequencing with nanopores.6 However, the harsh environment for the lipid membrane used for supporting the biological nanopore has limited its further development. On the other hand, solid-state nanopores offer a number of advantages compared with the biological nanopores such as superior mechanical properties,7,8 multiplex detection,9 and high stability to complex environments.10 In recent years, significant progress has been made in DNA sequencing with solid-state nanopores.2,11,12 Note that conventional nanopores made from silicon nitride,13 aluminum oxide,14 and silicon oxide15 are several nanometers in thickness. As a result, a nanopore is occupied by many DNA bases at the same time in sequencing, which makes it difficult to detect a single-stranded DNA (ssDNA) molecule at single-base resolution. This problem shows that the resolution of DNA sequencing with solid state nanopores needs to be improved. A number of experiments and theoretical studies have been carried out to improve the resolution of DNA sequencing.16–21 For example, a sub-2 nm nanopore was used in DNA sequencing by Guo's22 and Wang's groups,23 where the force peak was considered as an effective index by which DNA nucleotides could be distinguished by simulating the stretching process of a DNA molecule through the graphene nanopore. Dekker et al. pointed out that the resolution of DNA sequencing could be improved and that the translocation time will decrease by lowering the hydrophobicity of graphene nanopores with non-covalently bound hydrophilic functional groups on a graphene nanopore surface.24 These studies greatly enhanced our understanding of DNA sequencing and paved a way to improve the resolution of DNA sequencing with solid-state nanopores. However, the error rate of DNA sequencing with solid-state nanopores is still too high for real-life applications and other ways to reduce the error rate for DNA sequencing with nanopores need to be developed.
Graphene nanopores have been investigated in DNA sequencing because of their single-atom thickness and unique mechanic properties. They have been used widely in DNA detection in recent years.25–27 In this work, single molecule sequencing with graphene nanopores to identify four bases was investigated by molecular dynamics (MD) simulation. Table 1 lists all the MD simulations we performed under various conditions. As shown in Fig. 1, an ssDNA molecule was observed translocating through a graphene nanopore under a certain electric field, and the translocation time was calculated to distinguish different types of bases. In this figure, the starting time t1 is defined as the time when the first atom of the DNA molecule starts to enter into the nanopore, whereas the end time t2 is defined as the time when the DNA molecule exits the nanopore completely. The time interval between t1 and t2 is defined as the DNA translocation time. By characterizing the profile of the translocation time for the DNA to pass through graphene nanopores of different diameters under various applied electric fields, we were able to distinguish the nucleotides of the DNA.
Table 1 Simulated systemsa
| |
Number of atoms |
Electric field (mV nm−1) |
Diameter of the pore (nm) |
KCl concentration (M) |
DNA (bp) |
Time (ns) |
| Sim represents simulation; I means that KCl ions were added to the system in the simulation; A, T, C and G represent the type of nucleotides. |
| SimIA1 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 564 564 |
100 |
1.6 |
1.0 |
poly(A)15 |
50 |
| SimIT1 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246 246 |
100 |
1.6 |
1.0 |
poly(T)15 |
50 |
| SimIC1 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 504 |
100 |
1.6 |
1.0 |
poly(C)15 |
50 |
| SimIG1 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335 335 |
100 |
1.6 |
1.0 |
poly(G)15 |
50 |
| SimIA2 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 564 564 |
200 |
1.6 |
1.0 |
poly(A)15 |
50 |
| SimIT2 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246 246 |
200 |
1.6 |
1.0 |
poly(T)15 |
50 |
| SimIC2 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 504 |
200 |
1.6 |
1.0 |
poly(C)15 |
50 |
| SimIG2 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335 335 |
200 |
1.6 |
1.0 |
poly(G)15 |
50 |
| SimIA3 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 564 564 |
400 |
1.6 |
1.0 |
poly(A)15 |
50 |
| SimIT3 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246 246 |
400 |
1.6 |
1.0 |
poly(T)15 |
50 |
| SimIC3 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 504 |
400 |
1.6 |
1.0 |
poly(C)15 |
50 |
| SimIG3 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335 335 |
400 |
1.6 |
1.0 |
poly(G)15 |
50 |
| SimIA4 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 564 564 |
600 |
1.6 |
1.0 |
poly(A)15 |
50 |
| SimIT4 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246 246 |
600 |
1.6 |
1.0 |
poly(T)15 |
50 |
| SimIC4 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504 504 |
600 |
1.6 |
1.0 |
poly(C)15 |
50 |
| SimIG4 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335 335 |
600 |
1.6 |
1.0 |
poly(G)15 |
50 |
| SimIA5 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735 |
100 |
2.0 |
1.0 |
poly(A)15 |
30 |
| SimIT5 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705 705 |
100 |
2.0 |
1.0 |
poly(T)15 |
30 |
| SimIC5 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713 713 |
100 |
2.0 |
1.0 |
poly(C)15 |
30 |
| SimIG5 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938 938 |
100 |
2.0 |
1.0 |
poly(G)15 |
30 |
| SimIA6 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735 |
200 |
2.0 |
1.0 |
poly(A)15 |
10 |
| SimIT6 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705 705 |
200 |
2.0 |
1.0 |
poly(T)15 |
10 |
| SimIC6 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713 713 |
200 |
2.0 |
1.0 |
poly(C)15 |
10 |
| SimIG6 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938 938 |
200 |
2.0 |
1.0 |
poly(G)15 |
10 |
| SimIA7 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735 |
400 |
2.0 |
1.0 |
poly(A)15 |
10 |
| SimIT7 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705 705 |
400 |
2.0 |
1.0 |
poly(T)15 |
10 |
| SimIC7 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713 713 |
400 |
2.0 |
1.0 |
poly(C)15 |
10 |
| SimIG7 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938 938 |
400 |
2.0 |
1.0 |
poly(G)15 |
10 |
| SimIA8 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735 |
600 |
2.0 |
1.0 |
poly(A)15 |
10 |
| SimIT8 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705 705 |
600 |
2.0 |
1.0 |
poly(T)15 |
10 |
| SimIC8 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713 713 |
600 |
2.0 |
1.0 |
poly(C)15 |
10 |
| SimIG8 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938 938 |
600 |
2.0 |
1.0 |
poly(G)15 |
10 |
| SimIA9 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735 |
50 |
2.0 |
1.0 |
poly(A)15 |
50 |
| SimIT9 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705 705 |
50 |
2.0 |
1.0 |
poly(T)15 |
50 |
| SimIC9 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713 713 |
50 |
2.0 |
1.0 |
poly(C)15 |
50 |
| SimIG9 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938 938 |
50 |
2.0 |
1.0 |
poly(G)15 |
50 |
| SimA5 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 831 |
50 |
2.0 |
0.0 |
poly(A)15 |
30 |
| SimT5 |
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 961 961 |
50 |
2.0 |
0.0 |
poly(T)15 |
30 |
| SimC5 |
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 921 921 |
50 |
2.0 |
0.0 |
poly(C)15 |
30 |
| SimG5 |
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105 105 |
50 |
2.0 |
0.0 |
poly(G)15 |
30 |
 |
| | Fig. 1 Initial structure of a system with an ssDNA and a graphene nanopore: (a) side view and (b) top view. The water molecules and ions are not shown for clarity. | |
2. Simulation details
System setup
To construct a graphene nanopore, the graphene sheet was set in the x–y plane with its center of mass at the origin (0, 0, 0) of the Cartesian coordinates; moreover, the atoms with their coordinates satisfying x2 + y2 < r2 were deleted, where r is the radius of the graphene nanopore. ssDNA fragments with different nucleotide compositions (as shown in Table 1) were constructed using the Hyperchem software (Version 7.0, Hypercube, Inc). Each system, which consisted of a nanopore and an ssDNA fragment, was solvated in a box of TIP3P28 water molecules and underwent a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-step energy minimization. 14 K+ were added into the system as counter-ions. Then, KCl ions were added into the box to match the same concentration as used in experiment.29 Note that DNA and KCl were modeled by the CHARMM27 force field30 and all carbon atoms in the graphene sheet were set to be neutral. The force field parameters for graphene were obtained from our previous work with σCC = 0.385 nm and εCC = −0.439 kcal mol−1 (ref. 31 and 32). All simulations were performed by the GROMACS 4.5.2 program,33 and all simulations were repeated in 3 times. The periodic boundary condition was applied to model the infinite graphene nanopore, and Ewald summation was used to recover the long range electrostatic interaction with a cutoff of 1.3 nm for the separation of the direct and reciprocal space summations. All atoms, including hydrogen atoms, were represented explicitly and the lengths of the bonds containing hydrogen atoms were fixed. The cutoff for the non-bonded van der Waals interaction was set by a switching function starting at 1.0 nm and reaching zero at 1.2 nm, and the time step was 2 fs. Note that the Langevin method was employed to maintain the temperature at 298 K with the pressure set at 101.3 kPa. Different bias voltages were applied in the simulations to drive the ions and ssDNA passing through the nanopores.
000-step energy minimization. 14 K+ were added into the system as counter-ions. Then, KCl ions were added into the box to match the same concentration as used in experiment.29 Note that DNA and KCl were modeled by the CHARMM27 force field30 and all carbon atoms in the graphene sheet were set to be neutral. The force field parameters for graphene were obtained from our previous work with σCC = 0.385 nm and εCC = −0.439 kcal mol−1 (ref. 31 and 32). All simulations were performed by the GROMACS 4.5.2 program,33 and all simulations were repeated in 3 times. The periodic boundary condition was applied to model the infinite graphene nanopore, and Ewald summation was used to recover the long range electrostatic interaction with a cutoff of 1.3 nm for the separation of the direct and reciprocal space summations. All atoms, including hydrogen atoms, were represented explicitly and the lengths of the bonds containing hydrogen atoms were fixed. The cutoff for the non-bonded van der Waals interaction was set by a switching function starting at 1.0 nm and reaching zero at 1.2 nm, and the time step was 2 fs. Note that the Langevin method was employed to maintain the temperature at 298 K with the pressure set at 101.3 kPa. Different bias voltages were applied in the simulations to drive the ions and ssDNA passing through the nanopores.
Analysis method
To describe the blockade current of a DNA molecule passing through a nanopore and to understand the phenomenon, time-dependent ionic current I(t) was calculated as follows:17| |
 | (1) |
where Lz is the length of the system in the z-direction, tint is set to 10 ps, N is the total number of atoms, including those of the DNA and ions, and qi is the charge of atom i. The translocation time Δttl of a DNA fragment through a nanopore was calculated as follows:where t1 is the time when the first atom of the DNA fragment enters into the nanopore and t2 is the time when the DNA fragment exits the nanopore completely. All DNA atoms were tracked with their positions; therefore, one could track the first atom that enters into the nanopore as well as the time t1. Similarly, if all atoms translocate through the position of graphene nanopore, t2 could be identified. The average blockade current for the DNA fragment to pass through the nanopore was calculated by| |
 | (3) |
3. Results and discussion
3.1 Effect of graphene diameter on DNA translocation
With the graphene nanopore of 1.6 nm diameter, the translocation time for the nucleotides is rather long. In our simulations, which were carried out for 50 ns, poly(A)15, poly(T)15, poly(C)15 and poly(G)15, were not observed to translocate through the nanopore completely under the electric field from 100 mV nm−1 to 600 mV nm−1 (SimIA1–SimIG4 in Table 1). The reason is that the diameter of ssDNA (∼1.1 nm) measured from experiments is almost comparable to that of the nanopore (1.6 nm), which makes it difficult for the DNA to pass through completely in the limited simulation time because of the steric effect. Based on our previous work,21 a large graphene nanopore can facilitate the translocation of ssDNA, but it decreases the identification at single nucleotide resolution. To achieve a balance between simulation time and resolution, a 2.0 nm graphene nanopore was selected for sequencing the DNA in our simulations. We found that poly(A)15, poly(T)15, poly(C)15, and poly(G)15 can translocate through the nanopore under a 100 mV nm−1 electric field (SimIA5–SimIG5 in Table 1) within 30 ns. The averaged blockade currents during the translocation of different nucleotides were calculated from the simulations (SimIA5–SimIG5 in Table 1), as shown in Fig. 2, and the order of the averaged blockade currents is T < C < A < G. Compared with the experimental order of T < G < C < A, the order of T, C, A is in accordance with that in the experiment6 with the exception that the blockade of G is much smaller than that of A in the experiment. However, the error rate in the experiment is always with the high blockade current of G, which indicates that the blockade current for G is not very stable. The reason that the blockade of G in our simulation is much higher than that in experiment is that the applied electric field (100 mV nm−1) in these simulations is much higher than that in the experiments, which makes it difficult to distinguish the blockade currents between A and G. Our results show that T and G can be identified from the blockade current very clearly because the blockade current for T is much lesser than that for G, which has been also observed experimentally.6,34 However, the difference in the blockade current between A and C is too small to be distinguishable with the 2.0 nm graphene nanopore. Another interesting phenomenon is that all the nucleotides tend to adsorb on the graphene nanopore surface after translocation. This observation has also been confirmed by experimental and theoretical works.17,24
 |
| | Fig. 2 The average blockade currents of different nucleotides poly(A)15, poly(T)15, poly(C)15, and poly(G)15 in the 2 nm graphene nanopore under an electric field at 100 mV nm−1. | |
3.2 Effect of electric fields on DNA translocation
In this study, we investigate the effect of electric field on DNA translocation time. Poly(A)15, poly(T)15, poly(C)15 and poly(D)15 were driven to pass through the 2 nm graphene nanopore by a series of electric fields ranging from 50 mV nm−1 to 600 mV nm−1. Under the 600 mV nm−1 electric field, the dynamics of poly(A)15 is rather different from that under the field at 100 mV nm−1. The applied electric field of 600 mV nm−1 is so high that the bases went through the nanopores instantaneously because at high electric fields, such as 600 mV nm−1, the dynamics of DNA molecule translocation through the nanopore was accelerated due to the higher electric field force on the DNA molecule. Although the thickness of graphene should be close to the spacing between two bases, the DNA molecule might bend in conformation and has less time to relax during the translocation process at a higher electric field (with fast translocation dynamics) and small nanopore. Therefore, the ratio of signal to noise decreased because two or more bases occupied the nanopore at the same time. This observation indicates that a high electric field is not appropriate for DNA sequencing with graphene nanopores because the field can increase the noise and decrease the resolution of DNA detection. To understand the effect of electric fields on the DNA translocation, the translocation time required for different polynucleotides to pass through the graphene nanopore under various electric fields was calculated. As shown in Fig. 3, the translocation times for different nucleotides are almost the same when the electric field is higher than 100 mV nm−1, reflecting that the translocation times of the nucleotides can hardly be distinguished with the 2 nm graphene nanopore under a high electric field. Based on Newton's equation, the entire movement of the DNA fragment can be calculated as follows:| |
 | (4) |
| |
 | (5) |
where Δf(t) is the total force on the DNA fragment caused by graphene atoms, water molecules and ions, which is time dependent. Under a high electric field, Δf(t) can be ignored. The acceleration a can be estimated by eqn (6), and the translocation time can be expressed by eqn (7) where L is the length of the DNA fragment. Thus, for a specified DNA fragment, the translocation time is calculated as an ideal case where DNA does not interact with the ion, water and graphene in the system and is only related to the electric field as expressed in eqn (8), where A is the parameter.| |
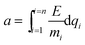 | (6) |
| |
 | (7) |
 |
| | Fig. 3 (a) Change of the translocation time of poly(A)15 with the electric field (black square) in the 2 nm graphene nanopore. The red line is the fitted curve; (b) change of the translocation times of different polynucleotides with different electric field in the 2 nm graphene nanopore. | |
As shown in Fig. 3(b), the curves obtained from fitting to eqn (8) are in good agreement with the translocation times from the simulations, especially under high electric fields. This verifies that the interactions between the bases and other components, such as ions and the graphene nanopores, can be ignored under a high electric field. This is also the reason why the translocation times for different bases are almost the same under high electric fields. Therefore, the different types of bases could not be distinguished by translocation time under a high electric field.
To distinguish different bases of ssDNA by the translocation time, a lower electric field of 50 mV nm−1 was applied in the simulations with the 2 nm graphene nanopore. The translocation times of poly(G)15, poly(C)15, poly(A)15, and poly(T)15 in the nanopore are 13.2 ± 0.8 ns, 10.1 ± 0.6 ns, 4.8 ± 0.2 ns and 3.2 ± 0.1 ns, respectively, as shown in Fig. 4. The translocation time for poly(G)15 is ca. 13.2 ns in the electric field of 50 mV nm−1 and is ca. 6.4 ns in that of 100 mV nm−1. With a much lower electric field, the translocation time for all types of nucleotides is extended. This indicates that the speed of translocation can be decreased with a lower electric field, which is consistent with the results from our previous work21 and the experimental work from other groups.27 In addition, the gaps between the translocation times of four types of nucleotides are much larger in 50 mV nm−1 than those in 100 mV nm−1. The gap between the translocation times of poly(G)15 and poly(A)15 is ca. 3.1 ns in the electric field of 50 mV nm−1 and ca. 1.9 ns in that of 100 mV nm−1. This indicates that a single nucleotide can be identified easily in the electric field of 50 mV nm−1. As displayed in Fig. 4, the order of the translocation times for the four nucleotides is poly(G)15 > poly(C)15 > poly(T)15 > poly(A)15, which is in accordance with the results from Derrington's experiments with the biological MspA nanopore.35 These results clearly show that, under a low electric field, it is possible to distinguish four bases from the translocation times with a 2 nm graphene nanopore. However, it is also very important that the applied electric field should not be too low for a DNA fragment to pass through the nanopore because the interaction between the DNA fragment and graphene nanopore is very strong.17,36 For example, as has been shown in our previous work, the fluctuation of translocation time is relatively large under the electric field of 30 mV nm−1 because the DNA fragments could stick strongly to the graphene nanopore.37 Therefore, to select a suitable electric field providing the best balance between the fluctuation of translocation time and the resolution of the DNA sequencing is very important.
 |
| | Fig. 4 The translocation times of poly(G)15, poly(C)15, poly(A)15, and poly(T)15 through 2 nm graphene nanopore with 1 M KCl. The applied electric field is 50 mV nm−1. | |
3.3 Effect of ions
The radial distribution functions (RDF) in this section was defined as a distribution of K+ ions around the center of mass of each polynucleotide in the sequencing with 2 nm graphene nanopore and an electric field of 50 mV nm−1. This was calculated from the last 10 ns trajectory to investigate the effect of ions on the ssDNA translocation. As shown in Fig. 5(a), the first three peaks in the K+–poly(G)15 RDF are much higher than those in the RDFs of K+–poly(A)15, K+–poly(C)15 and K+–poly(T)15. Moreover, the second peak of the K+–poly(A)15 RDF is much higher than that in the K+–poly(C)15 and K+–poly(T)15 RDFs. Therefore, the coordination number of K+ ions around poly(G)15 is always higher than that around the other three polynucleotides. If more K+ ions are close to poly(G)15, then the hydration of the base is higher, making dehydration of the base difficult, and thus could extend the translocation time of the polynucleotide.
 |
| | Fig. 5 (a) RDFs between K+ and the polynucleotides. (b) The coordination number of K+ around each polynucleotide. | |
Moreover, increase in the hydration of the polynucleotide poly(G)15 can decrease the hydrophobic interaction between the base and the graphene nanopore and facilitate the desorption process of the polynucleotide from the nanopore. The translocation time of the polynucleotide will decrease with the acceleration of the desorption process. Therefore, the translocation time of the polynucleotide is the result of the dehydration effect and the desorption process, which can be affected by the hydration of ions. To study in detail the effect of K+ ions on the DNA translocation, systems (SimA5–SimG5) without KCl ions but with only 14 K+ ions as counterions were simulated under the same condition as those for SimIA5–SimG5. Fig. 6 shows that without KCl, the translocation times for poly(A)15, poly(T)15, poly(C)15, and poly(G)15 are 12.1 ± 1.2 ns, 10.1 ± 0.9 ns, 10.5 ± 0.8 ns, and 12.5 ± 1.1 ns, respectively. We noted that with 1 M KCl, the corresponding values are 4.8 ± 0.2 ns, 3.2 ± 0.1 ns, 10.1 ± 0.6 ns, and 13.2 ± 0.8 ns. This indicates that, in the absence of KCl, the difference in the translocation time between different polynucleotides is much smaller than that in the presence of 1 M KCl ions. Without KCl, the translocation times of poly(A)15 and poly(T)15 are much longer than those with 1 M KCl. In accordance with Luo's results,38 the translocation time of poly(A)15 is greatly prolonged in the absence of KCl ions. The reason is probably that the hydration of the ssDNA in the absence of K+ is much weaker than that in the presence of K+ ions; thus, the hydrophobic graphene nanopore has a much stronger interaction with the ssDNA in the solution.
 |
| | Fig. 6 The translocation times of poly(G)15, poly(C)15, poly(A)15, and poly(T)15 through the 2 nm graphene nanopore in the absence of KCl. The applied electric field was 50 mV nm−1. | |
In a relatively low electric field such as 50 mV nm−1, factors such as DNA–graphene interaction and effect of ions is comparable to the electric field force, and they are the main reasons that the polynucleotide could be identified reasons that the polynucleotide could be identified by its translocation time. Compared with the dehydration effect of the polynucleotide poly(G)15, increase in the interaction between the polynucleotide and nanopore may have a much larger influence on the translocation time, and thus greatly prolong the translocation times of poly(A)15 and poly(T)15. However, the translocation time of poly(C)15 passing through the graphene nanopore in the absence of KCl ions is almost as same as that in the presence of 1 M KCl. In the absence of KCl, the translocation time of poly(G)15 changes a little. For these two polynucleotides, the dehydration and desorption effects may cancel each other in the solution without KCl ions. Thus, our studies indicate that, in the absence of KCl, the difference in the translocation time between different polynucleotides is much lesser than that in 1 M KCl solution, indicating that under a given electric field, the resolution of ssDNA sequencing decreases greatly in the solution without KCl ions.
4. Conclusion
In this work, the translocation time of ssDNA through graphene nanopores was investigated by MD simulations. We found that with a graphene nanopore of appropriate diameter, such as 2 nm, the resolution of DNA sequencing by translocation time could be greatly improved compared with the case of using a larger nanopore as was discussed in a previous work.21 Different nucleotides such as A, T, C, and G can be identified by their characteristic translocation times. The recognition of a graphene nanopore for different nucleotides can be improved significantly by applying a low electric field. Because the applied field in the experiment is much lower than that in our simulations, our results provide a possible way to increase the resolution of DNA sequencing, which is based on the translocation time of DNA. Moreover, ion effects were found to be very important to the resolution of DNA detection. As the interaction between a graphene nanopore and a polynucleotide can affect the translocation time of the polynucleotide through the nanopore, it is possible to adjust the translocation time by chemical decoration of the nanopore surface. Our future work will focus on the influence of graphene nanopore modification on the resolution of DNA sequencing.
Acknowledgements
This work was financially supported by the National Natural Science Foundation of China (Grant no. 21273200, 21074115 and 21403049), MOE (J20091551), the Zhejiang Provincial Natural Science Foundation of China (Grant no. LY13F040006, LY13F04006 and LY14B030008), the Zhejiang Provincial Science and Technology Plan Project Number (no. 2014C33220) and Zhejiang University (2011XZZX002, 2011QNA3014). The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the parallel computer centre (PDC) through the project “Multiphysics Modeling of Molecular Materials”, SNIC 020/11-23.
References
- J. J. Kasianowicz, E. Brandin, D. Branton and D. W. Deamer, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 13770–13773 CrossRef CAS.
- R. dela Torre, J. Larkin, A. Singer and A. Meller, Nanotechnology, 2012, 23, 385308 CrossRef PubMed.
- T. Z. Butler, J. H. Gundlach and M. A. Troll, Biophys. J., 2006, 90, 190–199 CrossRef CAS PubMed.
- D. Branton, D. W. Deamer, A. Marziali, H. Bayley, S. A. Benner, T. Butler, M. Di Ventra, S. Garaj, A. Hibbs, X. Huang, S. B. Jovanovich, P. S. Krstic, S. Lindsay, X. S. Ling, C. H. Mastrangelo, A. Meller, J. S. Oliver, Y. V. Pershin, J. M. Ramsey, R. Riehn, G. V. Soni, V. Tabard-Cossa, M. Wanunu, M. Wiggin and J. A. Schloss, Nat. Biotechnol., 2008, 26, 1146–1153 CrossRef CAS PubMed.
- B. M. Venkatesan and R. Bashir, Nat. Nanotechnol., 2011, 6, 615–624 CrossRef CAS PubMed.
- E. A. Manrao, I. M. Derrington, A. H. Laszlo, K. W. Langford, M. K. Hopper, N. Gillgren, M. Pavlenok, M. Niederweis and J. H. Gundlach, Nat. Biotechnol., 2012, 30, 349–353 CrossRef CAS PubMed.
- A. Hozumi, D. F. Cheng and M. Yagihashi, ACS Appl. Mater. Interfaces, 2011, 3, 2224–2227 Search PubMed.
- C. C. Striemer, T. R. Gaborski, J. L. McGrath and P. M. Fauchet, Nature, 2007, 445, 749–753 CrossRef CAS PubMed.
- M. J. Kim, M. Wanunu, D. C. Bell and A. Meller, Adv. Mater., 2006, 18, 3149–3153 CrossRef CAS.
- Y. Yang, R. Liu, H. Xie, Y. Hui, R. Jiao, Y. Gong and Y. Zhang, J. Nanosci. Nanotechnol., 2013, 13, 4521–4538 CrossRef CAS PubMed.
- J. Hong, Y. Lee, G. A. Chansin, J. B. Edel and A. J. Demello, Nanotechnology, 2008, 19, 165205 CrossRef PubMed.
- Z. Chen, Y. B. Jiang, D. R. Dunphy, D. P. Adams, C. Hodges, N. G. Liu, N. Zhang, G. Xomeritakis, X. Z. Jin, N. R. Aluru, S. J. Gaik, H. W. Hillhouse and C. J. Brinker, Nat. Mater., 2010, 9, 667–675 CrossRef CAS PubMed.
- J. Li, D. Stein, C. McMullan, D. Branton, M. J. Aziz and J. A. Golovchenko, Nature, 2001, 412, 166–169 CrossRef CAS PubMed.
- B. M. Venkatesan, A. B. Shah, J. M. Zuo and R. Bashir, Adv. Funct. Mater., 2010, 20, 1266–1275 CrossRef CAS PubMed.
- A. J. Storm, J. H. Chen, X. S. Ling, H. W. Zandbergen and C. Dekker, Nat. Mater., 2003, 2, 537–540 CrossRef CAS PubMed.
- T. Ahmed, J. T. Haraldsen, J. J. Rehr, M. Di Ventra, I. Schuller and A. V. Balatsky, Nanotechnology, 2014, 25, 125705 CrossRef PubMed.
- C. Sathe, X. Q. Zou, J. P. Leburton and K. Schulten, ACS Nano, 2011, 5, 8842–8851 CrossRef CAS PubMed.
- A. Chitteth Rajan, M. R. Rezapour, J. Yun, Y. Cho, W. J. Cho, S. K. Min, G. Lee and K. S. Kim, ACS Nano, 2014, 8, 1827–1833 CrossRef PubMed.
- J. Eid, A. Fehr, J. Gray, K. Luong, J. Lyle, G. Otto, P. Peluso, D. Rank, P. Baybayan and B. Bettman, Science, 2009, 323, 133–138 CrossRef CAS PubMed.
- D. B. Wells, M. Belkin, J. Comer and A. Aksimentiev, Nano Lett., 2012, 12, 4117–4123 CrossRef CAS PubMed.
- L. Liang, P. Cui, Q. Wang, T. Wu, H. Agren and Y. Tu, RSC Adv., 2013, 3, 2445–2453 RSC.
- H. Qiu and W. Guo, Appl. Phys. Lett., 2012, 100, 083106 CrossRef PubMed.
- Z. Zhang, J. Shen, H. Wang, Q. Wang, J. Zhang, L. Liang, H. Ågren and Y. Tu, J. Phys. Chem. Lett., 2014, 5, 1602–1607 CrossRef CAS.
- G. F. Schneider, Q. Xu, S. Hage, S. Luik, J. N. H. Spoor, S. Malladi, H. Zandbergen and C. Dekker, Nat. Commun., 2013, 4, 2619 Search PubMed.
- S. Garaj, W. Hubbard, A. Reina, J. Kong, D. Branton and J. A. Golovchenko, Nature, 2010, 467, 190–193 CrossRef CAS PubMed.
- C. A. Merchant, K. Healy, M. Wanunu, V. Ray, N. Peterman, J. Bartel, M. D. Fischbein, K. Venta, Z. T. Luo, A. T. C. Johnson and M. Drndic, Nano Lett., 2010, 10, 2915–2921 CrossRef CAS PubMed.
- G. F. Schneider, S. W. Kowalczyk, V. E. Calado, G. Pandraud, H. W. Zandbergen, L. M. K. Vandersypen and C. Dekker, Nano Lett., 2010, 10, 3163–3167 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS PubMed.
- R. M. M. Smeets, U. F. Keyser, D. Krapf, M. Y. Wu, N. H. Dekker and C. Dekker, Nano Lett., 2006, 6, 89–95 CrossRef CAS PubMed.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS PubMed.
- L. J. Liang, Q. Wang, T. Wu, T. Y. Sun and Y. Kang, ChemPhysChem, 2013, 14, 2902–2909 CrossRef CAS PubMed.
- Y. Kang, Z. Zhang, H. Shi, J. Zhang, L. Liang, Q. Wang, H. Ågren and Y. Tu, Nanoscale, 2014, 6, 10666–10672 RSC.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS.
- J. L. Li, D. Stein, C. Qun, E. Brandin, A. Huang, H. Wang, D. Branton and J. Golovchenko, Biophys. J., 2003, 84, 134a–135a CrossRef.
- I. M. Derrington, T. Z. Butler, M. D. Collins, E. Manrao, M. Pavlenok, M. Niederweis and J. H. Gundlach, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 16060–16065 CrossRef PubMed.
- C. A. Merchant and M. Drndic, Methods Mol. Biol., 2012, 870, 211–226 Search PubMed.
- L. Liang, Z. Zhang, J. Shen, K. Zhe, Q. Wang, T. Wu, H. Agren and Y. Tu, RSC Adv., 2014, 4, 50494–50502 RSC.
- K. Luo, T. Ala-Nissila, S.-C. Ying and A. Bhattacharya, Phys. Rev. Lett., 2008, 100, 058101 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2015 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 564
564![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246
246![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504
504![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335
335![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 564
564![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246
246![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504
504![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335
335![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 564
564![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246
246![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504
504![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335
335![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 564
564![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 246
246![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 504
504![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 335
335![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735
735![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705
705![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713
713![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938
938![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735
735![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705
705![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713
713![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938
938![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735
735![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705
705![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713
713![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938
938![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735
735![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705
705![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713
713![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938
938![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735
735![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705
705![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 713
713![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 938
938![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831
831![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 961
961![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 921
921![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 105
105
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-step energy minimization. 14 K+ were added into the system as counter-ions. Then, KCl ions were added into the box to match the same concentration as used in experiment.29 Note that DNA and KCl were modeled by the CHARMM27 force field30 and all carbon atoms in the graphene sheet were set to be neutral. The force field parameters for graphene were obtained from our previous work with σCC = 0.385 nm and εCC = −0.439 kcal mol−1 (ref. 31 and 32). All simulations were performed by the GROMACS 4.5.2 program,33 and all simulations were repeated in 3 times. The periodic boundary condition was applied to model the infinite graphene nanopore, and Ewald summation was used to recover the long range electrostatic interaction with a cutoff of 1.3 nm for the separation of the direct and reciprocal space summations. All atoms, including hydrogen atoms, were represented explicitly and the lengths of the bonds containing hydrogen atoms were fixed. The cutoff for the non-bonded van der Waals interaction was set by a switching function starting at 1.0 nm and reaching zero at 1.2 nm, and the time step was 2 fs. Note that the Langevin method was employed to maintain the temperature at 298 K with the pressure set at 101.3 kPa. Different bias voltages were applied in the simulations to drive the ions and ssDNA passing through the nanopores.
000-step energy minimization. 14 K+ were added into the system as counter-ions. Then, KCl ions were added into the box to match the same concentration as used in experiment.29 Note that DNA and KCl were modeled by the CHARMM27 force field30 and all carbon atoms in the graphene sheet were set to be neutral. The force field parameters for graphene were obtained from our previous work with σCC = 0.385 nm and εCC = −0.439 kcal mol−1 (ref. 31 and 32). All simulations were performed by the GROMACS 4.5.2 program,33 and all simulations were repeated in 3 times. The periodic boundary condition was applied to model the infinite graphene nanopore, and Ewald summation was used to recover the long range electrostatic interaction with a cutoff of 1.3 nm for the separation of the direct and reciprocal space summations. All atoms, including hydrogen atoms, were represented explicitly and the lengths of the bonds containing hydrogen atoms were fixed. The cutoff for the non-bonded van der Waals interaction was set by a switching function starting at 1.0 nm and reaching zero at 1.2 nm, and the time step was 2 fs. Note that the Langevin method was employed to maintain the temperature at 298 K with the pressure set at 101.3 kPa. Different bias voltages were applied in the simulations to drive the ions and ssDNA passing through the nanopores.