Density functional investigations on the catalytic cycle of the hydrogenation of aldehydes catalyzed by an enhanced ruthenium complex: an alcohol-bridged autocatalytic process

Abstract

A novel ruthenium complex developed by Casey exhibits some outstanding features such as effective anti-dimerization, highlighted catalytic activity and a mild reaction condition. Density functional theory (DFT) was used to explore the catalytic cycle of the hydrogenation of PhCHO catalyzed by this enhanced ruthenium complex. The catalytic cycle of aldehyde hydrogenation involves two stages, hydrogen transfer and regeneration of the active catalyst, which can be achieved by means of a concerted outer-sphere hydrogen transfer and an intramolecular hydrogen migration, respectively. Hydrogen transfer is the rate-determining step in the total catalytic hydrogenation cycle, having a low free energy barrier of 16.2 kcal mol⁻¹. The hydrogenated product, alcohol, can remarkably improve the regeneration activity of the catalyst via an alcohol-mediated intramolecular hydrogen migration. The free energy barrier of regeneration of the active catalyst is only 13.8 kcal mol⁻¹. This catalytic hydrogenation of aldehyde is demonstrated to be an autocatalytic process.

---

Introduction

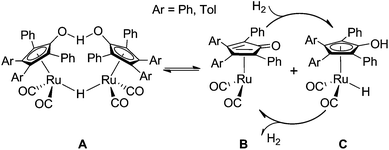
Hydrogenation of aldehydes and ketones is an important transformation for synthesizing novel chemicals and expanding the application of substrates.^1,2 These carbonyl compounds are commonly reduced using classic reagents such as LiAlH₄,^3–5 which generally require strictly anhydrous conditions and yield some amount of metal–salt waste. Metal–ligand bifunctional catalysts,⁶ by contrast, have gradually replaced these stoichiometric reducing agents as “green” surrogates in the hydrogenation of polar double bonds. Transition-metal-catalyzed hydrogenation of aldehydes and ketones exhibits a higher catalytic activity, indicating a lower cost and economical benefits in industrial production.⁷ Furthermore, as hydrogen is a renewable resource, utilizing H₂ in organic synthesis is favorable to avoid causing environmental pollution.⁸

Shvo’s catalyst,^9,10 discovered in the mid-1980s, is a successful and famous ligand–metal bifunctional catalyst, [Ph₄(η⁵-C₄CO)]Ru₂(CO)₄(μ-H) (Scheme 1), which is popularly applied in hydrogen-transfer reactions of alkynes, carbonyls, and imines and the oxidation of alcohols, amines, and other compounds.^11–17 Compound A, an air-stable and crystalline solid, itself cannot catalyze hydrogen transfer of aldehydes and ketones. According to a kinetic study on the hydrogenation, Casey demonstrated that only generating the reduced C complex by dissociation of the diruthenium-bridging hydride A under high H₂ pressure can the catalytic hydrogenation achieve. The oxidized B can be used to catalyze the dehydrogenation reaction of alcohol and so on.^18,19

Scheme 1 Shvo’s ligand–metal bifunctional complex.

To further improve the catalytic activity of ruthenium complexes, it is useful and applicable to understand the mechanisms involved in the use of Shvo’s catalyst. Since 2001, many experimental studies have been performed to study the mechanisms of the hydrogenation and dehydrogenation reactions catalyzed by Shvo’s catalyst.^18,20–24 Until 2007, Casey proposed a concerted outer-sphere hydrogen transfer mechanism based on the kinetics study of an iron-complex-catalyzed hydrogenation of aldehydes (Scheme 2).²⁵ However, due to the regeneration rate of the catalyst being too rapid, he was not able to observe the detailed process of catalyst regeneration or perform related studies.

Scheme 2 Catalytic hydrogenation catalyzed by Knölker’s iron-catalyst D.

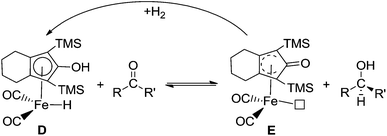
Inspired by Knölker’s iron-catalyst D, a more active ruthenium catalyst 1, [2,5-(SiMe₃)₂-3,4-(CH₂OCH₂)(η⁵-C₄COH)]Ru(CO)₂H, was successfully developed by Casey, which presented a significant enhancement relative to Shvo’s catalyst (Scheme 3).²⁶ In addition, there is no bridging hydride formation for complex 1 in toluene. This ruthenium hydride can catalyze the hydrogenation of both aldehydes and ketones under mild conditions (25 °C, 3 atm of H₂, Scheme 4). Understanding the nature of this advanced ruthenium complex 1 is very helpful and useful to further find and develop other, more highly active ruthenium catalysts. Actually, Casey and Guan once attempted to monitor the catalytic cycle, but they only observed the kinetic behavior of the hydrogen transfer of the catalytic hydrogenation between −68 and −54 °C under a non-hydrogen environment, as this hydrogenation rate was too rapid to follow at room temperature. However, a complete catalytic hydrogenation cycle should consist of the regeneration of catalyst 1 in addition to the hydrogen transfer. Lacking understanding of the catalyst regeneration, it is difficult to provide potent and cogent recommendations for the design of novel ruthenium catalysts and the modification of reaction conditions.

Scheme 3 The novel ruthenium complex 1 synthesized by Casey and Guan.

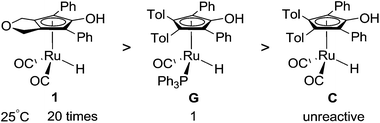Scheme 4 Relative catalytic activities for the hydrogenation of PhCHO in toluene at 25 °C under 3 atm H₂ pressure, obtained by Casey and Guan. (The unreactive nature of C is due to the formation of non-catalytic dimers such as A shown in Scheme 1).

Since a serious limitation was encountered by depending only on experimental techniques, the theoretical chemical method is an appropriate supporting technique for investigating the total catalytic hydrogenation cycle of PhCHO. Previously, many reasonable explanations and results given by the density functional method (DFT) regarding the mechanisms of Shvo’s and Knölker’s catalysts in catalyzing the hydrogen transfer of both aldehydes and ketones have been in good agreement with the experimental conclusions and observations.^27–29 In this work, a deep and detailed computational study was performed on the elementary steps involved in Casey’s modified ruthenium complex catalyzed aldehyde hydrogenation. The calculated results were expected to clarify the relationships between structures and actions in order to supply functional and reliable information for experimental work.

Computational details

Calculations for all geometries were carried out using the Gaussian 09 software package.³⁰ Optimizations were performed at the density functional theory (DFT) level by means of the hybrid B3LYP³¹ functional and LACVP* basis set. The effective core potential LANL2DZ³² along with its associated basis set was employed for ruthenium, and the main group elements (C, O, H, and Si) were calculated using the 6-31G* basis set. The structural parameters for the ruthenium complex 1 that were used in all calculations were obtained based on the X-ray crystal structure obtained by Casey and Guan.²⁶ The entire aromatic ligand of the ruthenium complexes is referred to as CpOH in this paper.

All calculations were done without any geometrical constraints. Frequency calculations were performed for all stationary points at the same level in order to identify the minima (zero imaginary frequency) and transition states (TS, only one imaginary frequency) and to provide the free energies at 298.15 K and 1 atm. Intrinsic reaction coordinate (IRC)³³ analysis was carried out to confirm that all stationary states were smoothly connected to each other. Solvent effects (in toluene) were included using the SMD model^34,35 with the M06 method (as implemented in Gaussian 09) by performing single-point calculations via the B3LYP-optimized geometries at the higher level of basis set, where the def2-TZVP³⁶ was employed for Ru and the 6-31++G** was used for main group elements. Zhao and Truhlar^37,38 reported that the M06 method has a high accuracy for the calculation of the thermochemistry and kinetics of transition metals and main-group elements.

A correction term of 1.8943 kcal mol⁻¹ must be added to the G(sol) calculations to convert the gas-phase standard free energies at a standard state of 1 atm to the appropriate standard state for a solution of 1 mol L⁻¹.^39,40 Then, solvation free energies ΔG(sol) were used in order to consider both entropic and solvent effects.

Results and discussion

The catalytic cycle mainly involves two stages for the hydrogenation of aldehyde catalyzed by Casey’s ruthenium complex (Scheme 5). The first stage is the hydrogen transfer from catalyst to substrate: 1 → 2 + PhCHO → 3 → 4 → 5 + PhCH₂OH → 6. An outer-sphere concerted hydrogen transfer mechanism has been demonstrated to be both a kinetically and thermodynamically reasonable pathway for this process according to previous experimental and theoretical studies. The second stage is the regeneration of the active catalyst 2: (i) 5 + H₂ → 2, (ii) 5 + PhCH₂OH + H₂ → 8 → 2 + PhCH₂OH, (iii) 5 + PhCH₂OH → 6 + H₂ → 8 → 2 + PhCH₂OH or (iv) 5 + PhCH₂OH → 6 + H₂ →2 + (PhCH₂OH)₂. To the best of our knowledge, there is no computational study on the regeneration of the active catalyst 2. Based on the hydrogenated products and intermediates, there are four possible pathways for the regeneration of the catalyst. The DFT method was then adopted to make a detailed investigation for the total catalytic cycle.

Scheme 5 Possible routes for the catalytic cycle of PhCHO hydrogenation catalyzed by Casey’s Ru-complex.

Hydrogen transfer process of PhCHO catalyzed by the ruthenium complex

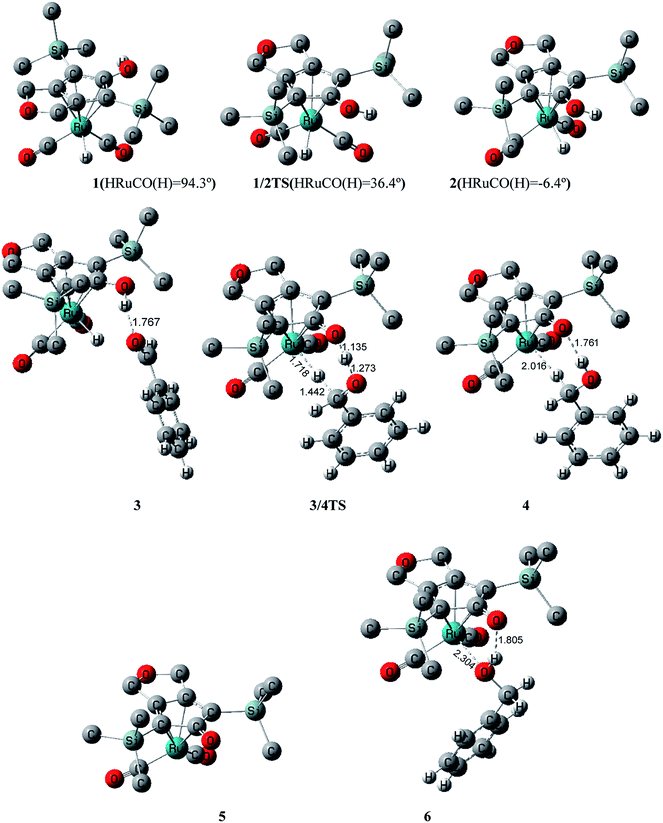
The initial geometry of Casey’s ruthenium catalyst was optimized at the B3LYP/LACVP* level in the gas phase. The most stable conformation 1 was obtained (Fig. 1), which was in good agreement with the X-ray crystal structure (Table S1 of ESI†). Benzaldehyde was used as the substrate in our calculations in order to approximate experimental conditions. It was found that 1 had a strong coordination interaction between the Cp ligand and the ruthenium, which improved the thermodynamic stabilization of 1 to a large extent. Fig. 1 shows that the dihedral angle of the H–Ru bond and the C–O(H) bond of the CpOH ligand is 94.3° in the 1 geometry. This indicated that these two bonds were nearly perpendicular to each other. However, the hydride ion of the H–Ru bond and hydroxyl group bond were oriented in opposite directions in 1, which was unfavorable to the outer-sphere concerted hydrogen transfer.

Fig. 1 Optimized structures for the hydrogen transfer of PhCHO catalyzed by 1. Distances are given in Å. HRuCO(H) indicates the dihedral angle. All hydrogen atoms connected to carbons in the CpOH ring were ignored.

According to our previous computational studies on Knölker’s catalyst,²⁹ conformation 1 actually was a non-rigid structure in toluene and facilely transformed to the other isomer 2 via the transition state 1/2TS. The dihedral angle of HRuCO(H) was reduced to 36.3° in 1/2TS, which indicated that conformation 1 transformed to 2 by means of an intramolecular rotation of the CpOH group. Fig. 2 shows that the activation free energy ΔG^≠(sol) for this isomerization reaction is only 5.3 kcal mol⁻¹, which represents a kinetically rapid step. In 2, the HRuCO(H) dihedral angle was only −6.4°, indicating that the H–Ru and C–O(H) bonds became almost coplanar. Thus the H⁺⋯H⁻ distance in complex 2 was greatly shortened, which was a more favorable structure for the transfer of two hydrogen atoms to the substrate. Additionally, this step was also thermodynamically facile due to the ΔG(sol) between 1 and 2 being only 1.2 kcal mol⁻¹. This indicated that 1 ⇋ 2 was actually a fast equilibrium in toluene.

Fig. 2 Free energy ΔG(sol) profiles (kcal mol⁻¹) for the hydrogen transfer of PhCHO catalyzed by Ru-catalyst 1. Values are relative to the free energies of 1 and PhCHO.

In the next step, the free PhCHO in system bound to the active catalyst 2 via a hydrogen bond interaction and formed an intermediate 3 in which the CpOH⋯OHCPh distance was 1.767 Å. Due to the effect of the entropic penalty, the thermodynamic stabilization of 3 was reduced to some extent. The reaction of 2 + PhCHO → 3 was endergonic by 7.5 kcal mol⁻¹. This indicated that the intermediate 3 was thermodynamically unstable in the hydrogenation process at room temperature, which was also in agreement with experimental observation. In particular, this hydrogen bond effectively shrunk the distance between catalyst and substrate, which made the migration of the hydrogen atom from 2 to PhCHO more favorable.

Then the intermediate 3 transformed into another intermediate 4 through the transition state 3/4TS in which the proton of the CpOH group and the hydride ion of the Ru–H bond concertedly added to the oxygen and carbon atoms of the aldehyde group, respectively. The free energy barrier ΔG^≠(sol) was only 8.7 kcal mol⁻¹ for the 3 → 4 reaction, which represented a kinetically facile step. In the geometry of 4, the newly formed PhCH₂OH was connected to the oxidized ruthenium complex via a hydrogen bond in which the CpO⋯HO distance was 1.761 Å and an agostic H-bonding interaction in which the Ru⋯H distance was 2.016 Å. Due to the failure of the ruthenium atom to achieve 18 electrons, the intermediate 4 was also thermodynamically unstable, with ΔG(sol) increased to 7.8 kcal mol⁻¹ compared with 1.

The dissociation of 4 produced the isolated ruthenium complex 5 and free PhCH₂OH. Due to 4 → 5 + PhCH₂OH being entropically favorable, this dissociation was exergonic by 2.1 kcal mol⁻¹. But 5 also did not satisfy the 18-electron structure of ruthenium. The free PhCH₂OH again connected to complex 5 by its hydroxyl group to obtain the complex 6, which was the final hydrogenated product, without the presence of H₂. In product 6, the oxygen atom of PhCH₂OH was coordinated to the unsaturated ruthenium center in order to achieve the 18-electron structure; the hydrogen atom of OH also formed a hydrogen bonding interaction with the oxygen atom of CpO. So the reaction of 5 + PhCH₂OH → 6 was exergonic by 3.0 kcal mol⁻¹.

However, 6 was not the most thermodynamically stable product in this hydrogenation, due to ΔG(sol) being 2.7 kcal mol⁻¹ for 1 + PhCH₂OH → 6. This was also the reason that crystals of 6 were not able to be obtained in experiments. But a structurally similar crystal was experimentally obtained for Knölker’s iron-catalyst. The distances Ru⋯O and CpO⋯HO–Bn were 2.304 and 1.805 Å in ruthenium complex 6, respectively, which were longer than the distances, 2.069 and 1.734 Å, of these bonds in the similar iron-complex geometry.²⁹ This meant that the coordination and hydrogen bonding interactions were reduced in ruthenium complex 6. This was because the coordination bond between oxygen and the 4d-orbital of ruthenium was to some extent weaker in comparison to the bond between oxygen and the 3d-orbital of iron.

In the catalytic cycle, the total free energy barrier was 16.2 kcal mol⁻¹ for the hydrogen transfer from 2 to 6, which was consistent with Casey and Guan’s experimental result of 15.3 kcal mol⁻¹. This was a kinetically facile process, so PhCHO was able to be hydrogenated at a very rapid rate by Casey’s ruthenium catalyst at room temperature.¹⁸

The regeneration of the active-catalyst 2

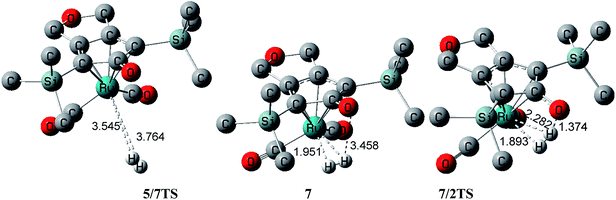
In accordance with dehydrogenated product 5, there are four possible pathways for the regeneration of the active-catalyst 2 under a H₂ atmosphere. In route (i), H₂ is directly added to Ru-complex 5, namely 5 + H₂ → 7 → 2. In routes (ii) and (iii), the catalyst 2 is regenerated with the aid of an alcohol bridge only involving one PhCH₂OH molecule; the detailed processes are 5 + H₂ → 7 + PhCH₂OH → 8 → 2 + PhCH₂OH and 5 + PhCH₂OH → 6 + H₂ → 8 → 2 + PhCH₂OH, respectively. In last route (iv), the regeneration of catalyst 2 is achieved via a double-alcohol bridge composed of a hydrogen bond, for which the steps are 5 + H₂ → 7 + (PhCH₂OH)₂ → 9 → 2 + (PhCH₂OH)₂.

Actually, both regeneration routes (i) and (ii) start with the addition of H₂ to the dehydrogenated Ru-complex 5. Fig. 3 shows that two σ-bond electrons of hydrogen coordinate to the unoccupied d-orbital of ruthenium through a transition state 5/7TS in this step, which has an extremely small free energy barrier of 0.8 kcal mol⁻¹ due to the ruthenium center urgently demanding extra electrons to achieve an 18 electron structure. A stable dihydride intermediate 7 was then obtained, in which H–H coordinated symmetrically with the Ru center, with both H⋯Ru distances being 1.951 Å (Fig. 4). The transformation 5 + H₂ → 7 was exergonic by 4.6 kcal mol⁻¹

Fig. 3 Free energy ΔG(sol) profiles (kcal mol⁻¹) for the regeneration route (i). Values are relative to free energies of 5 and H₂.

Fig. 4 Optimized structures for route (i). Distances are given in Å.

In route (i), one coordinated hydrogen atom directly migrated to the carbonyl oxygen of CpO from the Ru center of intermediate 7 via a transition state 7/2TS, and the catalyst 2 was then regenerated. The reaction 7 → 2 was exergonic by 7.1 kcal mol⁻¹, but it had a high free energy of 29.8 kcal mol⁻¹ which corresponded to a low reaction rate constant in the kinetics. From 7/2TS, the effective distance was 1.374 Å for hydrogen migration to the carbonyl oxygen of the CpO group. However, both H⋯O distances were 3.458 Å in the reactant 7 of this step. The coordinated H–H bond must twist from a horizontal to a vertical orientation in order to approach the carbonyl oxygen of CpO; one hydrogen atom of H–H moved away from ruthenium during this twisting and its coordination interaction was to some extent reduced due to the H–Ru distance being 2.282 Å in 7/2TS. In addition, the CpO group concertedly slipped towards the vertical hydrogen atom to further shrink the H⋯O distance. These geometric adjustments were favorable to intramolecular hydrogen migration, but an overly high strain was also created between CpO and ruthenium due to H–H strain. As a result, this led to a high total free energy barrier of 25.2 kcal mol⁻¹ for route (i).

In contrast to route (i), the intramolecular hydrogen migration was achieved with the help of an alcohol bridge in the pathways (ii) and (iii) (Fig. 5). The difference between routes (ii) and (iii) was the means of generation of a crucial intermediate 8. For route (ii), the intermediate 7 first linked to a generated PhCH₂OH via a hydrogen bonding interaction, because the CpO⋯HO–Bn distance was 1.810 Å in the produced intermediate 8 (Fig. 6). Due to the entropic penalty of forming the hydrogen bond, 7 + PhCH₂OH → 8 was endergonic by 7.8 kcal mol⁻¹. So it was in total endergonic by 3.2 kcal mol⁻¹ to generate 8 by means of 5 + H₂ → 7 + PhCH₂OH → 8.

Fig. 5 Free energy ΔG(sol) profiles (kcal mol⁻¹) for the regeneration route (ii). Values are relative to free energies of 5, H₂ and PhCH₂OH.

Fig. 6 Optimized structures for routes (ii) and (iii). Distances in Å.

Next, intermediate 8 underwent an intramolecular hydrogen migration with the assistance of an alcohol-bridge. In transition state 8/2TS, one hydrogen atom of H–H added to the hydroxyl oxygen of PhCH₂OH and the hydroxyl hydrogen concertedly transferred to the carbonyl oxygen of the CpO group. Due to the participation of PhCH₂OH, the CpO⋯H–H distance was enlarged to 2.806 Å compared with the direct transfer via 7/2TS, and it was only reduced by 0.652 Å relative to 7. This indicated that the geometric tension among the CpO, H–H and Ru-center was to a large extent eased by an alcohol-mediated bridge. Additionally, the closest distance between a hydrogen of H–H and the oxygen of PhCH₂OH was 2.676 Å in intermediate 8, but it shrank to 1.302 Å in 8/2TS. The shortened distance was 1.374 Å here, which is less than 2.084 Å between 7 and 7/2TS. This meant the migration of the hydrogen atom to the hydroxyl oxygen via 8 was more facile. Thus, route (ii) corresponded to a lower total free energy barrier, 13.8 kcal mol⁻¹, compared to the first route. Route (ii) was more kinetically favorable for the implementation of the regeneration of 2 than route (i).

Considering 6 as an alternative to intermediate 7, there was another means to generate intermediate 8, namely 5 + PhCH₂OH → 6 + H₂ → 8 (Fig. 7). In route (iii), 5 combined with the product PhCH₂OH prior to H₂ coordination and formed intermediate 6. Then H₂ coordinated to the ruthenium of 6 to replace the hydroxyl oxygen of alcohol. In the transition state 6/8TS of this step, the CpO⋯HO–Bn distance was 1.819 Å which meant the hydrogen bonding interaction still existed; whereas the Ru⋯OH distance was enlarged to 4.137 Å due to the replacement of OH by H₂ coordination (shown in Fig. 6). Due to the coordinated hydroxyl oxygen causing an obstruction to H₂ coordination, the free energy barrier was increased to 14.1 kcal mol⁻¹ for 6 + H₂ → 8. So the means of generating 8 in route (iii) corresponds to a total free energy barrier of 11.1 kcal mol⁻¹. The last step was the same as that of route (ii). The total free energy barrier was also 13.8 kcal mol⁻¹ in route (iii). However, the barrier of 5 + H₂ → 7 + PhCH₂OH → 8 in route (ii) was 7.9 kcal mol⁻¹ lower than that of 5 + PhCH₂OH → 6 + H₂ → 8 in route (iii). This indicated that the former was much more kinetically favorable for the production of intermediate 8, so route (ii) was more kinetically feasible compared with (iii).

Fig. 7 Free energy ΔG(sol) profiles (kcal mol⁻¹) for regeneration route (iii). Values are relative to free energies of 5, H₂ and PhCH₂OH.

It is well known that many intermolecular hydrogen bonds exist among alcohol molecules. This indicates that a long alcohol bridge involving two or more PhCH₂OH molecules can be formed via the intermolecular hydrogen bonding interactions. Since an alcohol-mediated bridge can effectively reduce the intramolecular geometric tension and actually increase the regeneration activity of catalyst 2, there is another interesting issue of whether or not a multiple-alcohol bridge can further improve the catalyst regeneration ability. Here a double-alcohol bridge was investigated first.

As shown in Fig. 8, the first step of route (iv) is the same as that of route (ii), which is the process of H₂ adding to ruthenium, 5 + H₂ → 7. From 7 to 9, a double-alcohol bridge bound to the carbonyl oxygen of the CpO group via a hydrogen bonding interaction in which the CpO⋯H distance was 1.745 Å (Fig. 9). From 9, the double-alcohol bridge established a looser geometry between ruthenium and the CpO group, in which the H–H⋯O distance was 2.075 Å. This structure was more favorable to the addition of hydrogen to the hydroxyl oxygen atom. However, it was highly endergonic by 15.6 kcal mol⁻¹ for 7 + (PhCH₂OH)₂ → 9. This was because the two alcohol molecules hydrogen bonded to dihydride 7 caused a very high entropic penalty which exceeded the stabilization of the structure caused by the hydrogen bonds.

Fig. 8 Free energy ΔG(sol) profiles (kcal mol⁻¹) for the regeneration route (iv). Values are relative to free energies of 5, H₂ and PhCH₂OH.

Fig. 9 Optimized structures for route (iv). Distances are in Å.

Then intermediate 9 transformed to catalyst 2 and free (PhCH₂OH)₂ through transition state 9/2TS with a free energy barrier of 9.6 kcal mol⁻¹. This barrier was 1.0 kcal mol⁻¹ lower than that of 8 → 8/2TS → 2 + PhCH₂OH, which indicated that a double-alcohol bridge was more favorable to the intramolecular hydrogen migration from ruthenium to the carbonyl oxygen of CpO. This can be attributed to the long alcohol bridge creating a looser geometry, the transition state 9/2TS, in which the H–H⋯OCp distance was 3.509 Å, very close to the value of 3.458 Å for dihydride 7. So the hydrogen of H–H only needed a slight movement and to be able to add to the hydroxyl oxygen of PhCH₂OH. Unexpectedly, the total free energy of route (iv) was 20.6 kcal mol⁻¹, which was not further reduced compared with 13.8 kcal mol⁻¹ for route (ii). Thus, these facts indicated that overly high entropic penalties caused by a multiple-alcohol bridge were finally unfavorable for increasing the regeneration activity of catalyst 2 relative to a single-alcohol bridge.

Complete catalytic cycle

As discussed in the above analyses, the complete catalytic cycle for the hydrogenation of PhCHO catalyzed by Casey’s Ru-complex actually included two processes. Fig. 10 shows that the first stage is the hydrogen transfer, 1 → 2 + PhCHO → 3 → 4 → 5 + PhCH₂OH → 6, giving rise to a total free energy barrier of 17.4 kcal mol⁻¹. Due to 2 + PhCHO → 3 merely being an endergonic reaction without any barrier, the concerted outer-sphere hydrogen transfer is the rate-determining step in this hydrogenation, namely 2 + PhCHO → 4. This corresponds to a free energy barrier of 16.2 kcal mol⁻¹.

Fig. 10 The autocatalysis cycle of the hydrogenation of benzaldehyde catalyzed by Casey’s ruthenium complex 1 (kcal mol⁻¹).

The second stage, regeneration of the active catalyst 2, 5 + H₂ → 7 + PhCH₂OH → 8 → 2 + PhCH₂OH, had a total free energy barrier of 13.8 kcal mol⁻¹. The step 7 + PhCH₂OH → 8 is also an endergonic reaction without a barrier, so the intramolecular hydrogen migration from ruthenium to the carbonyl oxygen of the CpO group is the rate-determining step in this regeneration of catalyst 2, namely 7 + PhCH₂OH → 2. The free energy barrier is 18.4 kcal mol⁻¹, which is far higher than the 0.8 kcal mol⁻¹ of the addition reaction, 5 + H₂ → 7. This means the pressure of H₂ does not determine the regeneration rate of catalyst 2, which is in good agreement with Casey’s experiments.²⁶

Comparing these two processes in the catalytic cycle, the total free energy barrier of hydrogen transfer is 3.6 kcal mol⁻¹ greater than that of catalyst regeneration. So the hydrogen transfer is the rate-determining step in the complete catalytic hydrogenation cycle. This indicates that the total free energy barrier for the catalytic cycle is 16.2 kcal mol⁻¹, which corresponds to a kinetically facile process. This is the reason that Casey’s Ru complex can catalyze hydrogenation of aldehydes in mild reaction conditions. However, the alcohol concentration is very low in an initial stage of hydrogenation. As a result, the actual reaction rate of regeneration is lower than that of hydrogen transfer, because the direct reduction from 5 to 2 corresponds to a higher free energy barrier of 25.2 kcal mol⁻¹ in this case. Thus, if extra alcohol is not added into the toluene solution before reaction, the hydrogenation rate can be significantly increased after the generation of PhCH₂OH in the preliminary stage of the catalytic cycle. These facts indicate that the catalytic hydrogenation of aldehydes is actually an autocatalytic process, because the generated alcohol can participate in the catalytic cycle and effectively decrease the free energy barrier of catalyst reactivation.

However, a comparison between regeneration routes (ii) and (iv) indicated that a multiple-alcohol bridge cannot further improve the regeneration activity of catalyst 2 relative to a single alcohol-mediated bridge due to overly high entropic penalties. This indicates that adding the proper concentration of alcohol to the reaction system is favorable for increasing the hydrogenation rate, while this effect can not be further improved after the concentration of alcohol exceeds that of Ru-catalyst in solution. So the overall hydrogenation rate is mainly controlled by hydrogen transfer step when sufficient quantities of PhCH₂OH are generated in the catalytic cycle.

Conclusions

The catalytic cycle of the hydrogenation of PhCHO catalyzed by Casey’s Ru-complex was studied in detail using the DFT method. Solvation effects in toluene were also considered, and were included in the calculated free energy profiles. This catalytic cycle actually involves two stages: hydrogen transfer and regeneration of active catalyst 2. The hydrogenation of aldehydes can be achieved via a concerted outer-sphere hydrogen transfer pathway. The regeneration of the active catalyst 2 can be achieved by means of an intramolecular hydrogen migration. Here an alcohol-mediated bridge displays a crucial function in enhancing the regeneration activity of catalyst 2.

This catalytic hydrogenation of aldehydes is actually an autocatalytic process. The hydrogen transfer is the rate determining step in the complete catalytic hydrogenation cycle. Additionally, the intramolecular hydrogen migration is the rate-determining step in the regeneration stage. This indicates that the pressure of H₂ does not determine the overall catalytic hydrogenation rate. Adding the proper concentration of alcohol into the toluene solution before reaction is favorable to significantly improve the regeneration activity of catalyst and thus effectively enhance the catalytic hydrogenation rate. However, this effect cannot be further improved when the concentration of alcohol exceeds that of Ru catalyst in solution.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (no. 21277082 and 21337001), Marie Curie International Research Staff Exchange Scheme Fellowship within the 7th European Community Framework Programme (no. 295132) and the Program for New Century Excellent Talents in University (NCET-13-0349).

Notes and references

1. H. U. Blaser, C. Malan, B. Pugin, F. Spindler, H. Steiner and M. Studer, Adv. Synth. Catal., 2003, 345, 103–151.
2. P. N. Rylander, in Hydrogenation Methods, Academic Press, New York, 1990.
3. B. M. Trost and I. Fleming, in Comprehensive organic synthesis: selectivity, strategy, and efficiency in modern organic chemistry, Pergamon Press, Oxford, England, 1st edn, 1991.
4. J. Seyden-Penne, in Reductions by the alumino- and borohydrides in organic synthesis, Wiley-VCH, New York, 2nd edn, 1997.
5. V. Fehring and R. Selke, Angew. Chem., Int. Ed., 1998, 37, 1827–1830.
6. M. Yamakawa, H. Ito and R. Noyori, J. Am. Chem. Soc., 2000, 122, 1466.
7. S. Enthaler, K. Junge and M. Beller, in Iron catalysis in organic chemistry: reaction and applications, Wiley-VCH, Weinheim, 2008 and references therein.
8. (a) D. B. Levin, L. Pitt and M. Love, Int. J. Hydrogen Energy, 2003, 29, 173–185; (b) J. I. Hayashi, S. Hosokai and N. Sonoyama, Process Saf. Environ. Prot., 2006, 84, 409–419; (c) A. J. Esswein and D. G. Nocera, Chem. Rev., 2007, 107, 4022–4047; (d) A. Kudo and Y. Miseki, Chem. Soc. Rev., 2009, 38, 253–278.
9. Y. Blum, D. Czarkie, Y. Rahamim and Y. Shvo, Organometallics, 1985, 4, 1459–1461.
10. Y. Shvo, D. Czarkie, Y. Rahamim and D. F. Chodosh, J. Am. Chem. Soc., 1986, 108, 7400–7402.
11. (a) R. Karvemu, R. Prabhakaran and K. Natarajan, Coord. Chem. Rev., 2005, 249, 911–918; (b) S. Gladiali and E. Alberico, Chem. Soc. Rev., 2006, 35, 226–236.
12. Y. Shvo, I. Goldberg, D. Czierkie, D. Reshef and Z. Stein, Organometallics, 1997, 16, 133–138.
13. N. Menashe, E. Salant and Y. Shvo, J. Organomet. Chem., 1996, 514, 97–102.
14. J. S. M. Samec and J. E. Bäckvall, Chem.–Eur. J., 2002, 8, 2955–2961.
15. J. S. M. Samec, A. H. Éll and J. E. Bäckvall, Chem.–Eur. J., 2005, 11, 2327–2334.
16. A. H. Éll, J. S. M. Samec, C. Brasse and J. E. Bäckvall, Chem. Commun., 2002, 10, 1144–1145.
17. (a) A. L. E. Larsson, B. A. Persson, B. Pugin and J. E. Bäckvall, Angew. Chem., Int. Ed., 1997, 36, 1211–1212; (b) B. A. Persson, A. L. E. Larsson, M. L. Ray and J. E. Bäckvall, J. Am. Chem. Soc., 1999, 121, 1645–1650; (c) J. Paetzold and J. E. Bäckvall, J. Am. Chem. Soc., 2005, 127, 17620–17621.
18. C. P. Casey, S. W. Singer, D. R. Powell, R. K. Hayashi and M. Kavana, J. Am. Chem. Soc., 2001, 123, 1090–1100.
19. C. P. Casey and G. A. Bikzhanova, Organometallics, 2002, 21, 1955–1959.
20. L. S. M. Samec, J.-E. Bäckvall, P. G. Andersson and P. Brant, Chem. Soc. Rev., 2006, 35, 237–248.
21. S. E. Clapham, A. Hadzovic and R. H. Morris, Coord. Chem. Rev., 2004, 248, 2201–2237.
22. G. Csjernyk, A. H. Éll, L. Fadini, B. Pugin and J.-E. Bäckvall, J. Org. Chem., 2002, 67, 1657–1662.
23. C. P. Casey, G. A. Bikzhanova, Q. Cui and I. A. Guzei, J. Am. Chem. Soc., 2005, 127, 14062–14071.
24. J. B. Johnson and J.-E. Bäckvall, J. Org. Chem., 2003, 68, 7681–7684.
25. C. P. Casey and H. Guan, J. Am. Chem. Soc., 2007, 129, 5816–5817.
26. C. P. Casey and H. Guan, Organometallics, 2012, 31, 2631–2638.
27. A. Comas-Vives, G. Ujaque and A. Lledós, Organometallics, 2007, 26, 4135–4144.
28. H. Zhang, D. Chen, Y. Zhang, G. Zhang and J. Liu, Dalton Trans., 2010, 39, 1972–1978.
29. X. Lu, Y. Zhang, P. Yun, M. Zhang and T. Li, Org. Biomol. Chem., 2013, 11, 5264–5277.
30. Gaussian 09 (Revision B.01), M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford CT, 2009.
31. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789; (c) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
32. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 (J. Chem. Phys., 1985, 82, 299–310).
33. (a) K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163; (b) K. Fukui, Acc. Chem. Res., 1981, 14, 363–368.
34. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 4538–4543.
35. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
36. X. Xu and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 80–90.
37. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167.
38. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
39. L. M. Pratt, S. Merry, S. C. Nguyen, P. Quan and B. T. Thanh, Tetrahedron, 2006, 62, 10821–10828.
40. L. M. Pratt, D. G. Truhlar, C. J. Cramer, S. R. Kass, J. D. Thompson and J. D. Xidos, J. Org. Chem., 2007, 72, 2962–2966.

---

Footnote

† Electronic supplementary information (ESI) available: Total electronic energies, thermal corrections to Gibbs free energies and Cartesian coordinates, and so on. See DOI: 10.1039/c4ra12466a

---