Phononic band structure in carbon microtube composites

Abstract

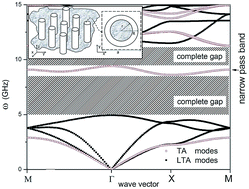
In this work we have investigated theoretically the dispersion relation of mechanical waves propagating in an elastic solid medium reinforced by carbon microtubes arranged periodically in a square lattice. Based on classical elasticity theory, we obtained a generalized wave equation ignoring microscopic size effects. The wave equation is solved using the plane wave expansion method and numerical routines. The results for structures with lattice parameters of the order of micrometers show the presence of gaps that depend on the thickness of the microtubes’ walls. Our findings show that hollow inclusions maintain as large gaps as their massive counterparts until the ratio of the inner to the outer microtube radius is less than 20%. Therefore such structures are suitable for mechanical vibrations management. As an example, with appropriate parameters we have proposed a GHz transversal phononic band pass filter. The phonon density of states were also computed.

---

1. Introduction

For a long time it has been known that the periodic potential in crystals gives rise to a set of quasi-continuum energy levels which form the so-called band structure of the materials. Over the last few decades, this concept was extended for other types of waves propagating in periodic systems, including electromagnetic waves (in photonic crystals),^1,2 acoustic and elastic waves (in phononic crystals),^3,4 plasmon waves (in plasmonic crystals)⁵ and spin waves (in magnonic crystals).⁶ The common physical property of these systems is to induce wave scattering and destructive interferences in some frequency ranges, leading to the formation of band gaps. In particular, the phononic metamaterials have received a great deal of attention due to their ability to tailor acoustic (in fluids) and elastic (in solids) mechanical waves, and even low-frequency acoustic phonons in nanostructures. This class of structures encompasses materials whose physical properties are determined from geometrical structuring, rather than their composition.

Early studies in bulk phononic crystals, i.e., structures assumed to extend infinitely along the three spatial directions, have shown that gaps may appear under conditions which concern mainly the contrast between the physical characteristics (density and elastic moduli) of the inclusions and the matrix, as well as the geometry, shape and filling fraction of the array of inclusions. The gaps may also be influenced by the physical nature of the host materials and their inclusions, which may be: solid/solid, fluid/fluid, or mixed solid/fluid composite systems.^7–13 Further works, beyond conventional binary component structures, including hollow,¹⁴ coated¹⁵ and rotated¹⁶ inclusions, give even more options to modulate the phononic band gap. The applications range from confinement or guiding of acoustic/elastic waves, improvements in transducers (opto-mechanical converters, for example), noise control and vibration shields. This research area has been coined Transformational Acoustics.¹⁷

Primarily, due to experimental convenience, the studies were limited to millimeter scale structures, like metal cylinder arrays immersed in air or water, and frequency band gaps ranging from kHz to MHz.^18,19 Recent works have reported the fabrication of hypersonic phononic crystals with frequency band gaps from GHz to THz.^20,21 The interest lies in phonon management which could allow heat control and coherent phonon emission,^22–25 for example. With the advent of GHz phononics, the so called phoxonic crystals have received special attention. They are microsized structures presenting both phononic as well as photonic band gaps.²⁶ From the photonic crystal (PtC) perspective, many devices have been proposed that allow for the realization of optical cavities, waveguides, high Q resonators, selective filters, lenses or superprisms. For example, Prather et al. experimentally demonstrated light self-collimation in silicon PtC plates, thus proposing an alternative to waveguides that does not require line defects.²⁷ Lin et al. proposed a PtC lens to couple THz radiation into silicon integrated devices. A 45% coupling efficiency was demonstrated experimentally.²⁸ Wong and Morales demonstrated enhanced photocurrent efficiency of a carbon nanotube device electromagnetically coupled to a GaAs photonic structure, which has application in the increase of the intensity of infrared light in the nanotubes for effective energy conversion.²⁹ Combining these possibilities with phonon management opens an entirely new path to manipulate light, sound and heat in micro-electro-mechanical systems.

The inclusions studied in this paper are comprised of carbon microtubes, a class of carbon structures with tubular morphology which have internal diameters in the range of microns. In analogy with carbon nanotubes, which have a noteworthy role in nanoscience, carbon microtubes have the potential to become a key material in mesoscopic technology.³⁰ Like carbon nanotube forests, periodic arrays of microtube structures have applications in light emission, ultracapacitors, solar cells, chemical and biological sensors, etc.³¹ From a practical experimental perspective our work is supported by Han et al.,^32–34 who developed a novel method for making carbon microtubes by thermal pyrolysis of composite fibers that contained a thermally removable polymer core, like poly(ethylene terephthalate), and a more thermally stable exterior, such as one made from a conducting polymer like polypyrrole. The method can be used to prepare micrometer- or submicrometer-sized carbon tubes of a few centimeters length with a controllable tube wall thickness ranging from less than 30 nm to a few micrometers.

The phononic metamaterial considered may also be understood as a reinforced composite, i.e., a material which has strong fibers immersed in a weaker matrix material, which greatly influences the mechanical properties of the matrix. There are numerous applications in the engineering industry. In nanotechnology, the properties of these structures have been motivating the development of metal, ceramic and polymer matrices reinforced by micro- and nanotubes of carbon.³⁵

The phononic band structure studied in this work is described by a generalized wave equation, according to classical elasticity theory, and solved by Fourier expansion of in plane waves. The frequency eigenvalue equation thus obtained is computed by standard numerical routines. Considering a structure with a lattice parameter of the order of micrometers and varying the internal radius of the microtubes, we have observed broader band gaps and narrow pass bands inside these gaps. The phonon density of states is calculated as well, aiming to motivate future study of transport problems involving phononic metamaterials.

2. Theory

There are two approaches for obtaining the phonon dispersion relation: atomic and continuous. The atomic approach calculates the dispersion from the interatomic forces using a discrete atomic model, which basically solves coupled motion equations for each atom vibrating around their equilibrium position. The solution of these equations results in a frequency spectrum (going up to tens of THz) which depends on the number of atoms considered. However, the method becomes computationally expensive when trying to describe smaller and smaller frequencies because the number of atoms considered in the calculations also increases. The continuous approach, on the contrary, considers the solid as a continuum medium, ignoring its atomic structure. Thus, such an approach is very useful to describe mechanical vibrations with wavelengths larger than hundreds or dozens of unit cells, which correspond to frequencies below 10 or 100 GHz, respectively. In short, the atomistic approach is more suitable to describe the optical and acoustic modes of high-frequency phonons (∼THz) while the continuum approach fits the description of low-frequency acoustic phonons (≲GHz).

In the scope of the latter, one can study mechanical perturbations in a medium through the generalized wave equation in the linear elastic regime,^36,37

ρ(r)ü_i(r, t) = ∂_j[C_ijmn(r)∂_mu_n(r, t)], (1)

where ρ is the matter density in the medium, C_ijmn is the elastic stiffness tensor and u_i is the displacement field (i = 1, 2, 3 are the rectangular coordinates). For isotropic periodic media

C_ijmn(r) = λ(r)δ_ijδ_mn + μ(r)(δ_imδ_jn + δ_inδ_jm), (2)

where λ and μ are periodic Lamé coefficients. More specifically, μ is the shear modulus and λ is a combination of two mechanical parameters like bulk modulus, elastic modulus, shear modulus and Poisson’s ratio.

The continuum model can be scaled to be used from macro to micro phononic crystals simply by adopting a change in scale of the frequency spectrum by the non dimensional factor Ω = ωa/2πc₀, where ω is the frequency, a is the lattice constant and c₀ is an effective wave velocity in the medium.^7,38 Thus we can say roughly that solid phononic structures with periodicity at the meter, millimeter or micrometer scale present frequency gaps in kHz, MHz or GHz, respectively. Recently, nonlocal³⁹ and surface/interface⁴⁰ effects were considered in band structure calculations of phononic crystals, showing deviations from classical continuum mechanics. Even in some quantum problems the classical theory can be applied with good results. As an example, we can cite Akatyeva and Dumitrica, who studied screw dislocation influences in the stability and properties of nanowires and nanotubes. They found that the existence of twisted nanostructures can be described using Eshelby’s twist linear elasticity mechanics.⁴¹

Several theoretical approaches have been used to study band structure and transmission spectra of mechanical waves. Among them, Plane Wave Expansion (PWE),⁷ Finite Element Method (FEM)⁴² and Finite Difference Time Domain (FDTD)⁴³ have been largely used since early works in photonic and phononic crystals. The PWE method, which is based on the Bloch theorem and the Fourier series expansion, is a simple and powerful method to investigate wave propagation and band structures in reciprocal space. However, being a Fourier space method, it suffers from the Gibbs phenomenon⁴⁴ and the convergence problem in phononic structures containing fluid. The FEM and FDTD methods overcome such difficulties, although their use is much less intuitive and requires more computational effort.

We have adopted the PWE method to solve the wave equation and determine the dispersion relation for a phononic structure formed by isotropic carbon microtubes in a soft matrix. We begin by expressing the displacement field using Bloch’s theorem and the harmonic approximation,

where k is a wave vector in the first Brillouin zone and G is a reciprocal lattice vector ranging from 1 to N_PW, the number of plane waves used in the expansion. Now, expanding ρ(r) and C_ijmn(r) in Fourier series, we can express eqn (1) as an eigenvalue equation,

ω²ρ_G′−Gu_k+Gⁱ = C_G′−G^ijmn(k + G′)_j(k + G)_mu_k+Gⁿ, (3)

which gives us the dispersion curves ω(k) and, hence, the phonon density of states for the acoustic modes. The Fourier coefficients ρ_G′−G and C_G′−G^ijmn can be expressed as
where α_G ≡ (ρ_G, C_G^ijmn) and the subscripts A and B refer to the inclusion and the host medium, respectively; f is the filling fraction that defines the cross-sectional area of a cylinder relative to a unit-cell area A_c = a², and is given by f = πR²(1 − f₁²)/a², where f₁ = r/R is the radius fraction; and F(G) is a structure function defined over the area of the inclusion

The phononic crystal studied here is a structure composed of an array of hollow carbon cylinders embedded in a soft isotropic solid medium arranged in a square lattice as shown in Fig. 1. We consider mechanical waves propagating in the xy plane, with vibrations polarized in the z axis known as transversal modes, or Z-modes, and vibrations polarized along the xy plane known as mixed longitudinal-transversal modes, or XY-modes. In order to describe the hollow cylinders, we evaluate F(G) according to

where J₁ is the Bessel function of the first kind. When r → 0, i.e., massive cylinders, the structure function reduces to the well-known expression F(G) = 2 f (GR)⁻¹J₁(GR).

Fig. 1 Representation of a phononic crystal with hollow inclusions immersed in a soft medium forming a square lattice in the xy plane. The unit cell has an area a² and a filling fraction πR²(1 − f₁²)/a².

Since we are assuming that the structure is isotropic, we can use eqn (2) to write eqn (3) as

In matrix form, we have a 3N_PW × 3N_PW block diagonalization problem

Solving these equations, we obtain the dispersion relation along the high symmetry direction for coupled vibrations in the xy plane (superior block matrix) and transversal vibration modes (inferior block matrix).

3. Results and discussion

The numerical calculations were performed using the GFortran Compiler⁴⁵ and standard numerical diagonalization routines. The matrix was chosen to be the one of a very low density medium in order to achieve a high contrast in the acoustic impedance. Such a medium can be considered, for example, as low density epoxy resin or polyethylene foam. High impedance mismatch can also be achieved using metallic (or even tungsten) inclusions. Physical parameters of the materials are listed in Table 1. The parameters for the phononic crystal structure (Fig. 1) were chosen to be: a = 2 → 4 μm, R = 1 μm and r = 0.0 → 0.8 μm.

Table 1 Physical parameters used in this work for a system composed of carbon microtubes immersed in a soft medium

	Density	Elastic modulus	Shear modulus
	ρ (kg m^−3)	λ (N m^−2)	μ (N m^−2)
Carbon	1800	130 × 10^9	88 × 10^9
Soft medium	120	6 × 10^9	2 × 10^9

---

Epoxy resin is an amorphous solid and is thus isotropic. The assumption of isotropic carbon microtubes is supported by Han et al.^32–34 In their work, the carbon tubes were prepared by heating the composite fibers in a quartz tube oven from room temperature to 1000 °C under a N₂ atmosphere. An annealing time of 0–3 h was employed after the temperature reached 1000 °C, before the carbon tubes were cooled to ambient temperature. They observed that the morphology of the sample specimen formed at 500 °C was still quite amorphous, with the crystallinity of the resulting carbon tubes increasing with annealing temperature. This suggests the possibility of a phase transformation from amorphous carbon matrices to a more ordered form during the thermal annealing process.

In Fig. 2 we observe complete band gaps formation in the frequency dispersion relations for acoustic longitudinal-transversal (LTA or XY) modes and acoustic transversal (TA or Z) modes. In Fig. 2A, the internal radius is r = 0.2R and the filling fraction is f = 0.335. The first complete gap appears between 4.9 and 8.6 GHz, i.e., a forbidden window of 3.7 GHz. A second gap appears right above, from 9.4 to 11.3 GHz. For higher frequencies, there are no more complete gaps, nevertheless there are still smaller gaps for XY or Z modes, called incomplete band gaps. In Fig. 2B where r = 0.6R and f = 0.223, there is an incomplete band gap for the XY mode with a width of 1.4 GHz. For both plots in Fig. 2, a = 3 μm was used. It is interesting to note the following: (a) for a = 2 μm (the carbon cylinder touches the unit cell frontier) no complete gap appears for any internal radius and filling fraction, as presented in Table 2; (b) the larger gaps were obtained for a = 3 μm; (c) smaller complete gaps were obtained for a = 4 μm. This is a clue that when the unit cell is very large the volume of the microtube is negligible, which results in no modification of vibrational modes of the medium where the former are immersed.

Fig. 2 Phononic band structure of the carbon microtube/soft matrix phononic crystal. The mixed longitudinal-transversal waves (black filled squares) and the pure transverse waves (red open squares) are plotted along the high symmetry directions of a square unit cell of parameter a = 3 μm. In (A) the internal radius is r = 0.2R and the filling fraction is f = 0.335. In (B), r = 0.6R and f = 0.223.

Table 2 Filling fraction (in percentage) for various values of internal radius and unit cell parameter

r (μm)	0.0	0.2	0.4	0.6	0.8
a = 2 μm, f (%)	78.5	75.4	66.0	50.3	28.3
a = 3 μm, f (%)	34.9	33.5	29.3	22.3	12.6
a = 4 μm, f (%)	19.6	18.8	16.5	12.6	7.1

---

The basic application of phononic crystals consists of suppressing, filtering and guiding mechanical vibrations in their interior. They are especially important in communication technology and reduction of noise in electronic circuits. The basic idea involves engineering the band gap and exploiting narrow pass band frequencies. In Fig. 2A, the narrow band at around 10 GHz, ranging between the first two complete band gaps, is an example of a possible filter for transversal vibrations. Moreover, it is interesting to note that this narrow pass band can be created without the introduction of defects within the structure.

Previous work on metallic cylinders in air has shown that due to the high impedance mismatch between the components, the transmission spectra were qualitatively the same for hollow or filled inclusions.¹⁴ However, for metallic cylinders immersed in water, the transmission spectra have shown a dependence on the thickness of the hollow inclusions, which are characterized by a narrow transmission peak with tunable frequency according to their inner radius.¹⁹ These results encompass a solid/fluid phononic structure. Our results encompass a solid/solid phononic structure, which exhibits transversal vibrational modes (shear modes). We also observed a high dependence of the band gaps magnitudes with the internal radius of the cylinders. This indicates that the radius mode dependence is related to the filling fraction of the phononic structure.

Fig. 3 presents the phonon density of states for the polarization modes of Fig. 2A, where r = 0.2R (dense lines). Also, we plot the density of states of the bulk soft medium, calculated from the dispersion relation in an empty lattice model. Note that the gap by itself is not entirely responsible for the reduction in the density of phonons; dispersionless phonon branches also contribute. The knowledge of the density of states allows the computation of important physical properties involving thermal and electronic transport, the reduction of thermal conductivity in phononic crystals being an intense research field in recent years.^22,23 Finally, the control of the heat diffusion process in semiconductors would represent an extraordinary breakthrough in micro-electro-mechanical systems and energy management.

Fig. 3 Density of states for the band structure shown in Fig. 2A (dense lines) and the density of states of the bulk matrix (sparse lines).

Fig. 4 shows the influence of the wall thickness on the phononic band structure. The two complete band gaps (see Fig. 2A), the incomplete band gap for XY modes (see Fig. 2B) and the width of the transversal phononic transmittance band are plotted as a function of the radius fraction of the microtubes, namely: a = 3 μm, R = 1 μm and r = 0.0–0.8 μm. From Fig. 4 one can also show that thick walled microtubes present a similar dispersion relation to microrods (massive microtube, r = 0), mainly because the filling fraction reduction is small: a reduction of 1.4% for f₁ = 0.2 and 5.6% for f₁ = 0.4, when compared with massive inclusions. The first gap disappears at f₁ = 0.6 and the second one at f₁ = 0.5. The incomplete gap XY remains until f₁ = 0.7. Above that, the filling fraction becomes so small (<10%, see Table 2) that no gap is formed. Further, the figure shows that the optimal configuration for the broader transversal pass band occurs for f₁ = 0.5.

Fig. 4 Variation of the first band gaps with radius fraction in the band structure of the carbon microtube/soft medium system.

4. Conclusions

In summary, we investigated the phononic band gaps of a 2D phononic crystal composed of isotropic carbon microtubes immersed in a soft matrix. The plane wave expansion method was used assuming an infinite medium and ignoring any boundary, surface or quantum size effects.

Considering a structure with a lattice parameter of the order of a few micrometers, we have obtained a band gap with width of about 4 GHz for thicker microtubes. A narrow pass band for transverse polarized vibrations within the gap was found, which has potential application as a high-frequency acoustic filter. Moreover, the phonon density of states, computed from the dispersion relation, is the first step in order to study thermal and electronic transport in phononic metamaterials. We believe that our work further enhances the knowledge of phononic band gap engineering¹⁰ considering hollow inclusions and the influence of diameter and wall thickness. Experimental support for this paper can be found in the results of Soliman et al.⁴⁶

Acknowledgements

This work was supported by CNPq, FAPEMIG, and CAPES, Brazil.

References

1. E. Yablonovitch, Phys. Rev. Lett., 1987, 58, 2059.
2. E. Yablonovitch, Phys. Rev. Lett., 1989, 63, 1950.
3. M. Sigalas and E. N. Economou, J. Sound Vib., 1992, 158, 377.
4. M. S. Kushwaha, et al., Phys. Rev. Lett., 1993, 71, 2022.
5. I. I. Smolyaninov, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 2454.
6. S. A. Nikitov, et al., J. Magn. Magn. Mater., 2001, 236, 320.
7. M. S. Kushwaha, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 47, 2313.
8. J. O. Vasseur, et al., J. Phys.: Condens. Matter, 1994, 6, 8759.
9. T. T. Wu, et al., Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 52, 094301.
10. I. Sliwa and M. Krawczyk, Acta Phys. Pol., A, 2005, 108, 943.
11. M. Sigalas, et al., Z. Kristallogr., 2005, 220, 765.
12. X. Z. Zhou, et al., J. Appl. Phys., 2009, 106, 014903.
13. Y. Pennec, et al., Surf. Sci. Rep., 2010, 65, 229.
14. J. O. Vasseur, et al., Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 056608.
15. S. Zhang and J. Chengs, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 65, 056608.
16. S. C. S. Lin and T. J. Huang, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 174303.
17. L. Fok, et al., MRS Bull., 2008, 33, 931.
18. R. Martinez-Sala, et al., Nature, 1995, 378, 241.
19. A. Khelif, et al., J. Appl. Phys., 2003, 94, 1308.
20. T. Gorishnyy, et al., Phys. Rev. Lett., 2005, 94, 115501.
21. D. F. Goether, et al., AIP Adv., 2011, 1, 042001.
22. P. E. Hopkins, et al., Nano Lett., 2011, 11, 107.
23. M. Maldovan, Phys. Rev. Lett., 2013, 110, 025902.
24. L. C. Guarnieri, et al., Phys. Procedia, 2012, 28, 57.
25. L. C. Guarnieri, et al., J. Supercond. Novel Magn., 2012, 26, 1.
26. A. Martínez, Photonic and Phononic Properties of Engineered Nanostructures III, Proc. of SPIE, 2013, p. 8632.
27. D. W. Prather, et al., Opt. Lett., 2004, 1, 50.
28. C. Lin, et al., Opt. Lett., 2005, 30, 1330.
29. B. Wong and A. Morales, J. Phys. D: Appl. Phys., 2009, 42, 055111.
30. S. Dumpala, et al., Smart Materials, Carbon Microtubes and Conical Carbon Nanotubes: Design and Applications, CRC Press, 2008, ch. 22.
31. Z. Ren, et al., Aligned Carbon Nanotubes: Physics, Concepts, Fabrication and Devices, Springer-Verlag, Berlin Heidelberg, 2013.
32. C. Han, et al., Chem. Mater., 1999, 11, 1806.
33. C. Han, et al., Chem. Mater., 2001, 13, 2656.
34. C. Han, et al., Chem. Mater., 2001, 13, 4180.
35. D. Gay, et al., Composite Materials: Design and Applications, CRC Press LLC, 2003.
36. N. W. Ashcroft and N. D. Mermin, Solid State Physics, Saunders College, Philadelphia, 1976, ch. 22.
37. L. Landau and E. Lifshitz, Theory of Elasticity, Pergamon, Oxford, 3rd edn, 1986.
38. R. Ramprasad and N. Shi, Appl. Phys. Lett., 2005, 87, 111101.
39. A. L. Chen and Y. S. Wang, Phys. E, 2011, 44, 317.
40. N. Zhen, Phys. E, 2013, 54, 125.
41. E. Akatyeva and T. Dumitrica, Phys. Rev. Lett., 2012, 109, 035501.
42. A. Movchan, et al., Mater. Sci. Eng., A, 2006, 431, 175.
43. M. M. Sigalas and N. García, J. Appl. Phys., 2000, 87, 3122.
44. E. W. Weisstein, “Gibbs Phenomenon”, From MathWorld-A Wolfram Web Resource, http://mathworld.wolfram.com/GibbsPhenomenon.html.
45. G. Fortran, Gnu Compiler Collection, http://gcc.gnu.org.
46. Y. M. Soliman, et al., Appl. Phys. Lett., 2010, 97, 081907.

---