Molecular dynamics simulation of deformation accumulation in repeated nanometric cutting on single-crystal copper
Abstract
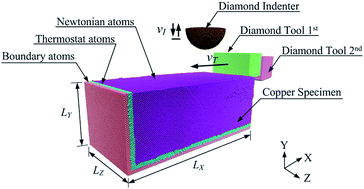
The machining-induced residual defects and stress in subsurfaces determine the mechanical properties of the finished surfaces of bulk materials. In this paper, three-dimensional molecular dynamics simulations of AFM-based nanoindentation using diamond indenters are conducted on machining-induced surfaces of single-crystal copper. The simulation results indicate that the residual defects and deformation introduced from the first nanometric cutting process induce dislocation nucleation and propagation in the successive nanometric cutting process. A large number of atomic defects and vacancies occur in the second nanometric cutting process, many more than in the first cutting process, leading to a significant change in mechanical properties. In addition, the quantitative analysis of the surface is obtained based on the Oliver–Pharr method. The results reveal that the machining-induced surface is softer than the pristine single-crystal copper surface. Based on the defect accumulation limitation, the hardness and surface potential energy of the machining-induced surface tend to be between the highest and lowest limitations.

 Please wait while we load your content...
Please wait while we load your content...