A facile strategy to achieve high conduction and excellent chemical stability of lithium solid electrolytes†
Shufeng Song,
Jia Lu,
Feng Zheng,
Hai M. Duong and
Li Lu*
Department of Mechanical Engineering, National University of Singapore, 9 Engineering Drive 1, Singapore 117576, Singapore. E-mail: luli@nus.edu.sg; Fax: +65-67791459; Tel: +65-65162236
First published on 18th December 2014
Abstract
Lithium solid electrolytes have shown their potential for high-energy density batteries. The use of solid electrolytes will also be able to overcome safety issues associated with conventional carbonate-based electrolytes. However, achieving the combination of high ionic conductivity and excellent electrochemical stability in lithium solid electrolytes is still a major challenge. Herein we report a facile strategy to achieve high conduction and excellent electrochemical stability by the substitution of Cl for O based on the concept of bottleneck size and binding energy. The ionic conductivities of Li10.42Si1.5P1.5Cl0.08O11.92 and Li10.42Ge1.5P1.5Cl0.08O11.92 are 1.03 × 10−5 S cm−1 and 3.7 × 10−5 S cm−1 at 27 °C, respectively, which are 13 orders of magnitude higher than that of the pure Li3PO4, and 1 order of magnitude higher than that of the pristine Li10.5Si1.5P1.5O12. The electrochemical stability with metallic lithium is up to 9 V vs. Li+/Li, which is one of the widest electrochemical windows of solid electrolytes. This research also addresses the crystal structure, lithium ion migration mechanism, and battery performance.
Introduction
Although lithium-ion batteries are now widely used in many electronic products, safety, energy density, and service life are still issues, which continue to plague lithium-ion batteries for the potential of mass market of electric vehicles and large-scale energy storage.1 There are two ways to increase the energy density, one of which is to increase the specific capacity and the other one is to increase the voltage potential of the cathode which is limited by current liquid electrolytes. Applying solid electrolytes to lithium batteries will eliminate the conventional voltage limitation (4.5 V vs. Li+/Li) of currently used carbonate-based electrolytes and open up the possibility of high-voltage operation with 5 V-class cathode materials.2 On the other hand, metallic lithium batteries exhibit the highest theoretical energy densities. Among many possible systems, Li–S and Li–O2 batteries are very attractive as candidates for next-generation high-energy density batteries. The use of solid electrolytes could potentially suppress the formation of lithium dendrites, that are caused by uneven current distributions at the metal–electrolyte interface during cycling.3A number of works reported new solid electrolytes, such as sulfide-based superionic conductors.4 Recently, a breakthrough has been achieved in inorganic sulfide-based electrolyte with extremely high room temperature conductivity of 10−2 S cm−1.5,6 Generally, sulfides have higher ionic conductivity than oxides but lower air and moisture stability than oxides. The hypersensitivity of the sulfides to air and moisture requires sophistically and tedious treatment procedures under dry inert gas atmosphere, which increase their processing cost.7 Moreover, the sulfides suffer inferior electrochemical stability due to reacting continuously with Li anode.8 In an effort to overcome inferior electrochemical stability, the lithium phosphorous oxynitride (LPON) electrolyte developed at Oak Ridge National Laboratories (ORNL) exemplifies the extremely good stability with Li metal anode. The ORNL group reports thin film batteries employing the LPON electrolyte, LiCoO2 cathode, and Li metal anode are capable of over 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 charge–discharge cycles with 0.001% capacity loss per cycle. Unfortunately LPON has relatively poor ionic conductivity of ca. 2 × 10−6 S cm−1.9
000 charge–discharge cycles with 0.001% capacity loss per cycle. Unfortunately LPON has relatively poor ionic conductivity of ca. 2 × 10−6 S cm−1.9
Although the advantages of non-flammable solid electrolytes are widely acknowledged, their low ionic conductivities or low chemical and electrochemical stabilities prevent them from practical applications. It is known that the ionic conductivity is given by:
| σ = Zenμ | (1) |
Experimental
Synthesis of halide-substituted solid solutions of Li3PO4 and Li4Si/GeO4 [Li10.5-xSi/Ge1.5P1.5ClxO12−x (0.05 ≤ x≤ 1.0)]
Li10.5-xSi/Ge1.5P1.5ClxO12−x (0.05 ≤ x≤ 1.0) was prepared by melt-casting method. All the raw materials were received from Sigma, and the stoichiometric amounts of Li2CO3 (99%, with 5 wt% excess to compensate for the loss of lithium during melting), SiO2 (99%), GeO2 (99.999%), NH4H2PO4 (98.5%), LiCl (99%), LiF (99%), and LiBr (99%) were weighed and ball-milled using zirconia balls for about 2 h in industrious ethanol in air. The mixed materials were pre-calcined at 700 °C for 2 h, subsequently, the calcined powder was melted at 1200–1250 °C, the sheet with thickness of about 1 mm was obtained after casting the melt using a rolling machine. For some specific samples, the F and Br were added to study their effects on ionic conductivity. Although the materials are not air-sensitive, to avoid possible interference from absorbed moisture, all the casted sheets were immediately transferred into an argon-filled glove box.Electrochemical characterization
For the ionic conductivity measurements, the sheets were cut to small pellet and the conducting silver paste was painted on both sides of the small sheet and sealed in a Swagelok cell. Electrochemical impedance spectroscopy (EIS) measurements were carried out using a Solartron 1260 + 1287 System, applying 100 mV in the frequency range 1 MHz–10 Hz, without any pressure applied. Activation energy was measured at the temperature range from 27 °C to 110 °C.Cyclic voltammogram (CV) of the samples made of Ag\Li10.42Si/Ge1.5P1.5Cl0.08O11.92 sheet\Li was measured using a linear sweep voltammetry between a voltage range from −0.5 V to 9 V vs. Li+/Li at a 1 mV s−1 scan rate.
Full cells using Li10.42Si/Ge1.5P1.5Cl0.08O11.92 as the electrolytes, 0.3Li2MnO3·0.7LiMn1.5Ni0.5O4 as the cathode and lithium metal as the anode were assembled in 2025 coin cells. The cathode powder was mixed with super P conductive carbon (TIMCAL Ltd.) and polyvinylidene fluoride (PVDF, Sigma) at a weight ratio of 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
: ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in an N-methylpyrrolildone (NMP, Sigma) solvent to form uniform slurries and then coated on Al foils. To reduce interfacial impedance between the cathodes and electrolytes, a very little drop of 1 M LiPF6 in EC–DEC (1
1 in an N-methylpyrrolildone (NMP, Sigma) solvent to form uniform slurries and then coated on Al foils. To reduce interfacial impedance between the cathodes and electrolytes, a very little drop of 1 M LiPF6 in EC–DEC (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by weight) as a buffer between solid electrolyte and cathode layer. Charge–discharge test was performed at a potential range between 2.0 and 5.0 V vs. Li+/Li at 0.1 C rate.
1 by weight) as a buffer between solid electrolyte and cathode layer. Charge–discharge test was performed at a potential range between 2.0 and 5.0 V vs. Li+/Li at 0.1 C rate.
Structural characterization
X-ray diffraction (Shimadzu XRD-6000 and 7000 Cu-Kα) was employed to detect crystallographic structure of the samples in air with no seal. Lattice constants and structures were analyzed by Rietveld refinement of the powder XRD data using GSAS software. The structure was drawn by VESTA software.Results and discussion
Fig. 1 represents typical Nyquist plots of Li10.42Si1.5P1.5Cl0.08O11.92 (square symbol) and Li10.42Ge1.5P1.5Cl0.08O11.92 (circle symbol) measured at 27 °C. It shows a depressed rather than ideal semicircle, inclined rather than vertical capacitive tail. The appearance of the tail at low frequencies in the case of ionically blocking electrodes is an indication that the pellet is ionically conducting in nature.14 Close examination of the Nyquist plot, there is only one semicircle, suggesting that the grain and grain boundary resistance be unable separated. The total conductivity of the pellet at 27 °C is calculated by the equation:
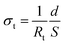 | (2) |
 | ||
| Fig. 1 Typical Nyquist plots of Li10.42Si1.5P1.5Cl0.08O11.92 (square symbol) and Li10.42Ge1.5P1.5Cl0.08O11.92 (circle symbol) measured at 27 °C. | ||
Fig. 2 shows the Arrhenius plots of Li10.42Si/Ge1.5P1.5Cl0.08O11.92 in the range between 27 °C and 110 °C. The activation energies for two types of solid electrolytes were calculated using the Arrhenius equation:
| σ = Aexp(−Ea/kT) | (3) |
Fig. 3 shows the effect of halide substitution on the room-temperature conductivity of Li10.5−xSi1.5P1.5Cl/FxO12−x (0.05 ≤ x≤ 1.0). The square symbol displays the conductivity variation with substitution of Cl for O. A maximum conductivity σLi ≈ 1.03 × 10−5 S cm−1 was found for x = 0.08. The solid circle symbol displays the conductivity variation with substitution of F for O. The maximum conductivity σLi ≈ 7.6 × 10−6 S cm−1 was lower than their Cl counterpart, while the conductivities of Li10.4Si1.5P1.5Cl0.05F0.05O11.9 and Li10Si1.5P1.5Cl0.25F0.25O11.5 (triangular symbol) are comparable with their Cl counterpart Li10.4Si1.5P1.5Cl0.1O11.9 and Li10Si1.5P1.5Cl0.5O11.5. Whereas, the conductivities of Li10.4Si1.5P1.5Cl0.05Br0.05O11.9 is much lower (≈7.4 × 10−6 S cm−1, not shown in this paper).
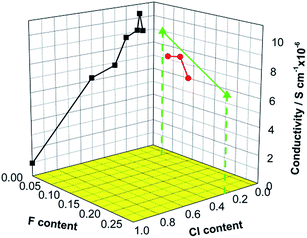 | ||
| Fig. 3 Effect of halide substitution on the room-temperature conductivity of Li10.5−xSi1.5P1.5Cl/FxO12−x (0.05 ≤ x≤ 1.0). | ||
It is worth noting that the activation energy versus Cl content displays an inverted peak with the conductivity (Fig. 4). The lowest activation energy observed in the composition of Li10.42Si1.5P1.5Cl0.08O11.92 that had the highest ionic conductivity.
A high conductivity is necessary but not a sufficient property to make an electrolyte to be useful in practical terms. A wide electrochemical window is also an essential parameter to ensure good performance in rechargeable lithium batteries. The electrochemical stability window has been evaluated by running a cyclic voltammogram of cells, in which Li and Ag serve as reference/counter and working electrodes, respectively. Fig. 5 displays the current–potential curve of Li10.42Si/Ge1.5P1.5Cl0.08O11.92. First, the potential was swept from open voltage (OCV) to −0.5 V (cathodic sweep) and then from −0.5 V to 9 V (anodic sweep). The cathodic current corresponding to lithium deposition, and the anodic current corresponding to lithium dissolution. No obvious current was observed except the ones due to the lithium deposition and dissolution, indicating that the Li10.42Si/Ge1.5P1.5Cl0.08O11.92 electrolytes have a wide electrochemical window up to 9 V vs. Li+/Li. Li10.42Si/Ge1.5P1.5Cl0.08O11.92 would be an alternative for stable protective solid electrolyte interphase and buffer film taking into account their excellent electrochemical stability with lithium metal and promising ionic conductivities.
All XRD patterns of Li10.5−xSi1.5P1.5ClxO12−x (0.05 ≤ x≤ 0.5) (Fig. S1†) show that the matrix of Cl substitution is in the solid solution with structure of γ-Li3PO4 (Powder Diffraction File 15-0760, space group Pnma). The orthorhombic structure of γ-Li3PO4 widely used as a host for preparing lithium solid electrolytes. In particular, the LPON, LISICON and thio-LISICON electrolyte materials based on γ-Li3PO4 structure have been well developed.17–19 Two different structures have been recognized in the system of solid solutions between Li3PO4 and Li4SiO4: the Li4SiO4-type phase and γ-Li3PO4-type phase with respective formulae of Li4−xSi1−xPxO4 (0 ≤ x≤ 0.12) and Li3+ySiyP1−yO4 (0 ≤ y≤ 0.42).20 In the Li4SiO4-type phase, vacancies can be introduced into the normal Li+ sites in the Li4SiO4 structure, while in the γ-Li3PO4-type phase, interstitial Li+ can be introduced into the γ-Li3PO4 structure. In the system, x = y = 0.5, it shows γ-Li3PO4-type phase judged from the XRD patterns (Fig. S1†), indicating an interstitial ion migration mechamism.
The crystal structure of Cl-substituted Li10.5−xSi1.5P1.5ClxO12−x (0.05 ≤ x≤ 0.5) was analyzed by the Rietveld method.21 The structure model of orthorhombic γ-Li3PO4 was adapted as the initial structure model with space group of Pnma (no. 62).22 Typical observed, calculated, and difference patterns for Rietveld refinement of Li10Si1.5P1.5Cl0.5O11.5 were shown in Fig. S2.† Table S1† lists the crystallographic data and details of the structure refinement. The resultant R-values reached Rwp = 0.0787, Rp = 0.0638. The Li1, Li2, Li3, P, Si, O1, O2, O3, Cl sites were the special positions of 8d, 4c, 8d, 4c, 4c, 8d, 4c, 4c, and 8d sites (the multiplicity and Wyckoff letter), respectively. The lattice constants were refined to be a = 5.012(7) Å, b = 6.116(6) Å, c = 10.599(8) Å.
Fig. 6 shows the lattice constants and volume of unit cell of pure Li3PO4 and Cl-substituted Li10.5−xSi1.5P1.5ClxO12−x solid solutions. The lattice constants and volume of unit cell of Cl-substituted Li10.5−xSi1.5P1.5ClxO12−x solid solutions are much larger than the pure Li3PO4,22 while the lattice constants and volume of unit cell vary very slightly when Cl concentration increases further, since the ionic radius of Cl− (1.81 Å) is much larger than that of O2− (1.4 Å).11 There are no simple correlation between lattice constants and ionic radii.23 Addressing the concept of bottleneck size and binding energy between mobile ions and the network anions, substitution of Cl for O increases the lattice constants and volume of unit cell, would enlarge the bottleneck size, then decrease the energy barriers (activation energy) and enhance the ionic conductivity. On the other hand, the ionicity of Li–Cl is smaller than that of Li–O due to the lower electronegativity of Cl− (3.16) than O2− (3.44). As the increase of Cl concentration, the Li+ cations would be rigidly bonded to the Cl− anions, which behaves as an obstacle for the ions migration, and increases the activation energy and decreases the ionic conductivity. Hence there should be an optimized Cl concentration with considerably large bottleneck size for Li+ ions migration and relatively small binding energy between Li–O/Cl, which may lead to the minimum activation energy and maximum ionic conductivity (Cl = 0.08). This has been demonstrated in Fig. 4.
 | ||
| Fig. 6 The lattice constants and volume of unit cell of pure Li3PO4 and Cl-substituted Li10.5−xSi1.5P1.5ClxO12−x solid solutions. | ||
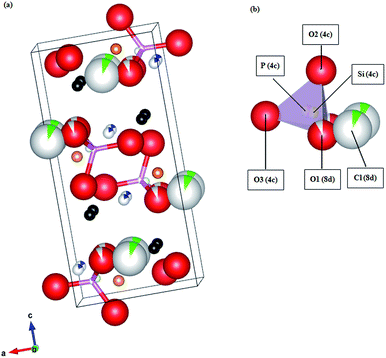
Fig. 7(a) illustrates the unit cell of Li10Si1.5P1.5Cl0.5O11.5. In an ideal crystal of γ-Li3PO4, the Li ions are located at two different crystallographically sites indicated with Li1 and Li2, using the Wyckoff labels, 8d and 4c, respectively. The d site accounts for 8 equivalent atomic sites, and the c site accounts for 4 equivalent atomic sites per unit cell. The O ions fully occupy three different sites designated as O1(8d), O2(4c) and O3(4c), and the P ions fully occupy the 4c sites. Since in an ideal crystal, all the lithium cations fully occupy their positions and are rigidly bonded to the framework, which creates no prerequisites for ion migration. In the real crystal of Li10Si1.5P1.5Cl0.5O11.5, Si and P ions share the same 4c sites due to partially substitution of Si for P (Fig. 7(b)). Noted that one site can just accommodate one atom, the P and Si ions cannot appear at 4c site at the same time, designating as white and pink spheres for P ions, and white and yellow spheres for Si ions in Fig. 7(b), indicating that they are occupied by P or Si exclusively. Cl and O ions share the same 8d sites due to partially substitution of Cl for O (Fig. 7(b)), designating as white and green spheres for Cl ions, and white and red spheres for O1 ions in Fig. 7(b), indicating that they are occupied by Cl or O exclusively. It is difficult to determine the exact positions of Cl ions due to their minor content and volatilization during preparation procedure. In the present work, we refine the crystal structure according to O1 sites occupied by Cl ions, and getting a reasonable agreement factors Rwp and Rp. However, the case that other O sites were occupied by Cl ions is also possible. 1.33 interstitial Li ions were introduced into unit per cell in the system of Li10Si1.5P1.5Cl0.5O11.5. There are two crystallographically inequivalent Li interstitial sites I and II, and four sites equivalent to I site and eight sites equivalent to II site.24 We firstly refine the crystal structure according to I site occupied by interstitial Li ions. However, it is unreasonable with the distance of 0.79 Å between interstitial Li ions and the neighbor O ions (not shown in this paper). Therefore, we supposed that the 1.33 interstitial Li ions occupy the interstitial II sites, designating as Li3 in Fig. 7 (white and blue spheres).
Interstitial migration of the lithium ion were showing in dimension 2a × 2b × 2c supercells in Fig. 8. The hypothesis of interstitial mechanism described here for ions diffusion within the type II voids suggest that possible mechanism for interstitial Li ion diffusion in all three crystallographic directions (Fig. 8(a)). We thus considered the possibly efficient diffusion path along the three crystallographic directions, by selecting shorter Li–Li distance to hop which indicating smaller migration barrier24 tabulated in Table 1. Fig. 8(b) described diffusion of an interstitial Li ion Li3(0.76472, 0.71260, 0.31232) to its equivalent site Li3(0.26472, 0.71260, 0.31232) along a axis. During the motion process, an interstitial Li ion Li3(8d) kicks out and replaces a neighboring Li1(8d) while the “kicked-out” Li1(8d) migrates to next neighboring Li3(8d) site, then kicks out Li1(8d) to take its equivalent site Li3(0.26472, 0.71260, 0.31232). It takes four steps from one interstitial site to its equivalent site, and the shortest Li–Li distance is 1.76 Å, and the largest Li–Li distance is 2.37 Å. The diffusion path along a axis is (Fig. 8(b)):
| Li3(8d) → Li1(8d) → Li3(8d) → Li1(8d) → Li3(8d) | (4) |
| Net direction | Step | Net distance/Å |
|---|---|---|
| a | Li3(0.76472, 0.71260, 0.31232) | 1.76, 2.37, 1.76, 2.37 |
| Li1(0.60328, 0.75030, 0.33631) | ||
| Li3(0.51472, 0.78740, 0.43768) | ||
| Li1(0.35328, 0.74970, 0.41369) | ||
| Li3(0.26472, 0.71260, 0.31232) | ||
| b | Li3(0.51472, 0.28740, 0.43768) | 2.0, 2.0 |
| Li2(0.66414, 0.37500, 0.47482) | ||
| Li3(0.51472, 0.46260, 0.43768) | ||
| c | Li3(0.48528, 0.53740, 0.56232) | 2.0, 2.82, 2.37, 2.0, 2.82, 2.37 |
| Li2(0.33586, 0.62500, 0.52518) | ||
| Li1(0.35328, 0.50030, 0.41369) | ||
| Li3(0.26472, 0.53740, 0.31232) | ||
| Li2(0.41414, 0.62500, 0.27518) | ||
| Li1(0.39672, 0.50030, 0.16369) | ||
| Li3(0.48528, 0.53740, 0.06232) |
The diffusion paths along b and c axis are similar with that along a axis, both are zigzag motions. The diffusion path along b axis is (Fig. 8(c)):
| Li3(8d) → Li2(4c) → Li3(8d) | (5) |
The diffusion path along c axis is (Fig. 8(d)):
| Li3(8d) → Li2(4c) → Li1(8d) → Li3(8d) → Li2(4c) → Li1(8d) → Li3(8d) | (6) |
The proposed diffusion paths show a slight anisotropy along the three crystallographic directions. Based on the diffusion steps from one interstitial site to its equivalent site and the Li–Li distance, it can be deduced that the diffusion path along b axis is the most efficient and major motion path of this solid solution. Fig. 8(e) shows the projection of Li sites of supercell of Li10Si1.5P1.5Cl0.5O11.5 on the b × c plane, which can visually deliver a zigzag diffusion path along b axis. Fig. 8(f) shows the 3D-zigzag network of lithium ions diffusion path along a × b × c axes. The diffusion along b axis combined with the diffusion along a × c axes.
The cathode material 0.3Li2MnO3·0.7LiMn1.5Ni0.5O4 which proves to be able to stably cycle in a wide potential window of 2.0–5.0 V has been adopted to evaluate the electrochemical performance of Li10.42Si1.5P1.5Cl0.08O11.92 and Li10.42Ge1.5P1.5Cl0.08O11.92. Fig. 9(a) and (b) show the charge–discharge curves of the hybrid electrolyte Li10.42Si1.5P1.5Cl0.08O11.92 and Li10.42Ge1.5P1.5Cl0.08O11.92 cells at 0.1 C rate. The charge and discharge capacities of Li10.42Si1.5P1.5Cl0.08O11.92 cell at the 1st cycle were 114.5 mA h g−1 and 114.1 mA h g−1, respectively, delivering almost 100% coulombic efficiency. The initial charge capacity of Li10.42Ge1.5P1.5Cl0.08O11.92 cell was 330.1 mA h g−1, much higher than the theoretical capacity of 0.3Li2MnO3·0.7LiMn1.5Ni0.5O4 (213 mA h g−1), whereas the initial discharge capacity was 133.2 mA h g−1. The charge and discharge capacities after 100 cycles were 81.6 mA h g−1 and 81.9 mA h g−1, respectively, with 100% coulombic efficiency for Li10.42Si1.5P1.5Cl0.08O11.92 cells (Fig. 9(c)). However, the discharge capacity was 11.2 mA h g−1 for Li10.42Ge1.5P1.5Cl0.08O11.92 cells after 23 cycles (Fig. 9(d)). The cycle performance of Li10.42Si1.5P1.5Cl0.08O11.92 cells was much better than that of Li10.42Ge1.5P1.5Cl0.08O11.92 cells.
Conclusions
To achieving the combination of high ionic conductivity and excellent electrochemical stability in lithium solid electrolytes still remains a major challenge. A facile strategy was proposed to achieve reasonably high conduction and excellent electrochemical stability by the substitution of Cl for O based on the concept of bottleneck size and binding energy. New electrolytes, Li10.42Si1.5P1.5Cl0.08O11.92 and Li10.42Ge1.5P1.5Cl0.08O11.92, were synthesized that showed promising ionic conductivity 1.03 × 10−5 S cm−1 and 3.7 × 10−5 S cm−1 at 27 °C respectively, 13 orders of magnitude higher than that of the pure Li3PO4, and 1 order of magnitude higher than that of the pristine Li10.5Si1.5P1.5O12, and superior electrochemical stability with metallic lithium up to 9 V vs. Li+/Li, one of the solid electrolytes with most wide electrochemical window. These series of new electrolytes are orthorhombic structure of γ-Li3PO4 with interstitial 3D-zigzag ions migration mechanism along b axis. The charge and discharge capacities of Li10.42Si1.5P1.5Cl0.08O11.92 cell at the 1st cycle were 114.5 mA h g−1 and 114.1 mA h g−1, respectively, with almost 100% coulombic efficiency. The coulombic efficiency was almost 100% after 100 cycles for Li10.42Si1.5P1.5Cl0.08O11.92 cells. This strategy holds promising potential to develop new solid electrolytes combined with high ionic conductivity and excellent electrochemical stability thus advance lithium ion battery technology by enabling the use of metallic lithium anode.Acknowledgements
This work was supported by SERC 2011 Public Sector Research Funding (PSF) Grant R-265-000-424-305.Notes and references
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587 CrossRef CAS.
- Z. C. Zhang, L. B. Hu, H. Wu, W. Weng, M. Koh, P. C. Redfern, L. A. Curtiss and K. Amine, Energy Environ. Sci., 2013, 6, 1806 CAS.
- L. Suo, Y. S. Hu, H. Li, M. Armand and L. Q. Chen, Nat. Commun., 2012, 4, 1481 CrossRef PubMed.
- R. Kanno and M. Maruyama, J. Electrochem. Soc., 2001, 148, A742 CrossRef CAS PubMed.
- N. Kamaya, K. Homma, Y. Yamakawa, M. Hirayama, R. Kanno, M. Yonemura, T. Kamiyama, Y. Kato, S. Hama, K. Kawamoto and A. Mitsui, Nat. Mater., 2011, 10, 682 CrossRef CAS PubMed.
- Y. Seino, T. Ota, K. Takada, A. Hayashi and M. Tatsumisago, Energy Environ. Sci., 2014, 7, 627 CAS.
- G. Sahu, Z. Lin, J. Li, Z. Liu, N. Dudney and C. D. Liang, Energy Environ. Sci., 2014, 7, 1053 Search PubMed.
- J. L. Schaefer, Y. Lu, S. Moganty, P. Agarwal, N. Jayaprakash and L. A. Archer, Appl. Nanosci., 2012, 2, 91 CrossRef CAS PubMed.
- W. C. West, J. F. Whitacre and J. R. Lim, J. Power Sources, 2004, 126, 134 CrossRef CAS PubMed.
- Y. Inagum and M. Itoh, Solid State Ionics, 1996, 86, 257 CrossRef.
- O. Bohnke, C. Bohnke, J. O. P. Ahmed, C. Lopez, H. Duroy, F. Berre and J. L. Fourquet, Chem. Mater., 2001, 13, 1593 CrossRef CAS.
- Y. Inaguma, Y. Matsui, J. Yu, Y. J. Shan, T. Nakamura and M. Itoh, J. Phys. Chem. Solids, 1997, 58(6), 843 CrossRef CAS.
- H. Y. Hong, Mater. Res. Bull., 1978, 13, 117 CrossRef CAS.
- J. T. S. Irvine, D. C. Sinclair and A. R. West, Adv. Mater., 1990, 2, 132 CrossRef CAS.
- B. Wang, B. C. Chakoumakos, B. C. Sales, B. S. Kwak and J. B. Bates, J. Solid State Chem., 1995, 115, 313 CrossRef CAS.
- Y. W. Hu, I. D. Raistrick and R. A. Huggins, J. Electrochem. Soc., 1977, 124, 1240 CrossRef CAS PubMed.
- J. B. Bates, N. J. Dudney, G. R. Gruzalski, R. A. Zuhr, A. Choudhury, D. F. Luck and J. D. Robertson, Solid State Ionics, 1992, 647, 53 Search PubMed.
- P. G. Bruce and A. R. West, J. Electrochem. Soc., 1983, 130, 662 CrossRef CAS PubMed.
- R. Kanno, H. Kawamoto and Y. M. Irie, Solid State Ionics, 2000, 130, 97 CrossRef CAS.
- A. Khorassani, G. Izquierdo and A. R. West, Mater. Res. Bull., 1981, 16, 1561 CrossRef CAS.
- H. Xie, J. A. Alonso, Y. T. Li, M. T. Fern and J. B. Goodenough, Chem. Mater., 2011, 23, 3587 CrossRef CAS.
- W. Baur and H. T. Ohta, J. Solid State Chem., 1982, 44, 50 CrossRef CAS.
- R. Ubic and G. Subodh, J. Alloys Compd., 2009, 488, 374 CrossRef CAS PubMed.
- Y. A. Du and N. A. W. Holzwarth, J. Electrochem. Soc., 2007, 154, A999 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra11287c |
| This journal is © The Royal Society of Chemistry 2015 |