Crystallization and molecular dynamics of ethylene-vinyl acetate copolymer/butyl rubber blends

Abstract

In this article, butyl rubber (IIR) was blended with ethylene-vinyl acetate copolymer (EVA) through a molten method. The crystal structure, morphology, crystallization and segmental dynamics were characterized. The crystal structure test indicated that IIR had no influence on the crystal form of EVA. Furthermore, the morphology showed that the blends changed from sea-island to a co-continuous structure. Moreover, the non-isothermal crystallization kinetics given by Mo’s model showed that the rate of crystallization became fast as the content of EVA increased. In addition, the segmental dynamics characterization illustrated that EVA suppressed the molecular motions of IIR to a different degree. Longer units were more influenced than shorter units. It was also found that both crystallization and molecular dynamics had a close relationship with the morphology.

---

Introduction

In the past decades, the nature of molecular mobility in the glass–rubber transition region of polymers always remained a hot topic of controversy in condensed matter physics.^1–5 For some particular polymers, more than one mode could be found in their dissipation spectra through non-linear fitting, which was first shown by Fitzgerald et al.⁴ The transition at low temperature was thought a glass transition (T_g); while the transition at high temperature was proposed as Rouse modes. Glass transition, called local segments motions (LSM), was involved by limitedly cooperative segments. However, Rouse modes referred to the motion of Gaussian sub-molecular chains. In recent years, an opinion proposed by Ngai et al. thought that a transition existed at the temperature range between glass transition and Rouse modes. They were called sub-Rouse modes, which had units that were longer than segments and shorter than Gaussian sub-molecular chains.⁵ The sub-Rouse mode was confirmed by many related works and tools;^6,7 an example is two-dimensional analysis.^8–10 Generally speaking, the LSM were classified as α processes and both Rouse and sub-Rouse modes were classified into α′ processes.

IIR, copolymerized by isobutylene and some isoprene, has been widely used in many fields. For its special damping behaviour, the IIR has been studied extensively by many scholars and institutions since 1950s.^1–16 In addition, EVA, as a common thermoplastic elastomer, has been universally applied in enhancing toughness, adhesives and so on.^16,17 The EVA had non-polar polyethylene segments and polar vinyl acetate segments, which could be used to blend with non-polar polymers and enhance their polarity. However, since Liao et al.¹⁸ found the space confinement in IIR composites, the asymmetric polymers blends have become a hot topic in the past 10 years.^19–22 Furthermore, other asymmetric many-body systems, copolymers, also obtained much attention, but those works are still at a fundamental stage.^23–25

Besides the dynamics of asymmetric polymer blends, the effect of networks on the crystallization of linear polymers was also important and attractive for polymer science. Studying crystallization kinetics was thought a good way to reflect the procedure of crystallization. Crystallization kinetics included isothermal and non-isothermal types. In contrast to the isothermal type, the non-isothermal crystallization kinetics had more practical value.²⁶ The Avrami equation was firstly used to study polymer crystallization kinetics. It is defined as

log[−ln[1 − X(t)]] = log C + n log t (1)

where X(t) is the relative crystallinity at a particular time, t is crystallization time, n is the Avrami exponent and C is a constant. However, it was thought that the Avrami equation could only be used for studying isothermal crystallization kinetics.²⁷ Based on Evans’ theory, which considered the effect of cooling rate on crystallization, the Ozawa method improved the Avrami equation to non-isothermal situations.²⁸ It is defined as

log[−ln(1 − X(T)] = log K(T) − m log φ (2)

where X(T) is the relative crystallinity at a particular temperature, K(T) is the cooling equation which refers to the type of nucleation, the rate of nucleation and the rate of crystal growth, φ is cooling rate and m is the Ozawa exponent which has similar meaning to Avrami equation. However, the Ozawa method more often failed (especially at the beginning or end of crystallization) when it was used to describe composites systems.²⁹ Combining Avrami and Ozawa methods, Mo et al. conducted a novel method for non-isothermal crystallization kinetics, which has been confirmed by many works.^30–33 This method seemed to be more applicable for composite system.^29,34

In this article, the crystal structure, morphology, crystallization and segmental dynamics of EVA/IIR blends were studied. It was desirable to investigate the effect of IIR on the crystallization of EVA and the influence of EVA on the dynamics of IIR. On the one hand, from a theoretical point of view, studying the crystallization and dynamics of EVA/IIR blends helps us to understand how the cross-linked IIR affects the crystallization of EVA and how the EVA affects the segmental of IIR. In fact, they are two popular topics for multi-component systems of polymers. On the other hand, from a practical point of view, EVA has nonpolar and polar segments, which can play the role of coupling agent to improve the compatibility of IIR to polar surface or materials. Moreover, the crystalline property of EVA has potential to enhance the mechanical and wear-resisting properties of the blends.

Experimental

Materials

IIR (268, industrial version) was purchased from Exxon Mobil co. Ltd. EVA (900, industrial version, the content of VA = 25%) was bought from Honam Petrochemical Corp. Tetramethyl thiuram disulfide (TMTD), sulphur and other raw materials are commercially available products.

Procedure

The 25 g IIR and EVA with a designed mass were respectively added in a torque rheometer (RG90, Haake co. Ltd.) for mixing. The rotate rate was set at 30 rad min⁻¹ and mixing temperature was set at 150 °C, with a mixing time of 20 min.

After mixing, we transferred the EVA/IIR blends to a two-roll equipment. The 0.5 g TMTD, 0.5 g sulphur and 0.25 g stearic acid were subsequently added to the blends during two-roll mixing. Furthermore, those blends were kept at room temperature for about 24 hours; then we took those IIR/EVA blends to moulds. The moulds were put on a plate vulcanizing machine. The blends were cured at 10 MPa pressure and 433 K about 30 min; thus the vulcanizates was obtained.

Characterizations

The morphology of the EVA/IIR blends was studied by scanning electron microscopy (SEM, JSM-5900LV, Jeol Corp., Ltd.). To prepare samples for SEM analysis, the blends were quenched in liquid nitrogen and cryogenically fractured. The fractured samples were eroded by hexane at room temperature for 30 min, thus the EVA phase was extracted preferentially. Before testing, these samples were sputter coated with Au.

Crystal structures were measured using wide angle X-ray diffraction (WAXD, XPert PRO MPD, PANalytical Corp., Ltd.) with Ni-filtered Cu Ka radiation (λ = 0.154 nm) at a generator voltage of 35 kV and a generator current of 25 mA. The scanning was at speed of 3.6 deg min⁻¹, beginning from 5 to 45 deg (2θ).

Crystallization characterization of EVA/IIR blends was conducted using differential scanning calorimetry (DSC, DSC823^e, Mettler Toledo Corp., Ltd.). For studying non-isothermal crystallization kinetics, the samples were first heated to 360 K at a rate of 30 K min⁻¹ and then kept at that temperature about 10 min. In this step, the original thermal stress history would be eliminated. The samples were then cooled and heated as a circle at rates of 5, 10, 15, 20 and 25 K min⁻¹; first cooling and second heating scans were recorded.

Dynamic mechanical analysis (DMA) was carried out on Q800 (TA Instruments Ltd.) by using a dual cantilever clamp and a testing method of temperature ramp-frequency sweep with a frequency of 1 Hz. The sample dimensions were 50 mm long, 12 mm wide and 3 mm thick. The oscillation strain amplitude was set to be 15 μm.

Results and discussion

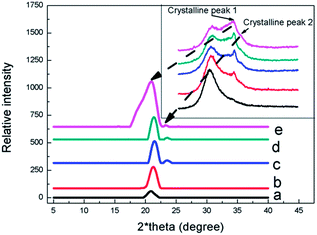
As shown in Fig. 1, the WAXD curves of EVA/IIR blends were displayed. In the upper inset, a big amorphous peak was seen at about 2*theta = 15 degree; and two weak crystal peaks were located at 2*theta = 21 degree (P₂₁) and 2*theta = 23 degree (P₂₃), respectively. After filtering the non-crystal peak, the concise pattern was illustrated at main-body of Fig. 1; the P₂₁ became higher as the content of EVA was increased, and the P₂₃ occurred when the content of EVA exceed about 33.33%, suggesting that crystal of EVA might have many flaws when the content of EVA was low. Moreover, the P₂₁ and P₂₃ displayed in all curves in Fig. 1, indicating IIR had no influence on the crystal form of EVA.

Fig. 1 WAXD patterns of EVA/IIR blends after extracting crystalline peaks. (a) Content of EVA in the blend (C_EVA) ≈ 16.66%; (b) C_EVA ≈ 23.07%; (c) C_EVA ≈ 33.33%; (d) C_EVA ≈ 38.46%; (e) C_EVA ≈ 42.85%. The upper inset shows original WAXD patterns.

Fig. 2 displays the morphology of EVA/IIR blends given by SEM measurements. When the content of EVA was low, the EVA phase, appearing as black concave areas, homogenously dispersed in the IIR phase. As the content of EVA was increased, the EVA and IIR phases formed a co-continuous structure (as shown in Fig. 2c). Here, the large area of continuous concave areas (extracted EVA phase) can be seen. A light collapse of the IIR phase was observed when the content of EVA was 42.85% (as shown in Fig. 2d). It can be predicted that the EVA phase would be the main body as the content of EVA is further increased.

Fig. 2 Morphology of EVA/IIR blends. The contents of EVA were 16.66% (a), 23.07 (b), 33.33% (c), and 42.85% (d). The EVA phase was removed.

In the present article, we used non-isothermal crystallization kinetics to reflect the crystallization behaviours of EVA/IIR blends. In Fig. 3a, the standard DSC heat flow curves are shown. As the cooling rate was increased, the crystallization exothermic peaks shifted to lower temperatures and became broader. It was also seen that the lower the cooling rate was, the earlier the crystallization started. The rate of heat release was proportional to the macroscopic rate of crystallization,^26–34 so Fig. 3b could be directly obtained from Fig. 3a. Using a simple relationship, the temperature at a certain relative crystallinity is related to the time at the same relative crystallinity as follow:

t = (T₀ − T)/φ (3)

where T₀ was the temperature at the beginning of crystallization, T was the temperature at the time (t) and t was the time of crystallization procedure.

Fig. 3 DSC thermograms of dynamic crystallization (a); relative crystallinity at different crystallization temperatures (b) and time (c). A sample with C_EVA = 16.66% was used as an example. (Curves in the three thermograms: (a) 5 K min⁻¹, (b) 10 K min⁻¹, (c) 15 K min⁻¹, (d) 20 K min⁻¹ and (e) 25 K min⁻¹.)

As the degree of relative conversion was related to the cooling rate and crystallization time, the relationship between cooling rate and the time of crystallization could be defined for a given degree of relative conversion.^29–31 Consequently, a new kinetics equation for dynamic crystallization was derived:

log φ = log f(T) − α log t (4)

where f(T) referred to the value of cooling rate chosen at unit crystallization time, when the system had a certain degree of relative crystallinity, and α was the ratio of the Avrami exponent to Ozawa exponent (i.e., α = n/m). The f(T) could be considered as a parameter to reflect the rate of crystal growth.^29–34 In addition, according to eqn (2), at a given degree of conversion, the plot of log φ vs. log t gave a series of straight lines as shown in Fig. 4.

Fig. 4 Mo plot of the dynamic crystallization. A sample with C_EVA = 16.66% was used as an example.

The good linearity of the plots verified the advantage of the combined approach (Mo’s model) applied in this paper. The values of log f(T) and α are listed in Table 1. As shown in Table 1, log f(T) increased as the content of EVA was increased, suggesting that a larger content of EVA resulted in a faster growth rate of crystal. Based on Fig. 2, we found that the bigger spherical particle-like phase and continuous phase of EVA would be beneficial to enhancing the growth rate of the crystal. There might be three reasons: First, with the increase of EVA content, the EVA phase would become bigger or continuous, and the molecules of EVA would gather together more easily. Secondly, EVA had polar VA segments, which would increase phase separation between EVA and IIR. The greater phase separation might offer larger space for PE segments arranging in the crystals. Thirdly, the crosslinked IIR could give a bigger pressure as the EVA phase became bigger for rubber elasticity. This pressure might be beneficial to crystallization.

Table 1 Parameters generated by the fitting processes of Mo’s model

Samples	Xc	log f(T) (±0.01)	α (±0.01)	R^2^a
a Fitting correlation coefficient of Mo’s model.
CEVA = 16.66%	80%	1.26	1.00	0.9776
	60%	1.19	1.04	0.9741
	50%	1.14	1.03	0.9794
	40%	1.10	1.04	0.9780
	20%	0.97	1.06	0.9621
CEVA = 23.07%	80%	1.32	1.37	0.9897
	60%	1.22	1.45	0.9947
	50%	1.17	1.51	0.9927
	40%	1.11	1.61	0.9870
	20%	0.85	1.88	0.9931
CEVA = 33.33%	80%	1.33	1.30	0.9979
	60%	1.22	1.37	0.9956
	50%	1.16	1.38	0.9942
	40%	1.08	1.40	0.9944
	20%	1.00	1.42	0.9843
CEVA = 38.46%	80%	1.35	0.99	0.9963
	60%	1.27	1.01	0.9982
	50%	1.22	1.03	0.9968
	40%	1.18	1.02	0.9957
	20%	1.07	1.08	0.9939
CEVA = 42.85%	80%	1.38	1.06	0.9975
	60%	1.30	1.06	0.9958
	50%	1.25	1.05	0.9940
	40%	1.22	1.04	0.9921
	20%	1.10	1.03	0.9854

---

The crystallization activation energy, or effective energy barrier (ΔE), has often been used to estimate the growth ability of a crystal. In this study, the Kissinger model³⁵ was applied to calculate the effective energy barrier. The Kissinger model is defined as follows:

ln(φ/T²_p) = constant − ΔE/RT_p (5)

where R was the universal gas constant and T_p was the temperature of the crystallization exothermic peaks in DSC curves. The Kissinger plot is shown in Fig. 5. Furthermore, ΔE can be obtained from the slope of the lines in Fig. 5 and are listed in Table 2. Generally speaking, a higher ΔE means more energy per unit of crystallization is required for the polymer chains to arrange in a crystal. According to Table 2, the crystallization activation energy estimated by Kissinger decreased as the content of EVA increased, which confirmed the result of non-isothermal crystallization kinetics given by Mo’s model.

Fig. 5 Kissinger plot for evaluating the crystallization activation energy of EVA/IIR composites.

Table 2 Parameters generated by the fitting processes of Kissinger’s model

Samples	ΔE (±0.01) kJ mol^−1	R^2^a
a Fitting correlation coefficient of Kissinger model.
CEVA = 16.66%	172.69	0.9678
CEVA = 23.07%	159.29	0.9608
CEVA = 33.33%	158.51	0.9401
CEVA = 38.46%	152.40	0.9439
CEVA = 42.85%	144.29	0.8969

---

The DMA was once thought as a sensitive tool for detecting all types of molecular modes in glass–rubber transition region.³⁶ As shown in Fig. 6, it was clear to see that the shoulder and maximum peaks of tan δ (i.e. tan δ = loss modulus/storage modulus) of EVA/IIR blend was suppressed to different extents as the content of EVA was increased. The maximum peak reduced from about 1.5 to 0.6; while the shoulder peak decreased from about 1.0 to 0.5. Such a difference in reducing degree might be resulted by the EVA had different influence on the different molecular motions. The longer units were more likely affected by the EVA than the shorter units.

Fig. 6 Effect of the content of EVA on the relaxation behaviour of IIR at 1 Hz.

The height of maximum and shoulder peaks was generally used for analysing space confinement.^18,21,37,38 In this paper, we propose a new method, which is based on difference spectra of DMA. We used the tan δ curve of pure IIR to subtract from the tan δ curve of EVA/IIR blends. The difference spectra show the decreasing values of tan δ with different EVA content, which indicated the space confinement effect. The larger decrease extent (Δtan δ) in the difference spectra was when the greater confinement effect existed. As shown in Fig. 7 Δtan δ increased with an increase of EVA content, whilst the Δtan δ spectrum changed from having a dual-peak shape to a shoulder-maximum shape. The change in spectrum shape made us recall another paper published by Ngai et al.³³ They used tricresyl phosphate (TCP) to dissolve polystyrene and the results showed that the dual-peak shape changed to shoulder-maximum shape when TCP was 25%. In fact, our experiment described herein was an inverse process of that described in Ngai’s paper. We focused on a confinement system, while they worked on a plasticity system. Thus, the changing of shape of Δtan δ referred to the sub-Rouse modes. In addition, as shown in the curve of “0–42.85%”, the Δtan δ of maximum > area between maximum and shoulder > shoulder. The molecular motions that exist in the glass–rubber transition region from high to low temperatures were Rouse modes, sub-Rouse modes and LSM, respectively. It is suggested that additional polymer had influence on Rouse modes > sub-Rouse modes > LSM. This result agrees well with other research in that the additional polymer had a larger effect on longer units.^{5,17,21,22,37–39} Furthermore, when the content of EVA went up to 33.33%, the Δtan δ increased quickly. Based on Fig. 2, we propose that the co-continuous phase structure has a larger space confinement than the sea-island phase structure.

Fig. 7 Difference spectra of DMA spectra. Content of EVA: up to 16.66%, 23.07%, 33.33%, 38.46%, 42.85%.

Conclusions

The result of WAXD showed that IIR had a rare influence on the crystal form of EVA. The morphology given by SEM illustrated that the phase of EVA/IIR changed from a sea-island structure to a co-continuous structure. In addition, according to non-isothermal crystallization kinetics achieved by Mo’s model, the IIR increased the rate of crystallization of EVA. The crystallization activation energy estimated by the Kissinger model agreed well with the result of Mo’s model, which showed that crystallization activation energy decreased as the content of EVA increased. Furthermore, EVA suppressed the molecular motions of IIR for space confinement. Based on difference spectra of DMA, it was found that the space confinement had a larger influence on longer units than shorter units.

Acknowledgements

This work was supported by open fund (PLN1429) of State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation (Southwest Petroleum University). And we also thank C. H. Wang (Centre of Experiments, College of Materials Science and Engineering, SWPU) for help with DSC measurements.

Notes and references

1. P. G. Debenedetti and F. H. Stillinger, Nature, 2001, 410, 259–267.
2. P. G. de Gennes, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 3365–3366.
3. P. W. Anderson, Science, 1995, 267, 1610.
4. E. R. Fitzgerald, L. D. Grandine and J. D. Ferry, J. Appl. Phys., 1953, 24, 650–655.
5. K. L. Ngai and D. J. Plazek, Rubber Chem. Technol., 1995, 68, 376–434.
6. X. B. Wu, C. S. Liu, Z. G. Zhu, K. L. Ngai and L. M. Wang, Macromolecules, 2011, 44, 3605–3610.
7. Y. C. Zhu, W. Zhou, J. J. Wang, B. Wang, J. R. Wu and G. S. Huang, J. Phys. Chem. B, 2007, 111, 11388–11392.
8. X. A. Wang, G. S. Huang, J. R. Wu, Y. J. Nie, X. J. He and K. W. Xiang, Appl. Phys. Lett., 2011, 99, 121902.
9. X. A. Wang, G. S. Huang, J. R. Wu, Y. J. Nie and X. J. He, J. Phys. Chem. B, 2011, 115, 1775–1779.
10. R. Zhang, X. R. He, H. Yu and K. Y. Chen, J. Macromol. Sci., Part B: Phys., 2014, 53, 1642–1653.
11. J. R. Wu, G. S. Huang, X. A. Wang, X. J. He and J. Zheng, Soft Matter, 2011, 7, 9224–9230.
12. J. F. Sanders and J. D. Ferry, Macromolecules, 1974, 7, 681–684.
13. W. H. Stockmayer, Pure Appl. Chem., 1967, 15, 539–554.
14. R. F. Boyer, J. Appl. Polym. Sci., 1986, 32, 4075–4107.
15. R. F. Boyer, J. Macromol. Sci. Phys., 1980, 18, 461–553.
16. X. R. He, R. Zhang, C. Y. Yang, Y. Q. Rong and G. S. Huang, Int. J. Adhes. Adhes., 2013, 44, 9–14.
17. X. R. He, R. Zhang, Q. Chen, Y. Q. Rong and Z. Q. Yang, Int. J. Adhes. Adhes., 2014, 50, 128–135.
18. F. S. Liao, A. C. Su and T.-C. J. Hsu, Polymer, 1994, 35, 2579–2586.
19. K. L. Ngai and S. Capaccioli, J. Chem. Phys., 2013, 138, 054903.
20. J. Colmenero, J. Chem. Phys., 2013, 138, 197101.
21. F. S. Zhang, G. S. He, K. M. Xu, H. Wu and S. Y. Guo, RSC Adv., 2014, 4, 20620–20625.
22. X. R. He, G. S. Huang, H. Zhou, L. X. Jiang and X. D. Zhao, Acta Polym. Sin., 2005, 1, 108–112.
23. R. Zhang, X. R. He and G. S. Huang, J. Polym. Res., 2014, 21, 388.
24. R. Zhang, X. R. He and H. Yu, Polymer, 2014, 55, 4720–4728.
25. X. R. He, H. Yu, R. Zhang and C. H. Yang, Int. Polym. Process., 2014, 3, 419–424.
26. X. R. He, S. R. Zheng, G. S. Huang and Y. Q. Rong, J. Macromol. Sci., Part B: Phys., 2013, 52, 1265–1282.
27. M. L. Di Lorenzo and C. Silvestre, Prog. Polym. Sci., 1999, 24, 917–950.
28. T. Ozawa, Polymer, 1971, 12, 150–158.
29. M. Naffakh, M. Remskar, C. Marco and M. A. Gomez-Fatou, J. Phys. Chem. B, 2011, 115, 2850–2856.
30. T. X. Liu, Z. S. Mo, S. G. Wang and H. F. Zhang, Polym. Eng. Sci., 1997, 37, 568–575.
31. T. X. Liu, Z. S. Mo and H. F. Zhang, J. Appl. Polym. Sci., 1998, 67, 815–821.
32. M. Q. Ren, Q. Y. Chen, J. B. Song, H. L. Zhang, X. H. Sun, Z. S. Mo, H. F. Zhang, X. Q. Zhang and L. S. Jiang, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 553–561.
33. J. W. Huang, J. Appl. Polym. Sci., 2007, 106, 2031–2040.
34. Z. S. Mo, Acta Polym. Sin., 2008, 7, 656–661.
35. H. E. Kissinger, J. Res. Natl. Bur. Stand., 1956, 57, 217–221.
36. J. R. Wu, G. S. Huang, Q. Y. Pan, J. Zheng, Y. C. Zhu and B. Wang, Polymer, 2007, 48, 7653–7659.
37. J. R. Wu, G. S. Huang, X. A. Wang, X. J. He and H. X. Lei, J. Polym. Sci., Part B: Polym. Phys., 2010, 48, 2165–2172.
38. J. R. Wu, G. S. Huang, X. A. Wang, X. J. He and H. X. Lei, J. Polym. Res., 2011, 18, 2213–2220.
39. K. L. Ngai and D. J. Plazek, Macromolecules, 2002, 35, 9136–9141.

---