Oxygen reduction on nanocrystalline ruthenia – local structure effects†
Daniel F. Abbottab,
Sanjeev Mukerjeeb,
Valery Petrykina,
Zdeněk Bastla,
Niels Bendtsen Halckc,
Jan Rossmeislc and
Petr Krtil*a
aDepartment of Electrocatalysis, J. Heyrovský Institute of Physical Chemistry, Academy of Sciences of the Czech Republic, Dolejškova 3, 18223 Prague, Czech Republic. E-mail: Petr.Krtil@jh-inst.cas.cz
bDepartment of Chemistry and Chemical Biology, Northeastern University, 360 Huntington Ave., Boston, MA 02115, USA
cCenter for Atomic-Scale Materials Design, Department of Physics, Technical University of Denmark, Building 307, 2800 Kgs. Lyngby, Denmark
First published on 25th November 2014
Abstract
Nanocrystalline ruthenium dioxide and doped ruthenia of the composition Ru1−xMxO2 (M = Co, Ni, Zn) with 0 ≤ x ≤ 0.2 were prepared by the spray-freezing freeze-drying technique. The oxygen reduction activity and selectivity of the prepared materials were evaluated in alkaline media using the RRDE methodology. All ruthenium based oxides show a strong preference for a 2-electron oxygen reduction pathway at low overpotentials. The catalysts' selectivity shifts towards the 4-electron reduction pathway at high overpotentials (i.e. at potentials below 0.4 V vs. RHE). This trend is particularly noticeable on non-doped and Zn-doped catalysts; the materials containing Ni and Co produce a significant fraction of hydrogen peroxide even at high overpotentials. The suppression of the 4-electron reduction pathway on Ni and Co-doped catalysts can be accounted for by the presence of the Ni and Co cations in the cus binding sites as shown by the DFT-based analyses on non-doped and doped catalysts.
Introduction
The fuel cell related electrocatalytic processes based on controlled hydrogen oxidation and oxygen reduction have recently gained importance mainly in connection with the increasing utilization of renewable energy sources. Despite efforts devoted to the optimization of existing systems, the performance of real fuel cells still lags behind the expectations and the cathodic oxygen reduction is seen as the performance limiting process. The electrochemical fuel cell reactions can also be generally employed in the energy storage mode using the excess electricity or solar energy to generate energetically useful hydrogen (produced along with the oxygen), leading to the introduction of the regenerative fuel cell concept.1,2 It also needs to be stressed that the regenerative fuel cell applications have sparked extensive catalyst development primarily for the oxygen evolution/reduction processes.Oxygen electrochemistry, including oxygen evolution as well as reduction, represents the simplest example of multiple electron charge transfer processes which have been extensively studied both experimentally as well as theoretically.3,4 In contrast to the development of suitable catalysts for independent oxygen evolution (OER) or oxygen reduction (ORR), the catalysts' application in regenerative fuel cells faces significant restrictions in terms of minimizing the energetic barriers of both kinetically irreversible processes. The fact that the oxygen evolution reaction proceeds solely on oxide covered surfaces disfavors the use of metal catalysts which are reported to be of superior activity in oxygen reduction. The oxide activity in the oxygen evolution was investigated in both acidic as well as alkaline media on various systems based on oxides of ruthenium,5–8 iridium,5,7–9 cobalt5,10 or manganese.5 Oxygen reduction studies on oxides are less frequent and are generally restricted to alkaline media. Oxygen reduction has been studied on rutile,11,12 spinel,13,14 perovskite15 and pyrochlore16,17 structural types based on ruthenium, manganese, nickel, cobalt and iridium oxides. The investigated oxide catalysts were the subject of electrochemical characterization which was phenomenologically analyzed in order to explain the possible reaction pathways leading to both 4-electron and 2-electron oxygen reduction processes. In contrast to the studies of oxygen evolution, no detailed investigations aiming at the role of the catalyst structure, including the local structure of the oxygen reduction active site, have been reported so far.
The theoretical approach allowing for the generalization of oxygen electrochemistry on oxides based on DFT calculations was recently reported.4,18,19 The DFT calculations identify the active sites for oxygen activation and the charge transfer to so-called coordination unsaturated sites (cus), the surface population of which is a function of the surface orientation. The cus surface sites feature (n − 1) oxygen bonding partners, where n is equal to number of metal–oxygen bonds present in the oxide bulk. It is believed that only cus sites can form the atop reaction intermediate(s), which are essential in the oxygen electrochemistry. In this respect one can easily predict that the catalytic activity and selectivity of oxide catalysts may be altered if one controls the population and stacking of the cus sites at the oxide surface. This trend has been shown for oxygen evolution on heterostatically doped ruthenia when the incorporation of lower valency cations, such as Ni,20–23 Co,24–27 Fe28 or Zn29,30 into ruthenia framework resulted in changes to both the activity and selectivity of anodic processes including oxygen and chlorine evolution. Similar systematic studies focused on other oxide systems are, so far, lacking.
This paper focuses on the role of the local structure of the oxide catalysts in the oxygen reduction reaction. We report on the ORR activity of model nanocrystalline ruthenia based catalysts with local structure controlled by doping with Ni, Co and Zn. The observed electrocatalytic activity and selectivity are related to the actual local structures and rationalized using DFT-based thermodynamic analysis of the oxygen reduction process.
Methods
Material preparation
Ruthenium dioxide and doped samples of the composition Ru1−xMxO2 (M = Co, Ni, Zn) were synthesized using the spray-freezing freeze-drying method as described in ref. 30 and 31. Generally, an 8 mM solution was prepared by dissolving the appropriate amount of Ru(NO)(NO3)3 (31.3% Ru, Alfa Aesar) in 100 mL of Millipore H2O. In the case of doped materials, a stoichiometric amount of the appropriate transition metal salt was added to the solution. Zinc-doped samples were prepared from the acetate precursor, Zn(C2H3O2)2·2H2O (99.5% ACS reagent grade, Fluka). Cobalt- and nickel-doped samples were prepared from the nitrate salts, Co(NO3)2·6H2O and Ni(NO3)2·6H2O (99.999% trace metal basis, Sigma Aldrich), respectively. The starting solution was then sprayed into liquid N2. The resulting ice slurry was collected in an aluminum tray pre-cooled with liquid N2 and quickly transferred to a freeze-dryer (FreeZone Triad Freeze Dry System 7400030, Labconco) pre-cooled to −30 °C. The frozen solvent was sublimated at reduced pressure (≈1.0 Pa) while the temperature was ramped according to the following program: −30 °C (1 h), −25 °C (5 h), −20 °C (4 h), −15 °C (6 h), 30 °C (4 h). After drying, the resulting powder was annealed in air at 400 °C for 1 hour.XRD, XPS and SEM characterization
The crystallinity of sample powders was characterized using a Rigaku Miniflex 600 powder X-ray diffractometer with CuKα radiation operating at 40 kV and 15 mA. The average sample compositions were evaluated with X-ray energy dispersive spectroscopy using a Hitachi S4800 scanning electron microscope (SEM) equipped with a Nanotrace EDX detector (Thermo Electron). Sample compositions did not deviate significantly from the projected ones. Particle size was evaluated by analyzing SEM images and averaging the size of 300 randomly chosen particles. The X-ray photoelectron spectra (XPS) of the prepared materials were measured using a modified ESCA 3 MkII multitechnique spectrometer equipped with a hemispherical electron analyzer operating in the fixed transmission mode. Al Kα radiation was used for electron excitation. The binding energy scale was calibrated using the Au 4f7/2 (84.0 eV) and Cu 2p3/2 (932.6 eV) photoemission lines. The spectra were collected at a detection angle of 45° with respect to the macroscopic surface normal. The studied materials were characterized using survey scan spectra and high resolution spectra of overlapping Ru 3d + C 1s photoelectrons, Ru 4s, Zn 2s and O 1s photoelectrons. The spectra were curve fitted after subtraction of Shirley background using the Gaussian–Lorentzian line shape and nonlinear least-squares algorithms. Quantification of the elemental concentrations was accomplished by correcting the photoelectron peak intensities for their cross sections and for the analyzer transmission function. The typical error of quantitative analysis by XPS is ∼10%.Electrochemical measurements
The electrochemical oxygen reduction activity of the prepared materials was assessed in a three-electrode single-compartment cell with a rotating ring-disk electrode (RRDE) setup (Pine Instruments, USA). The potential was controlled using an Autolab PGSTAT30 (EcoChemie, The Netherlands). Catalyst ink suspensions were prepared by sonicating 9.8 mg RuO2 or Ru1−xMxO2 (M = Co, Ni, Zn) with 5.00 mL Millipore water, 4.95 mL isopropyl alcohol, and 50 μL of 5 wt% Nafion® ionomer solution until the suspension was well dispersed. A 10.0 μL aliquot of the ink was drop cast on a 0.196 cm2 glassy carbon disk electrode equipped with a platinum ring to yield a total catalyst loading of approximately 50 μg cm−2. All experiments were conducted at room temperature in 0.1 M NaOH prepared from sodium hydroxide pellets (semiconductor grade, 99.99%, Sigma-Aldrich). A platinum wire served as the counter electrode and a saturated calomel electrode (SCE) served as the reference electrode. All potentials reported are quoted against RHE. Electrolyte solutions were saturated with O2 for 30 minutes prior to oxygen reduction measurements. The measured oxygen reduction currents were corrected for the contribution of the capacitive current by subtracting the cyclic voltammograms obtained under identical conditions in Ar saturated solution. Cyclic voltammograms were recorded at a scan rate of 20 mV s−1 and the potential of the platinum ring electrode was held at 1.1 V vs. RHE during all measurements. The ring collection efficiency was determined to be 0.275 according to the procedure described in ref. 32.DFT analysis of oxygen reduction
The thermodynamic analysis of the ORR on ruthenia based [110] surfaces was addressed using GPAW (grid-based projector-augmented wave) a DFT based code33 together with the ASE (atomic simulation environment).34 For all surfaces the exchange correlation functional, revised Perdew Burke Ernzerhof,35 was used. The grid spacing selected was 0.18 and the Brillouin zone was sampled using a 4 × 4 × 1 Monkhorst–Pack grid. The two model systems, the non-doped and Ni-doped ruthenia [110], were approximated using a 2 × 1 and a 3 × 1 supercell, respectively, with four atomic trilayers and with the bottom two trilayers fixed. The remaining layers and adsorbates were relaxed until the residual forces in all directions were less than 0.05 eV Å−1. The positions of the Ni atoms were modeled using the approach described in ref. 33. The calculations containing Ni were spin-polarized.Results and discussion
XRD and SEM characterization
X-ray diffraction patterns of all studied materials are shown in Fig. 1. In all cases the recorded patterns conform to a single phase tetragonal structure of the rutile type identical with that of RuO2 (PDF file #431027). The average size of coherent crystallite domains was evaluated using the Scherrer formula:
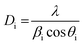 | (1) |
 | ||
| Fig. 1 Powder X-ray diffraction patterns for nanocrystalline RuO2 and Ru1−xMxO2 (M = Ni, Co, Zn) after annealing in air for 1 hour at 400 °C. | ||
The average coherent domain size ranged between 4.3 and 5.7 nm (see Table 1). Representative SEM images of the doped ruthenia are summarized in Fig. 2. The particle sizes evaluated from SEM micrographs agree with the coherent domain size values (see Table 1). Average sample compositions did not deviate significantly from the projected ones and are listed in Table 1.
| Actual composition | Coherent domain size [nm] | Strain [%] | a [Å] | c [Å] | Particle size [nm] |
|---|---|---|---|---|---|
| RuO2 | 5.7 | 0.46 | 4.470 | 3.120 | 7.6 ± 2.2 |
| Ru0.9Zn0.1O2−z | 4.9 | 0.61 | 4.526 | 3.108 | 8.9 ± 2.2 |
| Ru0.82Zn0.18O2−z | 5.5 | 0.00 | 4.519 | 3.099 | 5.8 ± 1.5 |
| Ru0.95Ni0.05O2−z | 5.3 | 0.00 | 4.515 | 3.096 | 7.2 ± 1.4 |
| Ru0.91Ni0.09O2−z | 5.0 | 0.00 | 4.501 | 3.079 | 7.9 ± 2.3 |
| Ru0.9Co0.10O2−z | 4.3 | 0.21 | 4.505 | 3.081 | 7.4 ± 1.8 |
 | ||
| Fig. 2 SEM images of nanocrystalline (a) RuO2, (b) Ru0.90Zn0.10O2, (c) Ru0.80Zn0.20O2, (d) Ru0.95Ni0.05O2, (e) Ru0.90Ni0.10O2, and (f) Ru0.90Co0.10O2 after annealing at 400 °C in air for 1 hour. | ||
Surface composition of all doped samples reflects the metastable character of the materials and previous thermal treatment which result in a dopant enrichment of the surface layer.21,37 This effect is most pronounced in the case of the Zn doped materials when the actual surface compositions of both studied materials correspond to Ru0.73Zn0.27O2.43 and to Ru0.63Zn0.37O2.23 for the materials with nominal Zn contents of 0.1 and 0.2, respectively. It needs to be noted that the apparent excess of the oxygen in the surface composition can attributed to surface OH groups as well as to adsorbed water.
Electrochemical measurements
All prepared ruthenia materials are active ORR catalysts in alkaline media. The ORR polarization curves for RuO2 and Ru1−xMxO2 (M = Ni, Co, Zn) samples are shown in Fig. 3. The disk current (iD) which reflects the oxygen reduction shows a pronounced peak at approximately 0.40 V to 0.55 V before approaching a mass transport controlled region. The disk current feature can be tentatively associated with a change in the Ru oxidation state from Ru(IV) to Ru(III).11,36 This process is usually connected with cation insertion into the oxide structure to balance the charge in cationic and anionic sub-lattices.37 The behavior giving rise to the peak in the disk current is also manifested in the ring current, indicating a pronounced formation of hydrogen peroxide in this potential region. The hydrogen peroxide formation in the 0.40 V to 0.55 V interval seems to be unaffected by the chemical composition of the catalyst. The formation of hydrogen peroxide seems to be suppressed with increasing rotation rate. The precise mechanism of this reduction process is, however, not evident. | ||
| Fig. 3 ORR polarization curves and ring currents at 1600 rpm for RuO2 and Ru1−xMxO2 (M = Ni, Co, Zn) electrodes at 20 mV s−1 in O2 saturated 0.1 M NaOH. Ering = 1.1 V vs. RHE. | ||
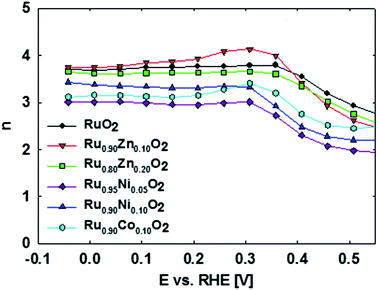
The overall ORR activity of the doped ruthenia catalysts is lower than that of the non-doped ruthenia. The ORR activity as reflected in the disk currents (iD) generally decreases for the Co- and Ni-doped samples. There is no apparent effect of the actual dopant concentration on the oxygen reduction disc currents. The corresponding ring currents (iR) are, however, higher than that of the non-doped ruthenia, particularly at high overpotentials (i.e. at potentials negative to 0.4 V vs. RHE). This shows a pronounced tendency of Co and Ni-doped materials to produce H2O2 namely at high overpotentials (n ranging between 3.0 and 3.4). In contrast, the Zn-doped materials show a preference for the 4-electron reduction pathway with n values ranging between approximately 3.6 and 3.8 while the activity remains comparable to that of the non-doped ruthenia. Also the selectivity of the doped ruthenia in oxygen reduction is controlled rather by the doping process itself than by the actual dopant content.
The observed behavior reflects the surface sensitivity of oxygen reduction on oxide surfaces, which can be related to the surface local structure. Quantitative visualization of this behavior is shown in Fig. 4, which plots the potential dependence of the average number of electrons transferred to an oxygen molecule on different doped ruthenium dioxide materials as calculated from the Koutecky–Levich equation:38
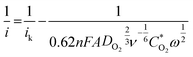 | (2) |
It has to be stressed that in contrast to the behavior known for metal electrocatalysts in acid media, the oxygen reduction on ruthenia based catalysts apparently forms primarily hydrogen peroxide, namely at low overpotentials. The observed selectivity of ruthenia-based catalysts in ORR shows a complex potential dependence which can be treated either by a phenomenological or a local structure sensitive approach.
Assuming a general phenomenological model of the oxygen reduction mechanism as proposed previously (see Fig. 5),40,41 oxygen can be reduced to water (4-electron pathway) either directly or sequentially with H2O2 as the main adsorbed intermediate.
 | ||
| Fig. 5 Phenomenological mechanism of oxygen reduction according to ref. 40. | ||
In principle, H2O2 either desorbs and can be detected on the ring or can be further reduced to water in the second 2-electron reduction process. The measured disk current summarizes the current contributions from the complete 4-electron reduction to H2O and the 2-electron reduction to H2O2 while the recorded ring current is proportional only to the amount of oxygen reduced to H2O2. In this respect a ratio of iD/iR can be used as an indicator of the actual mechanism which should yield a straight line proportional to k1/k2 when plotted against ω−1/2 (see Fig. 6).40
The actual iD/iR data deviate from linearity (see Fig. 6) as can be expected since the formalism incorporated in the scheme depicted in Fig. 5 disregards the nature of the individual reaction steps composing both 2- and 4-electron reduction pathways and their different dependence on the electrode potential.
 | ||
| Fig. 6 |ID/IR| vs. ω−1/2 plots for (a) RuO2, (b) Ru0.80Zn0.20O2, and (c) Ru0.90Ni0.10O2 presented data were extracted from RRDE experiments carried out in O2 saturated 0.1 M NaOH. | ||
The individual rate constants k1, k2 and k3 were evaluated from ORR data assuming that all three processes proceed simultaneously and that the values of k−1, k−2, and k−3, corresponding to reversed reactions, are negligible. The adsorption of oxygen on the electrode surface is also assumed to proceed sufficiently fast. The potential dependence of the rate constants for all considered catalysts in the overall oxygen reduction mechanism is shown in Fig. 7.
It seems that the conversion of H2O2 to H2O through the series pathway (k3) is negligible on all electrode surfaces at high overpotentials. It has to be noted, that although the k3 values are negligible with respect to k1 and k2 there is a significant difference between k3 of the Zn-doped and non-doped samples and those obtained for the Ni- and Co-doped samples. The values of k3 observed for Ni- and Co-doped samples are approximately one order of magnitude lower and seem to correspond to decreased tendency of these materials to reduce oxygen through the 4-electron pathway.
As follows from Fig. 7, the conversion of O2 to H2O2 appears to be the dominant process on ruthenium based oxides at low overpotentials. In this respect the reduction behavior of the ruthenia differs significantly from that of metals which prefer the 4-electron reduction at low overpotentials. The role of the chemical composition in selectivity of doped catalysts towards 2- and 4-electron reduction pathways can be visualized by the potential at which the catalytic system shows the same preference for the 4-electron and 2-electron reaction pathways, i.e. potential at which k1/k2 = 1 (see Fig. 8).
 | ||
| Fig. 8 The potential of equal rate in 2- and 4-electron reduction for different ruthenia based catalysts. | ||
A fundamental description of the oxygen reduction on oxide surfaces can be based on the thermodynamic analysis of the observed trend, which highlights the enhanced tendency of the Ni- and Co-doped materials to form hydrogen peroxide and reflects the local structure of the doped ruthenium oxides.
DFT analysis of oxygen reduction
A fundamental description of the oxygen reduction on oxide surfaces can be based on the thermodynamic analysis of the process utilizing the DFT modeling. Reverting to the formalism used for the oxygen evolution reaction we can describe the overall reduction process as a sequence of four consecutive concerted electron/proton transfers – if one aims for the complete 4-electron reduction – or of two consecutive electron/proton transfers if hydrogen peroxide is considered as the reaction product. The results of the DFT investigations of ORR reduction on ruthenium dioxide based catalysts are summarized in Fig. 9–12.A systematic description of the stable surface structures at different potentials represents a prerequisite step in the theoretical investigation of oxygen reduction on an oxide surface, which in this case is the [110] rutile surface of ruthenia. This procedure results in computational Pourbaix diagrams where the stable surface at any given potential features the highest stabilization (i.e. the most negative surface energy) of the system (see ESI† for details of the Pourbaix diagram construction).
Bearing in mind that the [110] oriented surface of a rutile type oxide features the transition metal cations in two local environments, cus and bridge, one can visualize the surface of non-doped ruthenium dioxide as changing from the surface structure characterized by protonated oxygen on cus sites and deprotonated oxygens in bridge sites (region C in Fig. 9) to the surface featuring vacant cus and protonated oxygens in bridge sites (region A in Fig. 9). Since the ORR was not observed at potentials positive to 0.7 V (vs.RHE) one can restrict the DFT investigations of the oxygen reduction on conventional RuO2 to the surface stable in the region A. In the case of doped ruthenia (as shown in the case of the Ni doped material presented in Fig. 10) one needs to consider the complexity arising from the chemical composition when both types of transition metal cations enter the cus and bridge positions. This variability in the chemical composition also increases the number of distinctive oxygen atoms available at the surface, the binding energy of which depends on their nearest neighbors. Although the electrode potential dependent variability of the surface structure is more pronounced in this case, the stable structure predicted for the potential range in which the ORR proceeds is qualitatively the same and corresponds to vacant cus sites complemented by protonated oxygen atoms connecting the bridge sites (see structure D in Fig. 10).
 | ||
| Fig. 9 Surface Pourbaix diagram for RuO2. Detailed description of the diagram construction is given in the ESI.† | ||
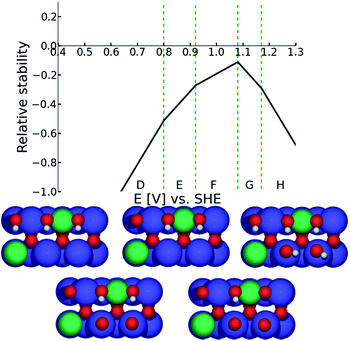 | ||
| Fig. 10 Surface Pourbaix diagram for Ni-doped RuO2. Detailed description of the diagram/s construction is given in the ESI.† | ||
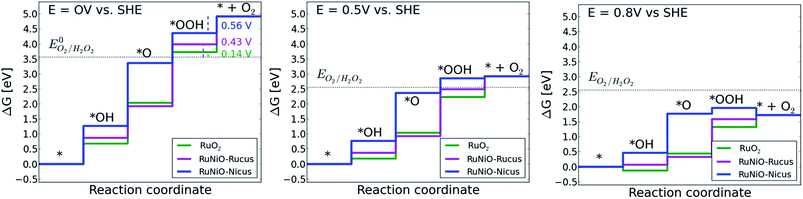
The DFT models predict that the entire process begins with oxygen adsorption at coordination unsaturated (cus) cationic sites. The behavior of both the non-doped and the doped ruthenia catalysts is controlled by the local structure and depends on the nature of the cation residing in the cus site as well as on the electrode potential. In the case that the cus site is occupied by a ruthenium cation (which are present on all investigated catalysts) the first electron reduction forms a rather strongly bound *OOH intermediate, which is more stable than the hydrogen peroxide at most reasonable electrode potentials (see Fig. 11). Consequently, the further reduction of the *OOH intermediate located on Ru cus site cannot form hydrogen peroxide unless one uses an rather strong external electric field to weaken the *OOH binding to the surface. The actual potential(s) at which hydrogen peroxide formation becomes thermodynamically allowed are indicated in the legend of the Fig. 11.
In the case that the cus site is occupied by an heteroatom, e.g. Ni or Co, (see Fig. 11) one observes a significantly weaker binding of the *OOH and *O compared with the Ru occupied cus sites. This fact decreases the potential at which the reduction on Nicus starts to contribute to the overall reduction process. The weak interaction of the *OOH with the heteroatom-containing cus site restricts the presence of such an adsorbate in the potential region with low total surface coverage, i.e. to relatively high over-potentials. It needs to be noted though, that the formation of hydrogen peroxide from *OOH confined on a heteroatom occurs at much more positive potentials than in the case of *OOH confined to Ru-containing cus sites and further reduction of the *OOH intermediate can proceed via the 4-electron or 2-electron reduction pathway with approximately the same probability.
Fig. 12 shows the dependence of the electrode potential needed to drive the oxygen reduction on oxide based surfaces either via the 4-electron (red) or 2-electron (blue) reaction pathway as a function of the reaction descriptor – i.e. adsorption energy of the *OOH intermediate. It needs to be noted that in a similar manner one may describe the reaction with the adsorption of *OH due to the interdependence of the adsorption energies of the intermediate formed in the first and third charge transfer step.3,33
Such a dual volcano plot has been used with great success in literature.42,43 The volcano curves presented in Fig. 12 clearly show a quantitative prediction of the thermodynamic preference of the 4-electron reduction pathway over the 2-electron reduction on strongly adsorbing cus sites. As follows from Fig. 11, oxygen reduction on Ni-doped ruthenia should proceed at slightly more positive potentials compared with the non-doped ruthenia as long as the cus sites are occupied with Ru cations. The reduction process on Ru occupied cus sites should show a pronounced preference for 4-electron reduction and the formation of hydrogen peroxide should be excluded for potentials positive of 0.14 V or 0.43 V (vs. RHE) for non-doped ruthenia and the Ni-doped material, respectively (see Fig. 11). The easier formation of hydrogen peroxide on the Ni-doped material should be compensated by an earlier onset of the oxygen reduction process as predicted for Ni-doped material. In the case of weakly adsorbing sites, e.g., in the case of Ni cus sites – there is no apparent thermodynamic preference for either the 4- or 2-electron reduction pathway. The DFT model predicts the onset of the oxygen reduction process to occur at potentials comparable with the ORR on non-doped ruthenia. The formation of hydrogen peroxide is possible at significantly more positive potentials (see Fig. 11).
Analyzing the experimental behavior of the ruthenium dioxide based catalysts for the oxygen reduction process in the light of the DFT results one can qualify the existence of two classes of catalysts – one favoring the 4-electron reduction (non-doped RuO2 and Zn-doped RuO2) and another showing significant activity in hydrogen peroxide production (Ni- and Co-doped ruthenia). Realizing that the Zn present in the Zn-doped ruthenia is itself redox inactive one can assume that the catalysts in the first group have all active cus sites occupied by Ru regardless of the actual chemical composition. The confinement of the catalytic activity to Ru itself justifies the selectivity towards 4-electron reduction pathway as it is shown in Fig. 4 and 8. In the case of the Co- and Ni-doped ruthenia the significant amount of hydrogen peroxide formed in the process can be attributed primarily to the Ni/Co cus sites although the Ru cus sites also contribute to the hydrogen peroxide formation at lower potentials. In contrast to the complementary oxygen evolution process, the Ni (or Co) ions located in the bridge sites, which play crucial role in the complementary anodic process,33 apparently have no effect on the oxygen reduction activity of these materials. A different role of the catalysts local structure in oxygen reduction is not entirely surprising given the irreversibility of oxygen evolution/reduction.
The DFT calculations, however, fail to explain pronounced formation of the hydrogen peroxide on all ruthenium based catalysts at low overpotentials (0.55–0.40 V) when the hydrogen peroxide on Ru cus sites should be thermodynamically excluded. Given the relatively short timescale of the RRDE experiments one may therefore suggest that the system fails to reach the thermodynamically stable surface structure on the experimental timescale and the hydrogen peroxide is released from meta-stable intermediates not reflected in the DFT calculations.
Conclusions
Nanocrystalline ruthenia based electrocatalysts offer a convenient model for investigating the role of the local structure in the oxygen reduction on oxide electrodes. The oxygen reduction related activity of RuO2 is comparable with that of the doped ruthenia. The selectivity of doped ruthenia catalysts differs from that of the RuO2 in which the non-doped as well as Zn-doped catalysts prefer 4-electron oxygen reduction while the Ni- and Co-doped ruthenia produce significant amount of hydrogen peroxide. The observed selectivity trends can be rationalized using a thermodynamic analysis of the oxygen reduction process based on DFT calculations.The DFT based analysis confines the oxygen reduction activity to cus sites the occupancy of which controls the selectivity of the oxygen reduction process. Oxygen reduction on non-doped ruthenium dioxide is controlled by the fourth electron transfer. Doping the ruthenium dioxide shifts the potential control to the first electron transfer. This trend can be attributed to decreasing occupancy of the cus sites with ruthenium. The strong adsorption of the *OOH intermediate on the Ru cus site steers the reaction mechanism towards 4-electron reduction pathway. Incorporation of reactive transition metal cations into bridge sites has negligible effect on the ORR activity. A confinement of the reactive transition metal into cus sites weakens the adsorption of the reaction intermediates and opens the 2-electron reaction pathway at relatively low overpotentials.
Acknowledgements
This work was supported by the Grant Agency of the Czech Republic (contract P108-12-1889) and European Commission within the Initial Training Network ELCAT (Project no. 214936). The support of the Danish Ministry of Science, Technology and Innovation though the CASE is also gratefully acknowledged.Notes and references
- G. Chen, S. R. Bare and T. E. Mallouka, J. Electrochem. Soc., 2002, A1092–A1099 CrossRef CAS PubMed.
- Y. Zhang, C. Wang, N. Wan and Z. Mao, Int. J. Hydrogen Energy, 2007, 32, 400–404 CrossRef CAS PubMed.
- M. T. M. Koper, J. Electroanal. Chem., 2011, 254–260 CrossRef CAS PubMed.
- I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martinez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Norskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- S. Trasatti, Electrochim. Acta, 1984, 29, 1503–1512 CrossRef CAS.
- M. Wohlfahrt-Mehrens and J. Heitbaum, J. Electroanal. Chem., 1987, 237, 251–260 CrossRef CAS.
- M. E. G. Lyons and S. Floquet, Phys. Chem. Chem. Phys., 2011, 13, 5314–5335 RSC.
- S. Song, H. Zhang, X. Ma, Z. Shao, R. T. Baker and B. Yi, Int. J. Hydrogen Energy, 2008, 33, 4955–4961 CrossRef CAS PubMed.
- S. Fierro, T. Nagel, H. Baltruschat and C. Comninellis, Electrochem. Commun., 2007, 9, 1969–1974 CrossRef CAS PubMed.
- A. J. Esswein, M. J. McMurdo, P. N. Ross, A. T. Bell and T. D. Tilley, J. Phys. Chem. C, 2009, 113, 15068–15072 CAS.
- C. C. Chang and T. C. Wen, J. Appl. Electrochem., 1997, 27, 355–363 CrossRef CAS.
- C.-C. Chang and T.-C. Wen, J. Electrochem. Soc., 1996, 143, 1485–1491 CrossRef CAS PubMed.
- F. Cheng, J. Shen, B. Peng, Y. Pan, Z. Tao and J. Chen, Nat. Chem., 2011, 3, 79–84 CrossRef CAS PubMed.
- M. Hamdani, R. N. Singh and P. Chartier, Int. J. Electrochem. Sci., 2010, 5, 556–577 CAS.
- J. Suntivich, H. A. Gasteiger, N. Yabuuchi, H. Nakanishi, J. B. Goodenough and Y. Shao-Horn, Nat. Chem., 2011, 3, 546–550 CrossRef CAS PubMed.
- H. S. Horowitz, J. M. Longo and H. H. Horowitz, J. Electrochem. Soc., 1983, 130, 1851–1859 CrossRef CAS PubMed.
- R. G. Egdell, J. B. Goodenough, A. Hamnett and C. C. Naish, J. Chem. Soc., Faraday Trans. 1, 1983, 79, 893–912 RSC.
- M. Garcia-Mota, A. Vojvodic, H. Metiu, I. C. Man, H.-Y. Su, J. Rossmeisl and J. K. Nørskov, ChemCatChem, 2011, 3, 1607–1611 CrossRef CAS.
- J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS PubMed.
- K. Macounova, M. Makarova, J. Jirkovsky, J. Franc and P. Krtil, Electrochim. Acta, 2008, 53, 6126–6134 CrossRef CAS PubMed.
- V. Petrykin, Z. Bastl, J. Franc, K. Macounova, M. Makarova, S. Mukerjee, N. Ramaswamy, I. Spirovova and P. Krtil, J. Phys. Chem. C, 2009, 113, 21657–21666 CAS.
- N. Krstajic and S. Trasatti, J. Electrochem. Soc., 1995, 142, 2675–2681 CrossRef CAS PubMed.
- N. Krstajic and S. Trasatti, J. Appl. Electrochem., 1998, 28, 1291–1297 CrossRef CAS.
- L. M. D. Silva, J. F. C. Boodts and L. A. DeFaria, Electrochim. Acta, 2000, 45, 2719–2727 CrossRef.
- L. M. D. Silva, J. F. C. Boodts and L. A. D. Faria, Electrochim. Acta, 2001, 46, 1369–1375 CrossRef.
- L. M. D. Silva, L. A. D. Faria and J. F. C. Boodts, J. Electroanal. Chem., 2002, 532, 141–150 CrossRef.
- V. Petrykin, K. Macounová, M. Okube, S. Mukerjee and P. Krtil, Catal. Today, 2013, 202, 63–69 CrossRef CAS PubMed.
- K. Macounová, M. Makarova, J. Franc, J. Jirkovský and P. Krtil, J. Electrochem. Soc., 2008, 11, F27–F29 Search PubMed.
- V. Petrykin, K. Macounova, J. Franc, O. Shlyakhtin, M. Klementova, S. Mukerjee and P. Krtil, Chem. Mater., 2011, 23, 200–207 CrossRef CAS.
- V. Petrykin, K. Macounova, O. A. Shlyakhtin and P. Krtil, Angew. Chem., 2010, 49, 4813–4815 CrossRef CAS PubMed.
- Y. D. Tretyakov and O. A. Shlyakhtin, J. Mater. Chem., 1999, 9, 19–24 RSC.
- U. A. Paulus, T. J. Schmidt, H. A. Gasteiger and R. J. Behm, J. Electroanal. Chem., 2001, 495, 134–145 CrossRef CAS.
- N. B. Halck, V. Petrykin, P. Krtil and J. Rossmeisl, Phys. Chem. Chem. Phys., 2014, 16, 13682–13688 RSC.
- S. R. Bahn and K. W. Jacobsen, Comput. Sci. Eng., 2002, 4, 56–66 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Norskov, Phys. Rev. B: Condens. Matter, 1999, 59, 7413–7421 CrossRef.
- M. Pourbaix, Atlas of Electrochemical Equilibria in Aqueous Solutions, Pergamon Press, Oxford, U.K., 1966 Search PubMed.
- K. Macounová, I. Jirka, A. Trojánek, M. Makarova, Z. Samec and P. Krtil, J. Electrochem. Soc., 2007, 154, A1077–A1082 CrossRef PubMed.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, John Wiley & Sons, Inc., New York, 2nd edn, 2001 Search PubMed.
- N. M. Markovic, H. A. Gasteiger and P. N. Ross, J. Phys. Chem., 1996, 100, 6715–6721 CrossRef.
- K. L. Hsueh, D. T. Chin and S. Srinivasan, J. Electroanal. Chem., 1983, 153, 79–95 CrossRef CAS.
- A. Damjanovic, M. A. Genshaw and J. O. M. Bockris, J. Phys. Chem., 1966, 45, 4057–4059 CrossRef CAS PubMed.
- S. Siahrostami, V.-C. Arnau, M. Karamad, D. Deiana, P. Malacrida, B. Wickman, M. Escudero-Escribano, E. A. Paoli, R. Frydendal and T. W. Hansen, Nat. Mater., 2013, 12, 1137–1143 CrossRef CAS PubMed.
- V. Viswanathan, H. A. Hansen, J. Rossmeisl and J. K. Nørskov, J. Phys. Chem. Lett., 2012, 3, 2948–2951 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c4ra10001h |
| This journal is © The Royal Society of Chemistry 2015 |