A reactive molecular dynamics study on the anisotropic sensitivity in single crystal α-cyclotetramethylene tetranitramine

Abstract

The anisotropic shock sensitivity in single crystal α-cyclotetramethylene tetranitramine (α-HMX) was investigated using the compress-shear reactive dynamics (CS-RD) computational protocol. Anisotropy in thermo-mechanical and chemical responses is found by measuring shear stress, energy, temperature, and chemical reactions during the dynamical process for shock directions perpendicular to the (010), (001), (100), (110), (011), (111), and (101) planes. We suggest that the internal energy accumulated within the duration of the surmounting shear stress barrier can be used as a useful criterion to distinguish the anisotropic sensitivity among various shock orientations. Accordingly, the α-HMX single crystal is predicted to be sensitive for the shock normal to the (010) plane, is intermediate to the (001) plane, and is insensitive to the (100), (110), (011), (111), and (101) planes. The molecular origin of the anisotropic sensitivity is considered to be the different intermolecular steric arrangements on the two sides of the slip plane induced by shock compression along various orientations. The shear deformation induced by shock compression along sensitive directions encounters strong intermolecular contact and has little intermolecular free space for geometry relaxation when molecules collide, leading to a high shear stress barrier and energy accumulation, which benefit a temperature increase and initial chemical bond dissociation that trigger further reactions. This validation of CS-RD indicates that this approach would be valuable in examining the anisotropic sensitivity of new energetic crystals and in evaluating which one would be least sensitive.

---

1. Introduction

Shock compression produces an unusual realm of pressure, temperature, and deformation on a short timescale that can induce a wide variety of physical and chemical changes in energetic materials (EMs), for instance, chemical reactions are initiated in shocked solids under suitable shock conditions.¹ A good understanding of the microscopic processes in shock-initiated EMs is needed for the development of a predictive capability regarding issues of explosive sensitivity, safety, and performance.

Although the role of molecular structure parameters on sensitivity of EMs has long been acknowledged,² the work by Dick brought a new dimension to this problem through his classic experiments. He and co-workers^3–12 observed direction dependences in mechanical behavior and shock wave initiation sensitivity of several energetic single crystals under plane shock wave loading. Single crystal pentaerythritol tetranitrate (PETN) is found to be insensitive for shocks normal to the (100) and (101) planes while it is sensitive for shocks normal to the (110) and (001) planes.^3–8 For single crystal β-cyclotetramethylene tetranitramine (β-HMX), the sensitivity to shock initiation is higher for the shock direction normal to the (010) plane than for the ones normal to the (110) and (011) planes.^10,11 Anisotropy in the wave profiles of single crystal cyclotrimethylene trinitramine (RDX) has also been observed under shock loadings up to 2.25 GPa,¹² but there is little direct experimental evidence on anisotropic detonation sensitivity. These discoveries have raised serious issues associated with safety, performance, and time burdens related to handling of these materials, as well as the cost associated with these issues. Even the small amount of plastic deformation in β-HMX as well as its anisotropic nature may be critical in determining the performance of polymer bonded explosives (PBX).¹³ For a PBX, if shock wave propagation and damage or initiation occur at scales less than their grain size, anisotropy in HMX single crystal must be considered.¹⁴

Thus, it is a pressing need to explore the anisotropic characteristics and find out the inherent mechanisms in energetic crystals. For the anisotropic sensitivity in PETN, Dick et al.^4–7 put forward a model based upon steric hindrance to shear, suggesting that sensitivity is related to the ease by which slip is allowed via available slip systems under shock compression. Because high potential energy barriers have to be overcome for hindered shear, such a deformation may excite the PETN molecules to very high energy vibrational states or cause direct bond rupture.^5–7 But this scenario was considered to be highly unconventional in terms of the concepts used in solid-state chemistry to explain chemical reactivity.^15,16 Jindal and Dlott¹⁶ argued that the orientation-dependence of shock-induced temperature increase may give rise to large anisotropies in thermo-chemical reactions. However, the preliminary assessment of anisotropic heating in PETN revealed that the temperature difference between the (110) and (100) orientations is insufficient to explain the very large chemical anisotropy observed experimentally.¹⁷ Gruzdkov and Gupta¹⁷ proposed a model that linked mechanical anisotropy to initiation chemistry, in which the steric hindrance concept was related to rotational conformations of PETN molecules through shear deformation, leading to local lattice polarization and consequently to ionic reactions. For β-HMX, most of the current studies focus on the plastic deformation mechanism that can be attributed to both mechanical twinning and slip,^18,19 and do not address the origin of anisotropic sensitivity. Zamiri et al.²⁰ presented a nonlinear anisotropic model for β-HMX crystal and found that certain crystallographic directions such as 〈110〉 are more prone to plastic deformation while some others like 〈010〉 remain completely elastic during uniaxial compression. They²⁰ suggested that the “softer” directions that are more prone to plastic deformation may lead to damage formation and localized temperature rise. If so, the 〈110〉 direction should be more sensitive than the 〈010〉 direction, but this is inconsistent with experimental results.^9–11

Despite numerous experimental and theoretical studies, there is no clear mechanism that explains the anisotropic sensitivity observed in shocked energetic single crystals, and the microscopic behavior responsible for the shock initiation observed on the macroscopic scale has not been well understood. Due to the hazardous nature of the experiments involved and the characteristics of molecular crystal, it is preferable to study the complex initiation process involving mechanical, chemical, thermodynamic changes by atomistic-scale computational modelling. First-principles calculation and molecular dynamics simulation of these materials at the atomic and molecular level thus provides an excellent opportunity for the investigation of the microscopic processes leading to shock initiation.

Conroy et al.^21–23 suggested that shear stress could be of importance in understanding the shock-induced anisotropy of EMs because it is usually considered to be the driving force behind plastic deformations in crystals and the source of mechano-chemical reactions behind the shock wave front. So they^21–23 performed a series of first-principles density functional theory (DFT) calculations for uniaxially compressed PETN and HMX crystals to find the relationship between shear stress and anisotropic sensitivity. The uniaxially compressed state of a crystal was used to mimic the state that the crystal experiences upon shock loading. A correlation between shear stress and sensitivity for PETN and HMX was found: the magnitudes of the calculated shear stresses are greater for the more sensitive directions than for the less sensitive ones.^21–23 Recently, Zybin et al.²⁴ developed a compress-shear reactive dynamics (CS-RD) computational strategy to examine the anisotropic shock sensitivity in PETN. The CS-RD method was developed to understand which aspects of the shock process are related to sensitivity by first compressing the crystals, followed by shear deformation along various slip systems. The hint that shear deformation is critical in understanding the sensitivity of EMs was provided by Plaskin's experiments showing that initiation of detonation occurs preferentially in directions with the maximum shear stress.²⁵ Simulation results for PETN²⁴ and β-HMX²⁶ showed dramatically different sensitivities for various shock directions that agreed completely with available experimental observations. Now that the CS-RD model has been validated to interpret the anisotropic sensitivity and to predict sensitive shock orientation for both PETN and β-HMX, for which the experimental data are most complete, it is suggested that this approach should be valuable for studying sensitivity of other EMs.

HMX molecule (C₄H₈N₈O₈) is an eight-membered ring of alternating carbon and nitrogen atoms, where two hydrogen atoms are bonded to each carbon atom and a nitro group is bonded to each nitrogen atom. There are three crystalline polymorphs of HMX: α, β, and δ, with the β polymorph (chair conformation) as the room-temperature stable form.²⁷ The α and δ polymorphs (boat conformations) are stable from approximately 377 to 429 K and approximately 429 to 549 K (melting point), respectively.^28,29 In this paper, we employ the CS-RD model using molecular dynamics method and ReaxFF force field^30,31 to investigate the anisotropic sensitivity in single crystal α-HMX for various shock directions. Analogous study on δ-HMX will be published in another paper. Our primary motivation is to access the possibility of this computational strategy in evaluating the sensitivity of various energetic single crystals, like the relative sensitivity of HMX polymorphs. The remainder of this paper is organized as follows: Simulation methods and procedures are described in Section II; Results and discussions are presented in Section III; Conclusions are drawn in Section IV.

2. Simulation methods and procedures

2.1 ReaxFF reactive force field

ReaxFF reactive force field,³⁰ a bond-order dependent potential parameterized from quantum mechanical (QM) calculations, provides accurate descriptions of bond breaking and bond forming. It has been demonstrated to be capable of describing the structures, energy surfaces, and reaction barriers for a variety of materials. Particularly important applications of ReaxFF have been to energetic materials that involve a complex sequence of reactions and multiple intermediates, many of which are difficult to detect, making it difficult to extract a mechanistic understanding. The ReaxFF reactive force field for nitramines coupled with molecular dynamics (MD) has been successfully used to study the complex and rapid reaction processes for RDX, HMX, TATB, and PETN subjected to various external loadings, including thermal, shock, and shear, providing mechanistic and conceptual information not readily available from experiments or QM.^24,32–40 The ability of ReaxFF-MD to efficiently study large-scale systems (millions of atoms) and complex dynamical processes with currently available computational facilities has been proved through these investigations.

ReaxFF-lg is an extension of ReaxFF, into which an additional term is added to account for London dispersion (van der Waals attraction).³¹ This provides a more accurate description of cell parameters for molecular crystals, which has been validated for RDX, PETN, TATB (triaminotrinitrobenzene), and nitromethane. Good agreements with experimental data have been obtained for crystal structures and equations of state. We have recently applied ReaxFF-lg to HMX, and the derived crystal structure is very close to experimental result.^26,41,42

In this study, we optimized the crystal structure of α-HMX starting from a unit cell with experimental lattice parameters using isothermal-isobaric molecular dynamics (NPT-MD) simulation at ambient condition (T = 300 K, P = 1 atm). This leads to lattice parameters of a = 15.09 Å, b = 23.81 Å, c = 5.89 Å, and V = 2115.91 ų, compared with experimental values of a = 15.14 Å, b = 23.89 Å, c = 5.91 Å, and V = 2138.70 ų.²⁸ The excellent agreement between calculated crystal structure and experimental result indicates that ReaxFF-lg is suitable for α-HMX.

2.2 Uniaxial compression and relaxation

The optimized crystal structure was uniaxially compressed along various shock directions. Here, we consider shock directions perpendicular to seven low index miller planes: (001), (010), (100), (110), (011), (111), and (101). We find that the direction normal to the (010) plane is softer than other orientations, leading to lower pressure at the same compression ratio. However, in shock-initiation anisotropy measurements, crystals in different orientations are not subjected to equal strain, but rather to approximately equal shock pressure.^4,5 To obtain comparative pressure, the compression ratio of 18% is applied for the (001), (100), (110), (011), (111), and (101) planes and 20% for the (010) plane. This compression leads to initial pressure of ∼10.0 GPa, corresponding to the pressure of our previous study on β-HMX.²⁶ These compressed unit cells were expanded to supercells (e.g. 2 × 2 × 4 for the (010) compressed system), which were then energy-minimized and equilibrated with fixed cell parameters using MD simulations at T = 300 K (denoted as NVT-MD) for 2 ps. The averaged full stress tensors over the structures obtained from the last 0.5 ps for the seven systems are summarized in Table S1 of the ESI.†

2.3 Slip systems selections from resolved shear stress

The full stress tensor induced by uniaxial compression along each shock direction was projected onto many slip systems, defined by a combination of slip planes and slip directions, to derive the resolved shear stress (RSS) for each slip system. Searching likely slip systems from many slip systems of single crystal in response to shock become a prior consideration. Since RSS is the driving force for potential shear deformation through slip system, we expect that possible slip systems for activation should be those with larger RSS. The angles between shock plane and slip plane (φ) and between shock direction and slip direction (ψ) are also expected to be close to 45° for these slip systems. Based on these criteria, we considered 50 possible slip systems with larger RSS and reasonable angles for the seven shock directions as listed in Table 1.

Table 1 The resolved shear stress (RSS) and angles between shock plane and slip plane (φ) and between shock direction and slip direction (ψ) for the 50 possible slip systems

Shock plane	Slip system	RSS/GPa	φ/°	ψ/°
(010)	{031}〈0−13〉	3.392	47.15	137.15
	{0−31}〈013〉	3.379	132.85	42.85
	{0−41}〈014〉	3.338	141.04	51.04
	{041}〈0−14〉	3.301	38.96	128.96
	{021}〈0−12〉	3.077	58.27	148.27
	{0−21}〈012〉	3.000	121.73	32.73
(001)	{301}〈10−3〉	2.394	43.84	133.84
	{−301}〈103〉	2.385	43.84	46.16
	{−401}〈104〉	2.349	52.01	37.99
	{401}〈10−4〉	2.292	52.01	142.01
	{−201}〈102〉	2.123	32.63	57.37
(100)	{−120}〈210〉	1.347	133.89	43.89
	{120}〈2−12〉	1.327	46.11	47.03
	{−130}〈310〉	1.256	122.68	32.68
	{201}〈10−2〉	1.195	46.41	43.59
	{−201}〈102〉	1.180	133.59	43.59
	{−130}〈31−3〉	1.171	122.68	38.62
	{−301}〈103〉	1.168	145.00	55.00
	{301}〈10−3〉	1.067	35.00	55.00
(110)	{−201}〈102〉	1.756	126.57	53.81
	{201}〈10−2〉	1.744	53.43	53.81
	{−301}〈103〉	1.694	135.62	61.72
	{301}〈10−3〉	1.674	44.38	61.72
	{−401}〈104〉	1.508	140.98	67.42
	{401}〈10−4〉	1.483	39.02	67.42
	{130}〈−310〉	1.442	25.24	115.24
	{140}〈−410〉	1.339	30.88	120.88
	{−101}〈101〉	1.317	111.48	43.73
(011)	{301}〈10−3〉	2.175	45.28	131.90
	{−301}〈103〉	2.174	45.28	48.10
	{401}〈10−4〉	2.115	53.15	139.33
	{−401}〈104〉	2.095	53.15	40.67
	{−201}〈102〉	1.997	34.60	58.59
	{201}〈10−2〉	1.973	34.60	121.41
(111)	{401}〈10−4〉	1.809	32.65	119.85
	{−201}〈102〉	1.798	55.03	38.46
	{301}〈10−3〉	1.731	26.05	113.03
	{−301}〈103〉	1.705	67.61	27.38
	{041}〈0−14〉	1.558	31.31	65.90
	{0−41}〈014〉	1.534	55.77	42.63
	{0−31}〈013〉	1.391	47.62	49.50
	{−101}〈101〉	1.378	38.58	54.22
(101)	{−201}〈102〉	1.582	54.09	35.91
	{401}〈10−4〉	1.545	30.82	120.82
	{301}〈10−3〉	1.413	23.72	113.72
	{−101}〈101〉	1.349	37.06	52.94
	{−101}〈2−12〉	1.059	37.06	61.89
	{041}〈0−14〉	1.042	42.86	54.58
	{0−31}〈313〉	1.025	36.03	57.85
	{031}〈0−13〉	0.983	36.03	61.31

---

2.4 Shear deformation dynamics simulations

For the sake of computational convenience, the compressed unit cell for each of the 50 slip systems was rotated so that the new x axis is slip direction and the new x–z plane is slip plane in a Cartesian coordinate system. We expanded these unit cells to large supercells, which were then energy minimized and relaxed using NVT-MD at 300 K for 2 ps. Take {021}〈0−12〉 slip system for the shock direction normal to the (010) plane for example, 4 × 4 × 2 unit cells were used in the a, b, and c directions to build a large supercell, leading to 1280 molecules and 35 840 atoms. The dimensions of the supercell are 89.585 Å × 103.927 Å × 30.180 Å along the a, b, and c axes. Shear deformation dynamics simulations were finally performed starting with these large optimized supercells for up to 8 ps by deforming the cells every 10 time steps (1.0 fs) at a constant shear rate 0.5 ps⁻¹. The nonequilibrium dynamics using microcanonical ensemble without temperature constraint (NVE-MD) was applied during the shear simulation. The CS-RD computational protocol was designed to capture the essential features of how shock processes relate to sensitivity while sufficiently efficient so that many different shock directions and slip systems can be considered at modest computational cost.

2.5 Chemical reaction analysis

To analyze the numerous reactions that occur during shear simulation, we carried out fragment analysis. The algorithm of molecule recognition in the fragment analysis uses MD trajectory and connection table with bond orders calculated by ReaxFF every step^32,36 and records the molecular components and their compositions every 0.05 ps. In this analysis, the bond order cutoff values for various atom pairs used to identify molecular fragments in the systems are tabulated in Table S2 of the ESI,† which were verified in previous study.^26,41 Thus, any two fragments are considered separate molecules if the bonds between them have bond orders smaller than cutoff values. These data were then used to plot time evolution profiles for reactants, intermediates, and products, providing detailed information about the initiation of chemical reactions. After determining the molecular fragments based on bond order cutoff values, the molecule recognition algorithm assigns a unique identification number to each molecular fragment (molecule ID) to trace the reaction pathways.

3. Results and discussion

3.1 Predictions of dominant slip systems

The 50 possible slip systems for the seven shock directions were selected to simulate the shear deformation. Each shock direction leads to several potential slip systems, each of which can lead to substantial differences in shear stress because of the different barriers they encounter during shear. The preferred slip systems for activation are expected to be with lower shear stress barrier (τ_max − τ₀), the maximum shear stress minus the initial shear stress, since it requires smaller stress to overcome the barrier and initiate slip motion. Thus, the lower shear stress barrier provides the criteria for identifying favorable slip systems. For the shock direction normal to the (010) plane, Fig. 1 presents the time evolutions of shear stress, potential energy, temperature, and initial reaction product NO₂ for the six possible slip systems during the shear simulations. The shear stress profile shown in Fig. 1(a) indicates that the slip systems {021}〈0−12〉 and {0−21}〈012〉 have lower barriers, making them more likely to be activated compared with the rest four slip systems, whose barriers are much higher. We find that the slip systems with higher barriers lead to faster energy change and temperature increase, particularly during the period of overcoming the barrier.

Fig. 1 Time evolutions of shear stress (a), potential energy per HMX molecule (b), temperature (c), and NO₂ fragment per HMX molecule (d) for the six possible slip systems along shock direction normal to the (010) plane during shear simulations.

For the other six shock planes, the shear simulation results for each possible slip system are plotted in Fig. S1–S6 of the ESI.† From these simulation results we can derive some key parameters such as the initio shear stress, shear stress barrier, temperature, and the formation time and the amount of the initial reaction product NO₂ for each slip system. These parameters are tabulated in Table 2. It is possible that a particular shock direction would trigger multiple slip systems and the CS-RD examines each possible slip system separately. The slip system exhibiting the lowest shear stress barrier to plastic deformation is most likely to be activated under shock loading, and we call such slip system the dominant slip system or the slip system expected to prevail. For each shock direction, we can select the dominant slip system and then access the sensitivity for various shock orientations. These slip systems are {021}〈0−12〉 for the (010) shock plane, {401}〈10−4〉 for the (001) shock plane, {−301}〈103〉 for the (100) shock plane, {−401}〈104〉 for the (110) shock plane, {−401}〈104〉 for the (011) shock plane, {401}〈10−4〉 for the (111) shock plane, and {401}〈10−4〉 for the (101) shock plane.

Table 2 Key parameters derived from the shear simulations of the 50 possible slip systems for the seven shock directions^a

Shock plane	Slip system	τ0/GPa	τmax − τ0/GPa	T/K	tf/ps	nNO2 per HMX/%	Sensitivity
a τmax − τ0 represents the shear stress barrier needed to be overcome during shear process, τ0 the initial shear stress, τmax the maximum shear stress, tf the formation time of the initial reaction product NO2, nNO2 the amount of NO2 per HMX molecule; T and nNO2 are measured at t = 4 ps; S: sensitive, M: intermediate, I: insensitive. The seven slip systems in bold font are dominant ones according to the lowest shear stress barrier criterion to access the sensitivity of various shock directions.
(010)	{031}〈0−13〉	2.826	2.500	1317	1.80	4.30
	{0−31}〈013〉	2.878	2.456	1306	1.60	3.52
	{0−41}〈014〉	2.861	2.652	1385	1.25	5.88
	{041}〈0−14〉	2.823	2.539	1389	1.40	6.10
	{021}〈0−12〉	2.711	1.953	1218	2.50	2.58	S
	{0−21}〈012〉	2.618	2.098	1237	2.05	2.89
(001)	{301}〈10−3〉	2.424	3.229	1311	1.95	2.75
	{−301}〈103〉	2.535	3.421	1335	1.80	3.15
	{−401}〈104〉	2.427	3.301	1185	2.30	1.79
	{401}〈10−4〉	2.461	3.217	1179	2.60	1.96	M
	{−201}〈102〉	2.374	3.456	1370	1.60	3.92
(100)	{−120}〈210〉	1.636	4.080	1416	1.20	6.34
	{120}〈2−12〉	1.578	3.620	1381	1.40	5.64
	{−130}〈310〉	1.465	3.150	1360	1.75	4.95
	{201}〈10−2〉	1.170	2.517	1218	2.40	1.65
	{−201}〈102〉	1.093	2.775	1293	2.20	3.04
	{−130}〈31−3〉	1.249	3.263	1329	1.55	3.91
	{−301}〈103〉	1.233	2.425	1151	2.90	0.92	I
	{301}〈10−3〉	0.954	2.498	1240	2.35	2.00
(110)	{−201}〈102〉	2.057	1.904	1173	2.80	1.22
	{201}〈10−2〉	2.080	1.815	1180	2.80	1.30
	{−301}〈103〉	1.587	1.746	1095	3.55	0.75
	{301}〈10−3〉	1.892	2.464	1122	3.45	0.75
	{−401}〈104〉	1.656	1.734	1107	3.25	0.54	I
	{401}〈10−4〉	1.514	1.933	1128	3.40	0.45
	{130}〈−310〉	1.234	2.457	1221	2.30	2.83
	{140}〈−410〉	1.126	2.214	1149	2.85	0.70
	{−101}〈101〉	1.531	2.719	1225	2.60	1.11
(011)	{301}〈10−3〉	1.894	2.908	1221	2.85	1.17
	{−301}〈103〉	1.858	2.739	1200	2.90	0.91
	{401}〈10−4〉	1.854	2.899	1107	3.15	0.71
	{−401}〈104〉	2.091	2.535	1102	3.30	0.36	I
	{−201}〈102〉	1.876	3.378	1352	2.10	2.63
	{201}〈10−2〉	2.042	3.006	1434	1.80	5.25
(111)	{401}〈10−4〉	1.914	2.477	1113	3.40	0.54	I
	{−201}〈102〉	2.097	3.304	1406	2.25	5.50
	{301}〈10−3〉	1.823	3.055	1199	2.90	0.94
	{−301}〈103〉	1.976	3.268	1243	2.45	2.08
	{041}〈0−14〉	1.488	2.983	1267	2.25	2.00
	{0−41}〈014〉	1.228	3.253	1275	2.15	2.43
	{0−31}〈013〉	1.266	2.980	1328	2.00	3.72
	{−101}〈101〉	1.387	2.673	1259	2.50	2.92
(101)	{−201}〈102〉	1.604	2.896	1377	2.45	3.88
	{401}〈10−4〉	1.533	2.461	1090	3.20	0.54	I
	{301}〈10−3〉	1.575	2.473	1160	2.90	0.63
	{−101}〈101〉	1.377	2.495	1241	2.30	1.88
	{−101}〈2−12〉	1.153	2.513	1199	2.55	1.67
	{041}〈0−14〉	1.146	3.555	1277	2.00	2.17
	{0−31}〈313〉	1.168	2.568	1286	2.10	3.17
	{031}〈0−13〉	1.081	3.659	1360	1.85	3.57

---

3.2 Anisotropic sensitivity

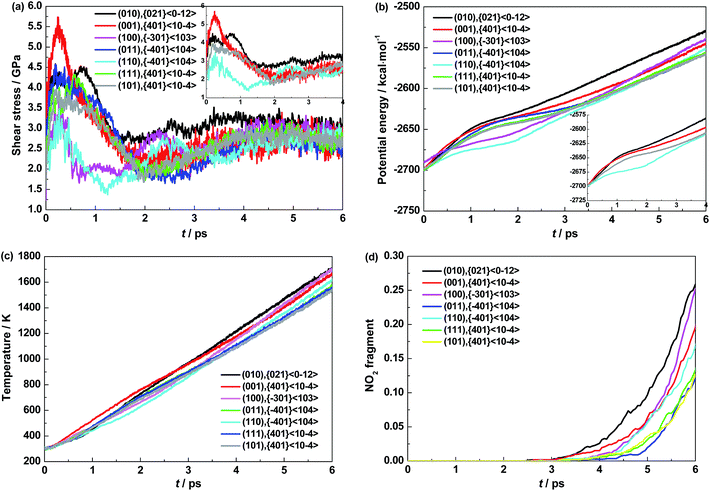
The physical and chemical responses to shear deformation of the seven dominant slip systems for the seven shock orientations are shown in Fig. 2. The time evolution of shear stress presented in Fig. 2(a) shows that the shear stress behaviors for the seven shock planes are different. For the (010) shock plane, the system exhibits shear stress that goes up to the maximum within the first 1 ps and then goes down during the next 1 ps, where we see two continuous peaks, illustrating that the slip motion encounters two continuous stress barriers that make it difficult to slip. In the case of the (001) shock plane, the system presents shear stress that maximizes rapidly within the first 0.3 ps and then declines gradually during the next 1.7 ps, indicating that the slip motion encounters stress barrier early and quickly and the barrier is hard to be surmounted. Similar shear stress profiles are observed for the (011), (111), and (101) shock planes, but the barriers are much smaller compared with the (001) shock plane, making the slips much easier. The (100) and (110) shock planes show analogous shear stress characteristics, namely, the stresses increase to the maximum very quickly within the first 0.3 ps and then decrease rapidly during the following 0.7 ps, suggesting that the slip motion runs into the stress barrier very early and overcomes it easily. Differing from other shock planes, the stresses then go up very slowly to a second local maximum at about 2.5 ps and go down gradually to reach the equilibrium at 4 ps. The second barrier is low and flat, making it easily to be surmounted. For all the seven shock planes, the shear stresses become equilibrated after 4 ps. Summarizing, the orientation-dependent shear stress behavior of α-HMX during the early stage of shear process is observed under mechanical shock compression.

Fig. 2 Comparisons of shear stress (a), potential energy per HMX molecule (b), temperature (c), and NO₂ amount per HMX molecule (d) of the seven dominant slip system for the seven shock directions during shear simulations.

Molecules across a slip plane are pushed into each other as they slip along a given slip direction. The resulted intermolecular contacts/overlap and collision/extrusion causes a fast increase of shear stress, that do work on the system, leading to the increments of energy and temperature. The molecules are most jammed together at the maximum of shear stress, and then relax back as the planes slide further. We consider that the shear stress barrier against slipping, which reflects the intermolecular steric arrangement on the two sides of the slip plane, comes from the periodic lattice structure of crystal. The anisotropic shear stress behavior for the seven shock directions indicates that the intermolecular steric arrangement depends on shock compression orientation, leading to different intermolecular entanglements. This would definitely leads to distinctions in energy and temperature changes and chemical reactions for different shock directions. Among the seven shock planes, the two continuous stress barriers for the (010) shock plane and the highest stress barrier for the (001) shock plane reveal stronger intermolecular contacts and collisions during slip, in comparisons with other shock planes.

The potential energy profile during shear process plotted in Fig. 2(b) can be separated into two stages, which corresponds to the time evolution of shear stress. Potential energy increases quickly with the increase of shear stress; it goes up at a slower rate during the stage where the shear stress relaxes from the maximum. Obviously, the change of potential energy during slip depends on shock orientation, relating to the anisotropic shear stress behavior. For the (010) shock plane, the increasing rate of potential energy during the first 1 ps is fast arisen from the two continuous shear stress barriers. In the case of the (001) shock plane, the potential energy rises more quickly during the first 0.5 ps than that for the (010) shock plane due to the higher stress barrier, leading to higher potential energy; but it becomes lower after 1 ps due to the shorter stress increasing time compared with the (010) shock plane. The time evolutions of potential energy for the (011), (111), and (101) shock planes are similar, showing slower increasing rates compared with the (001) and (010) shock planes attributed to the lower stress barrier. The (100) and (110) shock planes exhibit very analogue energy behavior, that is, two fast increasing stages appear because of the two discontinuous stress barriers. Although the increasing rates are lower than other shock planes, they still lead to comparative energy value with the (011), (111), and (101) shock planes at 4 ps. Note that, the change of potential energy proceeds a little more slowly than that for shear stress. Since the intermolecular contacts and collisions across the shear plane result in shear stress barrier, molecules need to deform in order to relax the shear stress and slip. This molecular deformation leads to the variation of intermolecular and intramolecular interactions, which compose to potential energy. Thus, the molecular deformation following shear stress accumulation leads to the lagged variation of potential energy.

To quantitatively compare the energy variation triggered by molecular deformation under imposed mechanical work for the seven shock planes, we calculated the accumulated potential energy (denoted as ΔE_p) before 4 ps as shown in Fig. 3. ΔE_p is about 120 kcal mol⁻¹ for the (010) shock plane, is 100 kcal mol⁻¹ for the (001) shock plane, and is 90 kcal mol⁻¹ for the (100), (110), (011), (111), and (101) shock planes, respectively, indicating that the change of potential energy is intense for the (010) shock plane, is moderate for the (001) shock plane, and is slight for the rest five shock planes. This demonstrates that the molecular deformation is severe for the (010) shock plane, is moderate for the (001) shock plane, and is weak for the (100), (110), (011), (111), and (101) shock planes.

Fig. 3 The accumulated potential energy ΔE_p and kinetic energy ΔE_k averaged on each HMX molecule of the seven dominant slip system for the seven shock directions during the process of surmounting shear stress barrier (t ≤ 4 ps).

Fig. 2(c) presents the evolution of temperature during shear simulation for the seven shock planes, showing that the increment of temperature is found to be most significant for the (010) shock plane, followed by the (001) shock plane. Temperature goes up from 300 K to 1218, 1179, 1151, 1107, 1102, 1113, and 1090 K for the (010), (001), (100), (110), (100), (111), and (101) shock planes, respectively. The kinetic energy accumulated (denoted as ΔE_k) within the first 4 ps is calculated to correlate with the temperature rise, which is also plotted in Fig. 3. As can be seen, ΔE_k for the (010), (001) and (100) shock planes are higher than that for the other shocks, suggesting that the kinetic energy changes most markedly for the (010) shock, closely followed by the (001) and (100) shock. Intermolecular contacts and collisions across slip planes during slip result in the increases of temperature and kinetic energy. The highest temperature and ΔE_k for the (010) shock plane further confirms its strong intermolecular contacts and collisions.

The accumulated internal energy (ΔE = ΔE_k + ΔE_p), on the other hand, reflects the mechanical work that is available to convert to thermal and chemical energy. The work done to overcome molecular interactions increases the temperature until it is high enough to break the weakest chemical bonds, followed by exothermic reactions that in turn contribute to temperature increase. Thus, the shocks with higher energy accumulation result in higher temperature and more reactions, whereas the ones with lower energy accumulation lead to lower temperature and less bond dissociation. Herein, we suggest that the accumulated internal energy within the duration of overcoming shear stress barrier correlates with shock sensitivity and thus provides a criterion to estimate sensitivity. For α-HMX, the accumulated internal energy averaged on each HMX molecule is 193.88, 173.80, 159.96, 161.16, 158.87, 162.69, and 157.97 kcal mol⁻¹ for the (010), (001), (100), (110), (011), (111), and (101) shock planes, respectively. Accordingly, the sensitivity of the seven shock planes is evaluated as follows (included in Table 2): the (010) shock plane is sensitive, the (001) shock plane is intermediate, and the (100), (110), (011), (111), and (101) shock planes are insensitive. Namely, the relative sensitivity for the seven shock planes is estimated to be (010) > (001) > (100)/(110)/(011)/(111)/(101). ΔE is highest for the (010) shock and lowest for the (101) shock, suggesting that the (010) shock exhibiting strong intermolecular contact and molecular deformation would lead to fast temperature rise and early chemical bond breaking, making it sensitive, whereas the (101) shock showing slight intermolecular contact and molecular deformation would result in slow temperature increase and tardy chemical reaction, making it insensitive.

To analyze the chemical reactions that occur during CS-RD simulations, we carried out fragment analysis. It is found that the decomposition of α-HMX is triggered by the N–NO₂ bond dissociation to form NO₂ fragment, consistent with previous studies.^43–45 Lewis et al.⁴³ performed ab initio calculations of reactive pathways for gas phase α-HMX and suggested that the N–NO₂ bond breaking is most energetically favorable at both the BLYP (41.8 kcal mol⁻¹) and B3LYP (40.5 kcal mol⁻¹) levels. It has also been concluded that N–NO₂ bond fission occurs at high temperature⁴⁶ and dominates the reaction at high-pressure limits⁴⁵ for HMX molecule. Fig. 2(d) presents the time evolutions of NO₂ for the seven shock orientations, showing that the initial chemical reaction occurs earlier and proceeds faster for the (010) and (001) shock planes compared with others. The formation time t_f as collected in Table 2 is about 2.5 ps for the (010) and (001) shock planes, and is about 3 ps or even later for the other five shock planes. At t = 4 ps, the population of NO₂ per HMX molecule approaches to 2.58%, 1.96%, 0.92%, 0.54%, 0.36%, 0.54%, and 0.54% for the (010), (001), (100), (110), (011), (111), and (101) shock planes, respectively. These data illustrate that the more sensitive shock directions lead to earlier and faster chemical reaction compared with less sensitive ones, which can be interpreted by faster temperature increase arising from stronger intermolecular entanglement during slip for more sensitive shock orientations.

Summarizing, the results from the early stage of slip are critical in understanding the anisotropic sensitivity under mechanical shock compression. The accumulated internal energy during this stage can be used as a useful criterion to distinguish sensitive directions from those that are likely to be less sensitive. The difference in internal energy accumulation leads to different temperature increasing rates and chemical reaction initiations within the first 3–4 ps.

During later process, fragments such as NO₃, H, HONO, HNO₃, NO, HO, O₂, and O appear subsequently as the chemical reactions progress, but the quantities of these fragments are much smaller than that for NO₂. A recent investigation of the coupled thermal and electromagnetic induced decomposition in bulk α-HMX from ReaxFF molecular dynamics simulations has found that the initial reactions involve NO₂ loss followed closely by HO, HONO, and H₂O formation.⁴⁶ The time evolution of the population of initial and intermediate products with relatively high concentrations for the sensitive (010) shock plane and the insensitive (101) shock plane are shown in Fig. 4. The snapshots of these products at the first time of their appearances from the MD trajectories for the two systems are presented in Fig. S8 and S9 of the ESI.† We find that NO₃ formation following N–NO₂ bond rupture becomes the secondary critical initial decomposition product under the coupled compression and shear loading. This is not the same as previous QM investigation for α-HMX molecule, which suggested that HONO elimination is the competing reaction channel with N–NO₂ bond dissociation due to comparative reaction barriers.⁴³ In the present work, the amounts of HONO and H are comparative, which are less than NO₃.

Fig. 4 Time evolutions of the fragments with relatively high concentrations formed during shear simulations for the (010) and (101) shock planes.

By tracking reaction pathways, we can explore the reaction mechanism for each reaction products. It is found that NO₃ is mainly generated from oxygen transfer via the following reactions:

(1) C₄H₈N₈O₈ + NO₂ → C₄H₈N₉O₁₀, C₄H₈N₉O₁₀ → C₄H₈N₈O₇ + NO₃;

(2) C₄H₈N₈O₈ → C₄H₈N₇O₅ + NO₃;

(3) C₄H₈N₈O₈ + NO₂ → C₄H₈N₈O₇ + NO₃

H forms directly from C–H bond breaking of C₄H₈N_8−nO_8−2n (n ≤ 2), especially C₄H₈N₇O₆, the product of HMX molecule after losing the first NO₂:

C₄H₈N_8−nO_8−2n → C₄H₇N_8−nO_8−2n + H (n ≤ 2)

HONO forms by NO₂ fragment attracting isolated H radical or the H atom on C₄H₈N_8−nO_8−2n (n ≤ 2):

(1) NO₂ + H → HONO

(2) C₄H₈N_8−nO_8−2n + NO₂ → C₄H₇N_8−nO_8−2n + HONO (n ≤ 2)

The formation of isolated O is mainly due to the N–O bond dissociation of C₄H₈N₇O₆ and HMX molecule, and is partially from NO₂ decomposition leading to NO and O:

(1) C₄H₈N₈O₈ → C₄H₈N₈O₇ + O;

(2) C₄H₈N₇O₆ → C₄H₈N₇O₅ + O

(3) NO₂ → NO + O

From above analyses, we conclude that the chemical reactions leading to initial products and intermediates are primarily the breaking of the chemical bonds that are located out of the C–N ring and are easily to be extruded, such as N–NO₂, N–O, and C–H bonds. This indicates that the intermolecular contacts and collisions during slip make these bonds active and easily to be broken.

More reaction channels and faster reaction rates are observed for sensitive directions compared with less sensitive ones, forming more products within shorter time. There are 219 and 117 kinds of reaction products counted up by the end of our simulation time (8 ps) for the (010) and (101) shock planes, respectively. Stable final products such as H₂O and N₂ are detected for the sensitive (010) shock plane, which are not observed for other shock planes. The undecomposed HMX molecule ratio at 8 ps is 6.48% for the sensitive (010) shock plane and is 23.30% for the insensitive (101) shock plane, confirming that the drastic reactions for the sensitive shock plane decomposes more HMX molecules. These elucidate that the differences in shear stress and energy accumulation exhibiting in early stage result in different chemical behaviors during later period, that is, the stronger intermolecular contacts and collisions and molecular deformations for sensitive directions make more chemical bonds excited and subsequent bond breakings, leading to more secondary reactions and violent reaction intensity, in comparisons with less sensitive ones.

As we concluded in previous study that the predicted anisotropic sensitivity for β-HMX does not vary with applied shear rate,²⁶ this is also valid for α-HMX. The simulation results at the shear rates of 0.25 ps⁻¹ for the (010), (001), and (101) shock planes are shown in Fig. S7 of the ESI,† which demonstrate that the order of sensitivity for the three directions is (010) > (001) > (101), the same as that at 0.5 ps⁻¹.

3.3 Mechanism analysis

To understand the molecular origin of the anisotropic shock sensitivity in α-HMX, we examined the intermolecular steric arrangements from the crystal structure after uniaxial compression for the sensitive (010) shock plane and the insensitive (101) shock plane as shown in Fig. 5. The black arrows and atoms labelled by atom type represent the intermolecular atoms that are close to each other and are likely to contact during shear deformation. For the sensitive (010) shock plane, these atoms are nitro group, hydrogen, and oxygen that are located out of the ring, which are easily to be extruded via intermolecular contacts and collisions, leading to the breakings of N–N bond, C–H bond, and N–O bond that dissociate NO₂, H, and O. And the inter-attractive hydrogen and oxygen atoms that are close to each other make it possible to generate HO and HONO fragments via intermolecular reactions. In the case of insensitive (101) shock plane, the atoms on the two sides of the slip plane are nitro groups, thus the H generation from C–H bond rupture is limited because of the lack of intermolecular extrusions. The intermolecular reactions leading to the formation of HO, HONO species are also reduced since no close contacts between oxygen and hydrogen atoms across the slip plane exist. Furthermore, it can be seen that the number of such atoms is larger and the intermolecular free space is smaller for the (010) shock plane than those for the (101) shock plane, suggesting that the shear deformation induced by the (010) shock encounters more contacts and there is less room for geometry relaxation when molecules collide, in comparisons with the (101) shock plane. Intermolecular free space can be reflected by intermolecular distance, so we calculated the radical distribution function (RDF) g(r) based on molecular center of mass for the two shocked systems after energy minimization, which is shown in Fig. S10 for the ESI.† These factors lead to greater molecular deformation that results in higher shear stress barrier and energy accumulation in the shear localized region for the (010) shock plane, benefiting temperature increase and initial chemical bond breaking that trigger further decomposition, making it more sensitive. This provides a possible explanation for the anisotropic sensitivity.

Fig. 5 Compressed crystal structure of α-HMX unit cell including the illustrations of intermolecular contacts during shear deformation. (a1) and (a2) represent the sensitive (010) shock plane with slip system {021}〈0−12〉, (b1) and (b2) present the insensitive (101) shock plane with slip system {401}〈10−4〉. The different colors represent different atom types: gray represents carbon atom, blue nitrogen atom, red oxygen atom, and white hydrogen atom. The black arrows and atoms labelled by atom type represent the intermolecular atoms that are close to each other and are likely to contact during shear deformation.

Intermolecular contacts and collisions resulting in the deformation of molecule can be revealed directly by the changes of energies describing bond stretching (E_bond), angle bending (E_val), dihedral distortion (E_tors), and intermolecular interactions (E_vdW). The time evolutions of these energy terms for the (010) and (101) shock planes are presented in Fig. 6, showing differences between the two shock directions. The variations of E_vdW, E_bond, E_val, and E_tors during the first 4 ps are larger for the (010) plane than those for the (101) plane, confirming the stronger intermolecular interactions and molecular deformations for the former compared with the latter. It has been suggested that the potential energy barrier for shear can be estimated by assuming a potential that describes the energy associated with bond and angle distortions of an individual molecule and with intermolecular interactions.¹⁷ According to this, the potential energy barrier is higher for the sensitive (010) shock plane in comparison with the insensitive (101) shock plane.

Fig. 6 Time evolutions of E_bond, E_val, E_tors, and E_vdW per HMX molecule for the (010) and (101) shock planes during shear simulation.

4. Conclusions

The physical and chemical responses of single crystal α-HMX to combined compression and shear loadings were investigated using the CS-RD computational protocol to explore the characteristics of EMs under shock compression along various directions. Based on the criterion of lowest shear stress barrier, the dominant slip system for each shock direction was selected to access the anisotropic behavior. Significant differences are found in shear stress, energy, temperature, and chemical reactions for shock directions normal to the (010), (001), (100), (110), (011), (111), and (101) planes, indicating anisotropy of this energetic crystal. The results from the early stage of slip are critical in understanding the anisotropic sensitivity under mechanical shock compression, which lead to different chemical behaviors during later process. According to the internal energy accumulated within the duration of surmounting shear stress barrier, the relative sensitivity for the seven shock planes is evaluated to be: (010) > (001) > (100)/(110)/(011)/(111)/(101), among which the (010) plane is most sensitive and the (101) plane is most stable. The molecular origin of the anisotropic sensitivity is the different intermolecular steric arrangements across the slip plane induced by shock compression along different orientations. The shear deformation induced by the (010) shock encounters more contacts and has less room for geometry relaxation when molecules collide, leading to higher shear stress barrier, faster energy and temperature increments, and stronger chemical reactions, making it more sensitive.

We have to stress here that the time scale is far too short and the shear rate is far too large for a realistic simulation of shock process, however, the CS-RD computational protocol was designed as a tool to quickly distinguish between sensitive and insensitive shock directions requiring only tens of thousands of atoms, which is indeed proved to be efficient and valuable. Considering that this protocol has been validated to predict the anisotropic sensitivity for PETN, β-HMX, RDX, and α-HMX, we suggest that this approach could provide a practical way to examine the anisotropic sensitivity for new energetic crystals and to assess which one would be least sensitive.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant no. 11402031, 11372053, and 11221202), and by the Foundation for Development of Science and Technology of CAEP, China (no. 2012A0101004 and 2014B0101014).

Notes and references

1. Z. A. Dreger, Understanding Shock-Induced Changes in Molecular Crystals in: Static compression of energetic materials, ed. S. M. Peiris and G. J. Piermarini, Springer-Verlag, Berlin, 2008, p. 241.
2. R. Cheret, Detonation of Condensed Explosives, Springer, New York, 1993.
3. J. J. Dick, Plane shock initiation of detonation in γ-radiated pentaerythritol tetranitrate, J. Appl. Phys., 1982, 53, 6161–6167.
4. J. J. Dick, Effect of crystal orientation on shock initiation sensitivity of pentaerythritol tetranitrate explosive, Appl. Phys. Lett., 1984, 44, 859–861.
5. J. J. Dick, R. N. Mulford, W. J. Spencer, D. R. Pettit, E. Garcia and D. C. Shaw, Shock response of pentaerythritol tetranitrate single crystals, J. Appl. Phys., 1991, 70, 3572–3587.
6. J. J. Dick, Molecular mechanics modeling of shear and the crystal orientation dependence of the elastic precursor shock strength in pentaerythritol tetranitrate, J. Appl. Phys., 1994, 76, 2726–2637.
7. J. J. Dick, Anomalous shock initiation of detonation in pentaerythritol tetranitrate crystals, J. Appl. Phys., 1997, 81, 601–612.
8. C. S. Yoo, N. C. Holmes, P. C. Souers, C. J. Wu, F. H. Ree and J. J. Dick, Anisotropic shock sensitivity and detonation temperature of pentaerythritol tetranitrate single crystal, J. Appl. Phys., 2000, 88, 70–75.
9. J. J. Dick, D. E. Hooks, R. Menikoff and A. R. Martinez, Elastic-plastic Wave Profiles in Cyclotetramethylene Tetranitramine Crystals, LA-UR-0 4–1229, 5 March 2004.
10. J. J. Dick, D. E. Hooks, R. Menikoff and A. R. Martinez, Elastic-plastic wave profiles in cyclotetramethylene tetranitramine crystals, J. Appl. Phys., 2004, 96, 374–379.
11. R. Menikoff, J. J. Dick and D. E. Hooks, Analysis of wave profiles for single-crystal cyclotetramethylene tetranitramine, J. Appl. Phys., 2005, 97, 023529.
12. D. E. Hooks, K. J. Ramos and A. R. Martinez, Elastic-plastic shock wave profiles in oriented single crystals of cyclotrimethylene trinitramine (RDX) at 2.25 GPa, J. Appl. Phys., 2006, 100, 024908.
13. M. R. Baer and C. A. Hall, Isentropic Loading Experiments of a Plastic Bonded Explosive and Constituents, J. Appl. Phys., 2007, 101, 034906.
14. C. O. Leiber, Aspects of the mesoscale of crystalline explosives, Propellants, Explos., Pyrotech., 2000, 25, 288–301.
15. A. R. West, Solid State Chemistry and its Applications, Wiley, New York, 1984, ch. 21, p. 666.
16. V. K. Jindal and D. D. Dlott, Orientation dependence of shock-induced heating in anharmonic molecular crystals, J. Appl. Phys., 1998, 83, 5203–5211.
17. Y. A. Gruzdkov and Y. M. Gupta, Shock Wave Initiation of Pentaerythritol Tetranitrate Single Crystals: Mechanism of Anisotropic Sensitivity, J. Phys. Chem. A, 2000, 104, 11169–11176.
18. P. J. Rae, H. T. Goldrein, S. J. P. Palmer, J. E. Field and A. L. Lewis, Quasi-Static Studies of the Deformation and Failure of PBX 9501, Proc. R. Soc. London, Ser. A, 2002, 458, 2227–2242.
19. P. J. Rae, D. E. Hooks and C. Liu, The Stress Versus Strain Response of Single β-HMX Crystals in Quasi-Static Compression, The 13th Symposium (International) on Detonation, Nor-folk, Virginia, USA, 23–28 July 2006, p. 293.
20. A. R. Zamiri and S. De, Modeling the Anisotropic Deformation Response of β-HMX Molecular Crystals, Propellants, Explos., Pyrotech., 2011, 36, 247–251.
21. M. W. Conroy, I. I. Oleynik, S. V. Zybin and C. T. White, First-principles investigation of anisotropic constitutive relationships in pentaerythritol tetranitrate, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 094107.
22. M. W. Conroy, I. I. Oleynik, S. V. Zybin and C. T. White, ANISOTROPIC CONSTITUTIVE RELATIONSHIPS IN ENERGETIC MATERIALS: PETN AND HMX, Shock Compression of Condensed Matter, ed. M. Elert, M. D. Furnish, R. Cliau, N. Holmes and J. Nguyen, American Institute of Physics, 2007, pp. 361–364.
23. M. W. Conroy, I. I. Oleynik, S. V. Zybin and C. T. White, First-principles anisotropic constitutive relationships in β-cyclotetramethylene tetranitramine (β-HMX), J. Appl. Phys., 2008, 104, 053506.
24. S. V. Zybin, W. A. Goddard III, P. Xu, A. C. T. van Duin and A. P. Thompson, Physical mechanism of anisotropic sensitivity in pentaerythritol tetranitrate from compressive-shear reaction dynamics simulations, Appl. Phys. Lett., 2010, 96, 081918.
25. I. Plaskin, C. S. Coffey, R. Mendes, J. Ribeiro, J. Campos and J. Direito, The 13th Symposium (International) on Detonation, ONR 351-07-01, 2006, p. 319.
26. T. T. Zhou, S. V. Zybin, Y. Liu, F. L. Huang and W. A. Goddard III, Anisotropic shock sensitivity for β-octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine energetic material under compressive-shear loading from ReaxFF-lg reactive dynamics simulations, J. Appl. Phys., 2012, 111, 124904.
27. C. S. Choi and H. P. Boutin, A study of the crystal structure of β-cyclotetramethylene tetranitramine by neutron diffraction, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1970, 26, 1235–1240.
28. H. H. Cady, A. C. Larson and D. T. Cromer, The crystal structure of α-HMX and refinement of the structure of β-HMX, Acta Crystallogr., 1963, 16, 617–623.
29. R. E. Cobbledick and R. W. H. Small, The crystal structure of the δ-form of 1,3,5,7-tetranitro-1,3,5,7-tetraazacyclooctane (δ-HMX), Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 1918–1922.
30. A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard III, ReaxFF: A Reactive Force Field for Hydrocarbons, J. Phys. Chem. A, 2001, 105, 9396–9409.
31. L. C. Liu, Y. Liu, S. V. Zybin and W. A. Goddard III, ReaxFF-lg: Correction of the ReaxFF Reactive Force Field for London Dispersion, with Applications to the Equations of State for Energetic Materials, J. Phys. Chem. A, 2011, 115, 11016–11022.
32. Q. An, Y. Liu, S. V. Zybin, H. Kim and W. A. Goddard III, Anisotropic Shock Sensitivity of Cyclotrimethylene Trinitramine (RDX) from Compress-and-Shear Reactive Dynamics, J. Phys. Chem. C, 2012, 116, 10198–10206.
33. A. Strachan, A. C. T. van Duin, D. Chakraborty, S. Dasgupta and W. A. Goddard III, Shock Waves in High-Energy Materials: The Initial Chemical Events in Nitramine RDX, Phys. Rev. Lett., 2003, 91, 098301.
34. A. Strachan, E. Kober, A. C. T. van Duin, J. Oxgaard and W. A. Goddard III, Thermal decomposition of RDX from reactive molecular dynamics, J. Chem. Phys., 2005, 122, 054502.
35. A. C. T. van Duin, Y. Zeiri, Y. F. Dubnikova, R. Kosloff and W. A. Goddard III, Atomistic-Scale Simulations of the Initial Chemical Events in the Thermal Initiation of Triacetonetriperoxide, J. Am. Chem. Soc., 2005, 127, 11053–11062.
36. L. Zhang, S. V. Zybin, A. C. T. Van Duin, S. Dasgupta, W. A. Goddard III and E. M. Kober, Carbon Cluster Formation during Thermal Decomposition of Octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine and 1,3,5-Triamino-2,4,6-trinitrobenzene High Explosives from ReaxFF Reactive Molecular Dynamics, J. Phys. Chem. A, 2009, 113, 10619–10640.
37. T. T. Zhou and F. L. Huang, Effects of Defects on Thermal Decomposition of HMX via ReaxFF Molecular Dynamics Simulations, J. Phys. Chem. B, 2011, 115, 278–287.
38. K. Nomura, R. K. Kalia, A. Nakano and P. Vashishta, Reactive nanojets: Nanostructure-enhanced chemical reactions in a defected energetic crystal, Appl. Phys. Lett., 2007, 91, 183109.
39. J. Budzien, A. P. Thompson and S. V. Zybin, Reactive Molecular Dynamics Simulations of Shock Through a Single Crystal of Pentaerythritol Tetranitrate, J. Phys. Chem. B, 2009, 113, 13142–13151.
40. Q. An, S. V. Zybin, W. A. Goddard III, A. J. Botero, M. Blanco and S. N. Luo, Elucidation of the dynamics for hot -spot initiation at nonuniform interfaces of highly shocked materials, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 220101.
41. T. T. Zhou, H. J. Song, Y. Liu and F. L. Huang, Thermal Shock Initiated Thermal and Chemical Responses of HMX Crystal from ReaxFF Molecular Dynamics Simulation, Phys. Chem. Chem. Phys., 2014, 16, 13914–13931.
42. T. T. Zhou and F. L. Huang, Thermal expansion behaviors and phase transitions of HMX polymorphs via reaxFF molecular dynamics simulations, Acta Phys. Sin., 2012, 61, 246501.
43. J. P. Lewis, K. R. Glaesemann, K. VanOpdorp and G. A. Voth, Ab Initio Calculations of Reactive Pathways for α-Octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine (α-HMX), J. Phys. Chem. A, 2000, 104, 11384–11389.
44. C. F. Melius, Molecular Decomposition Mechanisms Of Energetic Materials, J. Phys. Colloq., 1987, 48, 341–352.
45. S. W. Zhang and T. N. Truong, Branching Ratio and Pressure Dependent Rate Constants of Multichannel Unimolecular Decomposition of Gas-Phase-HMX: An Ab Initio Dynamics Study, J. Phys. Chem. A, 2001, 105, 2427–2434.
46. M. A. Wood, A. C. T. van Duin and A. Strachan, Coupled Thermal and Electromagnetic Induced Decomposition in the Molecular Explosive αHMX: A Reactive Molecular Dynamics Study, J. Phys. Chem. A, 2014, 118, 885–895.

---

Footnote

† Electronic supplementary information (ESI) available: The averaged full stress tensors for the seven shock planes after NVT-MD relaxation are collected in Table S1. Bond order cutoff values for various atom pairs used in the algorithm of molecule recognition are tabulated in Table S2. For the shock directions perpendicular to the (001), (100), (110), (011), (111), and (101) planes, the time evolutions of shear stress, potential energy, temperature, and initial reaction product NO₂ for each slip system during shear simulations are plotted in Fig. S1–S6. The shear simulation results at the shear rate of 0.25 ps⁻¹ for the (010), (001), and (101) shock planes are shown in Fig. S7. The snapshots of the initial and intermediate products at the first time of their appearances from the MD trajectories for the sensitive (010) shock plane and the insensitive (101) shock plane are presented in Fig. S8–S9. The radical distribution function (RDF) g(r) based on molecular center of mass for the two (010) and (101) shocked systems after energy minimization are shown in Fig. S10. See DOI: 10.1039/c4ra09943e

---