Surface energy of silk fibroin and mechanical properties of silk cocoon composites

Abstract

Silkworm cocoons are biological composite structures protecting the silkworms against environmental damage and physical attack by natural predators. In particular, some outdoor reared silk cocoons exhibit outstanding mechanical properties that are relevant to the higher level protection required to enhance the survival chance of silkworms while supporting their metabolic activity. The performance of composite materials strongly depends on the adhesion between the fiber reinforcement and matrix, with the surface properties of the fibers playing a key role in determining the level of adhesion achieved. For this reason it is important to study the surface properties of silk fibroin to further understand the composite properties of the cocoons. In this work, both the mechanical properties of the silk cocoons and silk fibroin were studied. The surface topography was examined using scanning probe microscopy (SPM), which revealed distinct longitudinal ridges and striations along the fiber axis of the four silk fiber types. The fibers were found to exhibit heterogeneity in surface energy as evidenced from inverse gas chromatography (IGC) measurements. The combination of excellent mechanical properties and the more energetically heterogeneous surface nature of the wild A. pernyi silk fibroin fibers correlates well with the excellent mechanical properties of the A. pernyi cocoons.

---

1. Introduction

Silkworm silk fibers are outstanding natural materials that have long been used for textiles.^1,2 Silk-based materials have recently found applications in a growing number of areas including biodegradable medical scaffolds, implantable functional devices and tissue engineering products.^3,4 While the properties of Bombyx mori (B. mori) cocoon silk and the major ampullate silks from a range of spiders have been extensively studied,^5–7 there are substantial knowledge gaps in understanding other silkworm silks including semi-domestic and wild silks and their cocoon structures. In nature, very thin and lightweight wild silkworm cocoons can protect silkworms from physical attacks from predators or environment while supporting their metabolic activity.^8,9 It is known that the wild silkworm silks such as Chinese tussah silkworm Antheraea pernyi (A. pernyi) and semi-domestic Antheraea assamensis (A. assamensis) silks are remarkably similar to the Golden Orb Web spider (Nephila Clavipes) silk and they have the excellent balance of strength, extensibility and toughness, presumably due to similar protein structure.¹⁰ Therefore the understanding of the mechanical property of such silkworm silks and their protective cocoon structure may provide insightful guidance for future bio-mimetic design of protective fibres and fibrous structures such as fabrics and textile composites.

A cocoon is a multilayer porous composite structure formed by continuous twin silk filaments (bave) bonded by silk gum (sericin). The compact cocoon structure is formed when a silkworm, along with spinning, wraps the twin silk filaments around its body through a gyrating motion of its head and cyclically bending and stretching of its body with different shapes in a programmed manner.^11,12 The mechanical performance of composites depends on the properties of individual component as well as on the interfacial compatibility between the constituting materials. The performance of composites strongly depends on the strength of the fiber/matrix interfacial zone, which controls the stress transfer process between the reinforcement and the matrix. However, it is difficult to evaluate the interface when the boundary between fiber and matrix is not clear. Composite interfaces can be characterized by analysing the surfaces of the fibers before they are impregnated with matrix.¹³ In the case of natural silk filaments, the interfacial properties can be examined through analysing the surface of the degummed fibers. Because the fiber/matrix interfacial region is closely related to the surface properties (e.g., surface energy, acid–base interactions, etc.) of both the fibers and matrix, characterization of the surface properties would be necessary to understand the adhesion, including the topography study and the IGC tests of degummed silk fibers for this work. Despite of the importance of surface energy parameters in preparation and properties in silk/polymer composites, the surface characteristics of silkworm silks are scarcely reported in literature.

Our previous work on interlaminar peel tests has shown that the wild silkworm cocoons are uniquely tough composite structures; the maximum work-of-fracture of the wild cocoons (A. pernyi and Antheraea mylitta, i.e. A. mylitta) was approximately 1000 J m⁻², which was almost 10 times the value for the domesticated cocoon (B. mori) and 3–4 times the value for the semi-domesticated cocoon (A. assamensis).^14,15 For some applications, natural fibers offer advantages over conventional synthetic fibers such as carbon and glass fibers as the reinforcement for composites, i.e. low cost, renewability, acceptable specific strength properties and biodegradability.^16,17 As one of the animal-based fibers, silk has received far less attention than plant-based fibers such as flax, jute, kenaf for the use as reinforcement in biocomposites.^18,19 As a result, further study of various silkworm silks and more particularly wild silkworm silks and their naturally built composite structures, i.e. cocoons, have important practical implications for the development of new biodegradable and renewable composite materials.

This work employs a range of techniques to characterize both the physical and chemical properties, including surface energy and surface energy heterogeneity, of both domestic and wild silkworm silk fibroin. In particular, inverse gas chromatography (IGC) was used in the present study to characterize the surface properties (surface area, surface energy, heterogeneity and acid–base properties) of several silk fibres.

2. Materials and methods

2.1 Materials

B. mori and A. assamensis silkworm cocoons were purchased from silk rearing houses in Northeast India; A. mylitta cocoons were collected from Central India and A. pernyi cocoons were collected from Northeast China. They were received as stifled cocoons, as commonly used prior to reeling silk filament for textile applications. The silk samples were degummed by washing the fibers for 30 min in a 1 wt% solution of Marseille soap and 0.5 wt% of Na₂CO₃ in boiling deionized water, followed by rinsing with deionized water. The process was repeated with fresh solutions twice for the B. mori and the Samia cynthia (S. cynthia) cocoons and three times for the A. pernyi and the A. assamensis cocoons. The degummed silk fibers were then air dried. During silk sampling, the temperature was held constant at ambient room temperature of 22 °C and the humidity was kept at 50–55%.

2.2 Physical characterization

2.2.1. Mechanical testing. An Instron MicroTester (Model 5848; force resolution, 0.5% of the indicated load; position resolution 0.02 μm) equipped with a 0.5 N load cell was used to measure the tensile properties of the silk fibroin. A gauge length of 20 mm with a measured error of 0.1 mm was used. The fibre was stretched until it broke and the strain rate was 50% per minute. The experiments were operated at 22 °C and the relative humidity was kept at 50–55%. 40 samples were tested for each silkworm silk type. The tensile properties of the cocoon walls were tested on an Instron 30K universal tester with a loading rate of 2 mm min⁻¹. The gauge length used was 10 mm and the cocoon wall samples were 5 mm wide. The tensile samples were cut using scissors at the center area of the cocoon along the major axis (i.e. the length direction of the samples is parallel to the major axis of the cocoon). The thickness of different cocoon wall samples is 393 ± 21 μm for B. mori, 243 ± 31 μm for S. cynthia, 277 ± 29 μm for A. assamensis, and 387 ± 31 for A. pernyi, respectively. The morphologies of the cocoons and the fracture surfaces from failed specimens were investigated by scanning electron microscopy (SEM) (Supra 55VP). The silk fibre cross-section was measured from the SEM images of 50 fibres and determined from the histogram graphs of size distribution. The 180 degree peel test, which is modified from the ASTM standard test D 1876-08 used for peel resistance of adhesives,¹⁹ was performed on a Lloyd LR30K tester with a 100 N load cell. The detailed experimental and data analysis methods can be found in ref. 14.

2.2.2. Scanning probe microscopy (SPM). SPM analysis was conducted on a Bruker MultiMode-8 tester in contact mode using silicon tip on cantilevers with a nominal force constant 40 N m⁻¹. Single degummed silk fiber was fixed on a metal substrate with double sided tape. The surface roughness was quantified by measuring the average roughness, R_a, which represents the arithmetic average of the deviations from the centre plane. The surface roughness calculations were based on the 1.2 μm × 1.2 μm height image after applying a 3rd order flattening routine using the V 1.40 NanoScope software.

2.3 Physicochemical properties of silk fibers – inverse gas chromatography (IGC)

Surface energy and specific surface area were analyzed using the IGC-Surface Energy Analyzer (Surface Measurement Systems, Alperton, Middlesex, UK). Approximately 1.5 g of each degummed silk fiber sample, cut at 5 cm lengths, was packed into individual 300 mm long by 4 mm inner diameter silanized glass columns (Surface measurement Systems, Alperton, Middlesex, UK).

In IGC, the adsorbent under investigation is placed into a column while a known adsorptive is used in the gas phase. As in analytical gas chromatography, the retention time is obtained as the fundamental parameter measured. The retention time can be converted into a retention volume, which is directly related to several physico-chemical properties of the solid (absorbent). Surface energetic heterogeneity profile can be represented by an energy distribution with surface coverage, which can provide more comprehensive understanding on the nature and population of different surface sites. IGC experiments with finite concentrations were conducted in pulse mode, by injecting a desired amount of probe molecule into the column via inert helium carrier gas. A series of n-alkanes (n-heptane, n-octane and n-nonane) and polar probes (chloroform, ethyl acetate, acetone, acetonitrile and 1,4-dioxane) were injected at a specific fractional surface coverage and their retention times measured for a broad range of fractional surface coverage. The retention times were then converted into retention volumes and the dispersive surface energy (γ^D_s) on a solid sample was determined in accordance with standard methodology as described by Jones.²⁰

Determination of the dispersive surface energy (γ^D_s) and specific free energy of desorption (ΔG⁰_SP), as well as the acidic and basic properties of a solid sample are well documented.²¹ The net retention volume (V_N), a fundamental surface thermodynamic property of the solid–vapor interaction, can be computed from eqn (1):

where j is the James–Martin correction, m is the mass of sample in the column (g), F is the carrier gas flow rate (cm³ min⁻¹), t_R is the retention time of the probe (minutes), t₀ is the mobile phase hold-up time (minutes), and T is the column temperature (K). γ^D_s can be calculated from the V_N of a series of non-polar reference probes (for example: n-hexane, n-heptane, n-octane and n-nonane) according to a standard methodology developed by Dorris and Gray where RT ln(V_N) is plotted against the number of carbon atoms of the alkane probe. γ^D_s can then be determined from the slope of the resulting linear regression, as reported in detail elsewhere.²²

Total surface energy (γ^T_s) was defined as the sum of the dispersive energy and the specific (γ^AB_s) energy contributions and the surface polarity was calculated as γ^AB_s/γ^T_s. On the other hand, the specific (acid–base) surface energy (γ^AB_s) can be obtained by first measuring the ΔG⁰_SP for different polar probe molecules (i.e. acetonitrile, acetone, ethanol, ethyl acetate and dichloromethane) on the materials. Employing the polarisation approach, the ΔG⁰_SP values are determined from a plot of RT ln(V_N) versus the molecular polarisabilities of the probes (P_D). The values obtained for a series of non-polar n-alkanes follow a linear relationship and ΔG⁰_SP for each polar probe is determined relative to this reference line.²³ The acid and base numbers, K_a and K_b, and hence the acid/base ratios (K_a/K_b) were determined according to the method of Gutmann.²⁴

3. Results and discussion

3.1 Mechanical properties of silk cocoons

The mechanical properties of cocoon walls vary considerably with the silk cocoon type. The tensile stress–strain curves of the cocoon walls are shown in Fig. 1 and the tensile property is summarized in Table 1. Among all the cocoon types, the A. pernyi cocoon wall exhibited the highest Young's modulus, breaking stress and breaking strain. The modulus of the wild A. pernyi was 872 MPa, which reached more than double the value of the other three cocoon types, i.e. domestic B. mori and S. cynthia, and semi-domestic A. assamensis. While the other three cocoon wall types had similar breaking stress (20 to 30 MPa) and breaking strain values (16% to 21%), the A. pernyi achieved a breaking stress of 56 MPa and a breaking strain of 41%. The high tensile stress and strain from the A. pernyi cocoon wall resulted in 5 to 11 time's larger absorbed energy during the loading process.

Fig. 1 Tensile stress–strain curves for different types of cocoon walls.

Table 1 Tensile properties of four type of silkworm cocoon walls

Cocoon wall type	Thickness (μm)	Nominal density (kg m^−3)	Young's modulus (MPa)	Maximum load (N)	Breaking stress (MPa)	Breaking strain (%)	Absorbed energy (J)
B. mori	393 ± 21	377 ± 15	365 ± 102	49 ± 8	30 ± 7	16 ± 1	0.09 ± 0.02
S. cynthia	243 ± 31	449 ± 56	238 ± 39	42 ± 9	20 ± 2	21 ± 5	0.17 ± 0.06
A. assamensis	277 ± 29	516 ± 28	342 ± 72	19 ± 1	23 ± 6	19 ± 7	0.05 ± 0.009
A. pernyi	387 ± 31	711 ± 44	872 ± 142	140 ± 13	56 ± 5	41 ± 6	0.6 ± 0.1

---

As a multilayer composite structure, the cocoon wall was tested not only along the in-plane direction but also along the interlaminar direction. Therefore, in addition to the tensile properties, the interlaminar peel resistance was also examined. The 180 degree peel tests showed that the maximum peeling load was 0.74 N and the average peeling load was 0.35 N for the B. mori cocoon. By comparison, the A. pernyi cocoon had a maximum peeling load of 4.45 N and an average peeling load of 2.51 N. The maximum work of fracture (WOF) of all tested cocoon layers was 981 J m⁻² from the A. pernyi outer layer, suggesting the highest interlaminar adhesion and bonding energy between the cocoon layers (Table 2). The toughness for the wild A. pernyi cocoon was approximately 10 times of the B. mori cocoon and twice the values of the S. cynthia and A. assamensis cocoon walls. The results are comparable to Chen et al.'s findings for the B. mori cocoon, where they observed similar nonlinear load–displacement relation with an average peeling load of 0.32 N and a WOF of 61 J m⁻² and also proved that the delamination of cocoon walls is mainly caused by the brittle fracture of the inter-layer sericin bonds.²⁵ As a result, the significantly higher bonding energy for the A. pernyi cocoon wall suggests the strongest fibroin/sericin bond in this cocoon type. The high toughness of the wild A. pernyi cocoon is presumably related to the higher level of protection against attack from predators and the hazardous outdoor physical environment.¹⁴

Table 2 Interlaminar peel properties of cocoon walls

Cocoon type	Wall thickness (μm)	Average peeling load (N)	Maximum peeling load (N)	Peel strength (N m^−1)	Work-of-fracture (J m^−2)
B. mori	393 ± 21	0.35 ± 0.05	0.74 ± 0.17	62 ± 6	119 ± 19
S. cynthia	480 ± 91	1.00 ± 0.45	1.58 ± 0.71	245 ± 99	437 ± 203
A. assamensis	277 ± 29	1.21 ± 0.56	1.43 ± 0.40	240 ± 89	322 ± 121
A. pernyi	387 ± 31	2.51 ± 0.55	4.45 ± 0.63	469 ± 75	981 ± 211

---

3.2 Cocoon morphology and tensile fracture

As shown in Fig. 2, the cocoon walls have a porous architecture with randomly distributed twin silk fibers bonded with sericin matrix. In comparison with the B. mori and S. cynthia cocoons, the silk fibers are more flat and wider in the A. pernyi and A. assamensis cocoon layers (Fig. 2a–d). In general, the fiber width varies along the out-of-plane direction, i.e. the fiber width reduces towards the interior of the cocoon. Therefore the cocoon has a graded porous structure with thinner fibers and smaller pores in the inner layers. The cross-sections of the cocoon wall and silk fibers reveal the fiber packing structure and the transversal geometrical shape of the silk fibers. It appears that the B. mori and the S. cynthia cocoons have a much more porous structure than the densely packed A. pernyi and A. assamensis cocoon walls. In particular, for the A. pernyi cocoon, the near-rectangular silk fibers are packed in parallel to the surface and form a compact brick-like fiber assembly. The B. mori silk fibers have a near-triangular-shaped cross-section and the S. cynthia silk fibers have more irregular fiber profiles.

Fig. 2 The outer layer, cross-section of different cocoon walls and the twin silk fibers from each type. (a), (a1) and (a2): B. mori; (b), (b1) and (b2): S. cynthia; (c), (c1) and (c2): A. assamensis; (d), (d1) and (d2): A. pernyi.

After tensile failure, among all the cocoon walls, only the A. pernyi showed a failed planar structure, all the other types turned completely fibrous due to the weaker bond in the 3D cocoon fibrous assembly (Fig. 3). It can be seen in the pulled B. mori silk fibres that the sericin shell detached from the fibroin core, indicating a weak bond between the fibroin and sericin. The fracture morphology shows the separation of the fibroin and sericin took place by the relative sliding of both surfaces. The S. cynthia silk exhibited a fibre split failure; the A. assamensis and the A. pernyi showed the ductile sericin matrix nature, which is in agreement with the reduced elastic modulus of these silk fibers as compared with B. mori (because of the large volume fraction of matrix which does not contribute to the fiber stiffness). Finally, the large elongation of wild silk fibers correlates well with the non-linear behaviour of composites prior to failure.^26,27 In all the three types of silk fibers other than B. mori, the sericin and the fibroin are not distinguishable in the other silk types.

Fig. 3 Tensile fracture of cocoon walls and enlarged view of broken silk fibers. (a) and (b) are B. mori; (c) and (d) are S. cynthia; (e) and (f) are A. assamensis; (g) and (h) are A. pernyi.

3.3 Mechanical property and surface topography of degummed silk fibers

Fig. 4 shows the tensile stress–strain curves of the degummed silk fibers. The stress–strain curves of the S. cynthia, A. assamensis and A. pernyi silk fibers have a distinct yield point followed by obvious strain hardening, which is similar to the spider major ampullate silks.⁵ In contrast, the B. mori silk lacks such distinct yield points and has much lower extensibility. It is interesting to see that the B. mori silk fibroin is almost as strong as the wild silk fibers despite the fact that the A. pernyi fibroin has a much higher breaking strain of 50% (Table 3). The A. pernyi fibers are 30% tougher than the domestic B. mori fibers and 100% tougher than the S. cynthia fibers. The mechanical properties of composite structure are generally determined by the fiber reinforcement properties, the fiber/matrix adhesion and the matrix properties. For the case of biological cocoon structure, the higher mechanical properties from the wild A. pernyi type are not only affected by the fibroin and sericin properties, but also dependent on the interfacial adhesion between the fibroin and sericin. The surface topography and roughness, and the surface energy of silk fibroin were consequently further investigated.

Fig. 4 Tensile stress–strain curves for degummed single silk fibers.

Table 3 Tensile properties of the degummed single silk fibers

Silk type	Single fiber cross-section area (μm^2)	Young's modulus (GPa)	Maximum load (cN)	Maximum stress (MPa)	Strain at maximum stress (%)	Toughness (J m^−3)
B. mori	74 ± 2	13.3 ± 1.8	4.7 ± 0.81	635 ± 108	22 ± 5	1.0 × 108
S. cynthia	196 ± 26	4.43 ± 0.60	5.6 ± 1.7	284 ± 88	34 ± 13	6.1 × 107
A. assamensis	231 ± 22	5.70 ± 0.47	11.4 ± 1.1	495 ± 48	51 ± 6	1.4 × 108
A. pernyi	350 ± 37	4.98 ± 0.56	14.9 ± 1.9	426 ± 55	51 ± 7	1.3 × 108

---

3.4 Silk fiber surface topography

The SPM images show the presence of distinct longitudinal ridges and striations along the fiber axis of the four silk fiber types (Fig. 5). The A. assamensis surface shows finer and lower grooves than the other three types. Surface roughness analysis was based on the SPM height images taken over a 1.2 μm by 1.2 μm area. The effect of fiber curvature needs to be removed before the surface roughness can be measured. In the current work this was done by applying a 3rd order flattening routine. The average roughness is 5.00 nm for B. mori, 7.29 nm for S. cynthia, 3.54 nm for A. assamensis and 6.76 nm for A. pernyi. The roughness value was the lowest for the A. assamensis which has the finest surface texture and the highest for the S. cynthia which was more than twice the value of the A. assamensis.

Fig. 5 SPM topography of degummed silk fiber surfaces. (a) B. mori; (b) S. cynthia; (c) A. assamensis; (d) A. pernyi. The z-color bar on the left ranges from −65 to 65 nm.

Increasing surface roughness of biomaterials has shown advantageous effects on the cell attachment for healing and bone formation.³ Silk fibroin is a native protein from silkworm fiber and is a remarkably stable and mechanically robust protein biomaterial, as evidenced by the ability to be autoclaved for sterilization and is amendable to ethylene oxide sterilization and gamma irradiation.²⁸ It can be conveniently employed in tissue engineering systems, drug release systems, bio-optics and bioelectronics applications.^1,29 The combination of excellent mechanical and surface properties of the wild A. pernyi silk fibroin may pave the way for its broader use for biomedical applications.

3.5 Surface energy

IGC can accurately determine the adsorption isotherms at ambient temperatures and atmosphere pressure using organic probe molecules. It allows the Brunauer, Emmett and Teller (BET) surface area to be measured, especially for the materials with low surface area. The sorption constant is related to the affinity of the solid with the adsorbate and the heat of adsorption. The BET surface area and the sorption constant for four types of silk fibroin are shown in Fig. 6. The S. cynthia, which has the highest surface roughness value, also has the highest BET surface area. In fact, the BET surface area results for silk fibroin follow the same sequence of the fiber surface roughness measurement. However, since the fineness of fibers is not the same for different silk fiber types and some silk fibers have pores, the BET surface area was affected by these factors as well. It is generally known that the higher the value of sorption constant, the higher the interaction.³⁰ Hence the surfaces of the A. assamensis, S. cynthia and B. mori silk fibroin may facilitate with better interaction with the absorbate.

Fig. 6 Specific surface area determined from Octane sorption isotherm.

Using IGC at finite concentration conditions generates surface energy (total, dispersive, specific or polar) as a function of surface coverage. Surface heterogeneity of silk fibers has not been sufficiently studied in silk fibers, despite its importance in many applications. There are two types of surface heterogeneity: structural and energetic. The former refers to the distribution of pore size and shape, being mainly a geometrical effect determined by the correlation between probe molecule size and pore diameter, whereas the latter refers to the distribution of surface sites of distinct energetic levels including surface groups, impurities and/or surface irregularities.³⁰ A completely flat line is indicative of an energetically homogeneous surface. The total surface energy traces (γ^T_s) for four types of silk fibers are shown in Fig. 7. All samples are energetically heterogeneous since the surface energy changes as a function of surface coverage. The total surface energy of the A. pernyi fibers varies from a minimum average value of 44 mJ m⁻² to a maximum value of 52 mJ m⁻² and the total surface energy of the B. mori fibers varies from a minimum average value of 43 mJ m⁻² to a maximum value of 52 mJ m⁻². The range of the total surface energy for the S. cynthia is from 41 mJ m⁻² to 47 mJ m⁻² and that for the A. assamensis is from 45 mJ m⁻² to 52 mJ m⁻².

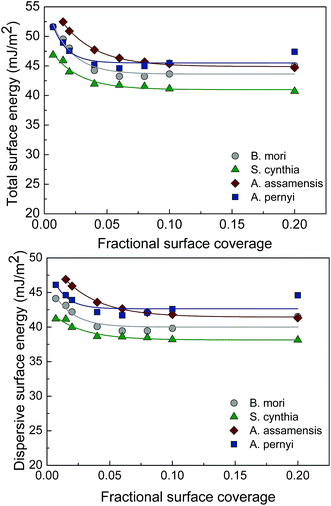Fig. 7 Total surface energy (γ^T_s and dispersive surface energy (γ^D_s for the degummed B. mori, S. cynthia, A. assamensis and A. pernyi silk fibers.

The total surface energy (γ^T_s) is made up of the dispersive (non-polar) interactions (γ^D_s) and the specific (acid–base or polar) contributions (γ^AB_s). The dispersive component arises from London, van der Waals and Lifshitz forces³¹ and the acid–base component arises from Lewis acid–base interactions and hydrogen bonds.²⁴ It can be seen from Fig. 7 and 8 that all the silk fibers are heterogeneous in both dispersive and acid–base surface energies. Dispersive surface energy (γ^D_s) profiles in Fig. 7 show that all silk fibers are energetically active and heterogeneous. The dispersive surface energy for the four silk samples changes as a function of surface coverage (up to 20% of surface coverage). The A. pernyi and the A. assamensis silk fibers have higher γ^D_s than the other two types. The A. assamensis silk fibers, in particular, also possess wider γ^D_s distribution, ranging from 41 to 47 mJ m⁻² compared to the B. mori (40–44 mJ m⁻²), S. cynthia (38-41 mJ m⁻²) and A. pernyi silk fibers (42–46 mJ m⁻²). Similar dispersive surface energy values for jute, silk floss, coir and sisal (41.9, 39.5, 39.1 and 38.4 mJ m⁻², respectively) have been reported.³² The higher γ^D_s of the A. pernyi and the A. assamensis silk fibers may be indicative of different surface groups with higher γ^D_s. The wider γ^D_s variation of the A. assamensis silk fibers indicates their surfaces contain more different levels of energetic sites.³³ The higher γ^D_s can also be an indication of more hydrophobic active sites. On the other hand, the polar surface energy profiles in Fig. 8 show energetically heterogeneous nature for all types of silks. In particular, the distribution of polar surface energy of the B. mori silk fibers varies from 3.5 to 7.5 mJ m⁻², which is higher than other types. This may be due to the presence of more polar surface groups on the B. mori silks. However, all silk fibers were degummed by using the soap-soda method. During the degumming process, sericin is hydrolyzed and solubilized and at least one type of non-covalent interaction such as hydrogen bonds was weakened. Therefore the polar surface energy would be affected by degumming as the result that the acid–base component of the total surface energy arises from Lewis acid–base interactions and hydrogen bonds.

Fig. 8 Polar surface energy (γ^AB_s), Gutmann acid (K_a) and base (K_b) number ratios for the degummed B. mori, S. cynthia, A. assamensis and A. pernyi silk fibers.

The surface chemistry of the samples was assessed using the Gutmann acid (K_a) and base (K_b) numbers, determined based on the Gutmann approach. Values of the samples were calculated using the Gibbs free energy values of polar probes at that particular surface coverage. It is clearly seen from Fig. 8 that the base numbers (K_b) are consistently higher than the acid numbers (K_a) (K_a/K_b < 1), indicating that the surfaces are generally more basic in nature,³⁴ which may be attributed to higher concentration of electron-donating surface functional groups. Fig. 8 shows that the acid–base ratios are higher for the B. mori and the A. assamensis silks which indicates that these silk samples possess marginally higher concentrations of electron-accepting surface functional groups. The work by Fowkes^35,36 has indicated that the acid–base interactions, in which one phase acts as an electron donor (base) and the other acts as an electron acceptor (acid), play a significant role in interfacial adhesion. As a result, surface modification of the fibers and/or the matrix of composites must be performed to modify the acid–base interactions at the matrix–fiber interface in order to improve the mechanical performance of the composites constituted by these fibers.

4. Conclusions

Four types of silk cocoons including the domesticated (B. mori and S. cynthia), semi-domesticated (A. assamensis) and wild type (A. pernyi) were investigated in this work. Among all cocoon types, the A. pernyi cocoon wall exhibited the highest Young's modulus, breaking stress and breaking strain, which also resulted in 5 to 11 time's larger absorbed energy during the loading process over other cocoon types. After tensile failure, among all the cocoon walls, only the A. pernyi showed a failed planar structure, all the other types turned completely fibrous due to the less strong bond in the 3D cocoon fibrous assembly. The morphology of the cocoon structures reveals that the A. pernyi cocoons have near-rectangular silk fibers packed in parallel to the surface and form a compact brick-like fiber assembly. However, the B. mori and the S. cynthia cocoons have much more porous structure with silk fibers having either near-triangular-shaped cross-section or irregular fiber profiles. The higher mechanical properties from the wild A. pernyi cocoon are not only affected by the fibroin and sericin properties, but also dependent on the interfacial adhesion between the fibroin and sericin. The fibroin surface roughness is higher for the S. cynthia (7.29 nm) and the A. pernyi (6.76 nm) cocoon types. The combination of excellent mechanical and more heterogeneous surface properties of the wild A. pernyi silk fibroin may pave the way for its broader use for biomedical applications. The surface energetics of materials are known to have important implications in processes involving interfacial interactions, as in wetting, coating, cohesion/adhesion etc. All silk fibroin samples are energetically heterogeneous, i.e. the surface energy changes as a function of surface coverage. The A. pernyi fibroin has higher dispersive surface energy and the A. assamensis fibroin has wider dispersive energy variation, suggesting their surfaces contain more different levels of energetic sites. The Gutmann acid–base values indicate that the silk fibroin surfaces are generally more basic in nature, which may be attributed to higher concentration of electron-donating surface functional groups.

Acknowledgements

The authors would like to acknowledge the funding support from the Australian Research Council (ARC) through a Discovery project DP 120100139. Dr Anett Kondor's assistance for the IGC data analysis is highly appreciated.

Notes and references

1. F. G. Omenetto and D. L. Kaplan, Science, 2010, 329, 528–531.
2. H. P. Zhao, X. Q. Feng, W. Z. Cui and F. Z. Zou, Eng. Fract. Mech., 2007, 74, 1953–1962.
3. C. Vepari and D. L. Kaplan, Prog. Polym. Sci., 2007, 32, 991–1007.
4. Q. Fang, D. Chen, Z. Yang and M. Li, Mater. Sci. Eng., C, 2009, 29, 1527–1534.
5. N. Du, Z. Yang, X. Y. Liu, Y. Li and H. Y. Xu, Adv. Funct. Mater., 2011, 21, 772–778.
6. N. Du, X. Y. Liu, J. Narayanan, L. Li, M. L. M. Lim and D. Li, Biophys. J., 2006, 91, 4528–4535.
7. Y. Liu, Z. Shao and F. Vollrath, Nat. Mater., 2005, 4, 901–905.
8. J. Zhang, R. Rajkhowa, J. Li, X. Y. Liu and X. Wang, Mater. Des., 2013, 49, 842–849.
9. F. Chen, D. Porter and F. Vollrath, Mater. Sci. Eng., C, 2012, 32, 772–778.
10. C. Fu, D. Porter, X. Chen, F. Vollrath and Z. Shao, Adv. Funct. Mater., 2011, 21, 729–737.
11. L. P. Lounibos, Anim. Behav., 1975, 23, 843–853.
12. T. Kaise, M. Miura, H. Morikawa and W. Iwasa, J. Insect Biotechnol. Sericol., 2003, 72, 171–175.
13. A. Kafi, M. Huson, C. Creighton, J. Khoo, L. Mazzola, T. Gengenbach, F. Jones and B. Fox, Compos. Sci. Technol., 2014, 94, 89–95.
14. J. Zhang, J. Kaur, R. Rajkhowa, J. Li, X. Liu and X. Wang, Mater. Sci. Eng., C, 2013, 33, 3206–3213.
15. J. Zhang, J. Kaur, R. Rajkhowa, J. Li, X. Liu and X. Wang, presented in part at the 8th International Conference on Structure Integrity and Fracture, Melbourne, 2013.
16. Y. Q. Zhao, H. Y. Cheung, K. T. Lau, C. L. Xu, D. D. Zhao and H. L. Li, Polym. Degrad. Stab., 2010, 95, 1978–1987.
17. H. Y. Cheung, K.-T. Lau, Y. F. Pow, Y. Q. Zhao and D. Hui, Composites, Part B, 2010, 41, 223–228.
18. B. Bax and J. Müssig, Compos. Sci. Technol., 2008, 68, 1601–1607.
19. D. Plackett, T. Løgstrup Andersen, W. Batsberg Pedersen and L. Nielsen, Compos. Sci. Technol., 2003, 63, 1287–1296.
20. M. D. Jones, P. Young and D. Traini, Adv. Drug Delivery Rev., 2012, 64, 285–293.
21. F. Thielmann, J. Chromatogr. A, 2004, 1037, 115–123.
22. G. M. Dorris and D. G. Gray, J. Colloid Interface Sci., 1980, 77, 353–362.
23. J. B. Donnet, S. J. Park and H. Balard, Chromatographia, 1991, 31, 434–440.
24. V. Gutmann, The donor–acceptor approach to molecular interactions, Plenum Press, New York, 1978.
25. F. Chen, D. Porter and F. Vollrath, Acta Biomater., 2012, 8, 2620–2627.
26. P. Poza, J. Pérez-Rigueiro, M. Elices and J. Llorca, Eng. Fract. Mech., 2002, 69, 1035–1048.
27. G. Nadiger and V. Halliyal, Colourage, 1984, 31, 23–32.
28. X. Hu, S. H. Park, E. S. Gil, X. X. Xia, A. S. Weiss and D. L. Kaplan, Biomaterials, 2011, 32, 8979–8989.
29. Y. Wang, H. J. Kim, G. Vunjak-Novakovic and D. L. Kaplan, Biomaterials, 2006, 27, 6064–6082.
30. N. Cordeiro, C. Gouveia, A. G. O. Moraes and S. C. Amico, Carbohydr. Polym., 2011, 84, 110–117.
31. F. M. Fowkes, Ind. Eng. Chem., 1964, 56, 40–52.
32. R. H. Mills, D. J. Gardner and R. Wimmer, J. Appl. Polym. Sci., 2008, 110, 3880–3888.
33. P. P. Ylä-Mäihäniemi, J. Y. Y. Heng, F. Thielmann and D. R. Williams, Langmuir, 2008, 24, 9551–9557.
34. J. Y. Y. Heng, D. F. Pearse, F. Thielmann, T. Lampke and A. Bismarck, Compos. Interfaces, 2007, 14, 581–604.
35. F. M. Fowkes, Rubber Chem. Technol., 1984, 57, 328–343.
36. F. M. Fowkes and M. A. Mostafa, Ind. Eng. Chem. Prod. Res. Dev., 1978, 17, 3–7.

---