Molecular spin qubits based on lanthanide ions encapsulated in cubic polyoxopalladates: design criteria to enhance quantum coherence†
José J.
Baldoví
ab,
Lorena E.
Rosaleny
a,
Vasanth
Ramachandran
c,
Jonathan
Christian
c,
Naresh S.
Dalal
c,
Juan M.
Clemente-Juan
a,
Peng
Yang
d,
Ulrich
Kortz
d,
Alejandro
Gaita-Ariño
*a and
Eugenio
Coronado
*a
aInstituto de Ciencia Molecular (ICMol), Universidad de Valencia, C/Catedrático José Beltrán 2, E-46980 Paterna, Spain. E-mail: alejandro.gaita@uv.es; eugenio.coronado@uv.es
bInstitut de Chimie Moléculaire et des Matériaux d'Orsay, CNRS, Université de Paris Sud 11, 91405 Orsay Cedex, France
cDepartment of Chemistry and Biochemistry, Florida State University, 32306 Tallahassee, FL, USA
dDepartment of Life Sciences and Chemistry, Jacobs University, P.O. Box 750 561, 28725 Bremen, Germany
First published on 7th September 2015
Abstract
The family of cubic polyoxopalladates encapsulating lanthanide ions [LnPd12(AsPh)8O32]5− where Ln = Tb, Dy, Ho, Er and Tm, is magnetically characterised and theoretically described by the Radial Effective Charge (REC) model and a phenomenological crystal-field approach using the full-hamiltonian, in the SIMPRE and CONDON packages respectively. The lack of anisotropy generates an extraordinarily rich energy level structure at low temperatures, which allows us to study how such a structure is affected by lifting the strict cubic symmetry and/or by applying an external magnetic field. In particular, we will explore the possibility of using these cubic Ln complexes as spin-qubits. We will focus on the Ho derivative. We find that it is possible to reach a regime where decoherence caused by the nuclear spin bath is quenched for moderate axial compression of the cube and small magnetic fields.
Introduction
The manipulation of quantum bits (or qubits) plays a key role in the next generation of quantum technologies, including the design of quantum-computing devices.1 There are many candidates for qubits, including superconducting circuits,2 quantum optical cavities,3 ultracold atoms4 and spin qubits.5,6 When dealing with spin qubits, molecules are the candidates of choice since many magnetic molecules possess a ground spin doublet which can be described in terms of a two-level quantum system.7 In this context, molecular magnetism provides an excellent basis for the design, preparation and modelling of molecular spin qubits.8–18 Still, the presence of a two-level quantum system is the minimum ingredient to have a qubit. The other two ingredients that make this quantum system really useful is the possibility to organize it and to make it “coherent” in order to have time to manipulate the spin before it looses its quantum information. Molecular systems are especially attractive for qubit organisation,19–24 but, on the downside, they often exhibit low quantum coherence. This phenomenon is produced by the uncontrolled interactions of the spin qubit with the spins of the environment and with the phonons. Thus, the three main sources of decoherence are the interactions with: (i) the nuclear spin bath (hyperfine interactions), (ii) the neighbouring electronic spins (dipolar interactions) and (iii) the phonon bath.25 Both hyperfine and dipolar interactions may, in principle, be controlled by a careful design of the molecular spin qubit.26 This requires the control of both its chemical composition and its electronic structure. In practice, it often means the control of the coordination environment around the metal ion embodying the spin qubit.In this context, mononuclear lanthanide complexes based on polyoxometalates (POMs) have shown some advantageous chemical, structural and electronic features that make them suitable for the goal of enhancing quantum coherence,27 including:
(i) They are robust magnetic molecules that keep their integrity in solid state, in solution, and also often on surfaces, thus being suitable for demanding physical experiments.
(ii) They can be functionalized to facilitate their processing.28,29
(iii) They can accommodate lanthanide ions at specific sites of the rigid POM structure, leading to mononuclear lanthanide complexes with specific topologies and high symmetry environments. This has already led to the design and characterization of single-molecule magnets (SMMs) and molecular spin qubits.30,31
(iv) In these complexes, diluted magnetic samples can be easily obtained from non-magnetic Yttrium samples doped with magnetic lanthanides; such a dilution allows to minimize the decoherence coming from dipolar interactions.32
(v) Nuclear spin-free samples can also be prepared, thus removing decoherence coming from hyperfine interactions.
In this work, we will focus on the family of cubic polyoxopalladates33,34 encapsulating lanthanide ions [LnPd12(AsPh)8O32]5− (in short: LnPd12) where Ln = Tb (1), Dy (2), Ho (3), Er (4) and Tm (5) (see Fig. 1).35,36 In a first step, we will model the magnetic properties of the five derivatives using the Radial Effective Charge (REC) model37 and a phenomenological crystal-field approach using the full hamiltonian38 in the CONDON package.39 Secondly, we will explore the consequences of reducing the symmetry around the lanthanide, or applying a magnetic field in a non-Kramers magnetic ion, such as Ho3+, on the quantum coherence of the molecular spin qubit. This systematic study will provide a quantitative and inexpensive estimate of decoherence times in this family of cubic polyoxopalladates.
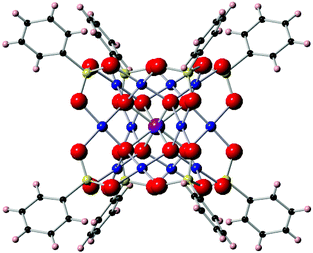 | ||
| Fig. 1 Ball and stick representation of LnPd12. Color code: Ln (violet), O (red), Pd (blue), C (black), As (yellow) and H (pink). | ||
Results and discussion
Magnetic characterization
Magnetic measurements on polycrystalline powder samples were carried out using a Quantum Design SQUID Magnetic Property Measurement System. The dc magnetic susceptibility was measured by varying the temperature from 2 K to 300 K under a constant magnetic field. Field dependent magnetization was measured at a constant temperature (T = 5 K) by varying the magnetic field from 0 T to 5 T. A gelatine capsule inserted in a plastic straw was used as sample holder. The measured susceptibility data were corrected for contributions from the sample holder and sample diamagnetism using Klemm constants.40Modelling the magnetic states of the family LnPd12
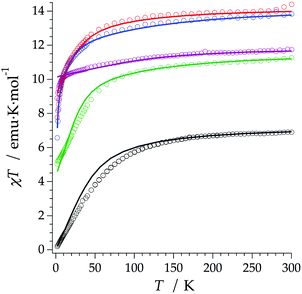
In this structure the lanthanoid (Ln) ion is encapsulated by the POM skeleton. The environment around the Ln exhibits a strict cubic Oh symmetry.35 The eight oxygen atoms are chemically equivalent, all coordinated to the Ln and three Pd(II) atoms. The magnetic susceptibility data of 1–4 from 2 to 300 K have been simultaneously fit using two parameters34 in the SIMPRE computational package.41 A satisfactory fitting of the χT product is obtained when Dr = 0.8 Å and Zi = 0.197 with a relative error of E = 3.02 × 10−3 (see Fig. 2). Both REC parameters, although similar to the ones obtained for the LnW10 and LnW22 families (Dr = 0.895 Å and Zi = 0.105),15 show small differences that can be attributed to the different electronegativity of the neighbour atoms: tungsten (2.36) and palladium (2.20), affecting slightly the lanthanide–oxygen bond in a different manner.42 The high symmetry of the compounds also provides only two non-vanishing crystal field parameters (CFPs) B40 and B60. Thus, we were also able to perform an individual fit of the two non-vanishing CFPs for each derivative using the full hamiltonian in the CONDON package using the CFPs calculated by SIMPRE as initial values. The CFPs and the energy level schemes calculated by the REC collective fit, the REC parameters in the full hamiltonian and the individual fit with CONDON are reported as ESI (see Tables SI1–SI6†). Those tables are also accompanied by the magnetic susceptibility (Fig. SI1–SI5†) and the magnetization curves (see Fig. SI6–SI10†). As the agreement with CONDON is almost perfect for the Ho derivative (considering only the five lowest energy levels, as can be seen in Table SI3†), we choose this system to perform in silico experiments using SIMPRE. This package, based on charge distributions, allows us to carry out a full set of inexpensive calculations with the aim of correlating the distortion of the cubic site and the influence of a magnetic field with the energy spectra.Enhancing quantum coherence in HoPd12
We theoretically studied the performance of complex 3 as a qubit. In particular, in this work we applied a recently developed extension to SIMPRE that calculates the hyperfine coupling to the nuclear spin bath and estimates decoherence time from this source (for details, see ESI†).22 Note that this approximation neglects other decoherence sources; therefore, it only provides an upper bound for the decoherence time. Nevertheless, it is a useful tool to provide a starting point towards an inexpensive theoretical quantification of decoherence for molecular spin qubits based on lanthanoids, and to advance beyond the stage of a qualitative characterization.Decoherence due to the coupling to the nuclear spin bath is unusually weak in POMs, compared with complexes with organic ligands. This is an expected result, in view of the low abundance of protons in the vicinity of the lanthanoid ion. Our calculations in this particular example have served to perform an analysis of the adequacy as molecular spin qubits of cubic or near-cubic systems such as 3. The most extraordinary feature in such highly symmetric systems is the abundance of degenerate or near-degenerate levels at low energies (see Tables SI1–SI3†). For example, in the case of the Ho derivative, there are 5 electron spin energy levels at energies within the range of conventional pulsed EPR.
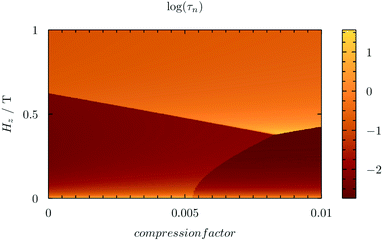
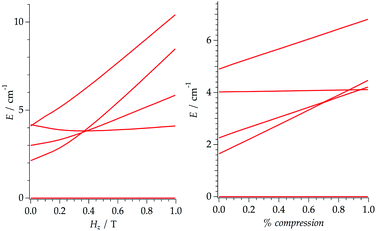
We have considered the possibility of distorting the cubic site by introducing a moderate axial compression of up to 1% (Δz/z, where the field is also applied as Hz). Of course, this physical effect can also be achieved, albeit less systematically, in a chemical way, by using ligands which generate a nearly cubic environment. In the Ho case we have calculated how different degrees of symmetry breaking (in our case, different axial compression ratios from 0 to 1%) and different applied fields (up to 1 T) alter decoherence times, τn. We performed 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 calculations for 200 compression factors and 400 applied magnetic fields. We found that the crossings of three levels create a “phase diagram” with three different zones (Fig. 3) that are distinguished by the character of the wave function of the first excited state. Fig. 4 depicts the triple crossing keeping constant either the compression (left) or the magnetic field (right).
000 calculations for 200 compression factors and 400 applied magnetic fields. We found that the crossings of three levels create a “phase diagram” with three different zones (Fig. 3) that are distinguished by the character of the wave function of the first excited state. Fig. 4 depicts the triple crossing keeping constant either the compression (left) or the magnetic field (right).
The different phases also have fairly different decoherence times, ranging from tens or hundreds of milliseconds up to 10 seconds, and thus, for clarity, we represent the logarithm of τn. These estimates need to be taken with caution. It is known that relatively long decoherence times can be obtained in cases such as the Cu(cmt)2 complex,43 or HoW10,30 where like in the present case nuclear spins are absent from the vicinity of the metal. Even in these complexes, actual experimental decoherence times are considerably shorter than the present nuclear-spin-only estimates: 68 μs (Cu(cmt)2) and 8 μs (HoW10).
The most significant finding is that in a fairly ample region (at fields between 0.4 and 0.5 T and at compressions from 0.5% to 1%) decoherence times that are at least two orders of magnitude above those calculated for lower fields or lower compressions are predicted. In this region the expectation value <Jz> for the first excited state is almost identical to that of the ground state. For example, for a compression of 0.85% and an applied field of 0.39 T the wave functions of the ground and first excited states are mainly composed by, respectively, the following MJ components: |ψ0> = 20%| − 8> + 70%| − 4> + 7.5%| + 4> + 2%| + 8>; |ψ1> = 32%| − 7> + 62%| − 3> + 4%| + 5> and they result in expectation values <Jz0> = −3.93 and <Jz1> = −3.86. In this particular case, another favourable circumstance is the fact that the transitions between |ψ0> and |ψ1> are allowed by EPR, as the two states are dominated by terms that differ in MJ = 1. As the two states of the qubit, |ψ0> and |ψ1> generate magnetic fields that are also almost identical, the nuclear spins around them, while affected magnetically by the presence of the Ho ion, will not be able to detect the state of the qubit. The wave function composition and Jz expectation values, of the ground and first excited states, and τn, for a compression of 0.85% and an applied field of 0.35 T, as well as for a compression of 0.78% and a magnetic field of 0.39 T, are reported in the ESI.† The key point is that, while the ground state is only slightly and continuously affected by a moderate change in the distortion or the magnetic field, the level crossings means that the first excited level has a completely different character at each of the three zones in the “phase diagram”.
This extremely unusual situation can provide an alternative strategy to the usual approach based on the use of magnetic molecules having a “large tunnelling gap”. For non-Kramers ions, large tunneling gaps mean an intense mixing of pseudo-classical “up” and “down” states. As a result, magnetic interactions are minimized, and both decoherence caused by the spin bath and decoherence caused by magnons are quenched. Unfortunately, at the same time rising tunneling gaps increase decoherence caused by phonons.44 Moreover, as transition energy has to be matched eventually by a microwave pulse in an EPR experiment, large tunneling gaps may be impractical in some cases. By using the condition <Jz0> ≈ <Jz1>, as in the present case, decoupling from magnetic interactions can be achieved without these detrimental side effects. Note that both achieve the same goal: when the nuclear spins are not coupled to the qubit state, they effectively disappear and cannot introduce any decoherence. Moreover, the same argument is valid for decoherence caused by neighbouring qubits: if the state of the qubit affects its <Jz> expectation value only marginally, decoherence caused by magnons vanishes. Thus, to operate the system, a third energy level would need to be used each time that the algorithm temporally requires a restoration of this interaction.
Note, however, that this extraordinary performance may come at a cost. Since the situation analysed above is close to two level crossings, there are two energy levels in the immediate vicinity. That means that small inaccuracies in the EPR pulses would result in transitions that would take the system out of the qubit space. One should also take into account that different decoherence sources are essentially additive, so that reducing the spin–spin interactions below certain level just means that most decoherence comes from interaction with phonons. Fortunately, POMs are also ideal systems in that regard, because of their rigidity.
Conclusions
We have performed an experimental and theoretical study of the LnPd12 family of polyoxopalladates, in which the lanthanoid ion presents a cubic coordination environment. The lack of anisotropy, which makes these systems unsuitable as SMMs, generates an extraordinarily rich energy level structure at low temperatures. We study the possibilities offered by these molecules when lifting the strict cubic symmetry and/or when applying an external magnetic field. While we simulate the distortion of the cube by introducing a physical compression, the same effect can be achieved chemically, by crystalline pressure or asymmetric substitution. We use a recently developed method to inexpensively estimate decoherence times from the coupling of the electronic spin with the nuclear spins, which is included in the SIMPRE program. In the non-Kramers Ho complex we find that, for moderate axial compression and in presence of small magnetic fields, it is possible to reach a regime where decoherence caused by the nuclear spin bath is quenched. This is achieved in the ground doublet when the two qubit states have virtually identical spin expectation values. In this regime the qubit states are invisible to the spin bath, and vice versa. This strategy is a generalisation of the well-known approach based on the presence of large tunnelling splittings. The strategy is quite general and can be applied to systems with a high degeneracy of levels near the ground state. Although a complete estimation of decoherence time requires taking into account all the possible sources of decoherence, this result should stimulate chemical and physical work on the design and study of nearly-cubic lanthanide complexes.Acknowledgements
The present work has been funded by the EU (ERC Advanced Grant SPINMOL and ERC Consolidator Grant DECRESIM), the Spanish MINECO (grant MAT2014-56143-R, CTQ2014-52758-P), and the Generalitat Valenciana (Prometeo and ISIC Programmes of excellence). A.G.-A. acknowledges funding by the MINECO (Ramón y Cajal contract). E.C. and J.J.B. acknowledge the Blaise Pascal International Chair for financial support. J.J.B. also thanks the Spanish MECD for an FPU predoctoral grant. U.K. thanks the German Science Foundation (DFG KO-2288/20-1 and KO-2288/8-1) and Jacobs University for research support, and also acknowledges the COST Actions CM1006 (EUFEN) and CM1203 (PoCheMoN). P.Y. thanks the CSC (China Scholarship Council) for a doctoral fellowship.Notes and references
- D. D'Alessandro and M. Dahleh, IEEE Trans. Autom. Control, 2001, 46, 866–876 CrossRef.
- M. H. Devoret and R. J. Schoelkopf, Science, 2013, 339, 1169–1174 CrossRef CAS PubMed.
- L. Duan, Nature, 2014, 508, 195–196 CrossRef CAS PubMed.
- C. Weitenberg, M. Endres, J. F. Sherson, M. Cheneau, P. Schauß, T. Fukuhara, I. Bloch and S. Kuhr, Nature, 2011, 471, 319–324 CrossRef CAS PubMed.
- J. J. Pla, K. Y. Tan, J. P. Dehollain, W. H. Lim, J. J. L. Morton, D. N. Jamieson, A. S. Dzurak and A. Morello, Nature, 2012, 489, 541–545 CrossRef CAS PubMed.
- D. Kaminski, A. L. Webber, C. J. Wedge, J. Liu, G. A. Timco, I. J. Vitorica-Yrezabal, E. J. L. McInnes, R. E. P. Winpenny and A. Ardavan, Phys. Rev. B: Condens. Matter, 2014, 90, 184419 CrossRef.
- J. Tejada, E. M. Chudnovsky, E. Del Barco, J. M. Hernández and T. P. Spiller, Nanotechnology, 2001, 12, 181–186 CrossRef CAS.
- S. Bertaina, S. Gambarelli, T. Mitra, B. Tsukerblat, A. Müller and B. Barbara, Nature, 2008, 453, 203–206 CrossRef CAS PubMed.
- S. Hill, R. S. Edwards, N. Aliaga-Alcalde and G. Christou, Science, 2003, 302(5647), 1015–1018 CrossRef CAS PubMed.
- V. Cerletti, W. A. Coish, O. Gywat and D. Loss, Nanotechnology, 2005, 16(4), R27 CrossRef CAS.
- A. Ardavan, O. Rival, J. J. L. Morton, S. J. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2007, 98, 057201 CrossRef.
- S. Bertaina, J. H. Shim, S. Gambarelli, B. Z. Malkin and B. Barbara, Phys. Rev. Lett., 2009, 103, 226402 CrossRef CAS ; Erratum Phys. Rev. Lett., 2014, 113, 109902.
- F. Meier, J. Levy and D. Loss, Phys. Rev. Lett., 2003, 90, 047901 CrossRef.
- J. J. Baldoví, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, Inorg. Chem., 2012, 51(22), 12565–12574 CrossRef PubMed.
- J. J. Baldoví, J. M. Clemente-Juan, E. Coronado, Y. Duan, A. Gaita-Ariño and C. Giménez-Saiz, Inorg. Chem., 2014, 53(18), 9976–9980 CrossRef PubMed.
- E. Abe, H. Wu, A. Ardavan and J. J. L. Morton, Appl. Phys. Lett., 2011, 98, 251108 CrossRef PubMed.
- S. Nakazawa, S. Nishida, T. Ise, T. Yoshino, N. Mori, R. D. Rahimi, K. Sato, Y. Morita, K. Toyota, D. Shiomi, M. Kitagawa, H. Hara, P. Carl, P. Höfer and T. Takui, Angew. Chem., Int. Ed., 2012, 124, 9998–10002 CrossRef PubMed.
- G. A. Timco, S. Carretta, F. Troiani, F. Tuna, R. J. Pritchard, C. A. Muryn, E. J. McInnes, A. Ghirri, A. Candini, P. Santini, G. Amoretti, M. Affronte and R. E. P. Winpenny, Nat. Nanotechnol., 2009, 4, 173–178 CrossRef CAS PubMed.
- D. Avisar and D. J. Tannor, Phys. Chem. Chem. Phys., 2015, 17, 2742–2749 RSC.
- J. Lehmann, A. Gaita-Ariño, E. Coronado and D. Loss, Nat. Nanotechnol., 2007, 2, 312–317 CrossRef CAS PubMed.
- J. J. Baldoví, E. Coronado, A. Gaita-Ariño, C. Gamer, M. Giménez-Marqués and G. Mínguez Espallargas, Chem. – Eur. J., 2014, 20, 10695–10702 CrossRef PubMed.
- L. E. Rosaleny and A. Gaita-Ariño, submitted.
- D. Aguilà, L. A. Barrios, F. Luis, A. Repollés, O. Roubeau, S. J. Teat and G. Aromí, Inorg. Chem., 2010, 49(15), 6784–6786 CrossRef PubMed.
- G. Aromí, D. Aguilà, P. Gamez, F. Luis and O. Roubeau, J. Am. Chem. Soc., 2014, 136, 14215–14222 CrossRef PubMed.
- S. Takahashi, I. S. Tupitsyn, J. van Tol, C. C. Beedle, D. N. Hendrickson and P. C. E. Stamp, Nature, 2011, 476, 76–79 CrossRef CAS PubMed.
- P. C. E. Stamp and A. Gaita-Ariño, J. Mater. Chem., 2009, 19(12), 1718–1730 RSC.
- J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Chem. Soc. Rev., 2012, 41(22), 7464–7478 RSC.
- A. Proust, R. Thouvenot and P. Gouzerh, Chem. Commun., 2008, 1837–1852 RSC.
- A. Proust, B. Matt, R. Villanneau, G. Guillemot, P. Gouzerh and G. Izzet, Chem. Soc. Rev., 2012, 41, 7605–7622 RSC.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, submitted.
- J. J. Baldoví, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and H. Prima-García, Chem. Commun., 2013, 49(79), 8922–8924 RSC.
- F. Luis, M. J. Martínez-Pérez, O. Montero, E. Coronado, S. Cardona-Serra, C. Martí-Gastaldo, J. M. Clemente-Juan, J. Sesé, D. Drung and T. Schurig, Phys. Rev. B: Condens. Matter, 2010, 82, 060403 CrossRef.
- E. V. Chubarova, M. H. Dickman, B. Keita, L. Nadjo, F. Miserque, M. Mifsud, I. W. C. E. Arends and U. Kortz, Angew. Chem., Int. Ed., 2008, 47, 9542–9546 CrossRef CAS PubMed.
- N. V. Izarova, M. T. Pope and U. Kortz, Angew. Chem., Int. Ed., 2012, 51, 9492–9510 CrossRef CAS PubMed.
- M. Barsukova, N. V. Izarova, R. N. Biboum, B. Keita, L. Nadjo, V. Ramachandran, N. S. Dalal, N. S. Antonova, J. J. Carbó, J. M. Poblet and U. Kortz, Chem. – Eur. J., 2010, 16, 9076–9085 CrossRef CAS PubMed.
- P. Yang, Y. Xiang, Z. Lin, B. S. Bassil, J. Cao, L. Fan, Y. Fan, M. Li, P. Jiménez-Lozano, J. J. Carbó, J. M. Poblet and U. Kortz, Angew. Chem., Int. Ed., 2014, 53, 11974–11978 CrossRef CAS PubMed.
- J. J. Baldoví, J. J. Borrás-Almenar, J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Dalton Trans., 2012, 41(44), 13705–13710 RSC.
- J. van Leusen, M. Speldrich, H. Schilder and P. Kögerler, Coord. Chem. Rev., 2015, 289–290, 137–148 CrossRef CAS PubMed.
- M. Speldrich, H. Schilder, H. Lueken and P. Kögerler, Isr. J. Chem., 2011, 51, 215–227 CrossRef CAS PubMed.
- S. G. Vulfson, Molecular Magnetochemistry, Gordon and Breach Science, Newark, NJ, 1998 Search PubMed.
- (a) J. J. Baldoví, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, J. Comput. Chem., 2013, 34, 1961–1967 CrossRef PubMed; (b) J. J. Baldoví, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, J. Comput. Chem., 2014, 35, 1930–1934 CrossRef PubMed.
- J. J. Baldoví, A. Gaita-Ariño and E. Coronado, Dalton Trans., 2015, 44, 12535–12538 RSC.
- K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2015, 5, 5304 CrossRef PubMed.
- S. Takahashi, I. S. Tupitsyn, J. van Tol, C. C. Beedle, D. N. Hendrickson and P. C. E. Stamp, Nature, 2011, 476, 76–79 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5qi00142k |
| This journal is © the Partner Organisations 2015 |