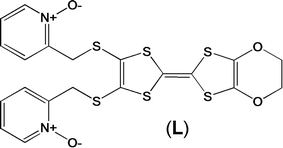
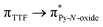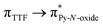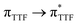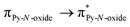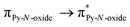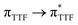Magnetic and photo-physical investigations into DyIII and YbIII complexes involving tetrathiafulvalene ligand†
K.
Soussi
a,
J.
Jung
a,
F.
Pointillart
*a,
B.
Le Guennic
a,
B.
Lefeuvre
a,
S.
Golhen
a,
O.
Cador
a,
Y.
Guyot
b,
O.
Maury
c and
L.
Ouahab
a
aInstitut des Sciences Chimiques de Rennes UMR 6226 CNRS-UR1, Université de Rennes 1, 35042 Rennes Cedex, France. E-mail: fabrice.pointillart@univ-rennes1.fr
bUniversité Claude Bernard Lyon 1, Institut Lumière Matière, UMR 5306 CNRS-Université Lyon 1, 10 rue Ada Byron, 69622 Villeurbanne Cedex, France
cLaboratoire de Chimie de l'ENS-LYON-UMR 5182, 46 Allée d'Italie, 69364 Lyon Cedex 07, France
First published on 26th October 2015
Abstract
Three lanthanide-based complexes involving a tetrathiafulvalene derivative (L) in which the lanthanide ion has a pseudo-D4d symmetry have been reported. One is a dinuclear compound of formula [Dy(hfac)3(L)]2 (1) while the two others are isostructural and described as mononuclear complexes of formulae [Ln(tta)3(L)]·xCH2Cl2 (LnIII = Dy and x = 1.41 (2); Yb and x = 2 (3)). The nuclearity of the species is driven by the nature of the ancillary ligands. Magnetic properties revealed that 1 and 3 behave as single molecule magnets, while 2 does not. The crystal field splitting of the ground multiplet state has been theoretically determined as well as the orientation of the easy axis of the ground MJ state. The results of ab initio calculations are in agreement with the experimental determinations of the anisotropy axis. Irradiation of the lowest-energy charge transfer bands of 3 led to an intense and resolved Yb-centred emission which can be correlated to the magnetic data. Thus 3 can be described as a redox-active luminescent field-induced single-molecule magnet.
Introduction
Single Molecule Magnets (SMMs) are fascinating objects which take a preponderant place in both the chemist and physicist communities owing to their potential applications in quantum computing,1 high-density memory data storage devices2 and spintronics.3 One of the actual challenges is to combine, in the same molecule, the SMM property with one or more subsequent physical properties in order to obtain a multifunctional SMM, such as for instance chiral SMM,4 ferroelectric SMM5 or luminescent SMM.6In this way, the use of lanthanide ions seems to be very promising since they display specific and unique physical and photophysical properties. On one side, they possess a strong magnetic anisotropy and a high magnetic moment, making them ideal candidates for SMM,7 and on the other side they display sharp emission lines ranging from the visible to the near infrared (NIR) region arising from f–f transitions.8 In order to exploit this potential, lanthanide ions must be coordinated to organic ligands acting as sensitizing antenna in a pre-organized way, resulting in the induction of a crystal (ligand)-field that monitors both the magnetic and luminescence properties.
For several decades, tetrathiafulvalene (TTF)-based ligands have been used for their electron donating ability and so for their electronic conductivity.9 Furthermore, their ability to form S⋯S short contacts and π–π stacking makes them attractive candidates as structural agents to organize the tridimensional arrangement in crystals and control the magnetic properties (magnetic isolation, SMM behaviour). In addition, their strong electronic delocalization is responsible for their interesting optical properties and this push–pull chromophore has been demonstrated to efficiently sensitize the lanthanide luminescence by the antenna effect.10
Considerable efforts have been made to better understand and ultimately predict the magnetic behaviour of lanthanide-based complexes and hence the crystal field effects. To this end, systematic experimental studies explored the magnetic properties of the original structure with the aim of establishing efficient magneto-structural correlations.10g,11
In parallel, theoretical investigations, based on electrostatic models or high level ab initio calculations, were undertaken to estimate the lanthanide crystal field and the orientation of the magnetic axis in molecular objects.12
Recently, some of us reported dinuclear complexes of lanthanide involving the (4,5-bis(2-pyridyl-N-oxidemethylthio)-4′,5′)-ethylenedithiotetrathiafulvene (L1) or -methyldithiotetrathiafulvene (L2) ligands which displayed either SMM or luminescence behaviour but not both simultaneously.10g It was demonstrated that a minor chemical change in the nature of the TTF-based ligand induces drastic magnetic modifications since [Dy(hfac)3(L2)]2 behaves as a SMM while [Dy(hfac)3(L1)]2 does not. In the present article, we continue the step-by-step study of this ligand family and report the slightly modified 4,5-ethylenedioxy-4′,5′-bis(2-pyridyl-N-oxidemethylthio)tetrathiafulvalene (L) (Scheme 1) ligand featuring the 4,5-ethylendioxy moiety instead of 4,5-ethylenedithio and 4,5-dimethylthio moieties for L1 and L2 respectively. This minor modification allows us to optimize the magnetic properties and to combine both luminescence and SMM behaviours in a single complex.
Experimental section
General procedures and materials
The precursors Dy(hfac)3·2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 13 (hfac− = 1,1,1,5,5,5-hexafluoroacetylacetonate anion), Ln(tta)3·2H2O
13 (hfac− = 1,1,1,5,5,5-hexafluoroacetylacetonate anion), Ln(tta)3·2H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14 (Ln = DyIII and YbIII; tta− = 2-thenoyltrifluoroacetonate anion) and 4,5-ethylenedioxy-4′,5′-bis(cyanoethylthio)tetrathiafulvalene15 were synthesized following previously reported methods. All other reagents were purchased from Aldrich Co., Ltd and used without further purification.
14 (Ln = DyIII and YbIII; tta− = 2-thenoyltrifluoroacetonate anion) and 4,5-ethylenedioxy-4′,5′-bis(cyanoethylthio)tetrathiafulvalene15 were synthesized following previously reported methods. All other reagents were purchased from Aldrich Co., Ltd and used without further purification.
Synthesis of the ligand 4,5-ethylendioxy-4′,5′-bis(2-pyridyl-N-oxidemethylthio)tetrathiafulvalene (L)
In a three-necked flask under an argon atmosphere, 0.432 g (1 mmol) of 4,5-ethylenedioxy-4′,5′-bis(cyanoethylthio)tetrathiafulvalene15c was dissolved in 30 mL distilled MeOH. In the dropping funnel, 0.115 g (5 mmol) of metallic sodium was added to 10 mL distilled MeOH and then added dropwise to a solution of 4,5-ethylenedioxy-4′,5′-bis(cyanoethylthio)tetrathiafulvalene under stirring. After the addition was over, the solution was stirred at room temperature for 4 hours. Then, in the dropping funnel, 0.419 g (3.3 mmol) of 2-(chloromethyl)pyridine-1-oxide16 was dissolved in 20 mL distilled MeOH and added dropwise to the solution and left under stirring overnight. Then 30 mL distilled water was added and stirred for 30 min, followed by the addition of 250 mL CH2Cl2. The resulting solution was washed with saturated NaHCO3 and distilled water. The organic phase was dried with MgSO4 and the solvent was removed under vacuum. The resulting powder was purified on an Al2O3 column with a 99/1 ratio of CH2Cl2/MeOH as the eluent. Yield: 200 mg (37%). 1H NMR (CDCl3): δ 4.12 (s, 4H), 4.26 (s, 4H), 7.23 (m, 4H), 7.33 (m, 2H), 8.26 (m, 2H). Single crystals were obtained by slow diffusion of n-hexane in a concentrated CH2Cl2 solution of L.Synthesis of complexes 1–3
Crystallography
Single crystals of L and 1 were mounted on a Nonius four circle diffractometer equipped with a CCD camera and a graphite monochromated MoKα radiation source (λ = 0.71073 Å, T = 293(2) K) while 2 and 3 were mounted on an APEXII Bruker-AXS diffractometer (MoKα radiation source, λ = 0.71073 Å, T = 150(2) K) for data collection, from the Centre de Diffractométrie (CDIFX), Université de Rennes 1, France. Structures were solved by direct methods using the SIR-97 program and refined by a full matrix least-squares method on F2 using the SHELXL-97 program17 for all the compounds. Crystallographic data are summarized in Table 1. Complete crystal structure results as a CIF file including bond lengths, angles, and atomic coordinates are provided in the ESI.†| Compounds | (L) | [Dy(hfac)3(L)]2 (1) |
| Formula | C20H16N2O5S6 | C70H38Dy2F36N4O20S12 |
| M/g mol−1 | 556.7 | 2705.8 |
| Crystal system | Monoclinic | Triclinic |
| Space group | P21/a (no. 14) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (no. 2) (no. 2) |
| Cell parameters | a = 13.2244(3) Å | a = 12.4879(3) Å |
| b = 12.1843(4) Å | b = 13.3816(4) Å | |
| c = 15.3079(4) Å | c = 15.6598(6) Å | |
| β = 107.908(2)° | α = 100.987(2)° | |
| β = 90.592(2)° | ||
| γ = 107.459(2)° | ||
| Volume/Å3 | 2347.06(11) | 2444.19(13) |
| Cell formula units | 4 | 2 |
| T/K | 293(2) | 293(2) |
| Diffraction reflection | 5.92 ≤ 2θ ≤ 54.20 | 2.66 ≤ 2θ ≤ 54.18 |
| ρ calc/g cm−3 | 1.575 | 1.799 |
| μ/mm−1 | 0.619 | 1.912 |
| Number of reflections | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 589 589 |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 277 277 |
| Independent reflections | 5151 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 729 729 |
| F o 2 > 2σ(Fo)2 | 3539 | 7750 |
| Number of variables | 298 | 689 |
| R int, R1, wR2 | 0.0625, 0.0509, 0.1327 | 0.0316, 0.0481, 0.1229 |
| Compounds | [Dy(tta)3(L)]·1.41CH2Cl2 (2) | [Yb(tta)3(L)]·2CH2Cl2 (3) |
| Formula | C45.41H30.54Cl2.82DyF9N2O10S9 | C46H32Cl4YbF9N2O10S9 |
| M/g mol−1 | 1486.2 | 1547.1 |
| Crystal system | Triclinic | Triclinic |
| Space group |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (no. 2) (no. 2) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (no. 2) (no. 2) |
| Cell parameters | a = 10.4634(8) Å | a = 10.4473(3) Å |
| b = 12.1092(10) Å | b = 12.0946(4) Å | |
| c = 23.9781(18) Å | c = 23.9969(7) Å | |
| α = 77.004(2)° | α = 76.5010(10)° | |
| β = 86.822(2)° | β = 86.0280(10)° | |
| γ = 74.808(2)° | γ = 74.7470(10)° | |
| Volume/Å3 | 2856.8(4) | 2844.4(15) |
| Cell formula units | 2 | 2 |
| T/K | 150(2) | 150(2) |
| Diffraction reflection | 1.74 ≤ 2θ ≤ 55.08 | 1.74 ≤ 2θ ≤ 55.00 |
| ρ calc/g cm−3 | 1.728 | 1.806 |
| μ/mm−1 | 1.853 | 2.246 |
| Number of reflections | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 912 912 |
39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 778 778 |
| Independent reflections | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 653 653 |
| F o 2 > 2σ(Fo)2 | 7773 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 826 826 |
| Number of variables | 711 | 732 |
| R int, R1, ωR2 | 0.0798, 0.0882, 0.2008 | 0.0219, 0.0387, 0.1033 |
Physical measurements
The elementary analyses of the compounds were performed at the Centre Régional de Mesures Physiques de l'Ouest, Rennes. 1H NMR spectra were recorded on a Bruker Ascend 400 spectrometer. Chemical shifts are reported in parts per million referenced to TMS for 1H NMR. Cyclic voltammetry was carried out in a CH2Cl2 solution, containing 0.1 M N(C4H9)4PF6 as the supporting electrolyte. Voltammograms were recorded at 100 mV s−1 at a platinum disk electrode. The potentials were measured versus a saturated calomel electrode (SCE) (EFc/Fc+ = 0.45 V). Absorption spectra were recorded on a Varian Cary 5000 UV-visible-NIR spectrometer equipped with an integration sphere. The luminescence spectra were recorded using a Horiba-Jobin Yvon Fluorolog-3® spectrofluorimeter equipped with a three-slit double grating excitation and emission monochromator with dispersions of 2.1 nm mm−1 (1200 grooves per mm). The steady-state luminescence was excited by unpolarized light from a 450 W xenon CW lamp and detected at an angle of 90° for diluted solution measurements or at 22.5° for solid state measurements (front face detection) by a red-sensitive Hamamatsu R928 photomultiplier tube. Spectra were reference corrected for both the excitation source light intensity variation (lamp and grating) and the emission spectral response (detector and grating). Near infrared spectra were recorded at an angle of 45° using a liquid nitrogen cooled, solid indium/gallium/arsenic detector (850–1600 nm). The dc magnetic susceptibility measurements were performed on a solid polycrystalline sample with a Quantum Design MPMS-XL SQUID magnetometer between 2 and 300 K in an applied magnetic field of 2 kOe in the 2–20 K temperature range and 10 kOe between 20 and 300 K for 3. For 1 and 2, 0.2 kOe is applied between 2 and 20 K, 2 kOe between 20 and 80 K and 10 kOe above 80 K. These measurements were all corrected for the diamagnetic contribution as calculated with Pascal's constants.Computational details
DFT geometry optimizations and TD-DFT excitation energy calculations of the ligand L were carried out using the Gaussian 09 (revision A.02) package18 employing the PBE0 hybrid functional.19 All atoms were described with the SVP basis sets.20 The first 50 monoelectronic excitations were calculated. In all steps, a modeling of bulk solvent effects (solvent = dichloromethane) was included through the Polarizable Continuum Model (PCM),21 using a linear-response non-equilibrium approach for the TD-DFT step.22 Molecular orbitals were sketched using the Gabedit graphical interface.23Wavefunction-based calculations were carried out on model structures of the LnIII-based complexes 1–3 (see below) by using the SA-CASSCF/RASSI-SO approach, as implemented in the MOLCAS quantum chemistry package (version 8.0).24 In this approach, the relativistic effects are treated in two steps on the basis of the Douglas–Kroll Hamiltonian. First, the scalar terms were included in the basis-set generation and were used to determine the spin-free wavefunctions and energies in the complete active space self-consistent field (CASSCF) method.25 Next, spin–orbit coupling was added within the restricted-active-space-state-interaction (RASSI-SO) method, which uses the spin-free wavefunctions as basis states.26 The resulting wavefunctions and energies are used to compute the magnetic properties and g-tensors of the lowest states from the energy spectrum by using the pseudo-spin S = 1/2 formalism in the SINGLE-ANISO routine.27 Cholesky decomposition of the bielectronic integrals was employed to save disk space and speed up the calculations.28 The atomic positions were extracted from the X-ray crystal structures. For the three complexes, only the modified TTF ligand L was simplified by suppressing the organic moieties beyond the central C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond. Moreover, in the case of the dimer 1, only one half of the molecule was considered. For 1 and 2, the active space of the self-consistent field (CASSCF) method consisted of nine 4f electrons of the DyIII ion spanning seven 4f orbitals, i.e. CAS(9,7)SCF. State-averaged CASSCF calculations were performed for all of the sextets (21 roots), all of the quadruplets (224 roots), and 300 out of the 490 doublets (due to software limitations) of the DyIII ion. Twenty-one sextets, 128 quadruplets, and 107 doublets were mixed through spin–orbit coupling in RASSI-SO. All atoms were described by ANO-RCC basis sets.29 The following contractions were used: [8s7p4d3f2g1h] for Dy, [4s3p2d] for the O directly coordinated to Dy, [3s2p] for other O atoms; [3s2p1d] for the N atoms; [4s3p] for the S atoms, [3s2p] for the C and F atoms and [2s] for the H atoms. A similar procedure was then applied to the YbIII complex 3. The active space consisted of 13 4f electrons in seven 4f orbitals, i.e. CAS(13,7)SCF. State-averaged CASSCF calculations were performed for the seven doublets of the YbIII ion, all of which were included in the RASSI-SO calculation. The effects of dynamical correlation were treated by means of a CASPT2 treatment on top of the spin-free wavefunctions. Similar basis set contractions were used except for Yb, which was described at the [8s7p4d3f2g] level.
C bond. Moreover, in the case of the dimer 1, only one half of the molecule was considered. For 1 and 2, the active space of the self-consistent field (CASSCF) method consisted of nine 4f electrons of the DyIII ion spanning seven 4f orbitals, i.e. CAS(9,7)SCF. State-averaged CASSCF calculations were performed for all of the sextets (21 roots), all of the quadruplets (224 roots), and 300 out of the 490 doublets (due to software limitations) of the DyIII ion. Twenty-one sextets, 128 quadruplets, and 107 doublets were mixed through spin–orbit coupling in RASSI-SO. All atoms were described by ANO-RCC basis sets.29 The following contractions were used: [8s7p4d3f2g1h] for Dy, [4s3p2d] for the O directly coordinated to Dy, [3s2p] for other O atoms; [3s2p1d] for the N atoms; [4s3p] for the S atoms, [3s2p] for the C and F atoms and [2s] for the H atoms. A similar procedure was then applied to the YbIII complex 3. The active space consisted of 13 4f electrons in seven 4f orbitals, i.e. CAS(13,7)SCF. State-averaged CASSCF calculations were performed for the seven doublets of the YbIII ion, all of which were included in the RASSI-SO calculation. The effects of dynamical correlation were treated by means of a CASPT2 treatment on top of the spin-free wavefunctions. Similar basis set contractions were used except for Yb, which was described at the [8s7p4d3f2g] level.
Results and discussion
Synthesis and crystal structures
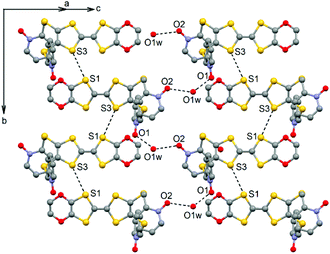
The ligand L (Scheme 1) was synthesized in order to study the influence of the ethylenedioxy (EDO) functionalization on the structural and magnetic properties. First, L was subjected to coordination with the Dy(hfac)3·2H2O precursor and the resulting dinuclear complex of formula [Dy(hfac)3(L)]2 (1) was compared to two previously published similar compounds.10c Then the hfac− ancillary ligands were substituted with the tta− ones leading surprisingly to the formation of new mononuclear complexes of formula [Ln(tta)3(L)]·xCH2Cl2 (LnIII = Dy and x = 1.41 (2); Yb and x = 2 (3)) and not to analogues of 1.L crystallized in the P21/a monoclinic space (Table 1). The asymmetric unit is composed of one molecule of L and one water molecule (Fig. 1). The central C5–C6 bond length (1.378(4) Å) confirms the neutral form of the ligand. Each 2-pyridine-N-oxide-methylthio arm is oriented to opposite sides with respect to the plane formed by the TTF core. The two N-oxide groups realize two hydrogen bonds (O1–O1w = 2.766(6) Å and O2–O1w = 2.783(6) Å) with the water molecule (Fig. 2). The L donors are stacked along the b axis with short S3⋯S1 contacts (3.577(2) Å).
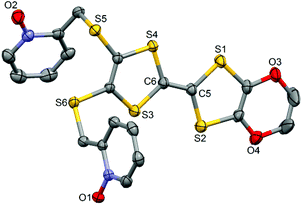 | ||
| Fig. 1 ORTEP view of the ligand L. Thermal ellipsoids are drawn at 30% probability. Hydrogen atoms are omitted for clarity. | ||
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (no. 2) triclinic space group (Table 1) and the asymmetric unit is composed of one half of the dinuclear unit (Fig. 3).
(no. 2) triclinic space group (Table 1) and the asymmetric unit is composed of one half of the dinuclear unit (Fig. 3).
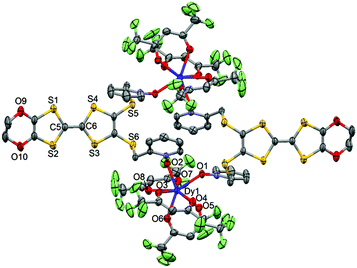 | ||
| Fig. 3 ORTEP view of the dinuclear complex [Dy(hfac)3(L)]2 (1). Thermal ellipsoids are drawn at 30% probability. Hydrogen atoms are omitted for clarity. | ||
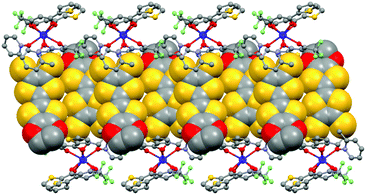
The value of the mean Dy–Ohfac distances is 2.359(4) Å (Table 2) that is comparable to what is observed in the previously reported dinuclear complexes involving the L1 and L2 ligands (2.340 Å).10g The arrangement of the ligands leads to a distorted square antiprism (D4d symmetry) coordination polyhedron around the DyIII ion. This distortion is visualized by continuous shape measures performed with SHAPE 2.1 (Table 3).30 The L donors form dimers through S3⋯S5 short contacts (3.691(3) Å) (Fig. 4). The shortest intra- and intermolecular Dy–Dy distances have been found to be equal to 9.314(5) Å and 9.039(5) Å, respectively.
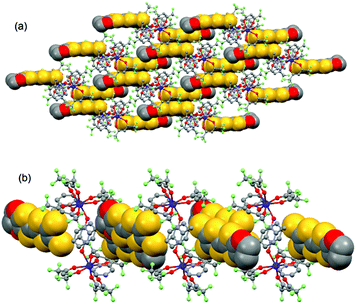 | ||
| Fig. 4 Crystal packing of 1 highlighting the intermolecular interaction between L ligands and the formation of the dimers of L. | ||
| Compounds | 1 | 2 | 3 |
|---|---|---|---|
| Ln1–O1 | 2.345(3) | 2.334(7) | 2.295(3) |
| Ln1–O2 | 2.309(4) | 2.349(7) | 2.308(3) |
| Ln1–O3 | 2.380(4) | 2.406(7) | 2.361(3) |
| Ln1–O4 | 2.402(4) | 2.376(7) | 2.326(3) |
| Ln1–O5 | 2.370(4) | 2.339(7) | 2.299(3) |
| Ln1–O6 | 2.323(4) | 2.327(7) | 2.286(3) |
| Ln1–O7 | 2.335(4) | 2.375(7) | 2.332(3) |
| Ln1–O8 | 2.404(4) | 2.362(7) | 2.316(3) |
| CShMSAPR-8 (square antiprism) D4d | CShMBTPR-8 (biaugmented trigonal prism) C2v | CShMTDD-8 (triangular dodecahedron) D2d | |
|---|---|---|---|
| 1 | 0.484 | 1.564 | 1.373 |
| 2 | 0.410 | 2.418 | 2.134 |
| 3 | 0.363 | 2.362 | 2.124 |
![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (no. 2) triclinic space group (Table 1) and the asymmetric unit is composed of one mononuclear unit (Fig. 5 and S1†) and two dichloromethane molecules of crystallization.
(no. 2) triclinic space group (Table 1) and the asymmetric unit is composed of one mononuclear unit (Fig. 5 and S1†) and two dichloromethane molecules of crystallization.
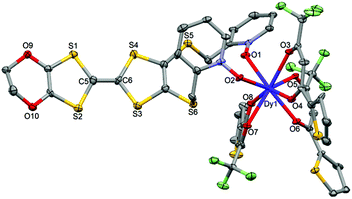 | ||
| Fig. 5 ORTEP view of the mononuclear complex [Dy(tta)3(L)] (2). Thermal ellipsoids are drawn at 30% probability. Hydrogen atoms and dichloromethane molecules are omitted for clarity. | ||
Using the Ln(tta)3·2H2O metal precursor, the two pyridine-N-oxide arms of one ligand are coordinated to the same lanthanide ion. The value of the mean Dy–Otta [Yb–Otta] distances is 2.359(7) [2.315(3)] Å (Table 2). The arrangement of the ligands leads to a distorted square antiprism (D4d symmetry) coordination polyhedron around the LnIII ion. This distortion is visualized by continuous shape measures performed with SHAPE 2.1 (Table 3).30 The L donors are “head-to-tail” stacked to form a regular pseudo-one-dimensional network of L. Two kinds of S⋯S contacts are identified between (i) the TTF cores (S4⋯S4 = 4.256(3) Å [4.223(4) Å]) and (ii) the thiophene ring and TTF core (S2⋯S9 = 4.067(3) Å [4.141(4) Å]) to form a mono-dimensional organic network along the a axis (Fig. 6). The shortest intermolecular Ln–Ln distances have been found to be equal to 9.789(7) [9.747(5)] Å.
Electrochemical properties
The cyclic voltammetry of L and the related complexes 1–3 is investigated to determine their redox properties. The values of the oxidation potentials are listed in Table 4. The cyclic voltammograms show two mono-electronic oxidations which correspond to the formation of a TTF radical cation and a dication, respectively (Fig. S2†). Upon coordination of the electron attracting Ln(hfac)3 or Ln(tta)3 moieties, both E11/2 and E21/2 are respectively slightly cathodically and anodically shifted compared with the potentials of the free ligands. The electrochemical properties attest the redox-activity of both L and complexes.| E 11/2/V | E 21/2/V | |||
|---|---|---|---|---|
| Ox E 11/2 | red E 11/2 | Ox E 21/2 | red E 21/2 | |
| L | 0.57 | 0.36 | 0.93 | 0.76 |
| 1 | 0.52 | 0.40 | 0.96 | 0.81 |
| 2 | 0.51 | 0.36 | 0.99 | 0.83 |
| 3 | 0.50 | 0.33 | 0.96 | 0.77 |
Magnetic properties
The static and dynamic magnetic properties of the three compounds have been measured. The χMT vs. T plots are shown in Fig. 7 while the magnetization curves at 2 K are shown in Fig. S3† (it must be mentioned that the data for 1 have been divided by two to fit with one DyIII per chemical unit). At room temperature the χMT are close to the expected values for isolated Dy(III) (6H15/2: 14.17 cm3 K mol−1) and Yb(III) (2F7/2: 2.57 cm3 K mol−1). All the χMT values decrease on cooling according to the thermal variation of the crystal field level population. Nevertheless, the two Dy(III) derivatives do not behave exactly in the same way although the coordination polyhedra look similar. The decrease is less steep for 2 than for 1 with however lower low temperature limits for 2 than for 1 (11.2 cm3 K mol−1 for 1 and 10.34 cm3 K mol−1 for 2). Differences are also visible in the magnetization curve at 2 K (Fig. S3†): while magnetization of 1 saturates at a value (4.97Nβ) close to that expected for the Ising component (MJ = ±15/2) of the 6H15/2 multiplet ground state, magnetization of 2 linearly increases with the magnetic field at higher values.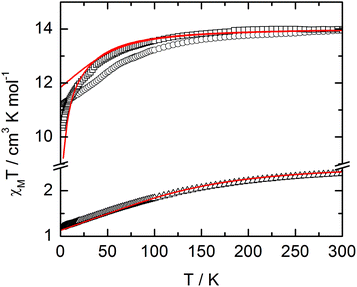 | ||
| Fig. 7 χ M T vs. T plots for compounds 1 (circles) (divided by two to fit with one DyIII per chemical unit), 2 (squares) and 3 (triangles) with simulated curves from ab initio calculations. | ||
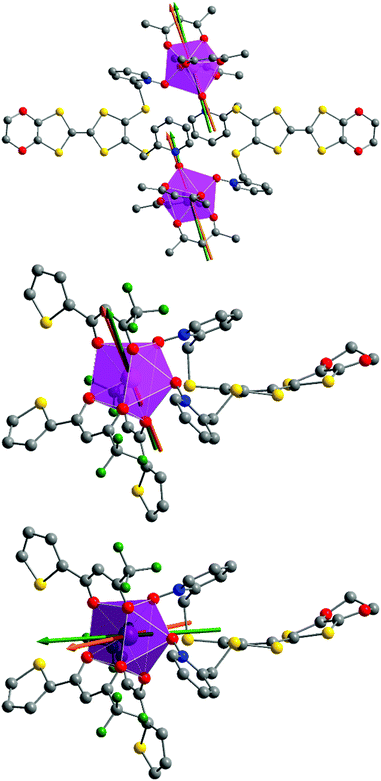
At this stage we decided to take advantage of the space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with one metallic site in the general position for both 1 and 2 to perform rotating single crystal magnetometry (ESI, Fig. S4–S7†) and to compare the orientations of principal magnetic axes with respect to molecular geometry. The principal values of g-tensors, in the frame of the effective spin 1/2 model, are given in Table 5 while the orientations of the principal axis with largest g value are given in Fig. 8. The most striking difference between 1 and 2 is the axiality: 1 is more Ising than 2 which suggests that 1 should be a better SMM than 2. Furthermore the orientation of the most magnetized axis differs significantly: it is oriented toward one oxygen atom of a pyridine-N-oxide moiety which is also coinciding with one of hfac− ligands in 1 whereas in 2, it is oriented between the two oxygen atoms of the two pyridine-N-oxide moieties. Ab initio calculations (see the Computational details section) confirm the large propensity of 1 to behave as a SMM. Indeed, at the SA-CASSCF/RASSI-SO level, both complexes present a predominant MJ = ±15/2 ground state. But due to the larger energy difference between the ground state and the first excited state in 1 than in 2 (80 cm−1vs. 15 cm−1), slighter mixing is observed for 1 than for 2 (Table S1†). This behaviour is also visible in the calculated principal values of the Zeeman tensors with gx = 0.04, gy = 0.06, gz = 19.46 for 1 whereas gx = 0.77, gy = 3.59, gz = 15.63 for 2 (Table 5). Finally, the orientations of the main magnetic anisotropy axes are well reproduced in both DyIII complexes.
with one metallic site in the general position for both 1 and 2 to perform rotating single crystal magnetometry (ESI, Fig. S4–S7†) and to compare the orientations of principal magnetic axes with respect to molecular geometry. The principal values of g-tensors, in the frame of the effective spin 1/2 model, are given in Table 5 while the orientations of the principal axis with largest g value are given in Fig. 8. The most striking difference between 1 and 2 is the axiality: 1 is more Ising than 2 which suggests that 1 should be a better SMM than 2. Furthermore the orientation of the most magnetized axis differs significantly: it is oriented toward one oxygen atom of a pyridine-N-oxide moiety which is also coinciding with one of hfac− ligands in 1 whereas in 2, it is oriented between the two oxygen atoms of the two pyridine-N-oxide moieties. Ab initio calculations (see the Computational details section) confirm the large propensity of 1 to behave as a SMM. Indeed, at the SA-CASSCF/RASSI-SO level, both complexes present a predominant MJ = ±15/2 ground state. But due to the larger energy difference between the ground state and the first excited state in 1 than in 2 (80 cm−1vs. 15 cm−1), slighter mixing is observed for 1 than for 2 (Table S1†). This behaviour is also visible in the calculated principal values of the Zeeman tensors with gx = 0.04, gy = 0.06, gz = 19.46 for 1 whereas gx = 0.77, gy = 3.59, gz = 15.63 for 2 (Table 5). Finally, the orientations of the main magnetic anisotropy axes are well reproduced in both DyIII complexes.
| 1 | 2 | 3 | ||||
|---|---|---|---|---|---|---|
| Exp. | Calc. | Exp. | Calc. | Exp. | Calc. | |
| g x | 1.19 | 0.04 | 7.24 | 0.77 | 5.84 | 5.96 |
| g y | 18.47 | 19.46 | 5.04 | 3.59 | 2.00 | 0.73 |
| g z | 3.14 | 0.06 | 15.86 | 15.63 | 1.77 | 0.33 |
For compound 3, χMT varies from 1.2 cm3 K−1 at 2 K to 2.38 cm3 K mol−1 at room temperature. At 300 K, χMT is close to the expected value for the ground state multiplet 2F7/2 (2.57 cm3 K mol−1). The orientation of the most magnetic axis determined from single crystal rotating magnetometry (ESI, Fig. S8†) is shown in Fig. 8. As for 1 and 2, ab initio calculations were performed on the YbIII compound 3. However, as usual for YbIII complexes,11h,33 dynamical correlation effects had to be taken into account by means of CASPT2 calculations (see the Computational details section). The χMT vs. T experimental curve is well reproduced by the calculations (Fig. 7) as well as the orientation of the easy magnetic axes (Fig. 8). The ground state is well separated from the first excited state (234 cm−1) and is mainly composed of MJ = ±5/2 (0.50) but with non-negligible contributions from MJ = ±7/2 (0.34) and MJ = ±5/2 (0.10). As could have been anticipated from dc magnetic data the dynamic susceptibilities of 1 and 2 differ significantly. 2 does not show any out-of-phase component of the ac susceptibility (χM′′) whatever the temperature (down to 1.8 K) and whatever the frequency of the oscillating field (between 1 and 1000 Hz) at zero external dc field. On the contrary, χM′′ is not null in zero external field for 1 at low temperature. It shows a frequency dependent signal below 7 K in the range 1–1000 Hz (Fig. 9).
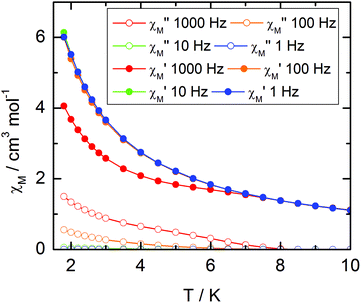 | ||
| Fig. 9 Temperature variations of the ac susceptibility components, χM′ and χM′′, of compound 1 measured in zero external dc field at various frequencies. Values are given for one metallic site. | ||
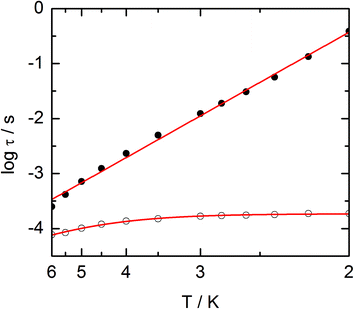
The frequency dependences of the two components at various temperatures have been treated using an extended Debye model (see ESI and Table S2†), which allows plotting the thermal variations of the relaxation time τ. It follows an Arrhenius law at high temperature modulated by a thermally independent regime at low temperature (Fig. 10). The complete set of data can be adjusted with the equation (τ−1 = τ0−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp
exp![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (−Δ/T) + τTI−1) with τ being the relaxation time, τ0 the intrinsic relaxation time, Δ the energy barrier and finally τTI the thermally independent relaxation time. The best agreement is obtained with τ0 = 9 ± 2 × 10−6 s, Δ = 16 ± 0.8 K and τTI = 1.85 ± 0.02 × 10−4 s.
(−Δ/T) + τTI−1) with τ being the relaxation time, τ0 the intrinsic relaxation time, Δ the energy barrier and finally τTI the thermally independent relaxation time. The best agreement is obtained with τ0 = 9 ± 2 × 10−6 s, Δ = 16 ± 0.8 K and τTI = 1.85 ± 0.02 × 10−4 s.
The application of an external dc field dramatically slows down the relaxation process in the thermally independent regime (Fig. S9†). The application of a moderate and constant external field removes the degeneracy of Kramer's doublet with no more direct relaxation between these two states. The most efficient field which is the one for which the relaxation is slowest is found close to 1 kOe. Then the frequency dependences of χM′ and χM′′ at various temperature but recorded at 1 kOe have been treated using the extended Debye model. The relaxation time obeys now the Arrhenius law (τ−1 = τ0−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Δ/T)) with τ0 = 1 ± 0.12 × 10−5 s, Δ = 21 ± 0.3 K. These values are of the same order of magnitude as in zero external field.
exp(−Δ/T)) with τ0 = 1 ± 0.12 × 10−5 s, Δ = 21 ± 0.3 K. These values are of the same order of magnitude as in zero external field.
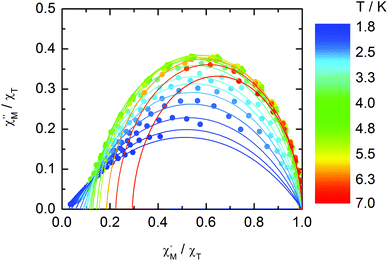
The normalized Cole–Cole plots (χM′′/χTvs. χM′/χT) at selected temperatures between 1.8 and 7.0 K are depicted in Fig. 11. They are flattened semicircles and the α values (Table S3†) indicate that a single relaxation time is mainly involved in the present relaxation process.
Compound 3 does not show any out-of-phase signal in zero external dc field whatever the temperature and the available oscillating field frequency in agreement with the calculated ground state (mainly MJ = ±5/2). However, at 1 kOe a frequency dependent out-of-phase signal shows up at lower temperatures than 4 K (Fig. 12) that may be due to the presence of a non-negligible contribution MJ = ±7/2 in the ground state wavefunction.
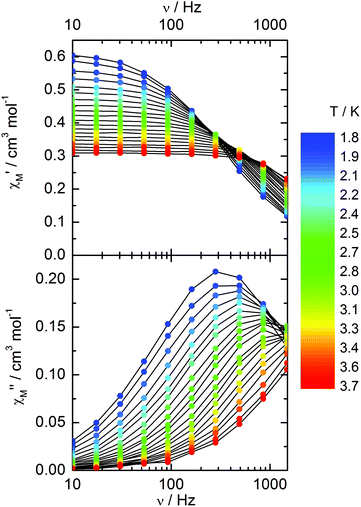 | ||
| Fig. 12 Frequency variations of the ac susceptibility components, χM′ and χM′′, of compound 3 measured at 1 kOe at various temperatures. | ||
The extended Debye model (Table S4†) allows to extract the temperature dependence of the relaxation which can then be treated in the frame of a thermally activated process only (τ−1 = τ0−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Δ/T) with τ0 = 1.9 ± 0.2 × 10−5 s and Δ = 6 ± 0.3 K (Fig. 13).
exp(−Δ/T) with τ0 = 1.9 ± 0.2 × 10−5 s and Δ = 6 ± 0.3 K (Fig. 13).
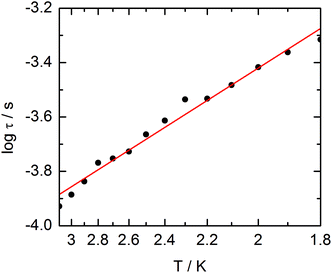 | ||
| Fig. 13 Temperature variations of the relaxation time of the magnetization measured at 1 kOe for compound 3. Full red line is the best fitted curve (see the text). | ||
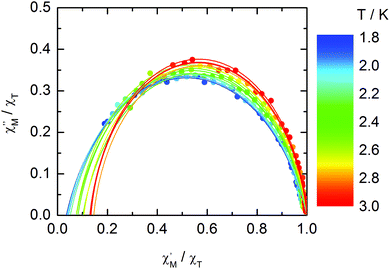
The normalized Cole–Cole plots (χM′′/χTvs. χM′/χT) at selected temperatures between 1.8 and 3.0 K are flattened semicircles due to α values close to 0.05 (Fig. 14 and Table S4†). This value indicates that a single relaxation time is mainly involved in the present relaxation process independently of the temperature. They almost all collapse into one semicircle which intercepts the x axis near the origin. The fast relaxing part of the magnetization is very small and is not related to the distribution of the relaxation time.
Photo-physical properties
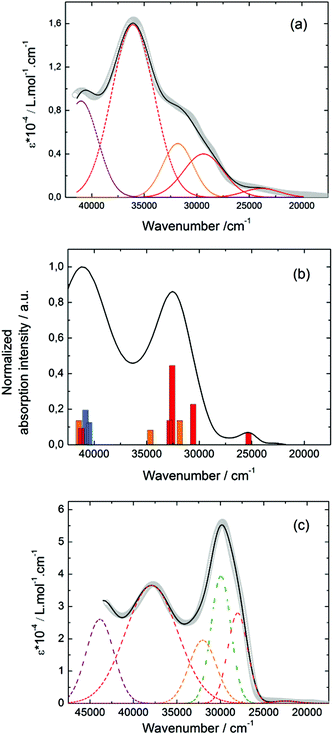
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1 and 36
400 cm−1 and 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1 were also attributed to ILCT transitions while the intermediate absorption band was attributed to intra-TTF excitations. Finally the highest energy absorption band centred at 41
100 cm−1 were also attributed to ILCT transitions while the intermediate absorption band was attributed to intra-TTF excitations. Finally the highest energy absorption band centred at 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (purple decomposition) was attributed to intra-ligand (IL) transitions. The replacement of the ethylenedithio fragment with an ethylenedioxy one does not induce significant changes in the absorption properties. The UV-visible absorption properties of the coordination complex 3 have been first studied in the solid-state (Fig. S10†) and then in CH2Cl2 solution (Fig. 15c). The absorption spectra have been decomposed into six and seven bands respectively for the solution and solid-state measurements (Table 7). The lowest-energy additional absorption band (15
000 cm−1 (purple decomposition) was attributed to intra-ligand (IL) transitions. The replacement of the ethylenedithio fragment with an ethylenedioxy one does not induce significant changes in the absorption properties. The UV-visible absorption properties of the coordination complex 3 have been first studied in the solid-state (Fig. S10†) and then in CH2Cl2 solution (Fig. 15c). The absorption spectra have been decomposed into six and seven bands respectively for the solution and solid-state measurements (Table 7). The lowest-energy additional absorption band (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1) which is observed in the solid-state spectra is due to the intermolecular CT.10c Additional intense absorption excitations have been observed around 27
500 cm−1) which is observed in the solid-state spectra is due to the intermolecular CT.10c Additional intense absorption excitations have been observed around 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–30
000–30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 that correspond to π–π* intra-tta− excitations.11c Complexations induce a weak red shift of the ligand-centered ILCT transition due to the moderate Lewis acid behavior of the Ln(tta)3 moieties enforcing the electron withdrawing character of the 2-pyridine-N-oxide fragments even if the electronic communication through the methylthio arms is expected to be very weak. Thus, the absorption bands are red-shifted 1300 cm−1 in coordination complexes compared to those in L. Since the shift value is determined from the data in CH2Cl2 solution, this is a first indication of the stability of the mononuclear complexes in such a solvent.
000 cm−1 that correspond to π–π* intra-tta− excitations.11c Complexations induce a weak red shift of the ligand-centered ILCT transition due to the moderate Lewis acid behavior of the Ln(tta)3 moieties enforcing the electron withdrawing character of the 2-pyridine-N-oxide fragments even if the electronic communication through the methylthio arms is expected to be very weak. Thus, the absorption bands are red-shifted 1300 cm−1 in coordination complexes compared to those in L. Since the shift value is determined from the data in CH2Cl2 solution, this is a first indication of the stability of the mononuclear complexes in such a solvent.
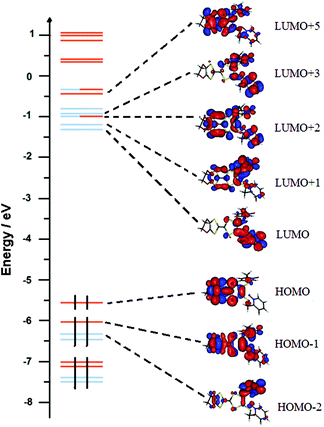 | ||
| Fig. 16 Molecular orbital diagram of L. The energy levels of the centred TTF and 2-methylpyridine-N-oxide orbitals are shown in orange and blue, respectively. | ||
| L (solid-state) | 3 (CH2Cl2 solution) | 3 (solid-state) | Type | |
|---|---|---|---|---|
| Energy exp. (cm−1) | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
— | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
Inter-LCT |
18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 800 |
ILCT | |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
ILCT | |
| — | 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
Itta | |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
ILCT | |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
ID | |
39![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 900 |
38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
IL |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1 (450 nm).
200 cm−1 (450 nm).
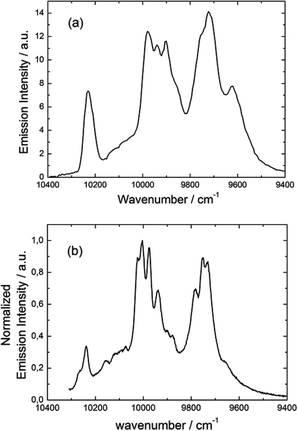 | ||
Fig. 17 Luminescence spectrum of 3 in the NIR range for λex = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 220 cm−1 (450 nm) in the solid state at 77 K (a) and luminescence spectrum obtained by direct irradiation of the f–f transitions (b). 220 cm−1 (450 nm) in the solid state at 77 K (a) and luminescence spectrum obtained by direct irradiation of the f–f transitions (b). | ||
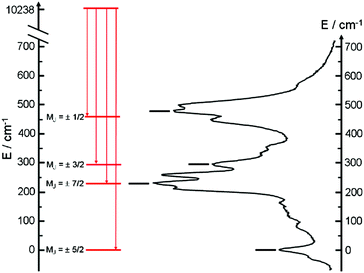
The almost complete absence of any residual ligand-centred emission in the visible region indicates that the energy-transfer process is rather efficient. As already observed in previously published TTF-based complexes of YbIII, the antenna-effect sensitization process is favored and proceeds through energy transfer from the singlet CT state of the L chromophore.11c–f Eight emission maxima and shoulders are clearly identified at the following energies: 9624 cm−1, 9722 cm−1, 9756 cm−1, 9860 cm−1, 9900 cm−1, 9940 cm−1, 9980 cm−1 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 230 cm−1. This number of contributions is higher than the degeneracy of the 2F7/2 ground state (Kramer's doublets) (maximum 4 contributions). By analogy with one of our previous studies11h,i 33a and the one by Auzel et al.35 the additional emission contributions could be attributed to transitions coming from the second and/or third MJ states of the 2F5/2 multiplet state. In order to discriminate between the vibronic contribution and the contribution of the excited multiplet state to explain the origin of these additional bands, the emission spectrum was recorded by direct laser excitation of the f–f bands (Fig. 17b).36 The two spectra are very similar although a partial quenching of the lowest-energy contribution (9624 cm−1) by a direct f–f sensitization can be observed. This decrease may be assigned to vibronic contributions. Assuming that the additional emission bands are due to the two MJ excited states of the 2F5/2 multiplet, the maximum number of expected transitions can be twelve. The total splitting is determined to be equal to 537 cm−1. The values of this splitting for a YbIII ion in a distorted and a regular37D3 symmetry are 455 cm−1 and 372 cm−1 respectively while a splitting of 528 cm−1 is found for a Yb complex in a lower symmetry up to 880 nm for an organometallic derivative.38 The value of 537 cm−1 seems to correspond to a quite low symmetry that is in agreement with the lowest symmetry of the coordination sphere around the YbIII ions in 3 (distorted square anti-prism). In addition, emission spectroscopy provides a direct probe of the ground state multiplet splitting which can be confronted with magnetic data (Fig. 18). Thus the energy splitting of the 2F7/2 ground state multiplet extracts from the experimental luminescence (MJ = ±5/2 (0 cm−1), MJ = ±7/2 (234 cm−1), MJ = ±3/2 (300 cm−1) and MJ = ±1/2 (488 cm−1)) is in perfect agreement with the results of MS-CASPT2/RASSI-SO calculations (MJ = ±5/2 (0 cm−1), MJ = ±7/2 (234 cm−1), MJ = ±3/2 (298 cm−1) and MJ = ±1/2 (467 cm−1)).
230 cm−1. This number of contributions is higher than the degeneracy of the 2F7/2 ground state (Kramer's doublets) (maximum 4 contributions). By analogy with one of our previous studies11h,i 33a and the one by Auzel et al.35 the additional emission contributions could be attributed to transitions coming from the second and/or third MJ states of the 2F5/2 multiplet state. In order to discriminate between the vibronic contribution and the contribution of the excited multiplet state to explain the origin of these additional bands, the emission spectrum was recorded by direct laser excitation of the f–f bands (Fig. 17b).36 The two spectra are very similar although a partial quenching of the lowest-energy contribution (9624 cm−1) by a direct f–f sensitization can be observed. This decrease may be assigned to vibronic contributions. Assuming that the additional emission bands are due to the two MJ excited states of the 2F5/2 multiplet, the maximum number of expected transitions can be twelve. The total splitting is determined to be equal to 537 cm−1. The values of this splitting for a YbIII ion in a distorted and a regular37D3 symmetry are 455 cm−1 and 372 cm−1 respectively while a splitting of 528 cm−1 is found for a Yb complex in a lower symmetry up to 880 nm for an organometallic derivative.38 The value of 537 cm−1 seems to correspond to a quite low symmetry that is in agreement with the lowest symmetry of the coordination sphere around the YbIII ions in 3 (distorted square anti-prism). In addition, emission spectroscopy provides a direct probe of the ground state multiplet splitting which can be confronted with magnetic data (Fig. 18). Thus the energy splitting of the 2F7/2 ground state multiplet extracts from the experimental luminescence (MJ = ±5/2 (0 cm−1), MJ = ±7/2 (234 cm−1), MJ = ±3/2 (300 cm−1) and MJ = ±1/2 (488 cm−1)) is in perfect agreement with the results of MS-CASPT2/RASSI-SO calculations (MJ = ±5/2 (0 cm−1), MJ = ±7/2 (234 cm−1), MJ = ±3/2 (298 cm−1) and MJ = ±1/2 (467 cm−1)).
Conclusions
Three DyIII and YbIII complexes involving the 4,5-ethylenedioxy-4′,5′-bis(2-pyridyl-N-oxidemethylthio)tetrathiafulvalene ligand (L) have been reported. The use of hfac− as ancillary ligands for the lanthanide precursor leads to the dinuclear complex 1 while the use of tta− leads to the mononuclear complexes 2 and 3. In all the compounds, the lanthanide ion is surrounded by a distorted O8 D4d symmetry environment. The electronic distribution around the DyIII ion in 1 and the YbIII ion in 3 favours an Ising system and single-molecule magnet behaviours. The Ising character was confirmed by ab initio calculations. Both the calculated and the experimental anisotropy axis have been determined and are in good agreement with each other. Interestingly, compound 2 does not display the out-of-phase component of the magnetic susceptibility whereas 1 does even if the nature of the neighbouring atoms and the symmetry of the coordination sphere are the same. That shows that a subtle change in the ligands can induce a drastic change in the magnetic behaviour. The ligand L guarantees an efficient sensitization of the YbIII luminescence by the antenna effect and the luminescence data for 3 can be correlated to the magnetic data. 3 thus enlarges the very scarce series of redox-active luminescent SMMs.Acknowledgements
This work was supported by the CNRS, Rennes Métropole, Université de Rennes 1, Région Bretagne, FEDER and Agence Nationale de la Recherche (no. ANR-13-BS07-0022-01). BLG thanks the French GENCI center for high-performance computing resources (project x2015080649).Notes and references
- (a) A. Dei and D. Gatteschi, Angew. Chem., Int. Ed., 2011, 50, 11852–11858 CrossRef CAS PubMed; (b) M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793 CrossRef CAS PubMed; (c) S. Hill, R. S. Edwards, N. Aliaga-Alcalde and G. Christou, Science, 2003, 302, 1015–1018 CrossRef CAS PubMed; (d) M. Hosseini, S. Rebic, B. M. Sparkes, J. Twamley, B. C. Buchler and P. K. Lam, Light: Sci. Appl., 2012, 1, e40 CrossRef.
- (a) R. Sessoli, H. L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 2002, 115, 1804–1816 CrossRef; (b) M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M.-A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194–197 CrossRef CAS PubMed; (c) M. Gu, X. Li and Y. Cao, Light: Sci. Appl., 2014, 3, e177 CrossRef CAS.
- (a) N. Papasimakis, S. Thongrattanasiri, N. I. Zheludev and F. J. Garcia de Abajo, Light: Sci. Appl., 2013, 2, e78 CrossRef; (b) S. Sanvito, Chem. Soc. Rev., 2011, 40, 3336–3355 RSC; (c) L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186 CrossRef CAS PubMed.
- S.-Y. Lin, C. Wang, L. Zhao, J. Wua and J. Tang, Dalton Trans., 2015, 44, 223 RSC.
- J. Long, J. Rouquette, J.-M. Thibaud, R. A. S. Ferreira, L. D. Carlos, B. Donnadieu, V. Vieru, L. F. Chibotaru, L. Konczewicz, J. Haines, Y. Guari and J. Larionova, Angew. Chem., Int. Ed., 2015, 54, 2236–2240 CrossRef CAS PubMed.
- X.-L. Li, C.-L. Chen, H.-P. Xiao, A.-L. Wang, C.-M. Liu, X. Zheng, L.-J. Gao, X.-G. Yanga and S.-M. Fang, Dalton Trans., 2013, 42, 15317–15325 RSC.
- (a) J. C. G. Bünzli and C. Piguet, Chem. Rev., 2002, 102, 1897 CrossRef; (b) R. Sessoli and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2328–2341 CrossRef CAS; (c) J. Luzon and R. Sessoli, Dalton Trans., 2012, 41, 13556–13567 RSC; (d) T. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 1729–1733 CrossRef PubMed.
- (a) J.-C. G. Bünzli, Acc. Chem. Res., 2006, 39, 53–61 CrossRef PubMed; (b) S. V. Eliseeva and J.-C. G. Bünzli, Chem. Soc. Rev., 2010, 39, 189–227 RSC; (c) S. V. Eliseeva and J.-C. G. Bünzli, in Springer series on fluorescence, in Lanthanide spectroscopy, Materials, and Bio-applications, ed. P. Hännen and H. Härmä, Springer Verlag, Berlin, 2010, ch. 1, vol. 7 Search PubMed; (d) Luminescence of Lanthanide Ions in Coordination Compounds and Nanomaterials, ed. A. De Bettencourt-Diaz, Wiley, 2014 Search PubMed.
- (a) H. Tanaka, H. Kobayashi, A. Kobayashi and P. Cassoux, Adv. Mater., 2000, 12, 1685–1689 CrossRef CAS; (b) S. Uji, H. Shinagawa, T. Terashima, C. Terakura, T. Yakabe, Y. Terai, M. Tokumoto, A. Kobayashi, H. Tanaka and H. Kobayashi, Nature, 2001, 410, 908–910 CrossRef CAS PubMed; (c) A. Kobayashi, E. Fujiwara and H. Kobayashi, Chem. Rev., 2004, 104, 5243–5264 CrossRef CAS PubMed; (d) T. Enoki and A. Miyasaki, Chem. Rev., 2004, 104, 5449–5478 CrossRef CAS PubMed; (e) E. Coronado and P. Day, Chem. Rev., 2004, 104, 5419–5448 CrossRef CAS PubMed; (f) L. Ouahab and T. Enoki, Eur. J. Inorg. Chem., 2004, 933–941 CrossRef CAS; (g) H. Fujiwara, K. Wada, T. Hiraoka, T. Hayashi, T. Sugimoto, H. Nakazumi, K. Yokogawa, M. Teramura, S. Yasuzuka, K. Murata and T. Mori, J. Am. Chem. Soc., 2005, 127, 14166–14167 CrossRef CAS PubMed; (h) R. Kato, Bull. Chem. Soc. Jpn., 2000, 73, 515–534 CrossRef CAS; (i) D. Lorcy, N. Bellec, M. Fourmigué and N. Avarvari, Coord. Chem. Rev., 2009, 253, 1398–1438 CrossRef CAS and references cited therein; (j) F. Pointillart, S. Golhen, O. Cador and L. Ouahab, Dalton Trans., 2013, 42, 1949–1960 RSC and references cited therein.
- (a) S. Faulkner, B. P. Burton-Pye, T. Khan, L. R. Martin, S. D. Wray and P. J. Skabara, Chem. Commun., 2002, 1668–1669 RSC; (b) S. J. A. Pope, B. P. Burton-Pye, R. Berridge, T. Khan, P. Skabara and S. Faulkner, Dalton Trans., 2006, 2907–2912 RSC; (c) F. Pointillart, T. Cauchy, O. Maury, Y. Le Gal, S. Golhen, O. Cador and L. Ouahab, Chem. – Eur. J., 2010, 16, 11926–11941 CrossRef CAS PubMed; (d) F. Pointillart, A. Bourdolle, T. Cauchy, O. Maury, Y. Le Gal, S. Golhen, O. Cador and L. Ouahab, Inorg. Chem., 2012, 51, 978–984 CrossRef CAS PubMed; (e) A. D'Aléo, F. Pointillart, L. Ouahab, C. Andraud and O. Maury, Coord. Chem. Rev., 2012, 256, 1604–1620 CrossRef; (f) F. Pointillart, B. Le Guennic, S. Golhen, O. Cador, O. Maury and L. Ouahab, Inorg. Chem., 2013, 52, 1610–1620 CrossRef CAS PubMed; (g) M. Feng, F. Pointillart, B. Le Guennic, B. Lefeuvre, S. Golhen, O. Cador, O. Maury and L. Ouahab, Chem. – Asian. J., 2014, 9, 2814–2825 CrossRef CAS PubMed; (h) F. Pointillart, B. Le Guennic, T. Cauchy, S. Golhen, O. Cador, O. Maury and L. Ouahab, Inorg. Chem., 2013, 52, 5978–5990 CrossRef CAS PubMed.
- (a) G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P. E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606–1610 CrossRef CAS PubMed; (b) M.-E. Boulon, G. Cucinotta, J. Luzon, C. Degl'Innocenti, M. Perfetti, K. Bernot, G. Calvez, A. Caneschi and R. Sessoli, Angew. Chem., Int. Ed., 2013, 52, 350–354 CrossRef CAS PubMed; (c) F. Pointillart, B. Le Guennic, S. Golhen, O. Cador, O. Maury and L. Ouahab, Chem. Commun., 2013, 49, 615–617 RSC; (d) J. Long, R. Vallat, R. A. S. Ferreira, L. D. Carlos, F. A. A. Paz, Y. Guari and J. Larionova, Chem. Commun., 2012, 48, 9974–9976 RSC; (e) K. Yamashita, R. Miyazaki, Y. Kataoka, T. Nakanishi, Y. Hasegawa, M. Nakano, T. Yamamura and T. Kajiwara, Dalton Trans., 2013, 42, 1987–1990 RSC; (f) K. Ehama, Y. Ohmichi, S. Sakamoto, T. Fujinami, N. Matsumoto, N. Mochida, T. Ishida, Y. Sunatsuki, M. Tsuchimoto and N. Re, Inorg. Chem., 2013, 52, 12828–12841 CrossRef CAS PubMed; (g) M. Ren, S.-S. Bao, R. A. S. Ferreira, L.-M. Zheng and L. D. Carlos, Chem. Commun., 2014, 50, 7621–7624 RSC; (h) G. Cosquer, F. Pointillart, J. Jung, B. Le Guennic, S. Golhen, O. Cador, Y. Guyot, A. Brenier, O. Maury and L. Ouahab, Eur. J. Inorg. Chem., 2014, 69–82 CrossRef CAS; (i) X. Yi, K. Bernot, V. Le Corre, G. Calvez, F. Pointillart, O. Cador, B. Le Guennic, J. Jung, O. Maury, V. Placide, Y. Guyot, T. Roisnel, C. Daiguebonne and O. Guillou, Chem. – Eur. J., 2014, 20, 1569–1576 CrossRef CAS PubMed.
- (a) J. J. Baldovi, J. M. Clemente-Juan, E. Coronado, Y. Duan, A. Gaita-Arino and C. Gimenez-Saiz, Inorg. Chem., 2014, 53, 9976–9980 CrossRef CAS PubMed; (b) J. J. Baldovi, J. M. Clemente-Juan, E. Coronado and A. Gaita-Arino, Inorg. Chem., 2014, 53, 11323–11327 CrossRef CAS PubMed; (c) N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551–2558 Search PubMed; (d) C. Y. Chow, H. Bolvin, V. E. Campbell, R. Guillot, J. F. Kampf, W. Werndorfer, F. V. Gendron, J. Autschbach, V. L. Pecoraro and T. Mallah, Chem. Sci., 2015, 6, 4148–4159 RSC; (e) L. Ungur, S.-Y. Lin, J. Tang and L. F. Chibotaru, Chem. Soc. Rev., 2014, 43, 6894–6905 RSC; (f) Y.-N. Guo, G.-F. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J. Tang, H.-J. Zhang, L. F. Chibotaru and A. K. Powell, J. Am. Chem. Soc., 2011, 133, 11948–11951 CrossRef CAS PubMed.
- M. F. Richardson, W. F. Wagner and D. E. Sands, J. Inorg. Nucl. Chem., 1968, 30, 1275–1289 CrossRef CAS.
- A. I. Vooshin, N. M. Shavaleev and V. P. Kazakov, J. Lumin., 2000, 91, 49–58 CrossRef.
- (a) N. Sevenstrup, K. M. Rasmussen, T. K. Hansen and J. Becher, Synthesis, 1994, 809 CrossRef; (b) M. Xu, Y. Ji, J. L. Zuo and X. Z. You, J. Heterocycl. Chem., 2005, 42, 847 CrossRef CAS; (c) L. Binet, J. M. Fabre, C. Montginoul, K. B. Simonsen and J. Becher, J. Chem. Soc., Perkin Trans. 1, 1996, 783 RSC.
- M. Polasek, M. Sedinova, J. Kotek, L. V. Elst, R. N. Muller, P. Hermann and I. Lukes, Inorg. Chem., 2009, 48, 455 CrossRef CAS PubMed.
- G. M. Sheldrick, SHELX97 – Programs for Crystal Structure Analysis (Release 97-2), Institut für Anorganische Chemie der Universität, Tammanstrasse 4, D-3400 Göttingen, Germany, 1998 CrossRef CAS, SIR97; A. Altomare, M. C. Burla, M. Camalli, G. L. Cascarano, C. Giacovazzo, A. Guagliardi, A. G. G. Moliterni, G. Polidori and R. Spagna, J. Appl. Crystallogr., 1999, 32, 115–119 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, Jr., J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision A.02, Gaussian Inc., Wallingford, CT, 2009 Search PubMed.
- (a) J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed; (b) C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- (a) M. Cossi and V. Barone, J. Chem. Phys., 2001, 115, 4708–4717 CrossRef CAS; (b) R. Improta, V. Barone, G. Scalmani and M. J. Frisch, J. Chem. Phys., 2006, 125, 054103–054109 CrossRef PubMed.
- A.-R. Allouche, J. Comput. Chem., 2011, 32, 174–182 CrossRef CAS PubMed.
- F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, P. A. Malmqvist, P. Neogrady, T. Bondo Pedersen, M. Pitonak, M. Reiher, B. O. Roos, L. Serrano-Andrés, M. Urban, V. Veryazov and R. Lindh, J. Comput. Chem., 2010, 31, 224–247 CrossRef CAS PubMed.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–288 CrossRef CAS.
- (a) P. A. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240 CrossRef CAS; (b) P. A. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189–194 CrossRef CAS.
- (a) L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112–064122 CrossRef CAS PubMed; (b) L. F. Chibotaru, L. Ungur and A. Soncini, Angew. Chem., Int. Ed., 2008, 47, 4126–4129 CrossRef CAS PubMed.
- F. Aquilante, P.-A. Malmqvist, T.-B. Pedersen, A. Ghosh and B. O. Roos, J. Chem. Theory Comput., 2008, 4, 694–702 CrossRef CAS.
- (a) B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS; (b) B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2005, 109, 6576–6586 Search PubMed; (c) B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov, P.-O. Widmark and A. C. Borin, J. Phys. Chem. A, 2008, 112, 11431–11435 CrossRef CAS PubMed.
- M. Llunell, D. Casanova, J. Cirera, J. M. Bofill, P. Alemany and S. Alvarez, S. SHAPE (version 2.1), Barcelona, 2013 Search PubMed.
- F. Habib, P.-H. Lin, J. Long, I. Korobkov, W. Werndorfer and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 8830 CrossRef CAS PubMed.
- G. Cosquer, F. Pointillart, S. Golhen, O. Cador and L. Ouahab, Chem. – Eur. J., 2013, 19, 7895–7903 CrossRef CAS PubMed.
- (a) J. Jung, T. da Cunha, B. Le Guennic, F. Pointillart, L. M. Pereira, J. Luzon, S. Golhen, O. Cador, O. Maury and L. Ouahab, Eur. J. Inorg. Chem., 2014, 3888–3894 CrossRef CAS; (b) F. Pointillart, J. Jung, R. Berraud-Pache, B. Le Guennic, V. Dorcet, S. Golhen, O. Cador, O. Maury, Y. Guyot, S. Decurtins, S.-X. Liu and L. Ouahab, Inorg. Chem., 2015, 54, 5384–5397 CrossRef CAS PubMed.
- G. Cosquer, F. Pointillart, B. Le Guennic, Y. Le Gal, S. Golhen, O. Cador and L. Ouahab, Inorg. Chem., 2012, 51, 8488–8501 CrossRef CAS PubMed.
- P. Goldner, F. Pell, D. Meichenin and F. Auzel, J. Lumin., 1997, 71, 137–150 CrossRef CAS.
- G. Zucchi, R. Scopelliti, P.-A. Pittet, J. C. G. Bünzli and R. D. Rogers, J. Chem. Soc., Dalton Trans., 1999, 931–938 RSC.
- F. R. Gonçalves Silva, O. L. Malta, C. Reinhard, H. U. Güdel, C. Piguet, J. Moser and J.-C. G. Bünzli, J. Phys. Chem. A, 2002, 106, 1670–1677 CrossRef.
- G. Lapadula, A. Bourdolle, F. Allouche, M. Conley, I. del Rosa, L. Maron, W. W. Lukens, Y. Guyot, C. Andraud, S. Brasselet, C. Copéret, O. Maury and R. A. Andersen, Chem. Mater., 2014, 26, 1062–1073 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 1407103–1407106. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5qi00087d |
| This journal is © the Partner Organisations 2015 |