Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ionic liquid effects on a multistep process. Increased product formation due to enhancement of all steps†
Sinead T.
Keaveney
,
Ronald S.
Haines
and
Jason B.
Harper
*
School of Chemistry, University of New South Wales, Sydney, NSW 2052, Australia. E-mail: j.harper@unsw.edu.au; Fax: +61 2 9385 6141; Tel: +61 2 9385 4692
First published on 17th July 2015
Abstract
The reaction of a series of substituted benzaldehydes with hexylamine was examined in acetonitrile and an ionic liquid. In acetonitrile, as the electron withdrawing nature of the substituent increases, the overall addition-elimination process becomes faster as does the build-up of the aminol intermediate. Under equivalent conditions in an ionic liquid, less intermediate build up is observed, and the effect on the rate on varying the substituent is different to that in acetonitrile. Extensive kinetic analysis shows that the ionic liquid solvent increases the rate constant of all steps of the reaction, resulting in faster product formation relative to acetonitrile; these effects increase with the proportion of ionic liquid in the reaction mixture. Differences in the equilibrium position of the addition step in the ionic liquid were found to account for both the decrease in intermediate build up relative to acetonitrile, as well as the differing trend in the overall rate of product formation as the substituent was changed. The microscopic origins of these ionic liquid effects were probed through temperature dependent analyses, highlighting the subtle balance of interactions between the ionic liquid and species along the reaction coordinate, particularly the importance of charge development in the transition state.
Introduction
There is a continually growing library of synthetic procedures available to chemists allowing many chemical transformations to be performed, although many of these methods are not without their drawbacks with a number of synthetic routes requiring elevated temperatures and prolonged periods of time to proceed. There are many different approaches to optimizing a specific transformation, such as catalysis,1,2 and irradiation,3 yet the use of solvents to control reaction outcome is an interesting alternative.4Ionic liquids, salts that are molten below 100 °C,5,6 have become of interest as solvents due to a number of attractive properties, including low vapour pressure7–9 and low flammability,9 compared to traditional molecular solvents. The extensive range of anions and cations available allows for tailor-made ionic liquids to be prepared, with specific physical and chemical properties obtained by simply varying the ion combination used; this makes them promising candidates as designer solvents.10,11 Further, it has been widely demonstrated that ionic liquids can affect reaction outcomes differently to organic solvents, with many reactions proceeding more readily and/or more selectively in ionic liquids.12–22 Despite this, the lack of understanding of these solvents is inhibiting their more widespread application, and hence a more thorough understanding of this reaction medium is of interest to all chemists, so the full potential of ionic liquids can be realized.
There has been much experimental10,12 and computational work23–27 that has sought to understand the microscopic origin of changes in the rate and the selectivity of organic processes in an ionic liquid, compared to molecular solvents. By systematically examining a number of well-understood organic processes, our group has been developing a set of principles that can be used to predict ionic liquid effects on organic reaction outcomes;4,28–39 this work has mainly focused on the effect of the solvent on reaction rate and product selectivity. In much of this work, entropic effects have dominated the changes in reaction outcome seen, with differences in the extent to which the ionic liquid solvates the reagents and the transition state driving the changes in reaction outcome observed. The body of work that has emerged in this area over recent years is beginning to shape our understanding of ionic liquid solvent effects, and will allow ionic liquids to be chosen and utilized more rationally in organic synthesis, although there is still much more work that needs to be done.
One aspect that has yet to be thoroughly examined is the effect that changing a substituent on a reactant has on the ionic liquid solvent effects; that is, how the rate of a reaction changes as the electronic perturbing ability of the substituent is varied, including whether a mechanism or rate-determining step change occurs. In molecular solvents, since the pioneering work of Hammett,40,41 substituent effects are generally well understood; it is relatively ‘easy’ to predict the substituent effects if there is a good understanding of the reaction mechanism, allowing specific substituents to be chosen to alter reaction outcome in a desired manner.42,43 It is also well known that changing the solvent can alter the substituent effects,42,43 hence it would be interesting to examine if this might be exploited in ionic liquids as a different solvent may allow access to different substituent effects than those seen in typical molecular solvents.
There have been few previous studies that have examined substituent effects in ionic liquids, with the two principal investigations focusing on the Menschutkin reaction.31,44 Both studies found that in molecular solvents the Hammett plot was non-linear due to a shift from a ‘tight’ or ‘closed’ transition state (i.e. the extent of bond formation and bond breaking are comparable) for electron withdrawing groups to more of a ‘loose’ or ‘open’ transition state (i.e. the extent of bond breaking is greater than the extent of bond formation) for electron donating groups. When using the ionic liquid 1-butyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide ([Bmim][N(CF3SO2)2], 1) both investigations found that the ionic liquid behaved in a similar fashion to molecular solvents, although the extent of bond breaking in the transition state, and hence positive charge development, was found to be greater in the ionic liquid.31,44
Previous work36,39 on the condensation of benzaldehyde 2a and hexan-1-amine 3 (Scheme 1) found that there was an increased rate constant for the rate-determining addition step when using an ionic liquid instead of acetonitrile. It was found that the critical interaction was between the ionic liquid cation and the nitrogen lone pair on the nucleophile 3, as on moving to the transition state there was an increase in disorder in the system, resulting in an entropically driven rate increase.
 | ||
| Scheme 1 The condensation of benzaldehydes 2 with the amine 3, which first undergoes addition to give the intermediate aminols 4 and then eliminates water to give the product imines 5. | ||
This manuscript describes efforts to extend this understanding and examines the effect of varying the para substituent on the electrophilic reagent (benzaldehydes 2a–f). This was carried out in order to examine the substituents effects of this two-step process to determine whether the fundamental understanding of substituent effects derived in molecular solvents can be applied in an ionic liquid. Consideration of the substituent effects was anticipated to also provide valuable insight into whether there are any changes in the reaction mechanism or rate-determining step between the different solvent types, which will contribute to the developing understanding of ionic liquid solvent effects.
Initially described are the outcome of the reactions in acetonitrile, and then in mixtures of the commonly used ionic liquid [Bmim][N(CF3SO2)2] 1 in acetonitrile to determine if the substituent effects are dependent on the proportion of ionic liquid in the reaction mixture. It is also of particular interest to examine the effect of the ionic liquid 1 on the elimination step, as this was not able to be determined previously.36,39 The ionic liquid solvent effects on elimination processes are not yet completely understood, with only a few examples in the literature.21,28,49–52 Hence, a thorough investigation of the effect of the ionic liquid on the outcome of the elimination process is an additional point of interest.
Experimental
Benzaldehydes 2a–f and hexan-1-amine 3 were all commercially available, and were either distilled (species 2a–c, 2e and 3) or sublimed (species 2d and 2f) under reduced pressure then stored at 253 K prior to use. Analytical grade deuterated acetonitrile was dried over molecular sieves for at least 48 h before use. The ionic liquid 1 was prepared according to literature methods:53,54 1-methylimiazole was treated with butyl bromide to afford the intermediate bromide salt ([Bmim][Br]), followed by salt metathesis with lithium bis(trifluoromethanesulfonyl)imide to give [Bmim][N(CF3SO2)2] 1. The ionic liquid 1 was dried to constant weight at 70 °C under reduced pressure immediately before use, and was found to have <0.1% water using Karl Fischer titration methodology and contained <0.1 mol% residual halide by ion chromatography.Reaction progress was monitored using 1H NMR spectroscopy on either a Bruker Avance III 400, Bruker Avance III 500 or Bruker Avance III 600 spectrometer with either a BBFO or TBI probe using ca. 0.5 mL of reaction mixture (details below) in a 5 mm NMR tube. Results were shown to be reproducible between the different spectrometers.
Kinetic analyses were carried out in solutions containing the benzaldehyde 2 of interest (ca. 0.02 mol L−1) and the amine 3 (ca. 0.25 mol L−1) at a given temperature and specific mole fraction of the ionic liquid, with the remaining solvent being made up by deuterated acetonitrile. NMR samples containing both the benzaldehyde 2 and amine 3 and the solvent mixture were prepared, and these samples were stored in liquid nitrogen to halt the reaction prior to analysis.
In each case the reaction was monitored in situ until more than 95% of the benzaldehyde 2 was consumed, with the spectrometer set to the desired temperature for the duration of the reaction, and all kinetic analyses were performed in triplicate. NMR spectra were processed using either the Bruker TOPSPIN 1.3 software or the MestReNova 7.1.1 software. For the 4-methylbenzaldehyde 2b cases, where no intermediate build up was detected, the pseudo-first order rate constants for the reactions were calculated using integrations of the aldehyde signal in the starting material 2 at δ ca. 10.0, obtained from the processed 1H NMR spectra, by fitting the natural logarithm of the integrations to a linear function using the Microsoft Excel 14.4.3 LINEST function. Bimolecular rate constants (k2,A) were obtained from the pseudo-first order constants by dividing by the initial amine 3 concentration in the reaction mixture. Where appropriate, the activation parameters were then determined through fitting the obtained data using the Microsoft Excel 14.4.3 LINEST function to the bimolecular Eyring equation31,55 (eqn (1)).
 | (1) |
For aldehydes 2d–f, where intermediate build-up was detected, integrations of the aldehyde signal in the starting material 2 at δ ca. 10, the corresponding proton in the intermediate 4 at δ ca. 5 and the imine proton in the product 5 at δ ca. 8.5 were obtained from the processed 1H NMR spectra. This data was then numerically integrated (fourth-order Runge-Kutta) to fit the mechanism outlined in Scheme 2 using the SOLVE function in Microsoft Excel 14.4.3 to optimize the rate constants. This allowed determination of the unimolecular rate constants for the elimination step (k1,E) and the reverse of the addition process (k−1,A), and the pseudo-first order rate constant for the (forward) addition step (k1,A) which was then converted to the bimolecular rate constant (k2,A) by dividing by the initial amine 3 concentration in the reaction mixture. For the elimination step the activation parameters were determined using the unimolecular Eyring equation (eqn (2)).55
 | (2) |
 | ||
| Scheme 2 Mechanism to which the kinetic data was numerically integrated in cases where intermediate build-up was detected. | ||
Tables containing the exact mole fractions of ionic liquid 1 used in the reaction mixture, amine 3 concentrations, temperature and rate constants for all the systems described below can be found in the ESI.†
Results and discussion
Before discussing the effects of substituents on the electrophile on the reaction shown in Scheme 1, it is necessary to discuss how the mechanism of the reaction influences analysis of the kinetic data. The condensation of each of the benzaldehydes 2a–f with the amine 3 proceeds through an addition-elimination mechanism (Scheme 1); there is initial nucleophilic attack of the amine 3 onto the carbonyl of the benzaldehyde 2 and proton transfer to give the intermediate aminol 4; this has been found to proceed either via a concerted mechanism in the gas phase,56 or through a stepwise process in aqueous solutions.57 When performed in organic solvents, experimental work suggests that there is significant charge development in the transition state, which is consistent with either the concerted or stepwise mechanism.58 This addition step is then followed by the subsequent elimination of water from the aminol 4 to give the product 5. The apparent bimolecular rate constant (k2,app) for this two step process (that is, the rate constant of product formation) will depend on the rate constant of both the addition (k2,A) and elimination (k1,E) processes, as well the rate constant for the reverse of the addition process (k−1,A), as shown in eqn (3).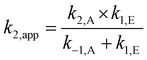 | (3) |
Previous work on the unsubstituted36 and methoxy substituted36,39 benzaldehydes 2c and 2a, respectively, found that for all the cases considered (different temperatures and different proportions of acetonitrile in a number ionic liquids) no build up of the intermediate 4 was ever detected. This indicated that the elimination step was significantly faster than the addition step, and hence that the addition step was rate-determining. This was unsurprising for these aldehydes as they bear an electron-donating group, which will deactivate them towards nucleophilic attack.
This previous work made an assumption that the bulk of any aminol 4 formed was converted to product 5 rather than reverting to starting material 2; that is k−1,A ≪ k1,E. This assumption was supported by the fact that for all systems considered (more than 25 solvent mixtures of 10 different ionic liquids) the apparent rate constant (k2,app) data produced linear Eyring plots. This could be due to the value k−1,A/k1,E being constant over the range of temperatures considered, and hence both the reverse addition and elimination processes have the same activation parameters in all solvent systems though it is considered that this is unlikely. Alternatively, a linear Eyring plot suggests that k−1,A is negligible compared to k1,E and that therefore k2,app = k2,A for aldehydes 2a and 2c (see eqn (3)). The validity of this assumption will be further reinforced in the subsequent discussions on the Hammett relationships.
One of the main conclusions from the previous investigations on benzaldehydes 2a36,39 and 2c36 was that the use of an ionic liquid accelerated the reaction due to an entropically favourable interaction between the cation of the ionic liquid and the nucleophilic nitrogen centre on the amine 3. It is important to note that the cation–nucleophile interaction also resulted in an enthalpic cost relative to the reaction in acetonitrile, yet the entropic benefit was more significant. In that work it was only possible to examine the addition process, as the elimination step was significantly faster than addition. Hence it was of interest to investigate the aldehydes 2b and 2d–f, firstly to examine the substituent effects on the process in acetonitrile and the ionic liquid 1, as well as a number of mixtures of acetonitrile and [Bmim][N(CF3SO2)2] 1 and, secondly, to attempt to monitor the second step of the reaction to allow the effects of the ionic liquid 1 on the elimination process to be examined. It was anticipated that increasing the electron withdrawing ability of the para substituent (σp) would further remove electron density from the electrophilic carbon, activating it and hence increasing k2,A. It was hoped that this increase in the rate constant of the addition step would result in k2,A no longer being significantly smaller than k1,E, leading to intermediate build-up and hence allowing k1,E to be determined.
Initially the reaction between the benzaldehydes 2 and hexan-1-amine 3 was monitored in acetonitrile; unsurprisingly for the methyl substituted aldehyde 2b, which has a substituent with a σp value intermediate to that of the substituents on substrates 2a and 2c, no intermediate build up was observed. Interestingly, for aldehydes 2d–f, containing an electron withdrawing group, significant build up of the intermediate aminol 4 was observed, allowing k2,A, k−1,A and k1,E to be determined (Table 1); importantly, for these cases k−1,A was found to be non-negligible when compared to k1,E. Firstly the substituent effects of the addition step will be discussed, and then the importance of k−1,A for the different substituents will be considered further.
| Substituent | k 2,A/10−3 L mol−1 s−1 | k −1,A/10−3 s−1 | K A/L mol−1 | k 1,E/10−3 s−1 | k 2,app/10−3 L mol−1 s−1 |
|---|---|---|---|---|---|
| a As the addition step was rate determining, no formation of the intermediate was detected using NMR spectroscopy so only k2,A could be determined. b k 1,E could be determined using a greatly increased nucleophile concentration ([3] = 2.5 mol L−1), yet under these conditions k2,A was too fast to be accurately measured and hence k−1,A and KA were unable to be determined. k2,A was determined from a different set of experiments using a lower nucleophile concentration. | |||||
| 2a R = MeO36,39 | 0.13 ± 0.02 | 0.13 ± 0.02 | |||
| 2b R = Mea | 0.27 ± 0.03 | 0.27 ± 0.03 | |||
| 2c R = H36 | 0.75 ± 0.06b | 7.51 ± 0.07b | 0.75 ± 0.06 | ||
| 2d R = Cl | 6.74 ± 0.03 | 7.51 ± 0.11 | 0.9 ± 0.1 | 1.73 ± 0.10 | 1.26 ± 0.12 |
| 2e R = CF3 | 33.0 ± 0.9 | 8.21 ± 0.23 | 4.0 ± 0.2 | 0.60 ± 0.05 | 2.26 ± 0.21 |
| 2f R = NO2 | 98.6 ± 5.4 | 7.03 ± 0.67 | 11.7 ± 1.2 | 0.24 ± 0.03 | 3.23 ± 0.35 |
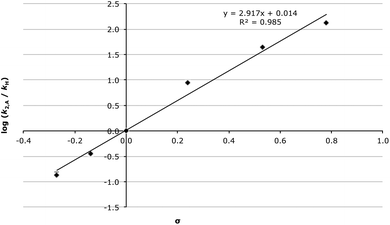
As the data in Table 1 shows, as the σp value of the substituent on the aldehyde substrate 2 was increased, there was an increase in the rate constant of the addition step (k2,A). The Hammett plot of k2,A (Fig. 1) is linear (R2 = 0.985), with gradient (or reaction constant, ρ) = 2.92 ± 0.09 indicating that this addition step is very susceptible to the electronic nature of the substituent. Such a large and positive ρ value suggests that there is a flow of electrons towards the aromatic ring when moving to the transition state. This trend is exactly as would be expected for this reaction type, and is consistent with related nucleophilic additions to carbonyl groups.59,60 It should be noted that it is feasible to separately fit the rate constants for σp ≤ 0 and σp > 0, and this results in large, positive ρ values for both fits (ρ = 3.19 ± 0.12 and ρ = 2.17 ± 0.06, respectively, Fig. S9†). A decreased reaction constant at higher σp could suggest that there is a shift from an open transition state for σp ≤ 0 to a more closed transition state for σp > 0.
The linearity of the fit in Fig. 1 is particularly important in the context of the earlier discussion suggesting that for aldehydes bearing an electron donating group k−1,A ≪ k1,E. The data in Table 1 and Fig. 1 assumes that k−1,A is negligible for aldehydes 2a–c where σp ≤ 0, but not for aldehydes 2d–f with σp > 0 where intermediate build up was readily observed; the values of k−1,A for these cases were determined from fitting as described in the Experimental section. This linear correlation yielding a ρ value as would be expected further reinforces the validity of the assumptions made, and indicates that for substrates bearing a para substituent with σp ≤ 0, k−1,A is not kinetically significant, and that for electron withdrawing substituents the value of k−1,A becomes kinetically significant. It is also important to highlight that during the fitting it was noted that k1,E was not sensitive to the values of k−1,A, hence the assumptions discussed above are only relevant for k2,A.
It is also of interest to examine the activation parameters of the addition step in acetonitrile, as these values will be compared to those determined in the ionic liquid 1 subsequently to determine the origin of any ionic liquid solvent effect. The activation parameters for the chloro substrate 2d were determined as an exemplar electron-withdrawing case to compare with the parent 2c and methoxy 2a aldehydes (Table 2).‡ It was found that with increasing σp of the substituent on the aldehyde 2 there was an increase in both the enthalpy and entropy of activation, with the increased entropy being more significant, leading to an overall reduction in the activation energy. This resulted in an increase in k2,A as the electron withdrawing nature of the substituent was increased (see Table 1 and Fig. 1).
The increased enthalpy of activation with larger σp suggests that as the electron-withdrawing ability of the substituent on the aldehyde 2 increases, the extent to which bonds are broken in the transition state increases. All of this is consistent with the transition state lying later along the reaction coordinate as σp increases. This is accompanied by an increase in the degrees of freedom in the transition state, as indicated by the less negative entropy of activation moving down Table 2.
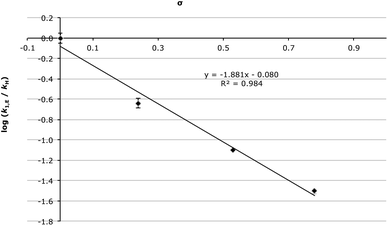
The substituent effects on the addition step have been thoroughly discussed, so it is now of interest to examine the substituent effects on the elimination step; note that k1,E was only able to be determined for aldehydes 2c–f. As the electron withdrawing ability of the substituent on the substrate 2 was increased the elimination rate constant (k1,E) decreased, with the Hammett plot of k1,E (Fig. 2) being linear (R2 = 0.984) with ρ = −1.88 ± 0.08. A negative ρ value suggests that on transition state formation there is a flow of electrons away from the aromatic ring, the opposite to what is seen for the addition step, and is consistent with positive change build up, with the ρ value comparable to that found for the hydrolysis of acetals.61 It is also important to note that the magnitude of ρ is smaller for the elimination step than for the addition step, indicating that the elimination process is less affected by the substituents’ electronic character than the addition case.
To determine the origin of these changes in the elimination rate constant, the activation parameters of the elimination process were determined for the chloro 2d, trifluoromethyl 2e and nitro 2f cases (Table 3). Interestingly the activation parameters for the trifluoromethyl 2e and nitro 2f cases were the same within uncertainty, while the activation parameters for the chloro 2d case were markedly different; although generally as the σp of the substituent increased, both the enthalpy and entropy of activation decreased. This data shows that for this unimolecular process, the rate decrease in the elimination step on going from substrate 2d to 2e to 2f is due to a decrease in the entropy of activation. This trend is consistent with the transition state lying earlier along the reaction coordinate as σp increases, resulting in a decreased extent of bond breaking with larger σp.
It is also interesting to note that as the electron withdrawing ability of the substituent increased (on going from chloro to trifluoromethyl to nitro) there was a shift in the equilibrium position of the addition process (KA, Table 1). As a result, despite the decreased elimination rate constant, the overall rate constant of the process (k2,app) still increases as the electron-withdrawing ability of the substituent was increased.
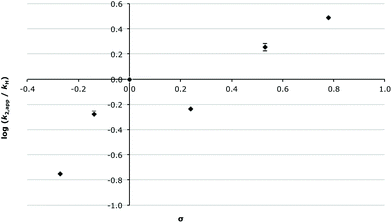
This last point is best demonstrated by the Hammett plot of the apparent second order rate constant (k2,app) for the overall process (Fig. 3); that is, k2,A for aldehydes 2a–c and k2,A × k1,E/(k−1,A + k1,E) for species 2d–f (eqn (3)). Clearly, with increased σp there is an increase in k2,app, indicating that as the electron-withdrawing nature of the substituent increases there is increased formation of the imine 5. Immediately apparent is that the Hammett plot is not linear but instead has decreasing slope with increasing σp; this is clearly demonstrated by the large change in ρ from ca. 3 at low values of σp to ca. 0.5 at the higher values of σp. This downwards curvature of a Hammett plot is consistent with a change in the rate-determining step of the process,42,59 which can also be clearly seen by the rate constants presented in Table 1 where the rate-determining step is addition for low σp and elimination for high σp. Further, it indicates a much greater dependence on the electronic nature of the substituent for the process that is rate determining at low values of σp than for the rate-determining step at high values of σp, as discussed earlier.
In summary, in acetonitrile the substituent effects on reaction outcome are relatively straightforward: increasing the electron withdrawing ability of the substituent increases the rate constant for the addition step with a concomitant decrease in the rate constant for the elimination process. This increase in k2,A, and the decrease in k1,E, results in a change in the rate determining step from addition to elimination as the electron withdrawing nature of the substituents increases.
Given the above, it is of interest to investigate how the ionic liquid 1 would affect the substituent effects observed in acetonitrile. For all the benzaldehydes 2a–f the reaction was conducted in a range of mole fractions of [Bmim][N(CF3SO2)2] 1 in acetonitrile.
Firstly the effect of the ionic liquid 1 on the addition step will be considered; as mentioned earlier previous work on the electron-donating aldehydes 2a and 2c found that as the proportion of an ionic liquid in the solvent mixture was increased there was a steady increase in k2,A.36,39 In those cases, the rate enhancement in the ionic liquid 1 was shown to be the result of an entropic benefit overcoming an enthalpic cost; this enthalpic cost corresponds to coordination and stabilisation of the nucleophile 3 by the cation of the ionic liquid (this can also be thought of as a decrease in the apparent nucleophilicity of hexan-1-amine 3 in [Bmim][N(CF3SO2)2] 1 relative to acetonitrile). On moving to the transition state, where the nucleophilic centre on 3 is no longer available to coordinate with the ionic liquid cation, there was an increase in disorder in the system resulting in a substantial entropic benefit relative to acetonitrile. For all substrates 2b and 2d–f as the amount of [Bmim][N(CF3SO2)2] 1 in the reaction mixture was increased there was a gradual increase in k2,A, as expected (Table 4, Fig. S2 and S5† for substrates 2d and 2e, respectively, and Fig. 4 and S1† for substrates 2f and 2b, respectively, where k2,A was determined at a number of different values of χIL). It is important to note the characteristic ‘dip’ in the mole fraction plot at χILca. 0.4, this has appeared many times in our previous work,28,36,39 and the source of this decrease in the rate constant at a particular proportion of ionic liquid is still under investigation. Importantly, for all substrates considered use of the ionic liquid 1 increases the rate constant of the addition step relative to acetonitrile, highlighting the utility of ionic liquids in promoting nucleophilic attack of a nitrogen centre onto a carbonyl group.
| Substituent |
k
2,A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a/10−3 L mol−1 s−1 a/10−3 L mol−1 s−1 |
||
|---|---|---|---|
| Acetonitrile | χ IL 0.2 | χ IL 0.9 | |
| a Uncertainties quoted represent the standard deviation of three replicates. | |||
| 2a R = MeO39 | 0.13 ± 0.02 | 0.49 ± 0.02 | 0.81 ± 0.04 |
| 2b R = Me | 0.27 ± 0.03 | 1.46 ± 0.06 | 2.83 ± 0.01 |
| 2c R = H36 | 0.75 ± 0.06 | 2.74 ± 0.03 | 4.86 ± 0.04 |
| 2d R = Cl | 6.74 ± 0.03 | 32.9 ± 1.5 | 37.4 ± 1.9 |
| 2e R = CF3 | 33.0 ± 0.9 | 93.1 ± 1.6 | 136 ± 3 |
| 2f R = NO2 | 98.6 ± 5.4 | 130 ± 16 | 250 ± 10 |
As the data in Table 4 shows, as the σp value of the substituent on the aldehyde substrate was increased there was an increase in the rate constant of the addition step (k2,A). The Hammett plot of k2,A at χILca. 0.2 (Fig. 5) is linear (R2 = 0.937), with ρ = 2.43 ± 0.16, as is the Hammett plot at χILca. 0.9 (Fig. S10†) with R2 = 0.967 and ρ = 2.41 ± 0.12. For these cases the linear correlation is not as strong as that seen in acetonitrile, and hence it is reasonable to consider two separate linear correlations for σp ≤ 0 and σp > 0; at χILca. 0.2 ρ = 2.77 ± 0.19 for σp ≤ 0, and ρ = 1.11 ± 0.11 for σp > 0 (Fig. 6), with a similar trend seen at χILca. 0.9 (Fig. S11†). For both mole fractions of [Bmim][N(CF3SO2)2] 1 in acetonitrile the magnitude of ρ is greater for σp ≤ 0 than σp > 0, suggesting that the reaction is more susceptible to electronic effects for electron donating substituents. Such a trend is indicative of a shift from an open transition state for σp ≤ 0 to a more closed transition state for electron withdrawing substituents; this is consistent with previous studies.19,31
Regardless of whether one or two linear fits are used, large, positive ρ values result, indicating that once again there is electron flow towards the aromatic system on moving to the transition state, and that while the addition step is very susceptible to the electronic nature of the substituent when in the ionic liquid 1, it is slightly less effected by the substituent than when in acetonitrile (where ρ = 2.92 ± 0.09). In order to investigate this further the activation parameters for the different substituents in acetonitrile and in the ionic liquid 1 (χILca. 0.2) need to be compared (Table 5).
| Substrate | χ IL | ΔH‡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a/kJ mol−1 a/kJ mol−1 |
ΔS‡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a/J K−1 mol−1 a/J K−1 mol−1 |
|---|---|---|---|
| a Uncertainties quoted are from the fit of the linear regression. | |||
| 2a R = MeO36,39 | 0 | 14.2 ± 1.0 | −333.1 ± 3.3 |
| 0.22 | 37.0 ± 0.9 | −242.1 ± 3.1 | |
| 2c R = H36 | 0 | 27.2 ± 2.5 | −272.1 ± 8.6 |
| 0.22 | 34.5 ± 1.5 | −233.2 ± 1.7 | |
| 2d R = Cl | 0 | 46.4 ± 3.7 | −185.2 ± 13.3 |
| 0.22 | 47.5 ± 3.0 | −168.1 ± 11.1 | |
As Table 5 shows, as σp increases the magnitude of the enthalpic cost when moving from acetonitrile to χIL 0.2 decreases; that is, the difference between the enthalpy of activation in acetonitrile and χIL 0.2 is largest for the methoxy substrate 2a, and is smallest for the chloro case 2d. The same trend is also seen for the entropy of activation; this is shown clearly in Table 6.
It is unlikely that on changing the substituent on the benzaldehyde 2 that the extent of interaction between the cation of the ionic liquid and the amine 3 would change, hence it is likely that these changes in activation parameters are the result of differences in the solvation of the transition state. This can be best explained by recalling what was discussed earlier for the addition step in acetonitrile: as σp increased both the enthalpy and entropy of activation increased and a later transition state was suggested. Such a change would also result in a greater build-up of charge (both on the oxygen and nitrogen centres) and hence a greater extent of interaction between the ionic liquid 1 and the transition state. The energetic result of such an interaction would be to decrease the enthalpy (benefit) and entropy of activation (cost) relative to acetonitrile; the opposite of the energetic result of cation–nucleophile 3 interaction. Therefore, increasing ionic liquid–transition state interaction would result in a greater ‘offsetting’ of the enthalpic cost and entropic benefit from the cation–nucleophile interaction, bringing the activation parameters for the ionic liquid 1 and acetonitrile closer together. This is clearly demonstrated in Table 6.
Another important consideration is the effect of use of an ionic liquid on the rate constant for the elimination step; for the chloro substrate 2d the rate constant was essentially unaffected by use of [Bmim][N(CF3SO2)2] 1 while for substrates 2e and 2f there is a gradual increase in k1,E as the proportion of ionic liquid in the reaction mixture was increased (Table 7, Fig. S3 and S6† for substrates 2d and 2e, respectively, and Fig. 7 for substrate 2f where k1,E was determined at a number of different values of χIL). Interestingly, this data shows that the magnitude of the rate enhancement seen when using the ionic liquid 1, relative to acetonitrile, increases as the electron-withdrawing ability of the substituent is increased.
| Substituent |
k
1,E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a/10−3 s−1 a/10−3 s−1 |
k 1,E (χIL 0.9)/k1,E (acetonitrile)b | ||
|---|---|---|---|---|
| Acetonitrile | χ IL 0.2 | χ IL 0.9 | ||
| a Uncertainties quoted represent the standard deviation of three replicates. b Uncertainties quoted are compounded from those previous in the table. | ||||
| 2d R = Cl | 1.73 ± 0.10 | 1.99 ± 0.03 | 1.73 ± 0.18 | 1.00 ± 0.12 |
| 2e R = CF3 | 0.60 ± 0.05 | 1.38 ± 0.05 | 2.62 ± 0.14 | 4.34 ± 0.10 |
| 2f R = NO2 | 0.24 ± 0.03 | 0.71 ± 0.08 | 1.27 ± 0.06 | 5.31 ± 0.15 |
In order to understand the microscopic origin of the changes in k1,E seen when using [Bmim][N(CF3SO2)2] 1 in the reaction mixture, the activation parameters of the elimination process were determined in a number of mixtures of [Bmim][N(CF3SO2)2] 1 and acetonitrile for aldehydes 2d–f (Table 8). For each case the activation parameters were determined in acetonitrile (as discussed earlier) and at χILca. 0.2 to allow comparison between the different substrates, with additional activation parameters determined for the trifluoromethyl 2e and nitro 2f cases to determine whether the activation parameters varied as the mole fraction of ionic liquid in the solvent mixture was changed.
| Substituent | χ IL | ΔH‡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a/kJ mol−1 a/kJ mol−1 |
ΔS‡![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a/J K−1 mol−1 a/J K−1 mol−1 |
|---|---|---|---|
| a Uncertainties quoted are from the fit of the linear regression. b The substrate 2f was not completely soluble in 1, so a small amount of acetonitrile was used to aid solubility resulting in a slightly decreased χIL. | |||
| 2d R = Cl | 0 | 90.3 ± 6.7 | 21.2 ± 24.1 |
| 0.22 | 71.8 ± 2.1 | −40.5 ± 7.6 | |
| 2e R = CF3 | 0 | 54.7 ± 3.5 | −111.8 ± 12.2 |
| 0.21 | 70.5 ± 4.1 | −48.6 ± 14.9 | |
| 0.95 | 67. 2 ± 2.1 | −55.5 ± 7.7 | |
| 2f R = NO2 | 0 | 55.2 ± 4.3 | −117.2 ± 14.9 |
| 0.06 | 72.6 ± 3.0 | -51.8 ± 11.0 | |
| 0.22 | 84.8 ± 2.6 | −6.1 ± 9.0 | |
| 0.88b | 87.6 ± 4.4 | 11.4 ± 16.2 | |
Immediately apparent is that the use of the ionic liquid 1 resulted in an increase in both the enthalpy and entropy of activation for the elimination step in the reaction of benzaldehydes 2e and 2f with the amine 3, relative to acetonitrile. Such a trend is indicative of the ionic liquid 1 ordering about and stabilising the species 4 to a greater extent than the transition state leading to the product 5. Based on previous studies that suggest that interaction between an ionic liquid cation and a nitrogen lone pair is important,28,31,33,35,36,38,39 it is reasonable to assume that the main interaction here is once again between the cation and the nitrogen lone pair on the aminol 4. Such an interaction would inhibit bond formation, resulting in an increased enthalpy of activation relative to acetonitrile. Once again the entropic benefit incurred when using the ionic liquid 1 is more significant than the enthalpic cost, resulting in an entropically driven rate enhancement; this further reinforces the importance of entropic effects when using ionic liquids. This conclusion is supported by kinetic studies on the base-induced, bimolecular elimination of a benzisoxazole, a nitrogen-containing substrate, where a similar trend in the activation parameters was found when using an ionic liquid.52
Interestingly, for the chloro substrate 2d there was the opposite trend in the activation parameters for the elimination step seen when using the ionic liquid 1; that is, a decrease in both the enthalpy and entropy of activation relative to acetonitrile. This can be readily rationalised by considering the earlier conclusion that the transition state of the chloro analogue 4d involves significantly more bond breaking and charge development than the trifluoromethyl and nitro cases. With greater charge separation there will be increased ionic liquid–transition state interaction, which would stabilise the transition state and be enthalpically favourable, yet the increased ordering would introduce an entropic cost. Hence, for the chloro case 4d, which involves significant build-up of charge in the transition state, it can be concluded that the extent of ionic liquid–transition state interaction is greater than the cation–nucleophile interaction, leading to the energetic result of the transition state interaction being dominant.
It is important to note that for all substrates 2d–f it is likely that there will be both cation–aminol 4 and ionic liquid–transition state interaction, and that the extent of charge development in the transition state will dictate which interaction is dominant. The importance of considering the subtle balance of the different interactions between the ionic liquid and species along the reaction coordinate has been highlighted in a number of different studies,12 and further demonstrates the complexity of ionic liquid solvent effects, along with reinforcing the importance of gaining a thorough understanding of this reaction media so that their effect on reaction outcome can be readily predicted.
Finally, for the elimination process it is also important to compare the Hammett plots in acetonitrile and the ionic liquid 1; in the ionic liquid 1 the log plot§ was linear at χIL 0.2, with gradient = −0.83 ± 0.08 (R2 = 0.955, Fig. S12†). This shows that: (1) build-up of positive charge in the transition state is key as was seen in acetonitrile, and (2) the magnitude of the slope is significantly smaller in the ionic liquid 1 than in acetonitrile. This suggests that the charge development in the transition state is decreased in the ionic liquid and hence k1,E is less susceptible to the electronic nature of the substituent when using the ionic liquid 5. At a higher mole fraction (χIL 0.9, Fig. S13†), the equivalent log plot was no longer linear; this is likely due to the very different ionic liquid–transition state interactions for the different substrates 2d–f, as discussed above.
For the electron-withdrawing cases the rate constants for the reverse of the addition step (k−1,A) were able to be determined (Table 9, and Fig. S4 and S7† for substrates 2d and 2e, respectively, and Fig. S8† for substrate 2f where k−1,A was determined at a number of different values of χIL), showing that use of the ionic liquid 1 also increased the rate constant of this process relative to acetonitrile. Importantly, while k−1,A remained relatively unchanged for substrates 2d–f in acetonitrile, when in the ionic liquid 1 there was a gradual decrease in k−1,A as σp increases.
While data for the substrate 2c is not available, a plot of the log of the rate data§ is linear, with gradient = −1.08 ± 0.12 (R2 = 0.951, Fig. S14†) at χIL 0.2, and gradient = −0.53 ± 0.05 (R2 = 0.947, Fig. S15†) at χIL 0.9. A negative value for the gradient suggests that on transition state formation there is a flow of electrons away from the aromatic ring. Interestingly, the magnitude of the slope decreases when moving from χIL 0.2 to 0.9, suggesting that with increasing amounts of the ionic liquid 1 in the reaction mixture k−1,A is less affected by the electron-withdrawing ability of the substituent. The implications of this change in k−1,A will be discussed in the context of k2,app below.
To conclude this work, it is now essential to see how the overall rate constant for the process (k2,app) changed when moving between acetonitrile and [Bmim][N(CF3SO2)2] 1, and to compare the Hammett plot of k2,app in acetonitrile and mixtures of acetonitrile and [Bmim][N(CF3SO2)2] 1. As the amount of the ionic liquid 1 in the reaction mixture was increased, there was a gradual increase in k2,app for all substrates 2a–f (Table 10). In other words, for all of the benzaldehydes 2a–f the use of the ionic liquid 1 resulted in an increase in the rate of imine formation relative to acetonitrile. This is significant as it further demonstrates the ability of ionic liquids to accelerate organic reactions, and highlights the utility of using an ionic liquid solvent to promote imine formation.
| Substituent |
k
2,app![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a/10−3 L mol−1 s−1 a/10−3 L mol−1 s−1 |
||
|---|---|---|---|
| Acetonitrile | χ IL 0.2 | χ IL 0.9 | |
| a Uncertainties quoted represent the standard deviation of three replicates. | |||
| 2a R = MeO39 | 0.13 ± 0.02 | 0.49 ± 0.02 | 0.81 ± 0.04 |
| 2b R = Me | 0.27 ± 0.03 | 1.46 ± 0.06 | 2.83 ± 0.01 |
| 2c R = H36 | 0.75 ± 0.06 | 2.74 ± 0.03 | 4.86 ± 0.04 |
| 2d R = Cl | 1.26 ± 0.12 | 1.58 ± 0.06 | 1.60 ± 0.15 |
| 2e R = CF3 | 2.26 ± 0.21 | 4.95 ± 0.34 | 9.99 ± 0.69 |
| 2f R = NO2 | 3.23 ± 0.35 | 8.41 ± 0.17 | 10.5 ± 0.69 |
Interestingly, in mixtures containing the ionic liquid 1 there was not a gradual increase in k2,app with increasing σp as seen for acetonitrile; this is best seen by considering the Hammett plot for k2,app in [Bmim][N(CF3SO2)2] 1 (Fig. 8 for χIL 0.2 and Fig. S16† for χIL 0.9). Clearly, the Hammett plot no longer shows a clear concave-down profile as seen for acetonitrile, with a similar trend seen across the range of proportions of ionic liquid used. It is important to note that the k2,app values for the electron withdrawing cases 2d–f lie lower than expected based on the acetonitrile Hammett plot (Fig. 3), with the chloro case 2d in particular standing out, as it slower than the parent benzaldehyde 2c.
The different shape of these Hammett plots highlight that the ionic liquid 1 is affecting the overall condensation process differently to acetonitrile. This difference can be rationalised by considering the three separate rate constants, discussed above, for the process in the ionic liquid 1, and how each would affect k2,app (see eqn (3), reproduced below). The key points are: (1) k2,A increases with larger σp, and hence changes in the rate constant of the addition step could not explain the decreased k2,app values for σp > 0; (2) k1,E decreases as the electron-withdrawing ability of the substituent increases, with the chloro substrate 2d having a particularly low k1,E value, hence this could contribute to the lower k2,app and (3) k−1,A also decreases as σp increases, with k−1,A being significantly larger for the chloro case 2d than for nitro 2f. By considering eqn (3) it is clear that this difference in k−1,A would have the largest impact on k2,app for all electron withdrawing substrates, and would account for the decreases in the apparent rate constant.
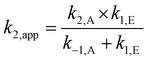 | (3) |
In other words, for the chloro substrate 1d the large rate constant for the reverse of the addition process shifts the equilibrium position of the addition step to the left, resulting in a significant decrease in the overall rate constant of formation of the imine 5. This decrease in k2,app is compounded by the lower k1,E values for substrate 1d, further decreasing k2,app. The magnitude of k−1,A decreases when moving from chloro 1d to trifluromethyl 1e to nitro 1f, resulting in the extent to which k2,app is decreased by k−1,A becoming less significant as σp increases. Importantly, this trend in k2,app further reinforces the assumptions described earlier that k−1,A is significant for σp > 0 and is not significant for σp ≤ 0: the k2,app values for aldehydes 2a–c follow the expected trend, with deviations seen only for the electron withdrawing substituents highlighting that the rate constant for the reverse of the addition process is only significant for σp > 0. It is also important to highlight than in acetonitrile k−1,A remains relatively unchanged between the electron withdrawing cases, resulting in a smooth concave-down profile of the Hammett plot of k2,app.
Lastly, the work presented throughout this manuscript suggests that the typically used substituent parameters describing electronic effects in molecular solvents are still valid in ionic liquid media for the reaction of substituted benzaldehydes 2a–f. The Hammett plots for each of the separate steps produced good linear correlations, with reaction constants in line with what would be expected for these reaction types.47 This allows us to suggest that it is not necessary to modify the substituent parameters when utilising ionic liquid solvents.
Conclusions
In summary, use of the ionic liquid 1 resulted in increased imine formation relative to acetonitrile, highlighting the possible synthetic utility of using an ionic liquid solvent for condensation reactions. Extensive kinetic analysis showed that the ionic liquid 1 increased the rate constant for each of the three individual steps that make up the reaction relative to acetonitrile, with the rate increases generally driven by the ionic liquid solvating the reagents to a greater extent than the transition state. The effect of changing the para substituent on the substrate 2 on the rate constant of each of the three processes was found to vary between acetonitrile and the ionic liquid 1, with the Hammett plot for the overall addition-elimination process being markedly different in [Bmim][N(CF3SO2)2] 1 than in acetonitrile. These differing substituent effects were found to arise due to the greater susceptibility of the ionic liquid 1 to respond to subtle changes in the extent of charge development in the transition state as the electronic nature of the substituent was varied; this is important as it is the first time that the sensitivity of an ionic liquid to differing degrees of charge development has been demonstrated through activation parameters. Overall, the importance of considering the delicate balance of microscopic interactions between the ionic liquid and species along the reaction coordinate has been further reinforced.Acknowledgements
STK acknowledges the support of the Australian government through the receipt of an Australian Postgraduate Award. JBH acknowledges financial support from the Australian Research Council Discovery Project Funding Scheme (Project DP130102331). The authors would like to acknowledge the NMR Facility within the Mark Wainwright Analytical Centre at the University of New South Wales for NMR support.Notes and references
- A. F. Trindade, P. M. P. Gois and C. A. M. Afonso, Chem. Rev., 2009, 109, 418–514 CrossRef CAS PubMed.
- C. S. Yeung and V. M. Dong, Chem. Rev., 2011, 111, 1215–1292 CrossRef CAS PubMed.
- A. de la Hoz, A. Diaz-Ortiz and A. Moreno, Chem. Soc. Rev., 2005, 34, 164–178 RSC.
- H. M. Yau, S. T. Keaveney, B. J. Butler, E. E. L. Tanner, M. S. Guerry, S. R. D. George, M. H. Dunn, A. K. Croft and J. B. Harper, Pure Appl. Chem., 2013, 85, 1979 CrossRef CAS.
- P. Wasserscheid and W. Keim, Angew. Chem., Int. Ed., 2000, 39, 3772–3789 CrossRef CAS.
- S. Z. El Abedin and F. Endres, Acc. Chem. Res., 2007, 40, 1106–1113 CrossRef CAS PubMed.
- K. R. Seddon, Kinet. Catal. Engl. Transl., 1996, 37, 693–697 CAS.
- C. L. Hussey, Pure Appl. Chem., 1988, 60, 1763–1772 CrossRef CAS.
- M. J. Earle, J. M. S. S. Esperanca, M. A. Gilea, J. N. Canongia Lopes, L. P. N. Rebelo, J. W. Magee, K. R. Seddon and J. A. Widegren, Nature, 2006, 439, 831–834 CrossRef CAS PubMed.
- J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576 CrossRef CAS PubMed.
- M. T. Clough, C. R. Crick, J. Grasvik, P. A. Hunt, H. Niedermeyer, T. Welton and O. P. Whitaker, Chem. Sci., 2015, 6, 1101–1114 RSC.
- S. T. Keaveney, R. S. Haines and J. B. Harper, in Encyclopedia of Physical Organic Chemistry, ed. U. Wille, Wiley, in press Search PubMed.
- J. P. Hallett, C. L. Liotta, G. Ranieri and T. Welton, J. Org. Chem., 2009, 74, 1864–1868 CrossRef CAS PubMed.
- G. Ranieri, J. P. Hallett and T. Welton, Ind. Eng. Chem. Res., 2008, 47, 638–644 CrossRef CAS.
- N. L. Lancaster, T. Welton and G. B. Young, J. Chem. Soc., Perkin Trans. 2, 2001, 2267–2270 RSC.
- H. Yanai, H. Ogura and T. Taguchi, Org. Biomol. Chem., 2009, 7, 3657–3659 CAS.
- C. Chiappe, D. Capraro, V. Conte and D. Pieraccini, Org. Lett., 2001, 3, 1061–1063 CrossRef CAS PubMed.
- R. Bini, C. Chiappe, E. Marmugi and D. Pieraccini, Chem. Commun., 2006, 897–899 RSC.
- R. Bini, C. Chiappe, C. S. Pomelli and B. Parisi, J. Org. Chem., 2009, 74, 8522–8530 CrossRef CAS PubMed.
- F. D'Anna, V. Frenna, R. Noto, V. Pace and D. Spinelli, J. Org. Chem., 2006, 71, 5144–5150 CrossRef PubMed.
- F. D'Anna, V. Frenna, V. Pace and R. Noto, Tetrahedron, 2006, 62, 1690–1698 CrossRef PubMed.
- M. J. Earle, S. P. Katdare and K. R. Seddon, Org. Lett., 2004, 6, 707–710 CrossRef CAS PubMed.
- S. T. Keaveney, J. B. Harper and A. K. Croft, RSC Adv., 2015, 5, 35709–35729 RSC.
- B. Kirchner, O. Hollóczki, J. N. Canongia Lopes and A. A. H. Pádua, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 202–214 CrossRef CAS PubMed.
- C. Chiappe and C. S. Pomelli, Phys. Chem. Chem. Phys., 2013, 15, 412–423 RSC.
- S. Zahn, M. Brehm, M. Brüssel, O. Hollóczki, M. Kohagen, S. Lehmann, F. Malberg, A. S. Pensado, M. Schöppke, H. Weber and B. Kirchner, J. Mol. Liq., 2014, 192, 71–76 CrossRef CAS PubMed.
- C. D. Hubbard, P. Illner and R. van Eldik, Chem. Soc. Rev., 2011, 40, 272–290 RSC.
- S. T. Keaveney and J. B. Harper, RSC Adv., 2013, 3, 15698–15704 RSC.
- B. Y. W. Man, J. M. Hook and J. B. Harper, Tetrahedron Lett., 2005, 46, 7641–7645 CrossRef CAS PubMed.
- H. M. Yau, S. A. Barnes, J. M. Hook, T. G. A. Youngs, A. K. Croft and J. B. Harper, Chem. Commun., 2008, 3576–3578 RSC.
- H. M. Yau, A. G. Howe, J. M. Hook, A. K. Croft and J. B. Harper, Org. Biomol. Chem., 2009, 7, 3572–3575 CAS.
- S. G. Jones, H. M. Yau, E. Davies, J. M. Hook, T. G. A. Youngs, J. B. Harper and A. K. Croft, Phys. Chem. Chem. Phys., 2010, 12, 1873–1878 RSC.
- H. M. Yau, A. K. Croft and J. B. Harper, Faraday Discuss., 2012, 154, 365–371 RSC.
- E. E. L. Tanner, R. R. Hawker, H. M. Yau, A. K. Croft and J. B. Harper, Org. Biomol. Chem., 2013, 11, 7516–7521 CAS.
- E. E. L. Tanner, H. M. Yau, R. R. Hawker, A. K. Croft and J. B. Harper, Org. Biomol. Chem., 2013, 11, 6170–6175 CAS.
- S. T. Keaveney, K. S. Schaffarczyk McHale, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2014, 12, 7092 CAS.
- B. J. Butler and J. B. Harper, New J. Chem., 2015, 39, 213–219 RSC.
- S. T. Keaveney, D. V. Francis, W. Cao, R. S. Haines and J. B. Harper, Aust. J. Chem., 2015, 68, 31–35 CrossRef CAS.
- S. T. Keaveney, R. S. Haines and J. B. Harper, Org. Biomol. Chem., 2015, 13, 3771–3780 CAS.
- L. P. Hammett, J. Chem. Phys., 1936, 4, 613–617 CrossRef CAS PubMed.
- L. P. Hammett, J. Am. Chem. Soc., 1937, 59, 96–103 CrossRef CAS.
- N. S. Isaacs, Physical Organic Chemistry, Addison Wesley Longman Limited, Harlow, 1998 Search PubMed.
- C. D. Ritchie and E. S. Lewis, J. Am. Chem. Soc., 1962, 84, 591–594 CrossRef CAS.
- R. Bini, C. Chiappe, C. S. Pomellic and B. Parisi, J. Org. Chem., 2009, 74, 8522–8530 CrossRef CAS PubMed.
- K. E. Johnson, R. M. Pagni and J. Bartmess, Monatsh. Chem., 2007, 138, 1077–1101 CrossRef CAS.
- Y. Chu, H. Deng and J.-P. Cheng, J. Org. Chem., 2007, 72, 7790–7793 CrossRef CAS PubMed.
- Z. Wang, H. Deng, X. Li, P. Ji and J.-P. Cheng, J. Org. Chem., 2013, 78, 12487–12493 CrossRef CAS PubMed.
- H. Deng, X. Li, Y. Chu, J. He and J.-P. Cheng, J. Org. Chem., 2012, 77, 7291–7298 CrossRef CAS PubMed.
- H. M. Yau, S. J. Chan, S. George, J. Hook, A. Croft and J. Harper, Molecules, 2009, 14, 2521–2534 CrossRef CAS PubMed.
- B. C. Ranu and R. Jana, J. Org. Chem., 2005, 70, 8621–8624 CrossRef CAS PubMed.
- F. D'Anna, S. L. Marca and R. Noto, J. Org. Chem., 2008, 73, 3397–3403 CrossRef PubMed.
- F. D'Anna, S. La Marca, P. Lo Meo and R. Noto, Chem. – Eur. J., 2009, 15, 7896–7902 CrossRef PubMed.
- H. Srour, H. Rouault, C. C. Santini and Y. Chauvin, Green Chem., 2013, 15, 1341–1347 RSC.
- S. Steines, P. Wasserscheid and B. Drießen-Hölscher, J. Prakt. Chem., 2000, 342, 348–354 CrossRef CAS.
- H. Eyring, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS PubMed.
- N. E. Hall and B. J. Smith, J. Phys. Chem. A, 1998, 102, 4930–4938 CrossRef CAS.
- M. Ciaccia and S. Di Stefano, Org. Biomol. Chem., 2005, 13, 646–654 Search PubMed.
- M. Ciaccia, R. Cacciapaglia, P. Mencarelli, L. Mandolini and S. Di Stefano, Chem. Sci., 2013, 4, 2253–2261 RSC.
- H. H. Jaffé, Chem. Rev., 1953, 53, 191–261 CrossRef.
- H. M. Yau, R. S. Haines and J. B. Harper, J. Chem. Educ., 2015, 92, 538–542 CrossRef CAS.
- B. Capon and K. Nimmo, J. Chem. Soc., Perkin Trans. 2, 1975, 1113–1118 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Rate constant data on which all the Hammett plots are based; additional Hammett plots, as referenced in the text; mole fraction dependent rate constant data and plots for all systems discussed, including the data on which the plots in Fig. 4 and 7 are based; temperature dependent kinetic data from which the activation parameters shown in Tables 2, 3, 5 and 8 are derived. See DOI: 10.1039/c5ob01214g |
| ‡ Attempts were made to determine the activation parameters for the substrates 2e and 2f, but due to the magnitude of k2,A for these cases the subtle changes in the rate constant with changing temperature were not sufficiently large to allow activation parameters to be accurately determined. |
| § As the rate constant for the unsubstituted case was not available, a ‘true’ Hammett plot could not be obtained. However, a plot of the log of the rate constants for the other species has a slope corresponding to the reaction constant so can be used for comparison. |
| This journal is © The Royal Society of Chemistry 2015 |