 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Invariom based electron density studies on the C/Si analogues haloperidol/sila-haloperidol and venlafaxine/sila-venlafaxine†
Peter
Luger
*a,
Birger
Dittrich
b and
Reinhold
Tacke
*c
aInstitut für Chemie und Biochemie – Anorganische Chemie, Freie Universität Berlin, Fabeckstraße 36a, D-14195 Berlin, Germany. E-mail: lugerp@zedat.fu-berlin.de
bInstitut für Angewandte und Anorganische Chemie, Universität Hamburg, Martin-Luther-King-Platz 6, D-20146 Hamburg, Germany
cInstitut für Anorganische Chemie, Universität Würzburg, Am Hubland, D-97074 Würzburg, Germany. E-mail: r.tacke@uni-wuerzburg.de
First published on 9th July 2015
Abstract
The subjects of this study are the structures and electron densities of the carbon/silicon analogues haloperidol/sila-haloperidol (1a/1b) and venlafaxine/sila-venlafaxine (2a/2b). The parent carbon compounds 1a (an antipsychotic agent) and 2a (an antidepressant) are both in clinical use. For haloperidol/sila-haloperidol, three published structures were studied in more detail: the structures of haloperidol hydrochloride (1a·HCl), haloperidol hydropicrate (1a·HPic) and sila-haloperidol hydrochloride (1b·HCl). For venlafaxine/sila-venlafaxine, the published structures of venlafaxine (2a), venlafaxine hydrochloride (2a·HCl; as orthorhombic (2a·HCl-ortho) and monoclinic polymorph (2a·HCl-mono)) and sila-venlafaxine hydrochloride (2b·HCl) were investigated. Based on these structures, the molecular electron densities were reconstructed by using the invariom formalism. They were further analysed in terms of Bader's quantum theory of atoms in molecules, electrostatic potentials mapped onto electron density isosurfaces and Hirshfeld surfaces. These studies were performed with a special emphasis on the comparison of the corresponding carbon/silicon analogues.
Introduction
Starting with the first pioneering studies on biologically active organosilicon compounds five decades ago, silicon chemistry is nowadays an established source of chemical diversity in drug design, with quite promising perspectives.1 Sila-substitution (carbon/silicon switch, carbon/silicon exchange) is one of the strategies that have been successfully used for the development of new silicon-based drugs.2 Based on this strategy, some years ago we have synthesized the silicon analogues of the dopamine D2 antagonist haloperidol (1a) and the serotonin/noradrenaline reuptake inhibitor venlafaxine (2a), sila-haloperidol (1b) and sila-venlafaxine (2b), and have evaluated the biological properties of these compounds (Fig. 1).3,4 As alcohols of the formula type R3COH (R = organyl) differ from the analogous silanols R3SiOH both in their chemical and physiochemical properties, replacement of the R3COH carbon atom of 1a and 2a by a silicon atom was very promising, because the OH groups of 1a and 2a are pharmacophoric groups. | ||
| Fig. 1 Chemical structures of haloperidol (1a), sila-haloperidol (1b), venlafaxine (2a), sila-venlafaxine (2b), bexarotene (3a) and disila-bexarotene (3b). | ||
Haloperidol (1a), which was developed in the late 1950s,5 is an antipsychotic agent that is still in clinical use for the treatment of schizophrenia, although it may cause severe extrapyramidal side effects, including parkinsonism and tardive dyskinesia.6 The pyridinium-type metabolite HPP+ was proposed to contribute to these neurotoxic side effects.7 As shown by radioligand binding studies at all five human dopamine receptor subtypes, the silicon analogue sila-haloperidol (1b) shows a 5-fold higher affinity for hD2 receptors than haloperidol (1a) itself, whereas the C/Si analogues 1a and 1b are approximately equipotent at all the other dopamine receptors (differences are less than 2-fold).3b As a result, the subtype selectivity of the silicon compound 1b for hD2 over the other dopamine receptors is higher than that of the parent carbon compound 1a. Functional studies at hD1 and hD2 receptors revealed similar results.3c As shown by studies in human and rat liver microsomes and hepatocytes, the metabolic fate of haloperidol (1a) and sila-haloperidol (1b) is quite different.3b,d Most importantly, a silicon analogue of the neurotoxic metabolite HPP+ is not formed in the metabolism of 1b; instead, two silanediols were detected.
Racemic venlafaxine (2a) is in clinical use as an antidepressant.8 Sila-substitution of 2a was found to dramatically influence the pharmacological selectivity profile with respect to serotonin, noradrenaline and dopamine reuptake inhibition. Upon C/Si exchange, the potency at serotonin transporters is reduced by approximately 2 orders of magnitude, whereas a small increase in potency was observed at the noradrenaline and dopamine transportes.4b Thus, the pharmacological selectivity profile of the silicon compound 2b was not suitable for its further development as an antidepressant. Instead, (R)-sila-venlafaxine ((R)-2b), a selective noradrenaline reuptake inhibitor, was preclinically developed as a drug for the treatment of emesis.4c,d Interestingly, the carbon analogue (R)-venlafaxine ((R)-2a) is a selective serotonin/noradrenaline reuptake inhibitor.4b
To understand the changes of the pharmacological selectivity profiles upon sila-substitution of 1a and 2a, we were interested to get some more information about the similarities and dissimilarities of the respective C/Si analogues on the molecular level. We have recently examined the similarities/dissimilarities of the retinoid agonists bexarotene (3a) and disila-bexarotene (3b) (Fig. 1) on the level of their molecular electron density distribution (EDD),9 which provides information about ligand–receptor interaction on an atomic scale beyond the structure, i.e., connectivity, bond lengths and angles. The invariom formalism10,11 provides the EDD and derived properties with only moderate effort, and we have therefore extended our investigations and have studied the EDD of the C/Si pairs 1a/1b and 2a/2b.
Invariom refinement and analysis of the electron density
For the C/Si pair haloperidol/sila-haloperidol (1a/1b), we made use of the known crystal structures of haloperidol hydrochloride (1a·HCl, CSD access code BIDFUQ12),3a haloperidol hydropicrate (1a·HPic, CUCYUV12)13 and sila-haloperidol hydrochloride (1b·HCl, BIDGAX12).3a In contrast to the neutral bexarotene (3a) and disila-bexarotene (3b) molecules studied before,9 compounds 1a·HCl, 1a·HPic and 1b·HCl are salts, i.e., they contain protonated haloperidol or sila-haloperidol as the cation in their solid-state structures. These three structures allow to compare the properties of (i) the two C/Si-analogous cations (protonated haloperidol versus protonated sila-haloperidol) and (ii) protonated haloperidol in the presence of two different counterions (chloride versus picrate).For the C/Si pair venlafaxine/sila-venlafaxine (2a/2b), we investigated four published data sets obtained from single-crystal X-ray diffraction experiments: venlafaxine (2a, OCALAG12) itself,14 two polymorphs of venlafaxine hydrochloride (2a·HCl) in orthorhombic (2a·HCl-ortho, WOBMUV12)15 and monoclinic form (2a·HCl-mono, WOBMUV0112)16 and sila-venlafaxine hydrochloride (2b·HCl, GEDBIB12).4b The data sets used refer to the respective racemates. These four structures allow to compare the properties of (i) the neutral venlafaxine (2a) molecule with the two ionic forms 2a·HCl-ortho and 2a·HCl-mono, (ii) the two chemically identical salts 2a·HCl-ortho and 2a·HCl-mono in different crystal systems (orthorhombic versus monoclinic) and (iii) the cations of the two forms of venlafaxine hydrochloride (2a·HCl-ortho and 2a·HCl-mono) with the cation of the silicon analogue sila-venlafaxine hydrochloride (2b·HCl).
The invariom formalism and the corresponding data base of aspherical scattering factors were applied. It relies on the Hansen & Coppens ‘multipole’ scattering-factor model.17 The procedure was similar to that described in some more detail in ref. 9, except that bond distances to hydrogen atoms were elongated to values from energy minimized structures of the respective model compounds also used in scattering-factor assignment. Hydrogen positions were idealized and constrained in a riding model; constraints were generated with the preprocessor program InvariomTool.18 After invariom transfer, refinement of positional and anisotropic displacement parameters for non-hydrogen atoms was carried out making use of the XD2006 program suite.19 In the case of the salt structures, full charge transfer was assumed, and the chlorine atom was treated as a chloride anion.
Special attention had to be payed to the invariom assignment for the disordered picrate in the structure of 1a·HPic, which was carried out with the program MoleCoolQt.20 It is a quite novel aspect that has so far not been well covered in the literature to model (partially) disordered structures with invarioms, although case studies with disordered solvent or side-chain disorder were already published.21 In principle, the procedure is straightforward. Initially the invariom scattering factor names of all atoms in a structure need to be known and assigned also to the disordered atoms. This can be done manually when there is only minor disorder, but it becomes impractical for larger disordered molecules. Then the density-normalized multipole populations that describe the deviation of valence electron density from a spherically symmetric distribution need to be modified. Disorder modeled with split occupancies already provides partial atomic occupancy parameters, and these then need to be multiplied with the DFT-derived multipole parameters of the invariom database. In the XD program such populations might already be a fraction of unity when an atom resides on a special position, and if applicable this also needs to be taken into account. A publication that reports on the tools that we have developed to facilitate the practical procedure using the example of a severely disordered cephalosporin antibiotic is in preparation.
Selected crystallographic and refinement data are summarized in Table 1 (for 1a·HCl, 1a·HPic and 1b·HCl) and Table 2 (for 2a, 2a·HCl-ortho, 2a·HCl-mono and 2b·HCl). In a next step, the molecular EDDs obtained in these studies were evaluated by topological analysis according to Bader's quantum theory of atoms in molecules (QTAIM formalism),22 using the subprogram XDPROP of XD2006.19
| Compound | 1a·HCl | 1a·HPic | 1b·HCl |
|---|---|---|---|
| a For further data, see ref. 3a and 13. | |||
| Formula | C21H24Cl2FNO2 | C27H26ClFN4O9 | C20H24Cl2FNO2Si |
| Crystal system | Monoclinic | Orthorhombic | Triclinic |
| Space group (No.) | P21/c (14) | Pna21 (33) |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (2) (2) |
| Z | 4 | 4 | 2 |
| V [Å3] | 1981.9(3) | 2723.8(2) | 1077.6(3) |
| (sinθ/λ)max [Å–1] | 0.64 | 0.76 | 0.63 |
| Unique reflections | 4168 | 7472 | 3895 |
| Observed reflections [Fo2 ≥ 2σ(Fo2)] | 3660 | 5784 | 3096 |
| Multipole refinement: | |||
| R(F) | 0.0300 | 0.0327 | 0.0339 |
| R all(F) | 0.0351 | 0.0512 | 0.0453 |
| R w(F) | 0.0268 | 0.0185 | 0.0265 |
| R(F2) | 0.0419 | 0.0387 | 0.0489 |
| R all(F2) | 0.0425 | 0.0432 | 0.0510 |
| R w(F2) | 0.0537 | 0.0364 | 0.0526 |
| Min/max Δρ [e Å–3] | –0.506/0.604 | –0.245/0.442 | –0.208/0.484 |
| Gof | 3.09 | 1.49 | 2.14 |
| N ref/Nv | 13.7 | 14.0 | 11.6 |
| Compound | 2a | 2a·HCl-ortho | 2a·HCl-mono | 2b·HCl |
|---|---|---|---|---|
| a For further data, see ref. 4b and 14–16. | ||||
| Formula | C17H27NO2 | C17H28ClNO2 | C17H28ClNO2 | C16H28ClNO2Si |
| Crystal system | Monoclinic | Orthorhombic | Monoclinic | Orthorhombic |
| Space group (no.) | P21/n (14) | Pca21 (29) | P21/n (14) | Pca21 (29) |
| Z | 4 | 4 | 4 | 4 |
| V [Å3] | 1566.9(7) | 1766.0(6) | 1740.9(19) | 1787.7(4) |
(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ)max [Å–1] θ/λ)max [Å–1] |
0.65 | 0.70 | 0.61 | 0.64 |
| Unique reflections | 3428 | 2474 | 3216 | 3825 |
| Observed reflections [Fo2 ≥ 2σ(Fo2)] | 2600 | 1629 | 1422 | 3664 |
| Multipole refinement: | ||||
| R(F) | 0.0323 | 0.0408 | 0.0450 | 0.0229 |
| R all(F) | 0.0595 | 0.1173 | 0.1465 | 0.0243 |
| R w(F) | 0.0283 | 0.0254 | 0.0598 | 0.0204 |
| R(F2) | 0.0345 | 0.0444 | 0.0719 | 0.0365 |
| R all(F2) | 0.0377 | 0.0748 | 0.0953 | 0.0367 |
| R w(F2) | 0.0567 | 0.0498 | 0.1186 | 0.0410 |
| Min/max Δρ [e Å–3] | –0.161/0.199 | –0.222/0.222 | –0.349/0.342 | –0.136/0.203 |
| Gof | 1.51 | 2.02 | 1.49 | 2.42 |
| N ref/Nv | 12.5 | 7.5 | 6.5 | 16.9 |
Results and discussion
Structural properties
The molecular structures of 1a·HCl, 1a·HPic and 1b·HCl as well as 2a, 2a·HCl-ortho, 2a·HCl-mono and 2b·HCl are displayed in ORTEP23 representations in Fig. 2 and 3, respectively, generated with PLATON.24 Atomic numbering schemes from the original publications (ref. 3a and 13 for 1a·HCl, 1a·HPic and 1b·HCl; ref. 4b and 14–16 for 2a, 2a·HCl-ortho, 2a·HCl-mono and 2b·HCl) were maintained. Therefore, atom numbering for 1a·HCl and 1b·HCl are identical, but differ from that of 1a·HPic, and the structures of 2a·HCl-ortho and 2a·HCl-mono agree in their atom numbering, but not with 2a or 2b·HCl. | ||
| Fig. 2 ORTEP23 representation24 of the molecular structures of 1a·HCl (a), 1a·HPic (b) and 1b·HCl (c) with their counterions. The used atomic numbering schemes are also shown. | ||
 | ||
| Fig. 3 ORTEP23 representation24 of the molecular structures of 2a (a), 2a·HCl-ortho (b), 2a·HCl-mono (c) and 2b·HCl (d), if applicable with their counterions. The used atomic numbering schemes are also shown. | ||
In all three structures, the piperidinium/silapiperidinium ring has a chair conformation, with the hydroxyl oxygen atom in an axial and the N-organyl group in an equatorial position. The already reported flattening of the silapiperidinium ring of 1b·HCl3a compared to the piperidinium rings of 1a·HCl and 1a·HPic is expressed quantitatively by the endocyclic torsion angles around the Si–C bonds, which are close to ±44°. This value is more than 10° smaller than that for the corresponding C–C torsion angles of 1a·HCl and 1a·HPic.
The inclination of the chlorophenyl ring with respect to the piperidinium/silapiperidinium ring as quantified by the torsion angle C8–C7–C1–C13 (or equivalent numbering in 1a·HPic) is alike in 1a·HPic and 1b·HCl (torsion angles 127.8(2)° and 130.4(2)°, respectively) but different compared with 1a·HCl (torsion angle 75.8(2)°). The major conformational difference is seen along the bond C18–C19 (or equivalent numbering in 1a·HPic). The torsion angle C17–C18–C19–C20 is −164.1(1)° for 1a·HCl, −82.6(2)° for 1a·HPic and 71.8(2)° for 1b·HCl, so that pronounced conformational flexibility exists along this bond. It follows that the molecular structures of the cations of compounds 1a·HCl, 1a·HPic and 1b·HCl are quite different.
The conformation of the tertiary amine 2a is completely different to those of the ammonium salts 2a·HCl-ortho, 2a·HCl-mono and 2b·HCl. This is due to an intramolecular hydrogen bond in 2a discussed below, which is not present in the ammonium salts. It follows that the molecular structures of the ammonium cations of 2a·HCl-ortho, 2a·HCl-mono and 2b·HCl are similar, but completely different from that of the tertiary amine 2a.
Intermolecular interactions
Hydrogen bonds between the ammonium cation and the counterion exist in all three haloperidol/sila-haloperidol structures studied (1a·HCl, 1a·HPic and 1b·HCl; Fig. 4, Table 3). The hydrogen bonds are OH⋯Cl and NH⋯Cl interactions for 1a·HCl and 1b·HCl and OH⋯O and NH⋯O contacts to oxygen atoms of the picrate anion of 1a·HPic. In the case of 1a·HCl and 1b·HCl, atom sequences O–H⋯Cl⋯H–N lead to infinite chains of cations linked to their chloride counterions. In the case of 1a·HPic, O–H⋯O–N–O⋯H–N interactions also lead to infinite chains of cations linked to the picrate counterion, where the twofold acceptor fragment O–N–O is one of the three nitrato groups of the picrate anion, and the N–H donor group of the piperidinium ring forms a bifurcated hydrogen bond with a neighbored oxygen atom of the picrate anion as a second acceptor. The special conformational situation at the bond C18–C19 of 1a·HCl allows an additional (weak) C–H⋯O contact to the adjacent cation. | ||
| Fig. 4 Intermolecular hydrogen bonds of 1a·HCl (a), 1a·HPic (b) and 1b·HCl (c) in the crystal, leading to a linkage between neighbored ammonium cations via the chloride (a, c) and picrate (b) counterion (SCHAKAL representations39). | ||
| Compound | D–H⋯A | D⋯A [Å] | H⋯A [Å] | ρ(rBCP) [e Å–3] | ∇2ρ(rBCP) [e Å–5] |
|---|---|---|---|---|---|
| a Symmetry code: 1 − x, 2 − y, −z. b Symmetry code: 1 − x, 1/2 + y, 1/2 − z. c Symmetry code: x, 5/2 – y, −1/2 + z. d Symmetry code: 1/2 + x, 1/2 − y, z. e Symmetry code: x, y, z. f Symmetry code: −1 + x, y, z. | |||||
| 1a·HCl | O1–H1⋯Cla | 3.194(1) | 2.24(2) | 0.13 | 1.88 |
| 1a·HCl | N1–HN⋯Clb | 3.038(1) | 2.02(2) | 0.21 | 2.71 |
| 1a·HCl | C15–H15B⋯O2c | 3.324(1) | 2.30(2) | 0.08 | 1.08 |
| 1a·HPic | O2A–H2O⋯O61Bd | 2.841(2) | 1.90(2) | 0.15 | 2.66 |
| 1a·HPic | N1A–H1N⋯O1Be | 2.703(1) | 1.73(1) | 0.24 | 3.85 |
| 1a·HPic | N1A–H1N⋯O62Be | 3.008(1) | 2.35(2) | 0.06 | 1.08 |
| 1b·HCl | O1–H1⋯Clf | 3.149(2) | 2.19(2) | 0.14 | 1.96 |
| 1b·HCl | N1–HN⋯Cle | 3.077(2) | 2.06(1) | 0.19 | 2.49 |
A summary of the hydrogen bonding topologies for the venlafaxine/sila-venlafaxine structures (2a, 2a·HCl-ortho, 2a·HCl-mono and 2b·HCl) is given in Fig. 5 and Table 4. An intramolecular O1–H1⋯N1 hydrogen bond exists in the neutral tertiary amine 2a, whereas in the ammonium salts 2a·HCl-ortho, 2a·HCl-mono and 2b·HCl intermolecular O–H⋯Cl and N–H⋯Cl hydrogen bonds establish O–H⋯Cl⋯H–N bridging sequences via the chloride counterion, leading to infinite chains of cations linked by their chloride counterions.
 | ||
| Fig. 5 Intermolecular hydrogen bonds of 2a·HCl-ortho (a) and 2b·HCl (b) in the crystal, leading to a linkage between neighbored ammonium cations via the chloride counterion (SCHAKAL representations39). The hydrogen bonding system of 2a·HCl-mono (not shown) is comparable. | ||
| Compound | D–H⋯A | D⋯A [Å] | H⋯A [Å] | ρ(rBCP) [e Å–3] | ∇2ρ(rBCP) [e Å–5] |
|---|---|---|---|---|---|
| a Symmetry code: x, y, z. b Symmetry code: x, 1 + y, z. c Symmetry code: 1 + x, y, z. d Symmetry code: −x, −y, −1/2 + z. | |||||
| 2a | O1–H1⋯N1a | 2.713(1) | 1.82(1) | 0.22 | 2.97 |
| 2a·HCl-ortho | O2–H2B⋯Cla | 3.178(3) | 2.22(2) | 0.13 | 1.97 |
| 2a·HCl-ortho | N1–H1A⋯Clb | 3.046(3) | 2.03(1) | 0.21 | 2.66 |
| 2a·HCl-mono | O2–H27⋯Clc | 3.212(5) | 2.28(2) | 0.12 | 1.62 |
| 2a·HCl-mono | N1–H28⋯Cla | 3.034(6) | 2.03(2) | 0.21 | 2.70 |
| 2b·HCl | O1–HO⋯Cld | 3.119(1) | 2.17(1) | 0.15 | 2.05 |
| 2b·HCl | N1–HN⋯Cla | 3.064(1) | 2.17(1) | 0.16 | 2.15 |
Hence, in all cases where chloride is the counterion (1a·HCl, 1a·HPic, 1b·HCl, 2a·HCl-ortho, 2a·HCl-mono, 2b·HCl), the pattern of intermolecular interaction is basically the same.
Bond topological and atomic properties
The molecular EDD of the title compounds as reconstructed from invariom fragments was subjected to a quantitative analysis according to Bader's QTAIM formalism.22 This analysis provides both bond critical points (BCPs, defined by the property that the gradient ∇ρ(r) vanishes at this point) and atomic properties by integration over the atomic basins bound by the zero flux surfaces of the gradient vector field, which subdivide a structure into transferable substructures.BCPs were located on all covalent bonds and on the H(donor)⋯X(acceptor) (X = Cl, O) linkages of the hydrogen bonds. ED values, Laplacians and ellipticities [ρ(rBCP), ∇2ρ(rBCP), ε], which provide information about the strength and nature of a bond, are summarized in Tables 5 and 6. It turned out, that – as expected – the obtained quantities are practically the same for comparable bond types so that only averages for the structures of 1a·HCl, 1a·HPic and 1b·HCl are listed in Table 5, while averages for the structures of 2a, 2a·HCl-ortho, 2a·HCl-mono and 2b·HCl are given in Table 6. Detailed lists for all seven compounds are provided in the ESI (Tables S1–S7†). Moreover, inspection of Tables 5 and 6 indicates a close agreement in all bond topological properties of comparable bonds of all compounds studied.
| Bond | Length [Å] | ρ(rBCP) [e Å–3] | ∇2ρ(rBCP) [e Å–5] | ε | N | C–C bond orderc |
|---|---|---|---|---|---|---|
| a The ellipticity ε is defined by (λ1/λ2) − 1, with λ1 and λ2 being the two principal negative curvatures of ρ(r) at a BCP and is a measure for the asphericity and hence the double bond character of a bond. b N = number of entries contributing to the average. c The bond order nb was calculated as nb = exp[C1(ρ(rBCP) − C2)], with C1 = 1.0229 and C2 = 1.6459.40 d Only 1b·HCl. e Not included for 1a·HPic, because of disorder. | ||||||
| C–C (aromatic) | 1.385(9) | 2.16(5) | −18.2(12) | 0.21(3) | 36 | 1.67 |
| C–C (single) | 1.522(8) | 1.71(2) | −11.5(4) | 0.04(2) | 18 | 1.07 |
| Si–Cd | 1.864(8) | 0.86(2) | +3.8(3) | 0.06(3) | 3 | |
(O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) )C–C )C–C |
1.498(15) | 1.79(4) | −12.7(5) | 0.08(3) | 6 | 1.16 |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Oe Oe |
1.213 | 2.95 | −32.9 | 0.09 | 2 | |
| C–O(H) | 1.424 | 1.82 | −13.1 | 0.04 | 2 | |
| Si–O(H)d | 1.623 | 1.01 | +17.3 | 0.07 | 1 | |
| C–N | 1.500(8) | 1.82(3) | −11.5(5) | 0.01(1) | 9 | |
| C–F | 1.339(3) | 1.92(1) | −16.6(2) | 0.01(1) | 3 | |
| C–Cl | 1.732(10) | 1.32(3) | −2.3(3) | 0.06(2) | 3 | |
| Bond | Length [Å] | ρ(rBCP) [e Å–3] | ∇2ρ(rBCP) [e Å–5] | ε | N | C–C bond orderc |
|---|---|---|---|---|---|---|
| a The ellipticity ε is defined by (λ1/λ2) − 1, with λ1 and λ2 being the two principal negative curvatures of ρ(r) at a BCP and is a measure for the asphericity and hence the double bond character of a bond. b N = number of entries contributing to the average. c The bond order nb was calculated as nb = exp[C1(ρ(rBCP) − C2)], with C1 = 1.0229 and C2 = 1.6459.40 d Only 2b·HCl. e Only 2a (neutral). f Only 2a·HCl-ortho, 2a·HCl-mono and 2b·HCl (charged). g Only 2a, 2a·HCl-ortho and 2a·HCl-mono. h Only 2b·HCl. | ||||||
| C–C (aromatic) | 1.392(8) | 2.14(2) | −17.5(7) | 0.21(2) | 24 | 1.65 |
| C–C (single) | 1.530(14) | 1.68(4) | −10.8(8) | 0.03(2) | 33 | 1.04 |
| Si–Cd | 1.88(3) | 0.86(2) | +3.6(1) | 0.05(1) | 3 | |
| C–Ne | 1.417(5) | 1.70(1) | −6.2(1) | 0.16(1) | 3 | |
| C–Nf | 1.494(9) | 1.85(3) | −11.4(5) | 0.01(1) | 9 | |
| C–O(H)g | 1.430(9) | 1.79(2) | −12.5(9) | 0.03(1) | 3 | |
| Si–O(H)h | 1.629 | 1.00 | +16.8 | 0.02 | 1 | |
| C(aromatic)–O | 1.359(8) | 2.08(2) | −18.6(10) | 0.09(1) | 4 | |
| H3C–O | 1.413(9) | 1.85(4) | −11.8(8) | 0.02(1) | 4 | |
If the central carbon atom in 1a·HCl/1a·HPic or 2a·HCl-ortho/2a·HCl-mono is replaced by a silicon atom (→1b·HCl or 2b·HCl), the following changes in bond topological properties are observed: for the longer Si–C and Si–O bonds (compared to the analogous C–C and C–O bonds), the ED values are much lower. For the Si–C bonds, the values of ρ(rBCP) and ∇2ρ(rBCP) are comparable to those reported for disila-bexarotene (3b),9 except that the Laplacian was slightly negative in 3b but is positive in the present cases. However, it was already noted that this is insignificant because the Laplacian along the Si–C bond has a steep slope close to the BCP and can easily change the sign in its vicinity as illustrated in Fig. 6 for 2b·HCl. For the Si–O bonds in 1b·HCl and 2b·HCl, the Laplacians of +17.3 and +16.8 e Å−5 are strongly positive. Si–O bonds were recently examined in detail by experiment and theory.25–27 The ρ(rBCP) values of the Si–O bonds reported were in the range 0.86 to 0.97 e Å−3; the corresponding Laplacians were +16.0 to +25.2 e Å−5 and are therefore in the same range as in 1b·HCl and 2b·HCl. This means that the Si–O bond has a highly ionic character. Fig. 6 shows the Laplacians along the non-polar C8–C7 and the polar C8–O2 bond in 2a·HCl-ortho and the analogous Si–C6 and Si–O1 bonds in 2b·HCl to illustrate their different character.
 | ||
| Fig. 6 Laplacian distributions along the C8–C7 and C8–O2 bonds in 2a·HCl-ortho (above) and along the Si–C6 and Si–O1 bonds in 2b·HCl (below). | ||
Atomic properties were calculated by integration over the atomic basins described above. The algorithm provided by XDPROP19 was used, which was introduced by Volkov et al.28 Since Bader volumes and charges are additive, it can easily be checked whether the calculation has worked properly. The atomic charges should sum up to the total charge of the considered species (e.g. zero in the neutral or +1 in the cationic case), and the sum of the atomic volumes multiplied by Z should reproduce the unit cell volume. This was fulfilled in all cases so that the integrations were accepted as correct.
A selection of atomic volumes and charges for 1a·HCl, 1a·HPic and 1b·HCl is given in Table 7 and for 2a, 2a·HCl-ortho, 2a·HCl-mono and 2b·HCl in Table 8. Only those atoms are listed where |q| > 0.15 e for one of the contributing structures (a complete list is given in the ESI; Tables S8–S14†). We note that for the hydrogen atoms only the two atoms involved in hydrogen bonding carry significant (positive) charges.
| Atoma | q [e] | V tot [Å3] |
|---|---|---|
| a Atom numbering according to 1a·HCl and 1b·HCl; the data for 1a·HPic refer to chemically equivalent atoms. b Affected by disorder or disordered neighbor atoms. c All further hydrogen atoms have charges and volumes in the range 0.05–0.14 e and 6–9 Å3, respectively. | ||
| C1/Si | 0.31/0.31/2.99 | 5.78/6.13/3.97 |
| O1 | −0.92/−0.93/−1.36 | 15.94/16.73/20.47 |
| O2 | −0.91/−b/−0.91 | 16.75/—b/18.44 |
| Cl1 | −1.18/—/−1.01 | 35.40/—/34.95 |
| Cl2 | −0.22/−0.22/−0.23 | 33.14/34.02/41.72 |
| F | −0.58/−0.58/−0.59 | 17.51/18.49/19.77 |
| N | −0.91/−0.81/−0.91 | 8.37/8.17/8.57 |
| C7 | −0.06/−0.05/−0.83 | 10.35/9.81/15.97 |
| C13 | −0.05/−0.02/−0.70 | 8.65/7.56/11.45 |
| C14 | 0.17/0.19/0.18 | 7.85/7.73/7.42 |
| C15 | 0.18/0.21/0.20 | 7.65/6.92/7.36 |
| C16 | −0.06/−0.03/−0.80 | 7.96/8.01/12.58 |
| C17 | 0.16/0.20/0.21 | 8.09/7.61/7.21 |
| C20 | 0.78/1.06b/0.79 | 7.94/6.66b/7.95 |
| C24 | 0.43/0.46/0.43 | 8.88/7.90/10.31 |
| HOc | 0.62/0.58/0.59 | 1.63/2.19/2.08 |
| HNc | 0.60/0.50/0.48 | 1.37/1.99/2.29 |
| Atoma | q [e] | V tot [Å3] |
|---|---|---|
| a Atom numbering according to 2a/2a·HCl-ortho = 2a·HCl-mono/2b·HCl. Note: atomic numbering for 2a·HCl-ortho and 2a·HCl-mono is the same. b All further hydrogen atoms have charges and volumes in the range 0.03–0.09 e and 6–10 Å3, respectively. | ||
| C5/C8/Si | 0.29/0.32/0.31/3.02 | 5.60/5.37/5.39/3.70 |
| O1/O2/O1 | −0.93/−0.94/−0.93/−1.37 | 14.52/14.64/14.89/18.76 |
| O2/O1/O2 | −0.91/−0.93/−0.93/−0.92 | 16.49/14.56/16.19/15.52 |
| Cl1/Cl1/Cl | —/−1.01/−1.00/−1.00 | —/38.28/37.36/37.10 |
| N1/N1/N | −0.81/−0.87/−0.89/−0.89 | 9.88/8.43/8.64/8.42 |
| C1/C15/C9 | 0.22/0.20/0.21/0.20 | 8.94/9.82/9.66/8.72 |
| C2/C16/C8 | 0.22/0.19/0.21/0.20 | 8.93/9.52/8.61/9.78 |
| C3/C14/C7 | 0.23/0.21/0.21/0.19 | 6.94/7.18/7.14/7.26 |
| C4/C7/C6 | 0.01/0.02/0.03/–0.78 | 6.78/6.66/6.47/10.26 |
| C6/C13/C5 | −0.04/−0.03/−0.01/−0.81 | 7.71/7.55/7.53/12.30 |
| C10/C9/C1 | −0.05/−0.01/0.00/−0.81 | 8.29/7.33/7.78/12.12 |
| C14/C4/C13 | 0.37/0.37/0.41/0.39 | 8.65/8.98/9.22/8.64 |
| C17/C17/C16 | 0.34/0.39/0.38/0.37 | 9.68/9.55/8.37/9.37 |
| HOb | 0.54/0.56/0.56/0.59 | 2.16/2.23/2.39/2.01 |
| HNb | —/0.48/0.47/0.48 | —/2.26/2.46/2.82 |
All three haloperidol/sila-haloperidol structures (1a·HCl, 1a·HPic and 1b·HCl) contain strongly negative centres at the two oxygen and at the piperidinium nitrogen sites, with charges close to −1 e. A moderately negative charge is found at the fluorine atom, whereas the second halogen atom at the chlorophenyl ring has only a rather small negative charge. While the atomic properties of 1a·HCl and 1a·HPic are very much alike, they are different from those of 1b·HCl in that the silicon atom exhibits a strongly positive charge with q ≈ +3 e. An Si atomic charge close to +3 e looks quite unexpected. However, there are examples in the literature supporting this finding. Already in 1998 Pedersen et al. have reported an Si charge of +3.35 e for a silatrane derivative, commented by these authors that this value is “somewhat counterintuitive”.29a The Bader formalism was also applied by Grabowsky et al. on a number of silicon derivatives.25,27 They made use of high resolution X-ray experimental data and periodic and non-periodic theoretical calculations and came to Si atomic charges in a range of +2.5 to +3.0 e. Experimental and theoretical ED studies on silicon compounds with large positive Bader charges of Si (e.g. +2.78 from experimental ED and +3.13 e from a B3LYP/6-311G** calculation) were also reported by Kocher et al.29b and Ott et al.29c In none of the above-mentioned references the invariom formalism was applied so that this aspect has obviously no influence on the Si charge.
The above-mentioned strongly negative charges are compensated by the adjacent covalently bound atoms. The piperidinium nitrogen atom for example carries a charge of −0.91/–0.81/–0.91 e in 1a·HCl/1a·HPic/1b·HCl, whereas the sum of the charges of the four direct neighbor atoms is +1.11/+1.10/+1.07 e. Hence, only an excess charge of 0.16–0.29 e is distributed in the environment of the nitrogen atom.
The atomic properties of the four venlafaxine/sila-venlafaxine structures (2a, 2a·HCl-ortho, 2a·HCl-mono and 2b·HCl; Table 8) can be discussed in the same manner as for the haloperidol/sila-haloperidol structures. Negative charges are found for hydroxyl and methoxy oxygen atoms and the nitrogen atom of the dimethylamino/dimethylammonio group. In the neutral tertiary amine 2a, the nitrogen atom carries a Bader charge of −0.81 e, while the sum of the charges of the three neighboring carbon atoms is +0.67 e, so that a small charge of −0.14 e remains. The situation is somewhat different for the ammonium salts 2a·HCl-ortho, 2a·HCl-mono and 2b·HCl, where the average charge at the nitrogen atoms is −0.88 e and that of the four nitrogen-bound atoms (including HN) is +0.20 e, hence slightly positive and comparable to the finding for 1a·HCl, 1a·HPic and 1b·HCl. There is also a significant difference in the volume of the nitrogen atom in the neutral and cationic form: in the neutral tertiary amine 2a, the atomic volume is by 1.5 Å larger than in the ammonium salts 2a·HCl-ortho, 2a·HCl-mono and 2b·HCl. As observed for 1b·HCl, the silicon atom of 2b·HCl has a strongly positive charge.
Molecular surfaces
In mutual drug–receptor recognition processes involving pharmacologically relevant molecules, molecular surfaces and the corresponding surface properties play an important role. That is why we consider both the electrostatic potential (ESP) mapped onto an EDD isosurface and the Hirshfeld surface:(i) The ESP was calculated by using the method of Volkov et al.30 with the XDPROP subprogram of XD200619 and colour coded onto the 0.0067 e Å−3 (= 0.001 a.u.) EDD isosurface (see Fig. 7–10).31 The study of the ESP is very helpful for understanding molecular polarization and reactivity behavior.
 | ||
| Fig. 7 Electrostatic potentials of the ammonium cations of 1a·HCl (a), 1a·HPic (b) and 1b·HCl (c) mapped onto the isoelectron density surface ρ = 0.0067 e Å−3.31 | ||
 | ||
| Fig. 8 Electrostatic difference potential 1b·HCl/1a·HCl.31 | ||
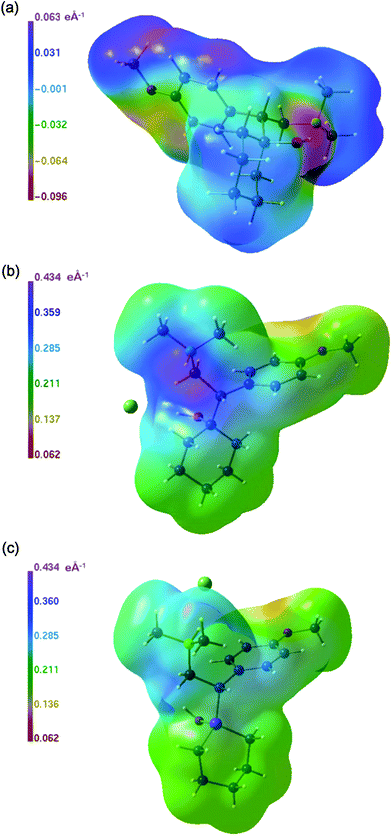 | ||
| Fig. 9 Electrostatic potentials of 2a (a), 2a·HCl-ortho (b) and 2b·HCl (c) mapped onto the isoelectron density surface ρ = 0.0067 e Å−3.31 | ||
 | ||
| Fig. 10 Electrostatic difference potential of 2b·HCl/2a·HCl-ortho.31 | ||
(ii) The Hirshfeld surface32,33 is defined by the ratio of the molecular EDD versus the crystal density when equal to 0.5. When the aspherical EDD is mapped by a colour code onto this surface, EDD concentrations are emphasized so that sites and strengths of intermolecular interactions become visible (see Fig. 11 and 12).31
 | ||
| Fig. 11 Hirshfeld surfaces of 1a·HCl (a), 1a·HPic (b) and 1b·HCl (c).31 | ||
 | ||
| Fig. 12 Hirshfeld surfaces of 2a (a), 2a·HCl-mono (b) and 2b·HCl (c).31 | ||
The ESP surfaces of the ammonium cations of 1a·HCl, 1a·HPic and 1b·HCl are displayed in Fig. 7. All three cationic structures have in common a polarization between the central region around the piperidinium/silapiperidinium fragment, with the strongest positive ESP, and the terminal p-chloro- and p-fluorophenyl rings, where the ESP is less positive. The ESP distribution supports findings regarding the atomic charges around the nitrogen atom as discussed above, in that the formal charge of +1 e of the cation is distributed over a larger range of the neighbored atoms. This was also observed earlier by a multipole refinement with high-resolution X-ray diffraction data of a protonated opioid derivative.34
The ESP distributions for the cations of 1a·HCl and 1a·Pic (Fig. 7a and 7b) are rather alike and compare well also with the major features of 1b·HCl (Fig. 7c). However, a detailed inspection of Fig. 7c reveals that the carbon environment of the silicon atom of 1b·HCl looks somewhat different. This is emphasized in the surface of the difference potential between 1b·HCl and 1a·HCl as shown in Fig. 8. Note that the figure legend indicates only a small potential difference of less than 0.1 e Å−1, which is however exclusively located in a torus shaped region around the silicon atom. Outside this region the difference potential is zero.
The ESP distributions for 2a, 2a·HCl-ortho and 2b·HCl are displayed in Fig. 9. The neutral molecule 2a has two negative surface regions around the oxygen atoms, a rather extended region at the methoxy oxygen atom and a smaller localized region at the hydroxyl oxygen atom (Fig. 9a); otherwise, the ESP surface is positive. The ESPs of 2a·HCl-ortho and 2a·HCl-mono are equal within the graphical error, so that only the ESP of 2a·HCl-ortho is shown (Fig. 9b). The surface region around the nitrogen atom is the most positive one, which is not true for the silicon analogue 2b·HCl (Fig. 9c). As a consequence, a negative region around the silicon atom is seen in the difference potential 2b·HCl minus 2a·HCl-ortho as shown in Fig. 10. The difference potentials in Fig. 8 and 10 are obtained by subtraction of very similar quantities, so that a more detailed quantitative interpretation does not seem justified.
The Hirshfeld surfaces of 1a·HCl, 1a·Pic and 1b·HCl are depicted in Fig. 11. The darkest colour is indicative of EDD concentrations, which coincide with the donor and acceptor sites of the hydrogen bonds listed in Table 3. Neither for 1a·Pic nor 1b·HCl further EDD concentrations are visible. For 1a·HCl, the weak C–H⋯O linkage is seen as an EDD concentration of medium strength above the hydrogen atom of the donor carbon atom C15 and at the acceptor oxygen atom O2. A further EED concentration above the terminal fluorine atom results from a short F⋯F contact of 2.627 Å (van der Waals radius of fluorine: 1.47 Å)35 between two molecules related via a crystallographic inversion centre. Comparable non-bonded F⋯F contacts shorter than the van der Waals distance have been reported earlier and examined on the basis of the electron density.36,37 Another non-negligible EDD concentration above one of the hydrogen atoms at C17 is caused by a weak contact to the chloride anion. Thus, EDD mapped onto the Hirshfeld surface is a very fine probe to recognize all intermolecular contacts in a crystal structure at one glance, whereas some of them might easily be overlooked in an analysis based on geometric criteria.
Intermolecular contacts of the venlafaxine/sila-venlafaxine structures are also visible on Hirshfeld surfaces as shown in Fig. 12, where coloured sites for the ammonium salts 2a·HCl-ortho, 2a·HCl-mono and 2b·HCl again indicate charge concentrations caused by the intermolecular contacts as discussed before (Fig. 12b and 12c). Consequently, the Hirshfeld surface of the tertiary amine 2a (Fig. 12a) is almost featureless, and the very weak signals are due to weak C–H⋯O contacts around 2.65 Å. The Hirshfeld surfaces of 2a·HCl-ortho and 2a·HCl-mono are practically identical, so that only the illustration for 2a·HCl-mono is shown (Fig. 12b). The only two strong EDD concentrations are found at the O–H and N–H donor sites. The same features are seen for the Hirshfeld surface of the silicon analogue 2b·HCl (Fig. 12c), where some additional weak signals indicate C–H⋯Cl contacts around 2.7–2.9 Å.
Conclusion
The electron density distribution of three haloperidol/sila-haloperidol (1a·HCl, 1a·HPic, 1b·HCl) and four venlafaxine/sila-venlafaxine (2a, 2a·HCl-ortho, 2a·HCl-mono, 2b·HCl) structures as provided by the invariom formalism was investigated. Although there is some conformational flexibility in the ammonium cations, the dominant intermolecular interactions are alike and consist of infinite cation⋯counterion⋯cation⋯chains. Only in the case of 1a·HCl, an additional weak C–H⋯O contact between two cations exists. In the neutral tertiary amine 2a, only an intramolecular O–H⋯N hydrogen bond is present. Hirshfeld surfaces make strong as well as weak intermolecular interactions visible and can therefore serve as a convenient tool for recognizing the influence of the entire crystal environment of a chemical system. The bond topological properties for the chemically comparable bonds agree well, except for the C–X/Si–X bonds (X = C, O). Pronounced differences between the carbon compounds and their corresponding silicon analogues (1a·HCl/1a·HPic versus1b·HCl and 2a/2a·HCl-ortho/2a·HCl-mono versus2b·HCl) are seen for the integrated atomic Bader charges. In all ammonium cations and in the neutral tertiary amine, the oxygen and nitrogen atoms are strongly negative centres. For the silicon compounds 1b·HCl and 2b·HCl, an additional positive centre at the silicon atom is found (Si atomic charge ≈ +3 e). Although these atomic charge distributions indicate some differences in the electronic structures of the C/Si analogues, the major features of polarization between the central piperidinium/silapiperidinium fragment and the terminal p-chloro- and p-fluorophenyl rings in the electrostatic potentials look similar for 1a·HCl, 1a·HPic and 1b·HCl. Only the electrostatic difference potential of 1b·HCl and 1a·HCl makes a significant non-zero region visible around the site, where the central carbon atom of 1a·HCl is replaced by a silicon atom (→1b·HCl). In case of the venlafaxine/sila-venlafaxine structures, the neutral tertiary amine 2a completely differs from the ammonium salts 2a·HCl-ortho, 2a·HCl-mono and 2b·HCl concerning conformation and electronic structure. The two ammonium cations of 2a·HCl-ortho and 2a·HCl-mono are conformationally and electronically equal. However, as also observed for the C/Si analogues 1a·HCl and 1b·HCl, there is a small but significant difference between the electrostatic potential of 2a·HCl/ 2a·HPic and the silicon analogue 2b·HCl, visible as a negative region around the silicon atom in the difference potential.As the C/Si analogues haloperidol/sila-haloperidol (1a/1b) and venlafaxine/sila-venlafaxine (2a/2b) differ in their pharmacological potency and selectivity, the respective ligand–receptor interactions must be different. From the structural and electronic properties derived from this study, two major effects could be responsible for this: differences in the conformational flexibility and/or differences in the electrostatic potentials in the neighborhood of the C/Si replacement site. While the relevant structural parameters of the title compounds were already obtained from conventional X-ray diffraction analyses, the invariom formalism based on these crystal structure analyses additionally provides the electronic structures, which allow a more detailed analysis of the mutual recognition of receptors and their ligands.
A novel aspect of this work was to exploit the major advantage of modeling disorder using theoretically predicted aspherical scattering factors rather than freely refined multipole populations. Since the latter would correlate with split occupancies, thereby invalidating the electron density model, the invariom model was successfully applied to a disordered structure, the picrate anion in 1a·HPic.
Finally, the question should be commented whether the results from an invariom approach can compete with those obtained from multipole refinement against high resolution X-ray data at low temperatures. This has been examined before in a comparative study on sucrose,38a where an invariom modeling of a room temperature low order data set (d = 0.85 Å) was compared with a multipole refinement of a 20 K high resolution data set (d = 0.43 Å).38b It was shown that there is an agreement of bond topological and atomic properties in the range of earlier introduced experimental transferability indices (found to be 0.09 e Å−3 and 2.8 e Å−5 for the EDs and the Laplacians at the bond critical points and 0.7 Å3 and 0.11 e for the atomic volumes and charges).38c Hence, it can be concluded that the quantitative findings of the invariom application data are reliable within the transferability indices quoted above.
References
- For reviews dealing with silicon-containing drugs, see: (a) R. Tacke and H. Linoh, in The Chemistry of Organic Silicon Compounds, Part 2, ed. S. Patai and Z. Rappaport, Wiley-VCH, Chichester, 1989, pp. 1143–1206 Search PubMed; (b) W. Bains and R. Tacke, Curr. Opin. Drug Discovery Dev., 2003, 6, 526–543 CAS; (c) G. A. Showell and J. S. Mills, Drug Discovery Today, 2003, 8, 551–556 CrossRef CAS; (d) J. S. Mills and G. A. Showell, Expert Opin. Invest. Drugs, 2004, 13, 1149–1157 CrossRef CAS PubMed; (e) P. K. Pooni and G. A. Showell, Mini-Rev. Med. Chem., 2006, 6, 1169–1177 CrossRef CAS; (f) S. McN. Sieburth and C.-A. Chen, Eur. J. Org. Chem., 2006, 311–322 CrossRef CAS PubMed; (g) S. Gately and R. West, Drug Dev. Res., 2007, 68, 156–163 CrossRef CAS PubMed; (h) A. K. Franz, Curr. Opin. Drug Discovery Dev., 2007, 10, 654–671 CAS; (i) N. A. Meanwell, J. Med. Chem., 2011, 54, 2529–2591 CrossRef CAS PubMed; (j) A. K. Franz and S. O. Wilson, J. Med. Chem., 2013, 56, 388–405 CrossRef CAS PubMed; (k) S. McN. Sieburth, Top. Med. Chem. DOI:10.1007/7355_2014_80; (l) R. Tacke and S. Dörrich, Top. Med. Chem. DOI:10.1007/7355_2014_55.
- For recent studies on sila-substituted drugs, see: (a) J. B. Bauer, W. P. Lippert, S. Dörrich, D. Tebbe, C. Burschka, V. B. Christie, D. M. Tams, A. P. Henderson, B. A. Murray, T. B. Marder, S. A. Przyborski and R. Tacke, ChemMedChem, 2011, 6, 1509–1517 CrossRef CAS PubMed; (b) M. J. Barnes, C. Burschka, M. W. Büttner, R. Conroy, J. O. Daiss, I. C. Gray, A. G. Hendrick, T. L. Hong, D. Kuehn, D. J. Miller, J. S. Mills, P. Mitchell, J. G. Montana, P. A. Muniandy, H. Rapley, G. A. Showell, D. Tebbe, R. Tacke, J. B. H. Warneck and B. Zhu, ChemMedChem, 2011, 6, 2070–2080 CrossRef CAS PubMed; (c) R. Tacke, R. Bertermann, C. Burschka, S. Dörrich, M. Fischer, B. Müller, G. Meyerhans, D. Schepmann, B. Wünsch, I. Arnason and R. Bjornsson, ChemMedChem, 2012, 7, 523–532 CrossRef CAS PubMed; (d) J. B. G. Gluyas, C. Burschka, S. Dörrich, J. Vallet, H. Gronemeyer and R. Tacke, Org. Biomol. Chem., 2012, 10, 6914–6929 RSC; (e) M. Geyer, E. Wellner, S. Saloman, U. Jurva, D. Armstrong and R. Tacke, ChemMedChem, 2015, 10, 911–924 CrossRef CAS PubMed.
- Sila-haloperidol: (a) R. Tacke, T. Heinrich, R. Bertermann, C. Burschka, A. Hamacher and M. U. Kassack, Organometallics, 2004, 23, 4468–4477 CrossRef CAS; (b) R. Tacke, F. Popp, B. Müller, B. Theis, C. Burschka, A. Hamacher, M. U. Kassack, D. Schepmann, B. Wünsch, U. Jurva and E. Wellner, ChemMedChem, 2008, 3, 152–164 CrossRef CAS PubMed; (c) R. Tacke, B. Nguyen, C. Burschka, W. P. Lippert, A. Hamacher, C. Urban and M. U. Kassack, Organometallics, 2010, 29, 1652–1660 CrossRef CAS; (d) T. Johansson, L. Weidolf, F. Popp, R. Tacke and U. Jurva, Drug Metab. Dispos., 2010, 38, 73–83 CrossRef CAS PubMed.
- Sila-venlafaxine: (a) J. O. Daiss, M. Penka, C. Burschka and R. Tacke, Organometallics, 2004, 23, 4987–4994 CrossRef CAS; (b) J. O. Daiss, C. Burschka, J. S. Mills, J. G. Montana, G. A. Showell, J. B. H. Warneck and R. Tacke, Organometallics, 2006, 25, 1188–1198 CrossRef CAS; (c) G. A. Showell, M. J. Barnes, J. O. Daiss, J. S. Mills, J. G. Montana, R. Tacke and J. B. H. Warneck, Bioorg. Med. Chem. Lett., 2006, 16, 2555–2558 CrossRef CAS PubMed; (d) J. B. H. Warneck, F. H. M. Cheng, M. J. Barnes, J. S. Mills, J. G. Montana, R. J. Naylor, M.-P. Ngan, M.-K. Wai, J. O. Daiss, R. Tacke and J. A. Rudd, Toxicol. Appl. Pharmacol., 2008, 232, 369–375 CrossRef CAS PubMed.
- P. A. J. Janssen, C. van de Westeringh, A. H. M. Jagenau, P. J. A. Demoen, B. K. F. Hermans, G. H. P. van Daele, K. H. L. Schellekens, C. A. M. van der Eycken and C. J. E. Niemegeers, J. Med. Pharm. Chem., 1959, 1, 281–297 CrossRef CAS.
- (a) D. F. Levinson, Clin. Ther., 1991, 13, 326–352 CAS; (b) D. E. Casey, Int. Clin. Psychopharmacol., 1995, 10, 105–114 Search PubMed.
- (a) B. Subramanyam, S. M. Pond, D. W. Eyles, H. A. Whiteford, H. G. Fouda and N. Castagnoli Jr., Biochem. Biophys. Res. Commun., 1991, 181, 573–578 CrossRef CAS; (b) W. Dauer and S. Przedborski, Neuron, 2003, 39, 889–909 CrossRef CAS.
- (a) V. L. Ellingrod and P. J. Perry, Am. J. Hosp. Pharm., 1994, 51, 3033–3046 CAS; (b) E. Schweizer, R. J. Thielen and A. Frazer, Exp. Opin. Invest. Drugs, 1997, 6, 65–78 CrossRef CAS PubMed; (c) R. L. Rudolph, Acta Psychiatr. Scand., 2002, 106(Suppl. 415), 24–30 CrossRef; (d) H. Sauer, S. Huppertz-Helmhold and W. Dierkes, Pharmacopsychiatry, 2003, 36, 169–175 CrossRef CAS PubMed; (e) M. A. Gutierrez, G. L. Stimmel and J. Y. Aiso, Clin. Ther., 2003, 25, 2138–2154 CrossRef CAS.
- P. Luger, M. Weber, C. Hübschle and R. Tacke, Org. Biomol. Chem., 2013, 11, 2348–2354 CAS.
- B. Dittrich, T. Koritsánszky and P. Luger, Angew. Chem., Int. Ed., 2004, 43, 2718–2721 CrossRef CAS PubMed.
- B. Dittrich, C. B. Hübschle, K. Pröpper, F. Dietrich, T. Stolper and J. J. Holstein, Acta Crystallogr., Sect. B: Struct. Sci., 2013, 69, 91–104 CAS.
- F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388 CrossRef PubMed.
- J. P. Jasinski, R. J. Butcher, Q. N. M. Hakim Al-Arique, H. S. Yathirajan and B. Narayana, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2009, 65, o2403–o2404 CAS.
- L. Tessler and I. Goldberg, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2004, 60, o1868–o1869 CAS.
- D. Vega, D. Fernández and G. Echeverria, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2000, 56, 1009–1010 Search PubMed.
- A. Sivalakshmidevi, K. Vyas, S. M. Rao and G. O. Reddy, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2002, 58, o1072–o1074 CAS.
- N. K. Hansen and P. Coppens, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Cryst., 1978, 34, 909–921 CrossRef.
- C. B. Hübschle, P. Luger and B. Dittrich, J. Appl. Crystallogr., 2007, 40, 623–627 CrossRef.
- A. Volkov, P. Macchi, L. J. Farrugia, C. Gatti, P. R. Mallinson, T. Richter and T. Koritsánszky, XD2006 – a computer program for multipole refinement, topological analysis of charge densities and evaluation of intermolecular energies from experimental and theoretical structure factors, University of Buffalo, NY, USA; University of Milano, Italy; University of Glasgow, UK; CNRISTM, Milano, Italy; Middle Tennessee State University, TN, USA, 2006 Search PubMed.
- C. B. Hübschle and B. Dittrich, J. Appl. Crystallogr., 2011, 44, 238–240 CrossRef PubMed.
- (a) B. Dittrich, T. Koritsansky, A. Volkov, S. Mebs and P. Luger, Angew. Chem., Int. Ed., 2007, 46, 2935–2938 CrossRef CAS PubMed; (b) K. Pröpper, J. J. Holstein, C. B. Hübschle, C. S. Bond and B. Dittrich, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2013, 659, 1530–1539 Search PubMed.
- R. F. W. Bader, Atoms in Molecules – A Quantum Theory, Clarendon Press, Oxford, UK, 1990 Search PubMed.
- C. K. Johnson, ORTEP Report ORNL-3794, Oak Ridge National Laboratory, Oak Ridge, TN, USA, 1965.
- A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155 CrossRef CAS PubMed.
- S. Grabowsky, Ph.D. Thesis, Freie Universität Berlin, Germany, 2009; see http://www.diss.fu-berlin.de/diss/receive/FUDISS_thesis_000000015999.
- S. Grabowsky, M. F. Hesse, C. Paulmann, P. Luger and J. Beckmann, Inorg. Chem., 2009, 48, 4384–4393 CrossRef CAS PubMed.
- S. Grabowsky, J. Beckmann and P. Luger, Aust. J. Chem., 2012, 65, 785–795 CrossRef CAS.
- A. Volkov, C. Gatti, Y. Abramov and P. Coppens, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2000, 56, 252–258 CrossRef PubMed.
- (a) B. Pedersen, G. Wagner and R. Herrmann, ECHET98, https://www.ch.ic.ac.uk/ectoc/echet98/pub/048/index.htm; (b) N. Kocher, J. Henn, B. Gostevskii, D. Kost, I. Kalikhman, B. Engels and D. Stalke, J. Am. Chem. Soc., 2004, 126, 5563–5568 CrossRef CAS PubMed; (c) H. Ott, C. Däschlein, D. Leusser, D. Schildbach, T. Seibel, D. Stalke and C. Strohmann, J. Am. Chem. Soc., 2008, 130, 11901–11911 CrossRef CAS PubMed.
- A. Volkov, H. F. King, P. Coppens and L. J. Farrugia, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2006, 62, 400–408 CrossRef PubMed.
- C. B. Hübschle and P. Luger, J. Appl. Crystallogr., 2006, 39, 901–904 CrossRef.
- J. J. McKinnon, A. S. Mitchell and M. A. Spackman, Chem. – Eur. J., 1998, 4, 2136–2141 CrossRef CAS.
- M. A. Spackman, J. J. McKinnon and D. Jayatilaka, CrystEngComm, 2008, 10, 377–388 CAS.
- S. Scheins, M. Messerschmidt, W. Morgenroth, C. Paulmann and P. Luger, J. Phys. Chem. A, 2007, 111, 5499–5508 CrossRef CAS PubMed.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- A. Bach, D. Lentz and P. Luger, J. Phys. Chem. A, 2001, 105, 7405–7412 CrossRef CAS.
- C. F. Matta, N. Castillo and R. J. Boyd, J. Phys. Chem. A, 2005, 109, 3669–3681 CrossRef CAS PubMed.
- (a) B. Dittrich, M. Weber, R. Kalinowski, S. Grabowsky, C. B. Hübschle and P. Luger, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 749–756 CAS; (b) D. M. M. Jaradat, S. Mebs, L. Chęcińska and P. Luger, Carbohydr. Res., 2007, 342, 1480–1489 CrossRef CAS PubMed; (c) S. Grabowsky, R. Kalinowski, M. Weber, D. Förster, C. Paulmann and P. Luger, Acta Crystallogr., Sect. B: Struct. Sci., 2009, 65, 488–501 CAS.
- E. Keller and J. S. Pierrard, SCHAKAL99, University of Freiburg, Germany, 1999 Search PubMed.
- P. Luger, M. Messerschmidt, S. Scheins and A. Wagner, Acta Crystallogr., Sect. A: Fundam. Crystallogr., 2004, 60, 390–396 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Bond critical points; atomic properties (charges and volumes); atomic coordinates, displacement parameters and multipole parameters for the haloperidol/sila-haloperidol structures (1a·HCl, 1a·HPic, 1b·HCl) and the venlafaxine/sila-venlafaxine structures (2a, 2a·HCl, 2a·HCl-ortho, 2b·HCl). See DOI: 10.1039/c5ob00728c |
| This journal is © The Royal Society of Chemistry 2015 |
