Nanoparticle self-assembly in mixtures of phospholipids with styrene/maleic acid copolymers or fluorinated surfactants

Abstract

Self-assembling nanostructures in aqueous mixtures of bilayer-forming lipids and micelle-forming surfactants are relevant to in vitro studies on biological and synthetic membranes and membrane proteins. Considerable efforts are currently underway to replace conventional detergents by milder alternatives such as styrene/maleic acid (SMA) copolymers and fluorinated surfactants. However, these compounds and their nanosized assemblies remain poorly understood as regards their interactions with lipid membranes, particularly, the thermodynamics of membrane partitioning and solubilisation. Using ¹⁹F and ³¹P nuclear magnetic resonance spectroscopy, static and dynamic light scattering, and isothermal titration calorimetry, we have systematically investigated the aggregational state of a zwitterionic bilayer-forming phospholipid upon exposure to an SMA polymer with a styrene/maleic acid ratio of 3 : 1 or to a fluorinated octyl phosphocholine derivative called F₆OPC. The lipid interactions of SMA(3 : 1) and F₆OPC can be thermodynamically conceptualised within the framework of a three-stage model that treats bilayer vesicles, discoidal or micellar nanostructures, and the aqueous solution as distinct pseudophases. The exceptional solubilising power of SMA(3 : 1) is reflected in very low membrane-saturating and solubilising polymer/lipid molar ratios of 0.10 and 0.15, respectively. Although F₆OPC saturates bilayers at an even lower molar ratio of 0.031, this nondetergent does not solubilise lipids even at >1000-fold molar excess, thus highlighting fundamental differences between these two types of mild membrane-mimetic systems. We rationalise these findings in terms of a new classification of surfactants based on bilayer-to-micelle transfer free energies and discuss practical implications for membrane-protein research.

---

Introduction

Aqueous mixtures of amphiphiles display a rich repertoire of colloidal self-assembly phenomena and give rise to diverse supramolecular structures.¹ In particular, the aggregational state at the nano- and mesoscales in mixtures of bilayer-forming and micelle-forming amphiphiles may greatly vary with composition, temperature, pressure, hydration, ionic strength, and other parameters.² Among the most prominent and important examples are combinations of a bilayer-forming polar lipid and a micelle-forming surfactant,^3,4 which have found widespread use for analytical and preparative purposes in the study of biological membranes and membrane proteins.^5,6 From a thermodynamic viewpoint, the supramolecular structures observed in such mixtures can, usually to a very good approximation, be treated as pseudophases.⁷

All other conditions remaining constant, the aggregational state at full hydration then may be captured in a two-dimensional pseudophase diagram, where the concentrations of lipid and surfactant serve as abscissa and ordinate, respectively (Fig. 1a). In the simplest case, a coexistence range lies between two other ranges hosting either only bilayers or only micelles, which is conceptually and formally equivalent to the appearance of a miscibility gap in mixtures of two liquids of limited mutual solubility. Oftentimes, the lipid and surfactant concentrations delimiting the coexistence range are described by straight lines referred to as saturation (SAT) and solubilisation (SOL) boundaries.^4,7 The slopes of these boundaries correspond to the compositions of bilayers (b) saturated with surfactant (S) and micelles (m) saturated with lipid (L), which are expressed in terms of the molar ratios R^b,SAT_S ≡ c^b,SAT_S/c_L and R^m,SOL_S ≡ c^m,SOL_S/c_L, respectively (cf. eqn (1) and (2) in ESI†). These ratios allow calculation of the bilayer-to-micelle partition coefficients, K^b→m_L = (1 + R^b,SAT_S)/(1 + R^m,SOL_S) < 1 and K^b→m_S = K^b→m_LR^m,SOL_S/R^b,SAT_S > 1, as well as the corresponding standard values of the bilayer-to-micelle transfer free energies, ΔG^b→m,o_L = −RT ln K^b→m_L > 0 and ΔG^b→m,o_S = −RT ln K^b→m_S < 0, for the lipid and the surfactant, respectively (eqn (3)–(6)). Contrariwise, the thermodynamics of solubilisation determine the experimentally observable saturating and solubilising molar ratios according to R^b,SAT_S = (1 − K^b→m_L)/(K^b→m_S − 1) and R^m,SOL_S = R^b,SAT_SK^b→m_S/K^b→m_L, respectively (eqn (7) and (8)).

Fig. 1 Phase diagrams of aqueous mixtures of a bilayer-forming lipid and a micelle-forming surfactant with a CMC of 1 mM as predicted for various bilayer-to-micelle transfer free energies. (a) Typical phospholipid and detergent: ΔG^b→m,o_L = 1.0 kJ mol⁻¹, ΔG^b→m,o_S = −1.0 kJ mol⁻¹. (b) Membranophobic surfactant: ΔG^b→m,o_L = 1.0 kJ mol⁻¹, ΔG^b→m,o_S = −10 kJ mol⁻¹. (c) Solubilisation-resistant lipid: ΔG^b→m,o_L = 10 kJ mol⁻¹, ΔG^b→m,o_S = −1.0 kJ mol⁻¹. (d) Mutual insolubility of lipid and surfactant: ΔG^b→m,o_L = 10 kJ mol⁻¹, ΔG^b→m,o_S = −10 kJ mol⁻¹. The slopes of the phase boundaries correspond to the surfactant/lipid molar ratios required for bilayer saturation and complete solubilisation, R^b,SAT_S and R^m,SOL_S, respectively. The predominant range is graphically highlighted in each panel.

Consequently, phase diagrams of amphiphile mixtures offer quantitative insights into and, conversely, are governed by the thermodynamics of composition-dependent self-assembly. For typical phospholipid/detergent combinations, all three of the above ranges are easily accessible (Fig. 1a), giving rise to the famous three-stage model of membrane solubilisation.³ By contrast, membranophobic surfactants with a strong preference for the micellar over the bilayer phase⁸ saturate membranes at very low concentrations, thus limiting the abundance of the purely vesicular range (Fig. 1b). At the other extreme, lipids with highly endergonic bilayer-to-micelle transfer free energies are responsible for the phenomenon of solubilisation resistance (Fig. 1c), which is particularly relevant to liquid–ordered domains, so-called “detergent-resistant membranes”, and gel-phase bilayers.^9,10 Unfavourable lipid/detergent interactions in both bilayer and micellar phases result in a large mixing gap, that is, a broad coexistence range (Fig. 1d). Finally, phase diagrams have numerous practical applications, since they predict the aggregational state as a function of sample composition, which can be exploited, for instance, in guiding membrane-protein reconstitution.^11–13

Owing to its simple yet sound theoretical foundation and predictive power, the pseudophase concept has become popular for the thermodynamic analysis and interpretation of nano- and mesoscale self-assembly phenomena in mixtures of lipids and detergents, a term we use here to refer to any “water-soluble amphiphile with the capacity to solubilise lipids or other hydrophobic molecules”.¹⁴ Recently, however, there has been growing interest in surfactants that fundamentally differ from conventional detergents with regard to chemical composition, lipid interactions, and self-assembly behaviour and, hence, appear to elude the pseudophase model.¹⁵ On the one hand, these include amphiphilic styrene/maleic acid (SMA) copolymers, which solubilise lipids and lipid-embedded proteins to generate SMA-bounded lipid discs known as SMA/lipid particles (SMALPs), lipodisqs, or native nanodiscs.^15–18 These colloidal aggregates provide a native-like bilayer environment to membrane proteins but remain amenable to nuclear magnetic resonance (NMR) and optical spectroscopies and other methods requiring small particle sizes.^17–25 On the other hand, fluorinated surfactants^8,26,27 possess very poor detergency, as they do not solubilise lipid membranes and are even believed not to interact with them at all, although there are notable exceptions.^8,28 Therefore, these compounds are employed for solubilising hydrophobic peptides and proteins in the presence of lipid bilayers^29,30 and in similar situations requiring a nanostructured environment that does not compromise membrane integrity or does so in a mild, tightly controllable manner.⁸ Taken together, SMA copolymers and fluorinated surfactants currently receive widespread attention as promising membrane-mimetic systems since they enable gentle solubilisation and stabilisation of membrane proteins, but the thermodynamics underlying their peculiar modes of action has remained obscure.

Herein, we show (i) how mixtures of phospholipids with either SMA or a fluorinated nondetergent surfactant, which exhibit extremely strong or poor detergency, respectively, can be made amenable to experimentation and quantitative analysis; (ii) that the pseudophase-diagram approach is a valuable conceptual tool for rationalising membrane solubilisation and nanoparticle formation by such unconventional surfactants; and (iii) how a broad range of chemically diverse surfactants may be classified in a unifying framework based on simple thermodynamic criteria.

Results and discussion

Solubilisation by styrene/maleic acid (3 : 1) copolymer

Random copolymers containing styrene and maleic acid units at various ratios are capable of extracting lipids and proteins directly from artificial^16–20 or native^21–25 bilayer membranes. This peculiarity sets them apart from other compounds that form disc-shaped colloidal particles developed for membrane-protein research, such as bicelles³¹ and protein-bounded nanodiscs.³² It has been suggested³³ that SMA-mediated disruption of phospholipid vesicles is initiated by penetration of its hydrophobic styrene moieties into the hydrocarbon core of the membrane and then proceeds through wrapping of the polymer chain around a lipid bilayer disc. Although mechanistic details remain to be elucidated, it seems that the excision of bilayer patches sets in at very low SMA contents in the membrane.³³ Thus, within the phase-diagram concept, phospholipid/SMA mixtures are expected to display low R^b,SAT_S values, above which further SMA addition shifts the equilibrium from polymer-saturated bilayers to SMA-bounded discs called SMALPs until all lipid is solubilised once R^m,SOL_S is reached.

To corroborate this solubilisation scenario and determine R^b,SAT_S and R^m,SOL_S values, we examined the formation of SMALPs by exposing large unilamellar vesicles (LUVs) formed from the zwitterionic, singly unsaturated phospholipid 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) to increasing concentrations of SMA(3 : 1). For this purpose, we found ³¹P NMR spectroscopy to be superior to more common techniques such as turbidimetry and light scattering (see below). Under our experimental conditions, the ³¹P NMR signal from phosphorus nuclei residing in LUV bilayers is broadened beyond detection.^8,34–36 Hence, any peak in the spectrum is expected to be entirely due to—and, thus, proportional to the amount of—solubilised phospholipid. At a given POPC concentration, an isotropic, Lorentzian-shaped ³¹P NMR signal appeared once the SMA(3 : 1) concentration exceeded a certain threshold, increased sharply upon further addition of polymer, and finally levelled off in overall intensity when a second breakpoint was reached (Fig. 2a). Both breakpoints observed in such titrations were proportional to the concentration of POPC (Fig. 2b), indicating that they reflect the onset and completion of solubilisation.^3,4,37 Accordingly, addition of SMA(3 : 1) to POPC LUVs initially leads to adsorption of the polymer to the bilayer membrane until the latter is saturated at R^b,SAT_S. A further rise in SMA(3 : 1) concentration results in solubilisation, which manifests as a linear increase in the area of the ³¹P NMR peak before the latter plateaus once all lipid is solubilised at R^m,SOL_S. Plotting the SMA(3 : 1) concentrations at the breakpoints versus the corresponding POPC concentrations produced a phase diagram (Fig. 2c) characterised by saturating and solubilising SMA(3 : 1)/POPC molar ratios of R^b,SAT_S = 0.099 ± 0.004 and R^m,SOL_S = 0.147 ± 0.005, respectively. The vesicle-to-SMALP transfer free energies derived therefrom amount to ΔG^b→m,o_L = (0.11 ± 0.01) kJ mol⁻¹ and ΔG^b→m,o_S = −(0.87 ± 0.09) kJ mol⁻¹ for POPC and SMA(3 : 1), respectively. The vanishing ordinate intercept of c^aq,o_s = 0 indicates that the concentration of free polymer is negligible.

Fig. 2 Solubilisation of POPC vesicles by SMA(3 : 1) at 25 °C as monitored by ³¹P NMR. (a) NMR spectra of 10 mM POPC initially present as LUVs upon exposure to increasing concentrations of SMA(3 : 1). (b) Peak areas, A, at four POPC concentrations as functions of SMA(3 : 1) concentration. Experimental data (circles) derived from titrations such as that in (a) and fits (lines) according to eqn (17)–(19). Error bars indicate standard deviations from three experiments. (c) Phase diagram of POPC/SMA(3 : 1). Experimental data (circles) obtained from breakpoints in (b) and linear fits (lines) according to eqn (1) and (2) marking the onset (SAT; red) and completion (SOL; blue) of solubilisation, respectively. Error bars indicate 95% confidence intervals of fits based on eqn (17)–(19).

In contrast with the clear-cut picture emerging from ³¹P NMR spectroscopy, interpretation of dynamic light scattering (DLS) data proved more challenging. Particle size distributions obtained either well below R^b,SAT_S or above R^m,SOL_S were unimodal and relatively narrow, with mean values and standard deviations of (160 ± 10) nm and (12 ± 1) nm being in excellent agreement with the hydrodynamic diameters expected for, respectively, LUVs (Fig. 3a) and SMALPs (Fig. 3b). By contrast, intermediate SMA(3 : 1) concentrations gave rise to multimodal size distributions indicative not only of coexisting LUVs and SMALPs but also of larger aggregates (Fig. 3a). The latter could represent agglomerated vesicles interconnected by polymer chains or even (hemi)fusion products. Their transient appearance and disappearance during solubilisation became more evident when the total light scattering intensity at an angle of 90°, the z-average diameter, and the polydispersity index (PDI) of a POPC suspension were monitored as functions of SMA(3 : 1) concentration (Fig. 3c). Both the z-average diameter and the PDI increased abruptly below R^b,SAT_S, that is, within the vesicular range. At the same subsolubilising SMA(3 : 1) concentration, a turbid slurry started to sediment in the sample vial, indicating that the steady decrease in light scattering intensity observed already below R^b,SAT_S was due to sedimentation of particles out of the scattering volume rather than a reduction in particle size prior to solubilisation. Formation of SMALPs above R^b,SAT_S, that is, within the coexistence range, gradually dissolved these large aggregates, thus reducing the z-average diameter and narrowing down the PDI. Beyond R^m,SOL_S, the dispersion became optically clear, and all three of the above quantities decreased monotonically with increasing SMA(3 : 1) concentration, reflecting a continuous reduction in SMALP size.³⁸

Fig. 3 Solubilisation of POPC vesicles by SMA(3 : 1) at 25 °C as monitored by DLS. (a, b) Intensity-weighted particle size distribution functions, f(d), versus hydrodynamic diameter, d, of 6 mM POPC initially present as LUVs upon exposure to increasing concentrations of SMA(3 : 1). (c) Total light scattering intensity at 90°, I, z-average diameter, z, and PDI as obtained from data in (a) and (b). Also indicated are the SAT and SOL boundaries (dashed lines) derived from ³¹P NMR (Fig. 2).

Lipid interactions of the fluorinated surfactant F₆OPC

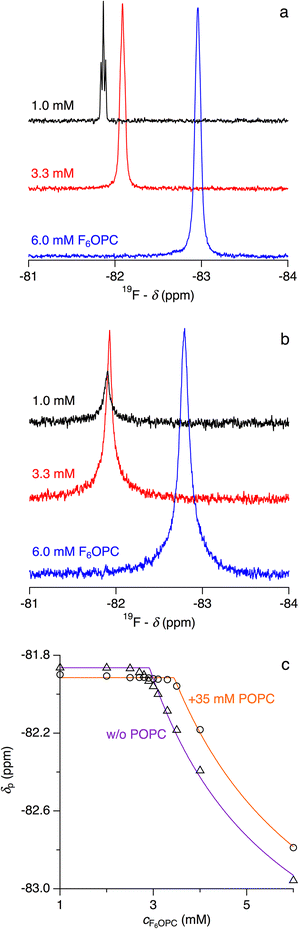
Fluorinated surfactants are used in situations requiring colloidal amphiphile properties without compromising the integrity of lipid membranes.^8,29,30 The fluorinated octyl phosphocholine derivative 3,3,4,4,5,5,6,6,7,7,8,8,8-tridecafluoro-n-octylphosphocholine (F₆OPC) self-assembles into spheroidal micelles above its CMC of 2.9 mM at 25 °C but behaves like a nondetergent, as it does not solubilise POPC vesicles even at high concentrations, at elevated temperature, and during prolonged incubation.⁸ In particular, no changes in light scattering intensity are observed on exposure of 100 μM POPC in the form of LUVs to 20 mM F₆OPC, that is, a 200-fold molar excess of fluorinated surfactant over lipid.⁸ Making the conservative assumption that such a measurement would pick up any reduction in vesicle number >10%, we conclude that ∼17 mM micellar F₆OPC (i.e., total concentration minus CMC) can solubilise no more than 10 μM POPC. Thus, complete solubilisation would require an F₆OPC/POPC molar ratio of R^m,SOL_S > 1000, attesting to the nondetergency of this fluorinated surfactant. From a thermodynamic perspective (eqn (5)), this sets a lower limit of ΔG^b→m,o_L > 17 kJ mol⁻¹ on the transfer free energy of the lipid.

Still, its extremely poor solubilising power does not mean that F₆OPC does not partition into lipid bilayers, although such interactions must be so weak as to elude standard protocols. In isothermal titration calorimetry (ITC) membrane-partitioning experiments, the heats measured during titration of monomeric F₆OPC with POPC are hardly discernible from dilution effects, and time-resolved fluorescence anisotropy reveals no changes in the nanosecond dynamics of the fluorescent bilayer probe 1,6-diphenyl-1,3,5-hexatriene (DPH) upon addition of F₆OPC to POPC vesicles.⁸ Nevertheless, the presence of lipid had a slight but significant and systematic influence on the concentration at which F₆OPC started to self-assemble into micelles, as borne out by ITC (Fig. 4) and ¹⁹F NMR spectroscopy (Fig. 5). In the absence of lipid, both methods determined a CMC of (2.9 ± 0.1) mM at 25 °C, in agreement with published data.⁸ The presence of POPC raised the apparent CMC, as manifested in a shift of the sigmoidal transition observed in ITC demicellisation experiments to higher F₆OPC concentrations (Fig. 4a). This shift was proportional to the concentration of lipid, furnishing a phase diagram (Fig. 4b) with a saturation threshold of R^b,SAT_S = 0.031 ± 0.004 and a bilayer-to-micelle transfer free energy of ΔG^b→m,o_S = −(8.7 ± 0.3) kJ mol⁻¹ (eqn (16)). Since the water-to-micelle transfer free energy is given as ΔG^aq→m,o_S = RT ln(CMC/55.5 M) = −(24.4 ± 0.1) kJ mol⁻¹, the water-to-bilayer transfer free energy amounts to ΔG^aq→b,o_S = ΔG^aq→m,o_S − ΔG^b→m,o_S = −(15.7 ± 0.4) kJ mol⁻¹.³⁹

Fig. 4 Weak interactions of F₆OPC with POPC LUVs at 25 °C as quantified by ITC. (a) Isotherms depicting heats of reaction, Q, (open symbols) obtained upon injection of 30 mM F₆OPC into buffer containing various POPC concentrations. Isotherms were vertically offset by −1.5 kJ mol⁻¹ each. Fits (solid lines) were done according to eqn (20). (b) Phase diagram of POPC/F₆OPC. The SAT boundary (red line) was obtained from linear regression of experimental values retrieved from eqn (20) (red circles with 95% confidence intervals). The SOL boundary (blue line) was estimated as described in the text. (c) Molar enthalpy change, ΔH_S, obtained from eqn (20) (circles with 95% confidence intervals) and linear fit according to eqn (23) (line) plotted as functions of the fraction of F₆OPC that partitioned into the bilayer as calculated from eqn (22).

Fig. 5 Weak interactions of F₆OPC with POPC bilayers at 25 °C as revealed by ¹⁹F NMR. (a) Representative spectra showing the –CF₃ resonance in the absence of POPC at different F₆OPC concentrations. (b) Spectra in the presence of 35 mM POPC under otherwise identical conditions. At 3.3 mM F₆OPC, micelles were observed in the absence of POPC but not in its presence. Peak broadening in the presence of LUVs was due to increased viscosity and fast exchange with the membrane-bound state. (c) ¹⁹F NMR peak chemical shift, δ_p, versus F₆OPC concentration in the absence (triangles) and presence (circles) of 35 mM POPC. Fits (lines) were done according to eqn (24).

Closer inspection of the ITC data allows parsing the exergonic ΔG^b→m,o_S value into enthalpic and entropic contributions. In the absence of lipid, demicellisation of F₆OPC was accompanied by an enthalpy change of −(4.0 ± 0.2) kJ mol⁻¹, which translates into a molar micellisation enthalpy of ΔH^aq→m_S = (4.4 ± 0.2) kJ mol⁻¹ upon correction for the fraction of monomeric surfactant in the syringe.^40,41 With increasing POPC concentration, the heats measured upon injection of micellar F₆OPC into the calorimeter cell below the CMC decreased in magnitude (Fig. 4a) because exothermic demicellisation was accompanied by an endothermic process ascribed to membrane partitioning. Plotting the molar heat of reaction against the fraction of F₆OPC that partitioned into the bilayer (eqn (22)) revealed a linear relationship (Fig. 4c), the slope of which returned a value of ΔH^b→m_S = −(17.4 ± 0.8) kJ mol⁻¹ for the bilayer-to-micelle transfer enthalpy. Hence, the free-energy gain accompanying the bilayer-to-micelle transfer of F₆OPC is entirely due to a markedly favourable enthalpy change, as might be expected for the removal of a fluorocarbon chain from a hydrocarbon matrix.

In the above considerations, we assumed the shift in the onset of micelle formation to arise from membrane partitioning of some F₆OPC, such that the aqueous surfactant concentration is slightly less than the total concentration. ¹⁹F NMR measurements corroborated this interpretation, as they revealed that the lowest F₆OPC concentration at which micelles appear (Fig. 5a) increased in the presence of POPC (Fig. 5b). Micellisation was reflected in a sudden change in the environment and, consequently, the chemical shift of fluorine nuclei when the concentration of F₆OPC exceeded the apparent CMC. With R^b,SAT_S = 0.031 derived from ITC (Fig. 4b), we expect a total POPC concentration of 35 mM, only half of which is accessible from the outside of the vesicles, to raise the onset of micellisation by 0.031 × 0.5 × 35 mM = 0.54 mM, which was indeed confirmed experimentally (Fig. 5c).

Thermodynamics of membrane solubilisation

Considerable efforts are being made towards replacing conventional detergents by milder nanostructured alternatives that should better preserve the native conformations and functions of membrane proteins. Among these, SMA copolymers and fluorinated surfactants appear particularly promising, but a better understanding of their interactions with phospholipid bilayer membranes is mandatory if one is to exploit their full potential. In particular, the powerful arsenal of experimental approaches and thermodynamic concepts that have proven invaluable for studying membrane partitioning and solubilisation by detergents^4,7 has remained largely unexplored for these surfactants. In the following, after setting the stage by reviewing the thermodynamic signatures of established detergents, we discuss the peculiarities of SMA(3 : 1) and F₆OPC in the framework of the pseudophase concept and propose a new classification of surfactants based on bilayer-to-micelle transfer free energies.

Synthetic head-and-tail detergents

The bilayer-to-micelle transfer free energies for many combinations of phospholipids and detergents consisting of a polar headgroup and a hydrocarbon tail are characterised by averages and standard deviations of ΔG^b→m,o_L = (1.2 ± 0.5) kJ mol⁻¹ and ΔG^b→m,o_S = −(0.7 ± 0.4) kJ mol⁻¹ (Table S1†). The latter value reflects a modest preference of the detergent for the micellar phase, while the former expresses a somewhat more pronounced preference of the lipid for the bilayer phase. Together, these thermodynamic hallmarks result in phase diagrams typically revealing saturation and solubilisation slopes of R^b,SAT_S = 1.4 ± 0.6 and R^m,SOL_S = 2.9 ± 1.1, respectively.

Gradual addition of detergent to a lipid bilayer initially results in partitioning of the detergent between the aqueous phase and the membrane, thus raising the chemical potentials of the detergent in both phases.⁷ Micelle formation begins once the chemical potentials in these two phases reach that in lipid-saturated micelles, just as micellisation in the absence of lipid would set in when the chemical potential of detergent monomers in the aqueous phase reaches that of pure detergent micelles. In both the bilayer and the micellar phases, the interactions of most head-and-tail detergents with lipids are adequately described by models assuming ideal or near-ideal mixing, such as regular solution theory.⁷ Consequently, these detergents tend to distribute homogeneously within each phase without forming stable domains or clusters. Membrane insertion of such curvophilic, cone-shaped molecules generates monolayer curvature stress and, if the detergent does not rapidly flip–flop across the membrane, additional bilayer curvature stress caused by asymmetric expansion of only one leaflet. The bilayer relaxes part of this stress by acyl chain disordering, which, in turn, results in membrane thinning and concomitant lateral expansion, as demonstrated by ²H solid-state NMR spectroscopy⁴² and time-resolved DPH fluorescence anisotropy.⁴³ The latter method also suggests that this relaxation mechanism is about equally effective for chemically diverse detergents as long as they distribute themselves evenly within the bilayer. The membrane's capacity to alleviate monolayer curvature stress by chain fluidisation appears to be exhausted once the hydrophobic thickness of one leaflet is reduced to ∼9 Å,⁴³ at which point the degree of acyl chain disorder reaches a critical threshold.⁴⁴

Bile salts, derivatives, and lipopeptides

Surfactants whose polar group is not clearly segregated from the hydrophobic moiety can be powerful detergents but appear to be more difficult to accommodate in a bilayer environment. This is exemplified by the naturally occurring bile salts cholate and deoxycholate and their synthetic derivatives 3-[(3-cholamidopropyl)dimethylammonio]-1-propanesulphonate (CHAPS) and 3-[(3-cholamidopropyl)dimethylammonio]-2-hydroxy-1-propanesulphonate (CHAPSO). By comparison with alkyl chain surfactants, ΔG^b→m,o_L = (0.6 ± 0.3) kJ mol⁻¹ is less endergonic and ΔG^b→m,o_S = −(1.6 ± 0.8) kJ mol⁻¹ is more exergonic for this class of detergents (Table S2†). These free energies translate into low saturation and solubilisation ratios of R^b,SAT_S = 0.2 ± 0.1 and R^m,SOL_S = 0.6 ± 0.2, respectively. By these measures, the strong detergency of these compounds results from their more unfavourable bilayer incorporation and the ease with which their micelles accommodate phospholipids. These properties can be traced back to the rigid, sterol-based scaffold, which does not impede micelle formation but is less compatible with incorporation into a bilayer environment. Therefore, and in contrast with head-and-tail surfactants, such detergents tend not to mix homogeneously but rather form clusters within the bilayer.⁴⁵ This renders it more difficult for the bilayer to counteract curvature stress, as inferred from the observation that membrane insertion of such compounds does not significantly increase acyl chain disorder,⁴³ and results in low saturation and solubilisation thresholds.

The same is true for surfactin (Table S3†), a Bacillus subtilis lipopeptide that interacts with and solubilises POPC membranes with transfer free energies of ΔG^b→m,o_L = 0.4 kJ mol⁻¹ and ΔG^b→m,o_S = −1.4 kJ mol⁻¹ and threshold ratios of R^b,SAT_S = 0.22 and of R^m,SOL_S = 0.46.⁴⁶ A similar case can be made for P2A2, a dipalmitoylated peptide originally designed for the delivery of biological probes and drugs across the blood–brain barrier.⁴⁷ Depending on the mixing ratio with phospholipids, P2A2 forms defined nanodiscs or liposomal assemblies and therefore can deliver both hydrophilic and hydrophobic cargos.⁴⁸ With a bilayer-to-micelle transfer free energy of ΔG^b→m,o_S = −5.6 kJ mol⁻¹, P2A2 is even more membranophobic than bile salts and their derivatives. More importantly, P2A2 provides a favourable micellar environment to POPC, whose bilayer-to-micelle transfer free energy amounts to only ΔG^b→m,o_L = 0.3 kJ mol⁻¹. Together, these unusual thermodynamic signatures give rise to extremely low critical ratios of R^b,SAT_S = 0.012 and R^m,SOL_S = 0.13. Accordingly, POPC membranes become saturated with lipopeptide when the latter accounts for only ∼1% of the molecules in the bilayer, and P2A2 can solubilise an ∼7-fold molar excess of POPC into mixed micelles. This enormous solubilising power is thought to arise from a disc-shaped micellar morphology, which can accommodate large amounts of lipid in a bilayer patch surrounded by P2A2 and, additionally, offers the advantage of preserving the biologically active, binding-competent conformation of the peptide moiety of P2A2.⁴⁸

Detergent activity of styrene/maleic acid copolymers

The transfer free energies describing the formation of SMALPs from POPC bilayers upon exposure to SMA(3 : 1) amount to ΔG^b→m,o_L = 0.11 kJ mol⁻¹ and ΔG^b→m,o_S = −0.87 kJ mol⁻¹. Accordingly, transfer of POPC from bilayer vesicles into SMALPs incurs only a minute free-energy cost and is much less unfavourable than solubilisation by any of the above detergents, including P2A2. In keeping with the definition of a detergent as being a “water-soluble amphiphile with the capacity to solubilise lipids or other hydrophobic molecules”,¹⁴ SMA(3 : 1) appears as an extremely powerful detergent. Hence, extraction of membrane proteins and lipids with the aid of SMA can be regarded as “detergent-free”^15–25 only insofar as no conventional, micelle-forming detergent is involved in this process. This is, of course, not in contradiction with the demonstrated usefulness of SMA as a mild, structure- and activity-preserving solubilising agent for membrane proteins and membrane-protein complexes.^15–25 In fact, the above values quantitatively demonstrate that, whereas SMA(3 : 1) is preferentially located in SMALPs rather than vesicular membranes, the lipid is almost indifferent, thus reflecting, from a thermodynamic perspective, the native-like properties of the bilayer disc forming the SMALP core.

Two words of caution are in place here: First, for most examples considered so far, the lipid and surfactant components are roughly similar in size, which justifies the use of thermodynamic formalisms based on mole fractions, thereby ignoring size differences between the two mixing components. This approximation is less good for mixtures of phospholipids with polymers such as SMA(3 : 1), whose number-average molar mass exceeds that of POPC by a factor of ∼5. Thus, low critical molar ratios of R^b,SAT_S = 0.099 and R^m,SOL_S = 0.147 translate into SMA(3 : 1)/POPC mass ratios of 0.52 g g⁻¹ and 0.77 g g⁻¹, respectively. These values are comparable to those of typical detergents such as n-octyl-β-D-glucopyranoside,⁴⁹ with R^b,SAT_S = 1.22 and R^m,SOL_S = 2.38 corresponding to detergent/POPC mass ratios of 0.47 g g⁻¹ and 0.91 g g⁻¹, respectively. Accounting for such size dissimilarities by more sophisticated solution theories would require more detailed knowledge of the molar-mass distribution of the polymer and the lipid/polymer interactions in vesicles and SMALPs. In the absence of such information, a quick calculation reveals that any such correction would have only a minor impact, though: for instance, multiplication of both R^b,SAT_S and R^m,SOL_S by the above factor of 5 yields modestly altered transfer free energies of ΔG^b→m,o_L = 0.37 kJ mol⁻¹ and ΔG^b→m,o_S = −0.62 kJ mol⁻¹. Second, another complication arises from the fact that lipid and polymer molecules do not mix homogeneously, as would be required for treating SMALPs as a pseudophase, but rather segregate into distinct domains; the same limitation applies to detergents that form clusters within lipid bilayers, as discussed in the preceding section.^43,45 In these cases, free-energy values should not be taken as thermodynamically rigorous measures but as phenomenological yet predictive descriptors.

Fluorinated surfactants: detergency vs. lipophobicity

By analogy to the poor miscibility of liquid hydrocarbons and fluorocarbons, fluorinated surfactants are usually assumed to be both hydrophobic and lipophobic, that is, reluctant to interact not only with water but also with lipids. We have recently shown,⁸ however, that fluorination and detergency are not mutually exclusive, as the fluorinated surfactant 3,3,4,4,5,5,6,6,7,7,8,8,8-tridecafluoro-n-octyl-β-D-maltopyranoside (F₆OM) readily partitions into POPC bilayers at low surfactant concentrations, with ΔG^aq→b,o_S = −25.3 kJ mol⁻¹, and solubilises them at higher concentrations. With transfer free energies of ΔG^b→m,o_L = 1.7 kJ mol⁻¹ and ΔG^b→m,o_S = −1.0 kJ mol⁻¹ and critical molar ratios of R^b,SAT_S = 1.0 and R^m,SOL_S = 3.0, F₆OM is indistinguishable from alkyl chain detergents as regards the thermodynamics of solubilisation (Table S3†). Nevertheless, this fluorinated detergent does not induce acyl chain disordering and, thus, appears to form clusters rather than being distributed homogeneously within the membrane.⁸

The present data show that F₆OPC, which carries the same fluorinated chain as F₆OM but a zwitterionic phosphocholine instead of a neutral maltose headgroup, interacts with hydrogenated phospholipids weakly but measurably. However, a distinction has to be made between the interactions in the bilayer membrane and those within the micellar phase. Comparably small absolute values of the water-to-bilayer transfer free energy of ΔG^aq→b,o_S = −15.7 kJ mol⁻¹ and the bilayer saturation threshold of R^b,SAT_S = 0.031 explain why earlier attempts failed in quantifying the weak membrane affinity of F₆OPC.⁸ Still, this interaction is significant enough to be quantified by dedicated calorimetric (Fig. 4) and NMR (Fig. 5) protocols. By contrast, incorporation of hydrogenated phospholipids into F₆OPC micelles is so unfavourable that no signs of solubilisation could be observed even under very harsh conditions excluding kinetic barriers,⁸ thus explaining why F₆OPC but not F₆OM can be used together with free-standing lipid bilayers.²⁹

Thermodynamic classification of surfactants

Surfactants are usually classified with respect to chemical properties such as headgroup ionisation and hydrophilic–lipophilic balance⁵⁰ or practical aspects such as their suitability for membrane-protein applications.^5,6 Here, we propose a classification based on thermodynamic grounds by considering the two critical mole ratios, R^b,SAT_S and R^m,SOL_S, or—equivalently but more revealingly—the bilayer-to-micelle transfer free energies, ΔG^b→m,o_L and ΔG^b→m,o_S. Since bile salts, their derivatives, lipopeptides, and SMA(3 : 1) display comparably low saturation and solubilisation thresholds, these strong detergents cluster in the lower left corner in a plot of R^m,SOL_Sversus R^b,SAT_S (Fig. 6a). A thermodynamic explanation for this empirical observation comes from the corresponding transfer free energies (Fig. 6b). At given ΔG^b→m,o_S, the transfer of phospholipids from bilayer membranes into mixed micelles is less unfavourable for these detergents, that is, ΔG^b→m,o_L is less endergonic. Conversely, at given ΔG^b→m,o_L, the bilayer-to-micelle transfer of the detergents themselves is more favourable, that is, ΔG^b→m,o_S is more exergonic.

Fig. 6 Thermodynamic classification of surfactants. (a) Surfactant/lipid ratios at the onset and completion of solubilisation, R^b,SAT_S and R^m,SOL_S, respectively. (b) Surfactant and lipid bilayer-to-micelle transfer free energies, ΔG^b→m,o_S and ΔG^b→m,o_L, respectively. Synthetic head-and-tail detergents (open black circles; average: full black circle) on the one hand and bile salts and their derivatives (open blue squares; average: full blue square), the lipopeptide surfactin (orange down triangle), the dipalmitoylated peptide P2A2 (brown diamond), and SMA(3 : 1) (green up triangle) on the other hand populate distinct ranges separated by a threshold (red dashed line) defined by ΔG^b→m,o_L = −0.65 ΔG^b→m,o_S. F₆OM (purple hexagon) behaves like a conventional detergent, whereas F₆OPC (not shown) is a nondetergent with R^m,SOL_S > 1000 and ΔG^b→m,o_L > 17 kJ mol⁻¹. Also indicated in both panels are the ranges where R^m,SOL_S = (2.37 ± 0.90)R^b,SAT_S (gray areas), as obtained from the average and standard deviation for all detergents. Numerical values and references are listed in Tables S1–S3.†

Qualitatively, it takes two properties for a detergent to be an efficient solubiliser. First, the detergent itself must display a clear preference for micellisation over membrane partitioning, as reflected in a markedly exergonic ΔG^b→m,o_S. Second, these micelles have to provide a suitable environment for the lipid in question, as manifested in an only moderately endergonic ΔG^b→m,o_L. Because bile salts, peptides, and polymers are less compatible with a bilayer structure than head-and-tail detergents are, one intuitively expects them to better fulfil the first prerequisite. Moreover, upon solubilisation, these strong detergents tend to give rise to discoidal nanostructures such as CHAPS(O)-containing bicelles,³¹ P2A2-bounded nanodiscs,⁴⁸ or SMALPs,^15–18 all of which provide a more membrane-like environment than spherical, ellipsoidal, or cylindrical micelles typically formed by head-and-tail detergents. More quantitatively, we can define a simple and unique thermodynamic criterion to distinguish two classes of surfactants: without exception, ΔG^b→m,o_L < −0.65ΔG^b→m,o_S for strong detergents such as bile salts, their derivatives, lipopeptides, and SMA(3 : 1), whereas relatively weak, synthetic head-and-tail detergents obey the relationship ΔG^b→m,o_L > −0.65ΔG^b→m,o_S (Fig. 6b; Tables S1–3†). By contrast, the ratio R^m,SOL_S/R^b,SAT_S = K^b→m_S/K^b→m_L and, thus, the difference ΔG^b→m,o_L − ΔG^b→m,o_S (eqn (9)), which determine the relative width of the coexistence range, are not significantly different between the two classes of surfactants (Tables S1 and S2†).

Heerklotz and Seelig⁵¹ have proposed a thermodynamic classification of detergents by correlating the CMC with the water-to-bilayer partition coefficient.⁵² The product of these two parameters decreases with increasing detergent strength, as it reflects a more pronounced preference for the micellar over the bilayer phase. Although relying exclusively on the partitioning behaviour of the detergent, ΔG^b→m,o_S, without considering that of the lipid, ΔG^b→m,o_L, this furnishes a sensible measure of detergency within the class of head-and-tail surfactants. This is because, in these cases, the bilayer-to-micelle transition is primarily governed by the intrinsic curvatures of both lipid and detergent, so that the product of the CMC and the partition coefficient provides a good predictor of R^b,SAT_S.⁵¹ However, this relationship breaks down when factors other than curvature come into play, as is the case with CHAPS, which is a much more potent detergent than would be expected from its high CMC and strong membrane affinity.⁵¹ At the other extreme is F₆OPC, which one would expect to be a powerful detergent because of its rather low CMC in conjunction with extremely low membrane affinity. Indeed, F₆OPC displays an unusually low R^b,SAT_S value. However, the micelles formed upon further addition of surfactant are virtually devoid of lipid because its transfer from a hydrocarbon into a fluorocarbon environment is very endergonic, thus resulting in an exceptionally high R^m,SOL_S value. Such effects, which are related to nonideal lipid/surfactant interactions rather than intrinsic curvature, must evade any approach based on a single transfer free energy but are readily captured by the present classification making use of both ΔG^b→m,o_L and ΔG^b→m,o_S.

Conclusions

Borrowing from concepts developed for conventional detergents not only furnishes insights into the peculiar properties of self-assembling amphiphilic copolymers and fluorinated surfactants but also highlights quantitative and qualitative differences.

The interactions of SMA(3 : 1) with lipid membranes follow the three-stage solubilisation scenario observed for many detergents. Polymer/lipid phase diagrams derived with the aid of ³¹P NMR spectroscopy pave the way for quantifying the effects of lipid composition and other conditions on solubilisation and define the subsolubilising concentration regime where membrane adsorption of the polymer can be scrutinised at equilibrium. Moreover, these phase diagrams predict the minimum polymer concentration required for complete solubilisation at a given lipid concentration, which is of practical importance for the use of SMA copolymers in membrane-protein research.

The fluorinated nondetergent surfactant F₆OPC partitions weakly but measurably into POPC bilayers. Once the membrane is saturated, F₆OPC forms micelles, which, however, do not solubilise lipid and do not compromise membrane integrity. Thus, F₆OPC qualifies as an amphiphile forming nanoparticles that are compatible with, for example, free-standing lipid bilayers, whereas the related fluorinated surfactant F₆OM is preferable in situations requiring mild detergent activity. The degree of detergency of new fluorinated surfactants can be tuned by judicious adjustment of headgroup properties and can be quantified with the aid of the ITC and ¹⁹F NMR protocols presented here.

Finally, we proposed a thermodynamic classification of surfactants based on the bilayer-to-micelle transfer free energies of both the lipid and the surfactant of interest. Synthetic head-and-tail detergents, including F₆OM, partition readily into membranes but form micelles that provide a rather poor environment to phospholipids, thus necessitating relatively high detergent concentrations for complete solubilisation. By contrast, bile salt detergents and their derivatives, natural and designed lipopeptides, as well as SMA(3 : 1) are more difficult to accommodate in lipid bilayers but fare much better in solubilising phospholipids at low detergent concentrations.

Experimental

Materials

POPC was from Lipoid (Ludwigshafen, Germany), F₆OPC from Anatrace (Maumee, USA), D₂O from Deutero (Kastellaun, Germany), and NaCl from VWR (Darmstadt, Germany). Sodium trifluoroacetate and 85% H₃PO₄ in D₂O were from Sigma–Aldrich (Steinheim, Germany) and 4-(2-hydroxyethyl)-1-piperazineethanesulphonic acid (HEPES) and tris(hydroxymethyl)aminomethane (Tris) from Carl Roth (Karlsruhe, Germany). SMA(3 : 1) copolymer solution (trade name Xiran SL25010 S25) was a kind gift from Polyscope (Geleen, Netherlands). All chemicals were obtained in the highest available purity.

Vesicle preparation

LUVs were prepared by suspension of POPC powder in buffer and 35-fold extrusion through two stacked 100-nm polycarbonate filters with a LiposoFast extruder (Avestin, Ottawa, Canada). Extruded vesicles revealed a unimodal size distribution with a mean diameter and standard deviation of (160 ± 10) nm in intensity-weighted size distributions obtained from DLS.

Preparation of SMA(3 : 1) stock solutions

The SMA copolymer used in this study had a styrene/maleic acid molar ratio of 3 : 1, a mass-average molar mass of M_w = 10 kg mol⁻¹, and a number-average molar mass of M_n = 4 kg mol⁻¹. SMA(3 : 1) stocks were prepared by dialysis of commercial Xiran SL25010 S25 solutions against buffer (50 mM Tris, 200 mM NaCl, pH 7.4) by use of a 5-mL QuixSep dialyser (Membrane Filtration Products, Seguin, USA) and a Spectra/Por 3 dialysis membrane (Spectrum Laboratories, Rancho Dominguez, USA) with a molar-mass cutoff of 3.5 kg mol⁻¹. Dialysis was performed for 24 h at room temperature with gentle stirring and with membrane and buffer exchange after 16 h. Final SMA(3 : 1) concentrations were determined by refractometry on an Abbemat 500 (Anton Paar, Graz, Austria) using a molar refractive index increment of dn/dc = 1.1178 M⁻¹. This value was obtained from an SMA(3 : 1) dilution series prepared from a nondialysed Xiran SL25010 S25 solution of known concentration. Molar concentrations were calculated from mass concentrations on the basis of the above number-average molar mass. Samples were aliquoted, stored at −20 °C, and thawed prior to use.

³¹P NMR spectroscopy

Stock solutions of 40 mM POPC in the form of LUVs and 17.5 mM SMA(3 : 1) in buffer (50 mM Tris, 200 mM NaCl, pH 7.4) were used to prepare samples containing 2.5, 5.0, 7.5, or 10.0 mM POPC, 0–5 mM SMA(3 : 1), and 10% D₂O for locking. After mixing, all samples were incubated at 25 °C for at least 24 h, which was found sufficient for equilibration, as evidenced by the fact that neither NMR nor DLS signals revealed further changes over a period of several weeks. Measurements were performed at 25 °C on an Avance 400 spectrometer (Bruker Biospin, Rheinstetten, Germany) operating at a ³¹P resonance frequency of 162 MHz using a 5-mm broadband inverse probe. 256 scans were acquired with an inverse-gated ¹H decoupling sequence using an acquisition time of 1.6 s, a sweep width of 9746 Hz, and a relaxation delay of 6 s. Data were multiplied by an exponential function with a line-broadening factor of 1.0 Hz before Fourier transformation. Chemical shifts were referenced to 85% H₃PO₄ in D₂O as external standard at δ = 0 ppm.

Dynamic light scattering

DLS experiments were carried out on a Zetasizer Nano S90 (Malvern Instruments, Worcestershire, UK) equipped with a 633-nm He–Ne laser and operating at a detection angle of 90°. Samples were thermostatted for 2 min before measurements were carried out at 25 °C in a 45-μL quartz glass cuvette with a cross-section of 3 mm × 3 mm (Hellma Analytics, Müllheim, Germany). Each sample was measured twice, once with the attenuator position automatically optimised for determination of size distributions and a second time with maximum open attenuator position to ensure comparability of total scattering intensities. The influence of all buffer components on viscosity and refractive index were accounted for during data analysis, which was performed by fitting experimentally determined autocorrelation functions with a non-negatively constrained least-squares function⁵³ to yield intensity-weighted particle size distributions and by cumulant analysis⁵⁴ to obtain z-average particle diameters and associated PDIs.

Isothermal titration calorimetry

Demicellisation experiments were done at 25 °C on a VP-ITC (Malvern Instruments) by titrating 30 mM F₆OPC from the injection syringe into the sample cell containing buffer (10 mM HEPES, 150 mM NaCl, pH 7.4). The influence of lipid on the onset of micellisation was assessed by performing the same kind of titration in the presence of 20, 35, or 50 mM POPC in the form of LUVs in both the syringe and the sample cell. Experimental settings included injection volumes of 10 μL, a reference power of 71 μJ s⁻¹, a filter period of 2 s, and time spacings of 7 min to allow the signal to reach the baseline before the next injection. Automated baseline adjustment and peak integration were done with NITPIC,⁵⁵ and the first injection was always excluded from further analysis.

¹⁹F NMR spectroscopy

Stock solutions of 60 mM POPC in the form of LUVs and 20 mM F₆OPC in buffer (10 mM HEPES, 150 mM NaCl, pH 7.4) were used to prepare NMR samples containing 1–6 mM F₆OPC in the absence or presence of 35 mM POPC. All samples contained 10% D₂O for locking. Spectra were recorded at 25 °C on an Avance 400 spectrometer (Bruker Biospin) operating at a ¹⁹F resonance frequency of 376 MHz using a broadband observe probe. 32 scans were acquired with proton decoupling using an acquisition time of 2.2 s, a sweep width of 29 762 Hz, and a relaxation delay of 1 s. Data were multiplied by an exponential function with a line-broadening factor of 1.0 Hz before Fourier transformation. Chemical shifts were referenced to sodium trifluoroacetate in 10% D₂O as external standard at δ = −76.55 ppm.

Acknowledgements

Dr. Harald Kelm (University of Kaiserslautern) is gratefully acknowledged for invaluable help with NMR experiments. We thank Prof. Heiko Heerklotz (University of Freiburg, Germany), Dr. Jana Broecker (University of Toronto, Canada), Jonas Dörr (Utrecht University, The Netherlands), and Johannes Klingler, Abraham Olusegun Oluwole, and Martin Textor (all University of Kaiserslautern) for illuminating discussions. This work was supported by the Deutsche Forschungsgemeinschaft (DFG) through International Research Training Group (IRTG) 1830, by the Carl Zeiss Foundation with a scholarship to R. C. A., and by the Deutsche Akademische Austauschdienst (DAAD) with grant no. 56041134 to S. K.

Notes and references

1. T. Heimburg, Thermal Biophysics of Membranes, Wiley-VCH, Weinheim, 2007.
2. R. Koynova and M. Caffrey, Chem. Phys. Lipids, 2002, 115, 107.
3. A. Helenius and K. Simons, Biochim. Biophys. Acta, 1975, 415, 29.
4. D. Lichtenberg, E. Opatowski and M. M. Kozlov, Biochim. Biophys. Acta, 2000, 1508, 1.
5. G. G. Privé, Methods, 2007, 41, 388.
6. K. Duquesne and J. N. Sturgis, Methods Mol. Biol., 2010, 601, 205.
7. H. Heerklotz, Q. Rev. Biophys., 2008, 41, 205.
8. E. Frotscher, B. Danielczak, C. Vargas, A. Meister, G. Durand and S. Keller, Angew. Chem., Int. Ed., 2015, 54, 5069.
9. S. Keller, A. Tsamaloukas and H. Heerklotz, J. Am. Chem. Soc., 2005, 127, 11469.
10. D. Lichtenberg, F. M. Goñi and H. Heerklotz, Trends Biochem. Sci., 2005, 30, 430.
11. N. Jahnke, O. O. Krylova, T. Hoomann, C. Vargas, S. Fiedler, P. Pohl and S. Keller, Anal. Chem., 2014, 86, 920.
12. M. Textor, C. Vargas and S. Keller, Methods, 2015, 76, 183.
13. M. Textor and S. Keller, Methods Enzymol., 2015 DOI:10.1016/bs.mie.2015.07.033.
14. D. Lichtenberg, H. Ahyayauch, A. Alonso and F. M. Goñi, Trends Biochem. Sci., 2013, 38, 85.
15. M. Jamshad, Y. P. Lin, T. J. Knowles, R. A. Parslow, C. Harris, M. Wheatley, D. R. Poyner, R. M. Bill, O. R. T. Thomas, M. Overduin and T. R. Dafforn, Biochem. Soc. Trans., 2011, 39, 813.
16. S. R. Tonge and B. J. Tighe, Adv. Drug Delivery Rev., 2001, 53, 109.
17. T. J. Knowles, R. Finka, C. Smith, Y. P. Lin, T. Dafforn and M. Overduin, J. Am. Chem. Soc., 2009, 131, 7484.
18. M. Jamshad, V. Grimard, I. Idini, T. J. Knowles, M. R. Dowle, N. Schofield, P. Sridhar, Y. Lin, R. Finka, M. Wheatley, O. R. T. Thomas, R. E. Palmer, M. Overduin, C. Govaerts, J. M. Ruysschaert, K. J. Edler and T. R. Dafforn, Nano Res., 2015, 8, 774.
19. M. C. Orwick, P. J. Judge, J. Procek, L. Lindholm, A. Graziadei, A. Engel, G. Gröbner and A. Watts, Angew. Chem., Int. Ed., 2012, 51, 4653.
20. M. Orwick-Rydmark, J. E. Lovett, A. Graziadei, L. Lindholm, M. R. Hicks and A. Watts, Nano Lett., 2012, 12, 4687.
21. A. R. Long, C. C. O'Brien, K. Malhotra, C. T. Schwall, A. D. Albert, A. Watts and N. N. Alder, BMC Biotechnol., 2013, 13, 41.
22. J. M. Dörr, M. C. Koorengevel, M. Schäfer, S. Scheidelaar, E. A. van der Cruijsen, T. R. Dafforn, M. Baldus and J. A. Killian, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 18607.
23. S. Gulati, M. Jamshad, T. J. Knowles, K. A. Morrison, R. Downing, N. Cant, R. Collin, J. B. Koenderink, R. C. Ford, M. Overduin, I. D. Kerr, T. R. Dafforn and A. J. Rothnie, Biochem. J., 2014, 461, 269.
24. S. Paulin, M. Jamshad, T. R. Dafforn, J. Garcia-Lara, S. J. Foster, N. F. Galley, D. I. Roper, H. Rosado and P. W. Taylor, Nanotechnology, 2014, 25, 285101.
25. D. J. K. Swainsbury, S. Scheidelaar, R. van Grondelle, J. A. Killian and M. R. Jones, Angew. Chem., Int. Ed., 2014, 53, 11803.
26. G. Durand, M. Abla, C. Ebel and C. Breyton, in Membrane Proteins Production for Structural Analysis, ed. I. Mus-Veteau, Springer, New York, 2014, pp. 205–250.
27. M. Abla, S. Unger, S. Keller, F. Bonneté, C. Ebel, B. Pucci, C. Breyton and G. Durand, J. Colloid Interface Sci., 2015, 445, 127.
28. F. H. Shepherd and A. Holzenburg, Anal. Biochem., 1995, 224, 21.
29. P. Raychaudhuri, Q. Li, A. Mason, E. Mikhailova, A. J. Heron and H. Bayley, Biochemistry, 2011, 50, 1599.
30. A. Kyrychenko, M. V. Rodnin, M. Vargas-Uribe, S. K. Sharma, G. Durand, B. Pucci, J. L. Popot and A. S. Ladokhin, Biochim. Biophys. Acta, 2012, 1818, 1006.
31. C. R. Sanders II and G. C. Landis, Biochemistry, 1995, 34, 4030–4040.
32. A. Nath, W. M. Atkins and S. G. Sligar, Biochemistry, 2007, 46, 2059.
33. S. Scheidelaar, M. C. Koorengevel, J. D. Pardo, J. D. Meeldijk, E. Breukink and J. A. Killian, Biophys. J., 2015, 108, 279.
34. M. L. Jackson, C. F. Schmidt, D. Lichtenberg, B. J. Litman and A. D. Albert, Biochemistry, 1982, 21, 4576.
35. M. Roux and P. Champeil, FEBS Lett., 1984, 171, 169.
36. D. Levy, A. Gulik, M. Seigneuret and J. L. Rigaud, Biochemistry, 1990, 29, 9480.
37. H. Heerklotz, A. D. Tsamaloukas and S. Keller, Nat. Protoc., 2009, 4, 686.
38. R. Zhang, I. D. Sahu, L. Liu, A. Osatuke, R. G. Comer, C. Dabney-Smith and G. A. Lorigan, Biochim. Biophys. Acta, 2015, 1848, 329.
39. We assumed that only the outer bilayer leaflet is accessible to F₆OPC, as (zwitter)ionic surfactants usually cannot rapidly translocate across POPC membranes at 25 °C,⁵⁶ particularly at low surfactant contents in the bilayer. If F₆OPC could quickly equilibrate across the membrane, saturation would occur at R^b,SAT_S = 0.016 ± 0.002, so that ΔG^b→m,o_S = −(10.4 ± 0.3) kJ mol⁻¹ and ΔG^aq→b,o_S = −(14.0 ± 0.4) kJ mol⁻¹.
40. J. Broecker and S. Keller, Langmuir, 2013, 29, 8502.
41. M. Textor and S. Keller, Anal. Biochem., 2015, 485, 119.
42. D. Otten, M. F. Brown and K. Beyer, J. Phys. Chem. B, 2000, 104, 12119.
43. M. Nazari, M. Kurdi and H. Heerklotz, Biophys. J., 2012, 102, 498.
44. Bilayer destabilisation in the thermodynamic context of solubilisation ought to be distinguished from other phenomena ascribed to detergent-induced membrane destabilisation, such as enhanced transbilayer lipid movement, permeability to polar solutes and ions, membrane (hemi)fusion, and vesicle agglomeration. These phenomena are not equilibrium processes and do not strictly correlate with one another and with the equilibrium process of membrane solubilisation.⁵⁷.
45. M. Haustein, M. Wahab, H. J. Mögel and P. Schiller, Langmuir, 2015, 31, 4078.
46. H. Heerklotz and J. Seelig, Eur. Biophys. J., 2007, 36, 305.
47. I. Sauer, H. Nikolenko, S. Keller, K. A. Ajaj, M. Bienert and M. Dathe, Biochim. Biophys. Acta, 2006, 1758, 552.
48. S. Keller, I. Sauer, H. Strauss, K. Gast, M. Dathe and M. Bienert, Angew. Chem., Int. Ed., 2005, 44, 5252.
49. O. O. Krylova, N. Jahnke and S. Keller, Biophys. Chem., 2010, 150, 105.
50. W. C. Griffin, J. Soc. Cosmet. Chem., 1949, 311.
51. H. Heerklotz and S. Seelig, Biophys. J., 2000, 78, 2435.
52. This is equivalent to comparing water-to-micelle and water-to-bilayer transfer free energies. Note that these authors⁵¹ used the so-called mole ratio partition coefficient, which is obtained by dividing the mole fraction partition coefficient (eqn (21)) by c_W(1 − X^b_S).
53. P. A. Hassan, S. Rana and G. Verma, Langmuir, 2014, 31, 3.
54. D. E. Koppel, J. Chem. Phys., 1972, 57, 4814.
55. S. Keller, C. Vargas, H. Zhao, G. Piszczek, C. A. Brautigam and P. Schuck, Anal. Chem., 2012, 84, 5066.
56. S. Keller, H. Heerklotz and A. Blume, J. Am. Chem. Soc., 2006, 128, 1279.
57. H. Ahyayauch, M. Bennouna, A. Alonso and F. M. Goñi, Langmuir, 2010, 26, 7307.

---

Footnote

† Electronic supplementary information (ESI) available: Theoretical background, data analysis, and literature values. See DOI: 10.1039/c5nr06353a

---