Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Synthesis, structure and gas-phase reactivity of the mixed silver hydride borohydride nanocluster [Ag3(μ3-H)(μ3-BH4)LPh3]BF4 (LPh = bis(diphenylphosphino)methane)†
Athanasios
Zavras
a,
Alireza
Ariafard
abc,
George N.
Khairallah
a,
Jonathan M.
White
a,
Roger J.
Mulder
d,
Allan J.
Canty
b and
Richard A. J.
O'Hair
*a
aSchool of Chemistry and Bio21 Institute of Molecular Science and Biotechnology, The University of Melbourne, Melbourne, Victoria 3010, Australia. E-mail: rohair@unimelb.edu.au
bThe School of Physical Sciences, University of Tasmania, Private Bag 75, Hobart, Tasmania 7001, Australia
cDepartment of Chemistry, Faculty of Science, Central Tehran Branch, Islamic Azad University, Shahrak Gharb, Tehran, Iran
dCSIRO Manufacturing, Bayview Avenue, Clayton, VIC 3168, Australia
First published on 16th October 2015
Abstract
Borohydrides react with silver salts to give products that span multiple scales ranging from discrete mononuclear compounds through to silver nanoparticles and colloids. The cluster cations [Ag3(H)(BH4)L3]+ are observed upon electrospray ionization mass spectrometry of solutions containing sodium borohydride, silver(I) tetrafluoroborate and bis(dimethylphosphino)methane (LMe) or bis(diphenylphosphino)methane (LPh). By adding NaBH4 to an acetonitrile solution of AgBF4 and LPh, cooled to ca. −10 °C, we have been able to isolate the first mixed silver hydride borohydride nanocluster, [Ag3(μ3-H)(μ3-BH4)LPh3]BF4, and structurally characterise it via X-ray crystallography. Combined gas-phase experiments (LMe and LPh) and DFT calculations (LMe) reveal how loss of a ligand from the cationic complexes [Ag3(H)(BH4)L3]+ provides a change in geometry that facilitates subsequent loss of BH3 to produce the dihydride clusters, [Ag3(H)2Ln]+ (n = 1 and 2). Together with the results of previous studies (Girod et al., Chem. – Eur. J., 2014, 20, 16626), this provides a direct link between mixed silver hydride/borohydride nanoclusters, silver hydride nanoclusters, and silver nanoclusters.
Introduction
The chemistry of alkali metal borohydrides reacting with silver salts has a rich history of over 60 years1 and continues to yield a variety of silver containing products, including silver borohydrides,2–4 silver hydrides5–10 and reduced silver species.11–16 These products span multiple scales ranging from discrete mononuclear compounds2–4 through to ligand capped silver nanoclusters,9–17 silver nanoparticles, and colloids capped with various species including BH4− (Scheme 1).18–21,‡ In 1952 Wiberg and Henle reported that at −80 °C silver perchlorate reacts with lithium borohydride to yield AgBH4 (eqn (1)), which decomposes when the temperature rises to −30 °C via hydrogen and BH3 loss (eqn (2)).2–4 Hydrogen can also be liberated via reaction with methanol (eqn (3)). Ab initio calculations suggested that the decomposition of AgBH4 should yield silver hydride (eqn (4)).23 Finally, there have been several reports that discrete mononuclear complexes of AgBH4 could be isolated when phosphine ligands were employed,2–4 ultimately leading to the X-ray crystallographic characterization of (Ph2MeP)3AgBH4 (Scheme 1(a)).4| AgClO4 + LiBH4 → AgBH4 + LiClO4 | (1) |
| AgBH4 → Ag + 0.5H2 + BH3 | (2) |
| AgBH4 + 3MeOH → Ag + 3.5H2 + B(OMe)3 | (3) |
| AgBH4 → AgH + BH3 | (4) |
In the last few years, several new silver nanoclusters have been isolated from reaction mixtures containing silver salts, sodium borohydride and either anionic ligands or neutral ligands and structurally characterised via X-ray crystallography. Structural reports include (i) silver hydride clusters [Ag2(μ2-H)L2]BF4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 (where L = 1,3-bis(2,6-diisopropylphenyl)imidazolin-2-ylidene (Scheme 1(b)), [Ag3(μ3-H)(μ3-Cl)LPh3]BF4
8 (where L = 1,3-bis(2,6-diisopropylphenyl)imidazolin-2-ylidene (Scheme 1(b)), [Ag3(μ3-H)(μ3-Cl)LPh3]BF4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9 and [Ag3(μ3-H)LPh3](BF4)2
9 and [Ag3(μ3-H)LPh3](BF4)2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 (where LPh = bis(diphenylphosphino)methane), [{Ag7(μ4-H)(E2P(OR)2}6] (R = iPr, E = Se),18 [Ag8H(S2P(OEt)2)6]+5, and [Ag11(H)(S2P(OEt)2)9]+ (Scheme 1(c)),6,7 (ii) the silver clusters Ag14(SC6H3F2)12(PPh3)8 (Scheme 1(d)),12 Ag16(dppe)4(SC6H3F2)14, {Ag32(dppe)5(SC6H4CF3)24}2− (dppe = 1,2-bis(diphenylphosphino) ethane, Scheme 1(e)),14 [Ag44(SAr)30]4− (where ArS is an arylsulfide, Scheme 1(f)),13 [Ag21{S2P(OiPr)2}12]+,15 Ag29(BDT)12(PPh3)4 (BDT = 1,3-benzenedithiol)16 and [Ag25(SR)18]−.17 Importantly, Liu et al. have shown that [{Ag7(μ4-H)(E2P(OR)2}6] (E = Se, S) are precursors to further growth into silver nanoparticles.24
10 (where LPh = bis(diphenylphosphino)methane), [{Ag7(μ4-H)(E2P(OR)2}6] (R = iPr, E = Se),18 [Ag8H(S2P(OEt)2)6]+5, and [Ag11(H)(S2P(OEt)2)9]+ (Scheme 1(c)),6,7 (ii) the silver clusters Ag14(SC6H3F2)12(PPh3)8 (Scheme 1(d)),12 Ag16(dppe)4(SC6H3F2)14, {Ag32(dppe)5(SC6H4CF3)24}2− (dppe = 1,2-bis(diphenylphosphino) ethane, Scheme 1(e)),14 [Ag44(SAr)30]4− (where ArS is an arylsulfide, Scheme 1(f)),13 [Ag21{S2P(OiPr)2}12]+,15 Ag29(BDT)12(PPh3)4 (BDT = 1,3-benzenedithiol)16 and [Ag25(SR)18]−.17 Importantly, Liu et al. have shown that [{Ag7(μ4-H)(E2P(OR)2}6] (E = Se, S) are precursors to further growth into silver nanoparticles.24
Here we report the “mass spectrometry directed synthesis” of the first mixed silver hydride/borohydride cluster [Ag3(μ3-H)(μ3-BH4)LPh3]BF4,25–27 and its structural characterization by X-ray crystallography. DFT calculations indicate that the loss of a ligand (L) under collision induced dissociation (CID) conditions results in a change in cluster geometry that facilitates decomposition of the ligated BH4−via loss of BH3 (cf.eqn (2)).
Results and discussion
Electrospray ionization mass spectrometry (ESI/MS) was used to monitor the identity of cationic silver clusters formed upon mixing silver(I) tetrafluoroborate with diphosphine ligands in cooled acetonitrile solutions and subsequently treating with excess NaBH4. The ligands bis(diphenylphosphino)methane (LPh) and bis(dimethylphosphino)methane (LMe) were added to an acetonitrile solution of AgBF4 (1.9 mg, 5 mM) with a ligand-to-metal ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
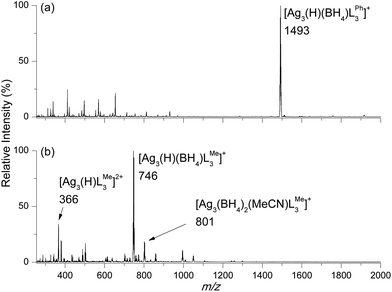
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 giving a clear solution. Addition of 15 equivalents of NaBH4 to each of these solutions gave an immediate colour change from colourless to light yellow for both LPhand LMe. ESI/MS analysis 5 minutes after the addition of NaBH4 are shown in Fig. 1. The bulkier LPh ligand yields the abundant peak [Ag3(H)(BH4)LPh3]+m/z 1493 (Fig. 1a), confirmed by high resolution mass spectrometry experiments (ESI Fig. S1a and b†). In contrast the LMe yields a mixture of silver clusters assigned as [Ag3(H)LMe3]2+m/z 366, [Ag3(H)(BH4)LMe3]+m/z 746 (Fig. 1b, ESI Fig. S2†) and [Ag3(BH4)2(MeCN)LMe3]+m/z 801. Since clusters formed from LPh were less prone to decomposition reactions in solution compared to those formed from LMe,28 the synthesis of crystalline material suitable for characterization was pursued for LPh.
1 giving a clear solution. Addition of 15 equivalents of NaBH4 to each of these solutions gave an immediate colour change from colourless to light yellow for both LPhand LMe. ESI/MS analysis 5 minutes after the addition of NaBH4 are shown in Fig. 1. The bulkier LPh ligand yields the abundant peak [Ag3(H)(BH4)LPh3]+m/z 1493 (Fig. 1a), confirmed by high resolution mass spectrometry experiments (ESI Fig. S1a and b†). In contrast the LMe yields a mixture of silver clusters assigned as [Ag3(H)LMe3]2+m/z 366, [Ag3(H)(BH4)LMe3]+m/z 746 (Fig. 1b, ESI Fig. S2†) and [Ag3(BH4)2(MeCN)LMe3]+m/z 801. Since clusters formed from LPh were less prone to decomposition reactions in solution compared to those formed from LMe,28 the synthesis of crystalline material suitable for characterization was pursued for LPh.
Structural characterization of (1) by ESI/MS, NMR and IR spectroscopy and X-ray crystallography
The crystals of (1) formed in the bulk synthesis were first analysed via ESI/MS in both the positive and negative ion mode. The former gave an almost identical mass spectrum to that shown in Fig. 1a (data not shown), while the latter gave an abundant signal due to the BF4− counter ion (ESI Fig. S3†). IR spectroscopy confirmed the presence of both BF4− and BH4− (ESI Fig. S4†).We next attempted to characterise 1via various NMR experiments (ESI Fig. S5–S16†). 1 was dissolved into cold CD3CN to produce a saturated solution and this solution immediately introduced into the pre-cooled NMR probe at −15 °C. The 1H NMR spectrum collected at −15 °C displayed a very broad multiplet centred at 0.5 ppm, attributed to coordinated BH4, from which no fine structure could be resolved (ESI Fig. S5†). This may be due to (i) the fluxional nature of the binding of BH4, (ii) the complex splitting patterns due to spin-active nuclei and isotopomers of silver (107/109Ag) and boron (10/11B) and (iii) the influence of the quadrupolar 10B nucleus. This signal collapsed into a broad singlet at 0.5 ppm under 11B-decoupling (ESI Fig. S6 and S7†). There was no apparent change to the signals upon 31P-decoupling (ESI Fig. S8 and S9†). The 1H NMR spectrum further displayed a broad multiplet centred at 4.5 ppm attributed to the coordinated hydride (ESI Fig. S5†), the peaks of which sharpened slightly under 31P-decoupling (ESI Fig. S8 and S9†). The 1H-decoupled 31P NMR spectrum displayed a broad peak at 0.56 ppm, shifted downfield from the free ligand resonance at 23.1 ppm (ESI Fig. S10†). The 1H-decoupled 11B NMR spectrum displays two resonances at 0.57 and 41.49 ppm attributable to BF4– and BH4, respectively (ESI Fig. S11†), as confirmed via the 19F-11B and 1H-11B HSQC NMR experiments (ESI Fig. S12 and S13† respectively). The 1H-decoupled 19F NMR spectrum displays a resonance at −150.16 ppm corresponding to BF4– (ESI Fig. S14†). The 1H-decoupled 13C NMR spectrum displays resonances attributable to coordinated phosphine ligand (ESI Fig. S15†).
Heating the sample from −15 °C to +25 °C in the NMR probe enabled the collection of 1H data at various temperatures. The most obvious change in the spectra with time at −15 °C and then upon heating was the increase in the intensity of the singlet at 4.56 ppm which is attributable to dissolved H2 and the corresponding reduction in the intensity of the coordinated hydride signal (ESI Fig. S16†).
This series of experiments required the preparation of several different samples, as it was noted that 1 appears to undergo decomposition/reactions in these highly concentrated solutions, ultimately resulting in precipitation of a black material after approximately 3 hours at 25 °C. This rapid change in solution, even at −15 °C, precluded the overnight or longer acquisition of a 109Ag NMR spectrum.
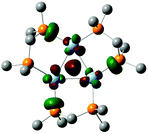
X-ray crystallography was used to determine the structure of [Ag3(H)(BH4)LPh3]BF4.§ The cation [Ag3(H)(BH4)LPh3]+ which has crystallographic 3-fold symmetry, Fig. 2, consists of a trinuclear core with silver(I) ions occupying the vertices of an equilateral triangle.
The Ag(1)–Ag(1) distances that connect the edges of the triangle are 2.9100(3) Å. The hydride H which lies on a crystallographic 3-fold axis is 0.96 Å displaced from the plane defined by the triangular silver(I) core and is coordinated to all silver(I) ions as a μ3-bridging ligand with a Ag(1)–H distance of 1.93(3) Å and Ag(1)–H–Ag(1) angle of 97.5(3)°. Relative to the μ3-hydride H, the opposing face of the trinuclear core has a μ3 borohydride with distorted tetrahedral geometry, the boron lies on the 3-fold axis of symmetry and three symmetry related hydrides (H1a) coordinate to the three silver atoms. Related μ3-borohydride binding to the metal triangle of Fe(CO)3 fragments has been reported for the trinuclear cluster [Fe3(μ-H)(μ3-BH4)(CO)9].27 The boron–hydrogen bond lengths for BH4− are: B(1)–H(1a) 1.10(3) Å and B(1)–(H1b) 1.07(6) Å. There are two types of bond angles in the BH4− tetrahedron: (i) H(1a)–B(1)–H(1a) 110.1(16)° and (ii) H(1a)–B(1)–H(1b) 108.9(16)°. The tetrahedral face H(1a)–H(1a)–H(1a), is parallel to the larger Ag(1)–Ag(1)–Ag(1) plane. Each of the three hydrogen atoms of BH4−, H(1a), are individually coordinated to one silver(I) ion where H(1a)–Ag(1) is 2.17(3) Å. The core is surrounded by three μ2-bridging phosphine ligands which coordinate to two silver(I) ions through P(1) and P(2): Ag(1)–P(1) is 2.4483(5) Å and Ag(1)–P(2) is 2.4486(5) Å. The distance between P(1) and P(2) within the chelate ring is 3.041 Å and the P(1)–C(20)–P(2) angle is 110.8(1)°. P(1) is below the plane of the trinuclear core and both C(20) and P(2) are above the plane with C(20) above P(2).
The phenyl rings extending from the phosphorus atoms adopt one of three distinct geometrical conformations. Both P(1) and P(2) have one phenyl ring towards the μ3-hydride. A pseudoequatorial phenyl ring in regards to the Ag3 triagnular plane extends from P(1). One phenyl ring from each P(2) extends toward the μ3-borohydride.
The structures of [Ag3(μ3-H)(μ3-BH4)LPh3]+, [Ag3(μ3-D)LPh3]2+ (ref. 10) and [Ag3(μ3-H)(μ3-Cl)LPh3]+ (ref. 9) are compared in Table 1. All structures consist of a trinuclear silver(I) core and maintain a triangular geometry. The dication [Ag3(μ3-D)LPh3]2+ has the longest Ag–Ag and Ag–P interactions at 3.1193 and 2.4632 Å respectively. All hydrides coordinate as μ3-bridging ligands where the longest Ag–H interaction exists in [Ag3(μ3-H)(μ3-Cl)LPh3]+ at 1.91(2) Å.
| [Ag3(μ3-D)LPh3]2+ | [Ag3(μ3-H)(μ3-Cl)LPh3]+ | [Ag3(μ3-H)(μ3-BH4)LPh3]+ | |
|---|---|---|---|
| Ag–Ag | 3.1193 | 2.8988(2) | 2.9100(3) |
| Ag-(H/D) | 1.83 | 1.91(2) | 1.93(3) |
| Ag-(Cl/BH4) | NA | 2.859(1) | 2.17(3) |
| Ag–P | 2.4632 | 2.4421(9) | 2.4486(5) |
The BF4− counterion is disordered over two crystallographic special positions, a −3 site with normal 1/6 occupancy and on a 3-fold axis with 50% the normal occupancy of 1/3, with the same position occupied the other 50% by a molecule of acetonitrile. The relative occupancy at these special positions were supported by SQUEEZE calculations29 which were not used to remove these disordered components. The Ag bound hydride and BH4 hydrides were located on Fourier difference maps and refined isotropically without restraint.
Unimolecular gas-phase chemistry of [Ag3(H)(BH4)L3]+
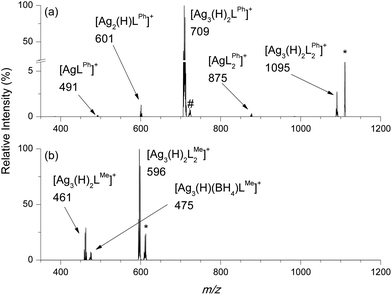
Given that AgBH4 is known to undergo thermal decomposition reactions that liberate BH3 (eqn (2)),1,23 we were interested in examining whether such reactions occur in the gas phase for isolated, stoichiometrically well defined cluster cations. Thus, CID was carried out in a 2D linear ion trap to probe the low-energy fragmentation pathways of [Ag3(H)(BH4)L3]+, where the cluster identity has been confirmed by high resolution mass spectrometry (HRMS).Mass selection and subsequent CID of [Ag3(H)(BH4)LPh3]+ (m/z 1493, HRMS (ESI Fig. S1a and b†)) to ca. 50% relative intensity yields [Ag3(H)(BH4)LPh2]+ (m/z 1109, HRMS (ESI Fig. S1c and d†)) via neutral ligand loss (eqn (5)) as the main fragmentation channel. [Ag3(H)2LPh2]+ (m/z 1095, HRMS (ESI Fig. S17a and b†)), [Ag3(H)(BH4)LPh]+ (m/z 723, (ESI Fig. S1e and f†)) and [Ag3(H)2LPh]+ (m/z 709, (ESI Fig. S17c and d†)); [Ag2(H)LPh]+ (m/z 601) and; [AgLPh]+ (m/z 491) are all also observed.
The main fragmentation channel of [Ag3(H)(BH4)LMe3]+ (m/z 747, HRMS (ESI Fig. S2†)) involves neutral ligand loss (eqn (5)) to form [Ag3(H)(BH4)LMe2]+ (m/z 610, Fig. 3b). Other ions observed include [Ag3(H)2LMe2]+ (m/z 596), [Ag3(H)(BH4)LMe]+ (m/z 475) and [Ag3(H)2LMe]+ (m/z 461).
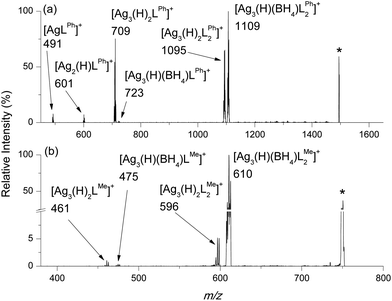 | ||
| Fig. 3 LTQ CID of (a) [Ag3(H)(BH4)LPh3]+, m/z 1493; (b) [Ag3(H)(BH4)LMe3]+, m/z 747. The most intense peak in the cluster is represented by the m/z value. *Refers to the mass-selected precursor ion. | ||
Energy-resolved CID (ERCID) was used in a 3D ion trap to determine whether the product ions in Fig. 3a are due to primary fragmentation pathways of [Ag3(H)(BH4)LPh3]+ or secondary fragmentation of primary fragment ions (ESI Fig. S18†). The onset of ligand loss (eqn (5)) begins at ca. 0.6 V and continues to steadily increase up until 0.8 V (ESI Fig. S18†). An increase in the collision voltage beyond this point results in the consumption of [Ag3(H)(BH4)LPh2]+ (m/z 1109) and the increase of [Ag3(H)2LPh2]+ (m/z 1095). These results suggest that the primary product ion upon CID of [Ag3(H)(BH4)LPh3]+ arises from ligand loss and that ions of lower m/z are from subsequent secondary fragmentation of [Ag3(H)2LPh2]+ (m/z 1095).
| [Ag3(H)(BH4)L3]+ → [Ag3(H)(BH4)L2]+ + L | (5) |
Unimolecular gas-phase chemistry of [Ag3(H)(BH4)L2]+
The primary product ions formed via ligand loss (eqn (5), Fig. 3) were mass selected and subjected to CID in the 2D ion trap (Fig. 4). Mass selection and subsequent CID of [Ag3(H)(BH4)LPh2]+ (m/z 1109, Fig. 4a) to ca. 30% relative intensity yields [Ag3(H)2LPh2]+ (m/z 1095) via neutral borane loss (eqn (5)) as a minor fragmentation channel and [Ag3(H)2LPh]+ (m/z 709) as the main fragmentation channel; (ii) [Ag2(H)LPh]+ (m/z 601) and; (iii) [AgLPh]+ (m/z 491) are all also observed. The main fragmentation channel upon CID of [Ag3(H)2LMe2]+ (m/z 596, Fig. 4b) involves neutral borane loss (eqn (6)). Other ions observed include [Ag3(H)(BH4)LMe]+ (m/z 475), and [Ag3(H)2LMe]+ (m/z 461).Once again, ERCID was used in a 3D ion trap to determine which of the product ions observed in Fig. 4a were primary (ESI Fig. S19†). [Ag3(H)2LPh2]+ (m/z 1095) begins to appear at 0.5 V upon CID [Ag3(H)(BH4)LPh2]+ (m/z 1109), which corresponds to BH3 loss (eqn (6)). A minor primary fragmentation channel assigned to neutral ligand loss (eqn (7)) is observed at around 0.6 V. Although decomposition reactions of coordinated ligands in metal complexes and clusters have been well studied in the gas-phase,30,31 this appears to be the first experimental report on the gas-phase decomposition of a coordinated BH4− ligand via BH3 loss. This reaction is related to that described by Wiberg and Henle (eqn (2)).1
| [Ag3(H)(BH4)L2]+ → [Ag3(H)2L2]+ + BH3 | (6) |
| [Ag3(H)(BH4)L2]+ → [Ag3(H)(BH4)L]+ + L | (7) |
Unimolecular gas-phase chemistry of [Ag3(H)(BH4)L]+
[Ag3(H)(BH4)LPh]+ (m/z 723), formed via sequential ligand losses (eqn (4) and (6)), was mass selected and allowed to undergo CID. The sole fragmentation channel observed is due to the loss of neutral BH3 (eqn (8)) (ESI Fig. S20†).| [Ag3(H)(BH4)L]+ → [Ag3(H)2L]+ + BH3 | (8) |
Unimolecular gas-phase chemistry of [Ag3(H)2Ln]+
The dihydride clusters [Ag3(H)2LPhn]+ where n = 2, 1 were subjected to ERCID using a 3D ion trap (ESI Fig. S21 and S22†). The major primary fragmentation of [Ag3(H)2LPh2]+ (m/z 1095) occurs via ligand loss (eqn (9)), with an onset requiring ca. 0.6 V. In contrast, The major primary fragmentation of [Ag3(H)2LPh]+ (m/z 708) involves AgH loss, as previously described,32 with the onset of fragmentation occurring at ca. 0.4 V.| [Ag3(H)2L2]+ → [Ag3(H)2L]+ + L | (9) |
| [Ag3(H)2L]+ → [Ag2(H)L]+ + AgH | (10) |
Computational study of BH4− decomposition triggered via ligand loss in the clusters [Ag3(H)(BH4)LMen]+ (n = 1–3)
To better understand how the number of diphosphine ligands, n, in the clusters, [Ag3(H)(BH4)Ln]+, influence the competition between decomposition of the ligated BH4− (eqn (11)) versus loss of a ligand (eqn (12)), we turned to DFT calculations to examine the structures and energetics of the reactants and products of eqn (11) and (12) for the case of clusters containing LMe ligands. The initial geometry for [Ag3(H)(BH4)LMe3]+ was that related to the core structure from the X-ray structure for 1. Thus changing the phosphine substitutent from Ph to Me has little effect on the core structure. To calculate fragment ion structures, either BH3 or LMe was removed and the resultant fragment was allowed to fully optimise.¶||| [Ag3(H)(BH4)Ln]+ → [Ag3(H)2Ln]+ + BH3 | (11) |
| [Ag3(H)(BH4)Ln]+ → [Ag3(H)(BH4)Ln−1]+ + L | (12) |
To understand why BH4− in [Ag3(H)(BH4)L3]+ bridges all three Ag atoms via three separate two-electron, two-centre (2e,2c) bonds, the structure and bonding of this cluster was analysed based on simple electron counting rules.33–37 As expected, a transition metal centre with a d10 electron configuration has four empty orbitals. Two of these four are always available for ligand coordination to give linear complexes [ML2]+. However, the availability of the other two orbitals depends on the identity of the L ligands. For example, if the L–M–L bond angle in [ML2]+ using the bidentate ligands is forced to be bent, the two extra orbitals become available and as a result the tetrahedral complex [ML4]+ is formed. Also, the monodentate L ligands with relatively weak σ-donor abilities increase the possibility of all four orbitals on the metal centre being available.
In [Ag3(H)(BH4)L3]+, the presence of the three bidentate phosphine ligands render all the four empty orbitals on three Ag centres susceptible to coordination. In such a case, the cluster has 3 × 4 = 12 available orbitals. Six of these twelve orbitals are occupied by the phosphine ligands. Three of them are involved in interaction with the hydride ligand (a μ3-bridging ligand) via a four-centre two-electrons bonding mode. Finally, the last three orbitals on Ag centres overlap with three filled B–H σ orbitals of BH4−, leading to coordination of BH4− in μ3-form. The 50 valence electron [Ag3(H)(BH4)L3]+ cluster is not expected to have direct metal–metal interactions, consistent with other related M3L6 clusters where M has a d10 electron configuration.35 This is highlighted by an examination of its HOMO, which suffers from the Ag–Ag anti-bonding interactions derived from the silver dxz orbitals (Fig. 6). The short Ag–Ag bond distances in [Ag3(H)(BH4)L3] (2.971–2.993 Å) can be mainly rationalised by the presence of the hydride ligand that creates the four-centre two-electron bonds with the Ag centres. A similar metal–metal bond distance was also observed by Harvey et al. in the [Pd3(H2PCH2PH2)3(CO)(H)]− cluster (2.932 Å), where the corresponding anti-bonding skeletal molecular orbitals are also fully occupied.38
With regards to the unimolecular fragmentation chemistry, the calculations indicate that the first loss of the ligand, L (eqn (12)), from [Ag3(H)(BH4)LMe3]+ results in transferring the hydride to Ag2 and causes this centre to adopt a mainly linear structure with a very weak interaction with Ag1 (Fig. 5). The presence of the very strong σ donating hydride ligand on the Ag2 centre makes the two empty orbitals on Ag2 less available and thus does not allow BH4− to strongly interact with them. In this case, BH4− is only able to interact with the Ag1 and Ag3 centres to give a μ2-coordination mode (Fig. 5). If we ignore the weak interactions between Ag centres in [Ag3(H)(BH4)LMe2]+, the Ag1 and Ag3 centres can be considered as three coordinate centres. For [Ag3(H)(BH4)LMe2]+, the Ag2–H σ orbital interacts with one of the empty orbitals on Ag3 and creates a 3-centre 2-electron bond between two silver(I) ions via a μ2-bridging hydride ligand.
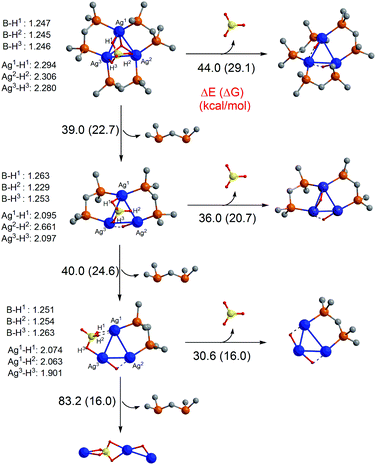 | ||
| Fig. 5 DFT calculated structures and energetics for the competition between BH3 loss and L ligand loss. Hydrogen atoms on the LMe ligands are omitted for clarity. | ||
From loss of a second LMe ligand, bonding in the product [Ag3(H)(BH4)LMe]+ can be viewed as interaction of the linear complex [BH4–Ag3–H]− with [Ag2LMe]2+ (Fig. 5). In this cluster, an Ag3–H σ orbital interacts with an empty orbital on Ag2, and BH4− bridges Ag3 to Ag1 through three of its B–H bonds. Therefore, each Ag(I) centre in [Ag3(H)(BH4)LMe]+ experiences a linear two coordinated environment.
Our calculations show that, in excellent agreement with the CID data, the BH3 loss becomes easier as the number of ligands, L, decreases. The loss of the ligand, L, increases the electron deficiency of the metal centres, leading to the stronger coordination of BH4− to the Ag centres, as evident from the shorter Ag–H(BH4) and longer B–H bond distances in [Ag3(H)(BH4)LMe]+ (Fig. 5). In other words, ligand loss enhances the acidity of Ag centres and makes them more prone to compete with BH3 for hydride abstraction. The better the competition, the easier the BH3 loss.
In contrast to BH3 loss (eqn (11)) neutral ligand loss (eqn (12)) from [Ag3(H)(BH4)LMe]+ is more difficult than that from [Ag3(H)(BH4)LMe3]+ and [Ag3(H)(BH4)LMe2]+, supported by the DFT calculations. This difference can be rationalised in terms of the molecular orbital approach.39 In general, the HOMO of d10 complexes (MLn) with a coordination number greater than two (n > 2) suffers from a slight anti-bonding interaction between L and M, leading to weakening of the M–L bonds. However, this anti-bonding interaction disappears in linear d10-ML2 complexes, causing the M–L bonds in ML2 to be much stronger than those in ML3 and ML4. As mentioned above, clusters [Ag3(H)(BH4)LMe3]+ and [Ag3(H)(BH4)LMe2]+ have the Ag centres not present as two-coordinate, and thus the loss of the ligand, L, from these clusters is relatively easy. By contrast, all the Ag centres in [Ag3(H)(BH4)LMe]+ are mainly two-coordinate, thereby not having the relevant anti-bonding interaction, forming very strong M–L bonds.
Conclusions
The sodium borohydride induced reduction of silver(I) salts to form nanoparticles has been described as a “black-box” synthesis.19 While it is now well established that there are different growth stages,18–20 the actual molecular species associated during growth to nanoparticles and the mechanisms for growth are not fully understood. By studying the formation and reactions of small ligand protected nanoclusters, we are able to better understand the fundamental interactions between silver salts and borohydride.We have previously shown that BH4− is a source of hydride for [Ag3(μ3-H)LPh3]2+ (ref. 10) and [Ag3(μ3-H)(μ3-Cl)LPh3]+ (ref. 9) at ambient conditions, however at −10 °C the decomposition of BH4− can be prevented and coordination to silver(I) ions can occur to yield [Ag3(μ3-H)(μ3-BH4)LPh3]BF4. This is the first silver nanocluster containing a “captured” borohydride anion, and may have relevance to binding of BH4− to silver nanoparticle surfaces,20,21 or bulk silver metal surfaces.40 Given that nanoclusters such as [{Ag7(μ4-H)(E2P(OR)2}6] are precursors to further growth into silver nanoparticles,21 it will be interesting to establish whether the nanoclusters [Ag3(μ3-H)(μ3-Cl)LPh3]BF4,9 [Ag3(μ3-H)LPh3](BF4)2,10 and [Ag3(μ3-H)(μ3-BH4)LPh3]BF4 can further grow into silver nanoparticles.
The current and previous32 gas-phase experiments and DFT calculations on [Ag3(H)2−x(BH4)xLn]+ clusters provide a direct link between mixed hydride/borohydride silver clusters (x = 1), dihydride silver clusters (x = 0)32 and silver clusters via discrete unimolecular reactions occurring for isolated clusters (Scheme 2). Thus CID triggers loss of the ligand, L (eqn (12)), resulting in a change in the binding mode(s) of the H and BH4 ligands (Fig. 5). Perhaps related reactions occur at the surfaces of silver nanoparticles, which might drive the development of catalysts for hydrogen storage applications.41
 | ||
| Scheme 2 Direct link established between mixed hydride/borohydride clusters (Black), dihydride clusters (Blue) and “all metal” clusters (Red) based on gas-phase unimolecular fragmentation reactions of mass selected clusters reported here using CID and in ref. 32 using laser-induced dissociation (LID). | ||
Experimental
Synthesis of solution phase silver clusters for MS analyses
Silver(I) tetrafluoroborate (1.9 mg, 0.010 mmol) and bis(diphenylphosphino)methane (3.8 mg, 0.010 mmol) in 20 mL acetonitrile were added to a 25 mL Quickfit Erlenmeyer flask equipped with a magnetic stirrer and stopper. The solution was cooled to ca.−10 °C by immersing the reaction flask in an ice/water bath above the solvent level. All reagents were kept in the dark and flasks covered in foil. Sodium borohydride (5.7 mg, 0.150 mmol) was added as a powder and the solution changed colour from clear to light yellow.Synthesis of crystalline [Ag3(H)(BH4)(LPh)3]BF4 (1)
Silver(I) tetrafluoroborate (194 mg, 1.0 mmol) and bis(diphenylphosphino)methane (384 mg, 1.0 mmol) in 100 mL acetonitrile were added to a 250 mL Quickfit round bottomed flask equipped with a magnetic stirrer and stopper. The solution was cooled to −10 °C by immersing the reaction flask in an ice/water bath above the solvent level. All reagents were kept in the dark and flasks covered in foil. Sodium borohydride (57.0 mg, 1.50 mmol), was added as a powder and the solution changed colour from clear to light yellow over ca. 5 minutes. The solution was filtered after stirring for 3 hours and frozen solid by immersing the flask in liquid nitrogen. While frozen, 100 mL of diethylether was added and the flask moved to the fridge. After 72 hours crystalline material was formed and characterised by X-ray crystallography.NMR spectroscopy experiments
The NMR experiments were performed on a Bruker Avance 400 NMR spectrometer (400.13 MHz 1H frequency) equipped with a 5 mm triple resonance broadband probe (BB/2H–1H/19F). Solutions for analysis by NMR were prepared by dissolving [Ag3(μ3-H)(μ3-BH4)LPh3]BF4 in 0.6 ml of deuteroacetonitrile. NMR experiments were performed with the sample held at temperatures between −15 °C and +25 °C (±0.1 °C). Chemical shifts for 1H experiments are referenced to the residual protonated solvent signal (CD2HCN, δ 1.94 ppm); 11B externally referenced to BF3·OEt2 capillary in CD3CN; 13C referenced to the solvent signal (CD3CN, δ 1.39 ppm); 19F externally referenced to a CFCl3 in CD3CN (δ 0.00 ppm); 31P externally referenced to a 85% H3PO4 capillary in CDCl3 (δ 0.00 ppm). One- and two-dimensional NMR experiments were acquired using standard Bruker library pulse sequences.Mass spectrometry
Mass spectra were recorded using a Finnigan hybrid linear quadrupole (LTQ) Fourier transform ion cyclotron resonance (FTICR) mass spectrometer. The silver clusters prepared in the solution phase were diluted to 50 μM and introduced into the mass spectrometer via a syringe pump set at a flow rate of 5 μL min−1 to the ESI capillary. The ESI conditions used, for optimum intensity of the target ions, typically were: spray voltage, 4.2–5.0 kV, capillary temperature, 250 °C, nitrogen sheath gas pressure, 5 (arbitrary units), capillary voltage 25 V, tube lens voltage 15 V. Selected ions were transferred to the FTICR cell for accurate mass measurement with the use of selected ion monitoring (SIM) and selected reaction monitoring (SRM) to obtain the most reliable results. The unimolecular fragmentation of silver clusters was examined via CID. The mass-selected precursor ion was depleted to 10–20% using a normalised collision energy typically between 20–25% and a mass selection window of 15 Th to isolate the full range of isotopes due to boron and silver isotopes.Energy resolved CID experiments were carried out using a Finnigan 3D ion trap (LCQ) mass spectrometer. The method of Broadbelt was adapted.42 The silver clusters were diluted to 50 μM and introduced into the mass spectrometer via a syringe pump set at 5 μL min−1 through a Finnigan ESI source. The source conditions used for optimum intensity of the target ions were: spray voltage 4.5–5.1 kV, capillary temperature 200 °C, nitrogen sheath gas pressure, 50 (arbitrary units), capillary voltage 30 V, tube lens voltage −55 V. The mass-selected precursor ion was isolated with a mass selection window of 15 Th. The normalised collision energy (NCE) was increased incrementally by 1.0% typically starting from a NCE where no fragmentation is observed, until reaching the NCE required for depleting the precursor ion to <5% relative intensity. The NCE was converted to an amplitude of the resonance excitation RF voltage (tick amp) as described in the ESI.† The relative intensity of precursor and product ions were plotted as a function of the increasing amplitude to determine: (i) the onset of precursor fragmentation and (ii) the assignment of product ions as primary or secondary fragments of the mass-selected silver cluster.
Crystallography
Intensity data for compound 1 was collected on an Oxford Diffraction SuperNova CCD diffractometer using Cu-Kα radiation, the temperature during data collection was maintained at 130.0(1) using an Oxford Cryostream cooling device. The structure was solved by direct methods and difference Fourier synthesis.43 The thermal ellipsoid plot was generated using the program ORTEP-3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 44 integrated within the WINGX45suite of programs. The BF4− counterion was disordered over two crystallographic special positions, a −3 site with normal 1/6 occupancy and on a 3-fold axis with 50% the normal occupancy of 1/3, with the same position occupied the other 50% by a molecule of acetonitrile. The Ag bound hydride and BH4 hydrides were located on Fourier difference maps and refined isotropically without restraint.
44 integrated within the WINGX45suite of programs. The BF4− counterion was disordered over two crystallographic special positions, a −3 site with normal 1/6 occupancy and on a 3-fold axis with 50% the normal occupancy of 1/3, with the same position occupied the other 50% by a molecule of acetonitrile. The Ag bound hydride and BH4 hydrides were located on Fourier difference maps and refined isotropically without restraint.
Crystal data for 1: C75H71B2F4P6Ag3·(0.25 CH3CN) M = 1589.63, T = 130.0(2) K, λ = 1.54184 Å, cubic, space group Pa![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) , a = 24.1922(1) Å, V = 14158.79(18) Å3, Z = 8, Dc = 1.491 mg M−3μ(Cu-Kα) 8.296 mm−1, F(000) 6428, crystal size 0.17 × 0.16 × 0.09 mm. 67033 reflections measured, 4996 independent reflections (Rint = 0.0442), the final R was 0.0279 [I > 3(I) 4853 data] and wR(F) (all data) was 0.0735.
, a = 24.1922(1) Å, V = 14158.79(18) Å3, Z = 8, Dc = 1.491 mg M−3μ(Cu-Kα) 8.296 mm−1, F(000) 6428, crystal size 0.17 × 0.16 × 0.09 mm. 67033 reflections measured, 4996 independent reflections (Rint = 0.0442), the final R was 0.0279 [I > 3(I) 4853 data] and wR(F) (all data) was 0.0735.
Density functional theory
Computational details.46–53 Gaussian 09![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 46 was used to fully optimise all the structures reported in this paper at the M06 level of density functional theory.47,48 The effective-core potential of Hay and Wadt with a double-ξ valence basis set (LANL2DZ) was chosen to describe Ag. The 6-31G(d) basis set was used for other atoms. Polarization functions were also added for Ag (ξf = 1.611). This basis set combination will be referred to as BS1. To further refine the energies obtained from the M06/BS1 calculations, we carried out single-point energy calculations for all of the structures with a larger basis set (BS2) at the M06 level of theory. BS2 utilises the def2-TZVP basis set on all atoms. Effective core potentials including scalar relativistic effects were used for silver atom. We have used the corrected potential energies obtained from the M06/BS2//M06/BS1 calculations throughout the paper unless otherwise stated.
46 was used to fully optimise all the structures reported in this paper at the M06 level of density functional theory.47,48 The effective-core potential of Hay and Wadt with a double-ξ valence basis set (LANL2DZ) was chosen to describe Ag. The 6-31G(d) basis set was used for other atoms. Polarization functions were also added for Ag (ξf = 1.611). This basis set combination will be referred to as BS1. To further refine the energies obtained from the M06/BS1 calculations, we carried out single-point energy calculations for all of the structures with a larger basis set (BS2) at the M06 level of theory. BS2 utilises the def2-TZVP basis set on all atoms. Effective core potentials including scalar relativistic effects were used for silver atom. We have used the corrected potential energies obtained from the M06/BS2//M06/BS1 calculations throughout the paper unless otherwise stated.
Acknowledgements
We thank the ARC for financial support via grants DP1096134 (to GNK) and DP150101388 (to RAJO and AJC). The authors gratefully acknowledge the generous allocation of computing time from the University of Tasmania and the National Computing Infrastructure. We thank Assoc. Prof. Paul Donnelly for useful discussions.Notes and references
- E. Wiberg and W. Henle, Z. Naturforsch., B: J. Chem. Sci., 1952, 7, 575–576 Search PubMed.
- J. C. Bommer and K. W. Morse, Inorg. Chem., 1980, 19, 587–593 CrossRef CAS.
- F. Cariati and L. Naldini, Gazz. Chim. Ital., 1965, 95, 201–205 CAS.
- E. B. Lobkovskii, M. Y. Antipin, A. P. Borisov, V. D. Makhaev, K. N. Semenenko and Y. T. Struchkov, Koord. Khim., 1981, 7, 307–310 CAS.
- C. W. Liu, H.-W. Chang, C.-S. Fang, B. Sarkar and J.-C. Wang, Chem. Commun., 2010, 46, 4571–4573 RSC.
- C. W. Liu, H.-W. Chang, B. Sarkar, J.-Y. Saillard, S. Kahlal and Y.-Y. Wu, Inorg. Chem., 2010, 49, 468–475 CrossRef CAS PubMed.
- C. W. Liu, P.-K. Liao, C.-S. Fang, J.-Y. Saillard, S. Kahlal and J.-C. Wang, Chem. Commun., 2011, 47, 5831–5833 RSC.
- B. K. Tate, C. M. Wyss, J. Bacsa, K. Kluge, L. Gelbaum and J. P. Sadighi, Chem. Sci., 2013, 4, 3068–3074 RSC.
- A. Zavras, G. N. Khairallah, T. U. Connell, J. M. White, A. J. Edwards, P. S. Donnelly and R. A. J. O'Hair, Angew. Chem., Int. Ed., 2013, 52, 8391–8394 CrossRef CAS PubMed.
- A. Zavras, G. N. Khairallah, T. U. Connell, J. M. White, A. J. Edwards, R. J. Mulder, P. S. Donnelly and R. A. J. O'Hair, Inorg. Chem., 2014, 53, 7429–7437 CrossRef CAS PubMed.
- A. Desireddy, B. E. Conn, J. Guo, B. Yoon, R. N. Barnett, B. M. Monahan, K. Kirschbaum, W. P. Griffith, R. L. Whetten, U. Landman and T. P. Bigioni, Nature, 2013, 501, 399–402 CrossRef CAS PubMed.
- H. Yang, J. Lei, B. Wu, Y. Wang, M. Zhou, A. Xia, L. Zheng and N. Zheng, Chem. Commun., 2013, 49, 300–302 RSC.
- H. Yang, Y. Wang, H. Huang, L. Gell, L. Lehtovaara, S. Malola, H. Hakkinen and N. Zheng, Nat. Commun., 2013, 4, 2422 Search PubMed.
- H. Yang, Y. Wang and N. Zheng, Nanoscale, 2013, 5, 2674–2677 RSC.
- R. S. Dhayal, J.-H. Liao, Y.-C. Liu, M.-H. Chiang, S. Kahlal, J.-Y. Saillard and C. W. Liu, Angew. Chem., Int. Ed., 2015, 54, 3702–3706 CrossRef CAS PubMed.
- L. G. AbdulHalim, M. S. Bootharaju, Q. Tang, S. del Gobbo, R. G. AbdulHalim, M. Eddaoudi, D.-e. Jiang and O. M. Bakr, J. Am. Chem. Soc., 2015, 137, 11970–11975 CrossRef CAS PubMed.
- C. P. Joshi, M. S. Bootharaju, M. J. Alhilaly and O. M. Bakr, J. Am. Chem. Soc., 2015, 137, 11578–11581 CrossRef CAS PubMed.
- J. Polte, X. Tuaev, M. Wuithschick, A. Fischer, A. F. Thuenemann, K. Rademann, R. Kraehnert and F. Emmerling, ACS Nano, 2012, 6, 5791–5802 CrossRef CAS PubMed.
- M. Wuithschick, B. Paul, R. Bienert, A. Sarfraz, U. Vainio, M. Sztucki, R. Kraehnert, P. Strasser, K. Rademann, F. Emmerling and J. Polte, Chem. Mater., 2013, 25, 4679–4689 CrossRef CAS.
- D. L. Van Hyning and C. F. Zukowski, Langmuir, 1998, 14, 7034–7046 CrossRef CAS.
- J.-S. Seo, D.-M. Son, H. Lee, J. Kim and Y. Kim, Bull. Korean Chem. Soc., 2009, 30, 2651–2654 CrossRef CAS.
- Q.-Q. Xu, X.-Y. Dong, R.-W. Huang, B. Li, S.-Q. Zang and T. C. W. Mak, Nanoscale, 2015, 7, 1650–1654 RSC.
- D. G. Musaev and K. Morokuma, Organometallics, 1995, 14, 3327–3334 CrossRef CAS.
- C. W. Liu, Y.-R. Lin, C.-S. Fang, C. Latouche, S. Kahlal and J.-Y. Saillard, Inorg. Chem., 2013, 52, 2070–2077 CrossRef CAS PubMed.
- V. D. Makhaev, Russ. Chem. Rev., 2000, 69, 727–746 CrossRef CAS.
- M. Besora and A. Lledós, Struct. Bonding, 2008, 130, 149–202 CrossRef CAS.
- J. Vites, C. Eigenbrot and T. P. Fehlner, J. Am. Chem. Soc., 1984, 106, 4633–4635 CrossRef CAS.
- A. J. Clark, A. Zavras, G. N. Khairallah and R. A. J. O'Hair, Int. J. Mass Spectrom., 2015, 378, 86–94 CrossRef CAS.
- P. Van der Sluis and A. L. Spek, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, A46, 194–201 CrossRef CAS.
- R. A. J. O'Hair, Gas Phase Ligand Fragmentation to Unmask Reactive Metallic Species, in Reactive Intermediates. MS Investigations in Solution, ed. L. S. Santos, Wiley-VCH, Weinheim, 2010, ch. 6, pp.199–227, ISBN: 978-3-527-32351-7 Search PubMed.
- R. A. J. O'Hair and N. J. Rijs, Acc. Chem. Res., 2015, 48, 329–340 CrossRef PubMed.
- M. Girod, M. Krstić, R. Antoine, L. MacAleese, J. Lemoine, A. Zavras, G. N. Khairallah, V. Bonačić-Koutecký, P. Dugourd and R. A. J. O'Hair, Chem. – Eur. J., 2014, 20, 16626–16633 CrossRef CAS PubMed.
- D. M. P. Mingos, T. Slee and Z. Lin, Chem. Rev., 1990, 90, 383–402 CrossRef CAS.
- D. M. P. Mingos and D. J. Wales, Introduction to Cluster Chemistry, Prentice Hall, 1990 Search PubMed.
- D. G. Evans and D. M. P. Mingos, J. Organomet. Chem., 1982, 240, 321–327 CrossRef CAS.
- D. M. P. Mingos, J. Organomet. Chem., 2004, 689, 4420–4436 CrossRef CAS.
- F. K. Sheong, W.-J. Chen and Z. Lin, J. Organomet. Chem., 2015, 792, 93–101 CrossRef CAS.
- C. Cugnet, D. Lucas, E. Collange, B. Hanquet, A. Vallat, Y. Mugnier, A. Soldera and P. D. Harvey, Chem. – Eur. J., 2007, 13, 5338–5346 CrossRef CAS PubMed.
- H. Batebi, F. Zarkoob, K. Daraei, B. F. Yates and A. Ariafard, J. Organomet. Chem., 2013, 748, 89–97 CrossRef CAS.
- M. C. Sison Escaño, E. Gyenge, R. Lacdao Arevalo and H. Kasai, J. Phys. Chem. C, 2011, 115, 19883–19889 CrossRef.
- W. Grochala and P. P. Edwards, Chem. Rev., 2004, 104, 1283–1315 CrossRef CAS PubMed.
- A. Colorado and J. Brodbelt, J. Am. Soc. Mass Spectrom., 1996, 7, 1116–1125 CrossRef CAS PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- L. J. Farrugia, J. Appl. Crystallogr., 1997, 30, 565 CrossRef CAS.
- L. J. Farrugia, J. Appl. Crystallogr., 1999, 32, 837–838 CrossRef CAS.
- M. J. Frisch, et al., Gaussian 09, revision D.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed. For the complete reference see the ESI.†.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- A. W. Ehlers, M. Böhme, S. Dapprich, A. Gobbi, A. Höllwarth, V. Jonas, K. F. Köhler, R. Stegmann, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 208, 111–114 CrossRef CAS.
- A. Höllwarth, M. Böhme, S. Dapprich, A. W. Ehlers, A. Gobbi, V. Jonas, K. F. Köhler, R. Stegmenn, A. Veldkamp, G. Frenking and R. Stegmann, Chem. Phys. Lett., 1993, 208, 237–240 CrossRef.
- K. Fukui, J. Phys. Chem., 1970, 74, 4161–4163 CrossRef CAS.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5nr05690j |
| ‡ There are other classes of silver nanoclusters that are formed without the use of borohydride salts.22 |
| § The crystallographic information file for [Ag3(μ3-H)(μ3-BH4)LPh3]BF4 has been deposited at the Cambridge Crystallographic Data Centre and assigned the code: CCDC 1419573. |
| ¶ While there is no significant change in the DFT calculated gas-phase structure of [Ag3(H)(BH4)LPh3]+ compared to the X-ray structure, detailed discussions of the calculations are limited to the LMe systems, as the Ag–P bond energies in [Ag3(H)(BH4)LPh3]+ are overestimated using the M06 functional. The same is also true when the B3LYP-D3BJ functional is applied. For example, the CID results show that loss of the phosphine ligand from [Ag3(H)(BH4)LPh3]+ is preferred to the BH3 loss while both the M06 and B3LYP-D3BJ functionals predict a reverse trend. This inconsistency is likely to arise from the overestimation of the magnitude of dispersive interactions in [Ag3(H)(BH4)LPh3]+ due to the presence of the aromatic rings. |
| || We have attempted to locate transition states for the BH3 loss reactions. In all cases we have been unable to locate a transition state and attempts led to the loss of BH3. |
| This journal is © The Royal Society of Chemistry 2015 |