Open Access Article
Open Access ArticleExcitation of Ni nanorod colloids in oscillating magnetic fields: a new approach for nanosensing investigated by TISANE
Philipp
Bender†
*a,
Annegret
Günther
b,
Dirk
Honecker‡
b,
Albrecht
Wiedenmann
c,
Sabrina
Disch
*d,
Andreas
Tschöpe
a,
Andreas
Michels
b and
Rainer
Birringer
a
aExperimentalphysik, Universität des Saarlandes, Postfach 151150, Geb. D2 2, D-66041 Saarbrücken, Germany. E-mail: nano@p-bender.de
bPhysics and Materials Science Research Unit, University of Luxembourg, 162A Avenue de la Faïencerie, L-1511 Luxembourg, Grand Duchy of Luxembourg
cInstitute Laue Langevin, 71 avenue des Martyrs, LSS, F38042 Grenoble, France
dDepartment Chemie, Institut für Physikalische Chemie, Universität zu Köln, Luxemburger Straße 116, D-50939 Köln, Germany. E-mail: sabrina.disch@uni-koeln.de
First published on 18th September 2015
Abstract
The response of a colloidal dispersion of Ni nanorods to an oscillating magnetic field was characterized by optical transmission measurements as well as small-angle neutron scattering (SANS) experiments using the TISANE (Time-dependent SANS experiments) technique. Exposed to a static magnetic field, the scattering intensity of the rod ensemble could be well described by the cylinder form factor using the geometrical particle parameters (length, diameter, orientation distribution) determined by transmission electronmicroscopy and magnetometry. An oscillation of the field vector resulted in a reorientation of the nanorods and a time-dependency of the scattering intensity due to the shape anisotropy of the rods. Analysis of the SANS data revealed that in the range of low frequencies the orientation distribution of the rods is comparable to the static case. With increasing frequency, the rod oscillation was gradually damped due to an increase of the viscous drag. It could be shown that despite of the increased friction in the high frequency range no observable change of the orientation distribution of the ensemble with respect to its symmetry axis occurs.
I. Introduction
In recent years several studies have been published, where the analysis of the relaxation behavior of magnetic nanoparticle ensembles has been utilized to characterize the rheological properties of the surrounding matrix on the nanoscale1–6 (nanorheology) or the specific binding of protein molecules on the particle surfaces7–21 (biosensor). The classical approach relies upon measuring the shift of the Brownian relaxation frequency by means of AC-susceptometry experiments (alternating magnetic fields), enabling the detection of viscosity changes (nanorheology)1–4 or the increase of the hydrodynamic particle volume (biosensor).7–17 Recently, application of rotating magnetic fields has been proposed5,18–21 to significantly enhance the sensitivity compared to AC-measurements.14 The phase lag between the particle magnetic moments with respect to the rotating field vector is determined as a function of rotation frequency, either by measuring the macroscopic magnetic moment of the ensemble14 or, in case of anisometric particles like nanorods, its optical extinction.5,19,20 In both cases the measured parameter – magnetic moment m ∝ 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ〉, transmitted light intensity I ∝ 〈cos2
Θ〉, transmitted light intensity I ∝ 〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ〉 – is an ensemble average which depends on the distribution P(Θ) of the angle Θ between the moments and the field vector. However, continuous rotation of magnetic nanoparticles is restricted to purely viscous matrices. To enable measurements of general viscoelastic matter, the application of oscillating magnetic fields has been proposed.6 In ref. 6 single domain uniaxial ferromagnetic Ni nanorods22–25 were used as probe particles and stimulated to an oscillating motion by an oscillation of the magnetic field vector with constant magnitude. Analysis of the frequency-dependent response of the colloidal dispersion was employed to determine the viscosities as well as the shear moduli of surrounding viscoelastic matrices on the nanoscale. For data analysis it was assumed that the orientation distribution P(Θ) of the nanorods corresponds to the static state even in the high-frequency range. However, in the particular case of rotating magnetic fields with constant magnitude, numerical simulations come to the conclusion that the orientation distribution P(Θ) of ferromagnetic nanorods not only depends on the magnitude of the field vector but also on the frequency ω.26 It can be shown that P(Θ) evolves from the static state at a given field strength with increasing frequency ω → ∞ towards an isotropic orientation distribution.26 Moreover numerical simulations come to the conclusion that the orientation distribution of magnetic particles exposed to static magnetic fields can be significantly altered by shear-flows and becomes in most cases asymmetric.27–30 Hence, the question arises whether the orientation distribution P(Θ) of magnetic dipoles in oscillating magnetic fields is also frequency-dependent.
Θ〉 – is an ensemble average which depends on the distribution P(Θ) of the angle Θ between the moments and the field vector. However, continuous rotation of magnetic nanoparticles is restricted to purely viscous matrices. To enable measurements of general viscoelastic matter, the application of oscillating magnetic fields has been proposed.6 In ref. 6 single domain uniaxial ferromagnetic Ni nanorods22–25 were used as probe particles and stimulated to an oscillating motion by an oscillation of the magnetic field vector with constant magnitude. Analysis of the frequency-dependent response of the colloidal dispersion was employed to determine the viscosities as well as the shear moduli of surrounding viscoelastic matrices on the nanoscale. For data analysis it was assumed that the orientation distribution P(Θ) of the nanorods corresponds to the static state even in the high-frequency range. However, in the particular case of rotating magnetic fields with constant magnitude, numerical simulations come to the conclusion that the orientation distribution P(Θ) of ferromagnetic nanorods not only depends on the magnitude of the field vector but also on the frequency ω.26 It can be shown that P(Θ) evolves from the static state at a given field strength with increasing frequency ω → ∞ towards an isotropic orientation distribution.26 Moreover numerical simulations come to the conclusion that the orientation distribution of magnetic particles exposed to static magnetic fields can be significantly altered by shear-flows and becomes in most cases asymmetric.27–30 Hence, the question arises whether the orientation distribution P(Θ) of magnetic dipoles in oscillating magnetic fields is also frequency-dependent.
In the current study an ensemble of Ni nanorods dispersed in water was exposed to oscillating magnetic fields with constant magnitude (μ0H = 6 mT) and varying frequency (ω = 0–18849.6 Hz). The evolution of the orientation distribution of the colloid was monitored by analyzing time-resolved SANS patterns. In order to achieve a sufficiently high time-resolution the novel TISANE-mode (Time-dependent SANS experiments) was employed, which was recently installed at the instrument D22 at the Institut Laue Langevin (ILL), Grenoble. The goal was to test if the orientation distribution remains comparable to the static state. This is an essential condition so that the relaxation behavior detected by means of ensemble averaging methods (e.g. magnetization and optical transmission measurements) can be analyzed by mean field approaches.6,26
II. Sample
A. Synthesis
The synthesis of colloidal dispersions of Ni nanorods involves several steps as described in detail in ref. 5. Briefly, the nanorods for this sample were prepared by current-pulsed electrodeposition of Ni31 from a Watts-bath32 into a nanoporous alumina template, which was prepared by a twofold anodization process.33 The rods were released from the template by dissolving the alumina in a 20 mM sodium hydroxide solution, which additionally contained polyvinyl-pyrrolidone (PVP) as surfactant. The PVP adsorbed on the rod surface and acted as steric stabilizer to prevent agglomeration during the following washing process which consisted of multiple centrifugation and redispersion steps in deuterium oxide (D2O). The final dispersion of rods in D2O had a total volume of ≈500 μl.B. Structural characterization
The structure of the rods was characterized by Transmission Electron Microscopy (TEM, JEOL JEM-2011, Fig. 1). The nanorods had a cylindrical shape and analysis of N = 100 particles revealed an average length l = 170 ± 4 nm (σl = 40 nm) and average diameter d = 23.8 ± 0.2 nm (σd = 2 nm). Using the volume of equally sized cylinders and the saturation magnetization of bulk Ni (MS = 4.85 × 105 A m−1(ref. 34)), the average magnetic moment of the rods can be estimated to mr = 3.7 × 10−17 Am2.C. Magnetic characterization
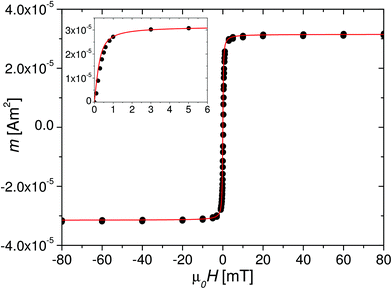
To characterize the magnetization behavior of the rod ensemble dispersed in D2O, the quasistatic magnetization curve of V = 135 μl of the colloidal dispersion was measured at T = 295 K with a Vibrating Sample Magnetometer (VSM, Lakeshore 7300). With diameters below about 40 nm the nanorods are expected to be single-domain particles, which are magnetized along their long-rod axes due to shape anisotropy.22–25 Dispersed in a liquid matrix the nanorods align preferentially parallel to a static external magnetic field,5,35 giving rise to the pseudo-superparamagnetic behavior observed in Fig. 2. The curve could be reasonably well described by a single Langevin function m(H) = mSL(ξ) = mS(coth(ξ) − 1/ξ) with ξ = mrμ0H/kBT, where μ0 = 4π × 10−7 V s (Am)−1 is the vacuum permeability and kB = 1.381 × 10−23 J K−1 the Boltzmann constant. The best fit result was obtained for a saturation moment mS = 3.2 × 10−5 Am2 and an average magnetic moment of mr = 3 × 10−17 Am2. The moment is below the average rod moment estimated from TEM, which can be attributed to a ≈1.5 nm thick oxide layer.36,37 From the saturation moment of the colloid the volume concentration of magnetic phase can be estimated to Vmag/V = 0.5‰. Additionally, the orientation of the rods at a given field strength can be extracted from the quasistatic magnetization behavior.38 The orientation distribution P(Θ) is symmetric around the field axis and can be represented by a tapered distribution with fixed characteristic polar angle between the moments and the field vector [Θ(H)] = arccos(L(H)). According to the magnetization measurement (Fig. 2) the Langevin function takes on a value of L = 0.978 at μ0H = 6 mT (ξ = 44), and hence the angle between the rod axes and the magnetic field vector is [Θ] = 12°. This value is important for the analysis of the optical transmission (OT) and SANS experiments where the response of the colloid to an oscillating field with magnitude μ0H = 6 mT was characterized.III. Nanorod colloids in oscillating fields
A. Experimental setups
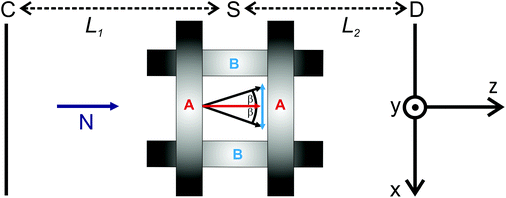
The time-resolved SANS experiments were performed on the instrument D22 at the ILL, Grenoble, using the newly implemented TISANE technique. The time-resolution in SANS experiments using a continuous neutron beam is generally limited to some ms due to frame overlap related to the wavelength broadening. The TISANE technique39 is a stroboscopic method, which allows to study fast cyclic processes down to the microsecond regime, where the neutron beam is chopped in neutron bunches of frequency ωn by means of a chopper located close to the monochromator in front of the collimation section. For this experiment unpolarized neutrons with a mean wavelength of λ = 6 Å and a wavelength spread of Δλ/λ = 10% were used. The distance between chopper (C) and sample (S) was L1 = 20.88 m (Fig. 3) and the area detector (D) with 128 × 128 pixels of 8 × 8 mm2 was placed L2 = 8 m behind the sample. The data acquisition was triggered with a frequency generator at given frequency ωd and one period was divided in 100 time channels with a channel width of t = 2π/(100 × ωd). For optimal time resolution, the frequency of the oscillating field (sample frequency ωs), the chopper frequency (ωn) and the data acquisition frequency (ωd) must satisfy the conditions39,40
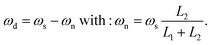 | (1) |
The rawdata treatment was carried out by means of the GRASP software package.41
B. Measurement protocol
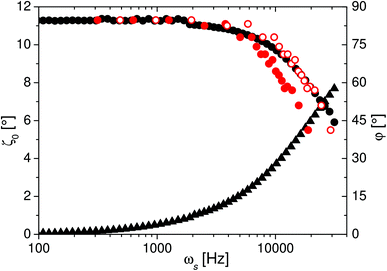
For both, the OT- as well as SANS-measurements, the response of the colloid to oscillating magnetic fields with magnitude μ0H ≈ 6 mT was monitored as a function of the frequency ωs. The fields were generated by applying a static field of 6 mT (with coil pair A in z-direction, Fig. 3) and an alternating field with magnitude 1.2 mT and frequency ωs perpendicular to it (with coil pair B in x-direction, Fig. 3). Due to the small amplitude of the excitation field the magnitude of the field vector can be considered as constant (μ0H = 6 ± 0.12 mT ≈ 6 mT). The angular position of the magnetic field vector in the x–z-plane is hence β(t) = β0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(iωst), with β0 = arctan(1.2/6) = 11.3°. The field stimulated an oscillation ζ(t) = ζ0(ωs)exp(i(ωst + ϕ(ωs))) of the nanorods, with the frequency-dependent amplitude ζ0(ωs) and phase shift ϕ(ωs) between the nanorod axes and the field vector. In case of the OT-measurements the phase shift ϕ(ωs) as well as the oscillation amplitude ζ0(ωs) were extracted from the oscillating transmitted light intensity as described in ref. 6, under the assumption that all nanorods are mutually aligned. The results of both quantities obtained from optical transmission are presented in the following section and used as the basis for the analysis of the SANS-experiments.
exp(iωst), with β0 = arctan(1.2/6) = 11.3°. The field stimulated an oscillation ζ(t) = ζ0(ωs)exp(i(ωst + ϕ(ωs))) of the nanorods, with the frequency-dependent amplitude ζ0(ωs) and phase shift ϕ(ωs) between the nanorod axes and the field vector. In case of the OT-measurements the phase shift ϕ(ωs) as well as the oscillation amplitude ζ0(ωs) were extracted from the oscillating transmitted light intensity as described in ref. 6, under the assumption that all nanorods are mutually aligned. The results of both quantities obtained from optical transmission are presented in the following section and used as the basis for the analysis of the SANS-experiments.
C. Experimental results
![[X with combining circumflex]](https://www.rsc.org/images/entities/i_char_0058_0302.gif) (ωs) is determined from the experimental data (Fig. 4) as X′′(ωs) = ζ0(ωs)/β0
(ωs) is determined from the experimental data (Fig. 4) as X′′(ωs) = ζ0(ωs)/β0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ (Fig. 5). Theoretically it is found that6
ϕ (Fig. 5). Theoretically it is found that6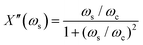 | (2) |
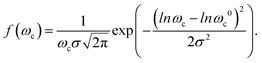 | (3) |
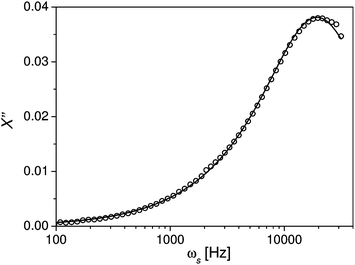 | ||
Fig. 5 Imaginary part X′′ of the response function of the nanorods as a function of frequency, determined by OT (open black circles). The black line is the fit with eqn (2) assuming a lognormal-distribution (eqn (3)) of the characteristic relaxation frequency ωc with ωc0 = 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460 Hz and σ = 0.58. 460 Hz and σ = 0.58. | ||
The best fit result shown in Fig. 5 was obtained for ωc0 = 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 460 Hz and the scatter parameter σ = 0.58, and thus the mean value of the characteristic frequency is 〈ωc〉 = ωc0
460 Hz and the scatter parameter σ = 0.58, and thus the mean value of the characteristic frequency is 〈ωc〉 = ωc0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(σ2/2) = 25
exp(σ2/2) = 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 391 Hz.
391 Hz.
Determination of the frequency-dependent response function from the time-dependent transmitted light intensity I(t) ∝ 〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ(t)〉 is based on the transmitted light intensity I ∝ 〈cos2
Θ(t)〉 is based on the transmitted light intensity I ∝ 〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ〉 in the static state. Implicitly it is thus assumed that the orientation distribution P(Θ) in the dynamic case corresponds to the static state, despite the distribution of relaxation frequencies and the growing viscous friction with increasing frequency. To gain information about the dynamic orientation distribution of ensembles of dipoles in time-modulated fields from OT- or magnetization measurements the experimental data has to be modeled with the Fokker–Planck-equation, as done e.g. in case of rotating fields.26 In contrast, a direct experimental access to the frequency-dependent orientation distribution of the individual particles is provided by the analysis of the time-dependent 2D SANS scattering patterns, as shown in the following.
Θ〉 in the static state. Implicitly it is thus assumed that the orientation distribution P(Θ) in the dynamic case corresponds to the static state, despite the distribution of relaxation frequencies and the growing viscous friction with increasing frequency. To gain information about the dynamic orientation distribution of ensembles of dipoles in time-modulated fields from OT- or magnetization measurements the experimental data has to be modeled with the Fokker–Planck-equation, as done e.g. in case of rotating fields.26 In contrast, a direct experimental access to the frequency-dependent orientation distribution of the individual particles is provided by the analysis of the time-dependent 2D SANS scattering patterns, as shown in the following.
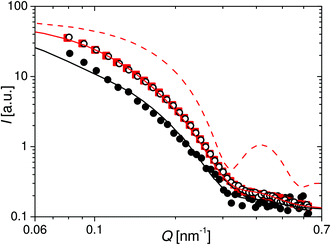 | ||
| Fig. 7 Red squares: SANS intensity I(Q) after circular averaging the 2D scattering pattern from Fig. 6 of the colloid in the static magnetic field. Red line: simulated intensity for an ensemble of Ni cylinders with the length and diameter distributions determined by TEM oriented parallel to the neutron beam (dashed) and with an angle of Θ = 12° between the cylinder axes and the neutron beam oriented symmetrically around the symmetry axis (straight). Black open circles: SANS intensity in the vertical sector of a random time channel of the time-resolved measurement for ωs = 157.1 Hz. Black full circles: SANS intensity in the horizontal sector of the time channel with minimal integrated intensity of the time-resolved measurement for ωs = 157.1 Hz. Black line: simulated intensity for an ensemble of Ni cylinders with the length, diameter and orientation distributions determined by TEM and VSM, rotated ζ = 11.3° out of the neutron beam. | ||
In general the unpolarized SANS intensity 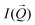 of a dilute particle system is given by43
of a dilute particle system is given by43
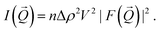 | (4) |
Here n is the number density of particles, Δρ the scattering length density difference between particle and solvent, V the volume of the particle and 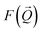 the form factor. Please note that in the following magnetic scattering contributions will be neglected due to the significantly smaller magnetic scattering length density contrast Δρm2 compared to the nuclear scattering length density contrast Δρn2 ≈ 6.6Δρm2 of the nanorods dispersed in D2O.44 The geometrical particle form factor of a cylinder with volume V, radius r and length l is given by43,45,46
the form factor. Please note that in the following magnetic scattering contributions will be neglected due to the significantly smaller magnetic scattering length density contrast Δρm2 compared to the nuclear scattering length density contrast Δρn2 ≈ 6.6Δρm2 of the nanorods dispersed in D2O.44 The geometrical particle form factor of a cylinder with volume V, radius r and length l is given by43,45,46
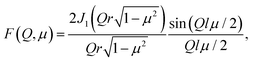 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ and the contributions in x- and y-direction are
Θ and the contributions in x- and y-direction areμx = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ Θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Φ, μy = sin Φ, μy = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ Θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Φ. Φ. | (6) |
To simulate the scattering data, a non-interacting ensemble of Ni cylinders dispersed in D2O was assumed, taking into account the length and diameter distributions determined by TEM (minus the oxide layer). As shown in Fig. 7, the simulated intensity I(Q) of such a cylinder ensemble aligned parallel to the field vector and hence to the neutron beam (Θ = 0°) shows significant differences compared to the experimental data, which indicates a significant orientation distribution in the experiment at Langevin-parameter ξ = 44. According to the quasistatic magnetization measurements, at a field strength of μ0H = 6 mT the characteristic angle between the rod moments and the field vector was [Θ] = 12°. To include an orientation distribution the orientation average
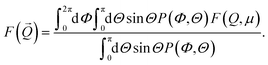 | (7) |
As shown in Fig. 7, the simulated intensity is in very good agreement with the experimental data when the polar angle is fixed at Θ = 12° (P(Θ) = δ(Θ − 12°)). Hence, the analysis of the SANS data in the static field agrees with the results of the magnetization measurements. In the following the cylinder model will be applied in order to extract the dynamic orientation distribution of the nanorod ensemble in oscillating magnetic fields from the time-dependent scattering patterns.
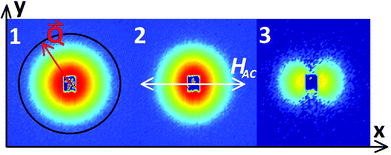
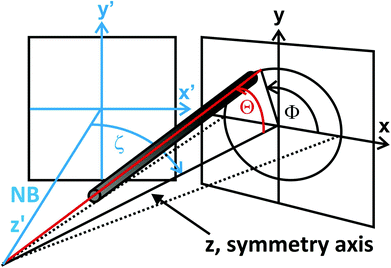
Application of the alternating excitation field in x-direction (Fig. 6) resulted in an oscillation of the field vector in the x–z-plane, stimulating an oscillation of the nanorod ensemble. In case of a rotation of the nanorods exclusively in the x–z-plane by the angle ζ, the orientation angles with respect to the neutron beam (in the following the z′-direction, as defined in Fig. 8) are
Θ′ = arccos(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ Θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζ − sin ζ − sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ Θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Φ Φ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζ) ζ) | (8) |
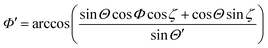 | (9) |
μx′ = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ′ Θ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Φ′ = sin Φ′ = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ Θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Φ Φ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζ + cos ζ + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ Θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ζ ζ | (10) |
μy′ = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ′ Θ′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Φ′ = sin Φ′ = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ Θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Φ. Φ. | (11) |
Thus, the SANS intensity I(Q) along the y′-direction does not change (compare eqn (6)) but tends to decrease along the x′-direction with increasing rotation (Fig. 6). In order to evaluate the anisotropic scattering patterns, analysis of the time-dependence of the nanorod oscillation was performed by integrating the intensity in ±10° sectors parallel to the alternating field as well as perpendicular to it, in each case for all 100 time channels.
Fig. 9 shows three examples of the integrated intensities detected for sample frequencies of ωs = 157.1 Hz, ωs = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 309.7 Hz and ωs = 18
309.7 Hz and ωs = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 849.6 Hz. For each frequency the intensity in the vertical sector is constant and corresponds to the radially-averaged scattering intensity of the sample in the static field (normalized intensity ∼1), whereas a significant modulation is observed in the horizontal sector. This observation verifies that the nanorod oscillation exclusively occurs in the x–z-plane. With increasing frequency the minimum of the time-dependent integrated intensity (at ωst = 90°, Fig. 9) shifts to larger values and can be explained by a damping of the nanorod oscillation due to the increasing viscous drag. In order to extract the magnitude of the average oscillation amplitude of the nanorod ensemble in analogy to the OT-measurements, the SANS measurement with the lowest sample frequency ωs = 157.1 Hz was used as reference. In this case it is safe to assume that the orientation distribution of the nanorod ensemble remains symmetric and rotates in phase with the field vector, i.e. the rotation angle ζ(t) of the symmetry axis of the nanorod ensemble equals the angle β(t) of the field vector at a given time channel ωst (Fig. 9).
849.6 Hz. For each frequency the intensity in the vertical sector is constant and corresponds to the radially-averaged scattering intensity of the sample in the static field (normalized intensity ∼1), whereas a significant modulation is observed in the horizontal sector. This observation verifies that the nanorod oscillation exclusively occurs in the x–z-plane. With increasing frequency the minimum of the time-dependent integrated intensity (at ωst = 90°, Fig. 9) shifts to larger values and can be explained by a damping of the nanorod oscillation due to the increasing viscous drag. In order to extract the magnitude of the average oscillation amplitude of the nanorod ensemble in analogy to the OT-measurements, the SANS measurement with the lowest sample frequency ωs = 157.1 Hz was used as reference. In this case it is safe to assume that the orientation distribution of the nanorod ensemble remains symmetric and rotates in phase with the field vector, i.e. the rotation angle ζ(t) of the symmetry axis of the nanorod ensemble equals the angle β(t) of the field vector at a given time channel ωst (Fig. 9).
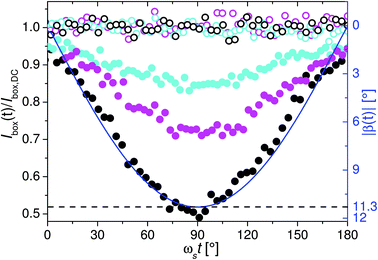 | ||
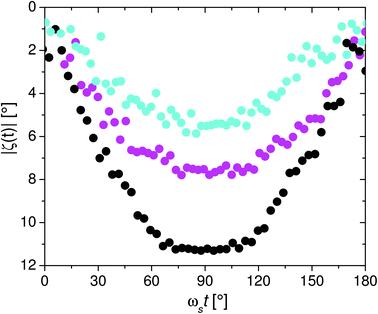
Fig. 9 Integrated intensities for sample frequencies of ωs = 157.1 Hz (black), ωs = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 309.7 Hz (magenta) and ωs = 18 309.7 Hz (magenta) and ωs = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 849.6 Hz (cyan) in the horizontal sector (full symbols) as well as in the vertical sector (open symbols) as a function of time. The integrated intensities were normalized to the sector area and divided by the normalized integrated intensity Ibox,DC of the static scattering pattern in the circular area indicated in Fig. 6. Phase shifts between the signal and the magnetic field were omitted by shifting the intensity on the time-scale, so that ωst = 90° corresponds to the minimum and hence maximal rotation of the nanorod ensemble out of the neutron beam. The blue line is the orientation of the magnetic field vector with respect to the neutron beam as a function of time. 849.6 Hz (cyan) in the horizontal sector (full symbols) as well as in the vertical sector (open symbols) as a function of time. The integrated intensities were normalized to the sector area and divided by the normalized integrated intensity Ibox,DC of the static scattering pattern in the circular area indicated in Fig. 6. Phase shifts between the signal and the magnetic field were omitted by shifting the intensity on the time-scale, so that ωst = 90° corresponds to the minimum and hence maximal rotation of the nanorod ensemble out of the neutron beam. The blue line is the orientation of the magnetic field vector with respect to the neutron beam as a function of time. | ||
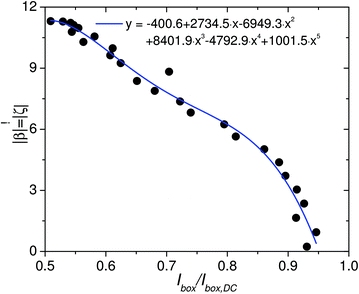
To correlate the integrated intensity with the rotation angle |ζ(t)|, the inverse function, i.e. |β(t)| as function of the measured integrated intensity for ωs = 157.1 Hz, was fitted with a phenomenological polynomial (Fig. 10). This calibration enabled to translate measured integrated intensities to |ζ(t)| (Fig. 11) and to determine the oscillation amplitude as function of ωs. The results of the given examples are for ωs = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 309.7 Hz ζ0 = 7.8° and for ωs = 18
309.7 Hz ζ0 = 7.8° and for ωs = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 849.6 Hz ζ0 = 5.5° (Fig. 11). A summary of the complete set for all measured frequencies is shown in Fig. 4. Comparison with the results of the OT shows a shift to smaller frequencies by a factor of 1.5. For this observation two possible explanations can be envisaged. First, the volume concentration Vmag/V of the colloid characterized by SANS was significantly larger compared to OT (VSANSmag/V = 100 × VOTmag/V = 0.5‰), which could result in hydrodynamic interactions between the oscillating nanorods. Second, using the integrated intensity from the measurement with ωs = 157.1 Hz as reference, it was implicitly assumed that the orientation distribution P(Θ) does not change with increasing frequency, identical to the data analysis of the OT measurements. However, if P(Θ) changes occur with increasing frequency, the data analysis would be incorrect and thus the obtained values for the oscillation amplitude by OT and SANS (Fig. 4) should not agree. Therefore, in the following, we focus on the time-dependent intensities I(Q) of the sectors in order to get insight into the dynamic orientation distribution of the nanorod ensemble.
849.6 Hz ζ0 = 5.5° (Fig. 11). A summary of the complete set for all measured frequencies is shown in Fig. 4. Comparison with the results of the OT shows a shift to smaller frequencies by a factor of 1.5. For this observation two possible explanations can be envisaged. First, the volume concentration Vmag/V of the colloid characterized by SANS was significantly larger compared to OT (VSANSmag/V = 100 × VOTmag/V = 0.5‰), which could result in hydrodynamic interactions between the oscillating nanorods. Second, using the integrated intensity from the measurement with ωs = 157.1 Hz as reference, it was implicitly assumed that the orientation distribution P(Θ) does not change with increasing frequency, identical to the data analysis of the OT measurements. However, if P(Θ) changes occur with increasing frequency, the data analysis would be incorrect and thus the obtained values for the oscillation amplitude by OT and SANS (Fig. 4) should not agree. Therefore, in the following, we focus on the time-dependent intensities I(Q) of the sectors in order to get insight into the dynamic orientation distribution of the nanorod ensemble.
As already shown in Fig. 9 the integrated intensity in the vertical sector for each frequency is constant and identical to the static case. Furthermore, the functional form of I(Q) is also identical to the circular averaged intensity of the ensemble aligned in the static field, as exemplarily shown for ωs = 157.1 Hz in Fig. 7. Therefore, it can be already concluded, that orientation distribution along the y-direction does not change with increasing frequency.
In Fig. 7I(Q) of the horizontal sector of the time channel with minimal integrated intensity for the frequency ωs = 157.1 Hz is displayed (black full circles). In this time channel the nanorod ensemble should be quasistatically (low frequency) rotated by the maximum angle ζ = 11.3° out of the neutron beam (z′-direction, Fig. 8). Under assumption of a coherent rotation of the entire ensemble (represented by the characteristic angle [Θ] = 12° and an symmetric distribution in Φ around the symmetry axis) the expected scattering intensity I(Q) (eqn (4)) in thehorizontal sector (x′-direction) is proportional to the form factor F(Q, μx′) (eqn (5) and (10)). Simulation of the orientation averaged SANS intensity (eqn (7)) resulted in good agreement with the experimental data, as shown in Fig. 7. This indicates that at a frequency of ωs = 157.1 Hz the orientation distribution of the rods around the symmetry axis at the maximum rotation angle is comparable to the static case.
In Fig. 12 and 13, the radially averaged intensity of the time channels with minimal integrated intensity (ωst = 90°) for ωs = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 309.7 Hz and ωs = 18
309.7 Hz and ωs = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 849.6 Hz are plotted, respectively. Comparison with I(Q) of the time channels from the measurement at ωs = 157.1 Hz with equal integrated intensities (i.e. equal average orientation) shows, that they are virtually identical. Additionally, the simulated intensities I(Q) for rotation angles ζ = 7.8° and 5.5° were in good agreement with the experimental data for ωs = 11
849.6 Hz are plotted, respectively. Comparison with I(Q) of the time channels from the measurement at ωs = 157.1 Hz with equal integrated intensities (i.e. equal average orientation) shows, that they are virtually identical. Additionally, the simulated intensities I(Q) for rotation angles ζ = 7.8° and 5.5° were in good agreement with the experimental data for ωs = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 309.7 Hz and 18
309.7 Hz and 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 849.6 Hz, respectively. In other words, the increasing value of the minimum integrated intensity is essentially the result of a reduced average oscillation amplitude of the nanorod ensemble at increasing frequency without a significant change in the orientation distribution function.
849.6 Hz, respectively. In other words, the increasing value of the minimum integrated intensity is essentially the result of a reduced average oscillation amplitude of the nanorod ensemble at increasing frequency without a significant change in the orientation distribution function.
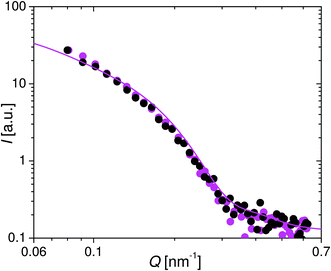 | ||
Fig. 12 Intensity after radially averaging in the horizontal sector of the time channel with minimal integrated intensity at ωs = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 309.7 Hz (magenta) and of the time channel with identical integrated intensity at ωs = 157.1 Hz (black, see Fig. 9). Full line is the simulated intensity of the ensemble when the symmetry axis is rotated by 7.8° out of the neutron beam. 309.7 Hz (magenta) and of the time channel with identical integrated intensity at ωs = 157.1 Hz (black, see Fig. 9). Full line is the simulated intensity of the ensemble when the symmetry axis is rotated by 7.8° out of the neutron beam. | ||
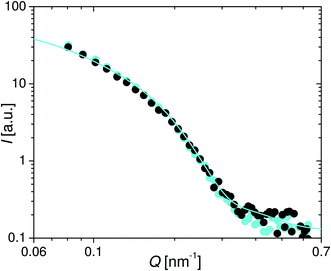 | ||
Fig. 13 Intensity after radially averaging in the horizontal sector of the time channel with minimal integrated intensity at ωs = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 849.6 Hz (cyan) and of the time channel with identical integrated intensity at ωs = 157.1 Hz (black, see Fig. 9). Full line is the simulated intensity of the ensemble when the symmetry axis is rotated by 5.5° out of the neutron beam. 849.6 Hz (cyan) and of the time channel with identical integrated intensity at ωs = 157.1 Hz (black, see Fig. 9). Full line is the simulated intensity of the ensemble when the symmetry axis is rotated by 5.5° out of the neutron beam. | ||
Overall it can be concluded that the orientation distribution of the rods around the symmetry axis is independent on the oscillation frequency up to 20 kHz and comparable to the static case. As a consequence, the mean-field approach introduced in ref. 6 to analyze the oscillation behavior of such nanorod ensembles in oscillating magnetic fields is justified. This also means, that the observed shift (Fig. 4) of the average oscillation amplitude of the nanorod ensemble to lower frequencies detected by SANS in comparison to OT, must be real. As previously mentioned, a possible explanation for this observation may be the significantly higher volume concentration Vmag/V of the colloid characterized by SANS compared to OT (VSANSmag/V = 100 × VOTmag/V = 0.5‰), which could lead to hydrodynamic interactions between the nanorods. To define an upper limit for the volume concentration, or rather for the average interparticle distance, so that such hydrodynamic interactions are negligible, would require a systematic investigation. However, it has to be emphasized that a possible structure formation (e.g. chains) in the concentrated nanorod colloid induced by dipolar interactions can be ruled out here, as the scattering intensity could be simulated in all cases by a dilute dispersion (no structure factor) of cylinders with the length and diameter distributions determined by TEM.
IV. Conclusions
The response of a colloidal dispersion of Ni nanorods to an oscillating magnetic field was characterized by SANS at the instrument D22 at the ILL, Grenoble, using the TISANE mode in the frequency range of 0 Hz ≤ ωs ≤ 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 849.6 Hz. In the static case the scattering intensity can be well described by the cylinder form factor using the structural parameters determined by TEM and VSM. An oscillation of the field vector resulted in a time-dependency of the SANS intensity due to the shape anisotropy of the magnetic nanorods. Analysis of the nuclear scattering data revealed that in the range of low frequencies (up to ωs = 157.1 Hz) the oscillation of the nanorod ensemble is in phase with the field vector and that the orientation distribution around the symmetry axis is comparable to the static case. With increasing frequency, the oscillation of the horizontal SANS intensity decreased due to damping of the nanorod rotation as a result of an increased viscous drag. The central result of the analysis of the scattering data in the high-frequency range is that despite the viscous drag and the polydispersity of the ensemble no change of the orientation distribution was observed. Consequently, the relaxation behavior detected by means of ensemble averaging methods (e.g. optical transmission measurements as additionally done in this study) can be correctly analyzed by mean field approaches, confirming the oscillating field method as a powerful alternative for nanosensing approaches.
849.6 Hz. In the static case the scattering intensity can be well described by the cylinder form factor using the structural parameters determined by TEM and VSM. An oscillation of the field vector resulted in a time-dependency of the SANS intensity due to the shape anisotropy of the magnetic nanorods. Analysis of the nuclear scattering data revealed that in the range of low frequencies (up to ωs = 157.1 Hz) the oscillation of the nanorod ensemble is in phase with the field vector and that the orientation distribution around the symmetry axis is comparable to the static case. With increasing frequency, the oscillation of the horizontal SANS intensity decreased due to damping of the nanorod rotation as a result of an increased viscous drag. The central result of the analysis of the scattering data in the high-frequency range is that despite the viscous drag and the polydispersity of the ensemble no change of the orientation distribution was observed. Consequently, the relaxation behavior detected by means of ensemble averaging methods (e.g. optical transmission measurements as additionally done in this study) can be correctly analyzed by mean field approaches, confirming the oscillating field method as a powerful alternative for nanosensing approaches.
Acknowledgements
We acknowledge the ILL for provision of neutron beamtime at the D22 and the Bundesministerium für Bildung und Forschung (BMBF) for financial support (Project: 05K10TS1). A. Michels acknowledges financial support from the FNR (Project No. INTER/DFG/12/07).References
- C. Barrera, V. Florian-Algarin, A. Acevedo and C. Rinaldi, Soft Matter, 2010, 6, 3662–3668 RSC.
- V. L. Calero-DdelC, D. I. Santiago-Quinonez and C. Rinaldi, Soft Matter, 2011, 7, 4497–4503 RSC.
- N. Frickel, R. Messing and A. M. Schmidt, J. Mater. Chem., 2011, 21, 8466–8474 RSC.
- E. Roeben, L. Roeder, S. Teusch, M. Effertz, U. Deiters and A. Schmidt, Colloid Polym. Sci., 2014, 292, 2013–2023 CAS.
- A. Günther, P. Bender, A. Tschöpe and R. Birringer, J. Phys.: Condens. Matter, 2011, 23, 325103 CrossRef PubMed.
- A. Tschöpe, K. Birster, B. Trapp, P. Bender and R. Birringer, J. Appl. Phys., 2014, 116, 184305 CrossRef PubMed.
- J. Connolly and T. G. S. Pierre, J. Magn. Magn. Mater., 2001, 225, 156–160 CrossRef.
- A. P. Astalan, F. Ahrentorp, C. Johansson, K. Larsson and A. Krozer, Biosens. Bioelectron., 2004, 19, 945–951 CrossRef CAS PubMed.
- S. H. Chung, A. Hoffmann, S. D. Bader, C. Liu, B. Kay, L. Makowski and L. Chen, Appl. Phys. Lett., 2004, 85, 2971–2973 CrossRef CAS PubMed.
- C.-Y. Hong, C. C. Wu, Y. C. Chiu, S. Y. Yang, H. E. Horng and H. C. Yang, Appl. Phys. Lett., 2006, 88, 212512 CrossRef PubMed.
- M. Strömberg, J. Göransson, K. Gunnarsson, M. Nilsson, P. Svedlindh and M. Stromme, Nano Lett., 2008, 8, 816–821 CrossRef PubMed.
- F. Öisjöen, J. F. Schneiderman, A. P. Astalan, A. Kalabukhov, C. Johansson and D. Winkler, Biosens. Bioelectron., 2010, 25, 1008–1013 CrossRef PubMed.
- K. Enpuku, Y. Tamai, T. Mitake, T. Yoshida and M. Matsuo, J. Appl. Phys., 2010, 108, 034701 CrossRef PubMed.
- J. Dieckhoff, T. Yoshida, K. Enpuku, M. Schilling and F. Ludwig, IEEE Trans. Magn., 2012, 48, 3792–3795 CrossRef CAS.
- T. Z. Gómez de la Torre, R. Ke, A. Mezger, P. Svedlindh, M. Stromme and M. Nilsson, Small, 2012, 8, 2174–2177 CrossRef PubMed.
- A. C. Bohorquez and C. Rinaldi, Part. Part. Syst. Charact., 2014, 31, 561–570 CrossRef CAS PubMed.
- R. S. Bejhed, T. Z. G. de la Torre, M. Donolato, M. F. Hansen, P. Svedlindh and M. Strömberg, Biosens. Bioelectron., 2015, 66, 405–411 CrossRef CAS PubMed.
- A. Ranzoni, J. J. H. B. Schleipen, L. J. van IJzendoorn and M. W. J. Prins, Nano Lett., 2011, 11, 2017–2022 CrossRef CAS PubMed.
- S. Schrittwieser, F. Ludwig, J. Dieckhoff, K. Soulantica, G. Viau, L.-M. Lacroix, S. M. Lentijo, R. Boubekri, J. Maynadié, A. Hütten, H. Brückl and J. Schotter, ACS Nano, 2012, 6, 791–801 CrossRef CAS PubMed.
- S. Schrittwieser, F. Ludwig, J. Dieckhoff, A. Tschöpe, A. Günther, M. Richter, A. Hütten, H. Brückl and J. Schotter, Small, 2014, 10, 407 CrossRef CAS PubMed.
- J. Dieckhoff, A. Lak, M. Schilling and F. Ludwig, J. Appl. Phys., 2014, 115, 024701 CrossRef PubMed.
- C. A. Ross, M. Hwang, M. Shima, J. Y. Cheng, M. Farhoud, T. A. Savas, H. I. Smith, W. Schwarzacher, F. M. Ross, M. Redjdal and F. B. Humphrey, Phys. Rev. B: Condens. Matter, 2002, 65, 144417 CrossRef.
- A. Günther, S. Monz, A. Tschöpe, R. Birringer and A. Michels, J. Magn. Magn. Mater., 2008, 320, 1340–1344 Search PubMed.
- P. Bender, A. Günther, A. Tschöpe and R. Birringer, J. Magn. Magn. Mater., 2011, 323, 2055–2063 Search PubMed.
- P. Bender, F. Krämer, A. Tschöpe and R. Birringer, J. Phys. D: Appl. Phys., 2015, 48, 145003 CrossRef.
- T. Yoshida, K. Enpuku, J. Dieckhoff, M. Schilling and F. Ludwig, J. Appl. Phys., 2012, 111, 053901 CrossRef PubMed.
- A. Satoh, J. Colloid Interface Sci., 2001, 234, 425–433 CrossRef PubMed.
- M. Aoshima, A. Satoh, R. W. Chantrell and G. N. Coverdale, J. Colloid Interface Sci., 2002, 253, 455–464 CrossRef CAS PubMed.
- A. Satoh, M. Ozaki, T. Ishikawa and T. Majima, J. Colloid Interface Sci., 2005, 292, 581–590 CrossRef.
- D. Soto-Aquino and C. Rinaldi, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2010, 82, 046310 Search PubMed.
- K. Nielsch, F. Müller, A.-P. Li and U. Gösele, Adv. Mater., 2000, 12, 582–586 Search PubMed.
- O. P. Watts, Trans. Am. Electrochem. Soc., 1916, 29, 395 Search PubMed.
- H. Masuda and M. Satoh, Jpn. J. Appl. Phys., 1996, 35, L126–L129 Search PubMed.
- R. Skomski, J. Phys.: Condens. Matter, 2003, 15, R841 Search PubMed.
- T. Klein, A. Laptev, A. Günther, P. Bender, A. Tschöpe and R. Birringer, J. Appl. Phys., 2009, 106, 114301 Search PubMed.
- P. Song, D. Wen, Z. X. Guo and T. Korakianitis, Phys. Chem. Chem. Phys., 2008, 10, 5057–5065 Search PubMed.
- R. Karmhag, G. A. Niklasson and M. Nygren, J. Appl. Phys., 2001, 89, 3012–3017 Search PubMed.
- C. P. Bean and J. D. Livingston, J. Appl. Phys., 1959, 30, S120–S129 Search PubMed.
- R. Gähler and R. Golub, ILL SC, 1999, 99, 73 Search PubMed.
- A. Wiedenmann, U. Keiderling, K. Habicht, M. Russina and R. Gähler, Phys. Rev. Lett., 2006, 97, 057202 Search PubMed.
- http://www.ill.eu/instruments-support/instrument-groups/groups/lss/grasp/home/ .
- P. Debye, Polar Molecules, New York, Dover, 1945 Search PubMed.
- J. S. Pedersen, Adv. Colloid Interface Sci., 1997, 70, 171–210 Search PubMed.
- Modern Techniques for Characterizing Magnetic Materials, ed. Y. Zhu, Springer, US, 2005, pp. 107–155 Search PubMed.
- G. Fournet, Bull. Soc. Fr. Mineral. Cristallogr.., 1951, 74, 39–113 Search PubMed.
- T. Maurer, F. Zighem, S. Gautrot, F. Ott, G. Chaboussant, L. Cagnon and O. Fruchart, Phys. Procedia, 2013, 42, 74–79 Search PubMed.
Footnotes |
| † Present address: Departamento CITIMAC, F. Ciencias, Universidad de Cantabria, 39005 Santander, Spain; E-mail: benderpf@unican.es |
| ‡ Present address: Institute Laue Langevin, 71 avenue des Martyrs, LSS, F38042 Grenoble, France |
| This journal is © The Royal Society of Chemistry 2015 |