Open Access Article
Open Access ArticleUnderstanding the nanoscale local buckling behavior of vertically aligned MWCNT arrays with van der Waals interactions†
Yupeng
Li
a,
Hyung-ick
Kim
b,
Bingqing
Wei
a,
Junmo
Kang
c,
Jae-boong
Choi
d,
Jae-Do
Nam
e and
Jonghwan
Suhr
*e
aDepartment of Mechanical Engineering, University of Delaware, Newark, Delaware 19716, USA
bKorea Institute of Industrial Technology, 189 Dongjin-ro, Jinju-si, Gyeongsangnam-do 660-805, Korea
cDepartment of Materials Science and Engineering, Northwestern University, Evanston, Illinois 60208, USA
dSchool of Mechanical Engineering, Sungkyunkwan University, Suwon, 440-746, South Korea
eDepartment of Polymer Science & Engineering, Department of Energy Science, Sungkyunkwan University, Suwon 440-746, Korea. E-mail: suhr@skku.edu
First published on 20th July 2015
Abstract
The local buckling behavior of vertically aligned carbon nanotubes (VACNTs) has been investigated and interpreted in the view of a collective nanotube response by taking van der Waals interactions into account. To the best of our knowledge, this is the first report on the case of collective VACNT behavior regarding van der Waals force among nanotubes as a lateral support effect during the buckling process. The local buckling propagation and development of VACNTs were experimentally observed and theoretically analyzed by employing finite element modeling with lateral support from van der Waals interactions among nanotubes. Both experimental and theoretical analyses show that VACNTs buckled in the bottom region with many short waves and almost identical wavelengths, indicating a high mode buckling. Furthermore, the propagation and development mechanism of buckling waves follow the wave damping effect.
Introduction
Since their discovery in 1991,1 carbon nanotubes (CNTs) have attracted great interest in new materials research and the mechanical properties of CNTs have been reported extensively. Recently, with the outstanding fatigue, resilience and good damping effect, ultra long VACNTs and continuous CNT composites have shown promising potential as engineered nanotube architectures in future applications, such as artificial skin type materials, energy absorbing materials and aircraft or wind turbine coatings. In these applications, the CNT arrays deform and recover together under compression, so the collective compressive behavior of CNTs has an influence on the compressive properties, and understanding of the collective compressive behavior becomes critically important.There are numerous studies on the compressive properties of VACNTs, showing a large amount of evidence on the buckling of VACNTs. It was firstly reported2 that VACNT blocks exhibited a viscoelastic behavior similar to soft-tissue, and a sharp stiffness increase in critical densification strain along with local buckling of VACNTs. The compression of VACNT films3 indicated that VACNTs exhibited foam-like viscoelastic behavior with local zigzag buckling waves and strong resilience. Similarly, local periodic buckling regions and stiffness of VACNTs under nano-indentation were reported4 in a low-cyclic compression. Also, local buckling behavior in the bottom region of VACNT turf5 and VACNT arrays6,7 with many short buckling waves was observed in compression. The periodic buckling waves were observed during electrical conductivity characterization of a VACNT block.8 And the stress–strain curve analysis of dense VACNT brushes also indicates progressive propagating buckling behavior.9 Moreover, an in situ compression test10 revealed the progressive propagation of periodic buckling of VACNT bundles from bottom to top, and another in situ compression experiment11 also indicated the large scale structural buckling and collapse of long VACNTs. These local buckling behaviors of VACNT were observed in many experiments and there are some research studies3,5,6,9–13 which employed the classical Euler's column buckling model14 with the formula:  , in order to predict the CNT buckling. Moreover, there are analytical modeling,13,15–18 numerical simulations,12,19 and experimental studies20–22 on buckling and post-buckling behavior of individual CNTs under an axial compression.
, in order to predict the CNT buckling. Moreover, there are analytical modeling,13,15–18 numerical simulations,12,19 and experimental studies20–22 on buckling and post-buckling behavior of individual CNTs under an axial compression.
However, the observed local buckling behavior is different from individual Euler column buckling due to the van der Waals interaction between nanotubes, so the compressive behavior of VACNT arrays is collective behavior and the nanotube interactions could change the buckling response significantly. The van der Waals interaction within bundles cannot be ignored due to the close distance between nanotubes, and CNTs are constrained by the van der Waals force from the adjacent nanotubes in the radial direction along the length, which can be considered as a lateral support. Consequently, VACNTs have lateral support effects from neighboring nanotubes and the buckling behavior may be different from individual Euler column buckling. Therefore, the van der Waals interactions between neighboring VACNTs cause CNT to buckle collectively as bundles and give rise to local buckling waves. There are many studies on the van der Waals interactions between parallel,23–25 and cross linked26 CNTs, and the interaction potential between CNTs,27 but no detailed studies have been reported on the effects of the van der Waals interactions on the collective buckling behavior of VACNTs.
Thus, in this paper, we have investigated and unraveled the buckling response of VACNTs with the van der Waals interactions as lateral supports by coupling experiments and modeling. This is the first time to interpret the unique local buckling behavior of VACNTs by considering the van der Waals interaction and to understand the propagation of local buckling with a wave damping effect.
Experimental and modelling
Characterization of buckling in quasi-static compressions
To study the buckling response of VACNTs under compression, uniform compression testing was performed using an Instron ElectroPuls E3000 machine at room temperature. Since the VACNTs (3 mm × 5 mm × 0.63 mm) were grown on a silicon substrate, the VACNT array with the silicon substrate was placed in the bottom compressive fixture, having the substrate contact with the bottom surface of the fixture with a pre-load of 0.02 N. Compressive strains were applied along the longitudinal direction of the VACNTs downwards under displacement control.All the tests were performed at the applied quasi-static loading rate of 100 μm min−1. The specimens were compressed from 4.7% to 80% strain by flat platens. The actuator kept the strain for 1 min and then released the strain, allowing the specimen to recover. The compressed VACNT arrays after recovery were monitored through SEM characterization and the buckling region was imaged for each strain-increase step.
van der Waals interaction modelling for lateral support
In order to explain the high mode buckling behavior of VACNTs observed in experiments, we developed analytical CNT models to take into account the van der Waals interaction between neighboring nanotubes, and then developed a finite element model accordingly. For the CNT model, the interaction between inter-tubes within a MWCNT is neglected, which simplifies the MWCNT to the equivalent CNT column. Therefore, the CNT is assumed to be a prismatic hollow continuous column with a ring cross-section. Since the distribution of VACNTs, the CNTs within bundles are assumed to be parallel to each other. The van der Waals interaction between CNTs was modeled with the Lennard-Jones pair potential28 and the interaction force between two parallel nanotubes is:23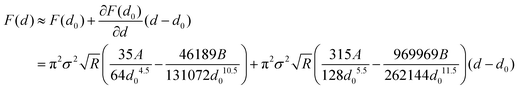 | (1) |
Thus, the equivalent spring constant per unit length is:
 | (2) |
With the supporting effect of van der Waals interaction, the corresponding lateral support is represented by converting the van der Waals interaction to the elastic modulus of the supporting medium accordingly:29
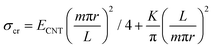 | (3) |
Results and discussion
Structural and morphological characterization
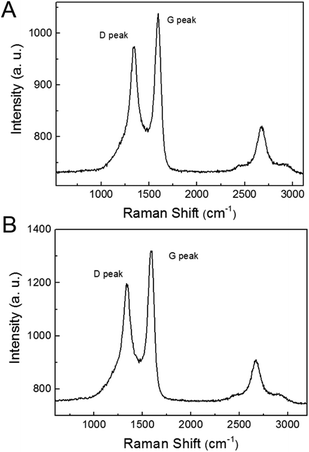
Fig. 1 shows structural and morphological characterization results of commercially available VACNTs. The CVD grown MWCNTs are vertically aligned and have a uniform length around 0.63 mm. Fig. 1A confirms the vertically aligned distribution of the MWCNTs. The MWCNTs are aggregated together as bundles (Fig. 1B) and have an average distance of several nanometers between adjacent CNTs (Fig. 1C), indicating the CNTs are very close to each other within the bundles and the effect of van der Waals interactions between them could be critical during compression. The outer diameter of these MWCNTs ranges from 7 nm to 10 nm, while the inner diameter ranges from 5 nm to 8 nm, and the number of graphitic layers of each nanotube is found to be around 3 (Fig. 1D). The aspect ratio of VACNTs is estimated to be nearly 6 × 104, which is extremely high. The characterization results provide clearly the structural and morphological features of VACNTs for experiments and modeling.To have further information on the defect degree of the VACNTs, which could also affect the stability and buckling behavior of CNTs, Raman spectroscopy with 633 nm excitation was employed (Fig. 2). We conducted the Raman spectroscopy measurements with 5 different VACNT samples and different characterization positions along the longitudinal direction of each sample. The Raman spectrum shows D-, G-, and 2D bands at 1323.5 cm−1, 1594.1 cm−1, and 2638.1 cm−1, respectively. In the Raman spectra of VACNTs, the average ratio of ID/IG peaks is around 0.78 before compression and 0.77 after compression; the standard deviation is less than 5%, indicating that the intrinsic properties of VACNTs do not change much during the compression process. This Raman spectrum result indicates the existence of disorder and defects in the graphitic structure of the VACNTs,30 which could lead to relatively weak resistance to an applied force and contribute to the instability of CNTs and propagation of buckling behavior during the compression process.
Buckling behavior characterization in quasi-static compressions
With all necessary structural and morphological properties of VACNTs, we utilized a strain increase compression test to investigate the buckling behavior of VACNTs. The SEM images in Fig. 3 indicate that the VACNTs exhibit local buckling behavior which develops progressively as the strain increases. Note that the buckling behavior develops from the bottom of the VACNT arrays. It could be attributed to the unbalanced friction between the bottom of the VACNTs and the silicon substrate, leading to a higher instability of VACNTs and also the smaller diameter of CNTs in the bottom as the effective catalyst size shrinks in the diffusing process to the substrate.31 As seen in Fig. 3A and D, the buckling waves develop progressively upward with new buckling waves propagating above the buckled region as the strain increases. Interestingly, the wavelength of the new buckling waves appears to be constant with the old ones. This buckling propagation and developing mechanism has not been studied in detail yet. And it could be explained in accordance with a wave damping effect,14 which was observed in previous experiments and modeling results, especially in shell buckling.32–36 Generally, a cylindrical shell under a uniform axial compression will have many axis-symmetrical buckling waves in the longitudinal direction due to the surrounding constraint force from its continuous shell structure, and the amplitudes of buckling waves will gradually decrease upwards, and eventually go to zero. Due to the van der Waals interactions from neighboring nanotubes, CNTs are constrained in the radial direction along the length and consequently have lateral support effects. Analogous to the shell buckling, the VACNT buckling with van der Waals lateral support also have many short buckling waves, which represents a high mode buckling, and the amplitudes of waves will decrease gradually under the wave damping effect. The detailed buckling propagation and the developing process are shown in the representative stress–strain curve in Fig. 3F with the corresponding buckling conditions (Fig. 3A–E). The stress–strain curve can be divided into the widely reported three-regions according to the buckling developing process: elastic region (0–5%), plateau region (5–60%), and densification region (70–85%). When strain is in the elastic region (<∼5%), the CNTs have only elastic deformation and there are no buckled waves. When the strain increases and exceeds the critical buckling strain, the buckling waves start to propagate from the bottom and the elastic modulus decreases correspondingly, indicating the critical buckling condition in Fig. 3A. With the strain increase, the bottom parts of CNTs deflect rapidly and then CNTs buckle at the first crests of the half buckling wave nearest to the bottom substrate. After the first half-wave is deformed, the second buckling half-wave sequentially begins to grow rapidly and so on. In this way, the buckling waves will progressively develop one by one upwards with the strain increase, shown in Fig. 3B–D, and the stress–strain curve shows almost a constant elastic modulus since it only needs a little more stress to force new buckling waves. Among these buckling waves, the half-wavelengths are almost identical because the initial buckling conditions, such as the CNT structure and Young's modulus, aspect ratio, and van der Waals interaction, have determined the length of all waves under critical buckling conditions. Meanwhile, the amplitudes of buckling waves will gradually decrease down to zero upwards in the buckling region and the rest parts of CNTs will still remain straight, following the wave damping effect.In Fig. 3F, when the strain is in the densification region (>∼70%), the elastic modulus will increase dramatically. The behavior of CNTs was changed from buckling to packing and folding in this region. Under these conditions, the collapse of the nanotube forest happens throughout the material and buckled nanotubes touch and press against one other as shown before in Fig. 3E. When this happens, the stress–strain curve rises sharply and the corresponding stiffness would simply be proportional to the relative density of bulk samples. Fig. 3E gives the corresponding buckling response in the densification region, showing almost uniform buckling half-waves along the longitudinal direction, which covers more than half the length of VACNTs. The gradually decreasing amplitudes in the top waves and the periodic developed half waves in the middle and bottom regions follow the wave damping effect when the strain keeps increasing up to a higher level. The observed half-wavelengths from the SEM images are around 9 μm at the top and middle region, and 6–8 μm at the bottom region. This slight increase in the wavelength indicates that the waves are heavily folded at the bottom and have weak recovery when the applied force is released. The difference in the wavelength between the top and bottom region is also reported in Cao et al.'s work.3 Overall, at a large strain, the decrease of the buckling wave amplitudes and the periodic propagating waves still follow the wave damping effect.
van der Waals interaction modeling characterization
With the above equations, a finite element CNT buckling model with lateral support was developed by converting the van der Waals interaction into a supporting medium and the simulation results are shown in Fig. 4. In Fig. 4A, the critical buckling mode keeps the 1st mode (whole column Euler buckling) when the aspect ratio is under ∼60. The critical buckling mode will become a high mode after that and the mode number will gradually increase with the aspect ratio. When the aspect ratio exceeds ∼6000, the critical buckling mode starts to remain constant around the 30th mode and the buckling region decreases from almost whole nanotube to nanotube ends. According to FEA analysis, with lateral support, the buckling mode of VACNTs will quickly increase to a high mode after the aspect ratio of 60 and have a nearly proportional correlation with the aspect ratio, but when the aspect ratio is over ∼6000, the local buckling behavior occurs and the buckling mode will start oscillate around number 30. Fig. 4B shows the simulation result of critical buckling conditions of VACNTs under experimental conditions (aspect ratio of 6 × 104), where the CNT buckles in the bottom region with ∼30th buckling mode, indicating the observed buckling response in the SEM images. The amplitudes of buckling waves are large in the bottom and gradually decrease to zero upwards, suggesting a wave damping effect. The half wave number of the FE result is around 15 at one end, which is higher than the experimental observation number 8. Among these half waves, the wavelengths are almost identical around 2.2 μm, while the experiment showed 6–8 μm. The differences between wavelengths and numbers might be caused by neglecting the multi-layered van der Waals interaction within the CNT, which could support the CNT considerably.17,37–39 Particularly, the CNTs in our experiments have only 2–3 graphitic-layered structure and will have great instability in compression, which might be overestimated in FE simulation due to its solid beam assumption. Also, the assumptions in the L-J potential and the conversion between van der Waals interaction24,40 and stiffness of supporting medium14 may contribute to the difference between FE and experimental results. In addition, there might be some differences between the actual VACNT structural properties and the SEM & TEM characterization, and the mechanical properties between FE simulation assumption and the actual CNT properties. But both FE simulation and experimental observation indicate high mode buckling behavior in the bottom region with many short buckling waves. And the propagation and developing mechanism of such buckling behavior follow the wave damping effect.Conclusions
In summary, the unique buckling behavior of VACNT arrays under compression was characterized experimentally and interpreted properly by employing the van der Waals interaction between VACNTs as the lateral support. Since van der Waals force from the adjacent nanotubes can constrain a VACNT in the radial direction, the buckling of VACNTs becomes a high mode buckling with many half buckling waves. The propagation and developing mechanism of VACNT buckling starts from the bottom of the nanotube and follows the wave damping effect. Furthermore, the study on such buckling behavior of VACNTs will significantly improve the understanding of collective mechanical properties of VACNT arrays and VACNT composites in compression, which could contribute to the use of engineered nanotube architectures in the building of synthetic biomaterials.Acknowledgements
The authors acknowledge the financial support from the National Science Foundation (Award No. 1104640) and the National Research Foundation of Korea (2014R1A2A2A01005496). The authors also want to acknowledge Dr Fei Deng for help in SEM and TEM characterization and our lab members for the discussion during experiments and modeling.References
- S. Iijima, Helical microtubules of graphitic carbon, Nature, 1991, 354(6348), 56–58 CrossRef CAS PubMed.
- J. Suhr, P. Victor, L. Ci, S. Sreekala, X. Zhang and O. Nalamasu, et al., Fatigue resistance of aligned carbon nanotube arrays under cyclic compression, Nat. Nanotechnol., 2007, 2(7), 417–421 CrossRef CAS PubMed.
- A. Cao, P. L. Dickrell, W. G. Sawyer, M. N. Ghasemi-Nejhad and P. M. Ajayan, Super-compressible foam like carbon nanotube films, Science, 2005, 310(5752), 1307–1310 CrossRef CAS PubMed.
- C. Cao, A. Reiner, C. Chung, S.-H. Chang, I. Kao and R. V. Kukta, et al., Buckling initiation and displacement dependence in compression of vertically aligned carbon nanotube arrays, Carbon, 2011, 49(10), 3190–3199 CrossRef CAS PubMed.
- A. A. Zbib, S. Mesarovic, E. T. Lilleodden, D. McClain, J. Jiao and D. F. Bahr, The coordinated buckling of carbon nanotube turfs under uniform compression, Nanotechnology, 2008, 19(17), 175704 CrossRef CAS PubMed.
- T. Tong, Y. Zhao, L. Delzeit, A. Kashani, M. Meyyappan and A. Majumdar, Height independent compressive modulus of vertically aligned carbon nanotube arrays, Nano Lett., 2008, 8(2), 511–515 CrossRef CAS PubMed.
- P. D. Bradford, X. Wang, H. Zhao and Y. T. Zhu, Tuning the compressive mechanical properties of carbon nanotube foam, Carbon, 2011, 49(8), 2834–2841 CrossRef CAS PubMed.
- V. L. Pushparaj, L. Ci, S. Sreekala, A. Kumar, S. Kesapragada and D. Gall, et al., Effects of compressive strains on electrical conductivities of a macroscale carbon nanotube block, Appl. Phys. Lett., 2007, 91(15), 153116 CrossRef PubMed.
- S. Pathak, Z. G. Cambaz, S. R. Kalidindi, J. G. Swadener and Y. Gogotsi, Viscoelasticity and high buckling stress of dense carbon nanotube brushes, Carbon, 2009, 47(8), 1969–1976 CrossRef CAS PubMed.
- C. P. Deck, J. Flowers, G. S. B. McKee and K. Vecchio, Mechanical behavior of ultralong multiwalled carbon nanotube mats, J. Appl. Phys., 2007, 101(2), 023512 CrossRef PubMed.
- S. B. Hutchens, L. J. Hall and J. R. Greer, In situ Mechanical Testing Reveals Periodic Buckle Nucleation and Propagation in Carbon Nanotube Bundles, Adv. Funct. Mater., 2010, 20(14), 2338–2346 CrossRef CAS PubMed.
- M. J. Buehler, Y. Kong and H. Gao, Deformation Mechanisms of Very Long Single-Wall Carbon Nanotubes Subject to Compressive Loading, Journal of Engineering Materials and Technology, 2004, 126(3), 245 CrossRef CAS.
- C. Ru, Column buckling of multiwalled carbon nanotubes with interlayer radial displacements, Phys. Rev. B: Condens. Matter, 2000, 62(24), 16962 CrossRef CAS.
- S. P. Timoshenko and J. M. Gere, Theory of elastic stability, Courier Dover Publications, 2009 Search PubMed.
- J. Wu, K. Hwang and Y. Huang, An atomistic-based finite-deformation shell theory for single-wall carbon nanotubes, J. Mech. Phys. Solids, 2008, 56(1), 279–292 CrossRef PubMed.
- A. Sears and R. C. Batra, Buckling of multiwalled carbon nanotubes under axial compression, Phys. Rev. B: Condens. Matter, 2006, 73(8), 085410 CrossRef.
- C. Ru, Degraded axial buckling strain of multiwalled carbon nanotubes due to interlayer slips, J. Appl. Phys., 2001, 89(6), 3426–3433 CrossRef CAS PubMed.
- C. Ru, Effective bending stiffness of carbon nanotubes, Phys. Rev. B: Condens. Matter, 2000, 62(15), 9973 CrossRef CAS.
- B. I. Yakobson, C. Brabec and J. Bernholc, Nanomechanics of carbon tubes: instabilities beyond linear response, Phys. Rev. Lett., 1996, 76(14), 2511 CrossRef CAS.
- H. J. Qi, K. B. K. Teo, K. K. S. Lau, M. C. Boyce, W. I. Milne and J. Robertson, et al., Determination of mechanical properties of carbon nanotubes and vertically aligned carbon nanotube forests using nanoindentation, J. Mech. Phys. Solids, 2003, 51(11–12), 2213–2237 CrossRef CAS PubMed.
- M. A. Poggi, J. S. Boyles, L. A. Bottomley, A. W. McFarland, J. S. Colton and C. V. Nguyen, et al., Measuring the compression of a carbon nanospring, Nano Lett., 2004, 4(6), 1009–1016 CrossRef CAS.
- M. Falvo, G. Clary, R. Taylor, V. Chi, F. Brooks and S. Washburn, et al., Bending and buckling of carbon nanotubes under large strain, Nature, 1997, 389(6651), 582–584 CrossRef CAS PubMed.
- E. G. Pogorelov, A. I. Zhbanov, Y.-C. Chang and S. Yang, Universal curves for the van der Waals interaction between single-walled carbon nanotubes, Langmuir, 2011, 28(2), 1276–1282 CrossRef PubMed.
- A. Popescu, L. M. Woods and I. V. Bondarev, Simple model of van der Waals interactions between two radially deformed single-wall carbon nanotubes, Phys. Rev. B: Condens. Matter, 2008, 77(11), 115443 CrossRef.
- C.-H. Sun, G.-Q. Lu and H.-M. Cheng, Simple approach to estimating the van der Waals interaction between carbon nanotubes, Phys. Rev. B: Condens. Matter, 2006, 73(19), 195414 CrossRef.
- A. I. Zhbanov, E. G. Pogorelov and Y.-C. Chang, van der Waals interaction between two crossed carbon nanotubes, ACS Nano, 2010, 4(10), 5937–5945 CrossRef CAS PubMed.
- C. Gao, Y. Z. Jin, H. Kong, R. L. Whitby, S. F. Acquah and G. Chen, et al., Polyurea-functionalized multiwalled carbon nanotubes: synthesis, morphology, and Raman spectroscopy, J. Phys. Chem. B, 2005, 109(24), 11925–11932 CrossRef CAS PubMed.
- L. A. Girifalco and R. A. Lad, Energy of Cohesion, Compressibility, and the Potential Energy Functions of the Graphite System, J. Chem. Phys., 1956, 25(4), 693 CrossRef CAS PubMed.
- O. Lourie, D. Cox and H. Wagner, Buckling and collapse of embedded carbon nanotubes, Phys. Rev. Lett., 1998, 81(8), 1638 CrossRef CAS.
- H. Kim, K.-Y. Chun, J. Choi, Y. Kim and S. Baik, Effects of Catalyst on the Super-Growth of Multi-Walled Carbon Nanotubes, J. Nanosci. Nanotechnol., 2010, 10(5), 3362–3365 CrossRef CAS PubMed.
- S. M. Kim, C. L. Pint, P. B. Amama, D. N. Zakharov, R. H. Hauge and B. Maruyama, et al., Evolution in catalyst morphology leads to carbon nanotube growth termination, J. Phys. Chem. Lett., 2010, 1(6), 918–922 CrossRef CAS.
- N. Jaunky and N. F. Knight Jr., An assessment of shell theories for buckling of circular cylindrical laminated composite panels loaded in axial compression, Int. j. solids struct., 1999, 36(25), 3799–3820 CrossRef.
- D. Karagiozova and N. Jones, Dynamic effects on buckling and energy absorption of cylindrical shells under axial impact, Thin-Walled Structures, 2001, 39(7), 583–610 CrossRef.
- D. Karagiozova, M. Alves and N. Jones, Inertia effects in axisymmetrically deformed cylindrical shells under axial impact, Int. J. Impact Eng., 2000, 24(10), 1083–1115 CrossRef.
- C. Bisagni, Numerical analysis and experimental correlation of composite shell buckling and post-buckling, Composites, Part B, 2000, 31(8), 655–667 CrossRef.
- H. Chai, The post-buckling response of a bi-laterally constrained column, J. Mech. Phys. Solids, 1998, 46(7), 1155–1181 CrossRef.
- S. Kitipornchai, X. Q. He and K. M. Liew, Buckling analysis of triple-walled carbon nanotubes embedded in an elastic matrix, J. Appl. Phys., 2005, 97(11), 114318 CrossRef PubMed.
- G. Román-Pérez and J. M. Soler, Efficient implementation of a van der Waals density functional: application to double-wall carbon nanotubes, Phys. Rev. Lett., 2009, 103(9), 096102 CrossRef.
- C. Ru, Effect of van der Waals forces on axial buckling of a double-walled carbon nanotube, J. Appl. Phys., 2000, 87(10), 7227–7231 CrossRef CAS PubMed.
- E. G. Pogorelov, A. I. Zhbanov, Y. C. Chang and S. Yang, Universal curves for the van der Waals interaction between single-walled carbon nanotubes, Langmuir, 2012, 28(2), 1276–1282 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5nr03581c |
| This journal is © The Royal Society of Chemistry 2015 |