 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Uncovering a law of corresponding states for electron tunneling in molecular junctions†
Ioan
Bâldea
*ab,
Zuoti
Xie
 *c and
C. Daniel
Frisbie
*c
*c and
C. Daniel
Frisbie
*c
aTheoretische Chemie, Universität Heidelberg, Im Neuenheimer Feld 229, D-69120 Heidelberg, Germany
bNational Institute for Lasers, Plasmas, and Radiation Physics, Institute of Space Sciences, Bucharest-Măgurele, Romania. E-mail: ioan.baldea@pci.uni-heidelberg.de
cDepartment of Chemical Engineering and Materials Science, University of Minnesota, Minneapolis, Minnesota 5545, USA. E-mail: zxie@umn.edu; frisbie@umn.edu
First published on 18th May 2015
Abstract
Laws of corresponding states known so far demonstrate that certain macroscopic systems can be described in a universal manner in terms of reduced quantities, which eliminate specific substance properties. To quantitatively describe real systems, all these laws of corresponding states contain numerical factors adjusted empirically. Here, we report a law of corresponding states deduced analytically for charge transport via tunneling in molecular junctions, which we validate against current–voltage measurements for conducting probe atomic force microscope junctions based on benchmark molecular series (oligophenylenedithiols and alkanedithiols) and electrodes (silver, gold, and platinum), as well as against transport data for scanning tunneling microscope junctions. Two salient features distinguish the present law of corresponding states from all those known previously. First, it is expressed by a universal curve free of empirical parameters. Second, it demonstrates that a universal behavior is not necessarily affected by strong stochastic fluctuations often observed in molecular electronics. An important and encouraging message of this finding is that transport behavior across different molecular platforms can be similar and extraordinarily reproducible.
1. Introduction
The idea of universality and the related law of corresponding states (LCS) trace back to van der Waals,1 who predicted that all fluids at equilibrium behave similarly; if appropriately renormalized, their parameters of state (pressure p, volume V and temperature T) obey the same equation | (1) |
In a fluid, the critical values (pc, Vc, and Tc) at the liquid–gas transition represent the natural units to define the reduced (dimensionless) parameters entering eqn (1)
| pR ≡ p/pc, VR ≡ V/Vc, and TR ≡ T/Tc | (2) |
Later on the notion of universality found its most fruitful realization in the renormalization group approach to phase transitions and critical phenomena.2 Laws of corresponding states were found for a series of equilibrium properties as well as transport coefficients (e.g., thermal conductivity, viscosity and self-diffusion) describing macroscopic fluids in the linear response regime.3–6 More recently, laws of corresponding states7,8 and universal behaviors9,10 have also been discussed for charge transport via hopping in organic semiconducting materials.
It might seem obvious that experimental data could exhibit a universal behavior only in situations, wherein, like those mentioned above, the fabrication of the materials/devices under investigation is a well-controlled process, and their properties are highly reproducible. From this perspective, attempting to find laws of corresponding states for molecular electronic devices seems to be extremely out of place; it is hard to expect universality for molecular junctions that are fabricated with a broad spectrum of different architectures and wherein measurements often yield conductance histograms having widths comparable to or larger than the most probable values.11–15 Nevertheless, and this is one of the most striking aspects of the results reported below, we demonstrate that the current–voltage (I–V) curves measured for molecular junctions based on two prototypical, completely different molecular series (oligophenylenedithiols and alkanedithiols) and commonly employed electrodes (Ag, Au and Pt) obey a remarkably simple LCS.
2. Results
2.1 Natural units for current and voltage
Similar to eqn (1), an LCS IRvs. VR relationship — expressing the I–V dependence in reduced, dimensionless quantities IR ≡ I/Ic and VR ≡ V/Vc—requires “critical” values for current Ic and voltage Vc to be used as natural units for these quantities. The challenge with respect to molecular junction measurements is to identify these natural units, given the fact that transport measurements on molecular junctions often yield featureless I–V curves (Fig. 1a). Our recipe is the following: recast the data as |V2/I| vs. V, and curves exhibiting maxima are obtained (Fig. 1b), which can be used to define the desired natural units Vc and Ic for voltage and current, respectively. The “critical” voltage Vc defined in this way represents an alternative to the so-called transition voltage introduced in recent molecular electronics studies;16–18 it characterizes the cross-over between a basically linear (ohmic) regime at (lower) biases V < Vc and pronounced non-linear regime at (higher) biases V > Vc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 (cf. ESI†). Importantly for the present analysis, Vc and Ic represent properties of a given junction.
19 (cf. ESI†). Importantly for the present analysis, Vc and Ic represent properties of a given junction.
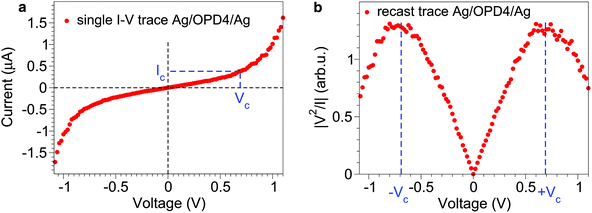 | ||
| Fig. 1 Natural units for voltage V and current I in molecular junctions. (a) Example of a typical featureless I–V curve measured in transport experiments. (b) By recasting it as |V2/I| vs. V, a maximum is obtained that can be used to define natural units Vc and Ic for voltage and current, respectively. These units are employed to define reduced biases (VR ≡ V/Vc) and currents (IR ≡ I/Ic), which satisfy an appealingly simple law of corresponding states, eqn (6), for the charge transport via tunneling in molecular junctions. | ||
So, we are led to define reduced, dimensionless voltage and current variables as
| VR ≡ V/Vc and IR ≡ I/Ic | (3) |
Notice that, similar to eqn (2), where the critical parameters are specific properties of a given fluid, our natural units Vc and Ic are essential characteristics of a given molecular device.
2.2 CP-AFM experimental results as basis for the presently reported LCS
Experimental results confirming the basis of the LCS consist, initially, of our own I–V measurements done on conducting probe atomic force microscope (CP-AFM) molecular junctions fabricated using two prototype molecular series and three widely employed electrode materials (M = Ag, Au, Pt), Fig. 2. One series, alkanedithiols, M/CnDT/M![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) M–S–(CH2)n–S–M (n = 8 to 11) has a σ-saturated aliphatic backbone. The other series, oligophenylenedithiols, M/OPDn/M
M–S–(CH2)n–S–M (n = 8 to 11) has a σ-saturated aliphatic backbone. The other series, oligophenylenedithiols, M/OPDn/M![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) M–S–(C6H4)n–S–M (n = 1 to 4) possesses π-electrons delocalized over aromatic rings.
M–S–(C6H4)n–S–M (n = 1 to 4) possesses π-electrons delocalized over aromatic rings.
 | ||
| Fig. 2 Experimental and theoretical results for oligophenylene- and alkane-dithiol-based CP-AFM junctions. (a) Schematic representation of a metal-molecule-metal junction made by contacting a self-assembled monolayer (SAM) of oligophenylene- (M/OPDn/M, n = 1 to 4) and alkane- (M/CnDT/M, n = 8 to 11) dithiol species with a conducting atomic force microscope tip. (b) The theoretical universal (red) curve of eqn (6) plotted along with ∼570 experimental IR–VR curves (black) measured for 24 different types of molecular junctions consisting of OPDn and CnDT molecules linked to metallic electrodes (M = Ag, Au, and Pt). (c) Comparison of the theoretical (red) curve, eqn (6), and the statistical average (blue line) of a statistical ensemble comprising ∼570 experimental curves analyzed. Error bars (black) represent standard statistical deviations. | ||
Fig. 2 displays an ensemble comprising ∼570 I–V curves measured up to biases (∼1.5 V) with pronounced nonlinearity for the 24 = 3 ×(4 + 4) aforementioned classes of CP-AFM junctions, which we have recast in the reduced variables IR and VR defined in eqn (3). Despite the variability in the molecular species and electrodes of the CP-AFM junctions considered, despite the fact that the ohmic (low bias) conductances G across these 24 classes vary over more than five orders of magnitude (ohmic resistances R ≡ 1/G are R ≈ 181 MΩ for Ag/C11DT/Ag and R ≈ 900 Ω for Pt/OPD1/Pt) and, to a lesser extent, within individual junctions of a given class (e.g., between the 28 individual I–V traces for Ag/OPD2/Ag, cf. Fig. S1a in the ESI†), all these reduced IR–VR curves are very close to each other: within statistical deviations (Fig. 2 and S1—S6 in the ESI†) and measurement errors (Fig. S8 and S9 in the ESI†), they collapse on a single universal IR–VR curve. This behavior exhibited by the reduced IR–VR curves (Fig. 2) clearly contrasts with the strong scattering in the raw I–V measurements depicted in Fig. 3.
 | ||
| Fig. 3 Unlike the normalized IR–VR curves of Fig. 2, the raw current–voltage I–V curves of the CP-AFM junctions analyzed in the present work exhibit a strong scattering. In panel a, all (∼570) I–V curves measured on the oligophenylene- (OPDn-) and alkane- (CnDT-)dithiol-based junctions are overlaid. Because of the different orders of magnitudes of the currents — similar to the low-bias conductance G (Gmin < G < Gmax range given in the left panels of Fig. S1–S6 in the ESI† for each type of molecule and electrode)—, the curves for the two molecular series OPDn and CnDT are also presented separately (panels b and c, respectively). | ||
2.3 Theoretical basis of the LCS
Most importantly, these experimental IR–VR curves excellently agree with a result that can be deduced theoretically. A preliminary comment is in order, however. It should be clear that a universal curve characterizing an experimental diversity of molecular junctions (and also applying to other experimental platforms, see below) can only follow if all these cases share a general common microscopic feature. It is implausible to expect universal transport behavior if demanding ab initio approaches or even sophisticated phenomenological models containing (many) system-specific parameters were needed to describe transport accurately for each of the cases considered here.20 So, it is most natural to assume (or at least to start the analysis by assuming) that the charge transport is dominated by a single molecular orbital, the HOMO or the LUMO, as schematically depicted in Fig. 4.For biases of interest, not much larger than Vc (the curves analyzed are almost unchanged upon reversing the bias polarity, so we choose Vc > 0 here), the current through a junction due to the tunneling mediated by a single level characterized by an energy offset ε0 relative to the electrodes’ Fermi energy can be expressed in closed analytical form (e is the elementary charge)21
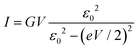 | (4) |
The values of the bias Vc and the current Ic at the maximum of the quantity |V2/I| can be immediately obtained by using eqn (4) as
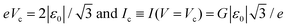 | (5) |
Eqn (5) expresses in mathematical form the physical fact that the cross-over values Vc and Ic represent properties of a given junction. It is noteworthy that, in particular, the peak bias Vc in Fig. 1b is directly related to the energy alignment ε0 relative to the Fermi energy of the dominant molecular orbital. Using the reduced quantities of eqn (3), we can recast eqn (4) in the form
 | (6) |
Eqn (6) is our “law of corresponding states” for the charge transport via tunneling through molecular junctions. The agreement between the theoretical result of eqn (6) and experiments, based on statistics performed over an ensemble comprising ∼570 I–V curves measured on a large variety of CP-AFM junctions (Fig. 2 and S1–S6 in the ESI†) is remarkable, particularly in view of the appealing simplicity of eqn (6).
The theory agrees with experiments even better than Fig. 2b (with ∼570 individual I–V traces) and Fig. 2c (statistically averaged measurements) may indicate. The theory stands the test of trace-by-trace analysis. For each class out of the 24 classes of junctions considered, we depict in Fig. S8 and S9 in the ESI† the individual IR–VR trace with the largest deviation from the theoretical curve, along with its vertical and horizontal error bars, which we refer to as “measurement errors”; they are related to uncertainties in identifying the bias V = Vc at the minimum location (Fig. S7 in the ESI†).
2.4 LCS beyond the CP-AFM platforms
Above, we have validated the LCS for the CP-AFM junctions fabricated and measured by us. To demonstrate that the class of universality is even broader, we present results in Fig. 5 for the reduced current–voltage curves reported for scanning tunneling microscope (STM) junctions by other groups.11,22–24 These data, spanning a spectrum of different molecules, also agree very well with the theoretical curve (cf.Fig. 5). | ||
| Fig. 5 Reduced current–voltage IR–VR curves for STM junctions. The theoretical curve of eqn (6) is plotted along with: (a) averages of 2151; 1661; 1661 I–V traces for the high- (H); medium- (M); low- (L) conductance phases of octanedithiol (C8DT) junctions with gold electrodes (cf.ref. 24) and (b) individual I–V traces measured for 4,4′-diaminostilbene,22 C8DT,23 and 44bpy ≡ 4,4′-bipyridine11 linked to gold electrodes. For these STM junctions, the ohmic resistance R varies over three orders of magnitudes [R ≈ 1.3 MΩ (ref. 11) to R ≈ 1.2 GΩ (L-phase, ref. 24)]. Notice that the 44bpy-based junction exhibits n-type conduction and was measured in solvent,11,25 in contrast to all the other junctions considered in this work, which are characterized by p-type conduction and measured in ambient conditions. | ||
2.5 How universal is the present LCS?
Section 2.3 made it clear that the physics underlying eqn (6) is the single-level picture. The examples presented above demonstrated that the present LCS applies to sufficiently broad classes of systems. Nevertheless, one cannot expect that, as general as it might be, an LCS like that presently discussed holds in all cases. Renormalization group theory speaks of some systems that belong to a certain universality class and other systems belonging to a different class of universality. Universal laws governing Fermi liquids do not apply to Luttinger liquids and vice versa; they belong to different classes of universality.We do not claim that the present LCS holds in all molecular junctions and do not rule out that cases to which it does not apply may exist. Still, as a last result reported in this paper, we want to show that this LCS also holds in situations where there is no straightforward reason why it should survive: namely, junctions wherein quantum interference effects26–29 occur. For illustration (Fig. 6), we will consider a schematic molecular junction consisting of a bridge comprising a donor moiety (D, onsite energy εD) and an acceptor moiety (A, onsite energy εA) connected to side group (S, onsite energy εS).
Exact results for this model can be obtained via straightforward Landauer-based calculations.30 Conductance G, energy-dependent transmission T(E), and current–voltage curves are depicted in Fig. 7. As a result of destructive quantum interference, the transmission T(E) and the conductance G are found to exactly vanish at E − εS = t2/tB and t2 + tBεS = 0, respectively. In Fig. 7, the green, blue and magenta colors correspond to situations where the coupling (t ≠ 0) to the side group S depresses via quantum interference the conductance G by factors of 10, 100, and 1000 with respect to the value without coupling (t = 0, coded as red color). For given values of εD, εA, εS, and tB (see legend of Fig. 7b), each of these situations is defined by a given value of t. The substantial decrease in G demonstrates that quantum interference effects are pronounced in those cases. Nevertheless, deviations from the LCS of eqn (6) of the IR–VR curves calculated for all those t-values are insignificant (cf.Fig. 7c).
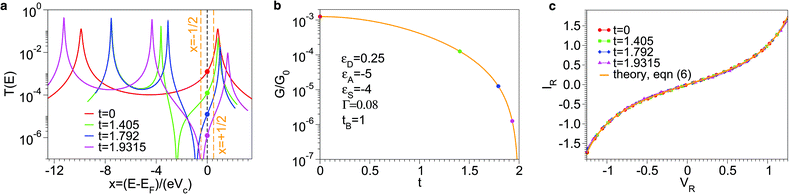 | ||
| Fig. 7 Results for the junction of Fig. 6: (a) energy-dependent transmission T, (b) conductance G, and (c) current–voltage curves in reduced variables. Quantum interference effects manifest themselves as a vanishing transmission and decreased conductance (G exactly vanishes for t2 + tBεS = 0). The orange vertical lines in panel a delimitate the energy window −eVc/2 < E − EF < eVc/2 that contributes to the current at the bias V = Vc. Parameter values as indicated in panel b. | ||
To conclude this analysis, nontrivial effects like quantum interference do not necessarily invalidate the present LCS.
3. Discussion
The starting point of eqn (1) was an equation (the van der Waals equation) proposed empirically and justified later microscopically based on certain assumptions.4 While its merit in bringing the notion of universality to the attention of scientific community is undeniable, we should remember that it represents a rather poor approximation of reality; empirical modifications of eqn (1) represent usual practice.6 Resorting to numerical coefficients determined via fitting is unavoidable to achieve a satisfactory description of the real systems (fluids) to which it refers.3,6 Later on, laws of corresponding states as expression of universal behaviors have been reported for a series of equilibrium2–4,6 and non-equilibrium5,7,8 properties, including full current–voltage curves for charge transport via hopping in semiconducting polymers.9,10 However interesting these findings are, like in all post-van-der-Waals developments for real fluids, the associated laws of corresponding states for charge transport via hopping contain empirical constants that can only be deduced by fitting experimental data.The fact that the present LCS, eqn (6), deduced analytically for charge transport via tunneling, contains no free parameters needing adjustment to experimental data is an important distinction from all the aforementioned cases. Whether p- or n-type (HOMO- or LUMO-mediated) conduction, whether STM-junctions containing a single-molecule or CP-AFM junctions consisting of a larger number molecules, which may furthermore significantly differ from junction to junction, the experimental current–voltage curves in reduced units collapse within errors on a single line agreeing with the theoretically predicted IR–VR curve free from any adjustable parameters.
This LCS is robust; it is not affected by the fact that, across the classes of junctions considered here, the conductance varies over more than five orders of magnitude. Significant spreads in conductance values from junction to junction for a given class11–15 do not affect this universal behavior either. So, the LCS is also robust against stochastic fluctuations related to, e.g., the large variability of contact binding mode (e.g., chemi- or physisorption) or geometry (e.g., atop, bridge or hollow24), which typically manifest themselves in very broad histograms.11–15 This is another striking contrast with the previously known laws of corresponding states that apply to systems or devices whose fabrication is highly reproducible. Thus, a bright side of the present LCS is that fundamental insight into the nanoscale charge transport of molecular junctions can be gained even with devices for which controllable fabrication still remains a desirable step for the future.
4. Conclusion
Universal laws extensively discussed in phase transitions and critical phenomena utilize physical properties at the critical point like those of eqn (2) as natural units to define relevant reduced dimensionless parameters. As expressed by eqn (3), in formulating the present LCS for tunneling transport, eqn (6), the cross-over voltage Vc (Fig. 1b) and the associated current value Ic at this bias (V = Vc) turned out to play an essential role in directly setting the natural units for bias and current. Similar to the critical parameters of eqn (1), it is possible to absorb all specific characteristics of molecular junctions in these natural units Vc and Ic, and the LCS is just the manifestation of this possibility. We believe that the present LCS is an important result for molecular electronics because it shows how straightforwardly results on charge transport can be compared across different platforms and how systems so extremely different at the molecular scale can obey a unique, parameter free, and simple equation.5. Methods
The metal-molecule-metal junctions were made based on molecules of oligophenylene dithiols (OPDn) and alkanedithiols (CnDT) bound to three types of electrodes (Ag, Au and Pt). Self-assembled monolayers (SAMs) of these molecules were formed by immersing clean template-stripped flat metal substrates31 in ethanol solution: OPDn (n = 1 to 4) at a concentration of ∼0.05 mM and CnDT (n = 8 to 11) at a concentration of 1 mM for ∼20 h. We measured about 570 current–voltage I–V characteristics for these (24 in total) types of CP-AFM junctions; details can be found elsewhere.32 The conductive AFM probes were made by coating the metals (Ag, Au and Pt) on contact mode AFM tips (DNP-10, Bruker Probes). The measurements were completed by mounting the substrates in the AFM and bringing the tip into contact with the SAM under ∼1 nN of applied compressive load. Voltages were applied to the tip with a Keithley model 236 electrometer operated in “DC mode”. The bias was swept at the tip, the sample was grounded and current–voltage characteristics were recorded. The measurements were carried out in an Ar-filled glove-box (H2O, O2 < 0.1 ppm). The inverse of the slope of the linear portion of the I–V characteristic at low biases was used to extract the ohmic resistance R = 1/G. The cross-over voltage Vc was estimated from the maximum of the quantity |V2/I| (Fig. 1 and S7 in the ESI†).Acknowledgements
I.B. thanks the Deutsche Forschungsgemeinschaft for financial support (DFG grant BA 1799/2-1). C.D.F. thanks the National Science Foundation (CHE-0616427) for financial support. Partial support was also provided by the National Science Foundation through the University of Minnesota MRSEC under Award Number DMR-0819885.References
- J. D. van der Waals, Ph.D. thesis, Leiden, The Netherlands, 1873.
- K. G. Wilson and J. Kogut, Phys. Rep., 1974, 12, 75–199 CrossRef.
- E. A. Guggenheim, J. Chem. Phys., 1945, 13, 253–261 CrossRef CAS PubMed.
- J. D. Boer, Physica, 1948, 14, 139–148 CrossRef.
- E. Helfand and S. A. Rice, J. Chem. Phys., 1960, 32, 1642–1644 CrossRef CAS PubMed.
- T. W. Leland and P. S. Chappelear, Ind. Eng. Chem. Res., 1968, 60, 15–43 CrossRef CAS.
- H. Bässler, Phys. Status Solidi B, 1993, 175, 15–56 CrossRef PubMed.
- R. H. Young, Philos. Mag. B, 1994, 69, 577–594 CAS.
- A. J. Kronemeijer, E. H. Huisman, I. Katsouras, P. A. van Hal, T. C. T. Geuns, P. W. M. Blom, S. J. van der Molen and D. M. de Leeuw, Phys. Rev. Lett., 2010, 105, 156604 CrossRef CAS.
- K. Asadi, A. J. Kronemeijer, T. Cramer, L. Jan Anton Koster, P. W. M. Blom and D. M. de Leeuw, Nat. Commun., 2013, 4, 1710 CrossRef PubMed.
- B. Xu and N. J. Tao, Science, 2003, 301, 1221–1223 CrossRef CAS PubMed.
- L. Venkataraman, J. E. Klare, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nature, 2006, 442, 904–907 CrossRef CAS PubMed.
- S.-Y. Jang, P. Reddy, A. Majumdar and R. A. Segalman, Nano Lett., 2006, 6, 2362–2367 CrossRef CAS PubMed.
- E. Lörtscher, H. B. Weber and H. Riel, Phys. Rev. Lett., 2007, 98, 176807 CrossRef.
- A. Mishchenko, D. Vonlanthen, V. Meded, M. Bürkle, C. Li, I. V. Pobelov, A. Bagrets, J. K. Viljas, F. Pauly, F. Evers, M. Mayor and T. Wandlowski, Nano Lett., 2010, 10, 156–163 CrossRef CAS PubMed.
- J. M. Beebe, B. Kim, J. W. Gadzuk, C. D. Frisbie and J. G. Kushmerick, Phys. Rev. Lett., 2006, 97, 026801 CrossRef.
- J. M. Beebe, B. Kim, C. D. Frisbie and J. G. Kushmerick, ACS Nano, 2008, 2, 827–832 CrossRef CAS PubMed.
- J. Kushmerick, Nature, 2009, 462, 994–995 CrossRef CAS PubMed.
- I. Bâldea, Europhys. Lett., 2012, 98, 17010 CrossRef.
- For the reason delineated in the main text, we do not believe that referring to ab initio calculations done for one or a few molecular species can be invoked to demonstrate a general LCS. Still, we want to mention that in a recent study on OPD-based junctions (Z. Xie, I. Bâldea, C. Smith, Y. Wu and C. D. Frisbie, Experimental and Theoretical Analysis of Charge Transport in Oligophenylene Dithiol Junctions as a Function of Molecular Length and Contact Work Function, preprint), we demonstrated that the HOMO energy offset ε0 deduced via the present eqn (6) agrees very well both with ab initio calculations and with UPS estimates (where the latter are available).
- I. Bâldea, Phys. Rev. B: Condens. Matter, 2012, 85, 035442 CrossRef.
- J. R. Widawsky, M. Kamenetska, J. Klare, C. Nuckolls, M. L. Steigerwald, M. S. Hybertsen and L. Venkataraman, Nanotechnology, 2009, 20, 434009 CrossRef CAS PubMed.
- W. Lee and P. Reddy, Nanotechnology, 2011, 22, 485703 CrossRef PubMed.
- S. Guo, J. Hihath, I. Diez-Pérez and N. Tao, J. Am. Chem. Soc., 2011, 133, 19189–19197 CrossRef CAS PubMed.
- I. Bâldea, Nanoscale, 2013, 5, 9222–9230 RSC.
- F. Sols, M. Macucci, U. Ravaioli and K. Hess, Appl. Phys. Lett., 1989, 54, 350–352 CrossRef PubMed.
- C. Patoux, C. Coudret, J.-P. Launay, C. Joachim and A. Gourdon, Inorg. Chem., 1997, 36, 5037–5049 CrossRef CAS.
- P. Debray, O. E. Raichev, P. Vasilopoulos, M. Rahman, R. Perrin and W. C. Mitchell, Phys. Rev. B: Condens. Matter, 2000, 61, 10950–10958 CrossRef CAS.
- M. Mayor, H. B. Weber, J. Reichert, M. Elbing, C. von Hänisch, D. Beckmann and M. Fischer, Angew. Chem., Int. Ed., 2003, 42, 5834–5838 CrossRef CAS PubMed.
- H. J. W. Haug and A.-P. Jauho, Quantum Kinetics in Transport and Optics of Semiconductors, Springer Series in Solid-State Sciences, Berlin, Heidelberg, New York, 2nd edn, 2008, vol. 123 Search PubMed.
- B. Kim, S. H. Choi, X.-Y. Zhu and C. D. Frisbie, J. Am. Chem. Soc., 2011, 133, 19864–19877 CrossRef CAS PubMed.
- V. B. Engelkes, J. M. Beebe and C. D. Frisbie, J. Am. Chem. Soc., 2004, 126, 14287–14296 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5nr02225h |
| This journal is © The Royal Society of Chemistry 2015 |


