Controlling the dynamics of Förster resonance energy transfer inside a tunable sub-wavelength Fabry–Pérot-resonator

Abstract

In this study we examined the energy transfer dynamics of a FRET coupled pair of chromophores at the single molecule level embedded in a tunable sub-wavelength Fabry–Pérot resonator with two silver mirrors and separations in the λ/2 region. By varying the spectral mode density in the resonator via the mirror separation we altered the radiative relaxation properties of the single chromophores and thus the FRET efficiency. We were able to achieve wavelength dependent enhancement factors of up to three for the spontaneous emission rate of the chromophores while the quenching due to the metal surfaces was nearly constant. We could show by confocal spectroscopy, time correlated single photon counting and time domain rate equation modeling that the FRET rate constant is not altered by our resonator.

---

1 Introduction

Förster resonance energy transfer (FRET) is probably the most prominent energy transfer mechanism between two fluorophores and is a widely used technique in life-science for determining small molecular distances.¹ This energy transfer is crucially dependent on the separation and orientation of two coupled chromophores and is mediated by near-field dipole–dipole coupling.² The Förster-transfer and similar energy-transfer mechanisms are important processes in nature i.e. photosynthesis³ and might be applied in photonic devices.⁴ During the last few years several studies have examined the influences of different environments on the FRET rate constant i.e. by coupling FRET-pairs to plasmonic particles.^5,6 But how the energy transfer rate constant can be altered by changing the local density of optical states (LDOS) is still under debate. Even contradicting statements can be found in the literature claiming no^7–9 or a linear^10–12 dependence of the transfer rate constant on the LDOS. One explanation for these contradictions can be found in the problem of describing the effective impact of the LDOS which is only a vague quantity if its spectral and spatial distribution affecting a dipole-emitter is not clarified. Thus, it is more explicit to separate the LDOS into energetically and spatially distributed modes with a certain density capable of coupling to the near-field and/or the far-field of an emitter.^13,14 Separating or specifically ruling out one of these influences is therefore inevitable for a deeper understanding of how the energy transfer process can be controlled. Another problem concerns the properties of the FRET-pair and the experimental determination of the transfer rate constant. Most commonly two spectrally matching fluorophores are labeled at two complementary DNA-strands ensuring a specific hybridization to adjust a fixed inter-chromophore distance. The often assumed rigid distance and its labeling with chromophores are nevertheless questionable regarding e.g. the hybridization thermodynamics,^15,16 structural and conformational changes of DNA¹⁷ confirmed by e.g. fluorescence microscopy experiments^18–20 revealing a broad distribution of FRET efficiencies of such labeled strands.

In this article, we examine the transfer dynamics of a FRET pair embedded in a λ/2-Fabry–Pérot-microresonator^21–24 by means of confocal microscopy and spectroscopy combined with pulsed laser excitation (λ = 488 nm, pulse width <100 ps, repetition rate 40 MHz) and time correlated single photon counting (TCSPC) for single molecule conditions. The FRET-pair, the resonator design and an energy level diagram are sketched in Fig. 1. Four types of samples were investigated: bare donors and FRET-pairs in free space and embedded in the microresonator. In all cases the concentration of donor chromophores or FRET-pairs was ∼10 × 10⁻⁹ mol l⁻¹ corresponding to an average number of around one chromophore or FRET-pair in a diffraction limited confocal volume, allowing us to measure fluorescence spectra and decay traces at the single-molecule level. The FRET-pairs consist of the fluorescent dyes Atto488 (donor) and Atto590 (acceptor) labeled on the same DNA-strand to prevent detection of false hybridized FRET-pairs or bare donors in the FRET-experiment. To stabilize this double labeled strand we hybridized a complementary unlabeled DNA-strand to the dye labeled strand. For further details concerning the sample design see the ESI.† The microresonator displayed in Fig. 1b allows us to control the LDOS at the location of the sample and its effect on the embedded emitters by controlling the mirror separation by piezo elements. The resonator exhibits a mirror separation dependent radiative enhancement of the spontaneous emission (i.e. the Purcell factor²⁵) ranging from a factor of 3 to nearly zero.^14,26–28

Fig. 1 (a) Double DNA-strand, with two FRET-coupled chromophores: Atto488 (donor) and Atto590 (acceptor) labeled to the green strand. (b) Fabry–Pérot-resonator: the mirrors consist of the following layers: (1) glass cover slide; (2) 1 nm Cr; (3) 40 nm Ag; (4) 1 nm Au; (5) 80 nm SiO₂; (6) 1 nm Au; (7) 60 nm Ag; (8) 1 nm Cr; (9) glass lens (f = 150 mm). The cavity length is tuned by using the piezoelectric stacks (A) implemented in a mirror mount (B). The sample (C) with embedded FRET-pairs or single donors within a thin film of PVA immersed with water (D) for reducing refractive index mismatches is placed on the bottom mirror which is mounted on the feed-back controlled sample scanning stage (E) of a confocal microscope. The same objective lens is used for excitation and fluorescence collection. A photodiode is used to measure white light transmission spectra of the resonator as a function of mirror spacing and hence determine the respective cavity resonance wavelength λ_res. (c) Simplified energy-level scheme of a FRET-system consisting of one donor and one acceptor. By absorbing a photon (blue wave) the donor is excited from the ground state D₀ to the intermediate vibronic level D^*₁ from where it relaxes quickly to the first electronically excited state D₁. Transitions back to D₀ can occur by either fluorescence with k^D_rad or various non-radiative decay channels with k^D_nrad. From the electronic excited state D₁ the energy can also be transferred with k_T to the acceptor chromophore, which is excited from the ground state A₀ to the intermediate vibronic level A^*₁ from where the first electronically excited state A₁ is populated. Relaxation to A₀ can occur radiatively or non-radiatively.

For analyzing the fluorescence in the time and spectral domain of a FRET-pair shown in Fig. 1c consisting of one donor, one acceptor and a one-directional energy transfer channel the transfer dynamics have to be expressed by the probabilities of finding one chromophore in its excited state given by the following rate equations:

where D_0,1 and A_0,1 are the probabilities of finding the donor and the acceptor chromophores in the electronic ground or excited state. The donor is excited by the focused pulsed laser beam with a time dependent rate k^D_exc(t) to a higher vibronic level D^*₁ of the first excited state. According to Kasha's rule vibronic relaxation occurs very fast such that the population can be neglected with respect to the lowest electronically excited state.²⁹ The donor may relax to its ground state with a non-radiative k^D_nrad, a radiative k^D_rad and an energy transfer rate constant k_T exciting in turn the acceptor to the vibronic level A^*₁ of the excited state. The acceptor can relax from its pure electronically excited state A₁ by non-radiative or radiative decay channels to its ground state A₀. 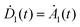Eqn (1) can be solved analytically for a quasi-stationary equilibrium , whereas the time evolution of D₁(t) and A₁(t) can be found only numerically. The energy transfer rate constant k_T as a measure of the dipole–dipole coupling depends on the spectral overlap of the donor fluorescence and acceptor absorption, the dipole–dipole separation in space and the mutual orientation of the transition dipole moments. The rate constant reaches its maximum value when the transition dipole moment of the acceptor is oriented parallel to the near-field induced by the donor or reaches zero if the transition dipole moment and field are perpendicular to each other.

In an altered photonic environment the decay rate constants have to be adapted to their dependency on the LDOS. The enhancement of the radiative rate can be calculated analytically³⁰ while in our Fabry–Pérot resonators the contributions to non-radiative relaxation by quenching due to the interaction of the emitters with the metallic mirrors are small.^9,31,32 This is because of the comparably large distances from the emitters to the metal surface which range between 70 and 125 nm adjusted by using a SiO₂-spacer layer on top of the silver. In the following, all radiative rate constants are denoted as functions of the on-axis transmission wavelength of the resonator λ_res which is experimentally directly accessible by white light transmission spectra of the resonator.

The total decay constant (or lifetime by τ^D_A = (k^D_A)⁻¹) for the donor in a FRET-pair can be expressed as

k^D_A = k^D + k_T = k^D_rad + k^D_nrad + k_T, (2)

which is the sum of the total decay constant of the bare donor k^D and the transfer rate constant k_T offering an additional decay channel. Therefore, the transfer rate constants can be determined by the experimentally accessible decay constants of the donor fluorescence for a specific resonance wavelength λ_res of the Fabry–Pérot cavity as

k_T(λ_res) = k^D_A(λ_res) − k^D(λ_res). (3)

Recording the on-axis transmission wavelengths allows one to calculate the radiative enhancement factor as a function of mirror separation.^24,30 For determining the transfer rate constants for a large number of different FRET-pairs and cavity lengths, the resonator was mounted on a scanning stage of a home built confocal microscope equipped with a spectrograph and a thermoelectrically cooled CCD-detector for recording fluorescence and transmission spectra and an avalanche photodiode (APD) for recording fluorescence decay curves by TCSPC. The pulsed and linearly polarized Gaussian laser beam was focused on the sample by using an objective lens (NA 1.46) which was able to collect also cavity off-axis emission. By installing a band-pass filter transmitting from 520–540 nm in front of the APD and switching between the photodiode and the CCD-camera it was possible to record fluorescence spectra of a FRET-pair and the decay curves at the very same lateral position representing exclusively the total decay of the donor chromophore inside the FRET-pair. A more detailed description of the microscope is given in the ESI.† First, the resonator was tuned to on-axis transmission wavelengths of around 500 nm for the lateral position of the detection volume by white light illumination. After that, the corresponding decay curve and fluorescence spectrum were recorded subsequently at the very same lateral position with integration times of 1 s by laser illumination. Then the confocal probing volume was laterally shifted by 1 μm and again the transmission and fluorescence were recorded. By a custom program (Labview) automatizing the procedure it was possible to investigate over 10 000 spatially separated volumes during all experiments. For the experiment with the FRET-pairs in the resonator ∼200 measured decay curves exceeded the threshold (30 counts per s in first time-bin) for determining the respective decay rate constants.

2 Results

Fig. 2a shows a free space ensemble spectrum of our FRET-pair consisting of the dyes Atto488 (donor) and Atto590 (acceptor) averaged over all measured confocal volumes to guarantee a homogeneous distribution of FRET-pairs in the sample volume. The emission with maximum intensity around 528 nm and a less intense vibronic contribution around 560 nm are assigned to the donor fluorescence while the red shifted contribution with its maximum around 620 nm is emitted by the acceptor. The gray shaded area represents the transmission range of the bandpass-filter installed in front of the APD selecting the donor fluorescence only for the time resolved measurements. In Fig. 2a the lower six panels show the fluorescence spectra (red lines) of FRET-pairs in the resonator recorded as a function of increasing mirror spacing, indicated by Lorentzian linefits to white light transmission spectra (black lines). The cavity fluorescence spectra (1)–(4) show only the blue wavelength bands of the donor. The donor's red wavelength vibronic band around 560 nm and the complete acceptor emission are suppressed. The cavity fluorescence spectra (5) and (6) show enhanced emission of the donor's long wavelength band and a part of the acceptor emission band around 610 nm. This behavior is in accordance with the resonance conditions for emission of fluorescent dipoles inside Fabry–Pérot-resonators, the mode spectrum given by the Purcell factor for this geometry and the angular detection efficiency of the objective lens.^23,30,33Fig. 2b shows measured fluorescence decay curves of the bare donor (blue dots) and the donor coupled to the acceptor (green dots) in free space, respectively. Both traces can be well fitted (black curves) to the convolution of a mono-exponential model function and the instrument response function (IRF, gray line). In panel (c) measured fluorescence decay curves of the bare donor (blue dots) and the donor coupled to an acceptor (green dots) in the resonator with an on-axis transmission wavelength of 530 nm matching the donor emission are displayed together with the fitted curves (black lines) consisting of a mono-exponential model function convolved with the IRF (gray line). Evaluating all recorded decay curves exceeding the pre-defined threshold in free space and in the cavity allows us to determine the statistically significant distributions. The determined 1200 bare donor decay constants k^D (blue bars) and 800 FRET-coupled donor decay constants k^D_A (green bars) in free space are shown in Fig. 3a by their relative occurrence. According to eqn (2) and the narrow distribution of the decay constants of the bare donor k^D the transfer rate constants k_T (brown bars) could be determined for each measured k^D_A as well as the FRET efficiency (yellow bars, lower panel) defined as E = k_T/[k^D + k_T]. For the bare donor, the distribution of the decay rates yields an average value of k^D = 0.309 ± 0.016 ns⁻¹, for the FRET-coupled donor decay rates k^D_A = 0.524 ± 0.137 ns⁻¹ and for the efficiency E = 0.448 ± 0.083. The significantly wider distribution of the FRET-coupled donor decay constants reflects the variation of the transfer rate constants and is in accordance with a mutual distribution of transition dipole moment orientations between the donor and acceptor in an amorphous polymer matrix.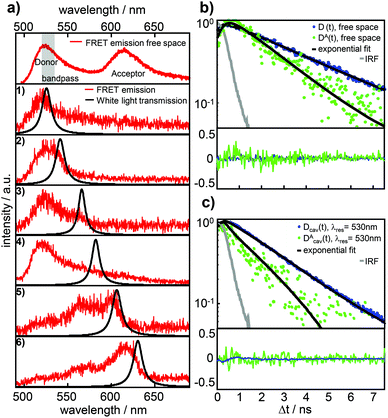

Fig. 2 (a) Top panel: free space ensemble fluorescence spectrum (red lines) of the FRET-pair Atto488 (donor) and Atto590 (acceptor). The gray area indicates the transmission of the bandpass filter placed in front of the APD to record decay curves of the donor fluorescence only. The six fluorescence spectra in the lower panels are from the same FRET-pair in a microresonator for different on-axis wavelengths of the resonator as illustrated by the black lines of the corresponding white light transmission spectra depending on the respective mirror separations. The change of the fluorescence spectra is in agreement with the expected effect of the cavity induced photonic environment, which is well described in the literature.^26–28 (b) Free space decay curves of donor fluorescence without (blue dots) and with (green dots) a coupled acceptor, recorded with a bandpass filter in front of the APD. (c) Fluorescence decay curves of donor D emitted photons without (blue dots) a coupled acceptor and the photons emitted by the donor D^A within the FRET-pair (green dots) in a microresonator with on-axis resonance wavelength 530 nm and a bandpass filter in front of the APD to select the donor fluorescence only. The black lines in (b) and (c) represent mono-exponential decay curves convolved with the instrument response function (IRF, gray line) fitted to the experimental data yielding the decay constants τ^D and τ^DA.

Fig. 3 (a) Histogram of total donor decay rates from different confocal volumes containing single bare donors (blue bars, k^D = 0.309 ± 0.016 ns⁻¹) and single FRET-pairs (green bars, k^D_A = 0.524 ± 0.137 ns⁻¹) in free space. The brown bars show the distribution of the energy transfer rates (k_T = 0.249 ± 0.079 ns⁻¹) determined by eqn (3). The panel below shows the distribution of the energy transfer efficiency in free space E_frsp (yellow bars, E_frsp = 0.448 ± 0.083 with: E_frsp = k_T/[k^D + k_T]). (b) Lifetimes τ^D and τ^D_A from mono-exponential fits of decay curves of single donor molecules without (blue dots) and with a coupled acceptor (green dots) as function of the on-axis resonance wavelength of the microresonator. The black line shows the simulated decay constant of the excited state of the donor inside the resonator. The gray line shows the simulation for the relaxation constant of the excited donor when coupled to an acceptor. The simulation of the lifetime of the FRET-coupled donor is based on the mono-exponential approximation and is the sum of the simulation of the pure donor (black line) and the mean transfer rate constant, determined from free space measurements.

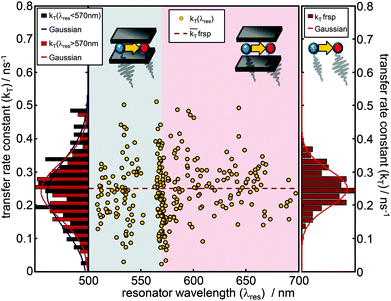
Fig. 3b shows the cavity modified lifetimes of the bare donors τ^D(λ_res) (blue dots) and of the donors within the FRET-pair τ^D_A(λ_res) (green dots) as a function of resonator wavelength. The bare donor lifetimes follow closely analytically calculated profile depending on the cavity length³⁰ (black curve) for molecules centered in the resonator with transition dipole moments parallel to the mirror surfaces. The gray line shows the modeled lifetimes τ^D_A(λ_res) assuming a cavity length independent transfer rate constant k_T with the mean free space value. The largest number of data points appear for cavity resonance wavelengths <600 nm i.e. when the cavity and the donor emission are in resonance.

Due to the narrow distribution of the bare donor decay rates k^D(λ_res) around the analytical solution, the transfer rate constants k_T(λ_res) can be determined by eqn (3) for each k^D_A(λ_res) and are displayed in Fig. 4 as yellow dots in the center graph. The transfer rate constants determined in this way can be divided roughly into two sections. The dots in the left section (blue shaded area) represent those rate constants which were determined for a resonator setting λ_res(L) < 570 nm i.e. when the donor emission is in resonance with the cavity. The dots in the right section (red shaded area) represent the transfer rate constants that have been determined where λ_res(L) > 570 nm i.e. when the acceptor emission is in resonance with the cavity. On the left side, the distributions of the transfer rate constants of both sections (donor resonance: dark blue; acceptor resonance: dark red) are visualized by histograms. The corresponding Gaussians show a mean transfer rate constant k_T of 0.233 ± 0.141 ns⁻¹ (λ_res < 570 nm) and 0.242 ± 0.112 ns⁻¹ (λ_res > 570 nm), respectively. On the right side, the distribution of the free space transfer rate constant (brown bars) is shown for comparison. The free space mean value is indicated as a dashed line in the center graph. All three distributions spread around the free space value, shaped symmetrically and show a large overlapping with mean values much closer to each other than their FWHM. Hence, the transfer rate constants determined for different transmission wavelengths show no significant dependence on the resonator wavelength.

Fig. 4 Transfer rate constants k_T(λ_res) (yellow dots) as a function of cavity resonance wavelength for the FRET-pair Atto488 and Atto590 inside an optical λ/2 microresonator. The yellow dots spread symmetrically around the free space mean value indicated by the brown dashed line and show no wavelength dependence. The dark blue bars (left panel) show the transfer rate constant distribution for λ_res < 570 nm with a mean value k_T(<570 nm) = 0.233 ± 0.141 ns⁻¹ and the red bars show the respective transfer rate constant distribution for λ_res > 570 nm with a mean value k_T(>570 nm) = 0.242 ± 0.112 ns⁻¹. The histogram on the right shows the distribution of k_T with a mean value of 0.249 ± 0.079 ns⁻¹ in free space.

3 Discussion

The presented results reflect the attempt to avoid the following three main obstacles of determining FRET-rate constants as a function of the LDOS achieved by the sample preparation, the design of the microresonator and the measurement procedure.

1: the intrinsic properties of a single FRET-pair and the corresponding transfer properties may vary with time due to conformational changes, bending or stretching of the DNA or the linker groups attached to the chromophores. This issue was faced by fixing the coupled chromophores in a PVA-matrix, preventing geometrical changes of the pair itself and the fluorophores with respect to each other over time. The TCSPC-histograms of the fluorescence decays (Fig. 2b) recorded with a collection time of 1 s are well described by a mono-exponential model function. Variations of orientation or distances within the FRET-pair during the acquisition time would lead to a multi-exponential decay behavior. The wide distributions of FRET-rate constants in free space and in the resonator can exclusively be ascribed to different conformational dispositions of the chromophores labeled to the DNA embedded in a rigid PVA matrix and reflect the results of previous studies.^34,35

2: the number of fluorescent dyes/FRET-pairs in the detection volume was chosen to be small enough to prevent averaging. Two or more FRET-pairs in the same detection volume would most likely have different donor decay rates resulting in double or multi exponential fluorescence decay curves. Thus, only decay curves fitting to the mono-exponential model function were further used in the evaluation. The distributions of the donor decay rates with and without the acceptor in free space and in the cavity show no significant asymmetric distortions or bimodal behavior. The design of the FRET-pair itself (see the ESI†) guarantees that we detected only fluorescent donors with linked acceptors. Hence, we can claim that our results were acquired at the single molecule level and the number of data-points and resonator separations are large enough allowing us to make statistically significant statements.

3: the influence of the photonic environment can be precisely controlled in particular for different lateral and axial locations and random orientations of the embedded emitters with respect to the resonator geometry defining the LDOS. The setup of our resonator allows one to accurately position the molecules in the center of the resonator by a thin PVA-film of several nanometer thickness and by spin coating on a well defined spacer layer of SiO₂ to ensure a well defined distance between the emitters and the mirrors. The near-field of a dipole can excite plasmons in the metal if the distance to the surface is small enough leading to a reduced fluorescence lifetime.³⁶ However, the distance between the chromophores and the mirrors is so large (80 nm, 80–240 nm) that non-radiative quenching by the silver mirrors has only a minor effect and is almost independent of the cavity resonance.^14,26–28 The measured lifetimes of the donor without the acceptor in the resonator (Fig. 3b), τ^D(λ_res), agree well with the model predicting radiative enhancement/inhibition according to the Purcell factor and a constant non-radiative decay.^14,26–28 The maximum enhancement of the LDOS in our approach tends toward a factor of 3, which seems to be still not enough to influence the FRET rate constant k_T.⁹

Due to these points, the reported results substantiate the assumption that the transfer rate constant of a closely spaced FRET pair is not influenced by the LDOS in our low-quality resonator. Nevertheless recent studies determined a scaling of the FRET-rate constant with the LDOS. Ghenuche et al. used FRET-pairs coupled to zero-mode waveguides milled in gold with diameters between 150 and 400 nm and determined an aperture size dependent rate constant.¹² Zhang et al.¹¹ observed altered energy transfer rates between donor–acceptor containing layers and an intermediate gold nanoparticle layer. This putative contradiction to our result is easily resolvable by regarding the effective mode distribution induced by the photonic environment. Our approach minimizes the coupling between the near-field modes of the emitter and the metal as the amplitude of the near field decays with R⁻³ and the cavity length is in the range of half a wavelength. Also Blum et al.⁸ found no enhancement of the FRET-rate constant in their experiments. They used one silver mirror with different separations to the FRET-pairs in order to vary the LDOS and achieved a maximum total enhancement factor of 1.5 assuming a constant non-radiative decay rate due to comparably large emitter–mirror separations. The main advantage of our method compared to most of the previously used techniques is based on the ability to control the LDOS in real-time at the location of one and the same quantum system by increasing or decreasing the mirror separations by using piezoelectrically movable mirrors and simultaneously observing white light transmission spectra. The approaches with nanoholes or nanoparticles on the other side benefit mainly from near-field coupling effects between the metal and emitter due to a smaller metal–emitter separation. This important insight allows one to tailor specific photonic devices for enhancing individual optical properties of FRET-coupled fluorophores without altering the intrinsic coupling properties of the FRET pair itself.

4 Conclusion

Using tunable Fabry–Pérot-λ/2-microresonators allows one to examine, control and characterize the spectral and temporal optical properties of e.g. natural energy-transfer coupled systems without changing the coupling mechanisms determined by their intrinsic structure.^9,24 We could show that the FRET rate constant is not altered by the effective LDOS of our resonator by time resolved measurements on fluorescent single FRET-pairs at different mirror separations.

Acknowledgements

Financial support from the German Research Council (DFG) for ME1600/13-1 is gratefully acknowledged. Special thanks are directed to Barbara Pohl (Biomers, Ulm, Germany) for her advice and discussions concerning the design and fabrication of the FRET-pair.

References

1. R. Roy, S. Hohng and T. Ha, Nat. Methods, 2008, 5, 507–516.
2. J. Lakowicz, Principles of Fluorescence Spectroscopy, Springer, 2006.
3. I. H. Stein, C. Steinhauer and P. Tinnefeld, J. Am. Chem. Soc., 2011, 133, 4193–4195.
4. M. Heilemann, P. Tinnefeld, G. S. Mosteiro, M. Garcia-Parajo, N. F. Van Hulst and M. Sauer, J. Am. Chem. Soc., 2004, 126, 6514–6515.
5. H. Y. Xie, H. Y. Chung, P. T. Leung and D. P. Tsai, Phys. Rev. B: Condens. Matter, 2009, 80, 155448.
6. V. Faessler, C. Hrelescu, A. A. Lutich, L. Osinkina, S. Mayilo, F. Jackel and J. Feldmann, Chem. Phys. Lett., 2011, 508, 67–70.
7. M. J. A. de Dood, J. Knoester, A. Tip and A. Polman, Phys. Rev. B: Condens. Matter, 2005, 71, 115102.
8. C. Blum, N. Zijlstra, A. Lagendijk, M. Wubs, A. P. Mosk, V. Subramaniam and W. L. Vos, Phys. Rev. Lett., 2012, 109, 203601.
9. F. Schleifenbaum, A. M. Kern, A. Konrad and A. J. Meixner, Phys. Chem. Chem. Phys., 2014, 16, 12812–12817.
10. P. Andrew and W. L. Barnes, Science, 2000, 290, 785–788.
11. X. Zhang, C. A. Marocico, M. Lunz, V. A. Gerard, Y. K. Gun'ko, V. Lesnyak, N. Gaponik, A. S. Susha, A. L. Rogach and A. L. Bradley, ACS Nano, 2014, 8, 1273–1283.
12. P. Ghenuche, J. de Torres, S. B. Moparthi, V. Grigoriev and J. Wenger, Nano Lett., 2014, 14, 4707–4714.
13. A. Caze, R. Pierrat and R. Carminati, Photonics Nanostruct. Fundam. Appl., 2012, 10, 339–344.
14. A. M. Kern, D. Zhang, M. Brecht, A. I. Chizhik, A. V. Failla, F. Wackenhut and A. J. Meixner, Chem. Soc. Rev., 2014, 43, 1263–1286.
15. K. J. Breslauer, R. Frank, H. Blocker and L. A. Marky, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 3746–3750.
16. W. Rychlik, W. J. Spencer and R. E. Rhoads, Nucleic Acids Res., 1990, 18, 6409–6412.
17. J. SantaLucia and D. Hicks, Annu. Rev. Biophys. Biomol. Struct., 2004, 33, 415–440.
18. R. M. Clegg, A. I. H. Murchie, A. Zechel and D. M. J. Lilley, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 2994–2998.
19. C. R. Sabanayagam, J. S. Eid and A. Meller, J. Chem. Phys., 2005, 122, 061103.
20. I. V. Gopich and A. Szabo, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 7747–7752.
21. A. Chizhik, F. Schleifenbaum, R. Gutbrod, A. Chizhik, D. Khoptyar, A. J. Meixner and J. Enderlein, Phys. Rev. Lett., 2009, 102, 073002.
22. S. Bar, A. Chizhik, R. Gutbrod, F. Schleifenbaum, A. Chizhik and A. J. Meixner, Anal. Bioanal. Chem., 2010, 396, 3–14.
23. A. I. Chizhik, A. M. Chizhik, A. M. Kern, T. Schmidt, K. Potrick, F. Huisken and A. J. Meixner, Phys. Rev. Lett., 2012, 109, 223902.
24. A. Konrad, A. L. Trost, S. Skandary, M. Hussels, A. J. Meixner, N. V. Karapetyan and M. Brecht, Phys. Chem. Chem. Phys., 2014, 16, 6175–6181.
25. E. M. Purcell, Phys. Rev., 1946, 69, 681–681.
26. M. Steiner, F. Schleifenbaum, C. Stupperich, A. V. Failla, A. Hartschuh and A. J. Meixner, ChemPhysChem, 2005, 6, 2190–2196.
27. M. Steiner, F. Schleifenbaum, C. Stupperich, A. V. Failla, A. Hartschuh and A. J. Meixner, J. Lumin., 2006, 119, 167–172.
28. M. Steiner, A. V. Failla, A. Hartschuh, F. Schleifenbaum, C. Stupperich and A. J. Meixner, New J. Phys., 2008, 10, 123017.
29. M. Kasha, Discuss. Faraday Soc., 1950, 9, 14–19.
30. G. Bjork, IEEE J. Quantum Electron., 1994, 30, 2314–2318.
31. M. Paulus, P. Cay-Balmaz and O. J. F. Martin, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5797–5807.
32. J. R. Lakowicz, Anal. Biochem., 2001, 298, 1–24.
33. A. Konrad, F. Wackenhut, M. Hussels, A. J. Meixner and M. Brecht, J. Phys. Chem. C, 2013, 117, 21476–21482.
34. A. A. Deniz, M. Dahan, J. R. Grunwell, T. J. Ha, A. E. Faulhaber, D. S. Chemla, S. Weiss and P. G. Schultz, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 3670–3675.
35. A. K. Wozniak, G. F. Schroder, H. Grubmuller, C. A. M. Seidel and F. Oesterhelt, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18337–18342.
36. K. H. Drexhage, Sci. Am., 1970, 222, 108–118.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5nr02027a

---