Nanoparticle characterization by means of scanning free grazing emission X-ray fluorescence

Abstract

Nanoparticles are considered for applications in domains as various as medical and pharmaceutical sciences, opto- and microelectronics, catalysis, photovoltaics, spintronics or nano- and biotechnology. The applications realized with nanocrystals depend strongly on the physical dimensions (shape and size) and elemental constitution. We demonstrate here that grazing emission X-ray fluorescence (GEXRF) is an element sensitive technique that presents the potential for a reliable and accurate determination of the morphology of nanoparticles deposited on a flat substrate (ready-to-use devices). Thanks to the scanning-free approach of the used GEXRF setup, the composition, shape and average size of nanoparticles are determined in short time intervals, minimizing the exposure to radiation. The (scanning-free) GEXRF technique allows for in situ investigations of the nanoparticulate systems thanks to the penetration properties of both the probe X-ray beam and the emitted X-ray fluorescence signal.

---

1. Introduction

Nanoparticles are used, or being evaluated for use, in many scientific fields like medicine, pharmacy, nano- and biotechnology, manufacturing, cosmetics, energy, electronics, photonics and environmental sciences. The characteristics of the nanoparticles differ pronouncedly from their bulk counterparts and are strongly influenced by their elemental constitution and their large surface-to-volume ratio (resulting from their physical dimensions and shape).¹ Indeed, the ratio of atoms or molecules having less neighbors and bonds than in a bulk matrix is increased, thus also the reactivity of the nanoparticles. Consequently, there is a demand for novel spectroscopic techniques which are able to deal with nanosized structures and to determine the morphology of the nanoparticles, in particular on ready-to-use devices. Indeed, the challenge during the synthesis of the nanoparticles is to tailor them in a controlled way in order to obtain specific sizes and shapes. Furthermore the characterization of these parameters is required in order to study their correlation with the nanoparticle properties, e.g. their catalytic activity, with regard to specific applications.

There are two main routes for nanoparticle formation, top-down and bottom-up approaches. In the top-down approach, nanometer-sized structures are engineered from bulk materials using a combination of lithography, micromachining methods, and etching.² Such approaches are technically challenging and although reproducible they do not readily lend themselves to large-scale production. A bottom-up approach involves the chemical growth of particles on an atom-by-atom basis until the desired particle size and shape are achieved. The growth process occurs spontaneously in super-saturated solutions and has been successfully used to create high-quality spherical, cubic, tubular and tetrahedral crystallites in kilogram quantities and above.^3,4

Some application domains like nanofabrication,^5–8 nanoelectronics,^9–11 and quantum dots^12–15 require that the produced particles are supported on flat substrates. This requirement can be achieved not only by post-synthesis deposition but also by direct growth on the substrate. The latter, however, limits at the same time the scope of spectroscopic techniques in the evaluation of the nanoparticle morphology on a ready-to-use device. In particular the class of metallic nanoparticles on insulating surfaces is difficult to investigate and the structural characterization presents a considerable experimental challenge. Indeed, besides the nanoscopic dimensions of the particles, the insulating substrate limits the possibility of using electron-based or ion-based probing techniques since they induce surface damage and can suffer from charging effects.^16,17 Noncontact atomic force microscopy (NC-AFM)^18–21 has opened the possibility of directly probing the local structure of nanoparticles on surfaces including some nanoparticles on insulators,^22–24 but, as for the electron and ion-based techniques, a controlled ultrahigh vacuum environment is usually required to achieve the best possible spatial resolution. While AFM provides direct information on the surface topography of individual nanoparticles, only confined areas can be scanned and element sensitive studies of the nanoparticle volume (core–shell nanoparticles) are not possible. While the discussed limitations show the areas where X-ray based approaches present the potential to champion current techniques for investigating nanoparticles, e.g. the imaging of nanoparticles on insulating substrates, the grazing emission X-ray fluorescence (GEXRF)^25–28 technique on which we report herein should not be seen as a direct competitor nor as a replacement of these well-established techniques which will continue to be the prime ones for routine imaging but rather as an additional, useful technique in this research area.

GEXRF offers elemental sensitivity and allows determination of the average nanoparticle size and shape, thus the nanoparticle morphology, of disperse distributions on the top of flat substrate surfaces without being affected by the limitations of electron-based or ion-based probes. Indeed, in GEXRF the sample is investigated by means of X-rays and therefore measurements can be realized under in situ conditions. No sample pretreatment and vacuum environment are necessarily required and moreover the technique is insensitive to the electric conduction properties of the sample. In contrast to imaging approaches with optical techniques it is furthermore not required to have a priori knowledge on the scattering properties of the nanoparticles. In the investigation of nanoparticles on the top of a substrate by means of GEXRF only the refractive index of the latter needs to be known. We demonstrate hereafter that the use of a scanning-free setup allows assessing the average size and the shape of the nanoparticles located in the investigated area in a single measurement at a fixed sample position in a reduced time interval during which the sample is exposed to X-ray radiation. This is of importance for radiation-sensitive samples. With regard to the actual applications, this allows for shape and size dependent studies of the nanoparticle properties. The size of the studied area, thus of the number of probed nanoparticles, depends essentially on the surface area irradiated with an X-ray probe beam. Moreover GEXRF, because of its element-sensitive character, allows investigating not only the morphology but also the composition and average homogeneity of multi-elemental particles. For example the technique may be applied to bimetallic nanoparticles which are of particular interest in the field of heterogeneous catalysis.²⁹

2. GEXRF on nanoparticles

The GEXRF technique was derived from the grazing incidence XRF (GIXRF) technique^30–33 through the principle of microscopic reversibility.³⁴ Both grazing XRF techniques offer nanometer-scale accuracy in the direction normal to the sample surface when investigating the elemental and structural composition of a sample. The probed sample volume below the sample surface can be tuned from a few nanometers to several hundred nanometers by varying the grazing incidence and grazing emission angle. The investigated, angle-dependent sample volume is restricted in GIXRF by using a monochromatic X-ray beam incident at grazing angles and in GEXRF by detecting only the X-ray photons emitted at grazing angles. In both techniques the respective grazing angles have to be well defined and the dependence of the XRF intensity on the grazing angle is measured. As a surface-sensitive technique GEXRF was applied towards trace-element measurements,^35–39 thin layered systems with respect to the determination of the layer thickness, density, roughness or oxidation^25,40–43 and towards (quantitative) depth-profiling experiments of the dopant distributions in ion-implanted samples.^44,45 Disperse particle distributions on the top of a reflecting surface were analyzed by both GEXRF^46,47 and GIXRF,^48–52 mainly in view of the investigation of the particle size.

While GIXRF and GEXRF are equivalent from a physical point of view,³⁴ from an experimental point of view the main difference between GIXRF and GEXRF is that the former setups are characterized by a large solid angle, whereas the latter setups can be easily combined with different X-ray excitation sources^53,54 and also with wavelength-dispersive detection setups.^25–28 Moreover, only GEXRF measurements can be realized in a scanning-free approach which allows acquiring the full angular profile in a single measurement without scanning in a sequential manner the XRF intensity at different grazing angles.⁵⁵ The latter setup offers in contrast to the conventional, scanning-based GEXRF setups a sufficiently large solid angle of detection to acquire the GEXRF intensity profiles in the angular range from 0° to above the critical angle in relatively short time intervals (of the order of minutes),⁵⁵ thus allowing reduction of the exposure time to X-ray radiation.

In the present paper, we show that the particle size and its shape can be accurately retrieved by means of GEXRF. For the investigation of nanoparticles deposited on the top of a substrate, GEXRF is suitable because of the homogeneous illumination and excitation of the XRF signal within the particle volume, even for particle sizes exceeding hundred nanometers when X-rays are used as the probe.

Despite the penetrating properties of X-rays compared to particle-based approaches, the grazing emission geometry provides two additional enhancement factors which are important with respect to the characterization of nanoparticles. First, the grazing emission geometry allows one to significantly reduce any background signal from the bulk volume of the substrate on which the nanoparticles are deposited. This allows measuring the XRF signal of the nanoparticles on the top of a substrate under almost background-free conditions, thus at significantly improved signal-to-noise ratios. Indeed, the X-ray photons emitted by atoms located in the bulk volume of the substrate towards the sharp interface separating the substrate from the surrounding environment (the optically denser medium since the refractive index of solids is smaller than unity in the X-ray domain) are refracted away from the surface upon transmission through this interface. For these X-ray photons, the propagation angle following the refraction process is larger than the critical angle. The latter depends on the X-ray energy and the substrate matrix. Thus, the angular range below the critical angle of total external reflection (≈1° or less in the hard X-ray regime) is simply inaccessible for the X-ray photons emitted by atoms located in the bulk matrix of the sample. Consequently, although X-ray fluorescence photons might be excited in a large substrate volume, only those emitted from above the refracting surface, i.e. from the deposited nanoparticles, or from within the extinction depth of the evanescent wave (≤3–5 nm) can be detected for grazing emission angles smaller than the critical angle of total external reflection. Given the element-sensitive character of XRF techniques, the particle and substrate contributions are distinguished by the energy of the emitted X-ray photons. In the angular range above the critical angle, the contribution of the bulk signal increases in a first approximation linearly with the grazing emission angle and is only modulated by the distribution of the atoms being the source of the X-ray signal of interest. Moreover, the grazing emission angles imply long emission paths within the sample and thus the emitted X-rays are still subject to strong attenuation.

A second enhancement factor is given by the total external reflection on the substrate surface of the X-ray photons emitted by the atoms located in the nanoparticles at an angle smaller than the critical angle towards the substrate surface (Fig. 1). Indeed, these X-ray photons do not penetrate into the substrate (the optically less dense medium for X-rays) but are reflected at an angle equal to that at which they were incident on the substrate surface (Fig. 1). Therefore in the angular regime below the critical angle, besides the direct emission towards the detector, a second detection path exists. Furthermore, the X-ray photons emitted via both possible detection paths may interfere with each other. Depending on the difference in the path length, constructive interference is possible which then provides in the ideal case a fourfold intensity increase rather than a twofold intensity increase as expected for the incoherent sum of the intensities. In addition, a modulation in the intensity increase by the substrate reflectivity also contributes to the measured intensities. Knowing the refractive index of the substrate for the energy of the measured X-ray signal, the interference pattern contains information on the shape and average size of a disperse nanoparticle distribution. Measuring the evolution of the emitted X-ray intensity as a function of the grazing emission angle in the angular range spanning from 0° to the critical angle allows therefore for an investigation of the nanoparticle's morphology.

Fig. 1 The dependence of the emitted X-ray intensity on the grazing emission angle can be measured in a scanning-free approach at a single sample–detector orientation by dispersing the angular scale along a position-sensitive detector. The solid angle, the covered angular range and the angular resolution depend on the sample-to-detector distance D and the detector pixel size Δh, respectively the detector height H. The XRF signal was excited by means of a synchrotron radiation beam (not shown). The grazing emission angles are discriminated by the individual pixels in the direction perpendicular to the substrate surface. The evolution of the XRF intensity with the grazing emission angle depends on the variation of the particle's cross-sectional atomic concentration f(z) with the distance z above the substrate surface (eqn (1) and Fig. 3). In the upper left panel, the dependence of the cross-sectional area with the height z for the represented spherical particle is shown, as well as for a conical particle with a base radius equal to its height and a prism particle with a base length equal to its height (cubical particle).

Finally, for emission angles larger than the critical angle only the X-ray photons emitted directly towards the detector contribute to the measurement (Fig. 1). The information from this angular regime can be used for quantitative measurements in terms of the surface concentration of the nanoparticles and the number of deposited atoms, without being disturbed by deviations from the linear intensity response due to a varying size and shape of the deposited particles as is the case for grazing angles below the critical angle.^38,56 However, other physical factors like secondary fluorescence (which to some extent can be avoided, respectively its contribution to the detected XRF signal can be estimated by appropriate tuning of the beam energy in a synchrotron radiation experiment) and different matrix effects might have to be considered.^38,57–59 We would like to stress that these effects do not affect the overall shape of the GEXRF intensity profile and consequently do not limit the presented retrieval procedure of the size and shape of the nanoparticles. Nevertheless, in the case of quantitative analysis of elemental concentrations, secondary fluorescence may have to be taken into account.

3. Experimental

The GEXRF measurements were realized at the X05DA Optics beam line⁶⁰ of the Swiss Light Source (SLS) with the scanning-free GEXRF setup which is schematically shown in Fig. 1 and described in ref. 55. The synchrotron radiation was produced using a bending magnet, monochromatized using a cryogenically cooled Si (111) channel cut monochromator and focused using a bendable toroidal mirror (1 : 1 focusing). The investigated Au nanoparticles with a diameter of ca. ≈ 10 nm (largely spaced ≈60 nm) on the top of a 1 cm² Si chip were fabricated by block-copolymer lithography.^61,62 The energy of the incident synchrotron radiation beam was selected as 12.1 keV which is above the L₃ (11.919 keV) but below the L₂ (13.734 keV) absorption edge of Au. The beam footprint on the sample surface was 4.1 mm by 200 μm. Thus, a larger surface area than with electron microscopy methods is covered in a single measurement. A scan of the substrate surface can be avoided and the size extracted from the angular intensity profile results from the average over a larger number of particles. The large footprint is explained by the small incidence angle of about 2.8° which was selected to efficiently excite the XRF signal from a large number of nanoparticles. The intensity dependence of the XRF signal on the grazing emission angle was recorded using a two-dimensional position-sensitive detector at a single sample–detector orientation. The GEXRF angular intensity profiles of the Au Lα₁, Lα₂, Lβ₁ and Ll characteristic lines were acquired in a single measurement without scanning through different sample or detector positions. The individual contributions were not discriminated by the detector, a PILATUS 100 K area detector,⁶³ since the latter did not allow for energy-discrimination of the incident signal as is possible with CCD detectors. While the relative contributions of the different radiative transitions are known,⁶⁴ the background signal originating from the elastic scattering on the Si substrate had to be corrected for with a complementary measurement at a beam energy below the Au L₃ edge in order to measure the shape of the angular intensity profile of this contribution. The relative difference in the critical angle for the two different beam energies was considered in the correction. The characteristic radiation from Si was rejected by the detector threshold. The area detector was set up so that its normal to the surface was perpendicular to the incident beam direction and parallel to the sample surface plane. The grazing emission angle of the emitted XRF photons, defined with respect to the substrate surface on which the nanoparticles were deposited, was discriminated by the position-sensitive detection along the direction perpendicular to the substrate surface. Each pixel in the dispersion direction corresponded to a different grazing emission angle whose value was determined by the geometry of the setup. The setup's angular resolution and covered angular range depend on the sample–detector distance D and the pixel size Δh (172 μm for the PILATUS detector) or the detector extension H.⁵⁵ For a sufficiently large sample–detector distance, as was the case for the used setup with D ≈ 1 m, the contribution to the angular resolution of the detector dimension perpendicular to the dispersion direction is almost negligible and the recorded photon counts can be summed along this direction which allows increasing the solid angle of detection.⁵⁵ As mentioned the GEXRF intensity profiles were recorded with the described setup simultaneously for different characteristic emission lines whose relative intensity contributions are known from tabulated values.⁶⁴ This increased the detection efficiency of the scanning-free GEXRF setup (see also Fig. 2).

Fig. 2 The grazing emission angular intensity profile for Au nanoparticles on the top of a Si substrate was measured with a scanning-free GEXRF setup. The best fit of the experimental data was obtained by assuming beforehand particles with a half-spherical shape (left hand panel). The particle size extracted from the fit was 10.6 ± 0.3 nm (diameter). It should be noted that this value corresponds to the best estimate of the average size of the nanoparticles localized within the area covered by the incident beam. The best fits when assuming other particle shapes are shown in the figure inset. The total acquisition time for the GEXRF profile was 780 s and the beam energy of the synchrotron radiation was 12.1 keV. The background signal originating from the substrate was corrected for by measuring its shape at a beam energy below the Au L₃ edge and taking the difference in the critical angle into account. On the right hand panel a scanning electron micrograph (SEM) of the investigated Au particles is shown, confirming when only isolated particles are considered, the average particle size retrieved by means of GEXRF. It can also be seen that SEM has difficulties with clustered particles, limiting the number of particles which can considered in the statistical evaluation of the particle size.

4. Theoretical approach

Derivations of the theoretical dependence of the X-ray intensity on the grazing emission angle for bulk and layered samples as well as for ion-implanted samples can be found in the literature.^65,66 For particles it was assumed that the atoms emitting the X-ray signal of interest are all in the same plane and the only refracting interface which has to be considered is that of the underlying substrate.⁶⁵ The former assumption, however, can only hold for very small particles and not for particles larger than several nanometers where the varying distance of the atoms emitting the XRF signal to the substrate surface cannot be neglected.⁶⁷ Depending on the nanoparticle morphology a varying cross-sectional area f(z), i.e. a changing number of atoms emitting the XRF signal, in the direction perpendicular to the substrate surface has to be considered. The theoretical dependence of the XRF intensity on the grazing emission angle φ is for particles extending to a height S measured from the substrate surface given bywhere r corresponds to the reflection coefficient of the substrate materialand n is the complex refractive index of the underlying substrate. For non-ideal substrate surfaces the surface roughness can be taken into account by an additional multiplication term.⁶⁸ The special cases of structured substrate surfaces and nanoparticles deposited near the substrate edge are also considered in the literature^69,70 and extensions towards layered supporting surfaces are also possible. In eqn (1) the second factor in the integrand accounts for the X-ray photons emitted directly towards the detector (first summand) and those emitted via a reflection on the substrate surface (second summand).

In eqn (1) the case of a low density particle surface coverage is considered meaning that the absorption of the emitted X-rays in neighboring nanoparticles can be safely neglected. In this case the X-ray intensity at emission angles above the critical angle are directly proportional to the number of emitting atoms and the mass calibration is straightforward with a calibration sample (a reference sample or a thin layer sample). Indeed, the contribution of the absorption of the emitted radiation was estimated, considering X-ray photon energies of several keV, to be of at most a few per cent with only a faint dependence on the grazing emission. The attenuation of the X-rays propagating at a grazing angle is also discussed in GIXRF in terms of shading by neighboring particles.^56,71 However, the shading effect, which can affect the mass calibration, is expected to be more important in GIXRF because in contrast to GEXRF the X-rays propagating at a grazing angle through the nanoparticles have energies above the elemental absorption edge, resulting in absorption cross-sections which are about an order of magnitude higher. An exception to this statement is the case of multi-elemental nanoparticles where the excited XRF signal of one element is above the absorption edge of another element. For the considered low density surface coverage the overall shape of the GEXRF intensity profiles will, however, not be affected. Indeed, the excitation or attenuation of XRF signals because of matrix effects in the nanoparticles is independent of the monitored grazing emission angle. Also, the average length of the emission path through neighbouring nanoparticles is short and does not vary significantly in the monitored angular range.

Another special case not considered by eqn (1) are periodic or dense (close to film-like structure) distributions of particles with a flat top. In this case not only reflections on the substrate surface but also the refraction on the upper particle interface (with the surrounding environment) needs to be taken into account. The angular intensity profile exhibits features of particle-like and layer-like surface distributions.^72,73 As in the present investigation only random (i.e. non-periodic) distribution patterns are considered, independent of the particle shape, this contribution is not needed to be taken into account since only particle-like contributions to the angular intensity profile are expected.

5. Results and discussion

In the following only low-density, monodisperse particle distributions as described in eqn (1) on the top of a Si substrate will be considered so that multiple reflections and the absorption of the emitted XRF signal within the (neighboring) nanoparticles can be safely neglected. In this case solving eqn (1) for the distribution f(z) would allow one to straightforwardly retrieve an analytical solution for the shape of the investigated nanoparticles provided that the optical parameters of the underlying substrate are sufficiently well-known to calculate the reflectivity r(φ). The case of the investigation of ion-implanted samples by means of GEXRF^44,45 is an analogous example in terms of retrieving the continuous distribution in the direction perpendicular to the substrate surface except that the atoms from which the emitted X-ray signal is monitored are located below the refracting surface. Through this analogy it can be assumed that the inversion of eqn (1) in order to isolate the distribution f(z) is also in the present case an ill-posed problem which cannot be easily solved, which is subject to instabilities caused by numerical errors and which requires regularization methods. The selected approach to investigate the experimental GEXRF intensity profile of Au nanoparticles deposited on the top of a Si surface was therefore to fit the experimental data with eqn (1) by using different parametrized functions describing each the atomic distribution f(z) for a different nanoparticle shape. The best fit of the experimental data allowed then not only to retrieve the shape of the probed nanoparticles but also to specify their average size. A future extension to be realized is the development of a genetic algorithm in which it would not be absolutely necessary to assume a given nanoparticle shape. The retrieved result was verified qualitatively by scanning electron microscopy (SEM). For a quantitative SEM analysis, a statistical analysis is necessary which requires the evaluation of many micrographs given the small area covered by a single micrograph. Also the analysis can be difficult if coalescence and agglomeration of nanoparticles occur.

The experimental result retrieved by means of GEXRF corresponds to a mean value of the nanoparticles which were within the lateral area covered by the incident X-ray beam used to excite the XRF signal. If polydisperse distributions are to be investigated, different particle sizes can be binned together in different average GEXRF intensity profiles and a weighted sum of the intensity profiles resulting from the different size contributions can be considered to fit the experimental data.⁴⁸ In this way the size repartition of the particles can be recovered.

The sensitivity of GEXRF to the size and shape of the nanoparticles is demonstrated in Fig. 3 for monoelemental and -disperse Co and Pt particles on the top of a Si substrate. To better depict the dependence of the GEXRF profiles on the particle size and shape, the intensities were normalized to 1 at an emission angle of 0.6°, which is fairly above the respective critical angles of Si for the energies of the Co Kα₁ and Pt Lα₁ lines considered in the calculation. This corresponds to a normalization of the number of atoms emitting the XRF signal. The selected examples are quadratic prism shaped particles with a base length of 10 nm, conical particles with a base diameter of 10 nm and spherical particles.

Fig. 3 Dependence of the Co Kα₁ and Pt Lα₁ GEXRF intensity profiles on the vertical particle size for monoelemental Pt (top row), and Co (middle row) nanoparticles with different shapes. In order to better illustrate the dependence on the particle size and shape of the evolution of the XRF intensity with the grazing emission angle, the intensities in the plots were normalized to 1 at an emission angle of 0.6°. The assumed particle shapes were prism with a 10 nm square base, conical with a 10 nm diameter base and spherical (from left to right). With respect to a dimensionless angular scale (top scale on the plots) identical angular intensity profiles can be observed for the Co and Pt. For a better comparison of the shape dependence, the bottom row shows the angular profiles of Co for the 3 different displayed shapes. The above examples show that size differences of the order of 1 nanometer or even better can be discriminated. This could also be inferred from the fitting error of the experimental example shown in Fig. 2, being on the order of 0.3 nm. The experimental error is, however, also influenced by the counting statistics and the physical size repartition of the nanoparticles.

For each of the particle shapes considered in Fig. 3, the evolution of the GEXRF intensity profile varies pronouncedly with the size of the particle. This shows that the particle size can be retrieved with good accuracy from a measured angular intensity profile. A limitation exists, however, for particles where the lateral density does not vary as a function of the height above the substrate surface, i.e. where f(z) is constant. Here only the height of the particles can be extracted but not their lateral extension and/or lateral shape. For example upright standing cylindrical particles would give rise to the same evolution of the angular intensity profiles as the square base prisms considered in Fig. 3 (left top and middle panels). For other particles the variation with z of the lateral density of atoms contributing to the XRF signal is encoded in the parametrization of f(z) and would therefore be considered in the fitting of an experimental angular intensity profile even if the shape type would be the same, e.g. conical particles with identical heights but different base diameters. Thus, not only the particle dimensions in the vertical direction but also the lateral dimensions can be retrieved for most of the particle shapes.

It can also be seen in Fig. 3 that the calculated angular intensity profiles depend not only on the particle size but also on the particle shape. Indeed, for particles of the same height, the calculated angular intensity profiles can be easily distinguished by the presence of multiple interference fringes as well as the position and width of the intensity maximum. If present, the interference fringes are visible for somewhat larger particles and the period, position and width of the fringes will allow for an accurate determination of the size. For smaller particles the position of the intensity maximum and the width of the intensity maximum are the best indicators of the size. Also, for particles with sizes of only a few nanometers the sensitivity to the shape is the smallest. In general, however, the evolution of the angular intensity profile depends pronouncedly on the particle shape and average size and from an experimental angular intensity profile the information on these two parameters can be reliably extracted as is demonstrated for Au particles on the top of Si (Fig. 2). A requirement is that the angular resolution of the setup is good enough, i.e. of the order of millidegrees, to resolve accurately the features (fringe frequency, intensity maximum peak position) in the experimental angular intensity profiles in the angular range between 0° and the critical angle for total external reflection.

In Fig. 3 the variation of the cross-sectional area is either described by a 0th or a 2nd order polynomial (see Fig. 1, upper left panel). With respect to a dimensionless angular scale (top axes in Fig. 3) where the grazing emission angle is divided by the respective critical angle of total external reflection it becomes apparent for each particle shape that the evolution of the angular intensity profile depends solely on the size of the nanoparticles but not on their elemental composition nor on the energy of the emitted X-ray signal. Thus, a database for the dependence of grazing angular XRF intensity profiles on the particle shape and size could be set up on the basis of the dimensionless angular scale. This shape-size database would be independent of the energy of the characteristic emission line, the elemental composition of the particles and the substrate material as long as the sources of the XRF radiation are uniformly distributed within the nanoparticles. Within the experimental limits discussed earlier the databases would even be identical for GEXRF and GIXRF. This would allow, by alleviating the dependence on the X-ray wavelength, for an easier and straightforward comparison of the investigations realized with both techniques. Indeed, GIXRF angular intensity profiles can be calculated⁷⁴ by means of a similar equation to eqn (1). When considering bimetallic nanoparticles, which can also be used instead of a modified particle morphology to enhance the electro-catalytic properties,⁷⁵ with uniform elemental distributions, the angular intensity profiles would exhibit the same dependence as for their monoelemental counterparts. Moreover, the GEXRF intensity profiles can be used as a fingerprint to check whether the elemental distributions within bimetallic particles are homogeneous, and how the spatial distributions differ.

Nanoparticles with a more complex structure can be investigated as well by means of GEXRF, e.g. core–shell particles. In Fig. 4 the case of spherical particles with a Co shell and a Pt core is considered. It is shown that the core diameter and the shell thickness have a significant influence on the evolution of the normalized angular intensity profiles. If the overall particle size is constant and only the diameter of the core is varied (Fig. 4, top row), i.e. the position of the center of mass of the atoms emitting the investigated X-ray signal is constant, the angular position of the intensity maximum does not change, neither for the XRF signal from the core nor for the one from the shell. However, the ratio of the XRF peak intensity to the one at emission angles above the critical angle changes in both angular intensity profiles, the one from the core and also the one from the shell. Therefore this ratio can be used as a first indicator of the size of the core. Regarding the overall shape of the normalized angular intensity profiles, the dependence on the core diameter, thus also the shell thickness, is more pronounced for the XRF signal from the core than for the XRF signal from the shell (Pt Lα₁ and Co Kα₁ in the selected example). If, however, the core diameter is kept fixed and the overall particle size is varied by changing the shell thickness, much more significant changes in the angular intensity profiles can be observed (Fig. 4, bottom row). In this case, the center of mass position of the emitting sources with respect to the substrate surface changes (as it did for monoelemental particles of a given shape but different sizes). Analogous to the size dependence observed for monoelemental spherical particles (Fig. 3, left top and middle panels) the position of the XRF intensity maximum moves towards smaller grazing emission angles with increasing particle dimensions (increasing shell thickness). In addition a second positive interference peak shows up in the angular dependence of the XRF signal originating from the core volume (Pt Lα₁) for larger shell thickness, meaning an increasing height of the core region above the substrate surface. Therefore, a dependence of the particle position above the substrate surface could be studied with core–shell particles, which might be of interest when using GEXRF to study, for example suspended particles.

Fig. 4 For core–shell nanoparticles, the shape of the GEXRF intensity profiles depends on the core diameter and the shell thickness. In the top panel, the changes in the Co Kα₁ and Pt Lα₁ XRF intensity profiles are shown for spherical monodisperse Co–Pt core–shell particle distributions with a diameter of 20 nm as a dependence of the core diameter. In the bottom panels, a core of 10 nm diameter was considered and the dependence on the particle diameter, thus the shell thickness, is represented.

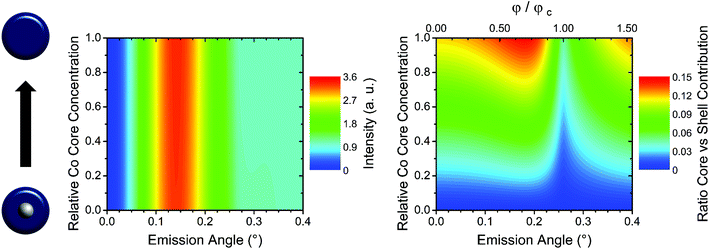
The study of nanoparticles by means of GEXRF is not only limited to the size dependence of core–shell particles with a monoelemental core and shell, but may also be extended to nanoparticles with multi-elemental compositions. In Fig. 5 a 20 nm in diameter particle with a 10 nm in diameter core composed of a CoPt alloy surrounded by a Co shell is considered. While the shape of the angular intensity profile for Pt Lα₁ does not vary with the Pt concentration in the core, the normalized angular intensity profile of Co Kα₁ exhibits a faint dependence, limited to the amplitude of the intensity peak, in the angular intensity profile and approaches that of a pure Co particle with decreasing Pt concentration in the core (Fig. 5, left panel). This is, however, not surprising, since the physical parameters in eqn (1) only show a very weak dependence on the chemical composition or the state of the elements located within the particles. Indeed, even if the energy of the monitored characteristic emission line of one of the elements in the particles shifts with the chemical state, the change in the refractive index of the substrate will only be minor (inverse dependence on the XRF energy). On the other hand, when combining GEXRF with a different X-ray based technique offering chemical sensitivity like fluorescence detected X-ray absorption (XAS) for example, the grazing emission geometry can also be of advantage in the case of core–shell particles where one element is present in the core and in the shell. Indeed, the relative contribution of the Co atoms in the core to the total intensity in the GEXRF profile varies with the grazing emission angle (Fig. 5, right panel). This allows optimizing the grazing emission angle with respect to the volume in the particle, the core or the shell, which may be preferentially studied by fluorescence detected XAS.

Fig. 5 For core–shell particles with a Co shell and a bimetallic CoPt core the elemental concentration of Co in the core influences the peak intensity in the GEXRF profile with respect to the intensity at emission angles above the critical angle (left panel). The contribution of the core region to the overall detected XRF intensity varies with the emission angle, allowing one to optimize the sensitivity to the core volume of the particle for X-ray emission based spectroscopy (XES) techniques (left panel). The grazing emission angle at which the contribution is maximal does not depend on the Co core concentration.

6. Conclusions

In summary it has been shown that GEXRF presents the potential for a reliable and accurate structural and compositional analysis of nanoscaled particles deposited on the top of an optically flat substrate. An experimental verification by GEXRF and SEM was performed for the Au particles on the top of Si while the Co, Pt and Co–Pt core–shell nanoparticles were considered on a simulation basis. Given their extreme properties some of the latter samples are difficult to synthesize so that an experimental verification as well as a cross-validation with other experimental techniques is still to be realized. Nonetheless it was shown that the shape of the GEXRF intensity profiles allows one to discriminate accurately between different nanoparticle sizes and shapes and moreover to investigate the structure of core–shell particles. For grazing emission angles smaller than the critical angle φ_c XRF photons emitted directly towards the detector or via a reflection on the substrate surface can be detected and interference effects between both emission paths have to be taken into account. The intensity dependence in this angular regime is sensitive to the size and shape of the investigated nanoparticles. For larger emission angles only the XRF photons directly emitted towards the detector can be detected. The information from this angular range can be used for quantification purposes. Moreover, in comparison with conventional GEXRF setups where the angular intensity profile is acquired in a series of sequential measurements the use of a scanning-free GEXRF setup allows for nanoparticle investigations at reduced exposition times to X-ray radiation. Furthermore, since GEXRF is an X-ray based method, experiments under atmospheric pressure can be envisaged. This helps in not only avoiding sample preparation issues but also allows for in situ measurements which are especially of importance if changes induced by chemical reactions, for example the chemical state of one or more reactants, are to be surveyed by combining GEXRF with fluorescence detected XAS. Note that information on the chemical states cannot be obtained with electron microscopy based approaches. In combination with the scanning-free GEXRF setup, XAS measurements can be realized by scanning the incident beam energy only and integrating afterwards for each incident energy the GEXRF profile or selecting the XRF intensity emitted at a specific emission angle. GEXRF measurements can also be realized with wavelength-dispersive setups^25–28 with the goal to combine this technique with chemical speciation methods requiring a high-energy resolution detector^76,77 like resonant X-ray emission spectroscopy (RXES) for example. This would present a promising approach for the (dynamic) investigation of the physical and chemical state of nanoparticles, if required during the synthesis of the nanoparticles, and the elemental distribution within the nanoparticles with respect to the substrate surface and allow straightforwardly for the investigation of size-dependent particle properties. By selecting the grazing emission angle to which the detection setup is sensitive, the grazing emission geometry is not only of advantage to optimize the detection efficiency and suppress background contributions from the substrate but it can also be profited from to optimize the sensitivity of the setup to a specific region of the volume of core–shell particles.

Acknowledgements

The authors thank the Swiss Light Source for provision of the beam time. The experiments were performed at the X05DA Optics beam line. Also the authors would like to thank Dr G. Tagliabue (ETH Zurich) for the Au on a Si chip sample.

References

1. C. de Mello Donegá, S. G. Hickey, S. F. Wuister, D. Vanmaekelbergh and A. Meijerink, J. Phys. Chem. B, 2003, 107, 489–496.
2. D. Xia, D. Li, Z. Ku, Y. Luo and S. R. J. Brueck, Langmuir, 2007, 23, 5377–5385.
3. O. Masala and R. Seshadri, Annu. Rev. Mater. Res., 2004, 34, 41–81.
4. J. Park, K. An, Y. Hwang, J.-G. Park, H.-J. Noh, J.-Y. Kim, J.-H. Park, N.-M. Hwang and T. Hyeon, Nat. Mater., 2004, 3, 891–895.
5. C. L. Cheung, A. Kurtz, H. Park and C. M. Lieber, J. Phys. Chem. B, 2002, 106, 2429–2433.
6. S. Helveg, C. Lopez-Cartes, J. Sehested, P. L. Hansen, B. S. Clausen, J. R. Rostrup-Nielsen, F. Abild-Pedersen and J. K. Norskov, Nature, 2004, 427, 426–429.
7. K. A. Dick, K. Deppert, L. S. Karlsson, L. R. Wallenberg, L. Samuelson and W. Seifert, Adv. Funct. Mater., 2005, 15, 1603–1610.
8. J. B. Hannon, S. Kodambaka, F. M. Ross and R. M. Tromp, Nature, 2006, 440, 69–71.
9. A. Bezryadin, C. Dekker and G. Schmid, Appl. Phys. Lett., 1997, 71, 1273–1275.
10. T. Morita and S. Lindsay, J. Am. Chem. Soc., 2007, 129, 7262–7263.
11. J. M. Mativetsky, S. A. Burke, S. Fostner and P. Grutter, Small, 2007, 3, 818–821.
12. C. B. Murray, C. R. Kagan and M. G. Bawendi, Annu. Rev. Mater. Res., 2000, 30, 545–610.
13. M. A. Reed, J. N. Randall, R. J. Aggarwal, R. J. Matyi, T. M. Moore and A. E. Wetsel, Phys. Rev. Lett., 1988, 60, 535–537.
14. M. Dahan, S. Lévi, C. Luccardini, P. Rostaing, B. Riveau and A. Triller, Science, 2003, 302, 442–445.
15. M. Howarth, W. Liu, S. Puthenveetil, Y. Zheng, L. F. Marshall, M. M. Schmidt, K. D. Wittrup, M. G. Bawendi and A. Y. Ting, Nat. Methods, 2008, 5, 397–399.
16. G. A. Bassett, Philos. Mag., 1958, 3, 1042.
17. J. M. Mativetsky, S. Fostner, S. A. Burke and P. Grutter, Phys. Rev. B: Condens. Matter, 2009, 80, 045430.
18. C. Barth and C. R. Henry, Phys. Rev. Lett., 2003, 91, 196102.
19. F. J. Giessibl, Science, 1995, 267, 68–71.
20. M. A. Lantz, H. J. Hug, R. Hoffmann, P. J. A. van Schendel, P. Kappenberger, S. Martin, A. Baratoff and H.-J. Güntherodt, Science, 2001, 291, 2580–2583.
21. S. A. Burke, J. M. Mativetsky, R. Hoffmann and P. Grütter, Phys. Rev. Lett., 2005, 94, 096102.
22. M. Goryl, F. Buatier de Mongeot, F. Krok, A. Vevecka-Priftaj and M. Szymonski, Phys. Rev. B: Condens. Matter, 2007, 76, 075423.
23. J. M. Mativetsky, S. Fostner, S. A. Burke and P. Grutter, Surf. Sci., 2008, 602, L21–L24.
24. O. H. Pakarinen, C. Barth, A. S. Foster and C. R. Henry, J. Appl. Phys., 2008, 103, 054313.
25. Y. Kayser, J. Szlachetko, D. Banaś, W. Cao, J.-Cl. Dousse, J. Hoszowska, A. Kubala-Kukuś and M. Pajek, Spectrochim. Acta, Part B, 2013, 88, 136–149.
26. M. Claes, P. de Bokx and R. Van Grieken, X-Ray Spectrom., 1999, 28, 224–229.
27. P. de Bokx, C. Kok, A. Bailleul, G. Wiener and H. Urbach, Spectrochim. Acta, Part B, 1997, 52, 829–840.
28. P. K. de Bokx and H. P. Urbach, Rev. Sci. Instrum., 1995, 66, 15–19.
29. W. Yu, M. D. Porosoff and J. G. Chen, Chem. Rev., 2012, 112, 5780–5817.
30. N. Alov, Inorg. Mater., 2011, 47, 1487–1499.
31. F. Meirer, A. Singh, P. Pianetta, G. Pepponi, C. Streli and T. Homma, TrAC, Trends Anal. Chem., 2010, 29, 479–496.
32. P. Wobrauschek, X-Ray Spectrom., 2007, 36, 289–300.
33. A. von Bohlen, Spectrochim. Acta, Part B, 2009, 64, 821–832.
34. R. S. Becker, J. A. Golovchenko and J. R. Patel, Phys. Rev. Lett., 1983, 50, 153–156.
35. T. Ashida and K. Tsuji, Spectrochim. Acta, Part B, 2014, 101, 200–203.
36. A. Kubala-Kukuś, D. Banaś, W. Cao, J.-Cl. Dousse, J. Hoszowska, Y. Kayser, M. Pajek, M. Salomé, J. Susini, J. Szlachetko and M. Szlachetko, Phys. Rev. B: Condens. Matter, 2009, 80, 113305.
37. J. Szlachetko, D. Banaś, A. Kubala-Kukuś, M. Pajek, W. Cao, J.-Cl. Dousse, J. Hoszowska, Y. Kayser, M. Szlachetko, M. Kavčič, M. Salome and J. Susini, J. Appl. Phys., 2009, 105, 086101.
38. Z. M. Spolnik, M. Claes, R. E. Van Grieken, P. K. de Bokx and H. P. Urbach, Spectrochim. Acta, Part B, 1999, 54, 1525–1537.
39. M. Claes, K. V. Dyck, H. Deelstra and R. Van Grieken, Spectrochim. Acta, Part B, 1999, 54, 1517–1524.
40. I. Koshelev, A. Paulikas, M. Beno, G. Jennings, J. Linton, M. Grimsditch, S. Uran and B. Veal, Oxid. Met., 2007, 68, 37–51.
41. M. L. Monaghan, T. Nigam, M. Houssa, S. D. Gendt, H. P. Urbach and P. K. de Bokx, Thin Solid Films, 2000, 359, 197–202.
42. T. Noma, K. Takada and A. Iida, X-Ray Spectrom., 1999, 28, 433–439.
43. G. Wiener, S. Kidd, C. Mutsaers, R. Wolters and P. de Bokx, Appl. Surf. Sci., 1998, 125, 129–136.
44. Y. Kayser, P. Hönicke, D. Banaś, J.-Cl. Dousse, J. Hoszowska, P. Jagodziński, A. Kubala-Kukuś, S. H. Nowak and M. Pajek, J. Anal. At. Spectrom., 2015, 30, 1086–1099.
45. P. Hönicke, Y. Kayser, B. Beckhoff, M. Müller, J.-Cl. Dousse, J. Hoszowska and S. H. Nowak, J. Anal. At. Spectrom., 2012, 27, 1432–1438.
46. K. Tsuji, Z. Spolnik, K. Wagatsuma, R. Van Grieken and R. D. Vis, Anal. Chem., 1999, 71, 5033–5036.
47. K. Tsuji, Z. Spolnik, K. Wagatsuma, J. Zhang and R. E. V. Grieken, Spectrochim. Acta, Part B, 1999, 54, 1243–1251.
48. M. Brücher, M. Chakif, E. L. Gurevich and R. Hergenröder, Spectrochim. Acta, Part B, 2014, 98, 60–64.
49. M. Menzel and U. E. A. Fittschen, Anal. Chem., 2014, 86, 3053–3059.
50. S. Motellier, S. Derrough, D. Locatelli, M. Amdaoud and K. Lhaute, Spectrochim. Acta, Part B, 2013, 88, 1–9.
51. M. K. Tiwari, K. J. S. Sawhney, T.-L. Lee, S. G. Alcock and G. S. Lodha, Phys. Rev. B: Condens. Matter, 2009, 80, 035434.
52. A. von Bohlen, M. Brücher, B. Holland, R. Wagner and R. Hergenröder, Spectrochim. Acta, Part B, 2010, 65, 409–414.
53. K. Tsuji, Spectrochim. Acta, Part B, 2005, 60, 1381–1391.
54. K. Tsuji, M. Huisman, Z. Spolnik, K. Wagatsuma, Y. Mori, R. Van Grieken and R. D. Vis, Spectrochim. Acta, Part B, 2000, 55, 1009–1016.
55. Y. Kayser, J. Szlachetko and J. Sá, Rev. Sci. Instrum., 2013, 84, 123102.
56. F. Reinhardt, J. Osan, S. Torok, A. E. Pap, M. Kolbe and B. Beckhoff, J. Anal. At. Spectrom., 2012, 27, 248–255.
57. A. Kuczumow, M. Claes, M. Schmeling, R. Van Grieken and S. de Gendt, J. Anal. At. Spectrom., 2000, 15, 415–421.
58. D. Hellin, J. Rip, V. Geens, T. Delande, T. Conard, S. De Gendt and C. Vinckier, J. Anal. At. Spectrom., 2005, 20, 652–658.
59. R. Klockenkämper and A. von Bohlen, Spectrochim. Acta, Part B, 1989, 44, 461–469.
60. U. Flechsig, A. Jaggi, S. Spielmann, H. Padmore and A. MacDowell, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 609, 281–285.
61. T. Lohmueller, E. Bock and J. P. Spatz, Adv. Mater., 2008, 20, 2297–2302.
62. J. Sá, G. Tagliabue, P. Friedli, J. Szlachetko, M. H. Rittmann-Frank, F. G. Santomauro, C. J. Milne and H. Sigg, Energy Environ. Sci., 2013, 6, 3584–3588.
63. C. Broennimann, E. F. Eikenberry, B. Henrich, R. Horisberger, G. Huelsen, E. Pohl, B. Schmitt, C. Schulze-Briese, M. Suzuki, T. Tomizaki, H. Toyokawa and A. Wagner, J. Synchrotron Radiat., 2006, 13, 120–130.
64. L. Storm and H. I. Israel, At. Data Nucl. Data Tables, 1970, 7, 565–681.
65. H. P. Urbach and P. K. de Bokx, Phys. Rev. B: Condens. Matter, 1996, 53, 3752–3763.
66. H. P. Urbach and P. K. de Bokx, Phys. Rev. B: Condens. Matter, 2001, 63, 085408.
67. A. Bekshaev and R. Van Grieken, Spectrochim. Acta, Part B, 2001, 56, 503–515.
68. D. K. G. de Boer, Phys. Rev. B: Condens. Matter, 1996, 53, 6048–6064.
69. A. Bekshaev and R. Van Grieken, Spectrochim. Acta, Part B, 2002, 57, 865–882.
70. A. Bekshaev, J. de Hoog and R. Van Grieken, Spectrochim. Acta, Part B, 2001, 56, 2385–2395.
71. U. E. A. Fittschen, M. Menzel, O. Scharf, M. Radtke, U. Reinholz, G. Buzanich, V. M. Lopez, K. McIntosh, C. Streli and G. J. Havrilla, Spectrochim. Acta, Part B, 2014, 99, 179–184.
72. F. Reinhardt, S. H. Nowak, B. Beckhoff, J.-Cl. Dousse and M. Schoengen, J. Anal. At. Spectrom., 2014, 29, 1778–1784.
73. S. H. Nowak, D. Banaś, W. Błachucki, J.-Cl. Dousse, W. Cao, P. Hönicke, J. Hoszowska, Ł. Jabłoński, Y. Kayser, A. Kubala-Kukuś, M. Pajek, F. Reinhardt, A. V. Savu and J. Szlachetko, Spectrochim. Acta, Part B, 2014, 98, 65–75.
74. M. Brücher, A. von Bohlen and R. Hergenröder, Spectrochim. Acta, Part B, 2012, 71–72, 62–69.
75. Z. Yin, Y. Zhang, K. Chen, J. Li, W. Li, P. Tang, H. Zhao, Q. Zhu, X. Bao and D. Ma, Sci. Rep., 2014, 4, 4288.
76. J. Sá, High-Resolution Xas/Xes: Analyzing Electronic Structures of Catalysts, CRC Press, 2014.
77. P. Glatzel and U. Bergmann, Coord. Chem. Rev., 2005, 249, 65–95.

---