Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
High performance multi-core iron oxide nanoparticles for magnetic hyperthermia: microwave synthesis, and the role of core-to-core interactions†
C.
Blanco-Andujar
 abc,
D.
Ortega
abc,
D.
Ortega
 cde,
P.
Southern
bc,
Q. A.
Pankhurst‡
*bc and
N. T. K.
Thanh‡
*ab
cde,
P.
Southern
bc,
Q. A.
Pankhurst‡
*bc and
N. T. K.
Thanh‡
*ab
aDepartment of Physics and Astronomy, University College London, Gower Street, London, WC1E 6BT, UK. E-mail: ntk.thanh@ucl.ac.uk; Fax: +44 (0)207 670 2920; Tel: +44 (0)207 491 6509
bUCL Healthcare Biomagnetics Laboratory, 21 Albemarle Street, London, W1S 4BS, UK. E-mail: q.pankhurst@ucl.ac.uk; Tel: +44 (0)20 3108 1124
cInstitute of Biomedical Engineering, University College London, Gower Street, London, WC1E 6BT, UK
dInstituto Madrileño de Estudios Avanzados en Nanociencia (IMDEA-Nanociencia), Cantoblanco, 28049, Madrid, Spain
eCentro Nacional de Biotecnología (CNB-CSIC) – IMDEA Nanociencia Associated Unit “Unidad de Nanobiotecnología”, Cantoblanco, 28049, Madrid, Spain
First published on 3rd December 2014
Abstract
The adoption of magnetic hyperthermia as either a stand-alone or adjunct therapy for cancer is still far from being optimised due to the variable performance found in many iron oxide nanoparticle systems, including commercially available formulations. Herein, we present a reproducible and potentially scalable microwave-based method to make stable citric acid coated multi-core iron oxide nanoparticles, with exceptional magnetic heating parameters, viz. intrinsic loss parameters (ILPs) of up to 4.1 nH m2 kg−1, 35% better than the best commercial equivalents. We also probe the core-to-core magnetic interactions in the particles via remanence-derived Henkel and ΔM plots. These reveal a monotonic dependence of the ILP on the magnetic interaction field Hint, and show that the interactions are demagnetising in nature, and act to hinder the magnetic heating mechanism.
Introduction
Hyperthermia therapy, or the application of supra-normal body temperatures as a direct or adjunct treatment for cancer, has been studied for decades due to the relatively high thermal sensitivity of malignant cells compared to healthy tissue.1,2 Heat can be delivered by a variety of techniques such as radiofrequency, microwave radiation, regional perfusion therapy, laser ablation or magnetic hyperthermia.3–5 The latter is an especially attractive approach due to the possibility of using targeted nanoparticles for specific accumulation in cancer tissues.6 Recent developments indicate that this technique could improve the therapeutic outcome for cancer patients, either as a stand-alone treatment or in conjunction with chemotherapy and/or radiotherapy.7,8 This has driven extensive research in the field, as exemplified by nearly 2000 reports§ and a growing number of reviews7,9–11 published in the last 5 years. Nonetheless, there is still doubt about its effectiveness, as the latest clinical trials have presented uncertain results.12Magnetic hyperthermia relies upon the fact that magnetic nanoparticles under the influence of an AC magnetic field generate heat, with this heat being affected by the concentration of nanoparticles, the strength of the magnetic field, the driving frequency and the heat capacity of the media, among other factors.6,7 The current development of magnetic hyperthermia is heavily focused on two aspects, namely the composition of the nanoparticles (where reproducibility and scalability are consistently found to be hard to achieve), and the instrumentation needed for applying external fields to generate the magnetic hyperthermia, and for measuring the resultant heat deposition in tissues. Regarding the instrumentation, the vast majority of the devices are purpose-built designs intended for in vitro testing, or at most pre-clinical in vivo testing. Clinical scale appliances are very much the exception to date, and are being developed by companies such as Magforce GmbH in Berlin13,14 and Resonant Circuits Ltd in London.15
The synthesis of magnetic nanoparticles for magnetic hyperthermia has been extensively studied with a view to improving their performance as heat sources. Their performance is usually characterised via the specific absorption rate (SAR) or intrinsic loss parameter (ILP) metrics,16 both of which describe the amount of energy absorbed/evolved per unit mass under the influence of an AC magnetic field. Reported materials with high SAR/ILP metrics encompass many different systems, including lanthanum manganites, mixed-cation ferrites, and core–shell or metallic nanoparticles.17–20 However, the undetermined or potential toxicity of many nanoparticle systems, as well as production scalability issues, have restricted their use in clinical trials.
Instead, materials research has been focused on the ferrimagnetic iron oxides maghemite (γ-Fe2O3) and magnetite (Fe3O4) because to their safe and well-known metabolic pathway in the human body, and their history of successful clinical use as MRI contrast agents. The main issue to be addressed here, rather than the discovery of new formulations, is to build on the existing knowledge and overcome the current practical limitation of their synthesis, in particular the reproducibility and scalability of the preparation methods. Unfortunately, to date many of the published and patented protocols have failed to be translated into an industrial setting, ready for large-scale production.
We report here on a solution to this problem, viz. a reproducible microwave-based method with a potential for scaling up synthesis of iron oxide nanoparticles (IONPs) with a high SAR/ILP design parameter. The use of a microwave reactor overcomes a critical confounding issue in the preparation of IONPs: the adsorption of precipitating agents (e.g. sodium bicarbonate) onto the surface of the intermediate oxyhydroxide species.21 Microwave radiation offers an easily controlled source of heating while also enabling some interesting specific effects such as selective heating,22–29 where, in solution, the surfaces of the nanoparticles absorb more microwave radiation than the core, leading to a local overheating that changes the particle surface energy and reactivity.30,31
This characteristic enables an effective and controllable exchange between undesirable surface-adsorbed species and other moieties deliberately added to the reaction medium, like coating agents. A wide range of coating molecules have been used to stabilize nanoparticles and ensure biocompatibility.32 Among these, we have found that citric acid (CA) possesses an optimal balance between biocompatibility, cellular transport and internalisation properties, as attested by its wide commercial availability and the many studies that have used it as a coating agent for biomedical applications.33–36 The free carboxyl groups provide stability and high surface negative charge density, which offers an excellent platform for further functionalisation, and improved cellular uptake.37,38
In this work we report on an investigation of the effect of the synthesis conditions on the properties of IONPs obtained by a coprecipitation method in a microwave reactor. As well as the beneficial effects of the microwave route with regard to the citric acid coatings that were produced, we also report on an unexpected controllability in the number and size of the individual magnetic nanocrystallites (‘cores’) that are present within the multi-core system. Such structures are common in magnetic nanoparticles,39,40 but hitherto there have been no reports on controllable routes to the synthesis of multi-core IONPs. Furthermore, we report on a detailed study of the magnetic interactions in the products – between cores within a multi-core structure, and between multi-core particles – and the influence that has on the magnetic heating performance. The optimal parameters for suitable products are thereby defined.
Experimental
Chemicals
Ferric chloride hexahydrate (FeCl3·6H2O, >99%), ferrous chloride tetrahydrate (FeCl2·4H2O, 99%), sodium carbonate (Na2CO3, 99%) and citric acid monohydrate (HOC(COOH)(CH2COOH)2·H2O, >99%) were obtained from Sigma Aldrich Ltd, UK, and were used as received.Microwave assisted coprecipitation of citric acid-coated iron oxide with sodium carbonate
Citric acid-coated iron oxide nanoparticles (CA-IONPs) were synthesised by coprecipitation of ferric and ferrous chloride salts with sodium carbonate and post-precipitation addition of a citric acid solution, with the aid of a SP-Discovery Microwave (CEM, USA). Briefly, a solution of FeCl2·4H2O (0.02 M) and FeCl3·6H2O (0.04 M) was transferred into a vial and sealed with a pressure cap. The solution was heated to 60 °C (50 or 300 W) and sodium carbonate aqueous solution (1 M) was added with a syringe pump (2 ml min−1) (WPI, UK). The solution was kept at this temperature for 10 or 60 min and then citric acid solution (refer to Table 1, 1 ml ddH2O) was added. The solution was maintained at 60 °C (50 or 300 W) for 10 or 60 min. The obtained nanoparticles were washed by magnetic separation and redispersed in ddH2O for further characterisation.| Sample | Step time (min) | MW power (W) | CA (mmol) | D TEM ± σTEM (nm) | D H (nm) | PDI | D XRD (nm) |
D
TEM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DH DH |
ILP (nH m2 kg−1) | N |
|---|---|---|---|---|---|---|---|---|---|---|
| CA-ioA | 60 | 50 | 1 | 13.1 ± 2.5 | 123.6 ± 0.4 | 0.19 | 13.2 | 0.10 | 1.8 | 520 |
| CA-ioB | 60 | 50 | 2 | 15.1 ± 3.5 | 59.2 ± 0.4 | 0.21 | 13.3 | 0.26 | 3.2 | 35 |
| CA-ioC | 60 | 300 | 1 | 13.2 ± 3.1 | 141.0 ± 1.0 | 0.20 | 12.7 | 0.10 | 1.9 | 730 |
| CA-ioD | 60 | 300 | 2 | 13.5 ± 3.5 | 49.5 ± 0.4 | 0.19 | 14.3 | 0.27 | 3.3 | 30 |
| CA-ioE | 10 | 50 | 1 | 14.0 ± 4.3 | 96.8 ± 0.8 | 0.20 | 13.7 | 0.14 | 2.7 | 200 |
| CA-ioF | 10 | 50 | 2 | 15.7 ± 3.3 | 58.7 ± 0.7 | 0.19 | 14.2 | 0.27 | 3.7 | 30 |
| CA-ioG | 10 | 300 | 1 | 13.7 ± 3.2 | 88.7 ± 0.8 | 0.21 | 12.5 | 0.15 | 2.4 | 160 |
| CA-ioH | 10 | 300 | 2 | 17.1 ± 3.2 | 65.8 ± 0.5 | 0.23 | 14.7 | 0.26 | 4.1 | 35 |
Characterisation of citric-acid coated iron oxide nanoparticles
The morphology, particle size and size distribution of IONPs were examined with a JEOL JEM 1200-EX transmission electron microscope (TEM) operated at an acceleration voltage of 120 kV. Samples were prepared by dropping the aqueous dispersion onto a carbon-coated copper grid and air-dried. The hydrodynamic diameter of the IONPs was measured by dynamic light scattering (DLS) using a Zetasizer nano (Malvern Instruments Ltd, UK). The crystal structure of IONPs was investigated with a PanAlytical X-ray diffractometer, using CoKα radiation (λ = 1.789010 Å). The diffraction patterns were collected from 2θ = 20° to 100°. Samples were prepared by pressing dried powders on a zero background silicon wafer. Field-dependent magnetisation, isothermal remanent magnetisation (IRM) and direct current demagnetisation (DCD) measurements of IONPs were carried out in a Quantum Design hybrid superconducting quantum interference device-vibrating sample magnetometer (SQUID-VSM) at 300 and 5 K, with applied fields up to 7 T. 57Fe Mössbauer spectra were collected from freeze-dried samples mixed with boron nitride and measured in transmission mode in a commercial spectrometer (SEE Co Inc, USA) working in constant acceleration mode, calibrated relative to metallic α-Fe at room temperature (RT).Magnetic heating measurements
The heat dissipation of the nanoparticle suspensions was evaluated with a magnetic alternating current hyperthermia ‘MACH’ system (Resonant Circuits Ltd, UK) operating at a frequency f = 950 kHz and a field amplitude H = 10.5 kA m−1. The generated heat was characterised with the ILP parameter, as defined by Kallumadil et al.,16 in preference to the alternatively used SAR, which is properly used only in a clinical context to refer to power dissipation per unit mass of tissue. Furthermore the SAR parameter is not an intrinsic property of a given system, as it is dependent on the field amplitude and frequency.41 Using the ILP parameter (eqn (1)), which is a constant in the clinically relevant region where the power generated by magnetic hyperthermia scales linearly with f and quadratically with H,42 allows comparisons to be made between measurements carried out under different f and H conditions.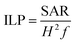 | (1) |
The obtained temperature profiles were fitted to the Box-Lucas model T(t) = A(1 − e−Bt),43 where A is the saturation temperature and B is a parameter related to the curvature of the heating curve. The product A × B at t = 0 is the initial heat rise rate, which is equivalent to the ΔT/Δt ratio used for calculating SAR values.
Study of magnetic interparticle interactions using Henkel plots
Fifty years ago, Henkel44 showed that it is possible to characterise magnetic interparticle interactions from a series of static magnetic measurements (IRM and DCD), in what have come to be known as Henkel plots. This approach is based on the Wohlfarth relationship as derived from the Stoner–Wohlfarth model for a system of non-interacting, single domain particles.45 According to the model, the Henkel plot of a non-interacting system is a straight line, and any deviations from that line are associated with interparticle interactions.A Henkel plot is obtained by first measuring the IRM curve, Mr(H), followed by the DCD curve, Md(H), and comparing the two. Initially the sample is demagnetised, with Mr(0) = 0. The IRM curve is obtained by sequentially cycling the applied field from zero to +H and back to zero (for each Mr(H) measurement), until a saturated state is reached at H = Hmax, for which increasing H no longer changes the measured Mr(H). The DCD curve is then obtained by reversing the direction of the applied field, and measuring the remanent magnetisation after sequential cycling of the field from zero to −H and back to zero, until the reverse-saturated state is reached at H = −Hmax. In a system of non-interacting magnetic particles, the reduced IRM and DCD curves follow the Wohlfarth relationship:
| md(H) = 1 − 2mr(H), | (2) |
| ΔM(H) = md(H) − [1 − 2md(H)]. | (3) |
ΔM(H) is referred to as the ‘delta M’ of the system, and is reported as a ‘delta M plot’ of ΔM versus H.46–48 The sign and magnitude of ΔM is determined by the nature and degree of the magnetic interactions. In particular, ΔM < 0 indicates demagnetising or ‘inhibiting’ interactions, while ΔM > 0 indicates magnetising or ‘enhancing’ interactions.49
Further information may be obtained by differentiating the mr and md curves with respect to H to find the energy barrier distributions for the IRM and DCD processes respectively. This then leads to an estimate of the mean interaction field in the system,48,49 which has the magnitude:
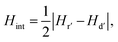 | (4) |
Results and discussion
Synthesis and structural characterisation
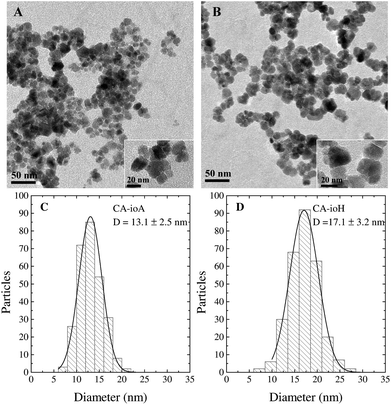
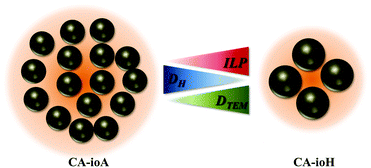
The synthesis of IONPs was carried out by a coprecipitation method with sodium carbonate in a microwave reactor. The reproducibility of the synthetic conditions was investigated to assess its feasibility towards mass-production. The sources of variation that could affect the reproducibility of the results were analysed and the rate of injection of sodium carbonate was identified as the “Achilles heel” of the reaction, as it is subject to human error. To overcome this limitation, a syringe pump was used to provide reproducible injection conditions. The reproducibility of this method is discussed in the ESI (Fig. S1–S4 and Table S1†).Sample details and experimental conditions used are listed in Table 1. The CA coated particles have a multi-core structure, wherein the spheroidal nanocrystallite cores, as studied by TEM, have an average core diameter (DTEM) ranging from ca. 13 nm to 17 nm for samples CA-ioA and CA-ioH, respectively (Fig. 1 and S5, ESI†). Increasing concentrations of citrate ions in solution produce a smaller hydrodynamic diameter (DH) with polydispersity index (PDI) of ca. 0.2, which indicate a well-controlled synthesis route (Table 1 and Fig. S6, ESI†). At the same time, DH of the particles varies across the series, ranging from ca. 50 nm to 140 nm for samples CA-ioC and CA-ioD, respectively. Assuming, for illustrative purposes, that the multi-core structure is that of a loose random packing of the constituent core particles, with a 60% v/v content,50 this would correspond, for example, to ca. N = 520 cores in sample CA-ioA, compared to ca. N = 35 cores in sample CA-ioH.
The capacity to produce such a wide range of multi-core systems via a single synthetic pathway is of great interest. The synthesis comprises coprecipitation of the individual core particle followed by citrate addition to yield a stable multi-core dispersion. The latter involves the partial dissolution of the core particles, and re-equilibration of the system. Specifically, the presence of citrate ions leads to the partial removal of Fe(II) from the surfaces of the core particles, which prompts the onset of a dissolution–recrystallisation process51 in which the released Fe(II) ions are chelated by the citrate ions52 and are reincorporated into the nanoparticles. This effect is enhanced by the microwave radiation due to local overheating and enhanced surface reactivity.22
The clearest trends in Table 1 are seen in the N parameter. At 1 mmol citric acid concentration, N ranges from 160–730, while at 2 mmol the range is much tighter, at 30–35. Changing the reaction time has a significant effect on the 1 mmol CA samples, with the slower reactions (60 min per step, 120 min total) leading to N = 520 and 730, and the faster reactions (10 min per step, 20 min total) yielding N = 160 and 200. Varying the microwave power from 50 to 300 W does not have a major effect in terms of the parameters listed in Table 1.
Room temperature XRD patterns from the complete set of freeze-dried samples primarily showed a single phase corresponding to an iron oxide with an inverse spinel structure (Fig. S7 and Table S2, ESI†). However, even with Rietveld analysis it was not possible to unambiguously distinguish whether the patterns corresponded to maghemite (γ-Fe2O3) or magnetite (Fe3O4) or a mixture of both, due to the similarity between the diffraction profiles of these structures. In addition, peak broadening due to the small core particle size throughout the series further complicated the phase characterisation.
Room temperature 57Fe Mössbauer measurements of the CA-ioA and CA-ioH samples were more conclusive, and were consistent with both samples comprising a mixture of magnetite and maghemite particles (see Fig. S8, ESI†). This was evidenced by a mean isomer shift (spectral centroid) of 0.40 ± 0.01 mm s−1 in both spectra, compared to the 0.32 mm s−1 of pure maghemite and 0.53 mm s−1 of pure magnetite. Recent work has established that an approximately linear correlation exists between the mean isomer shift and the magnetite-to-maghemite ratio,53 which for CA-ioA and CA-ioH indicates that around 25–35 wt% of the iron oxide is magnetite, with the remainder being maghemite.
Magnetic characterisation
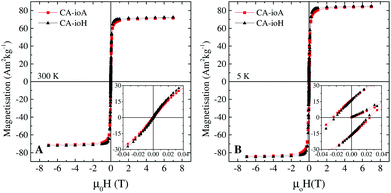
The magnetic properties of the samples are only marginally affected by changes in reaction conditions (Fig. S9, ESI†). Anhysteretic M(H) curves, and therefore superparamagnetic behaviour, were observed at 300 K (Fig. 2 and Table S3, ESI†), with an average saturation magnetisation of MS ≈ 72 Am2 kg−1. At 5 K the M(H) curves were hysteretic, having entered the magnetically blocked state (Fig. 2 and Table S3, ESI†).Magnetic heating experiments yielded the ILP values listed in Table 1, which ranged from a minimum of 1.8 nH m2 kg−1 for CA-ioA up to a maximum of 4.1 nH m2 kg−1 for CA-ioH. The ILP values increased approximately monotonically both with increasing DTEM and with decreasing DH (see Fig. 3), or, equivalently, with decreasing N (Table 1). These trends are illustrated in Scheme 1. It is also notable that half of the samples have ILPs in the range 3.2 to 4.1 nH m2 kg−1. These are unusually high values, higher than that of the best available commercial materials (see Table 2), and approaching the benchmark figures of 5.6 nH m2 kg−1 and 6.1 nH m2 kg−1 reported for 19 nm sized iron oxide nanocubes,54 and multi-core tiopronin-coated IONPs (with DXRD = 9 nm and DH = 135 nm).55
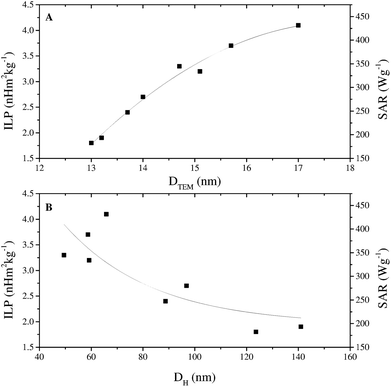 | ||
| Fig. 3 (A) ILP versus core size DTEM and (B) ILP versus hydrodynamic diameter DH for the citric acid coated iron oxide nanoparticle series listed in Table 1. SAR values are also indicated for reference. Solid lines are a guide to the eye. | ||
| Particle type | Coating | H (kA m−1) | f (kHz) | SAR (W g−1) | ILP (nH m2 kg−1) |
|---|---|---|---|---|---|
| Ferucarbotran | Carboxydextran | 5.7 | 900 | 90 | 3.116 |
| FluidMag-D | Starch | 5.7 | 900 | 80 | 2.716 |
| FluidMag-CT | Citric acid | 12.0 | 950 | 135 | 1.0 |
| Nanomag-D-spio | Carboxyl | 5.7 | 900 | 90 | 3.116 |
| CA-ioA | Citric acid | 10.5 | 950 | 190 | 1.8 |
| CA-ioH | Citric acid | 10.5 | 950 | 430 | 4.1 |
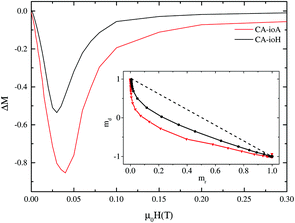
Magnetic interactions within the IONPs were explored via Henkel and ΔM plot measurements (Fig. 4) recorded at 5 K, i.e. at a temperature for which the samples were in the magnetically blocked, rather than the superparamagnetic state. Systematic deviations from the linear Wohlfarth relationship were found for all the samples. This is illustrated in Fig. 5, with monotonic correlations between the ILP and both the maximal deviation from the ΔM = 0 baseline, and the interaction field Hint. These data show conclusively that better magnetic heating is associated with less core-to-core magnetic interaction.
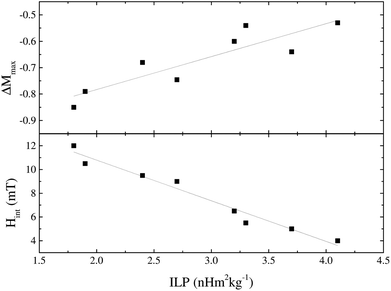 | ||
| Fig. 5 Parameters derived from the ΔM plots, ΔMmax and Hint, plotted against ILP, for the CA-io series. | ||
At first sight, this may seem a rather unexpected result. One might expect that stronger interparticle interactions would lead to an increased effective magnetic anisotropy energy barrier in the system, and therefore more hysteretic power losses, and more magnetic heating. However, this depends on whether the interactions help or hinder the magnetic heating process. The observed negative ΔM values indicate that demagnetising, as opposed to magnetising, interactions are in action.49 Such effects, which are typical of dipole–dipole interactions, tend to hinder the collective transition of an ensemble of magnetic entities from one state to another.
It is clear therefore that within these multi-core IONPs, the magnetic interactions, alongside the number, size and spatial arrangement of the cores, directly affect the final heating properties. Samples synthesised under lower concentrations of citric acid and longer reaction times have more strongly interacting multi-core interiors, but these interactions are demagnetising, and adversely affect the magnetic heating property. Conversely, higher concentrations of citric acid and shorter reaction times yield multi-core particles comprising a much smaller number of relatively large diameter cores, with relatively weak core-to-core magnetic interactions. These samples exhibit the highest ILP values.
Conclusions
The microwave-based synthesis of citric acid coated iron oxide magnetic nanoparticles presented here provides an efficient, controllable, and easily scalable way to produce multi-core materials for magnetic hyperthermia applications.Structurally, the core diameters and the hydrodynamic diameter of the multi-core particle as a whole have been found to be the main factors determining magnetic heating performance, with best results obtained for large cores (DTEM = 17 nm) in relatively small ensembles (DH = 65 nm). Magnetically, it was determined that demagnetising core-to-core interactions were present in all samples, to a lesser or greater effect. The best heating materials were those that had the least inter-core interaction, which is understood to be a result of the limiting effect of such magnetic interaction on the collective behaviour that underpins the magnetic heating effect. This new insight offers a prospect of further refinement of materials synthesis routes, including the microwave-assisted route discussed here, to achieve even better magnetic hyperthermia products.
Even without such refinement, the particles reported here had impressive heating metrics, with intrinsic loss parameters of order 3–4 nH m2 kg−1, placing them comfortably in the best 5% of such materials reported to date.16 Moreover, the use of these particles is not limited to magnetic hyperthermia as they have shown positive results for different applications such as MRI contrast agents for tracking of pancreatic islet transplants,56 and for the separation and detection of cholera bacteria from water samples.57
Lastly, it is notable that the core-to-core magnetic interactions found here are relatively weak (Hint ranging from 12 mT in CA-ioA to 4 mT in CA-ioH) compared to other systems, e.g. Hint ≈ 38 mT in core–shell iron/iron-oxide nanoparticles,48 and Hint ≈ 120 mT in nanocrystalline barium ferrites.49 This raises the possibility that an important future design strategy for producing new materials for magnetic hyperthermia might best be directed towards minimising the demagnetising interactions between cores, or, even more intriguingly, attempting to find ways to introduce positive, magnetising interactions, into multi-core nanoparticles. We are not aware of any such materials having yet been reported, and it is perhaps an interesting route for future research.
Acknowledgements
Nguyễn T. K. Thanh thanks the Royal Society for her University Research Fellowship. Cristina Blanco-Andujar thanks University College London and The Royal Institution of Great Britain for her PhD studentship. Daniel Ortega is grateful for the support received through the AMAROUT-II Marie Curie Action under the European Commission's FP7 PEOPLE-COFUND program and a Research Fund grant from the Royal Society of Chemistry.Notes and references
- A. Jordan, P. Wust, R. Scholz, B. Tesche, H. Fähling, T. Mitrovics, T. Vogl, J. Cervós-navarro and R. Felix, Int. J. Hyperthermia, 1996, 12, 705–722 CrossRef CAS.
- O. S. Nielsen, M. Horsman and J. Overgaard, Eur. J. Cancer, 2001, 37, 1587–1589 CrossRef CAS.
- A. Carpentier, R. J. McNichols, R. J. Stafford, J.-P. Guichard, D. Reizine, S. Delaloge, E. Vicaut, D. Payen, A. Gowda and B. George, Lasers Surg. Med., 2011, 43, 943–950 CrossRef PubMed.
- P. K. Sneed, P. R. Stauffer, M. W. McDermott, C. J. Diederich, K. R. Lamborn, M. D. Prados, S. Chang, K. A. Weaver, L. Spry, M. K. Malec, S. A. Lamb, B. Voss, R. L. Davis, W. M. Wara, D. A. Larson, T. L. Phillips and P. H. Gutin, Int. J. Radiat. Oncol., Biol., Phys., 1998, 40, 287–295 CrossRef CAS.
- W. Lee Titsworth, G. J. A. Murad, B. L. Hoh and M. Rahman, Anticancer Res., 2014, 34, 565–574 Search PubMed.
- W. Andrä and H. Nowak, Magnetism in medicine: a handbook, John Wiley & Sons, 2007 Search PubMed.
- D. Ortega and Q. A. Pankhurst, in Nanoscience: Volume 1: Nanostructures through Chemistry, ed. P. O'Brien, The Royal Society of Chemistry, Cambridge, 2012, vol. 1, pp. 60–88 Search PubMed.
- A. Hervault and N. T. K. Thanh, Nanoscale, 2014, 6, 11553–11573 RSC.
- I. Hilger, Int. J. Hyperthermia, 2013, 29, 828–834 CrossRef PubMed.
- S. Dutz and R. Hergt, Int. J. Hyperthermia, 2013, 29, 790–800 CrossRef PubMed.
- I. Andreu and E. Natividad, Int. J. Hyperthermia, 2013, 29, 739–751 CrossRef PubMed.
- S. Roussakow, Conf. Paper Med., 2013, 31 Search PubMed.
- U. Gneveckow, A. Jordan, R. Scholz, V. Bruss, N. Waldofner, J. Ricke, A. Feussner, B. Hildebrandt, B. Rau and P. Wust, Med. Phys., 2004, 31, 1444–1451 CrossRef.
- M. Johannsen, B. Thiesen, P. Wust and A. Jordan, Int. J. Hyperthermia, 2010, 26, 790–795 CrossRef PubMed.
- Resonant Circuits Ltd., London., http://www.resonantcircuits.com.
- M. Kallumadil, M. Tada, T. Nakagawa, M. Abe, P. Southern and Q. A. Pankhurst, J. Magn. Magn. Mater., 2009, 321, 3650–3651 CrossRef CAS PubMed.
- A. u. Rashid, A. Ahmed, S. N. Ahmad, S. A. Shaheen and S. Manzoor, J. Magn. Magn. Mater., 2013, 347, 39–44 CrossRef PubMed.
- C. Binns, P. Prieto, S. Baker, P. Howes, R. Dondi, G. Burley, L. Lari, R. Kröger, A. Pratt, S. Aktas and J. Mellon, J. Nanopart. Res., 2012, 14, 1–16 CrossRef.
- J. H. Lee, J. T. Jang, J. S. Choi, S. H. Moon, S. H. Noh, J. W. Kim, J. G. Kim, I. S. Kim, K. I. Park and J. Cheon, Nat. Nanotechnol., 2011, 6, 418–422 CrossRef CAS PubMed.
- B. Mehdaoui, A. Meffre, J. Carrey, S. Lachaize, L.-M. Lacroix, M. Gougeon, B. Chaudret and M. Respaud, Adv. Funct. Mater., 2011, 21, 4573–4581 CrossRef CAS.
- C. Blanco-Andujar, D. Ortega, Q. A. Pankhurst and N. T. K. Thanh, J. Mater. Chem., 2012, 22, 12498–12506 RSC.
- M. Baghbanzadeh, L. Carbone, P. D. Cozzoli and C. O. Kappe, Angew. Chem., Int. Ed., 2011, 50, 11312–11359 CrossRef CAS PubMed.
- R. Y. Hong, T. T. Pan and H. Z. Li, J. Magn. Magn. Mater., 2006, 303, 60–68 CrossRef CAS PubMed.
- V. Sreeja and P. A. Joy, Mater. Res. Bull., 2007, 42, 1570–1576 CrossRef CAS PubMed.
- W.-W. Wang, Y.-J. Zhu and M.-L. Ruan, J. Nanopart. Res., 2007, 9, 419–426 CrossRef CAS.
- C. Chen, Q. Long, X. Li and J. Xu, J. Bioact. Compat. Polym., 2008, 23, 490–500 CrossRef CAS PubMed.
- F. Y. Jiang, C. M. Wang, Y. Fu and R. C. Liu, J. Alloys Compd., 2010, 503, L31–L33 CrossRef CAS PubMed.
- S. Bhattacharya, D. Mallik and S. Nayar, IEEE Trans. Magn., 2011, 47, 1647–1652 CrossRef CAS.
- S. H. Liu, F. Lu, X. D. Jia, F. F. Cheng, L. P. Jiang and J. J. Zhu, CrystEngComm, 2011, 13, 2425–2429 RSC.
- S. J. Vallee and W. C. Conner, J. Phys. Chem. B, 2006, 110, 15459–15470 CrossRef CAS PubMed.
- O. Pascu, E. Carenza, M. Gich, S. Estradé, F. Peiró, G. Herranz and A. Roig, J. Phys. Chem. C, 2012, 116, 15108–15116 CAS.
- A. V. Bychkova, O. N. Sorokina, M. A. Rosenfeld and A. L. Kovarski, Russ. Chem. Rev., 2012, 81, 1026 CrossRef PubMed.
- A. Jedlovszky-Hajdú, F. B. Bombelli, M. P. Monopoli, E. Tombácz and K. A. Dawson, Langmuir, 2012, 28, 14983–14991 CrossRef PubMed.
- S. Srivastava, R. Awasthi, N. S. Gajbhiye, V. Agarwal, A. Singh, A. Yadav and R. K. Gupta, J. Colloid Interface Sci., 2011, 359, 104–111 CrossRef CAS PubMed.
- M. A. J. Hodenius, T. Niendorf, G. A. Krombach, W. Richtering, T. Eckert, H. Lueken, M. Speldrich, R. W. Gunther, M. Baumann, S. J. H. Soenen, M. De Cuyper and T. Schmitz-Rode, J. Nanosci. Nanotechnol., 2008, 8, 2399–2409 CrossRef CAS PubMed.
- B. Behdadfar, A. Kermanpur, H. Sadeghi-Aliabadi, M. D. Morales and M. Mozaffari, J. Solid State Chem., 2012, 187, 20–26 CrossRef CAS PubMed.
- Q. Bu, G. Yan, P. Deng, F. Peng, H. Lin, Y. Xu, Z. Cao, T. Zhou, A. Xue, Y. Wang, X. Cen and Y. L. Zhao, Nanotechnology, 2010, 21, 125105 CrossRef PubMed.
- E. Frohlich, Int. J. Nanomed., 2012, 7, 5577–5591 CrossRef PubMed.
- L. Gutiérrez, R. Costo, C. Grüttner, F. Westphal, N. Gehrke, D. Heinke, A. Fornara, Q. A. Pankhurst, C. Johansson, S. Veintemillas-Verdaguer and M. P. Morales, Dalton Trans., 2014 Search PubMed , unpublished work.
- L. A. W. Green, T. T. Thuy, D. M. Mott, S. Maenosono and N. T. K. Thanh, R. Soc. Chem. Adv., 2014, 4, 1039–1044 CAS.
- R. E. Rosensweig, J. Magn. Magn. Mater., 2002, 252, 370–374 CrossRef CAS.
- R. R. Wildeboer, P. Southern and Q. A. Pankhurst, J. Phys. D: Appl. Phys., 2014, 47, 495003 CrossRef.
- G. E. Box and H. Lucas, Biometrika, 1959, 46, 77–90 CrossRef.
- O. Henkel, Phys. Status Solidi B, 1964, 7, 919–929 CrossRef.
- E. P. Wohlfarth, J. Appl. Phys., 1958, 29, 595–596 CrossRef PubMed.
- P. E. Kelly, K. O'Grady, P. I. Mayo and R. W. Chantrell, IEEE Trans. Magn., 1989, 25, 3881–3883 CrossRef CAS.
- R. G. Calderon, L. F. Barquin and Q. A. Pankhurst, J. Magn. Magn. Mater., 2004, 272, E1177–E1179 CrossRef PubMed.
- M. Kaur, Q. Dai, M. Bowden, M. H. Engelhard, Y. Wu, J. Tang and Y. Qiang, Nanoscale, 2013, 5, 7872–7881 RSC.
- X. Batlle, M. G. delMuro and A. Labarta, Phys. Rev. B: Condens. Matter, 1997, 55, 6440–6445 CrossRef CAS.
- F. A. L. Dullien, Porous media: fluid transport and pore structure, Academic Press, San Diego, 2nd edn, 1992 Search PubMed.
- E. Tronc, J. P. Jolivet, P. Belleville and J. Livage, Hyperfine Interact., 1989, 46, 637–643 CrossRef.
- Y. Tamaura, K. Ito and T. Katsura, J. Chem. Soc., Dalton Trans., 1983, 189–194 RSC.
- G. M. da Costa, C. Blanco-Andujar, E. De Grave and Q. A. Pankhurst, J. Phys. Chem. B, 2014, 118, 11738–11746 CrossRef CAS PubMed.
- P. Guardia, R. Di Corato, L. Lartigue, C. Wilhelm, A. Espinosa, M. Garcia-Hernandez, F. Gazeau, L. Manna and T. Pellegrino, ACS Nano, 2012, 6, 3080–3091 CrossRef CAS PubMed.
- L. A. Thomas, L. Dekker, M. Kallumadil, P. Southern, M. Wilson, S. P. Nair, Q. A. Pankhurst and I. P. Parkin, J. Mater. Chem., 2009, 19, 6529–6535 RSC.
- Y. Wang, C. Blanco-Andujar, Z.-l. Zhi, P.-W. So, N. T. K. Thanh and J. C. Pickup, Chem. Commun., 2013, 49, 7255–7257 RSC.
- T. Q. Huy, P. V. Chung, N. T. Thuy, C. Blanco-Andujar and N. T. K. Thanh, Faraday Discuss., 2014 10.1039/c4fd00152d.
Footnotes |
| † Electronic supplementary information (ESI) available: Reproducibility studies and additional characterisation data including SQUID Magnetometry, TEM, ATR-FTIR, XRD and Mossbauer spectroscopy. See DOI: 10.1039/c4nr06239f |
| ‡ Joint last authors. |
| § Online search (Scopus) on 18/09/2014 using the keywords “magnet* + hypertherm*” under the terms “title + abstract + keywords” in the range of 2010-Present; with a total of 1948 results. |
| This journal is © The Royal Society of Chemistry 2015 |