Local manifestations of a static magnetoelectric effect in nanostructured BaTiO₃–BaFe₁₂O₉ composite multiferroics

Abstract

A study on magnetoelectric phenomena in the barium titanate–barium hexaferrite (BaTiO₃–BaFe₁₂O₁₉) composite system, using high resolution techniques including switching spectroscopy piezoresponse force microscopy (SSPFM) and spatially resolved confocal Raman microscopy (CRM), is presented. It is found that both the local piezoelectric coefficient and polarization switching parameters change on the application of an external magnetic field. The latter effect is rationalized by the influence of magnetostrictive stress on the domain dynamics. Processing of the Raman spectral data using principal component analysis (PCA) and self-modelling curve resolution (SMCR) allowed us to achieve high resolution phase distribution maps along with separation of average and localized spectral components. A significant effect of the magnetic field on the Raman spectra of the BaTiO₃ phase has been revealed. The observed changes are comparable with the classical pressure dependent studies on BaTiO₃, confirming the strain mediated character of the magnetoelectric coupling in the studied composites.

---

Introduction

Multiferroic materials demonstrating direct or indirect coupling between magnetic and electric degrees of freedom (magnetoelectric, ME, effect) have been a focus of attention for the scientific community in recent years, mainly due to a number of attractive technological applications¹ and a great potential for new investigations. Due to the fact that the ME effect occurs in a limited number of single phase materials, usually very weak, and at relatively low temperatures,² a popular alternative solution is composites of magnetostrictive (or piezomagnetic) and piezoelectric components.^3,4 ME coupling in such composites is a product property mediated by mechanical stress, arising at the interface when fields (magnetic/electric) are applied.^4c Conventionally, one distinguishes between the direct (change of the polarization under a magnetic field) and converse (change of the magnetization under an electric field) ME effects, both being the cross coefficients relating an extensive variable with an intensive one from the other respective thermodynamic field pairs. In the small signal regime, both ME coefficients should be the same due to the thermodynamic Maxwell relations. The other pair, relating electric and magnetic fields as well as magnetization and polarization (again both should be identical in value for small signals), is typically used in theory.^3,5

Most of the experimental and theoretical studies on multiferroic composites have so far been focused on measurements or simulation of the macroscopic integral ME response for different compositions,⁶ connectivity types,⁷ and morphologies of composites.⁸ Taking into account the crucial role of the interfaces and widely distributed connectivity schemes, there is a strong motivation to investigate local variations of the ME response with a high spatial resolution. This will not only allow microstructural control of the ME response, but should also provide new insights into the coupling mechanism, and thus open the door for controlling and tailoring the macroscopic ME effect. Such local measurements have become available only recently with the development of scanning probe microscopic techniques, such as piezoresponse force microscopy (PFM) and magnetic force microscopy (MFM), addressing ferroelectric and magnetic properties with nanoscale resolution,^9,10 and making possible direct monitoring of changes induced by electric or magnetic fields applied in situ.

At the moment, quite a few reports on scanning probe microscopic studies of ME coupling have been published.^11–13 However, only a modicum of these publications have been dedicated to studying the direct ME effect utilizing PFM under a magnetic field, even though PFM can be a more robust alternative compared to other local non-contact derivatives of AFM.

In the present work, we systematically study the local ME coupling in multiferroic composites by a combination of high resolution methods of PFM and spatially resolved confocal Raman microscopy (CRM). PFM is based on the detection of piezoelectric surface deformations, induced by the application of ac voltage to the sharp tip.¹⁰ It serves as a powerful method for imaging ferroelectric domain structures and studying the polarization reversal phenomena under the local electric bias (SSPFM). Raman spectroscopy, on the other hand, is a well-known method for the investigation of structural dynamics in a wide range of materials.¹⁴ The analytical advantages of Raman spectroscopy and the submicron spatial resolution (below the diffraction limit) of scanning confocal microscopy¹⁵ have been combined in the presented approach. Confocal Raman microscopy has recently been used for the visualization of domain structures in the bulk crystal and for reconstructing the domain kinetics in ferroelectric crystals.^16,17 The sensitivity of vibration modes to an induced strain makes CRM an interesting technique for the visualization of magnetoelectric coupling in multiferroic composites. Thus, joint application of these methods will give mutually complementary spatial maps of the ME response and provide synergetic new information about the studied materials.¹⁶

As the subject of our study we chose a bulk ceramic composite containing magnetostrictive barium hexaferrite (BaFe₁₂O₁₉) and piezoelectric barium titanate (BaTiO₃). This system has already been shown to manifest the ME effect at the nanoscale.¹³ However, direct macroscopic measurements of the ME coupling in these composites are limited due to the relatively high percolating electric conductivity. Therefore, the local measurements, which are, in general, free from such a limitation, are very useful for the evaluation of the ME potential of this system.

Experimental

The studied polycrystalline ceramic nanocomposites BaTiO₃–BaFe₁₂O₁₉ (65 : 35 weight%) were prepared using conventional powder processing techniques.¹³ The BaFe₁₂O₁₉ was synthesized from stoichiometric amounts of BaCO₃ and Fe₂O₃, mixed via mechanical milling and then calcined at 1200 °C for 2 h. Barium titanate was made from stoichiometric amounts of BaCO₃ and TiO₂, mixed via mechanical milling and then calcined at 1350 °C for 10 h. The crystal phases were confirmed by X-ray diffraction (XRD), and scanning electron microcopy (SEM) showed the grain sizes to be around 100–200 nm for the BaTiO₃ and 0.5–1 μm for the BaFe₁₂O₁₉ powders, respectively. To make the composites, the two components were well mixed by grinding in an agate mortar and then uniaxially pressed in a 10 mm diameter die with a pressure of 100 MPa. The composite was then sintered at 1200 °C for 2 h, achieving a relatively low composite density of around 4 g cm⁻³. The grain sizes in the composite were similar to those of the initial powders, with no significant grain growth occurring, and XRD showed that the two phases remained discrete and did not react.

Prior to the measurements, ceramic pellets were ground to a thickness of about 0.5 mm. One of the faces was polished up to 0.1 μm grit. A silver electrode was painted for electrical connection onto the other face. The PFM/MFM measurements were carried out with MFP-3D (Asylum Research) and Ntegra Prima (NT-MDT) commercial scanning probe microscopes. The PFM measurements were performed either in single frequency mode or in dual amplitude resonance tracking (DART-PFM) mode. In the first case, an ac voltage with amplitude V_ac = 5 V at frequency f = 50 kHz was applied to the tip. In the second case, the PFM signal is collected at two frequencies below and above the contact cantilever resonance frequency (550 kHz). This allows us to improve the signal to noise ratio. Switching spectroscopy PFM (SS-PFM) was performed using the MFP-3D system. A detailed explanation of the SS-PFM method can be found elsewhere.¹⁸ In our case, a train of dc voltage pulses with a constant duration τ_p = 25 ms and their amplitude changing stepwise from 0 to +V_max, then from +V_max to −V_max and back to 0 was applied to the tip (V_max = 30 V). Between the pulses, a small probing ac voltage was used to record the PFM signal in the DART mode. The resulting dc bias dependences of the piezoresponse, local piezoresponse hysteresis loops, were collected over a predefined spatial grid. The acquired data set was analyzed to yield spatial distribution of the polarization switching parameters, such as saturation amplitude, nucleation bias, etc.

Fresh uncoated doped silicon cantilevers (SEIHR, Nanosensors) with a spring constant k = 15 N m⁻¹ and resonant frequency f = 130 kHz were used for all PFM/SSPFM measurements. For MFM scans commercial cantilevers (ASYMFMHC) coated with a magnetic layer of Co/Fe (tip apex radius 45 nm; H_c > 5000 Oe) were utilized. A commercial variable magnetic field module (VFM2, Asylum Research) was used to apply an in-plane magnetic field up to 8 kOe during PFM measurements.

Raman spectra were recorded in the backscattering configuration at room temperature within 2D scanning using a confocal Raman microscope, Alpha300AR (WiTec GmbH). A He–Ne laser with λ = 633 nm and power 37 mW was used as a pumping source. Laser radiation was focused on the sample surface by an objective ×100 with numerical aperture 0.75. A diffraction grating with 600 g mm⁻¹ providing a spectral resolution of 1.9 cm⁻¹ was used for scattered light decomposition. The estimated spatial resolution of CRM was about 350 nm in the plane of the sample and about 500 nm in the vertical direction (depth). Raman measurements in the magnetic field were performed using a custom cell with permanent magnets providing a maximum magnetic field of H = 2.5 kOe. In order to efficiently mine the spatially resolved spectral data, which is usually dominated by overlapping contributions from the two phases, major data techniques including principal component analysis (PCA) and self-modelling curve resolution (SMCR) were utilized.

Results and discussion

Fig. 1 shows topography (a), vertical (b) and lateral (c) PFM images (the so-called mixed piezoresponse signal, A cos θ, is shown) measured in the single frequency mode (f_ac = 50 kHz, V_ac = 8 V), and MFM (phase) image (d) of the same spot. The PFM images show rather weak vertical and strong lateral responses. Hence, it can be inferred that the orientation of the polar axis of the individual grains lies at some angle to the sample normal, and is randomly distributed. The VPFM signal is only unipolar, which is often observed in multiferroic composites. In contrast, the LPFM signal shows both negative and positive values indicating the fact that domains are mainly separated by 90 degree walls. Concurrently, the piezoelectric inactive regions correlate with active ones in MFM mode. This verifies the fact that the two phases, piezoactive BaTiO₃ and magnetically active BaFe₁₂O₁₉, are juxtaposed to each other without obvious secondary phases.

Fig. 1 The typical topography (a), vertical PFM (b), lateral PFM (c), and MFM (phase) (d) images of the BaTiO₃–BaFe₁₂O₁₉ (65 : 35) composite ceramics. PFM images were taken in single frequency mode.

In order to study the effect of magnetic field on local polarization switching, we carried out SS-PFM mapping on a 16 × 16 point grid over a BaTiO₃ rich area (Fig. 2a). The obtained SS-PFM results are actually a 5-dimensional dataset composed of variation of the PFM phase and amplitude arrays as a function of the dc bias and spatial coordinates, (x, y). We analyzed the SS-PFM datasets using self-developed MATLAB routines to yield maps of the relevant parameters (Fig. 3). As shown in Fig. 3a, the map of the saturation VPFM amplitude extracted for SS-PFM data exhibits significant correlation with the maps of single frequency PFM on active regions (Fig. 1). The plotted values are as acquired, and no rejection algorithm was employed at this point to filter the data. Hence the saturation amplitude was used as a parameter to set a low pass filter for rejecting data arrays corresponding to the inactive regions. Using such a filter, fitting routines were developed in order to extract maps of the positive (Fig. 3c and d) and negative nucleation bias (Fig. 3e and f).¹⁹ The nucleation bias corresponds to the electric field when a stable enough switched domain (nucleus) appears and can be considered as a local analogue of the coercive field.¹⁸

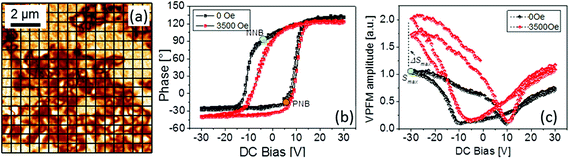Fig. 2 DART-PFM image of the BaTiO₃–BaFe₁₂O₁₉ (65 : 35) composite ceramics. The grid shows SS-PFM measurement points. The image was taken in another location than the one shown in Fig. 1. (a) Typical local piezoresponse hysteresis loops: phase (b) and amplitude (c), measured at zero magnetic field and at 3500 Oe. The coloured circles mark saturation amplitude (S_max), negative (NNB), and positive nucleation bias values (PNB).

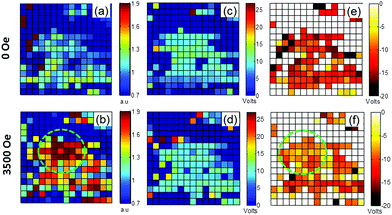Fig. 3 Maps of the saturation PFM amplitude, S_max (a, b), positive nucleation bias (c, d), and negative nucleation bias (e, f) obtained at the magnetic fields of 0 and 3500 Oe, respectively, for the region shown in Fig. 2a (all image scales are 4 × 4 μm). The magnetic field results in an increase of S_max and the variation of the nucleation bias. The dashed circle (green) highlights areas manifesting maximum changes.

Fig. 2b and c show an example of PFM phase–voltage and amplitude–voltage hysteresis loops measured at one of the grid points at magnetic fields of H = 0 and 3500 Oe. The loops measured at zero magnetic field are often distorted, that is, shifted towards either a positive or negative (as shown in Fig. 2) bias voltage. Such a shift indicates the presence of internal bias fields stabilizing an energetically more favorable orientation of the polarization along their directions, and resulting in an asymmetry of the switching process. This asymmetry can be quantified by comparison between the negative and positive nucleation bias voltages, NNB and PNB, marked by green and red dots in Fig. 2b, respectively. Fig. 4a shows histograms of the nucleation bias. In most cases NNB is larger than PNB. Moreover, analyzing a spatial distribution of the difference between these two biases, which can be considered as a measure of the strength and polarity of the internal fields, we found that the strong asymmetry is typical of the loops measured close to the interfaces between BaTiO₃ and BaFe₁₂O₁₉ grains, while the interior parts of the BaTiO₃ grains show more symmetric switching (Fig. 4c). The dominance of the negative offset of the PFM hysteresis loops correlates with the strong unipolarity of the VPFM signal measured for the as-sintered state (Fig. 1b). Indeed, a preferable direction of the internal fields may stimulate appearance of the preferable polarization orientation at the paraelectric–ferroelectric phase transition. The effect of self-polarization has often been observed for ferroelectric thin films and related to an internal bias field due to charged defects at the film–electrode interface.²⁰ Similarly, in our case the charge carriers seem to be accumulated at interfaces between BaTiO₃ and BaFe₁₂O₁₉ grains, resulting in strong internal bias fields in this area (see Fig. 4c). This effect is very likely if one considers the interface as a heterojunction between two semiconducting materials.²¹ As such, different work functions and band gaps (∼1 eV for BaFe₁₂O₁₉²² and ∼3.3 eV for BaTiO₃ ²³) result in the creation of a potential barrier at the interface. Free charges (few, but some are present) can be localized at such a barrier, resulting in the formation of a space charge layer. As the hexaferrite has a much narrower band gap, this phenomenon is not unlikely to occur in this combination with a ferroelectric.²¹

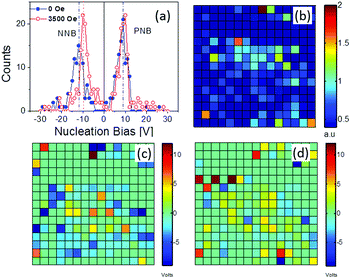Fig. 4 Corresponding to the maps shown in Fig. 3: histograms of the nucleation bias distributions (a). Maps of the difference between the saturation PFM amplitude (ΔS_max) measured with and without the magnetic field (b) and of the loop asymmetry (PNB + NNB)/2, measured at 0 Oe (c) and 3500 Oe (d) (all image scales are 4 × 4 μm).

Comparison between the loops measured with and without magnetic field reveals two apparent changes: (i) an increase of the saturation amplitude of the VPFM signal (S_max) and (ii) a reduction of the negative nucleation bias. Although an interpretation of these changes demands a rigorous theoretical model, we try to explain both effects separately and find a correlation between them based on the presumption of possible phenomena.

Fig. 4b shows a map of the difference between the saturation amplitudes with and without the magnetic bias. The strongest changes are observed in the vicinity of the interface between piezoelectric and magnetostrictive phases. Such an observation confirms that the ME effect in this composite occurs via a mechanical strain–stress transfer. The mechanical stress arising in BaTiO₃ grains due to the magnetostriction in adjacent BaFe₁₂O₁₉ grains seems to be localized in the vicinity of the interface and relaxes into the interior part of the grains.²⁴

The observed increase of the VPFM amplitude signal under a magnetic field, H, can have both intrinsic and extrinsic origins. The intrinsic origin is directly related to a change of the local polarization, ΔP, stimulated by the ME coupling, ΔP = αH, where α is the ME coefficient. It should result in the corresponding change of the local piezoelectric coefficient. According to the well-known relationship:²⁵

d₃₃ = εε₀QP₃ (1)

where ε is the relative dielectric permittivity, ε₀ is the dielectric permittivity of vacuum and Q is the electrostriction coefficient, a change in d₃₃ (namely Δd₃₃) can be magnetoelectrically induced as:

Δd₃₃ = εε₀QαH (2)

or correspondingly:

d₃₃ = εε₀Q(P₃⁰ + αH) (3)

Similar equations have been used in ref. 12. However, the authors of that article estimated d₃₃ from the slope of local hysteresis loops. Such an approach cannot be applied for a standard SS-PFM experiment, since the measured signal always corresponds to a deformation induced by a small ac voltage, independent of the value of the dc bias. Taking into account that in SS-PFM the polarization switching progresses via propagation of a new domain nucleated underneath the tip inside the oppositely polarized matrix^10,26 and that this new domain is maximal at large dc bias, one can estimate Δd₃₃ from the differences between S_max with and without magnetic field (ΔS_max). We would like to point out that in our composite, the ME effect is strain–stress mediated and, therefore, ΔS_max due to the intrinsic ME effect should be symmetric relative to the polarization polarity. In our case, however, we observed a substantially larger ΔS_max for the negative bias (upward polarization) than that for the positive bias (downward polarization). This difference may be a manifestation of an extrinsic contribution related to ME induced changes of polarization switching kinetics under the PFM tip.

Indeed, in the SS-PFM experiment the measured signal is proportional not only to the d₃₃ value, but also to the volume of the switched domain. One can assume that the application of a magnetic field affects the domain nucleation and growth processes. The applied magnetic field obviously results in mechanical stress acting on BaTiO₃ crystallites, due to the magnetostriction of adjacent BaFe₁₂O₁₉ grains. Such a stress can affect the energy equilibrium conditions, and facilitate (or impede) the growth of a new domain by different mechanisms.

One mechanism is related to a magnetic field induced variation of nucleation bias. Fig. 4a shows the distributions of positive and negative nucleation bias values extracted from the maps plotted in Fig. 3c–f. These distributions have a bimodal shape with two peaks corresponding to the most probable bias values. One can see that the application of the magnetic field results in a decrease of the NNB magnitude with the peak position shifting from −12 to approximately −9.5 V. At the same time, the shift of PNB lies within statistical errors. These changes cannot be explained by the lateral drift of the scanned area, which is estimated to be about 22 nm,²⁷ and is too small to be comparable to the tip apex diameter (∼20 nm).

The observed changes of the nucleation bias can be considered in the following way: as discussed above, the charges trapped in the vicinity of the interface result in an internal bias field and, correspondingly, in asymmetric polarization switching. Application of the magnetic field effectively lifts up the asymmetry of the domain nucleation by reducing the NNB values. We assume that the extra polarization appearing due to the ME coupling after the application of the magnetic field modifies the existing field balance. Obviously, the change of the polarization will result in a change of the related depolarizing field. The situation is somewhat similar to those in macroscopic measurements of the direct ME effect under open circuit conditions, when the applied magnetic field results in the appearance of an electric field.²⁸ Since our pristine state is unipolar (relative to the sample surface plane), the change of the depolarizing field will be unipolar too. Such changes can partially compensate for the defect-mediated negative bias, and facilitate nucleation of domains in the forward direction. A similar effect of the ME induced internal electric field on the symmetry of local polarization switching was proposed recently by H. Miao et al. in a bilayer Terfenol-D/PbMg_1/3Nb_2/3O₃–PbTiO₃ composite.²⁹ Contrary to our case, however, the internal field caused made the loops more asymmetric.

Besides the change of domain nucleation conditions, the domain propagation kinetics can also be affected by the magnetic field. Indeed, we observed that for the negative bias (upward domains), the maximal VPFM signal increases much more than for the downward polarization. This indicates that the domain for the upward polarization is propagating faster through the sample, and reaches a larger volume. Again, such facilitated kinetics can be attributed to the unipolar altering of the depolarizing field, which comes into play after the domain is nucleated.

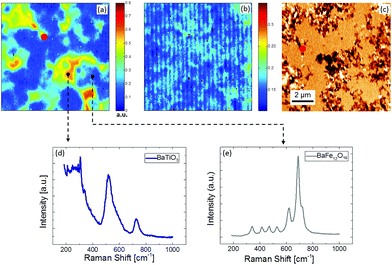
The confocal Raman imaging performed in a 10 μm × 10 μm region provides structural insights into the phase distribution. The 3D dataset was analyzed using PCA,³⁰ resulting in two principal spectral components corresponding to BaTiO₃ and BaFe₁₂O₁₉. The concentration of each component distributed over the scanned region has been represented by 2D maps (Fig. 5a). These maps reveal a tiny diffused interface between BaTiO₃ and BaFe₁₂O₁₉, and no spectral components corresponding to any impurity phase were found. The PFM image taken on the same spot shows that those active regions apparently correlate with BaTiO₃ (Fig. 5c). This confirms the validity of the observed PFM signal as originating from the piezoelectric displacement only, and not from electrochemical strain displacements. This also synergistically validates our approach of deconvolution of Raman spectra using PCA.

Fig. 5 BaTiO₃ concentration map (score maps) extracted from confocal Raman microscopy images using PCA. (a) Lack of fit map, (b) lateral PFM image of the same area (red point is shown for the correlation between images), (c) extracted components corresponding to the BaTiO₃ (d) and BaFe₁₂O₉ (e) Raman spectra.

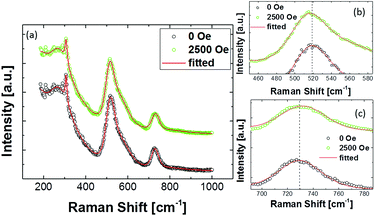
The Raman spectrum of BaTiO₃ was separated from the dataset using a combined statistical approach. This approach works in two steps, namely (i) recognition (PCA) and separation (SMCR) such that the recognition step works as a feedback for the separation step.³¹ Finally, two separate average spectra corresponding to BaTiO₃ and BaFe₁₂O₁₉ were extracted (Fig. 5d and e). The separation step essentially fits the two components (weighted) to each data array, while iteratively updating the weights as well as the components in order to achieve convergence using advanced algorithms.³² Ultimately, the extracted BaTiO₃ spectra corresponding to 0 and 2500 Oe magnetic field were fitted using 9 Gaussian–Lorentzian model functions, 7 of which correspond to the theoretical E₁, A₁, and B₁ modes of tetragonal BaTiO₃, and 2 peaks correspond to additional bands observed due to lattice disorder.³³ Comparison of the spectra reveals that the magnetic field induces a frequency shift of about 2.5 ± 1.0 cm⁻¹ for peaks around 520 cm⁻¹ (A₁ and E(TO) modes) and 720 cm⁻¹ (A₁ and E(LO) modes) (Fig. 6). The shifts occur in opposite directions: the frequency of the phonon modes at 520 cm⁻¹ decreases (mode softening), whereas for the modes at 720 cm⁻¹ it increases (mode hardening).

Fig. 6 Average Raman spectra of the BaTiO₃ phase extracted from the CRM images of BaTiO₃–BaFe₁₂O₁₉ (65 : 35) composite ceramics taken at the magnetic fields of 0 and 2500 Oe (a). Enlarged view around 520 cm⁻¹ (A₁ and E(TO) modes) (b) and 720 cm⁻¹ (A₁ and E(LO) modes) (c).

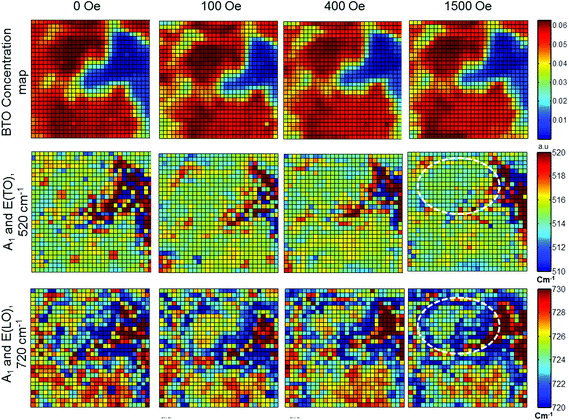
To obtain spatial maps of magnetic field induced changes in the Raman spectra of BaTiO₃, we performed a detailed study with better acquisition quality at another location of the sample, and at several values of magnetic field applied laterally using a homemade setup. In this case, the separation step was localized to a group of 4 points around each spatial grid point which was translated over the whole scan grid to yield separate BaTiO₃ spectra corresponding to each point. These local spectra were fitted to obtain peak parameters. Fig. 7 shows maps of the peak positions corresponding to the A₁ and E (TO) mode (520 cm⁻¹) and A₁ and E (LO) mode (720 cm⁻¹) spectral lines. Both peaks demonstrate a weak softening with increasing magnetic field. The shift value of the 520 cm⁻¹ peak is ∼0.6 cm⁻¹, whereas for the 720 cm⁻¹ peak it is about ∼2.5 cm⁻¹ at the maximum field, as inferred from the shift of histogram peaks (not shown) corresponding to the maps. We suppose that the hardening of the latter mode observed in the averaged spectrum is a result of the statistical interference between the strong Raman peak around 680 cm⁻¹ in BaFe₁₂O₁₉ and the peak at 720 cm⁻¹ in BaTiO₃. Since the separation step is sensitive to the sampling, a drift of the scan area can result in significant changes of the average spectrum, especially with the BaFe₁₂O₁₉ line being very strong. The field dependences of the Raman peaks at 520 and 720 cm⁻¹ reveal a monotonic and spatially persistent softening trend. Taking into account that the ME effect in the composite occurs via strain/stress coupling at the interface between BaTiO₃ and BaFe₁₂O₁₉, the observed phonon mode shifts can be related to the stress appearing in BaTiO₃ grains due to magnetostriction in adjacent BaFe₁₂O₁₉ grains. The stresses, which can be significant locally, may result in a cationic displacement, thus leading to the observed frequency changes.³⁴

Fig. 7 Spatial maps of the peak position of Raman modes of the BaTiO₃ phase at different magnetic fields, showing a softening in both modes with increasing magnetic field (all image scales 7 × 7 μm). The dashed circle (white) represents the correlated areas that also show maximum change at the highest magnetic field value. The bottom right image quite clearly shows the domination of the magnetostrictive stress at the interface.

It would be interesting to compare the obtained data with results of macroscopic measurements. However, to our knowledge there are no published reports on magnetic field induced changes in Raman spectra of BaTiO₃-based multiferroic composites. Li et al. studied the effect of a magnetic field on Raman spectra of Pb(Zr,Ti)O₃–CoFe₂O₄ bilayer composites, and found an ME induced decrease of the soft mode frequency of the Pb(Zr,Ti)O₃ layer.³⁵ In our case, however, the soft mode lies outside of the studied frequency range. Taking into account the stress mediated character of the ME coupling in our materials, we have compared our data with the results of high pressure effects on BaTiO₃ Raman spectra.^33,36 Significant changes, including the appearance of a second peak on the high-frequency asymmetric tail of the A₁ and E(TO) modes (in the 500–600 cm⁻¹ region) and broadening of the E(LO) phonon mode at 720 cm⁻¹, were reported only for pressures above 1 GPa,³³ which is definitely much higher than the magnetostrictive stress acting in our case. A rough approximation of the magnitude of induced stress level can be made by considering the magnetostriction of the order of λ ∼ 10⁻⁴ (ref. 37) and the elastic compliance of BaTiO₃c = 6.76 × 10⁻¹² m² N⁻¹ (stiffness ∼ 100 GPa). This gives a stress of the order of σ ∼ 10 MPa. It is worth noting that aforementioned experiments were performed under hydrostatic pressure, whereas magnetostriction provides an essentially anisotropic effect. Anisotropic stresses can lead to a splitting of the E mode, resulting in the observed frequency shift.

Conclusions

In this study, we performed a spatially resolved mapping of the ME effect in BaTiO₃–BaFe₁₂O₁₉ composites using high resolution microscopic techniques. Besides the intrinsic magnetoelectric change of the local piezoelectric coefficient, piezoresponse force microscopy revealed that the magnetic field affects the polarization switching process: domain nucleation and propagation. This is attributed to the ME induced modulation of the depolarization field. We found that the ME induced changes are mainly localized in the vicinity of the interfaces between piezoelectric and magnetostrictive phases. This fact agrees well with the idea of strain–stress mediated coupling for these composites. The SS-PFM studies revealed an asymmetry of the polarization switching related to the electric fields created by charge carriers trapped at the phase interfaces. These fields can provoke self-polarization that has often been observed in composite multiferroics, but was never rationalized. We observed that the magnetic field can modify the field balance at the interface indirectly. This can open up a new way of controlling the properties of the heterojunction between a ferroelectric and a semiconductor via the magnetoelectric effect. Confocal Raman microscopy has been demonstrated to be a powerful method for phase mapping in such composites. The magnetic field induced changes of Raman spectra of the BaTiO₃ phase show a similar behaviour to that observed in mechanically stressed BaTiO₃. The peak parameter maps revealed clear hot spots where stress mediated changes are mostly concentrated, supporting the fact that the stress generated by magnetostriction can be very high locally.

Acknowledgements

This work was supported by the European Commission within the FP7 Marie Curie Initial Training Network “Nanomotion” (grant agreement no. 290158). Deutsche Forschungsgemeinschaft is acknowledged for support via Forschergruppe 1509 “Ferroic Functional Materials”. RCP thanks the FCT Ciência 2008 programme for support. The equipment of the Ural Center for Shared Use “Modern nanotechnology” UrFU was used. The research was made possible in part by the Ministry of Education and Science of the Russian Federation (Agreement 14.594.21.0011, ID RFMEFI59414X0011).

Notes and references

1. (a) Y. H. Chu, L. W. Martin, M. B. Holcomb, M. Gajek, S. J. Han, Q. He, N. Balke, C. H. Yang, D. Lee, W. Hu, Q. Zhan, P. L. Yang, A. Fraile-Rodriguez, A. Scholl, S. X. Wang and R. Ramesh, Nat. Mater., 2008, 7, 478; (b) S. Fusil, V. Garcia, A. Barthelemy and M. Bibes, Annu. Rev. Mater. Res., 2014, 44, 91.
2. (a) T. Kimura, T. Goto, H. Shintani, K. Ishizaka, T. Arima and Y. Tokura, Nature, 2003, 426, 55; (b) C. A. Vaz, J. Hoffman, C. H. Ahn and R. Ramesh, Adv. Mater., 2010, 22, 2900.
3. M. Fiebig, J. Phys. D: Appl. Phys., 2005, 38, R123.
4. (a) C.-W. Nan, M. I. Bichurin, S. Dong, D. Viehland and G. Srinivasan, J. Appl. Phys., 2008, 103, 31101; (b) J. Ma, J. Hu, Z. Li and C.-W. Nan, Adv. Mater., 2011, 23, 1062; (c) M. Labusch, M. Etier, D. C. Lupascu, J. Schröder and M.-A. Keip, Comput. Mech., 2014, 54, 71.
5. J. F. Nye, Physical properties of crystals. Their representation by tensors and matrices, Clarendon Press, Oxford University Press, Oxford [Oxfordshire], New York, 1st edn, 1985.
6. (a) M. Etier, V. V. Shvartsman, Y. Gao, J. Landers, H. Wende and D. C. Lupascu, Ferroelectrics, 2013, 448, 77; (b) V. Corral-Flores, D. Bueno-Baques, D. Carrillo-Flores and J. A. Matutes-Aquino, J. Appl. Phys., 2006, 99, 08J503.
7. (a) G. V. Duong, R. Groessinger and R. Sato Turtelli, J. Magn. Magn. Mater., 2007, 310, 1157–1159; (b) C. Schmitz-Antoniak, D. Schmitz, P. Borisov, F. M. de Groot, S. Stienen, A. Warland, B. Krumme, R. Feyerherm, E. Dudzik, W. Kleemann and H. Wende, Nat. Commun., 2013, 4, 2051.
8. G. V. Duong and R. Groessinger, J. Magn. Magn. Mater., 2007, 316, e624.
9. (a) A. L. Kholkin, S. V. Kalinin, A. Roelofs and A. Gruverman, in Scanning Probe Microscopy, ed. S. V. Kalinin and A. Gruverman, Springer, New York, 2007, pp. 173–214; (b) R. K. Vasudevan, S. Jesse, Y. Kim, A. Kumar and S. V. Kalinin, MRS Commun., 2012, 2, 61; (c) U. Hartmann, Annu. Rev. Mater. Sci., 1999, 29, 53; (d) R. B. Proksch, T. E. Schäffer, B. M. Moskowitz, E. D. Dahlberg, D. A. Bazylinski and R. B. Frankel, Appl. Phys. Lett., 1995, 66, 2582.
10. V. V. Shvartsman and A. L. Kholkin, in Multifunctional polycrystalline ferroelectric materials. Processing and properties, ed. L. Pardo and J. Ricote, Springer, Dordrecht, New York, 2011, vol. 140, pp. 409–468.
11. (a) F. Zavaliche, H. Zheng, L. Mohaddes-Ardabili, S. Y. Yang, Q. Zhan, P. Shafer, E. Reilly, R. Chopdekar, Y. Jia, P. Wright, D. G. Schlom, Y. Suzuki and R. Ramesh, Nano Lett., 2005, 5, 1793; (b) Y. Geng, H. Das, A. L. Wysocki, X. Wang, S. W. Cheong, M. Mostovoy, C. J. Fennie and W. Wu, Nat. Mater., 2014, 13, 163; (c) F. Yan, G. Chen, L. Lu, P. Finkel and J. E. Spanier, Appl. Phys. Lett., 2013, 103, 42906; (d) M. Pan, S. Hong, J. R. Guest, Y. Liu and A. Petford-Long, J. Phys. D: Appl. Phys., 2013, 46, 55001.
12. G. Caruntu, A. Yourdkhani, M. Vopsaroiu and G. Srinivasan, Nanoscale, 2012, 4, 3218.
13. D. V. Karpinsky, R. C. Pullar, Y. K. Fetisov, K. E. Kamentsev and A. L. Kholkin, J. Appl. Phys., 2010, 108, 42012.
14. Raman Scattering in Materials Science, ed. W. H. Weber and R. Merlin, Springer, Berlin, Heidelberg, 2000.
15. T. Dieing, O. Hollricher and J. Toporski, Confocal Raman microcopy, Springer, Heidelberg, 2010, vol. 158.
16. V. Y. Shur and P. S. Zelenovskiy, J. Appl. Phys., 2014, 116, 66802.
17. (a) P. S. Zelenovskiy, V. Y. Shur, P. Bourson, M. D. Fontana, D. K. Kuznetsov and E. A. Mingaliev, Ferroelectrics, 2010, 398, 34; (b) V. Y. Shur, P. S. Zelenovskiy, M. S. Nebogatikov, D. O. Alikin, M. F. Sarmanova, A. V. Ievlev, E. A. Mingaliev and D. K. Kuznetsov, J. Appl. Phys., 2011, 110, 52013.
18. S. Jesse, A. P. Baddorf and S. V. Kalinin, Appl. Phys. Lett., 2006, 88, 62908.
19. S. Jesse, H. N. Lee and S. V. Kalinin, Rev. Sci. Instrum., 2006, 77, 73702.
20. A. L. Kholkin, K. G. Brooks, D. V. Taylor, S. Hiboux and N. Setter, Integr. Ferroelectr., 1998, 22, 525.
21. V. N. Fridkin, Ferroelectric semiconductors, Consultants Bureau, New York, 1st edn, 1980.
22. (a) A. Meftah, J. M. Costantini, N. Khalfaoui, S. Boudjadar, J. P. Stoquert, F. Studer and M. Toulemonde, Nucl. Instrum. Methods Phys. Res., Sect. B, 2005, 237, 563; (b) C. M. Fang, F. Kools, R. Metselaar, G. de With and R. A. de Groot, J. Phys.: Condens. Matter, 2003, 15, 6228.
23. S. H. Wemple, Phys. Rev. B: Condens. Matter, 1970, 2, 2679.
24. J. D. Eshelby, Proc. R. Soc. London, A, 1957, 241, 376.
25. G. Schulze, Z. Angew. Math. Mech., 1963, 43, 512.
26. M. Abplanalp, Piezoresponse scanning force microscopy of ferroelectric domains, Ph.D., Zürich, 2001.
27. P. Rahe, R. Bechstein and A. Kühnle, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct., 2010, 28, C4E31.
28. G. V. Duong, R. Groessinger, M. Schoenhart and D. Bueno-Basques, J. Magn. Magn. Mater., 2007, 316, 390.
29. H. Miao, X. Zhou, S. Dong, H. Luo and G. F. Li, Nanoscale, 2014, 6, 8515.
30. H. Shinzawa, K. Awa, W. Kanematsu and Y. Ozaki, J. Raman Spectrosc., 2009, 40, 1720.
31. K. Awa, T. Okumura, H. Shinzawa, M. Otsuka and Y. Ozaki, Anal. Chim. Acta, 2008, 619, 81.
32. D. D. Lee and H. S. Seung, Adv. Neural Inf. Proc. Syst., 2001, 13, 556.
33. U. D. Venkateswaran, V. M. Naik and R. Naik, Phys. Rev. B: Condens. Matter, 1998, 58, 14256.
34. A. K. Sood, N. Chandrabhas, D. V. S. Muthu and A. Jayaram, Phys. Rev. B: Condens. Matter, 1995, 51, 8892.
35. Z. Li, Y. Wang, Y. Lin and C. Nan, Phys. Rev. B: Condens. Matter, 2009, 79, 180406(R).
36. W. Zhang, L. Chen, C. Jin, X. Deng, X. Wang and L. Li, J. Electroceram., 2008, 21, 859.
37. (a) A. G. Chesnokov and E. P. Na, Phys. Solid State, 2001, 43, 1728 , 1730; (b) R. M. Bozorth, Phys. Rev., 1955, 99, 1788.

---