Multi-photon excited coherent random laser emission in ZnO powders

Abstract

We report the observation and analysis of anti-Stokes coherent random laser (RL) emission from zinc oxide (ZnO) powders excited by one-, two- or three-photon femtosecond laser radiation. The ZnO powders were produced via a novel proteic sol–gel, low-cost and environmentally friendly route using coconut water in the polymerization step of the metal precursor. One- and two-photon excitation at 354 nm and 710 nm, respectively, generated single-band emissions centred at about 387 nm. For three-photon excitation, the emission spectra showed a strong ultraviolet (UV) band (380–396 nm) attributed to direct three-photon absorption from the valence band to the conduction band. The presence of an intensity threshold and a bandwidth narrowing of the UV band from about 20 to 4 nm are clear evidence of RL action. The observation of multiple sub-nanometre narrow peaks in the emission spectra for excitation above the RL threshold is consistent with random lasing by coherent feedback.

---

Introduction

Random lasers (RLs) belong to a special class of lasers with optical feedback as a result of multiple light scattering in a disordered amplifying medium.^1,2 As in a conventional laser, the RL action occurs when, for excitation above a certain light intensity threshold, the optical gain of a luminescence transition is larger than the overall losses. First studied in 1966,³ a turning point in this field occurred in 1994⁴ after an unequivocal experimental demonstration in which a dye solution containing titanium dioxide (TiO₂) nanoparticles was observed to produce a laser-like emission, later named as an RL. Since then, multidisciplinary research has succeeded in exploiting strongly scattering disordered materials.^5,6 In addition to colloidal systems with different sizes and shapes of light scatterers,^7,8 RLs have been observed in polymers,⁹ photonic crystals infiltrated with a laser dye,¹⁰ dye-doped polymer film/TiO₂ nanomembrane arrangements¹¹ and cold atoms.¹² Of great technological importance are electrically excited RLs.^13–16

The question of coherent versus incoherent feedback from scattering media has been clarified^1,2,6 as well as the photon statistics.¹⁷ The lack of directionality resulting from the multiple scattering nature of the feedback mechanism has been tackled in different ways. One alternative exploited the surface plasmon excitation in a silver film.¹⁸ Random fiber lasers have also been demonstrated^19–22 as well as a planar microcavity with random gain layers.²³ Another important aspect, the lack of tunability, has been improved in a number of ways. In one approach, single particle resonances were exploited to provide resonant tunability.²⁴ Spatial profile and mode control have been used in a number of ways.^25,26 All these cited references are based on one-photon excitation (1PE) to obtain random lasing on the Stokes side of the excitation laser wavelength. Frequency up-conversion RLs with anti-Stokes emission have also been demonstrated based on two-photon absorption (2PA) processes in gallium arsenide²⁷ and zinc oxide (ZnO)²⁸ powders. An energy transfer process was also exploited to obtain an ultraviolet (UV) RL involving pairs of neodymium ions in a glass powder.²⁹ The anti-Stokes RLs have low spatial and temporal coherence analogous to the down-converted RLs, but have the advantage that light in the UV region may be obtained using an excitation laser operating in the visible or near-infrared range. Our group have demonstrated three-photon excited RLs in a dye/TiO₂ nanoparticle colloid³⁰ and in a ZnO-on-silicon (Si) nanostructured film.³¹ In the first study,³⁰ a highly efficient dye with a large three-photon absorption (3PA) cross-section was used.³² Excitation at 1350 nm with femtosecond pulses generated a visible coherent RL emission at about 560 nm by direct 3PA. In the second study,³¹ a ZnO nanostructured film was produced by a plasma immersion ion implantation and a deposition process. Femtosecond excitation at 802 nm and direct three-photon band-to-band absorption generated RL emission at 390 nm. In this example, the film structure led to a photon diffusion process in which interference had a negligible contribution in the feedback mechanism and, as a consequence, this RL falls in the category of non-resonant or incoherent feedback.

It is reported here that coherent up-converted RL emission as a result of direct 3PA in ZnO powders can be obtained by exciting with femtosecond pulses at 802 nm. This is the first time that an anti-Stokes coherent RL emission because of 3PA has been observed in powders with grains that act simultaneously as scatterers and amplifiers. The three-photon excitation (3PE) RL operated in the UV region (380–396 nm) and the observation of narrow peaks in the emitted UV spectrum for excitation above the RL threshold is consistent with random lasing with coherent feedback. The RL emission excited by one- and two-photons was characterized in the same sample for direct comparison.

ZnO is one of the most important large band gap semiconductors.³³ The versatility of ZnO arises from its 3.37 eV wide band gap and its high excitonic binding energy of 60 meV. Among its diversity of applications, ZnO has been used as a field emitter, as a front contact to solar cells, in liquid crystal displays and in light emitting diodes.³⁴ The antibacterial and antifungal properties of ZnO nanoparticles have also been demonstrated in biomedical applications.³⁵ Laser emission has been demonstrated in different ZnO morphologies (sub-micrometer particles, thin films, urchin-like structures and bulk samples) and temporal excitation regimes (femto- to nano-seconds),^36–39 including 1PE RL.^1,2,40

Experimental

The ZnO powders were synthesized following a new green synthesis route exploiting a proteic sol–gel, in which filtered coconut water was used in the polymerization step of the metal precursors. Using this method, the metal ions are believed to bind to the polymeric chains of the proteins present in the coconut water, forming a colloidal suspension (sol).⁴¹ The proteic sol–gel has the advantage of being a simple, low-cost, low toxicity synthesis route and has been successfully used to produce metal oxide nanoparticles and thin films with fine control of the size and agglomeration of the nanostructures.^42–44 In a typical procedure, zinc nitrate hexahydrate (Aldrich) was first dissolved in distilled water. Filtered coconut water was then added to the nitrate solution with gentle magnetic stirring for 30 min. The resulting sol was dried at 100 °C for 24 h and then pre-calcined at 200 °C for 5 h to form the precursor powder. The precursor powder was washed with distilled water followed by centrifugation to eliminate any residual potassium chloride derived from the coconut water. The washed precursor powder was then calcined at 1000 °C for 5 h. The morphology and crystallographic orientation of the ZnO grains were characterized using scanning electron microscopy (SEM) and X-ray diffraction (XRD). Fig. 1a shows an SEM image of the grains, which have a polyhedral shape with average dimensions of about 600 nm. The crystalline structural phase was confirmed using XRD (Fig. 1b).

Fig. 1 (a) SEM image of ZnO grains synthesized at 1000 °C. Grain sizes 500–700 nm. (b) XRD of ZnO grains. Inset: SEM image of compact ZnO powder at 1000× magnification.

For the RL excitation, a pulsed Ti:sapphire laser (802 nm, 100 fs, 1 kHz, pulse energy up to 1 mJ) or the output of an optical parametric amplifier at 354 nm or 710 nm was used. The pulse duration and repetition rate followed the Ti:sapphire excitation source. A mass of 26.4 mg of ZnO powder was placed in a sample holder (dimensions about 7 × 1.1 × 1.1 mm³) and a stripe excitation geometry was used with a cylindrical lens at an angle of 90° with respect to the sample face (inset of Fig. 2a). The stripe dimensions were adjusted for the different wavelengths used. For 1PE at λ_exc = 354 nm, a cylindrical lens (focal length 2.5 cm) was used and the excited region had a length of about 7 mm and a width of about 1.6 μm. For two-photon excitation (2PE) at λ_exc = 710 nm, the excited region had a length of about 7 mm and a width of about 3.2 μm. For 3PE, the excited area had a length of about 7 mm and a width of about 3.6 μm. The collected emission was analysed by a charge-coupled device spectrometer with an overall resolution >0.1 nm. All measurements were performed at room temperature.

Fig. 2 One-photon excited ZnO RL characteristics. (a) Peak intensity versus EPE (insets show the experimental setup and the emission spectrum for excitation below the threshold). (b) Line width reduction versus EPE (inset shows a typical spectrum for an EPE above the threshold). FWHM: full width at half maximum.

Results and discussion

The ZnO powders synthesized by the proteic sol–gel method had, in addition to optimum optical properties, a homogeneous size distribution and quasi-spherical grain morphology,⁴⁵ suggesting that they are excellent structures for use in RLs.

Next the RL emission as a result of 1PE and 2PE is reported. The results followed the same behavior as reported previously,^1,27,28,40 except that for the 2PE we observed an RL spiky spectrum, demonstrating the contribution of coherent feedback in the quasi-spherical ZnO grains. The agreement with the previous results indicates that the ZnO grains synthesized by this new method are of good quality. Fig. 2a shows the RL emitted intensity for 1PE (λ_exc = 354 nm) versus the excitation pulse energy (EPE). A threshold value of 0.54 μJ was obtained; the inset shows the stripe excitation geometry and an emission spectrum for excitation when the EPE was 0.47 μJ at 1 kHz.

Fig. 2b shows the bandwidth reduction as a function of the EPE and the bandwidth narrowing down to about 6 nm can be clearly seen. The inset shows a typical single shot spectrum obtained for an EPE of 1.1 μJ, above the RL threshold. Spikes because of coherent feedback can be observed.

Fig. 3 shows the RL characteristics for 2PE at λ_exc = 710 nm. Fig. 3a shows the RL emitted intensity versus the EPE and Fig. 3b shows the bandwidth reduction versus the EPE. In this instance, the threshold inferred from Fig. 3a is about 15 μJ and the bandwidth is narrowed to about 4 nm. The inset in Fig. 3a is a single-shot emitted spectrum for EPE below the threshold (11.6 μJ) and no spike was observed. The inset in Fig. 3b shows a similar single-shot spectral behavior for an EPE of 19 μJ above the threshold as in the 1PE example, again confirming the coherent feedback mechanism.

Fig. 3 Two-photon excited ZnO RL characteristics. (a) Peak intensity versus EPE (inset shows an emission spectrum below the threshold). (b) Line width reduction versus EPE (inset shows a typical spectrum for an EPE above the threshold).

The data shown in Fig. 2 and 3 can be compared with previously reported results.^15,16,40 The RL characteristics observed corroborate the quality of our samples compared to samples prepared by conventional methods. However, a new result was the demonstration of coherent feedback in the 2PE example. The emitted spectrum for excitation below the threshold in both instances showed a single band centered at 387 nm.

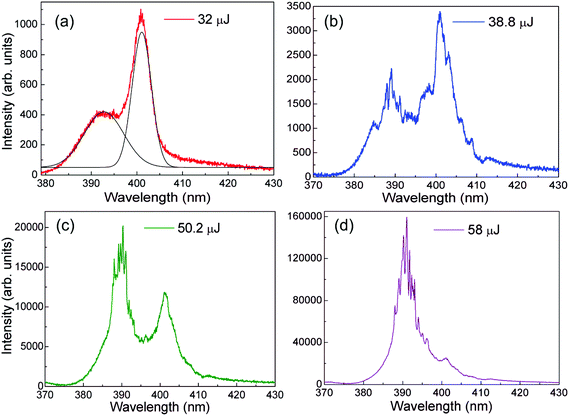
Interesting spectral behavior was observed with excitation at λ_exc = 802 nm, as shown in the luminescence spectra of Fig. 4, where two bands are present: a UV band centered at about 390 nm and a violet band centered at about 401 nm. Based on Özgür et al.,³³ we assigned the UV band to direct conduction-to-valence band decay, which was observed only with direct 3PE.

Fig. 4 (a)–(d) Emission spectra of ZnO powder in the UV-violet region for different excitation pulse energies. Solid black lines in (a) represent two Gaussian curves adjusted to the UV and violet bands to determine their FWHM.

Similar findings have been reported by our group using a ZnO-on-Si nanostructured film.³¹ The violet band centered at about 401 nm can be assigned to either second-harmonic generation (SHG) or luminescence induced by multi-photon absorption.^46–48 As shown by Dominguez et al.,³¹ it was verified that the violet emission is mainly because of SHG for low values of EPE (below 37 μJ) and this coexists with multi photon induced luminescence at energies higher than 37 μJ. It was confirmed that the emission at 401 nm is indeed SHG, because, on exciting the sample at 710 nm, the 401 nm band was no longer present although an emission at 355 nm was observed. Although the two bands centered at 390 and 401 nm are adjacent, we assumed Gaussian profiles for both bands to infer the FWHM for each of them (Fig. 4). A study of the intensity dependence of the violet and UV bands as a function of the EPE (Fig. 5a and b) helps to clarify the mechanisms involved. It is well known that, in the absence of saturation, the up-conversion intensity, I_UC, is proportional to (I_E)ⁿ, where n indicates the number of photons absorbed in the excitation process and I_E is the excitation intensity. Therefore, from Fig. 5a, which shows a slope corresponding to n ≈ 2, it can be concluded that the coexisting SHG and 2PA at an interstitial Zn energy level are responsible for the violet luminescence. A more detailed study of the SHG and multi-photon absorption in bulk ZnO and ZnO nanocrystals under visible and infrared femtosecond excitation has been reported previously.^46–50. On the other hand, for the UV emission, the slope of n ≈ 3.5 for low EPE corroborates the assumption of a direct band-to-band three-photon absorption process. The deviation from the theoretically expected slope n = 3, beyond the measurement uncertainty, is probably influenced by the onset of stimulated emission before the feedback due to scattering leads to lasing. For EPE larger than 45 μJ the data shown in Fig. 5b is highly nonlinear with slope ≈ 12.

Fig. 5 Peak intensities of the UV and violet bands versus EPE. The dots are experimental data and the lines represent numerical fits.

Fig. 6a illustrates the behavior of the violet and UV bands and shows two spectra at low (28.8 μJ) and high (63 μJ) EPE values. Double spectral bands can be clearly seen in both instances and they are both smooth at low EPE values, but at high energies the UV band is spiky. This behavior indicates that the feedback mechanism for RL emission is light scattering by the submicron-sized particles. To confirm the RL behavior, the emitted intensity and line width spectral reduction was studied as a function of the incident energy specifically for the UV band (Fig. 6b and c).

Fig. 6 (a) Spectral signature at low (28.8 μJ) and high (63 μJ) EPE values. (b) Peak intensity behaviour of the emission centred at 389 nm versus the EPE. Inset shows the threshold at 36.5 μJ. (c) Line width behaviour of the UV band showing the RL minimum bandwidth. Inset shows that the violet bandwidth remains essentially constant with a slight broadening.

To determine the RL threshold, it was first noted that the data shown in Fig. 5b, when plotted on a linear–linear graph (Fig. 6b), do not show the two inflexion points at about 36 μJ and 48 μJ clearly. Therefore the same data was plotted on the enlarged graph shown in the inset of Fig. 6b and then the RL threshold was determined at 36.5 μJ.

To understand the lasing behavior, three possible mechanisms are considered: (i) laser emission associated with the longitudinal modes of the Fabry–Pérot (FP) cavities formed by two opposite facets of the ZnO particles; (ii) whispering gallery mode lasing, a consequence of the total internal reflection of light inside a single particle; and (iii) random lasing because of multiple light scattering in random media. In case (i), the separation between two adjacent longitudinal modes is Δλ = λ²/2n_rL, where λ is the resonant wavelength, n_r is the refractive index and L is the FP cavity length. For ZnO grains with typical dimensions of about 600 nm and n_r = 2.45 at 390 nm, the spacing between two adjacent modes is about 50 nm. Only one mode would exist in the range 380–420 nm if the FP cavities formed by the two-end facets of the ZnO particles were responsible for the lasing effect. Consequently, laser action is ruled out because FP cavities were recorded as a multimode characteristic. However, the whispering gallery mode cannot be excited in sub-micrometer particles. The separation between two adjacent peaks in Fig. 4c and d is about 0.8 nm and this is compatible with particles with diameters of about 2 μm. Therefore, the only possible mechanism for coherent laser emission is the multiple scattering of light in the random media.

Two possibilities are usually considered to explain the presence of spikes in the RL spectrum. One possibility occurs in the Ioffe–Regel regime, when the mean free path is close to or smaller than the laser wavelength, λ, and the disorder parameter kl_t ≤ 1, where k = 2π/λand l_t is the transport mean free path.^1,2 Alternatively, coherent output may be because of extended modes^2,51 in a process that does not require either interference effects or localized modes. Mujumdar et al.⁵¹ demonstrated the contribution of coherent feedback for kl_t ranging from 35 to 5800.

Fig. 6a shows that the emitted spectrum in the RL regime has several spikes (line width about 0.3 nm), which is evidence of coherent feedback. The spiky curve on the left-hand side was obtained for an excitation energy of 63 μJ, whereas the smooth curve on the right-hand side corresponds to an EPE of 28.8 μJ, below the RL threshold. Considering the ZnO grains as spheres with a diameter of 600 nm, the scattering cross-section as calculated from Mie theory is 0.52 μm² at 390 nm. The transport mean free path, l_t, and the disorder parameter kl_t were estimated to be about 515 nm and about 8, respectively. Therefore our anti-Stokes RL is operating in the strong scattering regime, close to the Ioffe–Regel regime (l_t ∼ λ) and the emitted spikes are a result of the strong light confinement provided by ZnO particles enhanced by the stripe excitation geometry.

The increase in the RL threshold for 2PE and 3PE compared with 1PE is a consequence of the low efficiency of the non-linear optical absorption process.

Conclusion

In this paper, coherent RL action has been reported in the strong scattering regime and close to the Ioffe–Regel regime induced by simultaneous 3PA in ZnO powders. This is a demonstration of UV coherent random lasing excited by 2PA and 3PA in a semiconductor powder where the amplifying medium and scatterers are the same particles. One advantage of using a multi-photon excitation scheme to obtain random lasing in the UV region is that a high frequency excitation laser is not required. Our results open new windows for the potential application of RLs in speckle-free imaging⁵² using UV illumination, biomedical imaging⁵³ as well as their use in antibacterial treatments and photodynamic therapy.³⁵

Acknowledgements

We acknowledge financial support from the Brazilian agencies Conselho Nacional de Desenvolvimento Cientifico e Tecnológico (CNPq) and the Fundação de Amparo à Ciência e Tecnologia do Estado de Pernambuco (FACEPE). The work was performed in the framework of the Photonics National Institute (INCT de Fotônica) project and PRONEX/CNPq/FACEPE.

Notes and references

1. H. Cao, Waves in Random Media, 2003, vol. 13, p. R1.
2. D. S. Wiersma, Nat. Phys., 2008, 4, 359.
3. R. V. Ambartsumyan, N. G. Basov, P. G. Kryukov and V. S. Letokhov, IEEE J. Quantum Electron., 1966, 2, 442.
4. N. M. Lawandy, R. M. Balachandran, A. S. L. Gomes and E. Sauvain, Nature, 1994, 368, 436.
5. M. A. Noginov, Solid State Random Lasers, Springer, New York, 2005.
6. D. S. Wiersma, Nat. Photonics, 2013, 7, 188.
7. K. L. van der Molen, A. P. Mosk and A. Lagendijk, Opt. Commun., 2007, 278, 110.
8. J. U. Kang and J. B. Khurgin, Appl. Phys. Lett., 2006, 89, 221112.
9. A. Tulek, R. C. Polson and Z. V. Vardeny, Nat. Phys., 2010, 6, 303.
10. M. Notomi, H. Suzuki, T. Tamamura and K. Edagawa, Phys. Rev. Lett., 2004, 92, 123906.
11. C. T. Dominguez, Y. Lacroute, D. Chaumont, M. Sacilotti, C. B. de Araújo and A. S. L. Gomes, Opt. Express, 2012, 20, 17380.
12. Q. Baudouin, N. Mercadier, V. Guarrera, W. Guerin and R. Kaiser, Nat. Phys., 2013, 9, 356.
13. X. Ma, P. Chen, D. Li, Y. Zhang and D. Yang, Appl. Phys. Lett., 2007, 91, 251109.
14. X.-Y. Liu, C.-X. Shan, S.-P. Wang, Z.-Z. Zhang and D.-Z. Shen, Nanoscale, 2012, 4, 2843.
15. H. Zhu, C.-X. Shan, J.-Y. Zhang, Z.-Z. Zhang, B.-H. Li, D.-X. Zhao, B. Yao, D.-Z. Shen, X.-W. Fan, Z.-K. Tang, X. Hou and K.-L. Choy, Adv. Mater., 2010, 22, 1877.
16. Q. Qiao, C.-X. Shan, J. Zheng, H. Zhu, S.-F. Yu, B.-H. Li, Y. Jia and D.-Z. Shen, Nanoscale, 2013, 5, 513.
17. H. Cao, Y. Ling, J. Y. Xu and C. Q. Cao, Phys. Rev. Lett., 2001, 86, 4524.
18. M. A. R. C. Alencar, A. S. L. Gomes and C. B. de Araújo, J. Opt. Soc. Am. B, 2003, 20, 564.
19. C. J. S. de Matos, L. de S. Menezes, A. M. Brito-Silva, M. A. M. Gámez, A. S. L. Gomes and C. B. de Araújo, Phys. Rev. Lett., 2007, 99, 153903.
20. S. K. Turitsyn, S. A. Babin, A. E. El-Taher, P. Harper, D. V. Churkin, S. I. Kablukov, J. D. Ania-Castañón, V. Karalekas and E. V. Podivilov, Nat. Photonics, 2010, 4, 231.
21. Z. Hu, Q. Zhang, B. Miao, Q. Fu, G. Zou, Y. Chen, Y. Luo, D. Douguo, P. Wang, H. Ming and Q. Zhang, Phys. Rev. Lett., 2012, 109, 253901.
22. M. Gagné and R. Kashiap, Opt. Express, 2009, 17, 19067.
23. Q. Song, L. Liu, S. Xiao, X. Zhou, W. Wang and L. Xu, Phys. Rev. Lett., 2006, 96, 033902.
24. S. Gottardo, R. Sapienza, A. Blanco, D. Wiersma and C. López, Nat. Photonics, 2008, 2, 429.
25. N. Bachelard, J. Andreasen, S. Gigan and P. Sebbah, Phys. Rev. Lett., 2012, 109, 033903.
26. H. E. Türeci, L. Ge, S. Rotter and A. D. Stone, Science, 2008, 320, 643.
27. G. Zhu, C. E. Small and M. A. Noginov, Opt. Lett., 2008, 33, 920.
28. E. V. Chelnokov, N. Bityurin, I. Ozerov and W. Marine, Appl. Phys. Lett., 2009, 89, 171119.
29. M. A. S. de Oliveira, C. B. de Araújo and Y. Messaddeq, Opt. Express, 2011, 19, 5620.
30. A. S. L. Gomes, M. T. Carvalho, C. T. Dominguez, C. B. de Araújo and P. N. Prasad, Opt. Express, 2014, 22, 14305.
31. C. T. Dominguez, M. S. Vieira, R. M. Oliveira, M. Ueda, C. B. de Araújo and A. S. L. Gomes, J. Opt. Soc. Am. B, 2014, 31, 1975.
32. G. S. He, P. P. Markowicz, T.-C. Lin and P. N. Prasad, Nature, 2002, 415, 767.
33. Ü. Özgür, Ya. I. Alivov, C. Liu, A. Teke, M. A. Reshchikov, S. Doğan, V. Avrutin, S.-J. Cho and H. Morkoç, J. Appl. Phys., 2005, 98, 041301.
34. A. Janotti and C. G. Van de Walle, Rep. Prog. Phys., 2009, 72, 126501.
35. D. Sharma, J. Rajput, B. S. Kaith, M. Kaur and S. Sharma, Thin Solid Films, 2010, 519, 1224.
36. J. Fallert, R. J. B. Dietz, H. Zhou, J. Sartor, C. Klingshirn and H. Kalt, Phys. Status Solidi C, 2009, 6, 449.
37. C. Zhang, F. Zhang, T. Xia, N. Kumar, J.-I. Hahm, J. Liu, Z. L. Wang and J. Xu, Opt. Express, 2009, 17, 7893.
38. C.-H. Lu, T.-Y. Chao, Y.-F. Chiu, S.-Y. Tseng and H.-C. Hsu, Nanoscale Res. Lett., 2014, 9, 178.
39. J. Fallert, F. Stelzl, H. Zhou, A. Reiser, K. Thonke, R. Sauer, C. Klingshirn and H. Kalt, Opt. Express, 2008, 16, 1125.
40. H. Cao, Y. G. Zhao, S. T. Ho, E. W. Seelig, Q. H. Wang and R. P. H. Chang, Phys. Rev. Lett., 1999, 82, 2278.
41. M. A. Gomes, M. E. G. Valerio and Z. S. Macedo, J. Nanomater., 2011, 2011, 1.
42. P. R. J. Montes, M. E. G. Valerio, M. A. Macedo, F. Cunha and J. M. Sazaki, Microelectron. J., 2003, 34, 557.
43. J. V. A. Santos, M. A. Macedo, F. Cunha, J. M. Sazaki and J. G. S. Duque, Microelectron. J., 2003, 34, 565.
44. R. S. Silva and Z. S. Macedo, J. Therm. Anal. Calorim., 2011, 103, 587.
45. M. A. Gomes, M. E. G. Valerio, J. F. Q. Rey and Z. S. Macedo, Mater. Chem. Phys., 2013, 142, 325.
46. S. K. Das, M. Biswas, D. Byrne, M. Bock, E. McGlynn, M. Breusing and R. Grunwald, J. Appl. Phys., 2010, 108, 043107.
47. D. C. Dai, S. J. Xu, S. L. Shi, M. H. Xie and C. M. Che, IEEE Photonics Technol. Lett., 2006, 18, 1533.
48. C. F. Zhang, Z. W. Dong, G. J. You, R. Y. Zhu, S. X. Qian, H. Deng, H. Cheng and J. C. Wang, Appl. Phys. Lett., 2006, 89, 042117.
49. J. He, Y. Qu, H. Liu, J. Mi and W. Ji, Opt. Express, 2005, 13, 9235.
50. M. G. Vivas, T. Shih, T. Voos, E. Mazur and C. R. Mendonça, Opt. Express, 2010, 18, 9628.
51. S. Mujumdar, M. Ricci, R. Torre and D. S. Wiersma, Phys. Rev. Lett., 2004, 93, 053903.
52. B. Redding, M. A. Choma and H. Cao, Nat. Photonics, 2012, 6, 355.
53. J. H. Yu, J. H. Yu, S.-H. Kwon, Z. Petrášek, O. K. Park, S. W. Jun, K. Shin, M. Choi, Y. I. Park, K. Park, H. B. Na, N. Lee, D. W. Lee, J. H. Kim, P. Schwille and T. Hyeon, Nat. Mater., 2013, 12, 359.

---