Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hierarchical self-assembly of colloidal magnetic particles into reconfigurable spherical structures
Daniel
Morphew
and
Dwaipayan
Chakrabarti
*
School of Chemistry, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK. E-mail: d.chakrabarti@bham.ac.uk
First published on 8th April 2015
Abstract
Colloidal self-assembly has enormous potential as a bottom-up means of structure fabrication. Here we demonstrate hierarchical self-assembly of rationally designed charge-stabilised colloidal magnetic particles into ground state structures that are topologically equivalent to a snub cube and a snub dodecahedron, the only two chiral Archimedean solids, for size-selected clusters. These spherical structures open up in response to an external magnetic field and demonstrate controllable porosity. Such features are critical to their applications as functional materials.
While buckministerfullerene is a classic example of a spherical molecule,1 viral capsids with icosahedral symmetry showcase fascinating illustrations of molecular self-assembly into spherical structures in the realm of nature.2 Hollow spherical structures, apart from their aesthetic appeal due to their high degree of symmetry,3 have practical applications for their potential use as theranostic materials,4 heterogeneous catalysts,5 and metamaterials,6 and thus serve as attractive targets for self-assembly at different length scales.7–9 The ability to reconfigure such hollow spherical structures is critical to the design of responsive cages that can encapsulate guests and release them on demand.10 However, realisation of such architectures with nanoscale or microscale building blocks has been elusive,11 despite the promise of colloidal self-assembly,12 spurred especially by a recent surge in the synthesis of an exotic variety of colloidal building blocks.13,14 The key to the success of programmed self-assembly as a means of structure fabrication is the ability to encode the target structure into the building blocks.12 The scope for tuning the interactions between the building blocks is critical to performing this task. Although colloidal building blocks are appealing from this perspective,13,14 examples of colloidal self-assembly into target structures via a priori designed building blocks are still rather limited.15–17 Here we demonstrate in silico hierarchical self-assembly of rationally designed charge-stabilised colloidal magnetic particles into reconfigurable spherical structures.
We first describe the rationale that underpins our choice of building blocks in pursuit of targeted spherical assembly. Nanoscale and colloidal self-assembly can be governed by a multitude of forces.18,19 While van der Waals interactions tend to favour close-packed structures,20,21 the patchy colloids, which because of their heterogeneous surface chemistry offer highly directional interactions,22 are known to stabilise low-coordinated structures.16,17 Although computer simulation studies have now become indispensable for developing design principles, the complexity of the surface pattern predicted by in silico studies of patchy colloids is often beyond the reach of state-of-the-art experimental fabrication techniques.23 A potential alternative to patchy colloids for stabilising low-coordinated structures is dipolar particles.24,25 The common structural motifs observed for clusters of dipolar particles with a central dipole are linear chains, rings, and entangled knots for moderate strength of the dipole.21,25 Dipolar colloidal particles thus appear to be promising building blocks for target structures that are non-close packed at the microscale. In particular, we considered charge-stabilised colloidal magnetic particles because of the scope for tuning the electrostatic and magnetic interactions independently in experimental conditions without recourse to involved chemistry.25,26
Self-assembly of nano- and micro-particles governed by magnetic interactions results in a rich variety of novel structures and phases.27,28 Magnetic interactions can be due to permanent magnetic dipoles;26,29 alternatively, uniaxial magnetic fields are commonly used to induce magnetic interactions in the absence of permanent dipoles,15,30 though biaxial and triaxial magnetic fields have also been employed.31,32 Until recently, the focus has been on dipolar interactions with an isotropic excluded volume,27 for which the dipolar hard-sphere (DHS) model carrying a point-dipole at the center has been extensively studied,33 while soft interactions have also been considered.34,35 The DHS model successfully captures the tendency for dipolar particles to form chains and rings.33 While self-assembly into two-dimensional sheets has been observed for core–shell magnetic nanoparticles in the presence of an applied magnetic field,36 superparamagnetic colloidal particles confined at air–water interface due to gravity have served as excellent models for two-dimensional systems.37 A recent surge in the synthesis of colloidal magnetic particles, where an additional anisotropy attribute exists due to either shape15 or shift in the position of the dipole away from the center of a spherical excluded volume,26,38 or heterogeneous surface chemistry,29,39 has brought about a paradigm shift in magnetic colloids with the prospect of realising complex architectures via their self-assembly.40
In pursuit of targeted spherical assembly we explored a route to surface curvature via edge sharing of polygons, as exemplified by Platonic and Archimedean solids.41 A triangular face is simplest of its kind, featuring in many of these uniform convex polyhedra. In order to facilitate the formation of triangular motifs, we focused on spherical charge-stabilised colloidal magnetic particles, where a dipole is embedded at a location shifted away from the centre. Such building blocks resemble closely the colloidal magnetic particles, realised recently using an iron oxide inclusion buried below the surface of an organosilica polymer sphere, that formed planar trimers upon tuning the electrostatic repulsion.26 Our building block carries an off-centred dipole pointing radially outward.42,43 Here our results demonstrate hierarchical self-assembly of these colloidal building blocks into ground state structures that are topologically equivalent to a snub cube and a snub dodecahedron, the only two chiral Archimedean solids, for size-selected clusters. These spherical structures are shown to be reconfigurable by an external magnetic field, thus opening up the prospect of applications as responsive cages.
We employed a one-component treatment with an effective potential, widely used in colloid science,44 to model the charge-stabilised colloidal magnetic particles and used basin-hopping global optimisation45 to characterise the ground state structures. The spherical particles, with the centre of mass assumed to be at the centre, interact with each other via a screened electrostatic repulsion, given by the Yukawa potential.44 In addition, an anisotropic site, located away from the centre in a rigid framework, holds a permanent point-dipole directed radially outward. As detailed in Methods, the model parameters in the present case are the inverse Debye screening length λ−1, the strength of the dipole μD, the separation d between the location of the point-dipole and the centre of the particle, and the magnetic field strength B if the field is switched on. The shift distance is expressed in terms of a dimensionless fraction α = 2d/σ, where σ is the length scale in terms of which the Yukawa potential describing the screened electrostatic repulsion is defined.
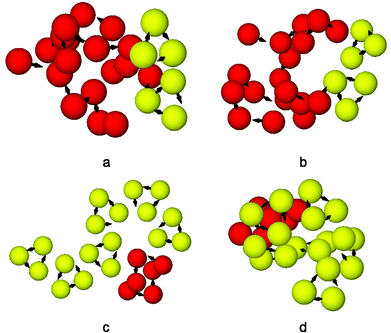
We assessed the relative stabilities of the global minima as a function of the cluster size. Fig. 1 shows the second finite difference of the energy for the global minimum of the cluster of size N, Δ2E(N), for N = 2–25 corresponding to a set of model parameters: λ−1 = 25, μ = 2, α = 0.6, and B = 0. Here Δ2E(N) = Vmin(N − 1) + Vmin(N + 1) − 2Vmin(N), where Vmin(N) is the potential energy of the global minimum of cluster containing N particles. The pronounced peaks in the Δ2E versus N plot indicate especially stable structures for the corresponding cluster size. Fig. 1 shows that the trimer, i.e. N = 3 cluster is indeed especially stable for this set of parameters. The corresponding structure, stabilised by the dipolar interactions with an arrangement of the dipoles in a closed loop (i.e. flux-closure state),46 is shown in Fig. 2a. Although the dipoles and the centres of the particles are coplanar in this triangular structure of three-fold rotational symmetry, the dipoles are not directed along the line joining the centres. This set of parameters was chosen so that the propensity to form triangular subunits continued as apparent in the first place for the N = 6 cluster [videFig. 2b]. It is evident in Fig. 1 that the N = 24 cluster is substantially stable while the N = 6, 12, 15, and 18 clusters are somewhat stable as well. Fig. 2c–e show the structures of the global minima for N = 12, 15, and 18 clusters, respectively, where a clear sign of hierarchical organisation of the triangular subunits, as seen in Fig. 2a, is evident. Note that the hierarchical organisation resulted in bowl-shaped structures with emergent four-fold and five-fold rotational symmetry for N = 12 and N = 15, respectively; however, for N = 18 a planar structure was observed with six-fold rotational symmetry.
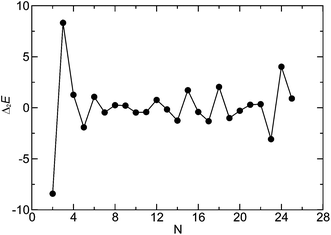 | ||
| Fig. 1 Second finite difference of the energy for the global minimum of the cluster of size N for N = 2–25. | ||
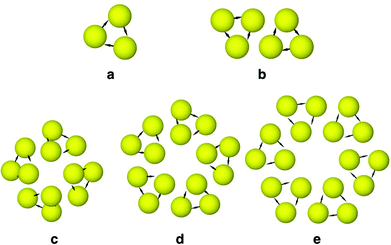 | ||
| Fig. 2 The structures of the global minima for the clusters of size (a) N = 3, (b) N = 6, (c) N = 12, (d) N = 15, and (e) N = 18. | ||
The surface curvature observed for the ground state structures of the N = 12 and N = 15 clusters was promising for possible spherical assembly for larger clusters. In a remarkable demonstration of hierarchical self-assembly, the ground state structure for the N = 24 cluster was indeed found to be a closed shell with octahedral (O) symmetry, as shown in Fig. 3. The structure is a non-uniform convex polyhedron composed of 32 triangular faces and 6 square faces and is topologically equivalent to a snub cube, a chiral Archimedean solid.41 8 of the triangular faces (shown in yellow) originate from the colloidal particles forming triangular subunits of three-fold rotational symmetry, while the rest of the faces emerge from the hierarchical self-assembly of these triangular subunits. It is noteworthy that the emergent triangular faces (shown in blue) are distinct from the symmetrical triangular faces and have slightly different edge lengths.
Following the characterisation of the closed shell structure for the ground state of the N = 24 cluster, it was rational to expect a structure that is topologically equivalent to a snub dodecahedron for the N = 60 cluster if the observed trend continued. However, the search for such a structure, anticipated to be formed via hierarchical self-assembly governed by highly directional interactions, proved to be elusive. In order to improve the efficiency of the search for larger clusters, the trimeric subunits with three-fold rotational symmetry, as shown in Fig. 2a, formed at the first stage of self-assembly for the N = 24 cluster were used as the building blocks instead. The effectiveness of this approach was assessed by examining the global minimum of the cluster of Nt = 8 such building blocks, which we call secondary building blocks as opposed to primary building blocks. The corresponding structure was also found to be of octahedral symmetry. When relaxed from this geometry, the N = 24 cluster with the primary building blocks was found to support the structure, shown in Fig. 3. This observation validated our approach with secondary building blocks in the reduced configuration space.
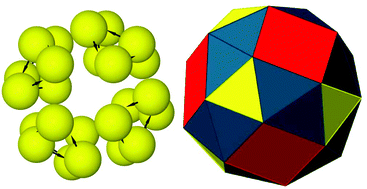
Our hunt for a likely spherical structure for a cluster of N = 60 colloidal magnetic particles therefore continued with Nt = 20 secondary building blocks for global optimisation runs before relaxing the global minimum with 60 primary building blocks. For the same set of parameters, Fig. 4 presents the ground state thus identified for the N = 60 cluster – a closed shell polyhedral structure that is topologically equivalent to a snub dodecahedron. The structure has icosahedral symmetry (I) and is composed of 80 triangular faces and 12 pentagonal faces. In this case, 20 of the triangular faces (shown in yellow), distinct from the 60 other triangular faces, are sustained by the colloidal particles forming triangular subunits of three-fold rotational symmetry, while the rest of the faces are emergent from the hierarchical self-assembly of these triangular subunits. As for the global minimum for the N = 24 cluster, the polyhedron is vertex-transitive but not uniform because of unequal edge lengths. Alongside the snub cube, the snub dodecahedron is a chiral Archimedean solid, existing in enantiomorphic forms. In fact, the snub dodecahedron can also be derived from the 120-vertex truncated icosidodecahedron by the process of alternation. Removal of alternate vertices leaves 60 of the vertices of the truncated icosidodecahedron to form a polyhedron topologically equivalent to one enantiomorphic form of snub dodecahedron. The other enantiomorphic form is formed by the set of other 60 vertices. The resulting polyhedron is vertex-transitive but not uniform, as shown in Fig. 4, and requires some deformation to transform into a snub dodecahedron. Similarly, two enantiomorphic forms of snub cube can be derived from the 48-vertex truncated cuboctahedron.
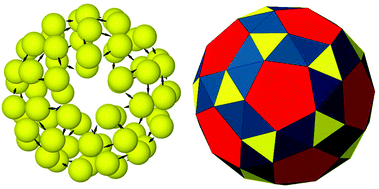 | ||
| Fig. 4 The structure of icosahedral (I) symmetry, topologically equivalent to a snub dodecahedron, identified as the global minimum for the N = 60 cluster of charge-stabilised colloidal magnetic particles. Two representations of the same structure are shown: (left) spherical particles with embedded dipoles, drawn not to scale; (right) the non-uniform convex polyhedron with the faces colour-coded to distinguish between distinct faces. 20 of the triangular faces, shown in yellow, are sustained by the colloidal particles forming triangular subunits of three-fold rotational symmetry, while the rest of the faces are emergent from the hierarchical self-assembly of these triangular subunits. The emergent triangular faces are in blue and the square faces are in red as in Fig. 3. | ||
We then examined the prospect of controlling the porosity of the spherical architectures by varying the salt concentration of the medium, which affects the inverse Debye screening length λ−1. The spherical structures for the N = 24 and N = 60 clusters were observed to be stable as λ−1 was increased from λ−1σ = 20 to λ−1σ = 50. For N = 24, the edge length of the trimeric subunits was then found to increase by ∼6%, resulting in a decrease in the edge length of the emergent faces by ∼4%. The reduced softness of the repulsive core is the dominant factor here, though an increase in λ−1 also shortens the range of the electrostatic repulsion. Over this experimentally accessible regime, the radius of gyration for the spherical structure remained practically constant. The spherical structures were found to be stable for a reasonably wide range of μD values, but for a relatively narrow range of α values.
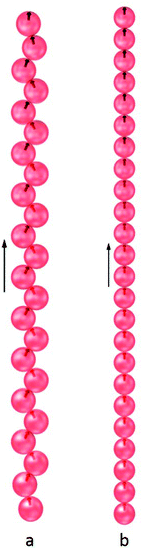
When subjected to an external magnetic field, the ground states of the N = 24 and N = 60 clusters retain their shell structures at low values for the field strength, but the symmetry is removed due to distortion. Above a threshold field, the shell structure collapses because of the tendency of the dipoles to align with the field. At a moderate field strength, the ground state structure, shown in Fig. 5a, was found to be a zig-zag chain as a result of competing dipolar interactions. For strong fields, the interaction of the dipoles with the field becomes dominant resulting in a linear chain aligned with the field (Fig. 5b). The hollow spherical structures, which enclose a well-defined space at the colloidal scale, can thus be reconfigured by the application of an external magnetic field above a threshold. This ability to reconfigure is critical to the design of responsive nano- or micro-cages capable of encapsulating guests and releasing them on demand.
The colloidal building blocks designed here are in close correspondence with the recently synthesised colloidal magnetic particles that used iron oxide inclusions located underneath the surface of the particles.26 While achieving precise control over the direction of the dipole moment in an off-centered position is a challenge,47 our model offers a design rule, which could be targeted realistically in pursuit of spherical self-assembly. As for the parameters, reasonable estimates in real units can be obtained by using εY = 4.1 × 10−21 J (of the order of kBT at room temperature) and σ11 = 10−6 m. These values will correspond in real units to μD ∼ 4 × 10−16 A m2, B ∼ 2 × 10−4 T, and λ = 40 nm, well within the experimentally accessible regime.26 The value of the Yukawa contact potential εY can be varied by an order of magnitude by controlling the colloidal charge number.34
We now present our results of Monte Carlo (MC) simulations of the finite-sized systems. For N = 24 colloidal magnetic particles, which are the primary building blocks for the hollow spherical structures reported here, we did not observe the formation of thermodynamically stable spherical structure even at effective temperature T = 0.1 when the finite-sized system was gradually cooled starting from a random configuration. The single-particle MC moves that were attempted proved to be inadequate to make the thermodynamically stable structure accessible with the primary building blocks within the length of the MC runs. An estimate of dimensionless time, reduced by the self-diffusion coefficient at infinite dilution D0 and particle diameter, per MC step can be obtained.48 For micron-sized colloidal particles it is reasonable to consider D0 ∼ 1 × 10−12 m2 s−1.49 The total length of the MC simulation run at the lowest temperature was thus estimated in real units to be of the order of hours (∼3 × 104 s). In the context of hierarchical self-assembly, cluster moves, though unphysical,48 could prove to be more efficient.50 Alternatively, we carried out Brownian Dynamics (BD) simulations as they involve collective motion. When BD simulations were performed at T = 0.1, the formation of more triangular subunits was indeed evident (Fig. 6). However, the assembly of any spherical structure was not observed in the timescale of these BD simulations either. The formation of the thermodynamically stable spherical structure upon cooling is thus hindered by kinetic trapping, which frustrates the assembly process. The strongly directional dipolar interactions provide kinetic traps, presumably because of the propensity to form chains as opposed to triangular units in the flux-closure state.
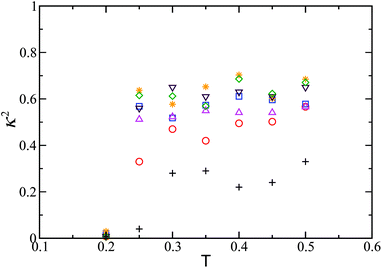
Since our global optimisation results identified a well-defined structural motif as the secondary building block for the next level of structural hierarchy, we carried out MC simulations also with these secondary building blocks, as seen in Fig. 2a. In these MC simulation runs constrained in spherical containers of different sizes, the thermodynamically stable spherical structure was indeed found to be formed for Nt = 8 as the temperature was gradually lowered. A measure of the spherically symmetric distribution of the particles in the 24-particle cluster was estimated in terms of the relative shape anisotropy κ2,51 which is bounded between 0 and 1. κ2 = 0 for a spherically symmetric distribution and κ2 = 1 for a linear arrangement as in Fig. 5b. Fig. 7 shows the evolution of the relative shape anisotropy κ2 as a function of effective temperature; a transition is marked by a fall in κ2, which indicates the formation of the spherical structure. The fall is relatively small for smaller containers because of the restriction imposed. Similar observation was made for Nt = 20.
The present study highlights a critical aspect of programmed self-assembly that has received little attention until recently.52–55 Here the task is to ensure that thermodynamically stable structures are kinetically accessible on the experimental time scale via removal of kinetic traps. Reversible association or contact formation allows for facile annealing of defects, and hence the removal of kinetic traps. Such reversibility is, however, often achieved at the expense of weak thermodynamic driving forces. It is relevant to note that this general idea has been corroborated, in particular, by a recent simulation study of a model of virus capsid assembly that employed rigid subunits corresponding to trimers of proteins.52 The competing thermodynamic and kinetic criteria suggest that an optimal condition has to be established for efficient self-assembly. In the presence of directional interactions, which strongly favour certain contacts, this task is even more challenging. In future, we will attempt to address this challenge.
Finally, we present preliminary data on the behaviour of these colloidal magnetic particles in the bulk, as observed in the canonical Monte Carlo simulations of N = 256 particles in a cubic periodic box at two values for the packing fraction: ϕ = 0.1 and ϕ = 0.01. A cluster analysis, shown in Fig. 8 and 9, reveals that the high-temperature vapour phase at either of these packing fractions largely consists of trimers and tetramers. At low temperatures, the cluster size distribution for the higher ϕ value tends to peak around a value in the limit of the system size, suggesting a percolating56 structure made of dipolar chains for the higher ϕ value (Fig. 8). In contrast, for the lower ϕ value, we observed a cluster phase57,58 at T = 0.1, where particles self-assembled into aggregates of different sizes as evident in Fig. 9.
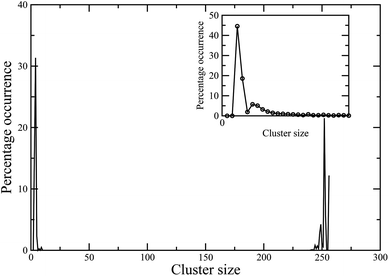 | ||
| Fig. 8 Cluster size distribution in the bulk system at the packing fraction ϕ = 0.1 at two different effective temperatures: T = 0.15 (main frame), T = 0.4 (inset). | ||
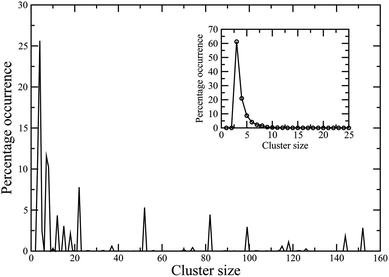 | ||
| Fig. 9 Cluster size distribution in the bulk system at the packing fraction ϕ = 0.01 at two different effective temperatures: T = 0.1 (main frame), T = 0.3 (inset). | ||
In conclusion, we have demonstrated rational design of colloidal magnetic particles forming thermodynamically stable hollow spherical structures via a remarkable hierarchical self-assembly. The ground state structures are topologically equivalent to a snub cube and a snub dodecahedron, the only two chiral Archimedean solids. The precision with which the subunits are formed parallels nature's mastery of creating hierarchically organised complex architectures. The manipulation of the electrostatic repulsion between the charge-stabilised colloidal magnetic particles allows for the porosity of the spherical structures to be controlled. The structures are shown to be responsive to an external magnetic field. The ability to reconfigure the hollow spherical structures is critical to the design of responsive supracolloidal cages for cargo delivery. The formation of thermodynamically stable spherical structures upon cooling is found to be hindered by kinetic trapping in the presence of the strongly directional dipolar interactions, presumably because of the propensity to form chains as opposed to triangular subunits. The presence of kinetic traps highlights the importance of the choice of an optimal condition for efficient self-assembly on the experimental timescale. It should be noted that even though the brute force simulations could not access the ground state within the length of the simulation time, which is of the order of hours, experiments often running over days might be able to do so.
Methods
The model
The potential energy V for a finite-sized system containing N charge-stabilised colloidal magnetic particles in the presence of a magnetic field is given by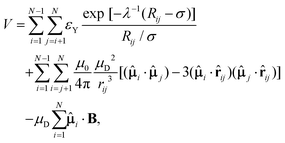 | (1) |
Here, Ri and ri are the position vectors for the centre of particle i and its embedded point-dipole, respectively, ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/b_char_e0b3.gif) i is the unit vector defining the direction of the dipole moment of the latter, whose magnitude is μD, and rij is the separation vector: rij = ri − rj with magnitude rij, so that the unit vector
i is the unit vector defining the direction of the dipole moment of the latter, whose magnitude is μD, and rij is the separation vector: rij = ri − rj with magnitude rij, so that the unit vector ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij = rij/rij. In the Yukawa description of screened electrostatic repulsion, λ−1 is the inverse Debye screening length and εY is the so-called contact potential. The units of energy and length are chosen as the Yukawa parameters εY and σ, respectively. The direction of the external field B = (0,0,B), when applied, was held fixed along the z-axis of the space-fixed frame. The magnetic dipole μD is given in reduced units of (4πεYσ3/μ0)1/2 and the magnetic field strength B is in [εYμ0/(4πσ3)]1/2, where μ0 is the permeability of free space. The model parameters are then the inverse Debye screening length λ−1, the strength of the dipole μD, the separation d between the location of the point-dipole and the centre of the particle, and the magnetic field strength B. The shift distance is expressed in terms of a dimensionless ratio α = 2d/σ, where σ is the length scale in terms of which the Yukawa potential is defined, offering an estimate of the size of the particle in the absence of a hard core.
ij = rij/rij. In the Yukawa description of screened electrostatic repulsion, λ−1 is the inverse Debye screening length and εY is the so-called contact potential. The units of energy and length are chosen as the Yukawa parameters εY and σ, respectively. The direction of the external field B = (0,0,B), when applied, was held fixed along the z-axis of the space-fixed frame. The magnetic dipole μD is given in reduced units of (4πεYσ3/μ0)1/2 and the magnetic field strength B is in [εYμ0/(4πσ3)]1/2, where μ0 is the permeability of free space. The model parameters are then the inverse Debye screening length λ−1, the strength of the dipole μD, the separation d between the location of the point-dipole and the centre of the particle, and the magnetic field strength B. The shift distance is expressed in terms of a dimensionless ratio α = 2d/σ, where σ is the length scale in terms of which the Yukawa potential is defined, offering an estimate of the size of the particle in the absence of a hard core.
Basin-hopping global optimisation
In order to elucidate the structures of colloidal clusters, the putative global minima on the potential energy surface were characterised by basin-hopping (BH) global optimisation.45 For the rigid-body description of the building blocks, the translational coordinates were represented by the Cartesian coordinates of the centre of the particle and the rotational coordinates by an angle-axis representation.59 Although the latter representation introduces a redundant orientational degree of freedom for each axially symmetric particle in this case, it has certain numerical advantages in the context of geometry optimisation.59The basin-hopping global optimisation method relies upon a hypersurface deformation, which results in a reduced configuration space spanned by local minima without altering the energies of any of these minima.45 In practice, the reduced configuration space is explored by proposing steps, each involving a perturbation from the current minimum in both the translational and rotational coordinates for rigid bodies, followed by local geometry optimisation to a minimum. For local minimisations, the limited-memory Broyden–Fletcher–Goldfarb–Shanno (LBFGS) algorithm was used.60 The gradient was calculated analytically.59 The proposed step was accepted or rejected on the basis of a Metropolis (or other suitable) criterion based on the relative energies of the two local minima. Since the objective is to escape from the basin of attraction of the current minimum, step sizes are much larger than those typically used in MC simulations of thermodynamic properties. A fictitious temperature was used to apply the Metropolis criterion. At least five independent basin-hopping global optimisation runs were performed starting from random initial structures and the lowest minimum found was proposed as the putative global minimum. Typically the convergence rate was between 80–100%.
Monte Carlo simulations
We performed Monte Carlo (MC) simulations for a system of N particles in a canonical ensemble, employing a constraining radius and hence an accompanying constraining volume to avoid evaporation. The system was cooled starting from a random configuration. At each temperature, simulations were run for 107, 108 or 109 MC steps, half of which were for equilibration. As the temperature was lowered, the total number of MC steps was gradually increased. Each MC step consisted of N attempts for single-particle translational and rotational moves each. For MC simulation, a quaternion representation was used for rotational coordinates.61 The temperature in the simulation is in the units of εY/kB, kB being the Boltzmann constant, and is referred to as the effective (or reduced) temperature. The step sizes were adaptive to achieve a target acceptance ratio of 0.45. At the lowest temperature, the translational step size was 2 × 10−2 in the reduced units, and the orientational step size was 1 × 10−2.We also performed MC simulations for N = 256 particles in a canonical ensemble under periodic boundary conditions in a cubic box at two packing fractions of ϕ = 0.1 and ϕ = 0.01. For isotropic interactions, the minimum image convention was applied and a spherical cut-off of half the box length was used. The Ewald summation technique was used with conducting boundary conditions for the long-ranged dipolar interactions.62 For MC simulation in the bulk, a unit vector representation was used for rotational coordinates. The systems were equilibrated at effective temperature T = 0.65, and then gradually cooled down to T = 0.1. The simulations were run for 106 steps above T = 0.3 and for 5 × 106 steps at and below T = 0.3, half of which were for equilibration. Each MC step consisted of N attempts for single-particle translational and rotational moves each. The step sizes were adaptive to achieve a target acceptance ratio of 0.45.
The cluster size distribution was obtained by the application of graph theory, where the system structure was treated as an undirected graph, the particles representing the vertices. There exists an edge between any two vertices if the separation between the corresponding particles is below a threshold rc = 1.25, beyond which the screened electrostatic repulsion practically vanishes. The number of connected components and their sizes were determined by the use of a depth first search method.63
The relative shape anisotropy κ2 for the distribution of particles was obtained from estimates of the radius of gyration Rg, asphericity b, and acylindricity c as follows:51
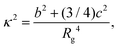 | (2) |
Brownian Dynamics simulations
We performed Brownian Dynamics (BD) simulations in the over-damped limit without hydrodynamic interactions for finite-sized cluster of N = 24 particles. In simulations, the position and orientation of each particle were propagated following a widely used BD algorithm.64 The translational and rotational diffusion coefficients at infinite dilution are given by appropriate Stokes laws with sticky boundary conditions. For BD simulations, the time is expressed in the units of σ2/Dt0, where Dt0 is the translational diffusion coefficient at infinite dilution. Starting from low-energy structures obtained in MC simulations for the N = 24 cluster, several BD simulations were run at T = 0.1 for 108 steps using the time step of Δt = 10−5 in the reduced units. In real units, the total length of these simulation runs was estimated to be 103 s.We thank Prof. Roy L. Johnston, Dr Stefano Sacanna, and Prof. Vinothan N. Manoharan for stimulating discussions. This work was supported by the Engineering and Physical Sciences Research Council of the UK and the University of Birmingham.
References
- H. W. Kroto, J. R. Heath, S. C. O'brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163 CrossRef CAS.
- D. L. Caspar and A. Klug, Cold Spring Harbor Symp. Quant. Biol., 1962, 27, 1–24 CrossRef CAS.
- A. Müller, Science, 2003, 300, 749–750 CrossRef PubMed.
- J. Song, L. Pu, J. Zhou, B. Duan and H. Duan, ACS Nano, 2013, 7, 9947–9960 CrossRef CAS PubMed.
- C. Song, Y. Wang and N. L. Ros, Angew. Chem., Int. Ed., 2013, 52, 3993–3995 CrossRef CAS PubMed.
- A. Benz, S. Campione, S. Liu, I. Montano, J. F. Klem, A. Allerman, J. R. Wendt, M. B. Sinclair, F. Capolino and I. Brener, Nat. Commun., 2013, 4, 2882 CAS.
- L. R. MacGillivray and J. L. Atwood, Angew. Chem., Int. Ed., 1999, 38, 1018–1033 CrossRef CAS.
- A. D. Dinsmore, M. F. Hsu, M. G. Nikolaides, M. Marquez, A. R. Bausch and D. A. Weitz, Science, 2002, 298, 1006–1009 CrossRef CAS PubMed.
- Y. He, T. Ye, M. Su, C. Zhang, A. E. Ribbe, W. Jiang and C. Mao, Nature, 2008, 452, 198–201 CrossRef CAS PubMed.
- R. P. Goodman, M. Heilemann, S. Doose, C. M. Erben, A. N. Kapanidis and A. J. Turberfield, Nat. Nanotechnol., 2008, 3, 93–96 CrossRef CAS PubMed.
- A. W. Wilber, J. P. K. Doye and A. A. Louis, J. Chem. Phys., 2009, 131, 175101 CrossRef PubMed.
- G. M. Whitesides and M. Boncheva, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4769–4774 CrossRef CAS PubMed.
- S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562 CrossRef PubMed.
- S. Sacanna, M. Korpics, K. Rodriguez, L. Colón-Meléndez, S.-H. Kim, D. Pine and G.-R. Yi, Nat. Commun., 2013, 4, 1688 CrossRef PubMed.
- D. Zerrouki, J. Baudry, D. Pine, P. Chaikin and J. Bibette, Nature, 2008, 455, 380–382 CrossRef CAS PubMed.
- Q. Chen, S. C. Bae and S. Granick, Nature, 2011, 469, 381–384 CrossRef CAS PubMed.
- J. W. R. Morgan, D. Chakrabarti, N. Dorsaz and D. J. Wales, ACS Nano, 2013, 7, 1246–1256 CrossRef CAS PubMed.
- F. Li, D. P. Josephson and A. Stein, Angew. Chem., Int. Ed., 2011, 50, 360–388 CrossRef CAS PubMed.
- Y. Min, M. Akbulut, K. Kristiansen, Y. Golan and J. Israelachvili, Nat. Mater., 2008, 7, 527–538 CrossRef CAS PubMed.
- V. N. Manoharan and D. J. Pine, MRS Bull., 2004, 29, 91–95 CrossRef.
- M. A. Miller and D. J. Wales, J. Phys. Chem. B, 2005, 109, 23109–23112 CrossRef CAS PubMed.
- Z. Zhang and S. C. Glotzer, Nano Lett., 2004, 44, 1407–1413 CrossRef.
- E. G. Noya, C. Vega, J. P. K. Doye and A. A. Louis, J. Chem. Phys., 2010, 132, 234511 CrossRef PubMed.
- K. Van Workum and J. F. Douglas, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2006, 73, 031502 CrossRef.
- A. Baskin, W.-Y. Lo and P. Král, ACS Nano, 2012, 7, 6083–6090 CrossRef PubMed.
- S. Sacanna, L. Rossi and D. J. Pine, J. Am. Chem. Soc., 2012, 134, 6112–6115 CrossRef CAS PubMed.
- A. Yethiraj and A. van Blaaderen, Nature, 2003, 421, 513–517 CrossRef CAS PubMed.
- M. Wang, L. He and Y. Yin, Mater. Today, 2013, 16, 110–116 CrossRef CAS PubMed.
- J. Yan, K. Chaudhary, S. C. Bae, J. A. Lewis and S. Granick, Nat. Commun., 2013, 4, 1516 CrossRef PubMed.
- R. M. Erb, H. S. Son, B. Samanta, V. M. Rotello and B. B. Yellen, Nature, 2009, 457, 999–1002 CrossRef CAS PubMed.
- J. E. Martin, R. A. Anderson and C. P. Tigges, J. Chem. Phys., 1998, 108, 7877–7890 Search PubMed.
- J. E. Martin, E. Venturini, G. L. Gulley and J. Williamson, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2004, 69, 021508 CrossRef.
- L. Rovigatti, J. Russo and F. Sciortino, Phys. Rev. Lett., 2011, 107, 237801 CrossRef.
- A.-P. Hynninen and M. Dijkstra, Phys. Rev. Lett., 2005, 94, 138303 CrossRef.
- A.-P. Hynninen and M. Dijkstra, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2005, 72, 051402 CrossRef.
- V. Malik, A. V. Petukhov, L. He, Y. Yin and M. Schmidt, Langmuir, 2012, 28, 14777–14783 CrossRef CAS PubMed.
- P. Keim, G. Maret and H. H. von Grünberg, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2007, 75, 031402 CrossRef CAS.
- L. Baraban, et al. , Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2008, 77, 031407 CrossRef.
- S. K. Smoukov, S. Gangwal, M. Marquezbc and O. D. Velev, Soft Matter, 2009, 5, 1285–1292 RSC.
- P. Tierno, Phys. Chem. Chem. Phys., 2014, 16, 23515–23528 RSC.
- P. R. Cromwell, Polyhedra, Cambridge University Press, Cambridge, 1997 Search PubMed.
- S. Kantorovich, R. Weeber, J. J. Cerda and C. Holm, Soft Matter, 2011, 7, 5217–5227 RSC.
- S. Kantorovich, E. Pyanzina and F. Sciortino, Soft Matter, 2013, 9, 6594–6603 RSC.
- C. N. Likos, Phys. Rep., 2001, 348, 267–439 CrossRef CAS.
- D. J. Wales and J. P. K. Doye, J. Phys. Chem. A, 1997, 111, 5111–5116 CrossRef.
- S. L. Tripp, R. E. Dunin-Borkowski and A. Wei, Angew. Chem., Int. Ed., 2003, 115, 5749–5751 CrossRef PubMed.
- A. A. Abrikosov, S. Sacanna, A. P. Philipse and P. Linse, Soft Matter, 2013, 9, 8904–8913 RSC.
- E. Sanz and D. Marenduzzo, J. Chem. Phys., 2010, 132, 194102 CrossRef CAS PubMed.
- T. Autenrieth, A. Robert, J. Wagner and G. Grübel, J. Appl. Crystallogr., 2007, 40, s250–s253 CrossRef CAS.
- S. Whitelam and P. G. Geissler, J. Chem. Phys., 2007, 127, 154101 CrossRef PubMed.
- D. N. Theodorou and U. W. Suter, Macromolecules, 1985, 18, 1206–1214 CrossRef CAS.
- M. F. Hagan, O. M. Elrad and R. L. Jack, J. Chem. Phys., 2011, 135, 104115 CrossRef PubMed.
- J. J. Juárez and M. A. Bevan, Adv. Funct. Mater., 2012, 22, 3833–3839 CrossRef PubMed.
- D. Klotsa and R. L. Jack, J. Chem. Phys., 2013, 138, 094502 CrossRef PubMed.
- L. D. Michele, F. Varrato, J. Kotar, S. H. Nathan, G. Foffi and E. Eiser, Nat. Commun., 2013, 4, 2007 Search PubMed.
- L. Rovigatti, J. Russo and F. Sciortino, Soft Matter, 2012, 8, 6310–6319 RSC.
- A. Stradner, H. Sedgwick, F. Cardinaux, W. C. K. Poon, S. U. Egelhaaf and P. Schurtenberger, Nature, 2004, 432, 492–495 CrossRef CAS PubMed.
- E. Mani, W. Lechner, W. K. Kegel and P. G. Bolhuis, Soft Matter, 2014, 10, 4479–4486 RSC.
- D. Chakrabarti and D. J. Wales, Phys. Chem. Chem. Phys., 2009, 11, 1970–1976 RSC.
- D. Liu and J. Nocedal, Math. Program., 1989, 45, 503–528 CrossRef.
- D. J. Evans, Mol. Phys., 1977, 34, 317–325 CrossRef CAS.
- A. Arnold and C. Holm, Adv. Polym. Sci., 2005, 185, 59–109 CrossRef CAS.
- S. Even, Graph algorithms, Cambridge University Press, 2nd edn, 2011 Search PubMed.
- G. Mériguet, M. Jardat and P. Turq, J. Chem. Phys., 2004, 121, 6078–6085 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2015 |