Confined surface plasmon sensors based on strongly coupled disk-in-volcano arrays

Abstract

Disk-in-volcano arrays are reported to greatly enhance the sensing performance due to strong coupling in the nanogaps between the nanovolcanos and nanodisks. The designed structure, which is composed of a nanovolcano array film and a disk in each cavity, is fabricated by a simple and efficient colloidal lithography method. By tuning structural parameters, the disk-in-volcano arrays show greatly enhanced resonances in the nanogaps formed by the disks and the inner wall of the volcanos. Therefore they respond to the surrounding environment with a sensitivity as high as 977 nm per RIU and with excellent linear dependence on the refraction index. Moreover, through mastering the fabrication process, biological sensing can be easily confined to the cavities of the nanovolcanos. The local responsivity has the advantages of maximum surface plasmon energy density in the nanogaps, reducing the sensing background and saving expensive reagents. The disk-in-volcano arrays also possess great potential in applications of optical and electrical trapping and single-molecule analysis, because they enable establishment of electric fields across the gaps.

---

1 Introduction

Plasmonic materials, defined as metallic nanostructures that support surface plasmon (SP) oscillations, constitute one of the most explored platforms for chemical sensing.¹ The sensitivity of surface plasmon resonance (SPR) to the dielectric environment in the vicinity of the metal surface forms the basis of many sensors.² In the context of chemical sensors, surface plasmon sensors offer a large range of advantages, including label-free detection,³ small (subwavelength) sensing area,^4,5 massive multiplexing,⁶ easy integration with microfluidics,⁷ and excellent sensitivity.⁸ All these favorable properties motivate intense research activities aimed at the development of different types of SPR-based sensors. Thin metal films,⁹ nanoparticles,^10,11 nanowires,¹² nanohole arrays^13–16 and topologically continuous films^17,18 have been widely investigated for higher sensing performances and practical uses in sensing devices.

With further extension of research it was realized that the key characteristics of a SPR-active substrate are either the nanogaps between the metal nanostructures or sharp features of single nanostructures, which produce high electric field enhancement under resonant excitation.¹⁹ Particularly, structures with small gaps not only provide a great enhancement in sensitivity but also are most efficient in optical and electrical trapping^20,21 and single-molecule analysis.^22,23 Because of the demand of high accuracy for fabricating a nanogap, scanning beam techniques such as electron beam lithography (EBL)²⁴ and focused ion beam lithography (FIB)^25,26 are the main fabrication methods. However, for cheaper translation into practical devices, there is a strong demand to explore the possibility of other low-cost and efficient techniques in fabricating plasmonic materials with the desired nanogaps. Moreover, fabrication of other plasmonic materials with small gaps, exploring the relationship between the unique properties and nanopatterned surfaces and making use of these is still in progress.

Herein, a simple colloidal lithography method is presented to fabricate a disk-in-volcano composite array with narrow gaps between the nanodisks and the wall of the nanovolcanos. We make use of the fact that the plasmon field can be centered inside a nanovolcano structure, and this is further enhanced by a metallic nanodisk in the center. In this way one also achieves narrow gaps for further field enhancement, and we have also shown that these gaps may be used to concentrate the analytes inside. This maximizes the analytical sensitivity up to 977 nm per RIU (refractive index unit) and enables an excellent linear dependence. The fabrication method is versatile, inexpensive and capable of patterning large areas in parallel at low cost and can be applied with only a few sophisticated equipment, yet with good control of structural parameters. Disk-in-volcano arrays with different hole diameters, heights and gap sizes are fabricated, and the corresponding optical performances are investigated.

2 Experimental

2.1 Materials

In all experiments ultrapure deionized water (18.2 MΩ cm) obtained from a Millipore water purification system was used. The glass slides (15 × 30 mm²) used as substrates were cleaned in an O₂ plasma cleaner for 2 min to create a hydrophilic and uniform surface. Polystyrene (PS) spheres with a diameter of 700 nm were purchased from Wuhan Tech Co., Ltd. 1-Methoxy-2-propanol-acetate (MPA) and 16-mercaptohexadecanoic acid (MHA) were purchased from Aldrich. Photoresist (BP212-37 positive photoresist, Kempur (Beijing) Microelectronics, Inc.) was diluted with MPA before use. The silver (99.9%) powder for vapor deposition was purchased from Sinopharm Chemical Reagent Co. Ltd. Carbon tetrachloride and carbon disulfide were purchased from Beijing Chemical Works and were used as-received.

2.2 Fabrication of disk-in-volcano arrays

30 wt%, 40 wt% and 50 wt% photoresists (diluted with MPA) were spin-coated onto the glass substrate cured at 88 °C for 1 h. Next the PS sphere (700 nm) monolayers were deposited on the as-prepared substrate by the interface method.²⁷ Oxygen reactive ion etching (RIE), performed with a Plasmalab Oxford 80 Plus system (ICP 65) (Oxford Instrument Co., UK), was applied for 270 s, 300 s and 330 s, generating PS spheres and circular truncated cones with different feature sizes. The RIE procedure was operated at a pressure of 10 mTorr, a flow rate of 50 sccm, a radio-frequency (RF) power of 100 W and inductively coupled plasma (ICP) power of 100 W. The as-prepared samples were mounted in a thermal evaporator to vertically deposit Ag (99.9%). After that the PS spheres were removed by sonication in toluene and the photoresist was washed away by ethanol, forming a nanovolcano array. Then silver was once again deposited on the as-prepared samples, forming the disks in the cavity. The thickness of Ag in the two deposition processes is controlled to fabricate samples with varied disk heights. But the total thickness is kept the same as 150 nm.

2.3 Finite-difference time-domain (FDTD) simulations

A commercial software package (FDTD Solutions v8.6.3, Lumerical Solutions Inc.) was used to perform the simulation of electromagnetic fields with the same structural parameters as extracted from the actual fabricated samples. The structure was excited by a normally incident, unit magnitude plane wave propagating in the z direction with an electric field polarization along the x-axis. A rectangular unit cell consisting of one unit in the center and four quartering units at the four corners was used under periodic boundary conditions in two dimensions, and perfectly matched layer (PML) boundary conditions were used on the top and bottom surfaces of the simulation domain. The auto non-uniform mesh was chosen in the entire simulation domain for higher numerical accuracy, while the time step Δt ≈ 2.73 × 10⁻¹⁷s was chosen to satisfy the Courant stability conditions. The mesh refinement is the conformal variant 2. Monitors of the frequency-domain field profile and the frequency-domain field and power were placed to calculate the distributions of SP energy and the transmission spectra in the continuous wave (CW) normalization state. The magnitude of the incident electric fields was taken to be unity and the enhancement of electromagnetic fields was evaluated. The optical parameters of Ag and SiO₂ were taken from Palik's handbook.

2.4 Human IgG–anti-human IgG immunoreaction

Disk-in-volcano arrays were firstly incubated overnight in a 4 mM 16-mercaptohexadecanoic acid (MHA) alcoholic solution. Then the protein immobilization experiment was carried out by the physical adsorption of human IgG (DingGuo Biotech. Co. Ltd, 50 μg mL⁻¹) on the MHA modified surface followed by blocking the surface with bovine serum albumin (BSA, 200 μg mL⁻¹). The recognition (DingGuo Biotech. Co. Ltd) was performed using concentrations of 10 μg mL⁻¹ anti-human IgG over 1 h. Before each recognition step, a specificity control experiment was performed using goat anti-rabbit IgG (DingGuo Biotech. Co. Ltd, 25 μg mL⁻¹).

2.5 Characterization

Scanning electron microscopy (SEM) images were taken using a JEOL JSM 6700F field emission scanning electron microscope with a primary electron energy of 3 kV, and the samples were sputtered with a layer of Pt ( ca. 2 nm thick) prior to imaging to improve conductivity. A Shimadzu 3600 UV-vis-NIR spectrophotometer was used to measure the transmission spectra. The RI of the liquids were measured using the Abbe refractometer.

3 Results and discussion

3.1 Fabrication and optical properties of disk-in-volcano arrays

Highly ordered disk-in-volcano arrays with a large area were fabricated based on a well-developed colloidal lithography approach.²⁸Fig. 1 shows the fabrication process of the disk-in-volcano array and a cross sectional schematic of a single disk-in-volcano. In brief, an ordered polystyrene (PS) sphere monolayer was first deposited onto a substrate coated by a photoresin film. Then reactive ion etching (RIE) with increasing duration was carried out to etch the photoresin film. Next, an Ag film was vertically deposited. After the PS spheres and photoresins were removed by toluene and ethanol, respectively, Ag was deposited onto the as-prepared sample once again. Because the bottom hole is larger than the top hole, disks are formed in the cavities, generating small nanogaps between the walls and the disks. In the fabrication process, the period (P), height of the volcano (H), height of the disk (h), and the hole diameters (d/D) are well controlled by the diameter of the PS spheres, thickness of photoresin films, the deposition procedure and the RIE procedure, respectively. The length of the gaps (l) is determined by the relative position between the disks and volcanos.

Fig. 1 Outline of the process for fabricating disk-in-volcano arrays. The central schematic shows a cross section of one disk-in-volcano and main structural parameters. The nanovolcano array in the left bottom schematic is made transparent to stress the relevance of the central structural element.

Fig. 2A and B show scanning electron microscopy (SEM) images of the disk-in-volcano arrays taken from a 30° tilt angle and top view, respectively. Fig. 2C shows the case when the nanovolcano array film is separated from the substrate while the disks are left intact. Moreover, the back of the disk-in-volcano array is shown in Fig. 2D. The red arrows point to the disks inside the volcanos. According to the SEM images the samples show a well-defined volcanic shape with a disk in each cavity. Small gaps emerge between the disks and the walls of the volcano, whose length is calculated and also measured as ≈20 nm according to the geometry and cross-sectional SEM images. Overall through this low-cost and controllable fabrication process, nanovolcano array films with disks in the volcano centers are prepared, generating the key feature of nanogaps. Besides it is noticed that against expectation the top holes possess a wide edge and the length (L) of the disks is a little larger than the top hole diameter. These results are due to the scattering of Ag vapor in the deposition processes. The structure shows a grainy surface, which is due to the RIE procedure and the nucleation process of Ag during the thermo-deposition.

Fig. 2 SEM images of disk-in-volcano arrays from (A) a 30° tilting view and (B) a top view. (C) SEM image of the disk-in-volcano array with the nanovolcano array separated from the substrate and the disks left. (D) SEM image of the reverse side of the sample. In (A–D), the bottom hole diameter D = 340 nm; the top hole diameter d = 220 nm; the height of the volcano H = 250 nm; the height of the disk h = 100 nm; the length of the gap l ≈ 20 nm; the diameter of the disk L = 240 nm; and the total thickness of the film is 150 nm. The red arrows point to disks inside the volcanos. (E) Measured and simulated transmission spectra of the disk-in-volcano array. Simulated distributions of the normalized electric field intensity at the peak wavelengths indicated by the (F) red, (G) blue, and (H) green dots in (E). The white dotted lines indicate positions of the structure. The scale bars correspond to 200 nm.

Fig. 2E presents an experimental transmission spectrum obtained from a substrate with the disk-in-volcano array. Finite-difference time-domain (FDTD) calculations were performed on the analogous structure and are represented as a dashed line. The measured profile is in qualitative agreement with the experimental results, yet there exist some deviations of the peak position and peak intensity. Three peaks appear at 609 nm, 737 nm and 1346 nm in the calculated spectrum, where the two former weak transmission peaks overlap, resulting in a broader resonance at ∼800 nm (P1 peak) in the measured spectrum. The overlap occurs, since the structure used in the simulations is not perfectly the same as the real structure. Because of the feature of the colloidal lithography technique, the inter-volcano space is not uniform, which would lead to a larger peak width. This makes the peaks with small width in simulations overlap in practical experiments. Moreover, the fact that the rough surface is not considered here and the edge is not as sharp as the designed structure assumed in the simulations would also cause the deviations in the peak position and the peak intensity.

FDTD modeling facilitates visualization of the electric field distribution in plasmonic structures. Fig. 2F–H show the time-averaged intensity maps of the total electric field at peak positions indicated by the red, blue and green dots, respectively. At the three wavelengths, strong SP excitation is concentrated in the nanogaps (top edge of the disks). It should be noted that the strong SP excitation appears in an annulus between the disk and the wall, leading to a large excited area. Except for the interaction between the disk and the inner volcano wall, the second major electric field is concentrated on the edge of the holes in Fig. 2F and on the bottom edge of the disk in Fig. 2G. These results indicate that strong localized SPRs (LSPRs) are excited in the disk-in-volcano arrays. Besides, SP energy is not only excited on the edge of the nanodisk but also under the film and in the glass substrate. The area and intensity are much larger than those for a single nanodisk (Fig. S1C†). These results indicate the excitation of a surface plasmon polariton (SPP). This can also be found in previous reports and confirms the fact that SPP and LSPR both can be excited on a structured metal film.²⁹ Considering the above analysis, the two peaks (indicated by the red and blue dots) at the short wavelengths are determined by a combination of SPP along the film and the LSPR concentrated in the gap and the edge of the holes and disks. However, for the P2 peak at 1306 nm, enhanced electric fields are only distributed in the gap (Fig. 2H). This indicates that LSPR excited by the coupling between the disk and the inner wall surface dominates the P2 peak. This conclusion is also supported by the simulated spectra of a single nano-volcano array and single disk array which are artificially separated from the composited disk-in-volcano array (Fig. S1A†). The nanovolcano array shows a peak at 624 nm which is mainly caused by the interaction of the LSPR on the holes and the SPP along the film.³⁰ This corresponds to the peak of the composited film at 607 nm. The disk array shows peaks at ∼700 nm, contributing to both the peaks at 607 and 737 nm. The correspondences prove that the peak at 607 nm derives from the nanovolcano array and disks; and the peak at 737 nm mainly derives from the disk. This is also in accord with the distributions of SP energy in Fig. 2F and G. Although the two figures are similar, there are some specific differences. SP energy is excited around the disk in both Fig. 2G and F, but the latter is much stronger than that in Fig. 2G, especially for the bottom edge of the disk. This indicates that the disk has contributed to both the first and second plasmon peaks, but contributes much more to the second plasmon peak. Furthermore, for the disk arrays the SP is excited on the disk–glass interface (Fig. S1C†) leading to the distribution of the electric field in the glass. For the composed film, LSPRs are excited above the substrate (in the gap) (Fig. S1B†), greatly reducing the substrate influence. This is quite advantageous for the sensing performance,³¹ which will become apparent in the following discussion. In summary, different SP modes and locations of excitation determined by the unique composited nanostructures are responsible for the transmission peaks.

3.2 Effects of structural parameters on optical performances

Disk-in-volcano arrays with different hole diameters are fabricated by controlling etching durations, as shown in Fig. 3A and B. All the other structural parameters are the same as those shown in Fig. 2A. The gaps between disks and the inner wall surface are also almost the same, because the size of the structure is proportionally reduced. As the hole diameter decreases, the intensity of the transmission peaks decreases and the peak positions shift to blue. For the samples with volcano heights of 400 nm and 600 nm, the trends of the change are the same, as the hole diameter decreases (Fig. S2A and B†). As a result more light is transmitted through the larger hole and interacts with the structure. Concluding from Fig. 3, the disk-in-volcano array with a large hole diameter is more appropriate for sensing applications because of the high transmission intensity and a concentration of the field in defined interstices.

Fig. 3 SEM images of disk-in-volcano arrays with hole diameters d/D = (A) 190/300 nm and (B) 150/250 nm. (C) Transmission spectra of the disk-in-volcano arrays with different hole diameters. The structural parameters H, h, and thickness of the film are the same as those in Fig. 2. The scale bars correspond to 500 nm.

Furthermore by applying photoresists with different thicknesses, disk-in-volcano arrays with different heights are fabricated (Fig. 4A and B). The gaps also become larger as the height increases. All other structural parameters are the same as those shown in Fig. 2A. Fig. 4C shows that more than one peak appears in the wavelength range of 400 to 900 nm as the height increases. This results from the fact that the interaction between the disk and the wall becomes much weaker as the height increases and each element would generate peaks by itself. At the longer wavelength, there is little contribution from the single element, and the interaction between the disk and the wall is the dominant element, therefore still keeping one peak. Also as the height increases, the gaps become larger leading to reduced coupling. This results in the reduction in transmission intensity and the red-shift of the peak positions. For the samples with top hole diameters of 190 nm and 150 nm, the trends in the peak position and transmission intensity are the same as the height of volcanos increases (Fig. S2C and D†). Concluding from Fig. 4, disk-in-volcano arrays with small heights, which possess small gaps and strong coupling, would be more appropriate for sensing applications due to the well-identified peak shapes and high transmission intensity.

Fig. 4 SEM images of disk-in-volcano arrays with volcano heights of (A) 400 nm and (B) 600 nm. The insets show the cross sectional SEM images. (C) Transmission spectra of the disk-in-volcano arrays with different heights of the volcano. The structural parameters D, d, L, h and the thickness of the film are the same as those in Fig. 2. The scale bars in the inset images correspond to 200 nm.

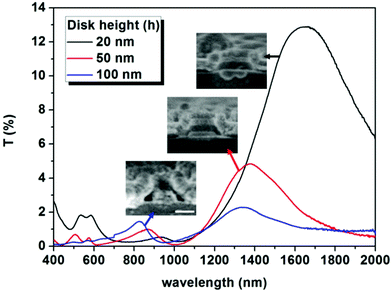
Disk-in-volcano arrays with different heights of disks were fabricated while other structural parameters were kept the same as those shown in Fig. 2A. The structures are shown in the inset SEM images in Fig. 5. For the samples with disk heights of 100 nm and 50 nm, the bottom side of the disks is a little larger than the top side, which results from the scattering of the Ag vapor. For the sample with the disk height of 20 nm the strength of the disk is weak and the thin disk bends to the section. The gap would experience an obvious increase as the height decreases. So the interaction between the disk and the wall would be much weaker as the gap increases, which also can be found in the simulated SP energy distributions of the samples with varied disk heights (Fig. S3†). However, the weakened coupling does not lead to the reduction in transmission intensity shown in Fig. 5, because of the fact that more light that would directly pass through the thinner disk mainly determines the transmission intensity. According to previous results, we consider that a small gap would lead to a strong coupling, resulting in a high sensitivity. Comprehensively considering transmission intensity and sensitivity, both of which are key factors for sensing applications, the three samples with different disk heights were all tested for sensing performances.

Fig. 5 Transmission spectra of disk-in-volcano arrays with disk heights of 20 nm, 50 nm and 100 nm. The insets show the SEM images of the disk-in-volcano arrays with disk heights of 100, 50 and 20 nm from the bottom up. The scale bar corresponds to 200 nm and applies to all the SEM images.

Overall according to the above demonstrations, a disk-in-volcano array with a large hole diameter and small gaps is the optimum selection to be tested for sensing performance, because it possesses high transmission intensity and strong coupling which can result in high sensitivity.

3.3 Sensing performances of disk-in-volcano arrays

For testing the sensing performance, the disk-in-volcano arrays with disk heights of 100 nm, 50 nm and 20 nm were immersed in a series of liquids with increasing refractive index (RI), and the transmission spectra were measured as shown in Fig. 6. Fig. 6A and B show the red-shifts (responding to the changes in RI) of the P1 transmission peaks of the samples with disk heights of 100 nm and 50 nm, respectively. The performance of the P1 peak of the sample with the disk height of 20 nm is not shown because the peak disappears as the RI increases. Significant red-shifts of the peaks are observed in Fig. 6A and B, which further show different sensitivities. Fig. 6C shows linear fits of the P1 transmission peaks in air as a function of the solution refractive index. Good linear responses are observed for both samples. The sensitivities indicated by the slope of the lines are calculated as 866 nm per RIU (the sample with 100 nm disk height, black line) and 977 nm per RIU (the sample with 50 nm disk height, red line), as shown in Table 1.

Fig. 6 Transmission spectra for P1 peaks of the disk-in-volcano arrays with disk heights of (A) 100 nm and (B) 50 nm measured by immersing the samples in a sequence of liquids with increasing RI: CCl₄ (1.46), CCl₄ : CS₂ = 2 : 1 (1.49), CCl₄ : CS₂ = 1 : 1 (1.53) and CS₂ (1.63). (C) Linear fits for the P1 peaks of the two samples.

Table 1 Sensitivity, coefficient of determination and relative RIS of the disk-in-volcano arrays with different disk heights

Peak	Disk height (nm)	Sensitivity (nm per RIU)	Adjust R^2	RIS (RIU^−1)
P1	100	866	0.98924	60
P1	50	977	0.98963	65
P2	100	949	0.99974	50
P2	50	838	0.99785	42
P2	20	834	0.99937	36

---

Moreover, changes of the P2 transmission peaks were also tested with respect to the sensing field. Peak shifts of the three samples are shown in Fig. 7. Linear fits of the peak wavelength vs. RI are shown in Fig. 7D, where a higher linearity is observed for the P2 peaks than for the P1 peaks. The sensitivities of the samples for the P2 peaks with disk heights of 100 nm, 50 nm and 20 nm are 949 nm per RIU, 838 nm per RIU and 834 nm per RIU, respectively. The values for the P1 and P2 peaks all are 2–10 times higher than those of the reported ordered two-dimensional (2D) nanohole arrays (400 nm per RIU),³² random 2D nanoholes (71–270 nm per RIU),^33,34 and nanoparticles and 2D nanoparticle arrays (76–200 nm per RIU).^35,36

Fig. 7 Transmission spectra for the P2 peaks of the disk-in-volcano arrays with disk heights of (A) 100 nm, (B) 50 nm and (C) 20 nm in the same liquids as those of Fig. 6. (D) Linear fits of the peak wavelength with increasing RI for the three samples.

To express the sensitivity in a way equally appropriate for different morphologies and parameters of metallic nanostructures with resonances in the spectral range from visible to infrared, the relative RIS has been introduced by Shumaker-Parry and coworkers.³⁷ The relative RIS is the ratio of sensitivity in eV per RIU to the light energy in eV at the resonance wavelength multiplied by 100% and is defined by the following equation:

ω _r is the resonance energy in units of eV, Δω/Δn the bulk RIS with units of eV per RIU. As shown in Table 1, the P1 peak of the sample with the disk height of 50 nm shows the highest relative sensitivity of 65% per RIU. This value is higher than the highest relative sensitivity of 38% per RIU measured for crescents,³⁷ the highest value of 40% per RIU for hematite–gold core–shells or rices³⁸ and the highest relative sensitivity of 61% per RIU for films perforated with nanoholes.⁸ Besides, the relative sensitivity of the P2 peaks becomes lower as the disk height decreases. Overall each peak of all the disk-in-volcano arrays shows high sensitivity and good linear dependence. Furthermore by tuning structural parameters, optimized samples can be well applied in SPR sensors. The sensitivity of the P1 peak of the sample with the disk height of 50 nm is the highest, but the linear dependence of the P2 peak is better than that of the P1 peak. The sensing performances of the P1 and P2 peaks offer alternative uses suitable for different cases.

The enhanced performance of the robust linear response results from the unique structure. The SP energy density is greatly enhanced because of the small gap between the disk and the inner volcano wall. Moreover, for the P2 peaks, the electric fields are exclusively distributed in regions above the planar substrate (in the gap) which are accessible to detected species. Hence, two essential features of the disk-in-volcano arrays, the more localized and enhanced SP field in the gaps and the full accessibility to the field enhancement region for the detected species, can explain the boost in sensitivity and excellent linear dependence. As the disk height decreases, the gaps become larger which results in weaker LSPR energy (Fig. S3†) leading to a reduction in the sensitivity of the P2 peak. However, an opposite trend is observed for the P1 peak. This can be explained by the different dominating elements for the P1 and P2 peaks. The former peak is determined by the combination of SPP and LSPR. The response resulting from the SPP is more sensitive than that resulting from the LSPR. If the LSPR energy becomes weaker, the SPP contributes more to the sensing performance. So the sensitivity increases as the gaps become larger. Also due to the contribution of the SPP, the P1 peak of the sample with the disk height of 50 nm shows a higher sensitivity than the P2 peak of the same sample. However, for the sample with the disk height of 100 nm, the LSPR is strong and mainly determines the P1 peak, which leads to lower sensitivity than that of the sample with the disk height of 50 nm. Besides, the total energy of the P1 peak for the sample with the disk height of 50 nm is weaker than that of the P2 peak. This leads to a sensitivity increase from the P1 to the P2 peak. Although the SPP would lead to higher sensitivity for the P1 peak, part of the field enhancement is distributed in the glass and is confined on the Ag surfaces, which increases the effect of the substrate. All of the SP energy would not be accessible to the detected species. This makes the linear dependence not as good as that of the P2 peak, which is determined by the LSPR distributed in air. Overall, the P1 peak of the disk-in-volcano array with the disk height of 50 nm shows the highest sensitivity; the P2 peak shows the best linear dependence. The enhancement in the sensing performance and the trend with tuning the structural parameters are well explained by the dominating elements and the distribution of the SP energy.

3.4 Sensor applications of disk-in-volcano arrays

To demonstrate the potential application of the disk-in-volcano array as a label-free biosensor a human IgG–anti-human IgG immunoreaction was carried out. Different from previous sensors, the sensing process can be easily confined in the cavity of the volcano by mastering the fabrication process. The local response is only determined by the LSPR energy in the gap. Therefore because of the strongest coupling the sample with the smallest gap was selected for the test. The process for confined sensing is shown in Fig. 8A–C. In brief, after the first-time deposition of Ag, the as-prepared sample was incubated overnight in a 4 mM 16-mercaptohexadecanoic acid (MHA) alcoholic solution (Fig. 8A). Then a layer of Ag was secondly deposited on the sample to not only form the disk in the cavity but also to cover the MHA grafted onto the outer surface, leaving the MHA in the cavity (Fig. 8B). After that, a protein immobilization experiment was carried out by the physical adsorption of human IgG on the inner surface of the cavity followed by blocking the surface with BSA. The recognition was performed using 10 μg mL⁻¹ anti-human IgG over 1 h (Fig. 8C). Before the recognition step, a specificity control experiment was performed using anti-rabbit IgG.

Fig. 8 (A–C) Schematics of the confined sensing process. (D) Transmission spectra of the disk-in-volcano array experiencing the immobilization experiments. It should be pointed out that, to make the spectra more clear and distinguishable, the curves are normalized (divided by max) and plotted with subsequent vertical offsets of 0.05 for each step.

Fig. 8D shows the spectra of the samples experiencing the immobilization experiments. According to the spectra, the formation of an IgG monolayer induced a ∼12 nm red shift. After the immobilization experiment with anti-rabbit adsorption, the peak shows almost no shift, indicating an excellent specificity. Through the recognition of anti-human IgG, a ∼8 nm red shift of the transmission peak is induced. The red-shift is comparable with those produced by SPP.^3,32 This results from the strong SP excitation in the small gap. For the confined sensing process, the SP energy is efficiently utilized; the sensing background would be much reduced through decreasing the detected area; and this process would save the reagent and make the sensing low-cost, especially if the reagent is extremely expensive and rare. All these favorable properties demonstrate the great potential for the application in advanced sensors.

4. Conclusions

In summary, two elements of a plasmonic structure, nanovolcano arrays and disks, are fabricated and integrated into a designed film through simple and efficient colloidal lithography. SPP, LSRP and the coupling between the two modes are all strongly excited by the composed disk-in-volcano arrays. Different optical performances are shown for samples with varied structural parameters, in which the sample with the smallest gap shows the strongest coupling. All disk-in-volcano arrays show great enhancement in sensitivity and strictly linear dependence based on the unique nanostructure. By tuning the structural parameters, an optimized sample for the response to changes of RI is found. Furthermore by simply changing the fabrication process, the species can be detected exclusively in the cavity, resulting in a confined sensor. This novel sensor concentrates the surface plasmon energy density, reduces the sensing background and saves expensive reagents. Moreover, the disk-in-volcano arrays with small gaps also present great potential in applications of optical and electrical trapping and single-molecule analysis.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (51073070, 51173068, 51373066) and “111” project (B06009).

Notes and references

1. A. G. Brolo, Nat. Photonics, 2012, 6, 709.
2. A. Krishnan, T. Thio, T. J. Kim, H. J. Lezec, T. W. Ebbesen, P. A. Wolff, J. Pendry, L. Martín-Moreno and F. J. García-Vidal, Opt. Commun., 2001, 200, 1.
3. X. Zhang, Z. Li, S. Ye, S. Wu, J. Zhang, L. Cui, A. Li, T. Wang, S. Lic and B. Yang, J. Mater. Chem., 2012, 22, 8903.
4. C. Escobedo, A. G. Brolo, R. Gordon and D. Sinton, Nano Lett., 2012, 12, 1592.
5. C. Escobedo, A. G. Brolo, R. Gordon and D. Sinton, Anal. Chem., 2010, 82, 10015.
6. A. Lesuffleur, H. Im, N. C. Lindquist, K. S. Lim and S.-H. Oh, Opt. Express, 2008, 16, 219.
7. A. De Leebeeck, L. K. S. Kumar, V. de Lange, D. Sinton, R. Gordon and A. G. Brolo, Anal. Chem., 2007, 79, 4094.
8. Y. Li, J. Pan, P. Zhan, S. Zhu, N. Ming, Z. Wang, W. Han, X. Jiang and J. Zi, Opt. Express, 2010, 18, 3546.
9. E. Kretschmann and H. Raether, Z. Naturforsch., A: Astrophys. Phys. Phys. Chem., 1968, 23, 615.
10. P. Mulvaney, Langmuir, 1996, 12, 788.
11. L. M. Liz-Marzán, Langmuir, 2006, 22, 32.
12. H. Wei, S. P. Zhang, X. R. Tian and H. X. Xu, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4494.
13. T. W. Ebbesen, H. J. Lezec, H. F. Ghaemi, T. Thio and P. A. Wolff, Nature, 1998, 391, 667.
14. B. Ai, Y. Yu, H. Möhwald and G. Zhang, Nanotechnology, 2013, 24, 035303.
15. S. Y. Lee, S.-H. Kim, S. G. Jang, Ch.-J. Heo, J. W. Shim and S.-M. Yang, Anal. Chem., 2011, 83, 9174.
16. H. Im, S. H. Lee, N. J. Wittenberg, T. W. Johnson, N. C. Lindquist, P. Nagpal, D. J. Norris and S.-H. Oh, ACS Nano, 2011, 5, 6244.
17. B. Ai, Y. Yu, H. Möhwald, L. Wang and G. Zhang, ACS Nano, 2014, 8, 1566.
18. C. J. Choi, Z. Xu, H.-Y. Wu, G. L. Liu and B. T. Cunningham, Nanotechnology, 2010, 21, 415301.
19. L. Tong, H. Wei, S. Zhang and H. Xu, Sensors, 2014, 14, 7959.
20. I. Ament, J. Prasad, A. Henkel, S. Schmachtel and C. Sonnichsen, Nano Lett., 2012, 12, 1092.
21. A. Kotnala and R. Gordon, Nano Lett., 2014, 14, 853.
22. D. Punj, M. Mivelle, S. B. Moparthi, T. S. van Zanten, H. Rigneault, N. F. van Hulst, M. F. García-Parajó and J. A. Wenger, Nat. Nanotechnol., 2013, 8, 512.
23. T. Sandén, R. Wyss, C. Santschi, G. Hassaïne, C. Deluz, O. J. F. Martin, S. Wennmalm and H. Vogel, Nano Lett., 2012, 12, 370.
24. E. Altewischer, C. Genet, M. P. van Exter, J. P. Woerdman, P. F. A. Alkemade, A. van Zuuk and E. W. J. M. van der Drift, Opt. Lett., 2005, 30, 90.
25. T. Ohno, J. A. Bain and T. E. Schlesinger, J. Appl. Phys., 2007, 101, 083107.
26. B. Brian, B. Sepulveda, Y. Alaverdyan, L. M. Lechuga and M. Kaell, Opt. Express, 2009, 17, 2015.
27. J. Rybczynski, U. Ebels and M. Giersig, Colloids Surf., A, 2003, 219, 1.
28. G. Zhang and D. Wang, Chem. – Asian J., 2009, 4, 236.
29. B. Ai, Y. Yu, H. Möhwald, G. Zhang and B. Yang, Adv. Colloid Interface Sci., 2014, 206, 5.
30. B. Ai, Y. Yu, H. Möhwald and G. Zhang, Adv. Opt. Mater., 2013, 1, 724.
31. A. Dmitriev, C. Hägglund, S. Chen, H. Fredriksson, T. Pakizeh, M. Käll and D. S. Sutherland, Nano Lett., 2008, 8, 3893.
32. A. G. Brolo, R. Gordon, B. Leathem and K. L. Kavanagh, Langmuir, 2004, 20, 4813.
33. A. Dahlin, M. Zäch, T. Rindzevicius, M. Kall, D. S. Sutherland and F. Höök, J. Am. Chem. Soc., 2005, 127, 5043.
34. T. Rindzevicius, Y. Alaverdyan, A. Dahlin, F. Höök, D. S. Sutherland and M. Käll, Nano Lett., 2005, 5, 2335.
35. N. Nath and A. Chilkoti, Anal. Chem., 2002, 74, 504.
36. K. D. Hartlen, A. P. T. Athanasopoulos and V. Kitaev, Langmuir, 2008, 24, 1714.
37. R. Bukasov and J. S. Shumaker-Parry, Nano Lett., 2007, 7, 1113.
38. H. Wang, D. W. Brandl, F. Le, P. Nordlander and N. J. Halas, Nano Lett., 2006, 6, 827.

---

Footnote

† Electronic supplementary information (ESI) available: Simulations of the composited disk-in-volcano array, and disk array and nanovolcano array; transmission spectra and simulated SP energy distributions of disk-in-volcano arrays with varied structural parameters. See DOI: 10.1039/c4nr05206d

---