Critical effect of pore characteristics on capillary infiltration in mesoporous films

Abstract

Capillary phenomena governing the mass-transport (capillary filling, condensation/evaporation) has been experimentally investigated in around 20 different silica thin films exhibiting various porosities with pores dimension ranging from 2 to 200 nm. Films have been prepared by sol–gel chemistry combined with soft-templating approaches and controlled dip coating process. Environmental ellipsometric porosimetry combined with electronic microscopy were used to assess the porosity characteristics. Investigation of lateral capillary filling was performed by following the natural infiltration of water and ionic liquids at the edge of a sessile drop in open air or underneath a PDMS cover. The Washburn model was applied to the displacement of the liquid front within the films to deduce the kinetic constants. The role of the different capillary phenomena were discussed with respect to the porosity characteristics (porosity vol%, pore dimensions and constrictions). We show that correlation between capillary filling rate and pore dimensions is not straightforward. Generally, with a minimum of constrictions, faster filling is observed for larger pores. In the case of mesopores (<50 nm in diameter), the presence of bottle necks considerably slows down the infiltration rate. At such a small dimension, evaporation/capillary condensation dynamics, taking place at the meniscus inside the porosity, has to be considered to explain the transport mode. This fundamental study is of interest for applications involving liquids at the interface of mesoporous networks such as nanofluidics, purification, separation, water harvesting or heat transfer.

---

Introduction

Porosity is intrinsically present in many materials and can be used to tune certain properties such as density, permeability, stiffness, etc. Nowadays, adjusting material porosity during material preparation has become a wide field of research and many strategies have been developed to control the size distribution, the density, the morphology, the interconnection, and the accessibility of pores in association with the processing methods.¹ Nanoporous materials are with no doubt highly interesting since they exhibit enhanced surface area that can reach several hundreds of square meters per gram, promoting thus surface interaction with the liquid or gaseous environments. While fluid behavior in model channels has been intensively investigated by the microfluidic community and is now rather well understood,² this is not the case for nanoporous materials. Indeed, due to the difficulties to analyze fluid conformation and transport in sub-100 nm pores, the literature remains sparse and considerable efforts are still needed to light up this black box. Single linear nanochannels with variable sizes and symmetries could be constructed by top-down nanofabrication recent technologies,³ and were used to address very important matters such as capillary filling,⁴ wall effects related to the Debye double layer,⁵ fast diffusion of heat,⁶ all testifying that fundamental properties of fluids confined in nanopores strongly differ from the bulk. Such top-down fabricated nanochannels are mainly used in nanofluidics for example for proteins and DNA separation and analysis.⁷ However, these are homogeneous single channels, while many 3D nanoporous networks are much more often encountered in conventional applications such as in separation,⁸ sensing,⁹ wetting,¹⁰ heterogeneous catalysis,¹¹ energy transfer,¹² optical thin films,^1betc. For all these domains of application, interactions of the nanoporous materials with liquid phases are crucial aspects that need to be addressed. Indeed, in presence of a liquid phase, one has to take into account the wetting, the natural capillary infiltration and the capillary condensation governed by liquid–vapor equilibriums. Knowing perfectly the structural characteristic of the porosity is of utmost importance to describe and predict dynamic exchanges governing the co-existence of solid–liquid–gas interpenetrated phases.

This work focuses on the relationship between the porous structure (porosity vol% and pore sizes deduced from water adsorption and desorption curves) and the liquid natural infiltration within the latter. To do so, we take advantages of the great variety of mesoporous materials that can be processed as thin coatings by the sol–gel approach, combining inorganic polycondensation, soft-templating and dip-coating.^1b Their preparation as thin layer offers practical experimental advantages such as being able to directly visualize the triple-phases line of a sessile drop standing on the coating flat surface, or the progression of the lateral fluid front during confined capillary filling. Here, in order to keep constant the material surface free energy, all films were composed of silica obtained from acid-catalysed sol–gel method. Selected fluids are water and ionic liquids since they both strongly interact with the matrices due to their high polarity, but differ in viscosity, surface tension, low saturated vapor pressure and thus volatility. Structures of the mesoporous films were assessed using scanning electron microscopy (SEM) and by environmental ellipsometry porosimetry (EEP). It is known that adsorption/desorption phenomena in porous materials can be interpreted in terms of chemical potential oversaturation for the capillary condensation and in terms of pore-blocking effects, cavitation, and equilibrium state for the desorption. In both cases the surface energy of the porous matrix plays a critical role.¹³ However, in the present study and for the sake of clarity in the discussion, we decided to interpret the isotherm and the presence of hysteresis through relative dimensions of pore and bottlenecks deduced from the Kelvin model. As a result, in order to be as consistent as possible, all silica materials were prepared in similar chemical conditions to prevent any large discrepancy in surface energy. The static water contact angle of the final silica materials (plain or porous coating) was measured to be 23° ± 8° and was introduced into the Kelvin's model to deduce the pore size distribution for both adsorption and desorption curves.¹⁴ Optical microscopy is used to follow, in situ and time-resolved, evolutions of liquid/vapor frontiers within the porous materials. In the first part of the article we will show that efficiency in capillary filling is associated to the presence of a steady “capillary ring” formed around a sessile drop. This ring is established and stabilized due to dynamic equilibrium between evaporation, capillary condensation and capillary filling. Its formation is observed in films with relatively high and fairly interconnected porosity. In the second part, the kinetics constants of capillary filling were deduced from the Washburn model using the propagation rate of the liquid front in conditions for which evaporation contribution was hindered. We show that correlation between capillary filling rate (lateral transport within the film) and pore dimensions (extracted from EEP isotherms due to transversal capillary condensation) is not straightforward, making all porous films not suitable as host matrix for liquid infiltration. Indeed the presence of bottlenecks evidenced on EEP isotherms, is found to play a major role especially in the case of mesopores (<50 nm in diameter). Here, evaporation at the moving front cannot be neglected. In particular, at the smaller dimensions, the mass transport driving force is very likely due to evaporation/condensation dynamics at the meniscus and at the pore interface. These results will be of paramount importance to further understand transport of solutes in confined infiltrated solutions for future nanofluidic systems or for heterogeneous catalysts among others.

Experimental

Films preparation

With the exception of the PPN sample, films were labeled with letters corresponding to the block copolymer responsible of the porosity in the sample, followed by a number corresponding to the various recipes used to prepare the films bearing different porosity (see Table 1). All films were processed onto (100) silicon wafers, from acid-catalyzed TEOS (TetraEthylOrthoSilicate – Aldrich) solutions, using dip-coating (ACEDIP from SolGelWay, Paris France, allowing controlled humidity, temperature and speed programing) followed by calcination under IR lamps (10 min at 450 °C). In these conditions, we assume that the free surface energy of the SiO₂ network is the same for each film. Films were deposited at a constant withdrawal speed of 10 mm s⁻¹. Thicknesses vary between 150 and 450 nm depending on the solution.¹⁵ We assume that because pores sizes are smaller than thicknesses, the later has no significant influence on the capillary effects. Component amounts, block copolymer types, and stirring times are reported in Table 1. PS1 and PS2 samples were prepared from initial inorganic solutions composed of 0.113 g of TEOS, 0.055 g of HCl/H₂O 1 M and 3 g of THF that were mixed and stirred for 12 hours. 0.04 g of PS-(80k)-b-PEO-(52k), namely, Polystyrene-b-Polyethylene oxide (obtained by PolymerSouce Inc. having a total molecular weight of 132 000 g mol⁻¹, a PEO weight fraction of 39%, and a polydispersity index of 1.05) was dissolved in 1 g THF before being added to the previous silica solution. The solution was then heated for 15 min at 70 °C in a closed bottle in order to become fully transparent. Then the solution was further stirred for 12 h before dip-coating in controlled atmosphere (RH < 5%, T = 22 °C). The same procedure was used to prepare PS2 films except that the initial silica solution was obtained by dissolving the precursor in 3 g of acetone (instead of THF). For F1 films, 1.94 g of TEOS, 0.23 g of HCl/H₂O 1 M, 0.52 g F127 (Aldrich), 0.81 g of H₂O and 17.5 g of ethanol (Normapur) were mixed and stirred for 12 hours before dip-coating at (RH < 5%). PPN films were prepared following the method already reported¹⁶ in which 20 mg of PS(54k)-b-PLA(36k) (Polystyrene-b-Polylactide obtained following the procedure described by Zalusky et al.¹⁷ having a total molecular weight of 90 000 g mol⁻¹, a PLA volume fraction of 34%, and a polydispersity index of 1.07) and 1 mL of chlorobenzene were mixed and stirred for 1 hour. The solution was spin coated on silicon substrate. The film was then exposed to saturated tetrahydrofuran (THF) vapors for 4 min in a closed glass vessel (0.2 L desiccator) at 25 °C with a reservoir of solvent (10 mL). The film was promptly removed from the vessel and allowed to dry at room temperature for a few minutes. The PLA sacrificial polymer was then selectively eliminated by hydrolysis of the PLA segments for 10 min in basic solution (MeOH, H₂O, NaOH 0.5 M). A second solution containing 4.5 g of TEOS (TetraEthylOrthoSilicate – Aldrich), 0.5 g of HCl/H₂O 1 M, 2 g of H₂O, 1.2 g of CTAB (CethylTriethylAmmonium Bromide – Aldrich) and 57 g of ethanol (Normapur) was stirred at room temperature for 12 hours. The solution was then used for dip-coating (SolGelWay, Paris France) onto the previously prepared nanoporous PS film in dry (RH < 5%) atmosphere. The hybrid sample was then stabilized at 70 °C for 1 h and then directly calcined at 450 °C for 10 min. For the other films, initial inorganic solutions were prepared with TEOS, HCl/H₂O 0.5 M and THF with proportions and aging times reported in Table 1. Final solutions were obtained by addition of the block copolymer (PolymerSource Inc.) into the TEOS solution and mixing also reported in Table 1. In the case of the PS6 sample 1 g of THF was added at the same time with the block copolymer (indicated by a **). In all cases, 1 hour after the addition of the block-copolymer, the solution was heated at 70 °C for 15 minutes to complete the dissolution of the block copolymer before further stirring. It's important to underline that similar solutions processed in different ways led to substantially different porosities. For instance for PS5 and PS6, the inorganic to organic ratio is the same than for PS1 but the dilution and stirring time change producing a thin film that is qualitatively different from PS1 in respect of pore shape. This is due to the well-known evolution of the silica degree of polycondensation related to relative hydrolysis and condensation kinetics. The spinodal phase separation responsible for the formation of the previously mentioned film is indeed very sensitive to the experimental parameters.

Table 1 Amount of inorganic solution, block copolymer and stirring time for the solutions used for the preparation of all the samples. See description in the text for *, **, *** and ****

Sample	TEOS (g)	HCl 0.5 M (g)	THF (g)	TEOS solution stirring	BCP type	BCP (g)	Final solution stirring
PS1	0.113	0.055	3.000	—	PS(80k)-b-PEO(52k)	0.040	12 hours
PS2*	0.113	0.055	3.000	—	PS(80k)-b-PEO(52k)	0.040	12 hours
PS3	0.358	0.174	3.168	4 days	PS(80k)-b-PEO(52k)	0.042	3 days
PS4	0.290	0.141	2.566	4 days	PS(80k)-b-PEO(52k)	0.068	3 days
PS5	0.295	0.144	2.611	4 days	PS(80k)-b-PEO(52k)	0.105	3 days
PS6**	0.290	0.141	2.566	4 days	PS(80k)-b-PEO(52k)	0.102	6 hours
Bj1	0.358	0.174	3.168	4 days	Brij C10	0.187	2 days
Bj2	0.290	0.141	2.566	4 days	Brij C10	0102	1 day
Bj3	0.557	0.271	4.929	4 days	Brij C10	0.392	2 days
F1***	1.940	1.04***	17.50***	—	F127	0.520	12 hours
F2	0.290	0.141	2.566	4 days	F127	0.102	1 day
PBd1	0.374	0.182	3.310	2 days	Pbd(11.8k)-b-PEO-(61k)	0.130	1 day
PBd2	0.474	0.231	4.195	15 days	Pbd(6k)-b-PEO(12k)	0.166	2 days
PS7	0.290	0.141	2.566	1 day	PS(16.4k)-b-PEO(36.4k)	0.102	1 day
PBd3	0.340	0.165	3.009	2 days	Pbd(40k)-b-PEO(60k)	0.117	1 day
PBd4	0.347	0.169	3.071	1 day	Pbd(32k)-b-PEO(43.5k)	0.130	1 day
Bj4	0.450	0.219	3.982	4 days	Brij C10	0.052	2 days
Bj5	0.368	0.179	3.257	4 days	Brij C10	0.086	2 days
PS8	0.350	0.170	3.097	4 days	PS(40k)-b-PEO(38k)	0.122	3 days
PPN****	—	—	—	—	PS(54k)-b-PLA(36k)	—	—

---

Film structural investigation

SEM images were obtained using field emission gun scanning electron microscopy (SEM-FEG) Zeiss Ultra 55 at 45° incidence. Ellipsometry measurements were performed on a UV-visible (from 240 to 1000 nm) variable angle spectroscopic ellipsometer (VASE – 2000 U Woollam), and the data analyses were performed with the Wvase32 software using Cauchy models. Pore volumes were estimated using the Bruggeman effective medium approximation model. Environmental ellipsometry porosimetry was investigated through water adsorption/desorption isotherm using an atmospheric control chamber as previously described.¹⁴ Pore size distributions were calculated using a model based on spherical geometry in the adapted Kelvin's equation.¹⁴ Capillary filling investigation were performed at 25° ± 2 °C and 30% ± 10% relative humidity. Water front propagation was recorded through the PDMS stamp using a Nikon Optiphot 500 optical microscope. Droplet edges for permeable and impermeable films were investigated using an Olympus Stylus 1 digital camera.

Results and discussion

In the present first part, the contact edge of a sessile water drop onto the two PS1 and PS2 typical mesoporous films are investigated and compared. Both films were prepared to have a thickness around 150 nm (deduced from ellipsometry), and similar apparent porosity (pore size around 60 nm and pore volume around 65% estimated from SEM-FEG images and environmental ellipsometry porosimetry (EEP)¹⁴ respectively) as shown in Fig. 1. Adsorption curves of both films show a sudden water uptake above 95% of relative humidity attributed to capillary condensation. At such high relative pressures, deducing the corresponding pore size through the Kelvin model is not relevant since a variation of 2% (sensor nominal error: ±2%) in the humidity reading would induce a considerable error in the corresponding calculated pore dimension. As a result, one can only conclude that the main population of the pores stands above 50 nm in diameter in both films, in agreement with the SEM images. For PS1, the desorption curve almost overlaps the adsorption one, suggesting very limited pore blocking effect associated to a small difference between the bottle-neck and the pore diameters. Therefore, a fairly good interconnectivity exists within the PS1 film porosity. Inversely for PS2, a type-IV hysteresis loop, attributed to bottle-necks. In the latter case, the desorption centered at 55% RH is probably due to cavitation or pore blocking. As a result, PS2 bearing 4.1 nm “bottlenecks” has a porosity that is much less homogeneous than the porosity of PS1. The initial desorption, occurring at around P/P₀ = 90% and concerning 25% of the total volume in the PS2 coating isotherm (Fig. 2f), corresponds likely to the fraction of pores emerging at the coating surface that are thus open to the atmosphere.

Fig. 1 (a), (d) Simplified schemes (b), (e) SEM images (c), (f) EEP adsorption/desorption isotherms (water volume versus relative humidity) of the PS1 and PS2 samples respectively. The lack of hysteresis in (c) suggests an internal structure of the thin film with large bottlenecks.

Fig. 2 (a) Scheme of the phenomena taking place when a water drop stands free on a thin film that allows wicking. (b) Picture and corresponding scheme representing a sessile water drop deposited onto the surface of PS1 and surrounded by its capillary ring. (c) and (d) Zoomed optical images of the triple line showing the presence of the capillary ring in PS1 and no capillary ring in PS2.

The difference in interconnectivity was obtained by varying solubility of the block-copolymer using different solvents. The homogeneous porosity in PS1 was obtained from an initial solution prepared with 100% THF (Fig. 1a–c), as opposed to the presence of small bottlenecks in PS2, for which the solvent was a mixture of 75% acetone and 25% THF (Fig. 1d–f), as described in the experimental section. The higher polarity of the acetone-rich solution decreases the solubility of the PS chains (without inducing precipitation in the present conditions). PS-b-PEO being amphiphilic, it forms discrete spherical micelles in the more polar acetone-rich medium, while it remains not assembled in the less polar THF medium. During liquid deposition, evaporation takes place inducing the simultaneous concentration of silica precursors and polymers as the silica cross-links, rigidifying thus the coating. During this process, micelles co-assemble into a percolated 3D-array of spheres with a minimal degree of coalescence for the acetone containing system. On the other hand, for the acetone-free system, the fast evaporation of THF drives the polymer to aggregate into a continuous 3D network, following a spinodal-type phase separation with the inorganic phase, promoting thus the formation of a homogeneous porosity. After thermal decomposition, both approaches yield coatings bearing a porosity network that corresponds to the inverse of the intermediate polymer network. The precursor to template ratio being identical in both systems, and the organic domain dimensions being fixed by the length of the polymer block, we obtained similar pore volume and pore size, but a more homogeneous interconnected network in pure THF (PS1) system (no hysteresis) than in presence of acetone (PS2). Physical–chemistry aspects governing the formation of different porosities with respect to the applied conditions have been analyzed and detailed for the present PS1 and PS2 cases, but will not be discussed for the other investigated films in Table 1.

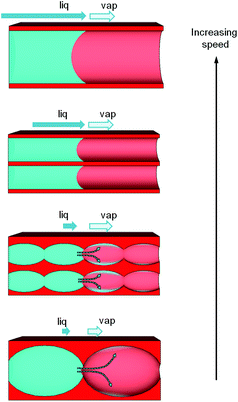
Fig. 2 illustrates what can be observed when a drop of water is deposited at the surface of the porous PS2 and PS1 films. After a few seconds, the sessile drop on the PS1 film is accompanied by a millimeter wide lighter ring formed at its periphery. Zooming on the drop triple-phase line as in Fig. 2b reveals that the latter ring is homogeneous all around the drop, and is stable as long as conditions for evaporation (RH and temperature) are steady. This ring corresponds to a fluctuation of optical interferences, induced by a local increase of the film refractive index, due to the presence of water into the porosity at the vicinity of the drop. We can thus call it “capillary ring”. The mechanism responsible for the establishment of this capillary ring is schemed in Fig. 2a. In the case of a sessile drop onto a porous thin film that allows wicking, the liquid from the drop reservoir enters the porosity and builds a radial flow outward of the triple contact line by capillarity.¹⁸ Evaporation occurs at the drop surface and all over the surface of the capillary ring, inducing a gradient of relative humidity (RH).

One expects thus that the relative humidity at the drop surface corresponds to the saturation (RH = 100%) and progressively decreases to match the ambient atmosphere away from the drop. The relative humidity is thus expected to decrease from saturation to ambient humidity radially from the drop triple line, causing an increase of evaporation rate when getting away from the drop. At a certain critical distance from the triple line, a stationary water-front is established (see Fig. 2a), where capillarity filling rate balances evaporation rate.

This situation can only exist if the relative humidity at the critical distance is inferior to the relative humidity of capillary condensation, which is above 95% in the present case, as deduced from the EEP investigations in Fig. 1c and f. Interestingly, the capillary ring is not observed for the PS2 sample (see Fig. 2d) in the same conditions. It is thus likely that the poorer interconnectivity of the PS2 structure, being the only structural difference with PS1, is responsible for the non-formation of the ring by capillary-driven out-flow from the drop. In other words, it seems that a direct relation exists between the presence of small bottlenecks, revealed by the hysteresis loop on the water adsorption/desorption isotherm (EEP), and a non-efficient capillary-driven filling.

In order to better understand the formation of this capillary ring, three additional films (PS3, PS4 and PS5) were prepared with increasing ratio of the same Block CoPolymer (BCP) (see Table 1) and were submitted to the sessile drop test. Fig. 3 displays the SEM images of the porous structure, the corresponding EEP isotherms, and the optical image of the sessile drop. The EEP adsorption/desorption isotherms are plotted in terms of the refractive index versus the relative humidity for a better comparison. As expected, capillary condensation occurs above 92% RH, suggesting that pores have dimension larger than 30 nm in all considered films. On the other hand, they show that the total volume of accessible porosity increases with the ratio of BCP, from 33% for PS3 to 54% for PS5, passing by 47% for the intermediate PS4. Interestingly, PS3 shows a large hysteresis with two desorption steps likely attributed to pore blocking (two populations) or pore blocking followed by cavitation; PS4 shows a narrower hysteresis attributed to pore blocking; while for PS5, desorption and adsorption curves are almost overlapping revealing limited pore blocking. From these, one can conclude that the bottlenecks are much smaller in PS3 than in PS4, while PS5 has the larger constrictions in its porosity. As can be seen on the corresponding SEM images, PS3 and PS4 samples show a micellar pore structure, responsible for the presence of the hysteresis loop, while PS5 shows a spinodal-phase-separated-type porosity. In accordance with what was previously observed, sessile drop images show that only the structure of PS5 allows the formation of a capillary ring.

Fig. 3 (a) SEM images (scale bar 300 nm) and corresponding images of a water drop deposited onto the surface of PS3, PS4 and PS5 films. Only sample PS5, which has a higher porosity vol%, shows a capillary ring. (b) EEP adsorption/desorption isotherms (film refractive index at wavelength 700 nm versus relative humidity) of PS3, PS4 and PS5 samples.

It confirms what was already demonstrated above that a more “open” or homogeneous porosity favors capillary filling. The same experience was repeated with films having smaller pores obtained with other BCP (see Table 1). In the same way, droplets deposited on films with lower porosity vol% do not generate a capillary ring (data not reported). In our case (3D bottom-up fabricated porous networks) porosities higher than 50% are needed for wicking to be observed. This statement has to be considered with attention since it is obvious that a set of separated parallel open linear channels in a dense matrix would allow capillary filling even for low values of the porosity vol% for the corresponding material. Therefore, the porosity vol% is not a direct and critical parameter by itself. However, it seems that the formation of a high porosity by the present templating approach, promotes the formation of networks with less pore-blocking effect, which then seems to be the critical parameter for efficient capillary filling. This is likely due to the fact that for an increasing content of BCP porogen the mechanism of porosity structuration evolves from a pure spherical-micelle-self-assembly towards a more and more spinodal phase separation assisted one, bearing larger bottlenecks.

In what follows, the dynamics of capillary filling was investigated by recording the advancement of the liquid front in the film porosity using a configuration where the direct transversal evaporation in the atmosphere is significantly hindered by applying a PolyDiMethylSiloxane (PDMS) stamp onto the top of the films (see Fig. 4a). PDMS is used because it permits a good and uniform covering of the film surface and because its transparency allows in situ visualization of the fluid front propagation with the help of an optical microscope. A drop of liquid is then applied at the edge of the stamp and the front progression underneath the stamp, where exchanges with atmosphere are minimized, is recorded using optical microscopy. This experiment was performed with all the different silica films reported in Table 1 using water as the volatile liquid and sometime 1-ethyl-3-methylimidazolium dicyanamide ionic liquid as the non-volatile one. While some films were instantaneously infiltrated by the liquid, some were not at all. For example, no capillary filling was observed underneath the stamp in the case of PS2 films, which is consistent with the absence of a capillary ring. On the other hand, rapid capillary filling was observed for PS1 films. The typical plots of the square of the fluid-front travelled distance L with respect to time t for water (black-squares) and for the ionic liquid (red-triangles), are shown in Fig. 4b for the PS1 film (data not shown for the other films).

Fig. 4 (a) Scheme of the phenomena taking place when a water drop stands at the edge of PDMS top cover (stamp) on a thin film that allows wicking. (b) Graphic displaying the diffusion limited capillary filling of the PS1 porous film with water and with (1-ethyl-3-methylimidazolium dicyanamide) ionic liquid, in the configuration illustrated in (a). Black (points and axes) corresponds to water, while red (points and axes) correspond to the ionic liquid. The initial position of the fluid corresponds to the edge of the PDMS stamp. Dots are experimental points and plain lines are linear fits of the first 20 points of both curves.

The experimental points corresponding to the early stage of the capillary filling with either water or ionic liquid, show that the square of the traveled distance is linear with time, which suggests a diffusion limited transport that perfectly fits expectation from the Washburn theory of capillary filling.¹⁹ The filling with the ionic liquid (red axes) is much slower than the filling for water due to its higher viscosity.²⁰ Interestingly, after 30 s of experiment, the water front tends to slow down more than predicted by the Washburn law, whereas the ionic liquid front still follows the linear regime. This is attributed to the evaporation of water at the advancing front within the porosity. Evaporation rate at the front is limited by the evacuation of the gaseous water outside of the porous network and is thus assumed to be constant during the experiment time frame. Because the liquid front speed progressively slows down with the covered distance, evaporation of water becomes more and more dominant with the front slowing down, a phenomena not accounted for in the classical Washburn prediction but which was reported for single slit nanochannels of less than 20 nm.²¹ This is evidently observed in the case of water and not in the case of ionic liquid as a result of the volatility difference. It has to be noticed that even if no PDMS is applied the ionic liquid fills the porous structure with the same law. Because the ionic liquid has a very low vapor pressure, no PDMS stamp is necessary, and filling the thin film porosity by capillarity can anyway be completed over time. The corresponding filling speed is expressed as the D parameter of the equation from Washburn theory of capillary filling (eqn (1)) and is reported in Table 2.¹⁹

L² = D × t (1)

Table 2 Porosity and capillary filling speed obtained for each analyzed film. Ads. RH and Des. RH correspond to humidity at which adsorption and desorption curves change inflection. SEM Diam. is the pore diameter estimated from SEM images; Ads. Diam. and Des. Diam. are pore diameters deduced from the EEP isotherm; Δ RH = Ads. RH – Des. RH represent the width of the isotherm. The porosity vol% is expressed in % of the whole film volume. D_water and D_IL are capillary filling speeds for water and ionic liquid, respectively. $ calculated using a cylindrical model

Sample	Ads. RH (%)	Des. RH (%)	SEM diam. (nm)	Ad. Diam. (nm)	Des. Diam. (nm)	Δ RH (%)	Por. vol. (%)	D water × 10^−2 (mm^2 s^−1)	D IL × 10^−2 (mm^2 s^−1)
PS6	99.4	97	180 ± 40	*	*	2.4	59	21	4.8
PS5	97.9	97.5	75 ± 20	*	*	0.4	54	7.9	3.8
PS1	96.8	96.5	60 ± 10	*	*	0.3	64	7.6	0.55
PPN	93.4	91.5	20 ± 4	17.1^$	15.2^$	1.9	86	7.0	1.2
Bj1	63.5	52.4	*	5.2	3.8	11.1	58	2.8	0.18
Bj2	59.3	48.0	*	4.6	3.4	11.3	59	2.1	0.020
Bj3	69.3	57.8	*	6.3	4.4	11.5	61	1.9	0.028
F1	68.9	48.0	*	6.2	3.4	20.9	55	1.4	*
F2	75.0	49.2	*	7.8	3.5	25.8	55	0.64	0.013
PBd1	83.5	33.0	*	12.0	2.3	50.5	50	0.21	*
PBd2	80.6	27.0	*	10.2	2.0	53.6	50	0.060	0.00017
PS7	88.5	42.9	*	17.5	3.0	45.6	55	0.044	*
PBd3	91.8	55.4	*	24.3	4.1	36.4	53	0.015	*
PBd4	93.0	60.9	*	27.5	4.8	32.1	53	0.0070	*
PS2	96.0	55.4	60 ± 5	*	4.1	40.6	63	—	—
PS3	93.3	50.5	*	29.9	3.6	42.8	33	—	—
PS4	95.8	69.4	50 ± 10	*	6.3	26.4	47	—	—
Bj4	37.0	22.8	*	2.6	1.8	14.2	32	—	—
Bj5	43.0	39.2	*	3.0	2.7	3.8	46	—	—
PS8	95.2	71.4	55 ± 15	*	6.8	23.8	47	—	—

---

In Table 2, D values are then correlated to the porosity characteristics (pore diameter and porosity) of the corresponding film, deduced from SEM images and/or EEP isotherms shown in Fig. 5, 6, 7, and 8. Pore diameters were calculated from the adsorption and desorption curves of the water EEP isotherm using the Kelvin's equation. The diameter at the desorption was assumed to be representative of the bottlenecks. As mentioned earlier, because EEP is not appropriated to determine pore size above 50 nm,¹⁴ estimation from SEM images was used when capillary condensation occurred above 95% RH. The symbol * is used in Table 2 when the corresponding value has not been determined. In the last two columns the values of the filling speed for water and ionic liquid are expressed as D from (eqn (1)). When no capillary filling could be observed under the PDMS stamps and through the formation of a capillary ring, the symbol – was used.

Fig. 5 SEM images and corresponding EEP adsorption/desorption isotherms (water volume versus relative humidity) of the PS5, PS6, PS1 and PPN samples (top section of Table 2).

Fig. 6 (Left) SEM images, (center) EEP adsorption/desorption isotherms (water volume versus relative humidity) and (right) pore size distribution of the Bj1, Bj2, Bj3, F1 and F2 samples of the intermediate section of Table 2. The samples are reported in decreasing order of the water filling speed.

Fig. 7 (Left) SEM images, (center) EEP adsorption/desorption isotherms (water volume versus relative humidity) and (right) pore size distribution of the PBd1, PBd2, PS7, PBd3 and PBd4 samples of the intermediate section of Table 2. The samples are reported in decreasing order of the water filling speed.

Fig. 8 (Left) SEM images, (center) EEP adsorption/desorption isotherms (water volume versus relative humidity) and (right) pore size distribution of the Bj4, Bj5, PS8 samples of the third section of Table 2.

Table 2 gives an overview of the samples with D values decreasing from top to bottom. Three sections can be roughly identified. The top section gathers films exhibiting larger pores and rather homogeneous porosity as evidenced by the quasi overlapping of the adsorption and desorption curves at high water relative pressure in the isotherm shown in Fig. 5. With the exception of the PPN sample, the typical porosity with limited bottlenecks observed by SEM is clearly originating from a phase separation mechanism. As expected for this type of porosity, larger pore dimension led to faster capillary filling.

Inflection of the adsorption and desorption curves between 30% and 40% RH for the PPN sample are due to internal porosity of the pillars,¹⁶ which is considered to have no significant effect on the capillary filling investigation as discussed later. The intermediate section gathers a set of samples exhibiting a type-IV hysteresis in their isotherms (see Fig. 6 and 7), typical of mesoporosity encountered in films prepared from micellar template. This type of structure is confirmed by the SEM images in Fig. 6 and 7, where more or less interconnected spherical-like pores are clearly evidenced.

These samples show values of pore diameter between 4.6 and 27.5 nm from adsorption, and values between 2.0 and 4.8 from desorption. All films could be infiltrated by capillarity, but in opposition to the top section, no evident relation can be found between pore dimension, or the pore volume, and the capillary infiltration rate in this intermediate section. However, it seems that films that present wider hysteresis (large values of ΔRH) are slower to infiltrate than films with narrower hysteresis, whatever the dimension of the pores and of the bottlenecks. This tendency will be further discussed later.

The last bottom section in Table 2 lists the samples that did not show any capillary infiltration under the PDMS stamp, neither the formation of a capillary ring around the sessile drop. The corresponding SEM images, EEP isotherms and pore size distributions are shown in Fig. 8 (EEP and SEM characterization of PS1, PS3 and PS4 films are already reported above).

All these samples exhibit various types of porosity with more or less wide hysteresis in their isotherm. Amongst these, one would expect that PS3 and PS8 allow capillary filling since their pore and constriction dimensions are close to PBd3 or PBd4 from the intermediate section. However, the porosity of PS3 and PS8 is below 50% vol, against 60% vol for PBd3 and PBd4, which may explain this difference in behavior. Indeed, for equivalent dimensions of pores and bottlenecks, a more porous structure would statistically have a higher number of interconnections (bottlenecks) per pores than a less porous structure. The number of interconnections per pore, that can also be related to the tortuosity taken into account in the Washburn model, strongly affects the liquid front propagation but much less the capillary condensation. In addition, EEP probes the porosity by infiltrating water in the pore under gaseous state and transversally through the film thickness (capillary condensation), while D is deduced from liquid water lateral transport in the film through capillarity. For such reasons, and regarding now all the pore characteristics and related capillary filling efficiency, it is difficult to draw a strict correlation between them. However, it would be interesting to discuss further the role of the bottlenecks and of their dimension with respect to the pore size. To do so, D values listed in Table 2 are plotted with respect to pore size for the two first sections in Fig. 9a and of the intermediate section only in Fig. 9b. Presence of bottlenecks can be visualized since both Ads. Diam. and Des. Diam. are reported. In the case of larger pores, where EEP could not be used to determine their dimension, a continuous bar is used that represents the approximated dimensions measured on the SEM images. First it is clear that samples from the first section allow faster filling than samples of the second section, since increasing the pore diameter (supposing no bottle-necks and uniform channels with thin hysteresis) means an increase of D, as expected from the Washburn theory. The trend in Fig. 9a is thus quasi linear (see the tendency line). The D value of the PPN sample is positioned above the tendency line, which is attributed to the lowest tortuosity associated to the uniformly standing periodical pillar array conformation. This is why such a structure is considered as ideal for fluid transportation in elongated wide thin channels. It is important to underline that the pillar inner porosity composed of 2 nm pores does not govern the filling. If it was the case the D value would be located below the tendency line. Even so, it is clear in Fig. 9 that porosity with smaller pores are associated with much lower D values. Concerning the capillary filling speeds of mesoporous samples from the intermediate section in Table 2, they are found at the left bottom corner of Fig. 9a graphic. This region of the graphic is displayed in Fig. 9b with the D axis given in logarithm scale for a better clarity. Pore and constriction dimensions for each film are linked by a horizontal rod to better visualize the width of the hysteresis. One can first observe that water filling speed ranges over three orders of magnitude while pore and constriction dimensions are found between 2 and 27.5 nm.

Fig. 9 (a) D values versus pore and constriction size. The blue bars correspond to the samples of the top section of Table 2 while the yellow and red points correspond to the mesoporous samples of the intermediate section (dashed line represents the global tendency and a guide for the eyes). (b) Zoom of (a) between 0 and 40 nm.

The bottleneck size (deduced from the desorption curve) ranges from 2 nm to 4.8 nm, while the pore diameter (deduced from the adsorption curve) varies from 4.6 nm to 27.5 nm. Quite anti-intuitively, despite a quasi-constant bottleneck size, films with larger pore size lead to slower filling speed by capillarity. The D value seems to increase linearly with the constriction size and decrease exponentially (logarithmic scale in Fig. 9b) with the pore size. This decrease is counterintuitive in respect of the known laws for liquid capillarity because an increase of pore size should lead to a faster filling even in presence of smaller constrictions. The most convenient way to describe this tendency is to consider the hysteresis width: for samples with small bottlenecks a large hysteresis means a slower filling while for samples with larger bottlenecks a large hysteresis totally inhibits the filling of the porosity. It has to be taken into account that exact values of the filling speed should be compared with caution due to tortuosity and pore volume discrepancies. However, the general tendency reveals that the thinner is the EEP hysteresis, the more efficient is the capillary filling. In order to explain this unexpected behavior, we need to reintroduce the evaporation/condensation equilibrium that establishes at the liquid front within the porous network. As already mentioned, evaporation at the liquid front within the porous network depends on the evacuation of the vapor phase and thus on the pore structure. It is therefore assumed to be constant in the same film during the capillary filling, and one may conclude that a decreasing gradient of vapor pressure exists from the liquid front. Knowing that capillary condensation occurs at vapor pressures below saturation in nanopores due to confinement, it is consistent to expect that evaporated water molecules may recondense in empty pores before the liquid front reaches them. The smaller the pores are, the lower is the critical vapor pressure for capillary condensation. This is to say that capillary condensation has to be seriously considered for smaller pores, for which capillary filling is very slow and condensation is possible for low vapor pressures. The influence of evaporation/condensation dynamics on the liquid front progression can be evidenced by plotting the ratio of D_water/D_ILversus pore and constriction dimensions, as shown in Fig. 10.

Fig. 10 D _water/D_IL values for samples reported in Table 2. The same code of Fig. 9 has been used to express the pore and constriction sizes.

Table 2 recalls that the Ionic Liquid progresses slower than water due to its higher viscosity. The difference in the D_water/D_IL values is attributed to the porosity structural characteristics and to the relative variation of viscosity of fluids in nanoconfinement (this point will be further discussed in the specific case of PPNs in a future article). Increasing the difference between the pore size (adsorption) and the bottleneck size seems to slow down the filling of the ionic liquid much more than in the case of water (even if water itself is slowed down). The ionic liquid has to penetrate in the porosity in a pure liquid way because its vapor pressure can be considered as null while water molecules can also diffuse (see Fig. 4) in the porosity under vapor phase. Here the vapor diffusion follows a Knudsen mode because the pore dimensions are much smaller than the mean free path. In these conditions, the diffusion of water molecules is governed by the collisions with the pore walls and the diffusivity is proportional to the pore dimension. Because IL progresses with no evaporation, D_water/D_IL is expected to remain low if water progression is governed by roughly the same mechanism of the IL (mainly liquid transport). On the other hand, if D_water/D_IL is high, mechanism of capillary filling differs for both volatile and non-volatile liquids (contribution of vapor phase transport). For samples with large pores and “open” porosity gathered in the top section of Table 2, D_water/D_IL fluctuates from 2 to 14, while for the mesoporous films of the intermediate section, D_water/D_IL can reach up to 353. The higher D_water/D_IL values for films bearing smaller pores indicate that the contribution of the capillary condensation, associated to vapor phase transport, to the water front progression is higher for smaller pores.

The mechanism of water filling in such porosities is thus cooperative between capillary filling and capillary condensation. A global picture of the system is illustrated in Fig. 11. In presence of bottlenecks, it is possible to imagine a mechanism of the water filling where the main part of the water molecules that contribute to the advancement of the water front evaporates from the front and condenses again in the next empty pores. The filling attributed to the vapor phase transport being limited by diffusion, the global observed filling rate would anyway follow the same mathematical law than the Washburn theory (with the squared length of the filled channel proportional to the time through a constant D). D includes thus two driving forces for filling that depend in a different way on the porosity characteristics. An adequate mathematical model could be derived here but this is out of the scope of this article. The tendency revealed in Fig. 9b can now be easily explained. For larger pores the relative humidity needed to fill them by capillary condensation is higher than that needed for smaller ones.

Fig. 11 Illustration of the capillary infiltration mechanism in the various porosities, taking into account the pore relative dimension and the presence of constrictions (bottlenecks), and the two driving forces related to liquid capillary transport and vapor capillary condensation. Liquid front progression proceeds faster from the bottom to the top.

Therefore, the time required for the vapor phase to reach the conditions for capillary condensation in the front nearby pores is longer for larger pores than for smaller ones. In presence of constrictions (bottlenecks) it results in a slower progression for larger pores than for smaller pores. It has to be noticed that in the case of porosities with bottle-necks and larger pore sizes the dynamics could be so slow for water, even with the evaporation/condensation mechanism, that no progression was observed.

In these cases, gathered in the last bottom section of Table 2, the critical vapor pressure for water capillary condensation in the front close-by porosity is never reached due to a too slow liquid progression (tortuosity and presence of solid dead-ends) compared to the vapor phase evacuation (diffusion away from the front). Similarly to solid dead-ends in the porous network, water flow blockage could also be related to air-trapping in the pores due to water condensation at the smaller pore intersections between larger pores. This can explain why the PS2 sample doesn't show any filling.

One must recall that evaporation depends on temperature and relative humidity and that the present experiment were performed at 25° ± 2 °C and 30% ± 10% RH as reported in the experimental section. However, the influence of external humidity has been investigated for sample Bj1 from Section 2 of Table 2, for which the transport through cooperative evaporation/condensation at the front prevails. No significant difference in front advancement rate was observed for three different relative humidity values (8%, 30% and 55% RH) applied in a close chamber. This suggests that the time scale of the water vapor exchange between the atmosphere and porosity to reach equilibrium is much longer than that of the evaporation/condensation occurring at the advancing front. In other words, when humidity in the atmosphere is below critical humidity for capillary condensation, the phenomena taking place at the front are not significantly influenced by the external humidity. On the other hand, when the experiment is performed above critical humidity for capillary condensation (at 100% RH), we additionally observed condensation of water at the edge of the PDMS stamp and the propagation of the front underneath the PDMS as expected.

Conclusions

In summary, we demonstrated that liquid natural infiltration in nanoporous materials is governed by a cooperative mechanism, involving liquid transport by capillarity and vapor transport through evaporation at the liquid front followed by capillary condensation. Relative contributions of both driving forces depend strongly on the porosity characteristics (pore volume fraction, relative dimensions of pores and bottlenecks). In the present cases of 3D porosities, a higher pore volume is associated to a lower tortuosity and to a faster capillary infiltration. For pores larger than ≈50 nm, the liquid transport by capillarity dominates and the filling is faster for larger pores as expected from the Washburn prediction, while the presence of constrictions (bottlenecks) tends to reduce the filling rate. In the mesoporous range, the evaporation at the liquid front can no more be neglected, and the capillary condensation dominates the filling when pore size increases and constrictions remain small. In this regime, for similar bottleneck dimensions, the liquid progression is faster with smaller pores than with large pores due to the easiness for the vapor phase to capillary condense in smaller pores. Some porosity shows no liquid infiltration at all, confirming that not all mesoporous materials are efficient for liquid infiltration and one must prefer homogeneous and bottleneck-free types showing narrow hysteresis in adsorption/desorption isotherms. The cooperative transport mechanism described in this fundamental study is also of paramount importance because it is likely to strongly affect the transport of solutes in confined infiltrated solutions in many applicative domains such as heterogeneous catalysts or nanofluidics.

Acknowledgements

We thank David Quéré, Cédric Boissiere and the reviewers for the useful discussions about fluid flow, wetting and contact angle characteristics in micro and nano channels. We also thank David Montero for his support for electron microscopy. Imaging and microanalysis were performed on a Su-70 Hitachi semfeg and a X-Max Oxford EDX detector, instruments facilitated by the IMPC (Institut des Matériaux de Paris Centre FR2482) financially supported by the C'Nano projects of the Region Ile-de-France. Labex Matisse is thanked for funding.

References

1. (a) D. Gu and F. Schüth, Chem. Soc. Rev., 2013, 43, 313–344; (b) C. Sanchez, C. Boissière, D. Grosso, C. Laberty and L. Nicole, Chem. Mater., 2008, 20, 682–737; (c) B. Rühle, M. Davies, T. Lebold, C. Bräuchle and T. Bein, ACS Nano, 2012, 6, 1948–1960.
2. (a) D. Mark, S. Haeberle, G. Roth, F. von Stetten and R. Zengerle, Chem. Soc. Rev., 2010, 39, 1153–1182; (b) S. Marre and K. F. Jensen, Chem. Sov. Rev., 2010, 39, 1183–1202; (c) A. Lenshof and T. Laurell, Chem. Sov. Rev., 2010, 39, 1203–1217.
3. (a) J. L. Perry and S. G. Kandlikar, Microfluid. Nanofluid., 2005, 2, 185–193; (b) S. J. Kim, Y.-A. Song and J. Han, Chem. Soc. Rev., 2010, 39, 912–922; (c) N. Kaji, Y. Okamoto, M. Tokeshi and Y. Baba, Chem. Soc. Rev., 2010, 39, 948–956; (d) F. Persson and J. O. Tegenfeldt, Chem. Soc. Rev., 2010, 39, 985–999.
4. K. M. van Delft, J. C. T. Eijkel, D. Mijatovic, T. S. Druzhinina, H. Rathgen, N. R. Tas, A. van den Berg and F. Mugele, Nano Lett., 2007, 7, 345–350.
5. (a) S. Pennathur and J. G. Santiago, Anal. Chem., 2005, 77, 6782–6789; (b) S. Kim, Y.-C. Wang, J. Lee, H. Jang and J. Han, Phys. Rev. Lett., 2007, 99, 044501.
6. R. Chein and J. Chuang, Int. J. Therm. Sci., 2007, 46, 57–66.
7. (a) G. B. Salieb-Beugelaar, K. D. Dorfman, A. van den Berg and J. C. T. Eijkel, Lab Chip, 2009, 9, 2508–2523; (b) D. Xia, J. Yan and S. Hou, Small, 2012, 8, 2787–2801; (c) T. Yasui, N. Kaji, R. Ogawa, S. Hashioka, M. Tokeshi, Y. Horiike and Y. Baba, Anal. Chem., 2011, 83, 6635–6640; (d) A. Balducci, P. Mao, J. Han and P. S. Doyle, Macromolecules, 2006, 39, 6273–6281.
8. H. Minakuchi, K. Nakanishi, N. Soga, N. Ishizuka and N. Tanaka, Anal. Chem., 1996, 68, 3498–3501.
9. (a) B. V. Harbuzaru, A. Corma, F. Rey, P. Atienzar, J. L. Jordá, H. García, D. Ananias, L. D. Carlos and J. Rocha, Angew. Chem., Int. Ed., 2008, 47, 1080–1083; (b) M. E. Calvo, S. Colodrero, N. Hidalgo, G. Lozano, C. López-López, O. Sánchez-Sobrado and H. Míguez, Energy Environ. Sci., 2011, 4, 4800.
10. P. Kim, M. J. Kreder, J. Alvarenga and J. Aizenberg, Nano Lett., 2013, 13, 1793–1799.
11. A. Corma, Chem. Rev., 1997, 97, 2373–2420.
12. (a) U. Bach, D. Lupo, P. Comte, J. E. Moser, F. Weissortel, J. Salbeck, H. Spreitzer and M. Gratzel, Nature, 1998, 395, 583–585; (b) A. Siria, P. Poncharal, A.-L. Biance, R. Fulcrand, X. Blase, S. T. Purcell and L. Bocquet, Nature, 2013, 494, 455–458.
13. (a) L. Sarkisov and P. A. Monson, Langmuir, 2001, 17(24), 7600–7604; (b) C. Fan, D. D. Do and D. Nicholson, Langmuir, 2011, 27(7), 3511–3526; (c) P. T. M. Nguyen, D. D. Do and D. Nicholson, Langmuir, 2013, 29(9), 2927–2934; (d) V. Kocherbitov and V. Alfredsson, J. Phys. Chem. C, 2007, 111(35), 12906–12913.
14. C. Boissiere, D. Grosso, S. Lepoutre, L. Nicole, A. B. Bruneau and C. Sanchez, Langmuir, 2005, 21, 12362–12371.
15. M. Faustini, B. Louis, P. A. Albouy, M. Kuemmel and D. Grosso, J. Phys. Chem. C, 2010, 114(17), 7637–7645.
16. M. Faustini, M. Vayer, B. Marmiroli, M. Hillmyer, H. Amenitsch, C. Sinturel and D. Grosso, Chem. Mater., 2010, 22, 5687–5694.
17. A. S. Zalusky, R. Olayo-Valles, C. J. Taylor and M. A. Hillmyer, J. Am. Chem. Soc., 2001, 123, 1519–1520.
18. J. Bico, U. Thiele and D. Quéré, Colloids Surf., A, 2002, 206, 41–46.
19. E. W. Washburn, Phys. Rev., 1921, 17, 273–283.
20. E. Quijada-Maldonado, S. van der Boogaart, J. H. Lijbers, G. W. Meindersma and A. B. de Haan, J. Chem. Thermodyn., 2012, 51, 51–58.
21. J. Haneveld, N. R. Tas, N. Brunets, H. V. Jansen and M. Elwenspoek, J. Appl. Phys., 2008, 104, 014309.

---