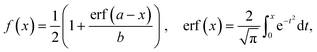Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Separation of cancer cells from white blood cells by pinched flow fractionation†
Marie
Pødenphant
a,
Neil
Ashley
b,
Kamila
Koprowska
b,
Kalim U.
Mir
c,
Maksim
Zalkovskij
d,
Brian
Bilenberg
d,
Walter
Bodmer
 b,
Anders
Kristensen
a and
Rodolphe
Marie
*a
b,
Anders
Kristensen
a and
Rodolphe
Marie
*a
aDTU Nanotech, Ørsteds Plads Building 345east, 2800 Kgs. Lyngby, Denmark. E-mail: rodolphe.marie@nanotech.dtu.dk; Tel: +45 4525 5753
bWeatherall Institute of Molecular Medicine, Department of Oncology, John Radcliffe Hospital, Headington, Oxford OX3 9D5, UK
cGenotype2Phenotype LLC (G2P), One Mifflin Place, Cambridge, MA 02138, USA
dNIL Technology ApS, Diplomvej 381, 2800 Kgs. Lyngby, Denmark
First published on 21st October 2015
Abstract
In this paper, the microfluidic size-separation technique pinched flow fractionation (PFF) is used to separate cancer cells from white blood cells (WBCs). The cells are separated at efficiencies above 90% for both cell types. Circulating tumor cells (CTCs) are found in the blood of cancer patients and can form new tumors. CTCs are rare cells in blood, but they are important for the understanding of metastasis. There is therefore a high interest in developing a method for the enrichment of CTCs from blood samples, which also enables further analysis of the separated cells. The separation is challenged by the size overlap between cancer cells and the 106 times more abundant WBCs. The size overlap prevents high efficiency separation, however we demonstrate that cell deformability can be exploited in PFF devices to gain higher efficiencies than expected from the size distribution of the cells.
1. Introduction
Circulating tumor cells (CTCs) are cells that have been shed from a tumor and entered the blood circulation. When shed from the primary tumor following adaptation to and colonization of the microenvironment of a secondary site, they form metastases which are responsible for over 90% of solid tumor-related deaths.1 CTCs, obtained through a simple venipuncture, can serve as a “liquid biopsy” to monitor tumor characteristics in real-time, including inter- and intratumoral heterogeneity. However, CTC isolation and subsequent characterization are technically challenging due to the low numbers among an abundance of white blood cells. A wide range of analytical methods for CTC detection, enrichment and isolation has been developed. They exploit CTC-specific properties, either biological such as surface marker expression or physical e.g. size, density or stiffness. Most of the available platforms utilize immunomagnetic capture using antibodies targeting the epithelial cell adhesion molecule-1 (EpCAM). Subsequent CTC detection is based on either direct antibody-based methods such as immunocytochemistry (ICC), immunofluorescence (IF) and fluorescence-activated cell sorting (FACS), or indirect nucleic acid-based methods which measure mRNA transcripts by reverse transcriptase-polymerase chain reaction (RT-PCR), or direct DNA isolation and sequencing.2 So far the only Food and Drug Administration (FDA) approved technology for the clinical monitoring of CTC counts in cancer patients is the CellSearch® system (Veridex). This system is based on an initial step of immunomagnetic enrichment of EpCAM-positive cells. Subsequent enumeration of CTCs is done using fluorescent microscopy to identify DAPI-positive, cytokeratin-positive and CD45-negative cells.3 AdnaTest® (AdnaGen AG) is an example of a system combining immunomagnetic enrichment of epithelial (EpCAM-positive) cells with multiplex RT-PCR to identify putative gene transcripts.4 Another strategy for the identification of CTCs is to enumerate and analyze proteins specifically secreted by viable tumor cells by use of EPISPOT (EPIthelial ImmunoSPOT). First CTCs are enriched by negative depletion using CD45 and subsequently cultured on a membrane coated with antibodies that capture secreted proteins such as cytokeratin 19, mucin 1, prostate-specific antigen or fibroblast growth factor 2.5 All antibody-based capture technologies have limitations as they likely capture only a subpopulation of the CTCs. Furthermore, most of them have high initial and running costs and require user specialization which limits wide spread use of these systems. In contrast passive size-separation in microfluidic devices is an alternative approach that is label-free and can potentially be performed on cost-effective single use devices, if they can be mass-produced. Microfluidic separation devices are also easy to operate and have low running costs especially if a simple pressure-driven flow is used to operate the device.6–9Rare cells have been separated from red blood cells (RBCs) and WBCs using different continuous label-free size-separation techniques. A successful separation is usually characterized by high recovery of the cancer cells, high removal of WBCs and RBCs,‡ and high sample throughput.
Geislinger et al. used non-inertial lift forces to sort MV3 skin cancer cells and RBCs with recoveries up to 100% for the cancer cells and a removal of 98% to 99% of the red blood cells.10 This was done at a throughput in the order of 106 cells per min. The MV3-cell line has an average size of 14 μm ± 2 μm, which is within the size range of WBCs, however in this study the removal of WBCs was not investigated. Loutherback et al.11 used deterministic lateral displacement arrays to separate MDA-MB-231 breast cancer cells from diluted whole blood. They measured a recovery of 86% at 10 mL min−1, but with a blood cell removal of only 75%. Bhagat et al.12 used inertial microfluidics to separate MCF-7 and MDA-MB-231 breast cancer cells spiked in whole blood with a recovery over 80% at a throughput of 108 cells per min. They measured a removal of both WBCs and RBCs of over 99%. The MCF-7 and MDA-MB-231 cell lines are relatively large with an average diameter of approx. 18 μm,12 consequently there is no size-overlap between these cancer cells and WBCs and it is not surprising that Loutherback et al. and Bhagat et al. measured such high recoveries and blood cell removals. The average diameter of CTCs is approx. 15 μm, but can be smaller, depending on their origin, which increases the size-overlap between WBCs and CTCs and is thus a challenge for any size-separation technique.
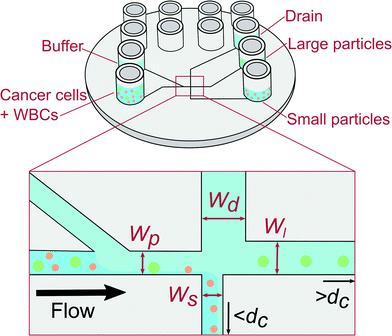
We use pinched flow fractionation (PFF) to separate WBCs from LS174T colon cancer cells. We chose LS174T cell as a convenient well characterised colorectal cancer derived cell line to model CTCs as their characteristics and size closely match those of CTCs. PFF is a continuous size-separation technique first presented by Yamada et al.13 The principle of our PFF devices is shown in Fig. 1. Briefly, a sample containing particles of different sizes is placed in one inlet and a carrier solution is placed in the other inlet. The solutions from both inlets are then pushed into the device, where they meet at a narrow channel called the pinched segment. The particles then get aligned against the channel side-wall under the high flow from the carrier solution, and they follow streamlines according to the position of their center of mass. Downstream, the pinched segment is split into three outlet channels: a small and large particle outlet channel, and a drain channel. Particles with a diameter below and above the critical diameter, dc, will flow towards the small and large particle outlet respectively, while the drain collects most of the buffer fluid to prevent dilution. The critical diameter dc can be adjusted by applying a pressure to the drain outlet and thus the devices can be adapted to any sample. We refer to this operation of the device as adjustable-PFF in the following. The PFF technique was first used to separate microbeads of different sizes using increasingly refined designs.14,15 PFF has also been applied to biological samples and used for separation of RBCs and WBCs,16 and detection of single nucleotide polymorphisms.17 Recently we used PFF to remove fat particles from cow milk samples for improved cell analysis.18
In this paper, we perform the separation of LS174T cancer cells from WBCs using PFF in order to mimic the isolation of CTCs from WBCs. Whole blood samples can rapidly be centrifuged to separate WBCs and CTCs from the remaining blood cells, and separating CTCs from WBCs is thus critical in isolating CTCs. We use LS174T colorectal adenocarcinoma cells as models for CTCs. They have a measured average size of 13.6 ± 2.1 μm, which is closer in size to CTCs than the often used breast cancer cell-lines. The LS174T cells have a large size overlap with WBCs, which vary in size from 5 μm up to 15 μm, see Fig. S1 in the ESI.† In our sample the WBCs have an average size of 7.1 ± 1.0 μm. We could thus expect a good removal of WBCs using an ideal separation with a critical diameter dc of 10 μm i.e. where all particles smaller than the critical diameter end up in the outlet for small particles. However, since the separation is not ideal for particles with a diameter close to dc, we expect the size overlap of the two cell types to decrease the removal of the WBCs. We demonstrate that a difference in cell deformability is the most likely reason for the unexpected separation efficiency, and show that we can exploit the apparent relatively large deformability of the WBCs to achieve both a cancer cell recovery and a WBC removal over 90%, which is better than expected from the size distribution of each cell type.
2. Materials and methods
2.1. Design
The PFF devices have two inlets and three outlets. The first outlet is for particles with a diameter below dc, the second for particles with a diameter above dc, while the third works as a drain for the buffer solution. A sketch of the designs is seen in Fig. 1.The dc of a PFF device with three outlets can be calculated from the channel geometry as follows.19 The flow rate through the pinched segment must equal the sum of flow rates through the outlet channels, due to mass conservation.
| Qpinched = Qsmall + Qlarge + Qdrain, | (1) |
| Qpinched = (1 + α + β)Qsmall, | (2) |
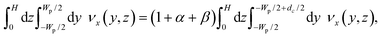 | (3) |
There are many sets of dimensions that yield the desired critical diameter, some more practical than others. The largest cell aggregates are expected to have a size of around 20 μm, therefore the channel height was chosen to be 30 μm to avoid clogging. The lengths were chosen by letting the outlet channels go straight from the pinched segment to the outlets. The injection molded chip has a diameter of 5 cm, so the channel lengths have to be in the centimeter range. Therefore only the channel widths were left to be optimized using eqn (3). We prepared two devices: the first device, referred to as non-adjusted PFF, has a dc that is suitable for separation when applying pressure to the sample and buffer inlet only. The second device has a dc that is adjusted by applying a pressure on the drain. It is referred to as adjustable PFF. The final design parameters are listed in Table S1 in the ESI.† In Table 1 we show that dc cannot be calculated, but must be measured experimentally.
| Calc. dc [μm] | Simulated dc [μm] | Measured dc [μm] | |
|---|---|---|---|
| Non-adjusted PFF | 13.1 | 10.2 | 7.6 ± 0.4 |
| Adjustable PFF | 8.3 | 7.7 | 5.8 ± 0.3 |
2.2. Fabrication
A nickel shim for injection molding was fabricated using standard clean room processes.21,22 A 150 mm silicon wafer was treated with hydrofluoric acid and coated with positive photoresist. The resist was developed and the silicon wafer was etched 30 μm using deep reactive-ion etching. The leftover resist was removed by plasma ashing and acetone. A nickel–vanadium seed layer was sputtered onto the wafer, and a 300 μm thick nickel layer was electroplated on top. Finally the silicon was removed using a KOH etch and the shim was cut out to fit in the injection molder. The devices were injection molded using the polymer TOPAS® 5013L-10 at a mold temperature of 120 °C, a holding pressure of 1500 bar and an injection rate of 20 cm3 s−1 to 45 cm3 s−1. The total injection and cooling time was around 70 s pr. device. The injection molder was equipped with a tool that creates 12 Luer fittings on each chip, which ensures easy connection to the equipment. Finally the microchannels on each chip were sealed with a 500 μm thick TOPAS® 5013L-10 foil using UV-assisted bonding. The chips and lids were exposed to UV-light from a mercury arc lamp for 30 s and then bonded at 120 °C and a pressure of 51 bar for 5 min using a P/O/Weber press.2.3. Cell culture and sample preparation
The following fluorescent polystyrene beads were used for experiments: 2.1 μm blue (Duke Scientific), 5.1 μm green (Magsphere Inc.), 7 μm green (Magsphere Inc.), 10 μm orange (Invitrogen), and 15 μm orange (Invitrogen). Bead solutions were prepared by mixing the different beads with Milli-Q water and 0.1% Triton X-100 to a total concentration of 5 × 105 particles mL−1. The solutions consisted of 15% 2.1 μm beads, 20% 5.1 μm beads, 40% 7 μm beads, 20% 10 μm beads and 5% 15 μm beads. All solutions were degassed in an ultrasonic bath before experiments. Milli-Q water and 0.1% Triton X-100 was used to wet the devices before the sample was introduced, and as buffer solution for all experiments with beads.The human colon adenocarcinoma LS174T cells were obtained from B. H. Tom (Northwestern University Medical Center, Chicago).23 The cell line was cultured in complete Dulbecco's Modified Eagle Medium (DMEM; Life Technologies) supplemented with 10% heat-inactivated fetal bovine serum (FBS; Life Technologies) and 1% penicillin/streptomycin (Invitrogen). Cells were incubated at 37 °C in a humidified environment at 10% CO2 and were grown to 60–80% confluence before next passage or further experiment.
Blood specimens were drawn from healthy donors after obtaining informed consent. All specimens were collected into BD Vacutainer CPT tubes (Becton Dickinson) containing sodium heparin/Ficoll and were processed within 2 hours according to the manufacturer's protocol. Following centrifugation at 1500 × g (room temperature) for 15 min, the white blood cell suspension was collected, washed twice in PBS (1000 × g, room temperature, 10 min), and finally the cells were suspended in FACSFlow.
For separation measurements, LS174T cells were stained with calcein AM (Molecular Probes) and WBC's with either Hoechst 33342 (Thermo Scientific) or CD45-PE (Becton Dickinson), and subsequently mixed in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
Before cell separation experiments devices were wet with degassed Milli-Q water and 0.1% Triton X-100 and then flushed with degassed buffer solution (FACSFlow, BD). All Luer fittings were then emptied and rinsed with FACSFlow to get rid of leftover Triton X-100. FACSFlow was used as buffer solution for all cell experiments.
2.4. Separation measurements
In this study, either solutions containing hard polystyrene spheres or WBCs spiked with LS174T cancer cells were used. In our study we perform an experiment with polymer beads to determine the critical diameter of a PFF separation for hard spheres. Previously, bead separation has mostly been demonstrated on simple solutions containing two bead types that do not overlap in size. These simple solutions do not represent biological samples very well and cannot be used to determine the critical diameter of a system. The bead sample is a blend of fluorescent polymer beads with diameters from 2.1 μm to 15 μm. The size distribution of the beads is continuous and there are small overlaps between beads of different colors, creating a good model system to determine the critical diameter of the separation over a continuous range of values.To conduct separation experiments, samples were pipetted into the Luer fittings on chip and pushed through the device using a pressure-driven flow controller (Fluigent MFCS-EZ). Experiments were monitored using an inverted fluorescence microscope (Nikon Eclipse TE2000-U) coupled to an EMCCD camera (Photometrics Cascade II:512) or a Brunel SP98F inverted fluorescence microscope (Brunel Microscopes Ltd). After experiments, images were taken of all particles in the two outlets and the drain. The images were analyzed using a script in MATLAB version R2013b software to extract the size distribution of each bead or cell type from the fluorescence images. The size of each particle was found by fitting circles to the beads/cells and calculating the corresponding diameter.
2.5. Critical diameter measurements
The separation efficiency of the cancer cell measurements was evaluated by calculating the recovery of cancer cells and the removal of WBCs, which we define as the number of cells in the targeted outlet divided by the total number of cells,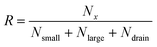 , where Nx is set to Nsmall for WBC removal and Nlarge for cancer cell recovery. No particles went to the drain for most of the pressure settings used in the experiments except for particles appearing very large such as aggregates of cells. After experiments we measured the size of all particles in the outlets, and used the size distributions to determine the critical diameter, dc. For each particle size the probability for going towards the large particle outlet is estimated as the proportion of particles in the large particle outlet. In the ideal case the estimated probability could be described by a step function jumping from 0 to 1 at dc. However particles with a size close to dc have a finite probability for going towards either outlet. The best estimate for dc is determined as the size where particles have a 0.5 probability of going towards the large particle outlet, and this size is found by fitting the estimated probability to an error function modified to output values between 0 and 1:
, where Nx is set to Nsmall for WBC removal and Nlarge for cancer cell recovery. No particles went to the drain for most of the pressure settings used in the experiments except for particles appearing very large such as aggregates of cells. After experiments we measured the size of all particles in the outlets, and used the size distributions to determine the critical diameter, dc. For each particle size the probability for going towards the large particle outlet is estimated as the proportion of particles in the large particle outlet. In the ideal case the estimated probability could be described by a step function jumping from 0 to 1 at dc. However particles with a size close to dc have a finite probability for going towards either outlet. The best estimate for dc is determined as the size where particles have a 0.5 probability of going towards the large particle outlet, and this size is found by fitting the estimated probability to an error function modified to output values between 0 and 1:where a and b are fitted parameters describing position and slope of the function. MATLAB was used to fit the error function to the data. The stated uncertainties in measured parameters correspond to half the distance from the upper to the lower bounds on the 95% confidence interval. Error bars on plots represent the standard deviation. Information on how the error bars were calculated can be found in the ESI.†
2.6. Simulations
The devices were simulated in the finite element simulation software COMSOL version 4.3. The critical diameter of the devices was determined using semi-3D simulations as described by Vig and Kristensen.24 Effects relating to cell deformation were investigated using 3D simulations of a section around the pinched segment. No-slip boundary conditions were applied to all channel walls, and the pressures at the inlets and outlets were set to values used in the experiments. Furthermore it was assumed that particles do not disturb the flow.3. Results and discussion
3.1. Hard sphere measurements
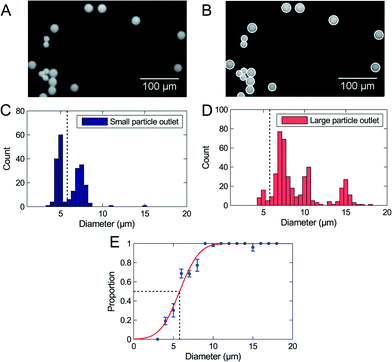
A blend of polymer beads with a broad size distribution was separated by size through the device in order to test the method for determining the critical diameter dc. For the initial experiments the sample flow rates were 30 μL h−1 to 50 μL h−1 depending on the design, and the flow was not adjusted by any pressure at the outlets. The experiments were run until at least 1000 beads had been sorted, equivalent to 2 μL of sample. The setup allows processing of larger samples, however, this would prevent optical visualization of beads in the outlets. All beads were counted and analyzed, and we extracted the critical diameter of the separation using our described method. Fig. 2 shows the result of a separation in an adjustable PFF device. The 2 μm beads are not represented on the figure because they were not fully pinched.The data fits well to the error function, but the analysis method results in a critical diameter of 5.8 μm ± 0.3 μm, which is much smaller than the expected diameter of 8.6 μm. The size distribution in Fig. 2 shows that the majority of 5 μm beads are collected in the small particle outlet, while the majority of 7 μm beads are collected in the large particle outlet. It is therefore reasonable that the critical diameter is in the range 5 μm to 7 μm, as measured.
The bead measurements show that the critical diameter is different from the calculated value. The displacement of beads due to an effect at the end of the pinched segment described by Vig and Kristensen24 could explain this discrepancy. Using semi-3D simulations they showed that at the corner at the end of the pinched segment, streamlines are squeezed closer to the wall than in the pinched segment. This corner effect forces particles to follow streamlines further away from the wall, and will decrease the critical diameter. We made similar semi-3D finite element simulations, and found a modified critical diameter, by measuring the shortest distance from the wall to the outer streamline going into the small particle outlet.
The distance from the pinched segment wall to the outer streamline was measured as 4.2 μm, corresponding to a critical diameter of 8.4 μm, which is close to the value of 8.3 μm found from the calculations. The smallest distance from the corner to the outer streamline was 3.85 μm, corresponding to a critical diameter of 7.7 μm. The same simulation was carried out on both designs, and the simulated critical diameters are summarized in Table 1, together with the critical diameters calculated from the geometry of the designs, and the critical diameters determined from bead experiments.
The corner effect accounts for some of the difference between calculated and measured critical diameter. Other influences on the critical diameter include deviations in the replication of the design during the fabrication and particle disturbances of the flow. The results indicate that the measurement of the critical diameter presented in Fig. 2 is more accurate than the theoretical calculations and the simulations. An advantage of PFF is that the critical diameter can be changed by applying pressure to the outlets. Using our new analysis method, microliter-sized bead samples can be used to find the optimal flow conditions, before experimenting on valuable cell samples.
It has previously been reported that filters with a size of 8 μm work well for cancer cell enrichment,25 thus 8 μm was expected to be the ideal critical diameter. The adjustable PFF devices have a critical diameter that is too small for separation of CTCs and WBCs. It can be increased by applying a pressure at the drain, and it was found that a pressure of 40% of the buffer inlet pressure was suitable such that the critical diameter for hard spheres is 8 μm.
There is no limitation to the adjustability of the dc in a PFF device. However it does not make sense to reduce the dc below the pinching width or increase it above the size of the biggest particles that can flow freely in the device (about 2/3 of the depth).
3.2. Cancer cell separation by PFF
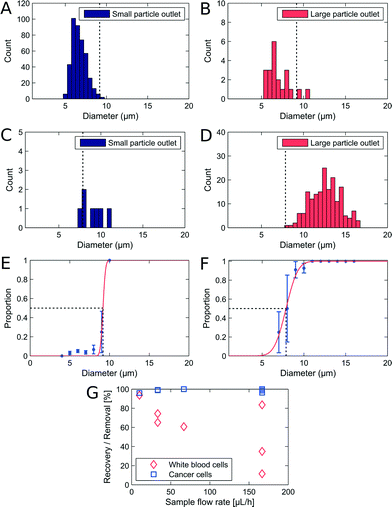
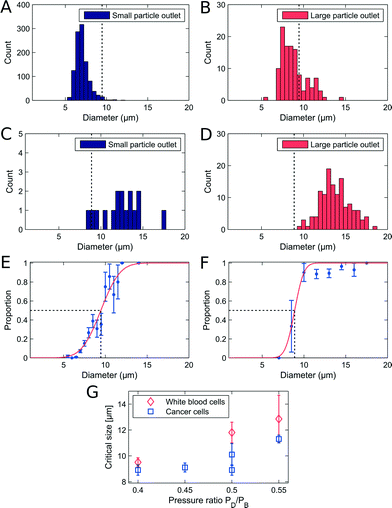
We used non-adjusted PFF devices to separate WBCs and cancer cells. We have measured the critical diameter of the device to be 7.6 μm with polymer beads. The devices were initially run with a sample flow rate of 10 μL h−1. We show the size distribution of each cell type in the small and large particle outlet in Fig. 3A–D. From the histograms we plot the proportion of WBCs in the large particle outlet (Fig. 3E) and of cancer cells in the large particle outlet (3F) as a function of cell size.In the non-adjusted PFF device with a critical diameter of 7.6 μm calibrated with polymer beads, we find at 10 μl h−1 flow rate nearly all WBCs up to a diameter of 9 μm in the small particle outlet, and nearly all cancer cells with a diameter of 7.9 μm and above in the large particle outlet.
The first observation is that the critical diameter for cancer cells is 7.9 μm ± 0.15 μm, similar to polymer beads. However, the critical diameter for WBCs is larger, 9.2 μm ± 2.1 μm. This difference in critical diameter is an advantage and resulted in a recovery of 96% cancer cells together with a removal of 93.6% WBCs. We spiked the WBC sample with LS174T cells at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, however, we observe that in the outlets the WBCs are more frequent. We observed that cancer cells sediment faster in the inlets. Therefore we expect to have a lower frequency for the cancer cells.
1, however, we observe that in the outlets the WBCs are more frequent. We observed that cancer cells sediment faster in the inlets. Therefore we expect to have a lower frequency for the cancer cells.
A good separation that should allow for isolation of CTCs was obtained, however, the experiment was performed at sample flow rates that are too low for applications where at least 10 mL of sample must be sorted. We investigated how increasing flow rates affect the recovery and removal of cells. The results from a series of experiments are seen on Fig. 3G. The CTC recovery is independent of flow rates, however the WBC removal drops rapidly as the flow rate is increased. A possible reason is that the inertia of the WBCs increases with increasing flow rates, and eventually becomes large enough to deflect them from the streamlines going around the corner and into the small particle outlet. This also explains why cancer cell recovery is unaffected, since the cancer cells move along straight trajectories into the large particle outlet. The throughput of a PFF device can be increased by increasing the depth. In our device the depth is limited by the maximum aspect ratio allowed by the nickel electroplating step and the replication in polymer by injection moulding.
3.3. Cancer cell separation by adjustable-PFF
The adjustable-PFF devices were also tested with WBC samples spiked with cancer cells to demonstrate that the critical diameter of PFF devices can be adjusted without loss of separation efficiency. A sample flow rate of 50 μL h−1 was used, and the critical diameter was adjusted by applying a pressure at the drain outlet. The results are shown in Fig. 4A–F.The measured recovery and removal are comparable to the values measured for the non-adjusted PFF devices at equivalent flow rates, see Fig. 3G. Thus we show that PFF devices with an arbitrary critical diameter can be tuned to fit the separation of a specific sample.
A difference in critical diameter between cell types was again observed in the measurements as seen in Fig. 4E. Here the critical diameter of each cell type is plotted for experiments where the pressure on the drain was changed relative to the pressure on the buffer inlet. As expected the critical diameter for both cell types increases with an increasing pressure on the drain, and the critical diameter of the WBCs stays above the critical diameter of the cancer cells, thus ensuring that the overall separation efficiency is high. The difference in critical diameter is an advantage and is exploited to get a better separation than expected from the overlapping size distributions.
3.4. How cell deformability influences PFF
We demonstrated that WBCs have a larger critical diameter than cancer cells in a PFF device. We can estimate that the difference in dc for the WBCs and the cancer cells improves the removal of WBCs from 85.8% to 93.6%.§ A possible source of error on the critical diameter measurements is that cancer cells are expected to be less spherical than WBCs. This would lead to an overestimation of the shortest axis of the cancer cells when measured by fluorescence imaging. The critical diameter of cancer cells would then be overestimated, which would mean that the difference in critical diameter between WBCs and cancer cells is indeed even more pronounced that we observe here. We hypothesize instead that the difference in critical diameter is due to a difference in deformability at high shear rate/deformation that would make the cancer cells appear more rigid than the WBCs and explain why they had a measured critical diameter closer to the one for beads (7.6 μm).Our hypothesis may seem contradictory with the result of mechanical studies on cancer cells such as AFM studies26,27 that show cancer cells are more deformable than other cells. However, in most mechanical measurements of cells, the Young's modulus is measured locally.28 In our device, the whole cell is deformed in a Pouiseuille flow in a capillary as described elsewhere.29–33
We investigated three possible effects in the PFF devices that could make the cell deformability influence the critical size of the cell separation: The elongation flow when cells move from the sample inlet channel to the pinched segment, the shear rate in the pinched segment, and squeezing at the corner between the pinched segment and the outlet channels.
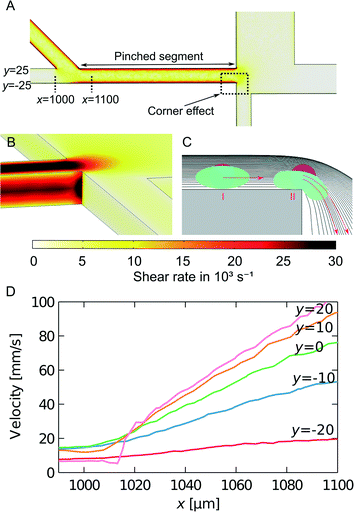
We model the shear rate experienced by cells when travelling from the inlet to the pinched segment by finite element simulations, as seen in Fig. 5A. The largest cell deformation is expected to be at the corner at the end of the pinched segment, where the corner effect causes hard spheres or cells to change to streamlines further away from the wall, whereas soft cells can deform and follow the streamlines they occupy in the pinched segment. We estimated the shear rates at the corner between the pinched segment and the small particle outlet channel using 3D simulations. The results from the simulations are seen in Fig. 5B. The shear rate is constant along the wall and then increases at the corner to approx. 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s−1 for a sample flow rate of 33 μL h−1. This is much larger than the shear rates used by Beech et al.34 to deform red blood cells in lateral displacement structures. Thus the shear rates are large enough to deform soft cells, which will then get an increased critical diameter, while hard cells will get a decreased critical diameter due to the so-called corner effect. This is illustrated in Fig. 5C. The high shear rates combined with the corner effect enhance the separation of hard and soft particles with overlapping sizes, which is very advantageous when separating cancer cells from WBCs.
000 s−1 for a sample flow rate of 33 μL h−1. This is much larger than the shear rates used by Beech et al.34 to deform red blood cells in lateral displacement structures. Thus the shear rates are large enough to deform soft cells, which will then get an increased critical diameter, while hard cells will get a decreased critical diameter due to the so-called corner effect. This is illustrated in Fig. 5C. The high shear rates combined with the corner effect enhance the separation of hard and soft particles with overlapping sizes, which is very advantageous when separating cancer cells from WBCs.
Increasing the throughput of the device must be achieved while keeping the flow velocity and shear rate at the same level. This is possible by increasing the depth of the device.
We have also estimated the shear rate in the pinched segment. A top-view 3D simulation of the pinched segment is seen in Fig. 5A. The illustrated plane is at a middle height, and the highest shear rate is found along the wall in the pinched segment. For a sample flow rate of 33 μL h−1 the maximum shear rate is approx. 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s−1. It is in the same order of magnitude as the shear rate at the corner and is expected to contribute to cell deformation as well.
000 s−1. It is in the same order of magnitude as the shear rate at the corner and is expected to contribute to cell deformation as well.
Finally when cells move from the sample inlet channel to the pinched segment, they experience an increase in velocity due to the incoming fluid from the buffer inlet. Simulations were used to investigate this elongation flow. It is assumed that the cells travel at a height in the middle of the channel. The velocity along streamlines starting at different positions in the sample inlet is plotted in Fig. 5D. The plot shows that the cells move at a constant velocity and then experience a linear velocity change as they move into the pinched segment. The change in velocity gives rise to a shear rate equal to the slope of the velocity curve. As opposed to the other cell deformation contributions, the shear rate from the elongation flow depends on the position of the cells before they are aligned. This could therefore decrease the separation efficiency. However the maximum shear rate is approx. 1000 s−1, which is much smaller than the shear rates along the wall and at the corner of the pinched segment. Thus elongation flow is not expected to contribute to cell deformation.
In our device the cells are in contact with the channel wall when they experience high shear rate. The time scale is much smaller than the relaxation time (1.1 s for WBCs in ref. 35). This situation may be comparable to the situation of margination studied by Fedosov et al.35 In this study, the shear rate is in the order of 100 s−1 and the deformation is 5%. Others report deformability up to 30% for WBCs adherent to a surface under similar conditions (in ref. 35 and references therein). We estimate that the cells experience a shear rate more than two orders of magnitude larger in our PFF device. We can thus reasonably expect that cancer cells and WBCs would deform 4% and 17% respectively in order for their size to appear to be 7.6 μm at the time of the separation.¶ Considering the rather large deformation, the observation that cancer cells have a larger nucleus may be relevant to our discussion and could explain why above a certain deformation, the cancer cells appear less deformable than WBCs. This has already been exploited by Tang et al., who used microfilters to separate cancer cells from whole blood. They observed that WBCs were able to deform and squeeze through 6.5 μm filters, while cancer cells were caught because of their rigid nucleus.36
Finally, in this discussion it may be important to consider the dynamics of potential deformations. In our experiment the cell viability is not expected to change since Hur et al.30 did not see a significant change when using inertial focusing with high shear stresses to classify cells according to deformability. This may be due to the very short exposure to high shear rates as it is in contrast with the loss of cell viability at prolonged flow above 300 s−1 reported by Barnes et al.37
We have shown that the high shear rate combined with the corner effect in PFF devices may be the reason for the improved separation of cancer cells and WBCs. It should be noted that cell deformation has previously been used to improve other microfluidic size-separation devices based on deterministic lateral displacement arrays34 and inertial microfluidics.30
4. Conclusion
We have separated cancer cells and WBCs at efficiencies over 90% using injection molded PFF devices. We measured the size of all separated cells and showed that there is a significant difference in critical diameter between WBCs and cancer cells. We suggest this comes from a difference in cell deformability, which improves the separation efficiency. We have used finite element simulations to investigate the cell deformation at three critical places on the devices, and the largest contribution is the shear rate at the corner of the pinched segment, just before the separation.We have demonstrated that the critical diameter of PFF devices can be changed successfully without a loss of separation efficiency. The highest separation efficiencies were obtained at sample flow rates of 10 μL h−1. At higher flow rates the cancer cell recovery was unaffected, whereas the WBC removal decreased. We believe the WBC trajectories changed because of increased inertia of the cells. Further investigations are needed to determine the exact cause and improve the PFF design, so a higher sample throughput can be accomplished without a decrease in WBC removal.
Acknowledgements
The authors gratefully acknowledge funding from the European Commission under the Seventh Framework Programme (FP7/2007–2013) under grant agreements number 278204 (Cell-o-matic).References
- A. F. Chambers, A. C. Groom and I. C. MacDonald, Nat. Rev. Cancer, 2002, 2, 563–572 CrossRef CAS PubMed.
- C. Alix-Panabières and K. Pantel, Lab Chip, 2014, 14, 57–62 RSC.
- S. Riethdorf, H. Fritsche, V. Müller, T. Rau, C. Schindlbeck, B. Rack, W. Janni, C. Coith, K. Beck and F. Jänicke, et al. , Clin. Cancer Res., 2007, 13, 920–928 CrossRef CAS PubMed.
- T. Fehm, O. Hoffmann, B. Aktas, S. Becker, E. F. Solomayer, D. Wallwiener, R. Kimmig and S. Kasimir-Bauer, Breast Cancer Res., 2009, 11, R59 CrossRef PubMed.
- C. Alix-Panabières, J.-P. Vendrell, M. Slijper, O. Pellé, E. Barbotte, G. Mercier, W. Jacot, M. Fabbro and K. Pantel, Breast Cancer Res., 2009, 11, R39 CrossRef PubMed.
- D. Gossett, W. Weaver, A. Mach, S. Hur, H. Tse, W. Lee, H. Amini and D. Di Carlo, Anal. Bioanal. Chem., 2010, 397, 3249–3267 CrossRef CAS PubMed.
- X. Zhe, M. L. Cher and R. D. Bonfil, Am. J. Cancer Res., 2011, 1, 740 Search PubMed.
- L. R. Huang, E. C. Cox, R. H. Austin and J. C. Sturm, Science, 2004, 304, 987–990 CrossRef CAS PubMed.
- H. W. Hou, M. E. Warkiani, B. L. Khoo, Z. R. Li, R. A. Soo, D. S.-W. Tan, W.-T. Lim, J. Han, A. A. S. Bhagat and C. T. Lim, Sci. Rep., 2013, 3, 1259 Search PubMed.
- T. M. Geislinger and T. Franke, Biomicrofluidics, 2013, 7, 044120 CrossRef PubMed.
- K. Loutherback, J. D'Silva, L. Liu, A. Wu, R. H. Austin and J. C. Sturm, AIP Adv., 2012, 2, 042107–042107 CrossRef PubMed.
- A. A. S. Bhagat, H. W. Hou, L. D. Li, C. T. Lim and J. Han, Lab Chip, 2011, 11, 1870–1878 RSC.
- M. Yamada, M. Nakashima and M. Seki, Anal. Chem., 2004, 76, 5465–5471 CrossRef CAS PubMed.
- J. Takagi, M. Yamada, M. Yasuda and M. Seki, Lab Chip, 2005, 5, 778–784 RSC.
- Y. Sai, M. Yamada, M. Yasuda and M. Seki, J. Chromatogr. A, 2006, 1127, 214–220 CrossRef CAS PubMed.
- C. Cupelli, T. Borchardt, T. Steiner, N. Paust, R. Zengerle and M. Santer, Microfluid. Nanofluid., 2013, 1–13 Search PubMed.
- A. Larsen, L. Poulsen, H. Birgens, M. Dufva and A. Kristensen, Lab Chip, 2008, 8, 818–821 RSC.
- M. Pødenphant, R. Marie, T. Olesen, M. Matteucci and A. Kristensen, Microelectron. Eng., 2014, 124, 53–57 CrossRef.
- K. B. Andersen, S. Levinsen, W. E. Svendsen and F. Okkels, Lab Chip, 2009, 9, 1638–1639 RSC.
- H. Bruus, Theoretical microfluidics, Oxford University Press, USA, 2008, vol. 18 Search PubMed.
- S. Tanzi, P. F. Østergaard, M. Matteucci, T. L. Christiansen, J. Cech, R. Marie and R. Taboryski, J. Micromech. Microeng., 2012, 22, 115008 CrossRef.
- P. Utko, F. Persson, A. Kristensen and N. B. Larsen, Lab Chip, 2011, 11, 303–308 RSC.
- B. H. Tom, L. P. Rutzky, M. M. Jakstys, R. Oyasu, C. I. Kaye and B. D. Kahan, In Vitro, 1976, 12, 180–191 CrossRef CAS PubMed.
- A. L. Vig and A. Kristensen, Appl. Phys. Lett., 2008, 93, 203507 CrossRef.
- G. Vona, A. Sabile, M. Louha, V. Sitruk, S. Romana, K. Schütze, F. Capron, D. Franco, M. Pazzagli and M. Vekemans, et al. , Am. J. Pathol., 2000, 156, 57–63 CrossRef CAS PubMed.
- M. J. Rosenbluth, W. A. Lam and D. A. Fletcher, Biophys. J., 2006, 90, 2994–3003 CrossRef CAS PubMed.
- S. E. Cross, Y.-S. Jin, J. Rao and J. K. Gimzewski, Nat. Nanotechnol., 2007, 2, 780–783 CrossRef CAS PubMed.
- B. D. Hoffman and J. C. Crocker, Annu. Rev. Fluid Mech., 2009, 41, 259–288 Search PubMed.
- H. Noguchi and G. Gompper, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 14159–14164 CrossRef CAS PubMed.
- S. C. Hur, N. K. Henderson-MacLennan, E. R. McCabe and D. Di Carlo, Lab Chip, 2011, 11, 912–920 RSC.
- M. Abkarian and A. Viallat, Soft Matter, 2007, 38, 653–657 Search PubMed.
- M. J. Rosenbluth, W. A. Lam and D. A. Fletcher, Lab Chip, 2008, 8, 1062–1070 RSC.
- O. Otto, P. Rosendahl, A. Mietke, S. Golfier, C. Herold, D. Klaue, S. Girardo, S. Pagliara, A. Ekpenyong, A. Jacobi, M. Wobus, N. Toepfner, U. F. Keyser, J. Mansfeld, E. Fischer-Friedrich and J. Guck, Nat. Methods, 2015, 12, 199–202 CrossRef CAS PubMed.
- J. P. Beech, S. H. Holm, K. Adolfsson and J. O. Tegenfeldt, Lab Chip, 2012, 12, 1048–1051 RSC.
- D. A. Fedosov and G. Gompper, Soft Matter, 2014, 10, 2961–2970 RSC.
- Y. Tang, J. Shi, S. Li, L. Wang, Y. E. Cayre and Y. Chen, Sci. Rep., 2014, 4, 6052 CAS.
- J. M. Barnes, J. T. Nauseef and M. D. Henry, PLoS One, 2012, 7, e50973 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Figure with measured reference sizes, table with design parameters and note on how error bars were calculated. See DOI: 10.1039/c5lc01014d |
| ‡ Recovery is calculated as the percentage of cancer cells in the targeted outlet compared to the total number of cancer cells in all outlets. Removal is the percentage of blood cells removed from the targeted outlet compared to the total number of blood cells in all outlets. |
| § Counting all WBCs larger than 7.9 μm in the small particle outlet as being in the large particle outlet. |
| ¶ Assuming dc decreases from 7.9 μm (cancer cells) and 9.2 μm (WBCs) to 7.6 μm (beads). |
| This journal is © The Royal Society of Chemistry 2015 |