Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Microfluidic droplet handling by bulk acoustic wave (BAW) acoustophoresis†
Ivo
Leibacher‡
*,
Peter
Reichert‡
and
Jürg
Dual
Institute of Mechanical Systems (IMES), Department of Mechanical and Process Engineering, Swiss Federal Institute of Technology (ETH Zurich), Tannenstrasse 3, CH-8092, Zurich, Switzerland. E-mail: leibacher@imes.mavt.ethz.ch; reichert@imes.mavt.ethz.ch; Web: http://www.zfm.ethz.ch/~leibacher Tel: +41 44 632 52 93
First published on 3rd June 2015
Abstract
Droplet microfluidics has emerged as a prospering field for lab-on-a-chip devices, where droplets serve as liquid vessels e.g. for biochemical reagents. Key to the fluid processing in droplet format are the controlled droplet handling and movement on the microscale. Hence this paper proposes droplet handling by combining droplet microfluidics with bulk acoustic wave (BAW) acoustophoresis. BAW acoustophoresis has formerly focused on cell and particle handling, whereas here we determine the various abilities of this method for the field of droplet microfluidics. In silicon microdevices, water-in-oil droplets of 200 μm size were generated for a set of unit operations including droplet fusion, focusing, sorting and medium exchange around 0.5–1 MHz acoustic frequency. Compared to existing droplet handling methods, the shown method is simple in fabrication, robust in operation and versatile to meet the needs of various droplet processing microfluidic devices.
1. Introduction
The miniaturization of fluid handling has led to the prospering field of “droplet microfluidics”.1–5 At the microscale, surface tension forms fluid samples into stable, separate droplets, which are – like a vessel – compartmentalizing a fluid of interest for fluidic laboratory procedures. A main goal is the processing of droplets, i.e. reagents, on microfluidic devices termed “lab-on-a-chip” or μTAS.6–8 Droplet microfluidics matches the demand towards fast, high-throughput, cheap, portable and batch-compatible fluidic instruments. Vast application possibilities of droplet microfluidics range from biological experiments9,10 (where droplets are biological samples or containers for cell encapsulation),11 pharmaceutics12 and chemical reactions13 (where droplets are reaction vessels replacing macroscopic beakers and test tubes) to material synthesis14 (based on droplet-shaped material structures).In the branch of segmented flow microfluidics, droplets are dispersed in an immiscible carrier fluid, as it is the case in this paper. Often water-in-oil droplets are employed because of their potential in experimental biology,9 where each droplet is a microfluidic analog to an aqueous fluid sample in a test tube, separated by an inert carrier oil. This droplet format offers many advantages for fluid handling at the microscale, once the droplet handling is enabled. An alternative to segmented flow microfluidics is called digital microfluidics, where discrete sessile drops are handled on planar substrates of open microfluidic platforms.15
For droplet handling, hydrodynamic,16 electric17 and acoustic forces18 can be employed amongst others, as reviewed in literature.2,19,20 An ideal handling method is a contact-free, controllable external force field which acts selectively and on demand on dispersed fluid droplets. Acoustic methods, termed “acoustofluidics” or more specific “acoustophoresis” in this context, fulfill these criteria. Unlike other methods, acoustophoresis works on a broad range of droplets with few physical requirements, as long as droplets differ from the continuous liquid in terms of density and speed of sound. Compared to electric methods, acoustic methods are simple and robust in terms of manufacturing and operation, since they do not require in-chip electrodes close to the fluidic channel. Furthermore, a high biocompatibility of acoustic methods has been reported,21 which is crucial for biological samples such as a cell-in-droplet.
Regarding acoustic droplet handling, most work so far has been dealing with surface acoustic waves22 (SAW). In segmented flow microfluidics, an acoustic field is generated in PDMS microchannels on a piezoelectric ground plate with interdigitated transducers (IDT). The acoustic field acts on droplets by acoustic radiation forces23 or acoustic streaming.24 Also in digital microfluidics devices, SAW are employed for droplet handling.15,25 Compared to the earlier work on SAW acoustophoresis, our method differs as it builds on a bulk acoustic wave (BAW) approach. BAW are defined as compressional waves in a solid that propagate through the bulk material (here a silicon microdevice), whereas SAW propagate along the surface of a material (as e.g. the mentioned piezoelectric ground plate). BAW acoustophoresis has formerly been studied for the handling of cells and particles, as recently reviewed in a tutorial series.26 In BAW acoustophoresis, an ultrasonic standing wave is generated in a fluid-filled channel by a bulk piezoelectric transducer rather than by IDTs. The piezoelectric transducer excites bulk waves and resonance in channels within an acoustically hard material, often silicon. Comparisons between the SAW and BAW will be discussed.
In this paper, we propose the BAW approach for droplet handling unit operations such as droplet fusion, focusing, sorting and medium exchange, all with one acoustophoretic method. The novel contribution of this paper lies in the combination of droplet microfluidics with BAW acoustophoresis, which offers application potential for various droplet processing microfluidic devices.
2. Operating principle
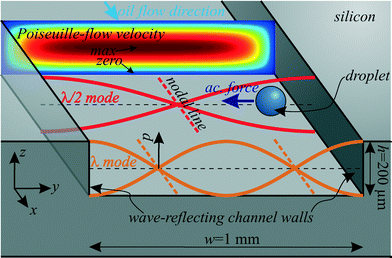
The platform for the following acoustophoretic droplet handling operations consisted of microfluidic channels (width w = 1 mm, height h ≈ 200 μm) in a silicon substrate, as illustrated in Fig. 1 and 2.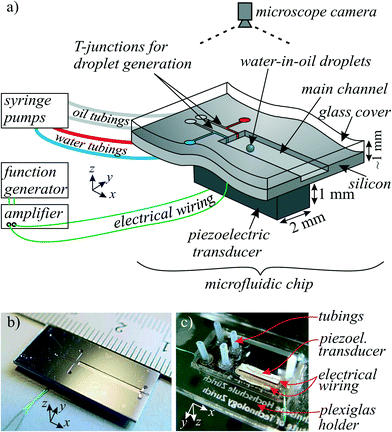 | ||
| Fig. 1 a) Sketch of the microfluidic device and setup for acoustophoretic droplet handling. b) Photograph of the device front side with centimeter scale. c) Photograph of the device back side. | ||
Water-in-oil droplets (silicone oil) were generated with T-junction27,28 and flow focusing device (FFD)28 geometries (detailed in the Methods & materials section) and were moving downstream in a continuous flow inside the channel. Droplet diameters ranged from 100 μm to 250 μm.
To generate an ultrasonic field within the fluidic domain, a piezoelectric transducer was glued underneath the channel, transforming a sinusoidal voltage into mechanical vibration at a tunable frequency f = ω/(2π). This BAW excitation design is known from cell and particle acoustophoresis and is often called “transversal resonator”.29 The piezoelectric substrate excites bulk waves in the silicon and in the silicone oil. The characteristic acoustic impedance Z = ρc (density times speed of sound) is much higher for the acoustically hard silicon than for silicone oil. Therefore, a large part of the bulk waves is reflected at the fluid/structure interface30 at the left and right channel walls, and they can be modeled approximately by hard wall conditions.31 This boundary then results in certain fluid resonance modes across the channel width w, when a traveling wave is superposed with a counter propagating reflected wave to result in a standing wave. Resonance occurs when a standing wave of n·λ/2 = w fits between the reflecting left and right channel walls with n = 1,2,3… for the first, second and third harmonic and the acoustic wavelength λ. The corresponding resonance frequencies are fresn = ccn/(2w) with the speed of sound cc in the continuous phase liquid (silicone oil). If the transducer is tuned to such a resonance frequency, this leads to the formation of an ultrasonic standing wave in the fluid. As an example, the first and second resonance modes with λ/2 and λ across the channel are shown in Fig. 2. Since the channel height is h ≪ λ/2, no disturbing resonances in z-direction are expected.
These standing wave fields exert acoustic radiation forces on acoustically contrasting droplets within the continuous phase liquid. For spherical droplets/particles with radius r ≪ λ (long-wavelength range) far away from walls and other droplets, the acoustic radiation force F can be calculated with the Gor'kov potential32 in the acoustic domain. For a droplet in a 1D standing wave field as shown in Fig. 2 with plotted pressure p(y,t) = pA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(kyy)e−iωt, the analytic calculation for the force Fy in y-direction yields33
cos(kyy)e−iωt, the analytic calculation for the force Fy in y-direction yields33
Fy = F·ey = 4πΦkyr3Eac![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(2kyy) sin(2kyy) | (1) |
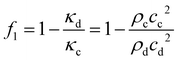 | (2) |
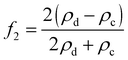 | (3) |
The fluiddynamic system had a small Reynolds number Re ≈ 0.01, small Weber number We ≪ 1 and small Bond number Bo ≪ 1, which means that surface tension and viscous forces advantageously dominate over inertial and gravity effects. This leads to stable, discrete droplets and controllable laminar flows.
Despite the low Bond number, the water droplets slowly sediment in the suspending oil. Due to a hydrophobic channel coating, the droplets wet the channel walls only slightly upon contact. However, sedimented droplets tend to move slower in the oil flow than droplets in the channel center because of the oil flow profile which has zero fluid velocity at all channel walls (no-slip condition). More precisely, the oil flow in the main channel can be approximated analytically with a Poiseuille-flow35 as also plotted in Fig. 2. The movement of the water droplets in x-direction is determined by the drag forces (Stokes' drag) of this Poiseuille-flow.
Regarding the scaling with the droplet size, acoustophoresis is also expected to work with droplets of a smaller size around 10 μm, since acoustophoresis is also capable of handling micrometer-sized cells.36 The acoustic radiation force scales down with the droplet volume according to eqn (1), yet for the handling of small droplets the force can be increased by a higher acoustic frequency (typically up to 10 MHz in BAW acoustophoresis)37 or a higher pressure amplitude. However, towards the lower micrometer range, a crossover from radiation force-dominated droplet motion to acoustic streaming-induced, drag force-dominated droplet motion is expected,38 because the Stokes' drag scales linearly with the droplet radius (unlike the radiation force which scales linearly with the droplet volume).
The components of the acoustofluidic system comprise several resonances.39 First, the ultrasonic standing wave in the water is a fluid resonance. Secondly, the silicon device structure has certain structural resonance modes. Thirdly, the piezoelectric transducer has coupled electromechanical transducer resonances (e.g. the thickness modes) which can be characterized mechanically as well as electrically. All three resonances interact with the whole acoustofluidic system, and they can also be coupled to each other. Ultimately it is a strong fluid resonance which drives acoustophoresis. However, ideally the structural and the transducer resonance frequencies are designed to match the fluid resonance frequency. Once all three resonance frequencies are matched, even lower power is required at the transducer to excite strong acoustophoretic forces.
3. Methods and materials
3.1 Fabrication
Microfluidic channels were dry-etched ∼200 μm deep in a silicon wafer (425 μm thick) by an inductive coupled plasma (ICP) system. The T-junction and FFD nozzles for droplet generation were designed to have a width of 40–60 μm. Fluidic inlets and outlets were provided by back side etching of holes at the channel ends. The wafer front side was covered with a glass wafer (thickness 500 μm) by anodic bonding. To achieve hydrophobic channel walls as required for water-in-oil droplets, the channels were flushed with a hydrophobic agent (Aquapel) and then dried in an oven (50 °C, 30 min).To connect the syringe pumps with the chip, teflon tubes (0.75 mm inner diameter) were first flanged with the “Easy flange kit” (Cetoni GmbH), then positioned on the chip with instant adhesive and glued and sealed with epoxy adhesive. The silicon chips were then mounted on laser-cut 2.5D Plexiglas holders of microscopy slide size, 75 mm × 25 mm.
3.2 Excitation
To excite a mechanical vibration, a piezoelectric transducer was cut to a size of 9 mm × 2 mm out of a 1 mm thick plate of Ferroperm piezoceramics Pz26. This piezoelectric block was glued on the bottom of the device with conductive epoxy (Epo-Tek H20E). For electrical excitation, the top and bottom electrodes of the piezoelectric block were connected to a function generator (Tektronix AFG 3022B) with a power amplifier (ENI 2100L) in between. The applied excitation voltages were in the range of 40–70 Vrms. As described in literature,40,41 frequency modulation around the estimated acoustophoretic resonance frequency can be employed to result in a more robust device operation.3.3 Droplet generation, dispersed and continuous phase liquid
The dispersed phase liquid was deionized water with density ρd= 998 kg m−3 and speed of sound cd = 1497 m s−1 at room temperature.31 For the continuous fluid, we chose silicone oil (Dow Corning 200 fluid) with kinematic viscosity v = 20 cSt, dynamic viscosity η = 19 mPa s, density ρc = 947 kg m−3 and surface tension γ = 0.0206 N m−1 to air at 25 °C. In flow focusing nozzles, except in the fusion experiments, ~0.1% surfactant (Span 80) was added to the oil for enhanced droplet generation and to stabilize the droplets.27 As in earlier work30 (section 3.1), the speed of sound cc of the silicone oil was determined by a pulse-echo time measurement (with an Olympus Panametrics 5800PR). With 1 MHz and 5 MHz transceivers for longitudinal waves, we measured cc = 1004 m s−1 in the silicone oil.Water-in-oil droplets were mostly generated with T-junctions,27,28 which is an established method to provide monodisperse droplets. Fig. 3 illustrates the design more precisely, where droplets pinched off in a ~50 μm wide channel and were then moved to a 1 mm wide main channel, where acoustophoresis was intended. With this geometry, depending on the flow rate of water and oil, droplets with diameters from 100 μm to 250 μm were generated in the dripping or squeezing regime,28 depending on the capillary number, which relates surface tension to viscous forces. The high aspect ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 between channel depth and width might also have promoted the droplet break-up as in step emulsification.42 To actuate the fluid flows, up to 4 syringe pumps (Cetoni neMESYS) were connected to the channel inlets.
1 between channel depth and width might also have promoted the droplet break-up as in step emulsification.42 To actuate the fluid flows, up to 4 syringe pumps (Cetoni neMESYS) were connected to the channel inlets.
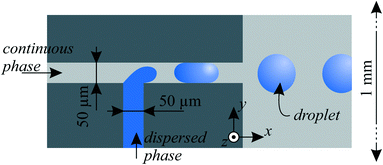 | ||
| Fig. 3 Droplet generation in microfluidic channels with a T-junction geometry. The channel depth was etched 200 μm in z-direction in the silicon substrate. | ||
The hydrodynamic steady state simulation in Fig. 5c was obtained with a FEM software (Comsol Multiphysics).
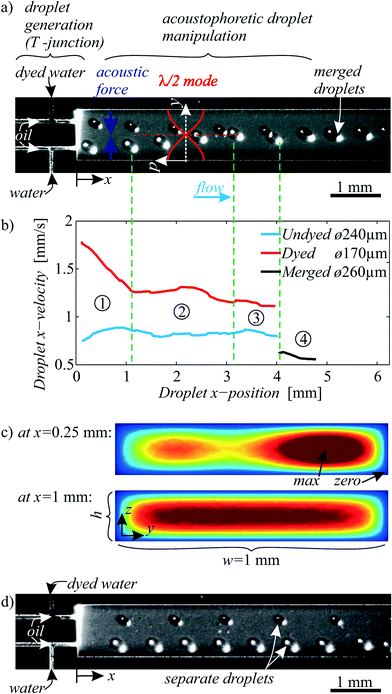 | ||
| Fig. 5 a) Generation and subsequent fusion of light and dark droplets by acoustophoresis for fluid sample handling applications. Piezoelectric excitation generated an acoustic field in the main channel, which was tuned to a resonance mode at 464 kHz with λ/2 from the upper to the lower channel wall. Droplets in the field experienced an acoustic radiation force towards the pressure node on the channel centerline. A corresponding “ESI† Movie S1” is available online. b) Droplet velocities tracked by video analysis. c) Simulated oil flow velocity in the main channel cross section. d) The same experiment as in a), yet without ultrasound is shown as a negative control, where droplets did not merge. | ||
3.4 Optical setup
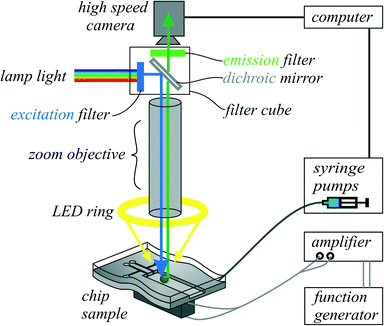
Videos and images were recorded with a high-speed camera (HiSpec 1 Mono, Fastec Imaging) mounted on an objective (Navitar 12× UltraZoom). The reflective silicon devices were illuminated from top as in bright-field microscopy: the light of a LED lamp was introduced in parallel to the optical axis by a half-transparent mirror. Because of the high reflectivity of silicon, this lighting setup resulted in bright illumination as required for high-speed imaging. For droplet and particle motion analysis by feature tracking, we employed a video analysis software (Xcitex ProAnalyst).3.5 Fluorescent imaging
The experiments of Fig. 6 with fluorescent fluids and particles were observed with the setup in Fig. 4 including a zoom microscope (Zeiss Axio Zoom V16).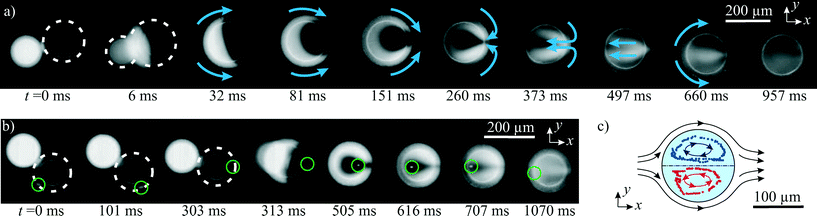 | ||
| Fig. 6 a) Acoustophoretic droplet fusion in a time series, stitched together from 10 frames of high-speed fluorescent imaging. Mixing of the fluorescein-dyed droplet with the undyed water droplet was observed despite the low Re number. (Droplet ∅ ≈ 200 μm, excitation at 463 kHz, total oil flow rate 33 μl min−1. The corresponding video sequence is shown in the “ESI† Movie S1”.) b) Fusion experiment with a cell-surrogating fluorescent particle (encircled green) in the droplet. c) The tracked particle paths (dotted) reveal the flow field (arrows) in the droplet. | ||
As a fluorescent dye, we chose fluorescein with a maximum excitation wavelength of λex,max = 485 nm and a maximum emission wavelength of λem,max = 515 nm. Fluorescent polystyrene particles (Kisker PFP-6052) with a diameter of 6–7.9 μm were used. These particles have a maximum excitation wavelength of λex,max = 470 nm and a maximum emission wavelength of λem,max = 480 nm. To visualize the fluorescence, a filter set (Zeiss 38HE) with an excitation filter, an emission filter and a dichroic mirror was chosen. Out of the spectrum of the incoming white light (from a Zeiss HXP 200c lamp), an excitation filter was filtering wavelengths from 450 nm to 490 nm. The filtered light was reflected with a dichroic mirror in the direction of the camera axis towards the sample. The fluorescent fluid and particles to be investigated were then emitting light at a higher wavelength, which passes the dichroic mirror (beam splitter: 495 nm). The emission filter was a band pass from 500 nm to 550 nm. Additionally, a white LED ring light was attached, so the channel borders became visible as white lines.
4. Results and discussion
4.1 Droplet fusion
All but the simplest fluidic laboratory procedures require two fluids to be mixed. Hence in droplet microfluidics, fusion of two droplets enables reaction initiation, reagent dosing, dilution and incubation of cells which are suspended in droplets. Droplet fusion is the microfluidic analog to pipetting two samples together in a macroscale test tube.In Fig. 5a, the on-demand one-to-one merging of two droplets in continuous flow was induced by focusing them on the channel centerline (corresponding to a pressure nodal line) with BAW acoustophoresis. A resonance mode with a standing pressure wave of λ/2 = w across the channel width w = 1 mm was tuned. The resonance frequency of f = 464 kHz was found to perform best in the experiment. A simple 1D calculation gives fres1 = cc/λ = (1004 m s−1)/(2 mm) = 502 kHz, which is 8% higher than in the experiment. Such differences are usually found, since the complex 3D fluid–structure coupled acoustic problem with compliant silicon boundaries is only vaguely approximated by the 1D calculation with hard wall boundaries. A control experiment without ultrasound in Fig. 5d illustrates a parallel movement of the dyed and undyed droplets without merging.
As soon as the two droplets come close at a position around x = 4 mm, additional hydrodynamic effects and secondary acoustic forces37 (similar to Bjerknes forces) come into play. In general, for two close-by droplets of similar material properties, the secondary acoustic force leads to an attraction of the droplets to each other. The primary acoustic radiation forces according to eqn (1) were generally much stronger than secondary acoustic forces in our experiments, however the primary forces decrease to zero in the pressure node on the channel centerline, so there the secondary forces might be influential.
In Fig. 5b, the droplet kinematics was studied by video tracking. In step (1), the dyed and undyed droplet enter the main channel, driven by an oil flow (15 μl min−1 in total) and with a rate around 1–10 Hz in our experiments. The dyed droplet was faster, denoting a higher oil flow rate in the upper T-junction, which results in the qualitatively simulated flow profile at x = 0.25 mm in Fig. 5c. Therefore, and also because the flow rate was smaller for the dyed water (0.2 μl min−1) than for the undyed water (0.5 μl min−1), the dyed and undyed droplet were generated with a different size: Higher oil flow rate and lower water flow rate lead to the generation of smaller water droplets at the T-junction. The diameter of the undyed droplet was larger than the channel height h = 190 μm, whereas the dyed droplets were smaller than the channel height. Hence the undyed droplets were squeezed in z-direction to a disk-like shape, whereas the dyed droplets remain spherical. In step (2), as simulated in Fig. 5c the oil flow profile is equilibrated to a Poiseuille-flow (like in Fig. 2), yet the droplet contact with the channel top and bottom slowed the large undyed droplets down. The faster dyed droplet was therefore found to catch up with the larger droplet, resulting in a synchronized fusion of droplet pairs in step (4). The merged droplet was even slower due to friction at the channel top and bottom.
Fig. 5 shows not only the fusion, but also the focusing of droplets on the channel centerline. Analog to the focusing of cells/particles in microfluidic systems,43 such focusing of droplets is meaningful e.g. prior to droplet counting and detecting steps. Besides channels of rectangular crossection like here, BAW acoustophoresis is advantageously known to work also in tubes with circular crossection44 for 2D focusing in the tube center. This allows simple droplet focusing without sheath flows, with similar application potential as the focusing of cells in flow cytometry.45
Good fluid mixing within the droplet is crucial for many applications, yet mixing is difficult at low Reynolds numbers. Therefore, we assessed the mixing within the droplets by fluorescence microscopy. (The fluorescent imaging setup is outlined in chapter 3.5) Fig. 6a shows the fusion of a pure water droplet (dark) with a fluorescently dyed water droplet (fluorescein, appears white). In the image series, good mixing was observed to happen in less than a second. Further studies19,46 give a more detailed insight into the fluiddynamic mixing behaviour of coalesced droplets.
In Fig. 6b, a cell-surrogating fluorescent particle was placed in the pure water droplet, which can serve as a container for cell studies.11 This particle followed the fluid flow in the droplet according to Stokes' drag. By tracing the particle in a video analysis software, the internal fluid flow in the droplet was observed as visualized in Fig. 6c. With the discussed disk-like shape of the droplets, two counter-rotating fluid flows were generated by the viscous drag on the interface between the silicone oil and the water droplet, which was slower than the oil. This flow contributed to the fluid mixing in the droplet.
According to a recent review,19 the fusion of droplets can be obtained by several passive and active methods. One also has to distinguish between fusion of non-stabilized droplets (which requires two droplets to be brought into contact as shown here) and fusion of surfactant-stabilized droplets (where the interfacial tension between two touching droplets has to be overcome).
Passive hydrodynamic droplet fusion methods16,47,48 base on specially designed channel geometries, which cause two sequent droplets to come into contact and merge. The advantage of passive methods is their simplicity, yet passive methods lack the possibility for controlled on-demand fusion and they are often slower than active methods. The hydrodynamic, geometrically mediated mechanism to bring two droplets in contact is often a coalescence chamber which is wider than the main channel.16,48 Another mechanism traps a first droplet until a second droplet arrives and collides with the trapped droplet.47 Other passive fusion methods base on surface tension effects. Two droplets can be merged at a junction of two channels, where the surface wettability of a micro-lancet induces the droplet fusion.49 A further approach builds on a surface energy pattern on the channel walls to trap a first droplet until a second droplet collides and merges.50 Selective droplet fusion has also been achieved by adapted surfactant concentration of the droplets.51,52
Active methods53–58 for droplet fusion employ controllable physical effects driven by an additional external energy. Electric fusion of droplets has been achieved by electrocoalescence,53,57,58 where a high-frequency voltage induces merging of adjacent surfactant-stabilized droplets. In a study with a picoinjector device, a second fluid could be injected into droplets by use of an electric field that locally destabilized the interface of the droplet passing an injection channel, so that the second fluid could be fused with/injected in the droplet.54 Active acoustic droplet fusion of non-stabilized droplets has been demonstrated with SAW55 by trapping a first droplet in a flow until a second droplet collides and merges.
Active and passive fusion methods can also be combined. As an example in literature,56 a passive, geometrically mediated approach with a widened fusion chamber brought two droplets in proximity, and an additional high-frequent electric field overcame the surface tension and induced fusion. Compared to these methods, BAW acoustophoresis offers an alternative method with the benefits of an active, biocompatible method and yet a simple setup, as further discussed in the conclusion. Compared to the reviewed methods above, BAW acoustophoresis mainly offers a controllable kinematic solution to bring two droplets in contact for subsequent fusion. Further work might analyze whether acoustic agitation favors the merging of surfactant-stabilized interfaces, similar as in electric fusion, and the merging of droplet pairs with partly surfactant-stabilized surfaces.52
4.2 Droplet sorting
To isolate droplets of interest out of a population, a droplet sorting mechanism is required. The combination of a droplet sensor (e.g. a fluorescence detector) with a sorting mechanism allows for fluorescence-activated droplet sorting (FADS),59 in analogy to the indispensable FACS technology for cells.Also BAW acoustophoresis allows to sort droplets at a channel bifurcation as demonstrated in Fig. 7. By turning the acoustophoretic transducer on/off, in Fig. 7a and b the droplet paths were switched between upper and lower outlet. The flow rates were 0.08 μl min−1 water and 25 μl min−1 oil, which resulted in much smaller droplets than in the last section. Alternatively, switching the transducer frequency between 463 kHz and 979 kHz allowed to switch between the λ/2 and the λ mode, whereby the nodal lines of these fields directed the droplets to the upper/lower outlet, as illustrated in Fig. 7c and d. The flow rates were 0.4 μl min−1 water and 37 μl min−1 oil.
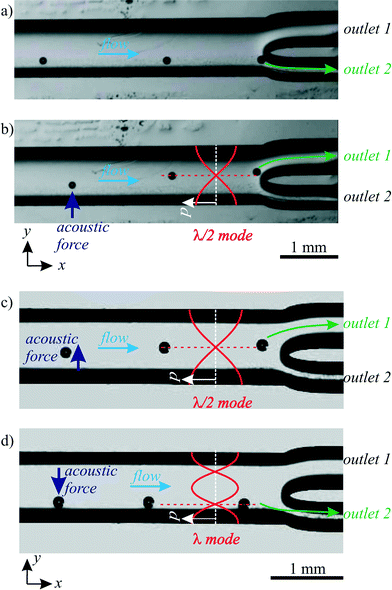 | ||
| Fig. 7 Sorting of droplets in upper/lower outlet. a) No ultrasound, droplets followed the flow to the lower outlet. b) Excitation at 463 kHz generated a λ/2 mode, which deflected droplet paths to the upper outlet. In c) and d), droplets were sorted by switching the excitation frequency between 463 kHz and 979 kHz, corresponding to the λ/2 and the λ mode, respectively. The corresponding “ESI† Movie S2” is available online. | ||
The speed of sorting is crucial for biologically oriented high-throughput experiments with vast numbers of droplets. In our experiments, droplets were sorted with a rate of several droplets per second, whereas literature reports much faster sorting of up to 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 droplets per second by electric fields.60,61 Yet we believe the sorting speed of BAW acoustophoresis has the potential to be highly increased with a precisely engineered channel bifurcation, accurately pulsed acoustic signals and flows, optimized acoustic fields with fine frequency tuning, device construction with a high Q factor and a main channel length with improved droplet migration time between inlet and outlet (currently in the order of a second). The droplet migration time and thereby the sorting speed can also be improved by higher acoustic forces at higher pressure amplitudes and higher acoustic frequencies, and by avoiding friction at contacts between droplets and channel walls. Accordingly, BAW acoustophoresis of particles has recently been reported with a sorting speed of 150 particles per second.62 Another approach for event-triggered ultrasonic cell sorting has been achieved by acoustic radiation forces acting on an interface between two liquids,63 whereby fluidic movement was generated as the sorting mechanism. This approach also addresses ultrasonic manipulation of two liquids with different acoustic properties.64
000 droplets per second by electric fields.60,61 Yet we believe the sorting speed of BAW acoustophoresis has the potential to be highly increased with a precisely engineered channel bifurcation, accurately pulsed acoustic signals and flows, optimized acoustic fields with fine frequency tuning, device construction with a high Q factor and a main channel length with improved droplet migration time between inlet and outlet (currently in the order of a second). The droplet migration time and thereby the sorting speed can also be improved by higher acoustic forces at higher pressure amplitudes and higher acoustic frequencies, and by avoiding friction at contacts between droplets and channel walls. Accordingly, BAW acoustophoresis of particles has recently been reported with a sorting speed of 150 particles per second.62 Another approach for event-triggered ultrasonic cell sorting has been achieved by acoustic radiation forces acting on an interface between two liquids,63 whereby fluidic movement was generated as the sorting mechanism. This approach also addresses ultrasonic manipulation of two liquids with different acoustic properties.64
Regarding other acoustic droplet sorting methods, binary droplet sorting was reported by directing the flow of the continuous fluid with traveling SAW-induced acoustic streaming.24,65 Different from this work, droplet sorting in 5 outlets has been demonstrated23 with standing SAW acoustic radiation forces, which act directly on the dispersed droplets rather than by drag forces as the acoustic streaming. Alternatively, sorting by high frequency ultrasound beams has been reported.66 Compared to these earlier mechanisms and as outlined in the conclusion, BAW acoustophoresis is an advantageously simple alternative with a different type of construction in acoustically hard channel structures.
4.3 Droplet washing/medium exchange
Dispersed droplets are carried and individually separated from each other by the continuous phase liquid. Similar to cell washing and medium exchange in particle acoustophoresis,36,67,68 the acoustophoretic transfer of droplets to another continuous phase is feasible. This transfer allows droplet washing and the movement of droplets into a continuous phase with another surfactant. Since surfactants can increase the surface tension between two phases, the movement of a droplet from a surfactant-free to a surfactant-carrying continuous phase liquid enables to stabilize droplets in a continuous flow mode.In Fig. 8, water droplets experienced an exchange of their suspending continuous phase from the dyed oil (center inlet) to the undyed oil (lower inlet) in the lower third of the channel. This was feasible because the acoustic radiation force acted selectively on the dispersed water droplet due to its spherical shape and its acoustic contrast to the surrounding silicone oil, which was not affected by the ultrasound. The flow rates were 13 μl min−1 in the top undyed oil inlet, 17 μl min−1 dyed oil in the middle inlet, 0.2 μl min−1 water and 10 μl min−1 undyed oil in the bottom inlet. The oil flows were balanced to guide the dyed oil to the middle outlet, but close to the bottom outlet, where the droplets were directed.
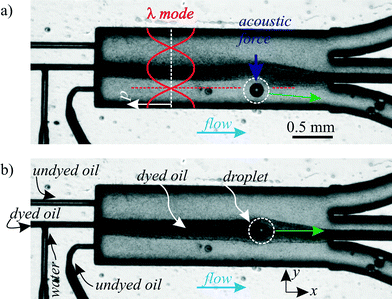 | ||
| Fig. 8 a) Exchange of the continuous phase liquid of dispersed droplets (∅ ≈ 150 μm) with a λ mode at 970 kHz. b) Negative control without ultrasound: the droplet remained in the dyed oil and left through the center outlet. A corresponding “ESI† Movie S3” is available online. | ||
In the shown experiment, the droplets covered a distance of slightly less than λ/4 in y-direction. Hence the maximum droplet size for a complete medium exchange depends on the frequency: lower frequencies allow the handling of larger droplets.
5. Conclusion
The presented acoustophoretic droplet handling enables a palette of active fluid handling operations for segmented flow droplet microfluidics.Compared to the alternative SAW acoustophoresis method, the BAW method has complementary benefits. SAW devices for segmented flows are usually restricted to piezoelectric ground plates where the surface acoustic wave propagates, and acoustically soft polydimethylsiloxane (PDMS) channels have to be bonded on top. Differently, the BAW method allows various configurations of channel and device geometries, where the driving ultrasonic transducer can be placed more freely on the device, even at some distance to the channel, and without any on-chip electrode fabrication. This renders the BAW method rather versatile with yet a simple setup. However, BAW acoustophoresis requires channel walls of an acoustically contrasting material (e.g. acoustically hard silicon, glass or a wall/air interface), and it is restricted to certain discrete resonance modes in the channel (called “harmonics”), whereas SAW enables more complex moving operations by varying frequencies over a continuous range.69
Compared to operating frequencies of 20–40 MHz70 and up to 150 MHz71 for standing SAW, BAW devices are typically working at a lower frequency range of 0.1–10 MHz.37 These lower operation frequencies lead to longer wavelengths, allowing the handling of larger droplets up to ∼500 μm size in larger channels of ∼1 mm width or even more. On the other hand, by scaling down the device size and scaling up the frequency, the setup can also accommodate smaller droplets, if the need arises.
So far, fusion, focusing, sorting and medium exchange have been shown separately in this paper. Yet with the presented method, it is well possible to combine them within one single channel, e.g. to fuse two droplets at first and sort them at a channel bifurcation right afterwards with a different acoustic frequency than the fusion. Another possibility is seen in the surfactant-free droplet merging, followed by a medium change to a continuous phase fluid which contains stabilizing surfactants. As inspired by cell/particle acoustophoresis, further work might also address acoustophoretic droplet-specific separations,37 droplet storing, and droplet trapping,72 for example to observe the long-time behaviour of cells in droplets under the influence of certain biochemical substances.
In view of applications, the shown contactless fluid sample handling by bulk acoustic waves offers significant benefits for fluid handling instruments e.g. in laboratory diagnostics and analytics, biochemical and pharmaceutical research and material science.
Acknowledgements
The authors would like to express their gratitude for funding by ETH Zurich and acknowledge the support by the ETH microscopy and screening center. The authors are inventors on a patent application (PCT/EP2015/050388) related to the reported approach.References
- X. Casadevall i Solvas and A. deMello, Chem. Commun., 2011, 47, 1936–1942 RSC.
- S.-Y. Teh, R. Lin, L.-H. Hung and A. P. Lee, Lab Chip, 2008, 8, 198–220 RSC.
- A. Huebner, S. Sharma, M. Srisa-Art, F. Hollfelder and J. B. Edel, et al. , Lab Chip, 2008, 8, 1244–1254 RSC.
- A. D. Griffiths and D. S. Tawfik, Trends Biotechnol., 2006, 24, 395–402 CrossRef CAS PubMed.
- D. S. Tawfik and A. D. Griffiths, Nat. Biotechnol., 1998, 16, 652–656 CrossRef CAS PubMed.
- P. S. Dittrich, K. Tachikawa and A. Manz, Anal. Chem., 2006, 78, 3887–3908 CrossRef CAS PubMed.
- A. Manz, N. Graber and H. M. Widmer, Sens. Actuators, B, 1990, 1, 244–248 CrossRef CAS.
- S. Haeberle and R. Zengerle, Lab Chip, 2007, 7, 1094–1110 RSC.
- Y. Schaerli and F. Hollfelder, Mol. BioSyst., 2009, 5, 1392–1404 RSC.
- A. B. Theberge, F. Courtois, Y. Schaerli, M. Fischlechner, C. Abell, F. Hollfelder and W. T. Huck, Angew. Chem., Int. Ed., 2010, 49, 5846–5868 CrossRef CAS PubMed.
- J. Clausell-Tormos, D. Lieber, J.-C. Baret, A. El-Harrak, O. J. Miller, L. Frenz, J. Blouwolff, K. J. Humphry, S. K. Oster and H. Duan, et al. , Chem. Biol., 2008, 15, 427–437 CrossRef CAS PubMed.
- P. S. Dittrich and A. Manz, Nat. Rev. Drug Discovery, 2006, 5, 210–218 CrossRef CAS PubMed.
- A. J. Demello, Nature, 2006, 442, 394–402 CrossRef CAS PubMed.
- A. Günther and K. F. Jensen, Lab Chip, 2006, 6, 1487–1503 RSC.
- J. Berthier, Micro-drops and digital microfluidics, William Andrew, 2012 Search PubMed.
- Y.-C. Tan, Y. L. Ho and A. P. Lee, Microfluid. Nanofluid., 2007, 3, 495–499 CrossRef.
- D. R. Link, E. Grasland-Mongrain, A. Duri, F. Sarrazin, Z. Cheng, G. Cristobal, M. Marquez and D. A. Weitz, Angew. Chem., Int. Ed., 2006, 45, 2556–2560 CrossRef CAS PubMed.
- J. Friend and L. Y. Yeo, Rev. Mod. Phys., 2011, 83, 647 CrossRef.
- C. N. Baroud, F. Gallaire and R. Dangla, Lab Chip, 2010, 10, 2032–2045 RSC.
- R. Seemann, M. Brinkmann, T. Pfohl and S. Herminghaus, Rep. Prog. Phys., 2012, 75, 016601 CrossRef PubMed.
- M. Wiklund, Lab Chip, 2012, 12, 2018–2028 RSC.
- X. Ding, P. Li, S.-C. S. Lin, Z. S. Stratton, N. Nama, F. Guo, D. Slotcavage, X. Mao, J. Shi and F. Costanzo, et al. , Lab Chip, 2013, 13, 3626–3649 RSC.
- S. Li, X. Ding, F. Guo, Y. Chen, M. I. Lapsley, S.-C. S. Lin, L. Wang, J. P. McCoy, C. E. Cameron and T. J. Huang, Anal. Chem., 2013, 85, 5468–5474 CrossRef CAS PubMed.
- T. Franke, A. R. Abate, D. A. Weitz and A. Wixforth, Lab Chip, 2009, 9, 2625–2627 RSC.
- S. Collignon, J. Friend and L. Yeo, Lab Chip, 2015, 15, 1942–1951 RSC.
- H. Bruus, J. Dual, J. Hawkes, M. Hill, T. Laurell, J. Nilsson, S. Radel, S. Sadhal and M. Wiklund, Lab Chip, 2011, 11, 3579–3580 RSC.
- T. Thorsen, R. W. Roberts, F. H. Arnold and S. R. Quake, Phys. Rev. Lett., 2001, 86, 4163–4166 CrossRef CAS.
- G. Christopher and S. Anna, J. Phys. D: Appl. Phys., 2007, 40, R319 CrossRef CAS.
- A. Lenshof, M. Evander, T. Laurell and J. Nilsson, Lab Chip, 2012a, 12, 684–695 Search PubMed.
- I. Leibacher, S. Schatzer and J. Dual, Lab Chip, 2014, 14, 463–470 RSC.
- H. Bruus, Lab Chip, 2012a, 12, 20–28 Search PubMed.
- L. P. Gor'kov, Phys.-Dokl., 1962, 6, 773–775 Search PubMed.
- H. Bruus, Lab Chip, 2012b, 12, 1014–1021 Search PubMed.
- Y. K. K. Yosioka, Acustica, 1955, 5, 167–173 Search PubMed.
- H. Bruus, Lab Chip, 2011, 11, 3742–3751 RSC.
- A. Lenshof, C. Magnusson and T. Laurell, Lab Chip, 2012b, 12, 1210–1223 Search PubMed.
- T. Laurell, F. Petersson and A. Nilsson, Chem. Soc. Rev., 2007, 36, 492–506 RSC.
- R. Barnkob, P. Augustsson, T. Laurell and H. Bruus, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 056307 CrossRef.
- J. Dual, P. Hahn, I. Leibacher, D. Moller and T. Schwarz, Lab Chip, 2012, 12, 852–862 RSC.
- O. Manneberg, B. Vanherberghen, B. Onfelt and M. Wiklund, Lab Chip, 2009, 9, 833–837 RSC.
- I. Leibacher, J. Schoendube, J. Dual, R. Zengerle and P. Koltay, Biomicrofluidics, 2015, 9, 024109 CAS.
- R. Dangla, E. Fradet, Y. Lopez and C. N. Baroud, J. Phys. D: Appl. Phys., 2013, 46, 114003 CrossRef.
- X. Xuan, J. Zhu and C. Church, Microfluid. Nanofluid., 2010, 9, 1–16 CrossRef.
- G. Goddard and G. Kaduchak, J. Acoust. Soc. Am., 2005, 117, 3440–3447 CrossRef CAS PubMed.
- G. Goddard, J. C. Martin, S. W. Graves and G. Kaduchak, Cytometry, Part A, 2006, 69, 66–74 CrossRef PubMed.
- F. Sarrazin, L. Prat, N. Di Miceli, G. Cristobal, D. Link and D. Weitz, Chem. Eng. Sci., 2007, 62, 1042–1048 CrossRef CAS PubMed.
- X. Niu, S. Gulati and J. B. Edel, et al. , Lab Chip, 2008, 8, 1837–1841 RSC.
- N. Bremond, A. R. Thiam and J. Bibette, Phys. Rev. Lett., 2008, 100, 024501 CrossRef.
- N.-N. Deng, S.-X. Sun, W. Wang, X.-J. Ju, R. Xie and L.-Y. Chu, Lab Chip, 2013, 13, 3653–3657 RSC.
- L. M. Fidalgo, C. Abell and W. T. S. Huck, Lab Chip, 2007, 7, 984–986 RSC.
- L. Mazutis, J.-C. Baret and A. D. Griffiths, Lab Chip, 2009, 9, 2665–2672 RSC.
- L. Mazutis and A. D. Griffiths, Lab Chip, 2012, 12, 1800–1806 RSC.
- M. Zagnoni, C. N. Baroud and J. M. Cooper, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 046303 CrossRef.
- A. R. Abate, T. Hung, P. Mary, J. J. Agresti and D. A. Weitz, Proc. Natl. Acad. Sci., 2010, 107, 19163–19166 CrossRef CAS PubMed.
- M. Sesen, T. Alan and A. Neild, Lab Chip, 2014, 3325–3333 RSC.
- E. Brouzes, M. Medkova, N. Savenelli, D. Marran, M. Twardowski, J. B. Hutchison, J. M. Rothberg, D. R. Link, N. Perrimon and M. L. Samuels, Proc. Natl. Acad. Sci., 2009, 106, 14195–14200 CrossRef CAS PubMed.
- M. Chabert, K. D. Dorfman and J.-L. Viovy, Electrophoresis, 2005, 26, 3706–3715 CrossRef CAS PubMed.
- K. Ahn, J. Agresti, H. Chong, M. Marquez and D. A. Weitz, Appl. Phys. Lett., 2006a, 88, 264105 Search PubMed.
- J.-C. Baret, O. J. Miller, V. Taly, M. Ryckelynck, A. El-Harrak, L. Frenz, C. Rick, M. L. Samuels, J. B. Hutchison and J. J. Agresti, et al. , Lab Chip, 2009, 9, 1850–1858 RSC.
- A. Sciambi and A. R. Abate, Accurate microfluidic sorting of droplets at 30 kHz, Lab Chip, 2015, 15(1), 47–51 RSC.
- K. Ahn, C. Kerbage, T. P. Hunt, R. Westervelt, D. R. Link and D. Weitz, Appl. Phys. Lett., 2006b, 88, 024104–024104 Search PubMed.
- O. Jakobsson, C. Grenvall, M. Nordin, M. Evander and T. Laurell, Lab Chip, 2014, 14, 1943–1950 RSC.
- L. Johansson, F. Nikolajeff, S. Johansson and S. Thorslund, Anal. Chem., 2009, 81, 5188–5196 CrossRef CAS PubMed.
- S. Deshmukh, Z. Brzozka, T. Laurell and P. Augustsson, Lab Chip, 2014, 14, 3394–3400 RSC.
- L. Schmid, D. A. Weitz and T. Franke, Sorting drops and cells with acoustics: acoustic microfluidic fluorescence-activated cell sorter, Lab Chip, 2015, 14(19), 3710–3718 RSC.
- C. Lee, J. Lee, H. H. Kim, S.-Y. Teh, A. Lee, I.-Y. Chung, J. Y. Park and K. K. Shung, Lab Chip, 2012, 12, 2736–2742 RSC.
- P. Augustsson, L. Åberg, A.-M. Swärd-Nilsson and T. Laurell, Microchim. Acta, 2009, 164, 269–277 CrossRef CAS.
- S. Li, X. Ding, Z. Mao, Y. Chen, N. Nama, F. Guo, P. Li, L. Wang, C. E. Cameron and T. J. Huang, Lab Chip, 2015, 15, 331–338 RSC.
- X. Ding, S.-C. S. Lin, B. Kiraly, H. Yue, S. Li, I.-K. Chiang, J. Shi, S. J. Benkovic and T. J. Huang, Proc. Natl. Acad. Sci., 2012, 109, 11105–11109 CrossRef CAS PubMed.
- J. Shi, D. Ahmed, X. Mao, S.-C. S. Lin, A. Lawit and T. J. Huang, Lab Chip, 2009, 9, 2890–2895 RSC.
- T. Franke, S. Braunmüller, L. Schmid, A. Wixforth and D. Weitz, Lab Chip, 2010, 10, 789–794 RSC.
- M. Evander and J. Nilsson, Lab Chip, 2012, 12, 4667–4676 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: 1) Video of droplet fusion, corresponding to Fig. 5 and Fig. 6a. 2) Video of droplet sorting, corresponding to Fig. 7. 3) Video of droplet medium exchange, corresponding to Fig. 8. See DOI: 10.1039/c5lc00083a |
| ‡ I. Leibacher and P. Reichert contributed equally to this work and were listed in alphabetical order (joint first authors). |
| This journal is © The Royal Society of Chemistry 2015 |